Optimising Mechanical Performance of Additive Manufactured Composites for Biomedical Applications
Abstract
1. Introduction
2. Materials and Experimental Methodology
2.1. Materials and Manufacturing Methods
2.2. ML Metrics and Assessment
2.2.1. Data Preprocessing
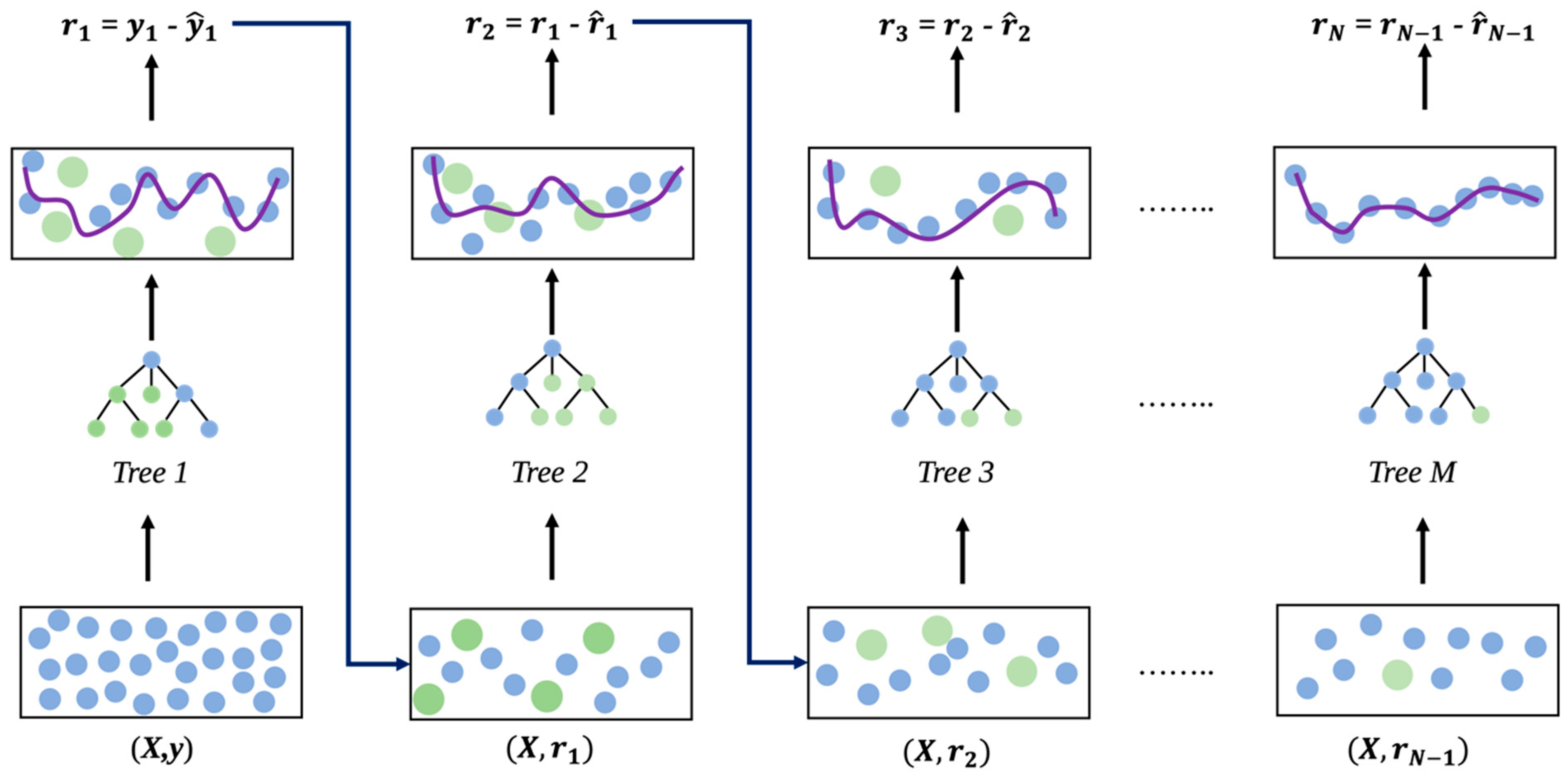
2.2.2. Selection of Regression Algorithms
3. Results and Discussion
3.1. Tensile Results
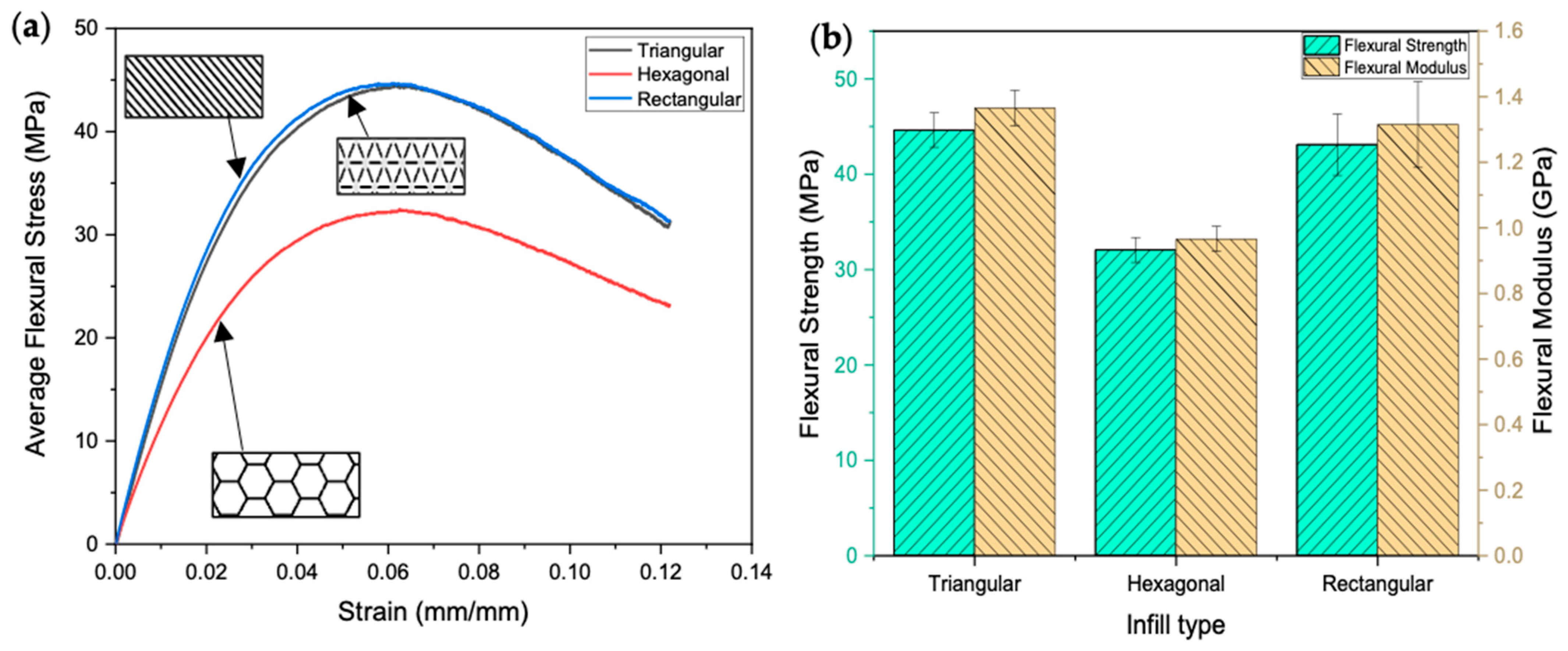
3.2. Flexural Results
3.3. ML Set-Up, Results, and Discussion
3.3.1. ML Data Set up
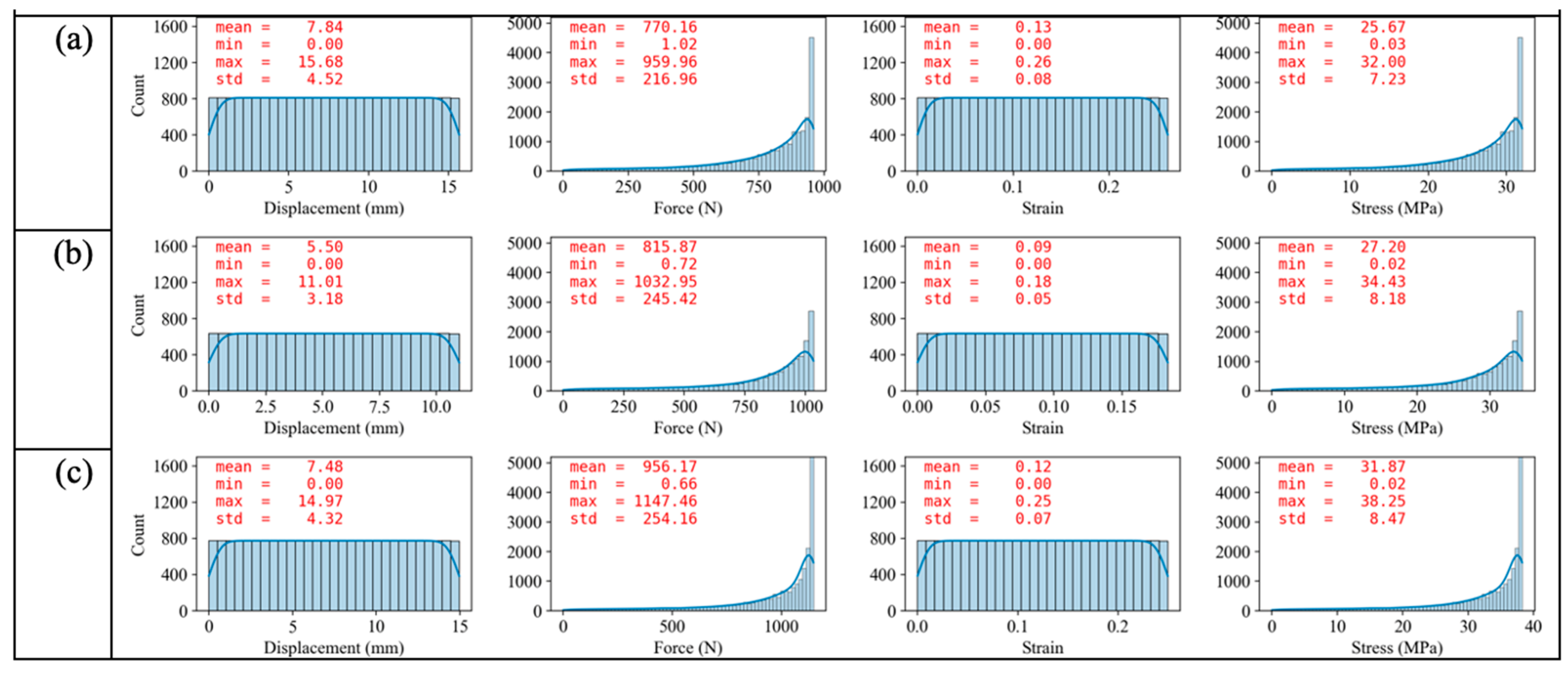
3.3.2. Data Assessment of Mechanical Properties
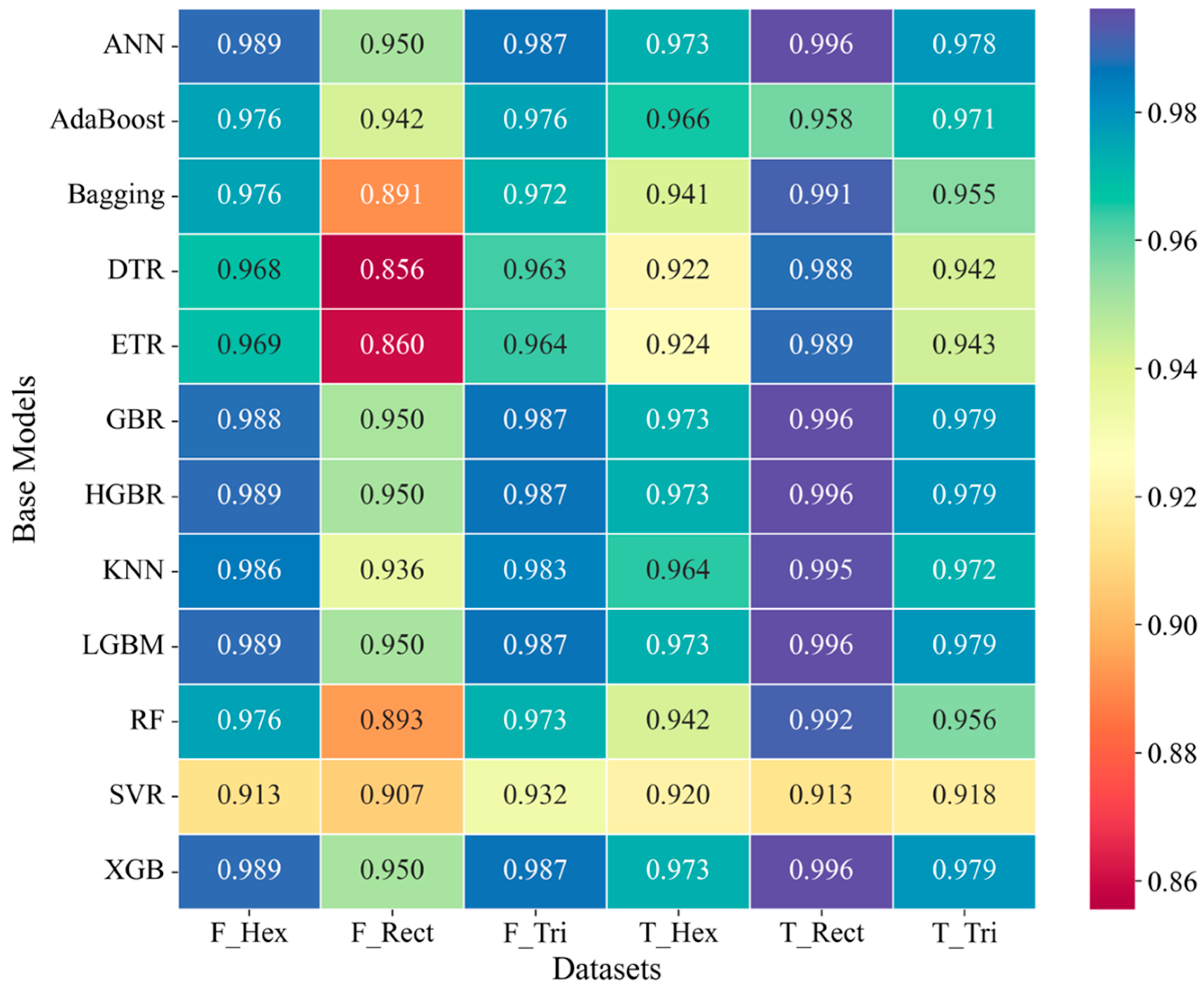
3.3.3. Evaluation of Regressor Algorithms
3.3.4. Hyper-Parameter Tuning Analysis
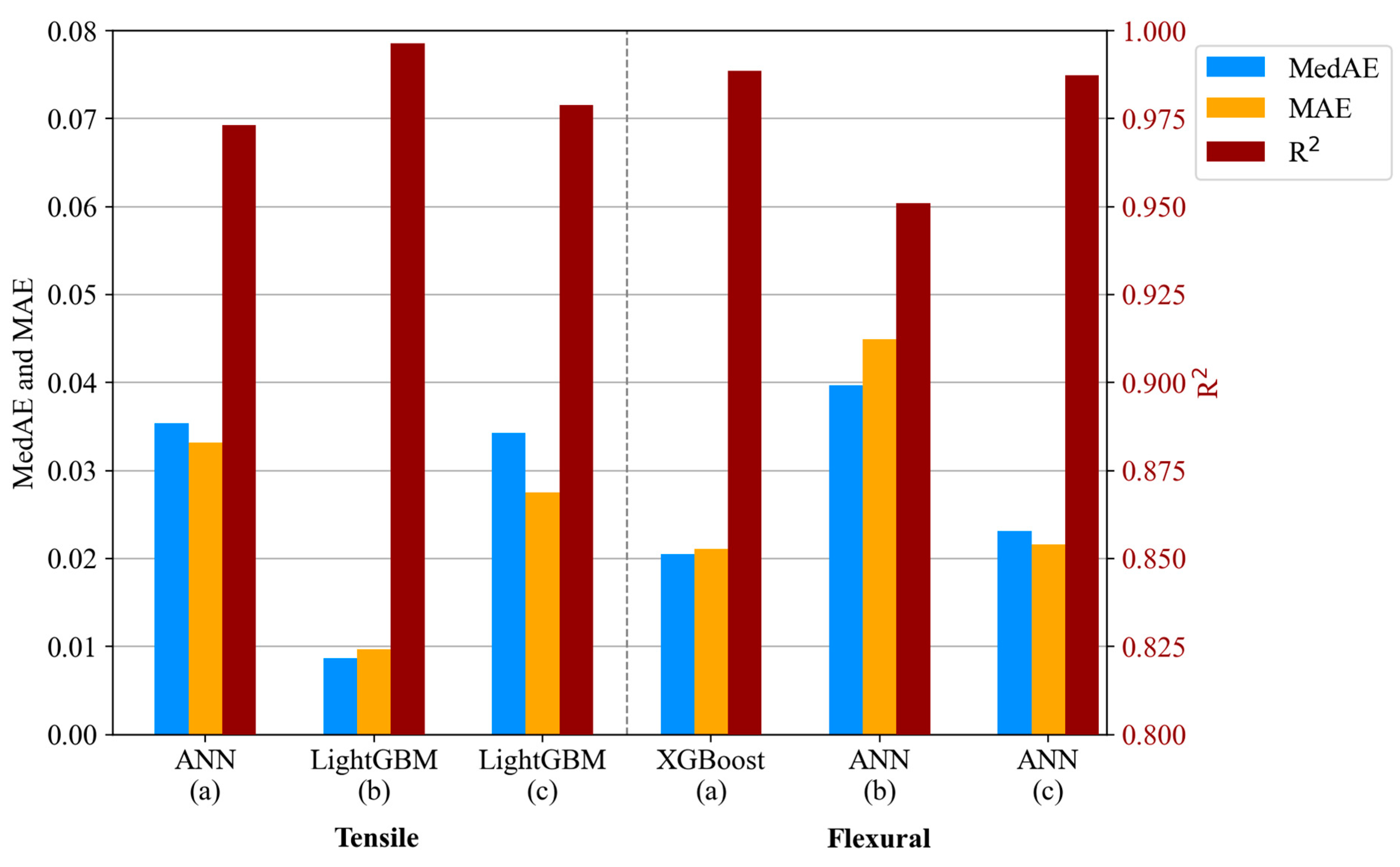
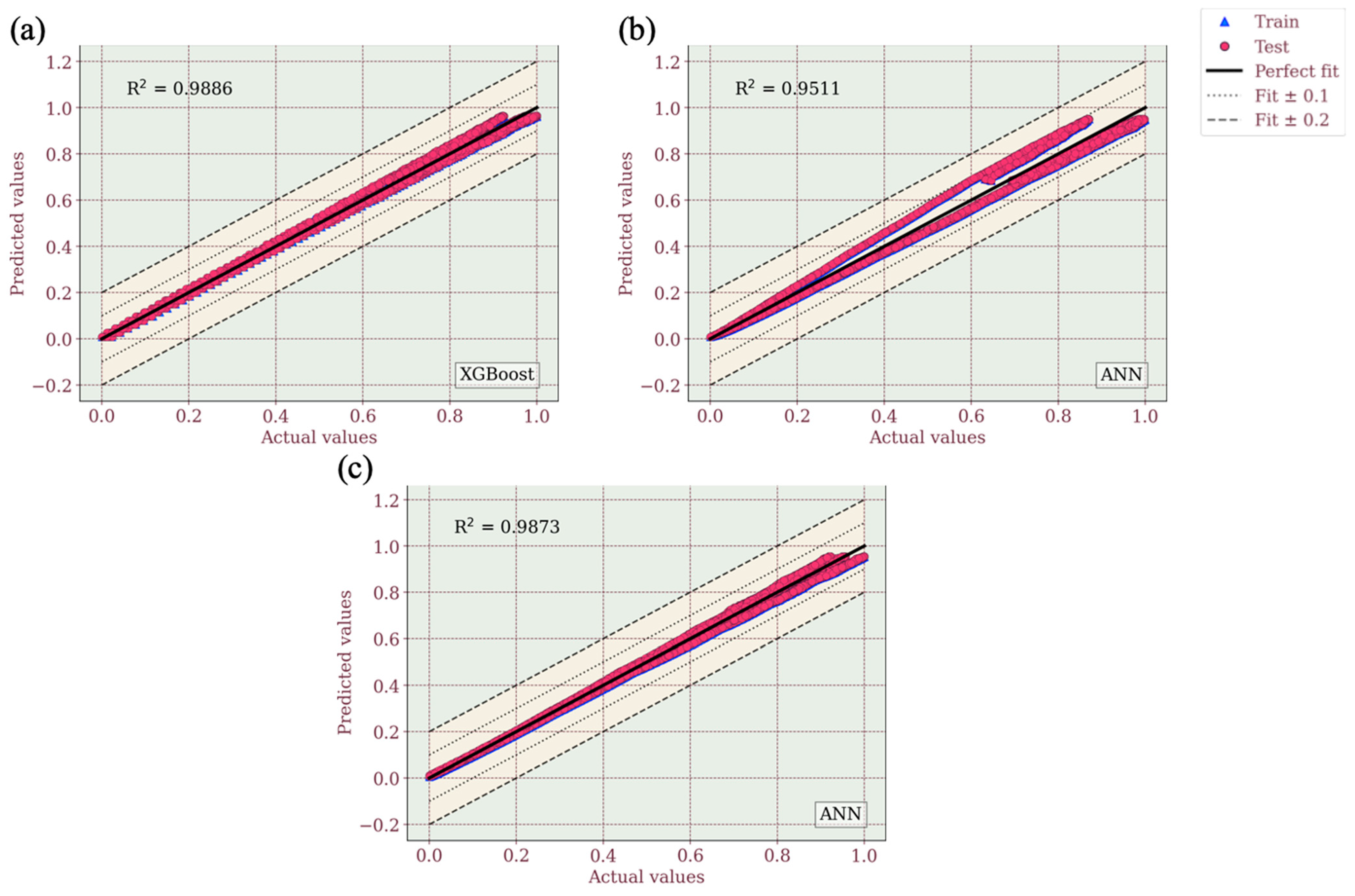
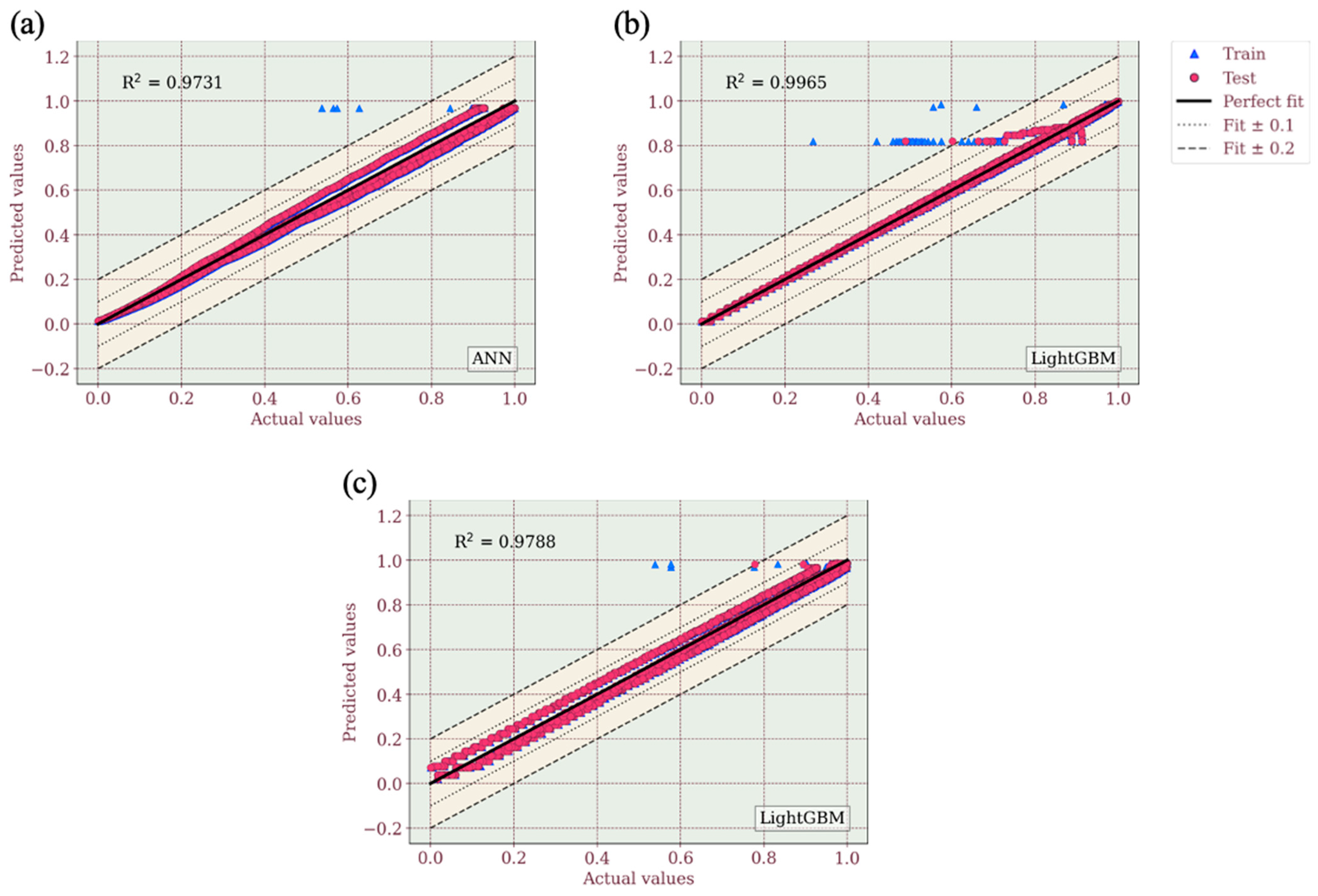
3.3.5. ML Model Performance
4. Conclusions
- The Triangular patterned samples exhibited superior tensile strength (37.01 ± 1.44 MPa) and stiffness (0.728 ± 0.018 GPa), surpassing Rectangular (33.40 ± 2.40 MPa; 0.661 ± 0.020 GPa) and Hexagonal (31.35 ± 1.30 MPa; 0.541 ± 0.037 GPa) configurations. Conversely, the hexagonal pattern displayed the weakest tensile strength and lowest stiffness, coupled with the highest variability in both properties (tensile SD = 1.30 MPa; stiffness SD = 0.037 GPa). Its superiority stems from its interconnected geometry, which facilitates uniform stress distribution and improves resistance to deformation, ensuring structural stability under load. Conversely, its weaknesses likely originate from its nodal junctions, which are susceptible to failure under stress, and its lightweight honeycomb structure, which reduces load-bearing efficiency.
- Regarding flexural properties, the triangular infill exhibited the highest bending strength (44.63 MPa) and flexural modulus (1.37 GPa), attributed to its efficient load distribution and structural integrity. In contrast, the hexagonal infill demonstrated the lowest bending strength (32.07 MPa) and flexural modulus (0.97 GPa), suggesting potential limitations in structural applications. The rectangular infill displayed intermediate values (43.1 MPa for strength and 1.31 GPa for modulus) but exhibited greater variability in performance.
- The developed ML framework accurately predicts the tensile and flexural behaviour of Onyx composites across various infill parameters, with models like LightGBM, XGBoost, and ANN achieving R-squared values above 0.95. For tensile properties, XGBoost performed best for hexagonal stacking, while ANN excelled in rectangular and triangular configurations. In flexural properties, ANN outperformed in hexagonal sequences, whereas LightGBM achieved the highest accuracy for rectangular and triangular sequences, though its predictions for the rectangular sequence showed higher variability. This study highlights the potential of ML-driven modelling for material optimisation, particularly in biomedical applications. While ensemble learning and deep learning approaches show promise, further refinement and dataset expansion is needed to enhance model generalisability for real-world applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive Manufacturing of Carbon Fiber Reinforced Thermoplastic Composites Using Fused Deposition Modeling. Compos. B Eng. 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Petersen, R. Carbon Fiber Biocompatibility for Implants. Fibers 2016, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Hoglund, R.; Smith, D.E. Continuous Fiber Angle Topology Optimization for Polymer Composite Deposition Additive Manufacturing Applications. Fibers 2019, 7, 14. [Google Scholar] [CrossRef]
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly Oriented Carbon Fiber-Polymer Composites via Additive Manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef]
- Arif, M.F.; Kumar, S.; Varadarajan, K.M.; Cantwell, W.J. Performance of Biocompatible PEEK Processed by Fused Deposition Additive Manufacturing. Mater. Des. 2018, 146, 249–259. [Google Scholar] [CrossRef]
- Durga Prasada Rao, V.; Rajiv, P.; Navya Geethika, V. Effect of Fused Deposition Modelling (FDM) Process Parameters on Tensile Strength of Carbon Fibre PLA. Mater. Today Proc. 2019, 18, 2012–2018. [Google Scholar] [CrossRef]
- Papon, E.A.; Haque, A. Fracture Toughness of Additively Manufactured Carbon Fiber Reinforced Composites. Addit. Manuf. 2019, 26, 41–52. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Hu, Y.; Wang, H. Additive Manufacturing of Carbon Fiber-Reinforced Plastic Composites Using Fused Deposition Modeling: Effects of Process Parameters on Tensile Properties. J. Compos. Mater. 2017, 51, 451–462. [Google Scholar] [CrossRef]
- Wang, K.; Xie, X.; Wang, J.; Zhao, A.; Peng, Y.; Rao, Y. Effects of Infill Characteristics and Strain Rate on the Deformation and Failure Properties of Additively Manufactured Polyamide-Based Composite Structures. Results Phys. 2020, 18, 103346. [Google Scholar] [CrossRef]
- Belarbi, Y.E.; Benmahiddine, F.; Hamami, A.E.A.; Guessasma, S.; Belhabib, S. Hygrothermal and Microstructural Investigation of PLA and PLA-Flax Printed Structures. Fibers 2022, 10, 24. [Google Scholar] [CrossRef]
- Al Rashid, A.; Ikram, H.; Koç, M. Additive Manufacturing and Mechanical Performance of Carbon Fiber Reinforced Polyamide-6 Composites. Mater. Today Proc. 2022, 62, 6359–6363. [Google Scholar] [CrossRef]
- Martulli, L.M.; Barriga Ruiz, P.; Rajan, A.; Bárnik, F.; Sága, M.; Bernasconi, A. Infill Shape Effects on Bending Stiffness of Additively Manufactured Short Fibre Reinforced Polymer Sandwich Specimens. J. Reinf. Plast. Compos. 2021, 40, 927–938. [Google Scholar] [CrossRef]
- Yasa, E.; Ersoy, K. Dimensional Accuracy and Mechanical Properties of Chopped Carbon Reinforced Polymers Produced by Material Extrusion Additive Manufacturing. Materials 2019, 12, 3885. [Google Scholar] [CrossRef] [PubMed]
- Breuer, K.; Stommel, M. Prediction of Short Fiber Composite Properties by an Artificial Neural Network Trained on an Rve Database. Fibers 2021, 9, 8. [Google Scholar] [CrossRef]
- Omigbodun, F.T.; Osa-Uwagboe, N.; Udu, A.G.; Oladapo, B.I. Leveraging Machine Learning for Optimized Mechanical Properties and 3D Printing of PLA/CHAP for Bone Implant. Biomimetics 2024, 9, 587. [Google Scholar] [CrossRef]
- Osa-uwagboe, N.; Udu, A.G.; Ghalati, M.K.; Silberschmidt, V.V.; Aremu, A.; Dong, H.; Demirci, E. A Machine Learning-Enabled Prediction of Damage Properties for Fiber-Reinforced Polymer Composites under out-of-Plane Loading. Eng. Struct. 2024, 308, 117970. [Google Scholar] [CrossRef]
- Gayatri, V.M.; Dave, A.; Chaganti, K. Artificial Neural Network Based Prediction of Tensile Strength of Hybrid Composites. Mater. Today Proc. 2018, 5, 19908–19915. [Google Scholar] [CrossRef]
- Huang, H.; Hadigheh, S.A.; Aghabalaei Baghaei, K. Influences of Fibre Shape on the Transverse Modulus of Unidirectional Fibre Reinforced Composites Using Finite Element and Machine Learning Methods. Compos. Struct. 2023, 312, 116872. [Google Scholar] [CrossRef]
- Cai, R.; Wen, W.; Wang, K.; Peng, Y.; Ahzi, S.; Chinesta, F. Tailoring Interfacial Properties of 3D-Printed Continuous Natural Fiber Reinforced Polypropylene Composites through Parameter Optimization Using Machine Learning Methods. Mater. Today Commun. 2022, 32, 103985. [Google Scholar] [CrossRef]
- Alhaddad, W.; He, M.; Halabi, Y.; Yahya Mohammed Almajhali, K. Optimizing the Material and Printing Parameters of the Additively Manufactured Fiber-Reinforced Polymer Composites Using an Artificial Neural Network Model and Artificial Bee Colony Algorithm. Structures 2022, 46, 1781–1795. [Google Scholar] [CrossRef]
- Meiabadi, M.S.; Moradi, M.; Karamimoghadam, M.; Ardabili, S.; Bodaghi, M.; Shokri, M.; Mosavi, A.H. Modeling the Producibility of 3d Printing in Polylactic Acid Using Artificial Neural Networks and Fused Filament Fabrication. Polymers 2021, 13, 3219. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, R.; Singh, J.; Gupta, V. Predicting the Compressive Strength of Additively Manufactured PLA-Based Orthopedic Bone Screws: A Machine Learning Framework. Polym. Compos. 2022, 43, 5663–5674. [Google Scholar] [CrossRef]
- Nikiema, D.; Balland, P.; Sergent, A. Study of the Mechanical Properties of 3D-Printed Onyx Parts: Investigation on Printing Parameters and Effect of Humidity. Chin. J. Mech. Eng. Addit. Manuf. Front. 2023, 2, 100075. [Google Scholar] [CrossRef]
- Booker, L.B.; Goldberg, D.E.; Holland, J.H. Classifier Systems and Genetic Algorithms. Artif. Intell. 1989, 40, 235–282. [Google Scholar] [CrossRef]
- Alexandropoulos, S.-A.N.; Kotsiantis, S.B.; Vrahatis, M.N. Data Preprocessing in Predictive Data Mining. Knowl. Eng. Rev. 2019, 34, e1. [Google Scholar] [CrossRef]
- Luo, G. A Review of Automatic Selection Methods for Machine Learning Algorithms and Hyper-Parameter Values. Netw. Model. Anal. Health Inform. Bioinform. 2016, 5, 18. [Google Scholar] [CrossRef]
- Salman, M.T.; Siddle, D.R.; Udu, A.G. Machine Learning Approach to Predict the DC Bias for Adaptive OFDM Transmission in Indoor Li-Fi Applications. IEEE Access 2025, 13, 9627–9641. [Google Scholar] [CrossRef]
- Dudescu, M.C.; Racz, L.; Popa, F. Effect of Infill Pattern on Fatigue Characteristics of 3D Printed Polymers. Mater. Today Proc. 2023, 78, 263–269. [Google Scholar] [CrossRef]
- Lubombo, C.; Huneault, M.A. Effect of Infill Patterns on the Mechanical Performance of Lightweight 3D-Printed Cellular PLA Parts. Mater. Today Commun. 2018, 17, 214–228. [Google Scholar] [CrossRef]
- Rybarczyk, J.; Górski, F.; Kuczko, W.; Wichniarek, R.; Siwiec, S.; Vitkovic, N.; Păcurar, R. Mechanical Properties of Carbon Fiber Reinforced Materials for 3D Printing of Ankle Foot Orthoses. Adv. Sci. Technol. Res. J. 2024, 18, 191–215. [Google Scholar] [CrossRef]
- Tyagi, B.; Dixit, K.; Sahai, A.; Sharma, R.S. Characterization of Flexural and Compressive Behavior in Polylactic Acid Composites for Low-Cost Transtibial Prosthetic Applications: Influence of Reinforcements. J. Appl. Polym. Sci. 2024, 141, e55319. [Google Scholar] [CrossRef]
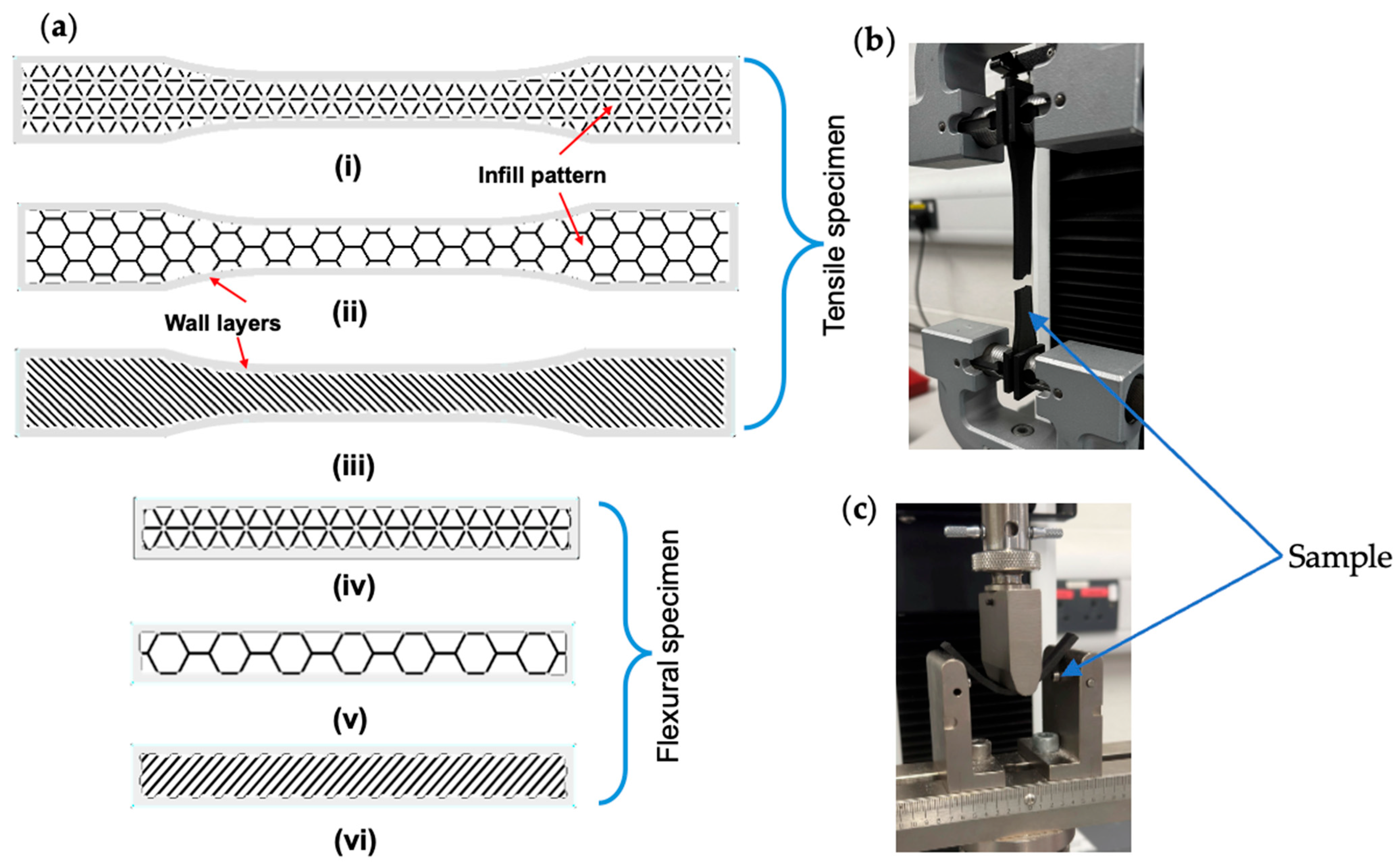



| Parameter | Value |
|---|---|
| Tensile Modulus | 2.4 GPa |
| Tensile stress at yield | 40 MPa |
| Tensile stress at break | 37 MPa |
| Flexural Strength | 71 MPa |
| Flexural Modulus | 3.6 GPa |
| Density | 1.4 g/cm3 |
| Parameter | Value |
|---|---|
| Layer height | 0.125 mm |
| Nozzle diameter | 0.4 mm |
| Nozzle temperature | 270 °C |
| No. of layers | 24 |
| Wall loops | 4 |
| Infill type | Triangular/Hexagonal/Rectangular |
| Infill | 28% |
| Top/bottom layers | 4/4 |
| Model | Attribute | Range | Selected Value | Mean Test Score |
|---|---|---|---|---|
| AdaBoost | learning rate | [0.01, 0.1, 0.5, 1] | 0.01 | 0.9745 |
| loss | [‘linear’, ‘square’, ‘exponential’] | exponential | ||
| n_estimators | [50, 100, 200, 500] | 500 | ||
| ANN | activation | [‘relu’, ‘tanh’] | relu | 0.9787 |
| alpha | [0.0001, 0.001, 0.01] | 0.01 | ||
| batch_size | [32, 64, 128, 200, ‘auto’] | 32 | ||
| hidden_layer_sizes | [(50,), (100,), (50, 50), (100,50)] | (100,50) | ||
| learning rate | [‘constant’, ‘adaptive’, ‘invscaling’] | constant | ||
| max_iter | [200, 300, 400] | 200 | ||
| solver | [‘lbfgs’, ‘sgd’, ‘adam’] | lbfgs | ||
| GBR | learning rate | [0.1, 0.01, 0.001] | 0.1 | 0.9787 |
| n_estimators | [100, 200, 300] | 100 | ||
| max_depth | [3, 5, 7] | 3 | ||
| min_samples_split | [2, 5, 10] | 10 | ||
| min_samples_leaf | [1, 2, 4] | 2 | ||
| max_features | [‘auto’, ‘sqrt’, ‘log2’] | auto | ||
| Hist GBR | learning rate | [0.01, 0.05, 0.1] | 0.05 | 0.9787 |
| max_depth | [None, 5, 10, 20] | 5 | ||
| max_iter | [100, 200, 300] | 300 | ||
| min_leaf_nodes | [15, 31, 63] | 15 | ||
| min_samples_leaf | [10, 20, 50] | 20 | ||
| k-NN | algorithm | [‘brute’, ‘kd_tree’, ‘ball_tree’, ‘auto’] | auto | 0.9744 |
| leaf_size | [5, 10, 20, 30] | 30 | ||
| n_neighbors | [3, 5, 7, 8] | 8 | ||
| weights | [‘uniform’, ‘distance’] | uniform | ||
| LightGBM | learning rate | [1, 0.1, 0.01, 0.001] | 0.1 | 0.9787 |
| max_depth | [None, 1, 3, 5, 7, 10] | 3 | ||
| min_child_samples | [5, 10, 20, 30] | 5 | ||
| n_estimators | [100, 200, 300] | 100 | ||
| num_leaves | [31, 50, 100, 200] | 31 | ||
| XGBoost | colsample_bytree | [0.8, 0.9, 1.0] | 0.8 | 0.9787 |
| gamma | [0, 0.1, 0.2] | 0 | ||
| learning rate | [0.1, 0.01, 0.001] | 0.1 | ||
| max_depth | [3, 5, 7] | 3 | ||
| min_child_weight | [1, 3, 5] | 1 | ||
| n_estimators | [100, 200, 300] | 100 | ||
| subsample | [0.8, 0.9, 1.0] | 0.8 |
| Hex | Rect | Tri | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R-Squared | MedAE | MAE | R-Squared | MedAE | MAE | R-Squared | MedAE | MAE | ||||||||||
| Model | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test |
| AdaBoost | 0.9606 | 0.9610 | 0.0375 | 0.0376 | 0.0381 | 0.0381 | 0.9725 | 0.9737 | 0.0225 | 0.0227 | 0.0291 | 0.0290 | 0.9748 | 0.9749 | 0.0294 | 0.0295 | 0.0302 | 0.0303 |
| ANN | 0.9728 | 0.9731 | 0.0339 | 0.0340 | 0.0329 | 0.0329 | 0.9947 | 0.9963 | 0.0071 | 0.0070 | 0.0098 | 0.0095 | 0.9787 | 0.9787 | 0.0345 | 0.0346 | 0.0272 | 0.0274 |
| GBR | 0.9731 | 0.9727 | 0.0345 | 0.0349 | 0.0325 | 0.0329 | 0.9957 | 0.9963 | 0.0084 | 0.0085 | 0.0096 | 0.0097 | 0.9792 | 0.9785 | 0.0341 | 0.0349 | 0.0270 | 0.0276 |
| HistGBR | 0.9728 | 0.9730 | 0.0350 | 0.0350 | 0.0327 | 0.0329 | 0.9954 | 0.9965 | 0.0087 | 0.0086 | 0.0098 | 0.0096 | 0.9789 | 0.9788 | 0.0344 | 0.0349 | 0.0272 | 0.0275 |
| KNN | 0.9733 | 0.9657 | 0.0328 | 0.0370 | 0.0320 | 0.0365 | 0.9958 | 0.9955 | 0.0082 | 0.0092 | 0.0094 | 0.0105 | 0.9793 | 0.9732 | 0.0326 | 0.0369 | 0.0269 | 0.0308 |
| LightGBM | 0.9728 | 0.9730 | 0.0344 | 0.0344 | 0.0327 | 0.0328 | 0.9955 | 0.9965 | 0.0086 | 0.0087 | 0.0099 | 0.0097 | 0.9788 | 0.9788 | 0.0340 | 0.0343 | 0.0272 | 0.0275 |
| XGBoost | 0.9728 | 0.9730 | 0.0345 | 0.0344 | 0.0327 | 0.0328 | 0.9953 | 0.9964 | 0.0088 | 0.0087 | 0.0099 | 0.0097 | 0.9789 | 0.9788 | 0.0343 | 0.0345 | 0.0272 | 0.0275 |
| Hex | Rect | Tri | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R-Squared | MedAE | MAE | R-Squared | MedAE | MAE | R-Squared | MedAE | MAE | ||||||||||
| Model | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test |
| AdaBoost | 0.9542 | 0.9544 | 0.0356 | 0.0356 | 0.0392 | 0.0393 | 0.9248 | 0.9259 | 0.0477 | 0.0477 | 0.0523 | 0.0523 | 0.9507 | 0.9513 | 0.0362 | 0.0362 | 0.0401 | 0.0402 |
| ANN | 0.9884 | 0.9884 | 0.0192 | 0.0195 | 0.0209 | 0.0212 | 0.9503 | 0.9511 | 0.0396 | 0.0397 | 0.0449 | 0.0449 | 0.9868 | 0.9873 | 0.0240 | 0.0231 | 0.0219 | 0.0216 |
| GBR | 0.9887 | 0.9884 | 0.0194 | 0.0204 | 0.0207 | 0.0214 | 0.9508 | 0.9501 | 0.0409 | 0.0416 | 0.0451 | 0.0459 | 0.9870 | 0.9869 | 0.0233 | 0.0232 | 0.0217 | 0.0218 |
| HistGBR | 0.9886 | 0.9886 | 0.0200 | 0.0204 | 0.0208 | 0.0211 | 0.9505 | 0.9507 | 0.0410 | 0.0414 | 0.0453 | 0.0456 | 0.9869 | 0.9871 | 0.0238 | 0.0233 | 0.0218 | 0.0216 |
| KNN | 0.9889 | 0.9857 | 0.0193 | 0.0219 | 0.0204 | 0.0234 | 0.9512 | 0.9378 | 0.0412 | 0.0456 | 0.0443 | 0.0504 | 0.9871 | 0.9839 | 0.0220 | 0.0245 | 0.0215 | 0.0241 |
| LightGBM | 0.9886 | 0.9886 | 0.0200 | 0.0206 | 0.0208 | 0.0211 | 0.9505 | 0.9507 | 0.0412 | 0.0414 | 0.0453 | 0.0456 | 0.9868 | 0.9871 | 0.0236 | 0.0231 | 0.0218 | 0.0216 |
| XGBoost | 0.9887 | 0.9886 | 0.0200 | 0.0205 | 0.0208 | 0.0211 | 0.9505 | 0.9506 | 0.0411 | 0.0417 | 0.0452 | 0.0456 | 0.9869 | 0.9871 | 0.0239 | 0.0237 | 0.0218 | 0.0217 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qadir, A.; Udu, A.G.; Osa-uwagboe, N. Optimising Mechanical Performance of Additive Manufactured Composites for Biomedical Applications. Fibers 2025, 13, 79. https://doi.org/10.3390/fib13060079
Qadir A, Udu AG, Osa-uwagboe N. Optimising Mechanical Performance of Additive Manufactured Composites for Biomedical Applications. Fibers. 2025; 13(6):79. https://doi.org/10.3390/fib13060079
Chicago/Turabian StyleQadir, Abdul, Amadi Gabriel Udu, and Norman Osa-uwagboe. 2025. "Optimising Mechanical Performance of Additive Manufactured Composites for Biomedical Applications" Fibers 13, no. 6: 79. https://doi.org/10.3390/fib13060079
APA StyleQadir, A., Udu, A. G., & Osa-uwagboe, N. (2025). Optimising Mechanical Performance of Additive Manufactured Composites for Biomedical Applications. Fibers, 13(6), 79. https://doi.org/10.3390/fib13060079







