Short-Beam Shear Fatigue Behavior on Unidirectional GLARE: Mean Shear Stress Effect, Scatter, and Anisotropy
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
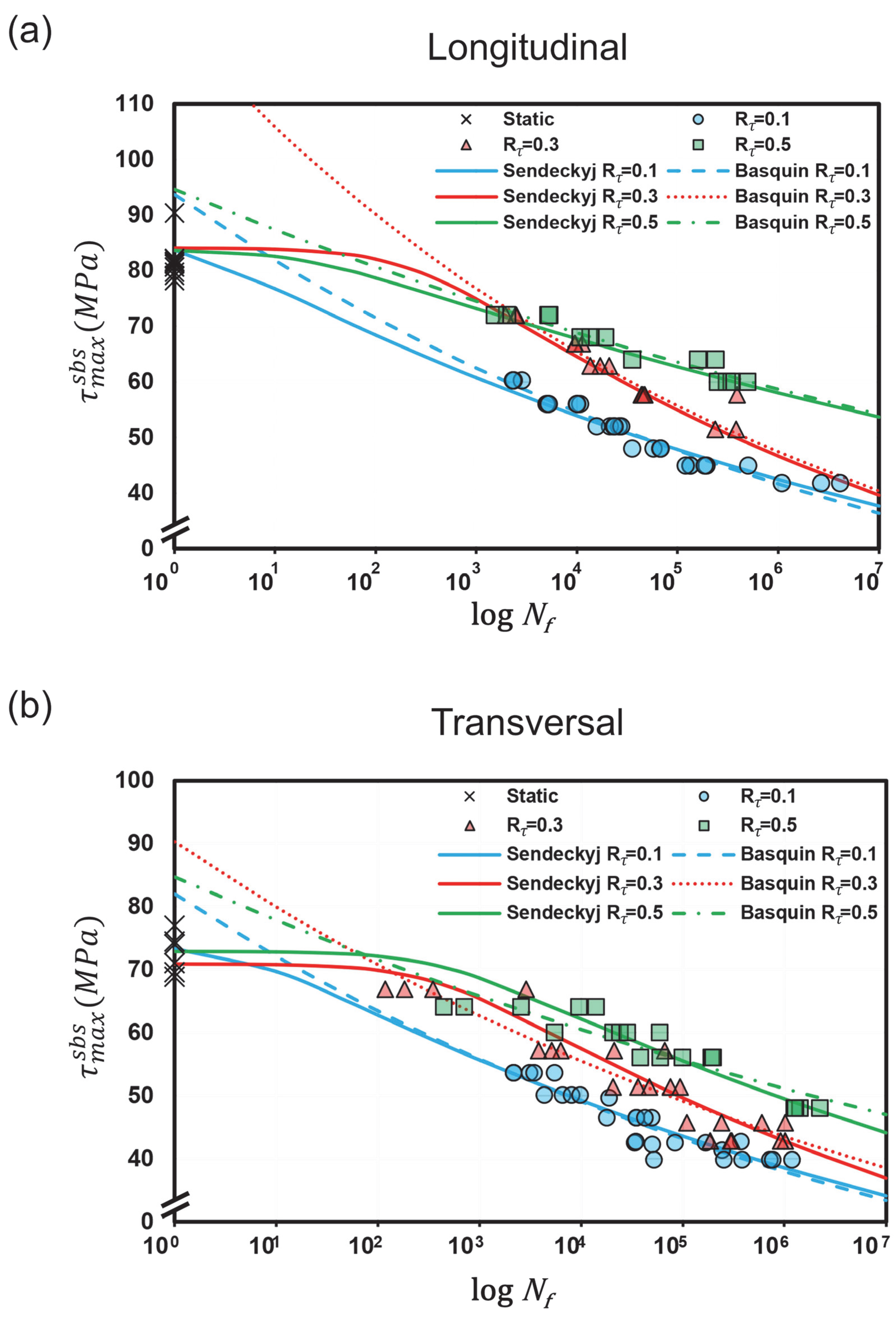
3.1. Scatter and Anisotropy
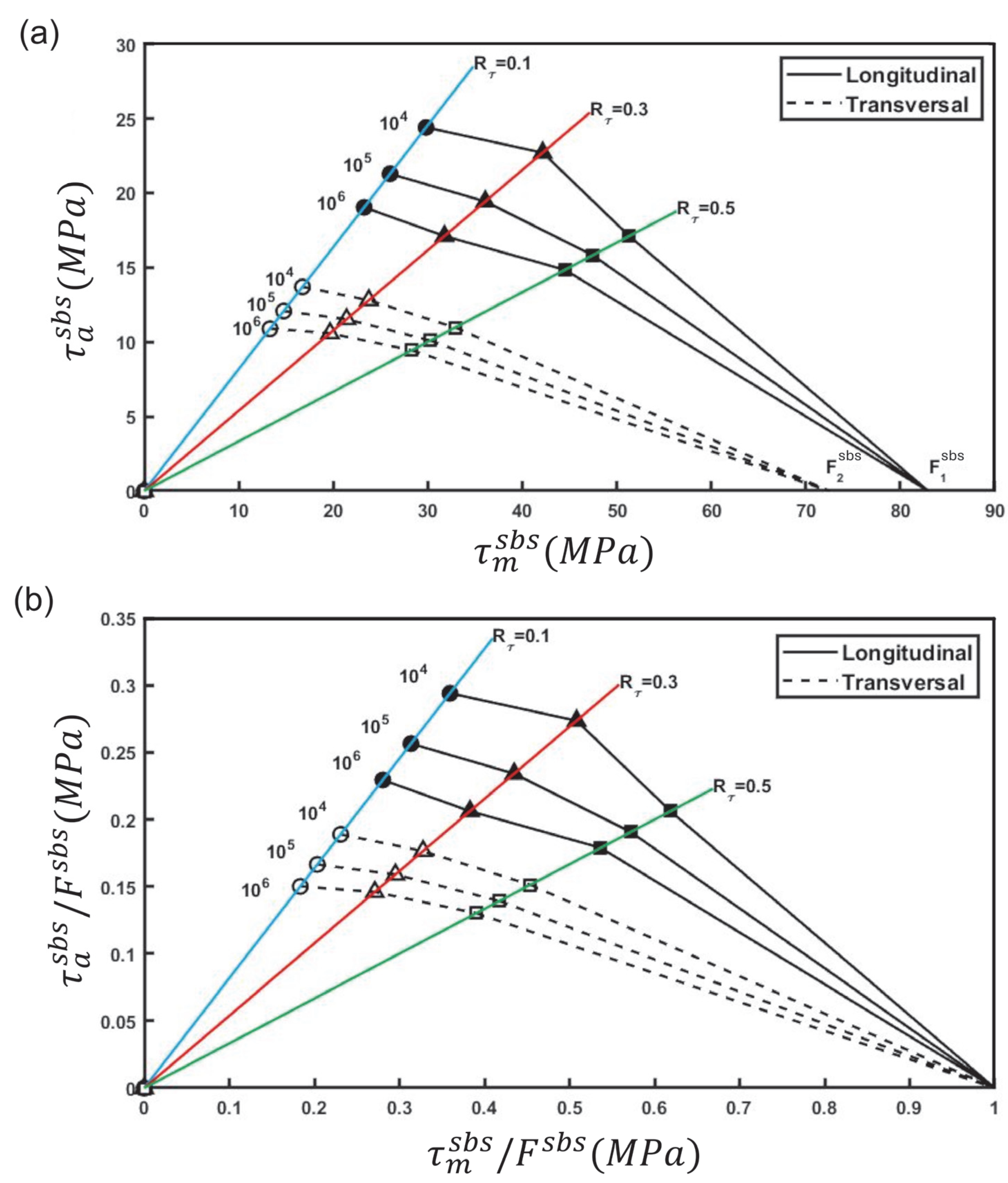
3.2. Mean Shear Stress Effect
3.3. Fractographic Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| exponent in Basquin’s relation | |
| b | specimen width |
| CLD | constant life diagram |
| E | tensile modulus of elasticity |
| FML | fiber metal laminate |
| quasi-static short-beam strength | |
| ultimate tensile strength | |
| tensile yield stress | |
| G | exponent in the Sendeckyj model |
| GFRP | glass fiber-reinforced polymer |
| t | specimen thickness |
| l | specimen length |
| N | number of cycles |
| Nf | number of cycles at failure or SBS fatigue life of a specimen |
| P | force |
| P(i) | force at ith data point observed during the fatigue test |
| shear stress ratio | |
| SBS | short-beam shear. |
| probability of survival after N cycles | |
| shape factor in Weibull distribution | |
| scale factor in Weibull distribution | |
| normal stress | |
| shear stress amplitude or SBS amplitude | |
| SBS stress value observed at ith data point in one cycle | |
| maximum SBS stress value observed in one cycle | |
| minimum SBS stress value observed in one cycle | |
| parameter of Basquin relation for shear stresses |
References
- Vlot, A.; Gunnink, J.W. (Eds.) Fibre Metal Laminates, An Introduction, 1st ed.; Springer Science + Business Media: Dordrecht, The Netherlands, 2001; ISBN 978-1-4020-0391-2. [Google Scholar] [CrossRef]
- Bieniaś, J.; Dadej, K.; Surowska, B. Interlaminar Fracture Toughness of Glass and Carbon Reinforced Multidirectional Fiber Metal Laminates. Eng. Fract. Mech. 2017, 175, 127–145. [Google Scholar] [CrossRef]
- Giallanza, A.; Parrinello, F.; Ruggiero, V.; Marannano, G. Fatigue Crack Growth of New FML Composites for Light Ship Buildings under Predominant Mode II Loading Condition. Int. J. Interact. Des. Manuf. 2020, 14, 77–87. [Google Scholar] [CrossRef]
- Asghar, W.; Nasir, M.A.; Qayyum, F.; Shah, M.; Azeem, M.; Nauman, S.; Khushnood, S. Investigation of Fatigue Crack Growth Rate in CARALL, ARALL and GLARE. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1086–1100. [Google Scholar] [CrossRef]
- Castrodeza, E.M.; Bastian, F.L.; Perez Ipiña, J.E. Fracture Toughness of Unidirectional Fiber–Metal Laminates: Crack Orientation Effect. Eng. Fract. Mech. 2005, 72, 2268–2279. [Google Scholar] [CrossRef]
- Jones, R.M. Macromechanical Behavior of a Laminate. In Mechanics of Composite Materials; Taylor & Francis: Philadelphia, PA, USA, 1999; pp. 260–276. [Google Scholar]
- O’Brien, K. Fracture Mechanics of Composite Delamination. In ASM Handbook Volume 21: Composites; ASM International: Materials Park, OH, USA, 2001; p. 241. ISBN 978-0-87170-703-1. [Google Scholar]
- Al-Azzawi, A.S.; Kawashita, L.F.; Featherston, C.A. Predicting Interlaminar Damage Behaviour of Fibre-Metal Laminates Containing Adhesive Joints under Bending Loads. J. Reinf. Plast. Compos. 2021, 41, 073168442110517. [Google Scholar] [CrossRef]
- Alderliesten, R.C. Fatigue. In Fiber Metal Laminates, An Introduction; Vlot, A., Gunnink, J.W., Eds.; Springer Science + Business Media: Berlin/Heidelberg, Germany, 2001; pp. 155–171. [Google Scholar]
- Chen, Y.; Wang, Y.; Wang, H. Research Progress on Interlaminar Failure Behavior of Fiber Metal Laminates. Adv. Polym. Technol. 2020, 2020, 3097839. [Google Scholar] [CrossRef]
- Alderliesten, R. Fatigue and Fracture of Fibre Metal Laminates; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-319-56226-1. [Google Scholar]
- Süsler, S.; Bora, M.Ö.; Uçan, C.; Türkmen, H.S. The Effect of Surface Treatments on the Interlaminar Shear Failure of GLARE Laminate Included AA6061-T6 Layers by Comparing Failure Characteristics. Compos. Interfaces 2023, 30, 627–643. [Google Scholar] [CrossRef]
- Amaral, L.; Zarouchas, D.; Alderliesten, R.; Benedictus, R. Energy Dissipation in Mode II Fatigue Crack Growth. Eng. Fract. Mech. 2017, 173, 41–54. [Google Scholar] [CrossRef]
- Bieniaś, J.; Dadej, K. Fatigue Delamination Growth of Carbon and Glass Reinforced Fiber Metal Laminates in Fracture Mode II. Int. J. Fatigue 2020, 130, 105267. [Google Scholar] [CrossRef]
- Lessard, L.B.; Eilers, O.P.; Shokrieh, M.M. Modification of the Three-Rail Shear Test for Composite Materials under Static and Fatigue Loading. ASTM Int. 1997, 1242, 217–233. [Google Scholar] [CrossRef]
- ASTM D4255-20; Test Method for In-Plane Shear Properties of Polymer Matrix Composite Materials by the Rail Shear Method. ASTM International: Conshohocken, PA, USA, 2020.
- ASTM D3518-18; Test Method for In-Plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45 Laminate. ASTM International: Conshohocken, PA, USA, 2018.
- ASTM D5379-19; Test Method for Shear Properties of Composite Materials by the V-Notched Beam Method. ASTM International: Conshohocken, PA, USA, 2019.
- May, M.; Hallett, S.R. An Assessment of Through-Thickness Shear Tests for Initiation of Fatigue Failure. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1570–1578. [Google Scholar] [CrossRef]
- ASTM D2344-22; Test Method for Short-Beam Strength of Polymer Matrix Composite Materials and Their Laminates. ASTM International: Conshohocken, PA, USA, 2022; pp. 1–8.
- Kotik, H.; Ipiña, J.P. Frequency Effect in Short-Beam Shear Fatigue of a Glass Fiber Reinforced Polyester Composite. Int. J. Fatigue 2016, 90, 116–124. [Google Scholar] [CrossRef]
- Kotik, H.G.; Ipiña, J.E.P. Suggested Modifications of the ASTM D2344-16 Short-Beam Shear Test Method to Be Applied to Fiber Metal Laminates. J. Test. Eval. 2019, 49, 1213–1221. [Google Scholar] [CrossRef]
- Liu, C.; Du, D.; Li, H.; Hu, Y.; Xu, Y.; Tian, J.; Tao, G.; Tao, J. Interlaminar Failure Behavior of GLARE Laminates under Short-Beam Three-Point-Bending Load. Compos. Part B Eng. 2016, 97, 361–367. [Google Scholar] [CrossRef]
- Kulkarni, R.R.; Chawla, K.K.; Vaidya, U.K.; Koopman, M.C.; Eberhardt, A.W. Characterization of Long Fiber Thermoplastic/Metal Laminates. J. Mater. Sci. 2008, 43, 4391–4398. [Google Scholar] [CrossRef]
- Majerski, K.; Surowska, B.; Bienias, J. The Comparison of Effects of Hygrothermal Conditioning on Mechanical Properties of Fibre Metal Laminates and Fibre Reinforced Polymers. Compos. Part B Eng. 2018, 142, 108–116. [Google Scholar] [CrossRef]
- Bellini, C.; Di Cocco, V.; Iacoviello, F.; Sorrentino, L. Comparison between Long and Short Beam Flexure of a Carbon Fibre Based FML. Procedia Struct. Integr. 2020, 26, 120–128. [Google Scholar] [CrossRef]
- Kubit, A.; Trzepiecinski, T.; Kłonica, M.; Hebda, M.; Pytel, M. The Influence of Temperature Gradient Thermal Shock Cycles on the Interlaminar Shear Strength of Fibre Metal Laminate Composite Determined by the Short Beam Test. Compos. Part B Eng. 2019, 176, 107217. [Google Scholar] [CrossRef]
- Gupta, R.K.; Mahato, A.; Bhattacharya, A. Damage Analysis of Carbon Fiber Reinforced Aluminum Laminate under Short Beam and Single Edge Notch Beam Bend Test. Int. J. Mech. Sci. 2021, 198, 106393. [Google Scholar] [CrossRef]
- Bellini, C.; Di Cocco, V.; Iacoviello, F.; Sorrentino, L. Influence of Structural Characteristics on the Interlaminar Shear Strength of CFRP/Al Fibre Metal Laminates. Procedia Struct. Integr. 2019, 18, 373–378. [Google Scholar] [CrossRef]
- Khalid, M.Y.; Arif, Z.U.; Al Rashid, A.; Shahid, M.I.; Ahmed, W.; Tariq, A.F.; Abbas, Z. Interlaminar Shear Strength (ILSS) Characterization of Fiber Metal Laminates (FMLs) Manufactured through VARTM Process. Forces Mech. 2021, 4, 100038. [Google Scholar] [CrossRef]
- Bieniaś, J.; Jakubczak, P.; Droździel, M.; Surowska, B. Interlaminar Shear Strength and Failure Analysis of Aluminium-Carbon Laminates with a Glass Fiber Interlayer after Moisture Absorption. Materials 2020, 13, 2999. [Google Scholar] [CrossRef] [PubMed]
- Hamill, L.; Hofmann, D.C.; Nutt, S. Galvanic Corrosion and Mechanical Behavior of Fiber Metal Laminates of Metallic Glass and Carbon Fiber Composites. Adv. Eng. Mater. 2018, 20, 1700711. [Google Scholar] [CrossRef]
- Zheng, X.; Li, Y.; Luo, P. Preparation and Mechanical Properties of Light-Weight Fiber Metal Laminates Based on Magnesium-Rare Earth Alloy. Mater. Today Commun. 2022, 33, 104822. [Google Scholar] [CrossRef]
- Kotik, H.G.; Ipiña, J.P. Short-Beam Shear Fatigue Behavior of Fiber Metal Laminate (Glare). Int. J. Fatigue 2017, 95, 236–242. [Google Scholar] [CrossRef]
- Surowska, B.; Dadej, K.; Jakubczak, P.; Bieniaś, J. Short-Beam Shear Fatigue Life Assessment of Thermally Cycled Carbon–Aluminium Laminates with Protective Glass Interlayers. Arch. Civ. Mech. Eng. 2021, 21, 50. [Google Scholar] [CrossRef]
- Harris, B. A Parametric Constant-Life Model for Prediction of the Fatigue Lives of Fibre-Reinforced Plastics. In Fatigue in Composites; Harris, B., Ed.; CRC Press LLC.: Boca Raton, FL, USA; Woodhead Publishing Limited: Cambridge, UK, 2003; pp. 546–568. [Google Scholar]
- Sutherland, H.J.; Mandell, J.F. Optimized Constant-Life Diagram for the Analysis of Fiberglass Composites Used in Wind Turbine Blades. J. Sol. Energy Eng. 2005, 127, 563–569. [Google Scholar] [CrossRef]
- Kawai, M.; Koizumi, M. Nonlinear Constant Fatigue Life Diagrams for Carbon/Epoxy Laminates at Room Temperature. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2342–2353. [Google Scholar] [CrossRef]
- Vassilopoulos, A.P. Introduction to the Fatigue Life Prediction of Composite Materials and Structures: Past, Present and Future Prospects. In Fatigue Life Prediction of Composites and Composite Structures; Vassilopoulos, A.P., Ed.; CRC Press LLC.: Boca Raton, FL, USA; Woodhead Publishing Limited: Great Abington, Cambridge, 2010; pp. 1–38. [Google Scholar]
- Vassilopoulos, A.P.; Keller, T. Fatigue of Fiber-Reinforced Composites; Engineering Materials and Processes; Springer: London, UK, 2011; ISBN 978-1-84996-180-6. [Google Scholar]
- Kotik, H.; Ipiña, J.P. Influence of Unifilo® Ply in the Interlaminar Shear Fatigue Resistance of GFRP. Procedia Mater. Sci. 2015, 8, 139–147. [Google Scholar] [CrossRef]
- Bevan, L.G. Axial and Short Beam Shear Fatigue Properties of Cfrp Laminates. Composites 1977, 8, 227–232. [Google Scholar] [CrossRef]
- Tonatto, M.L.P.; Tarpani, J.R.; Amico, S.C. Short-Beam Shear Fatigue Behavior of Round Curved Pultruded Composite. Mech. Adv. Mater. Struct. 2021, 29, 5579–5587. [Google Scholar] [CrossRef]
- QA Reports No. B0319B-2, B1008B-1, B0904A-3; Structural Laminates Company: New Kensington, PA, USA, 1994.
- Basquin, O. The Exponential Law of Endurance Tests. Am. Soc. Test Mater. 1910, 10, 625–630. [Google Scholar]
- Sendeckyj, G. Fitting Models to Composite Materials Fatigue Data. In Test Methods and Design Allowables for Fibrous Composites; ASTM International: West Conshohocken, PA, USA, 1981; pp. 245–260. [Google Scholar]
- ASTM E739-10; Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-) Fatigue Data. ASTM International: Conshohocken, PA, USA, 2015; pp. 1–7.
- Whitney, J. Fatigue Characterization of Composite Materials. In ASTM STP 723 Fatigue of Fibrous Composite Materials; ASTM International: West Conshohocken, PA, USA, 1981; pp. 133–152. [Google Scholar]
- Mandell, J.; Meier, U. Effects of Stress Ratio, Frequency, and Loading Time on the Tensile Fatigue of Glass-Reinforced Epoxy. In Long-Term Behavior of Composites STP 813; ASTM International: West Conshohocken, PA, USA, 1983; pp. 55–77. [Google Scholar]
- Kensche, C.W. Fatigue of Materials and Components for Wind Turbine Rotor Blades; European Commission, Directorate-General XII, Science, Research and Development: Brussels, Belgium, 1996; ISBN 92-827-4361-6. [Google Scholar]
- Gao, Q.; Xin, H.; Correia, J.A.; Mosallam, A.S.; Berto, F. Probabilistic Fatigue Life Analysis Considering Mean Stress Effects of Fiber Reinforced Polymer (FRP) Composites. Int. J. Fatigue 2022, 162, 106951. [Google Scholar] [CrossRef]
- Schijve, J. Fatigue and Scatter. In Fatigue of Structures and Materials; Springer: Dordrecht, The Netherlands, 2009; pp. 373–394. [Google Scholar]
- Movahedi-Rad, A.V.; Keller, T.; Vassilopoulos, A.P. Stress Ratio Effect on Tension-Tension Fatigue Behavior of Angle-Ply GFRP Laminates. Int. J. Fatigue 2019, 126, 103–111. [Google Scholar] [CrossRef]
- Greenhalgh, E.S.; Rogers, C.; Robinson, P. Fractographic Observations on Delamination Growth and the Subsequent Migration through the Laminate. Compos. Sci. Technol. 2009, 69, 2345–2351. [Google Scholar] [CrossRef]
- Greenhalgh, E.S. Failure Analysis and Fractography of Polymer Composites, 1st ed.; Woodhead Publishing Limited: Cambridge, UK, 2009; ISBN 978-1-84569-217-9. [Google Scholar]
- Lang, R.W.; Manson, J.A.; Hertzberg, R.W. Mechanisms of Fatigue Fracture in Short Glass Fibre-Reinforced Polymers. J. Mater. Sci. 1987, 22, 4015–4030. [Google Scholar] [CrossRef]
- Gamstedt, E.; Sjögren, B. Micromechanisms in Tension-Compression Fatigue of Composite Laminates Containing Transverse Plies. Compos. Sci. Technol. 1999, 59, 167–178. [Google Scholar] [CrossRef]
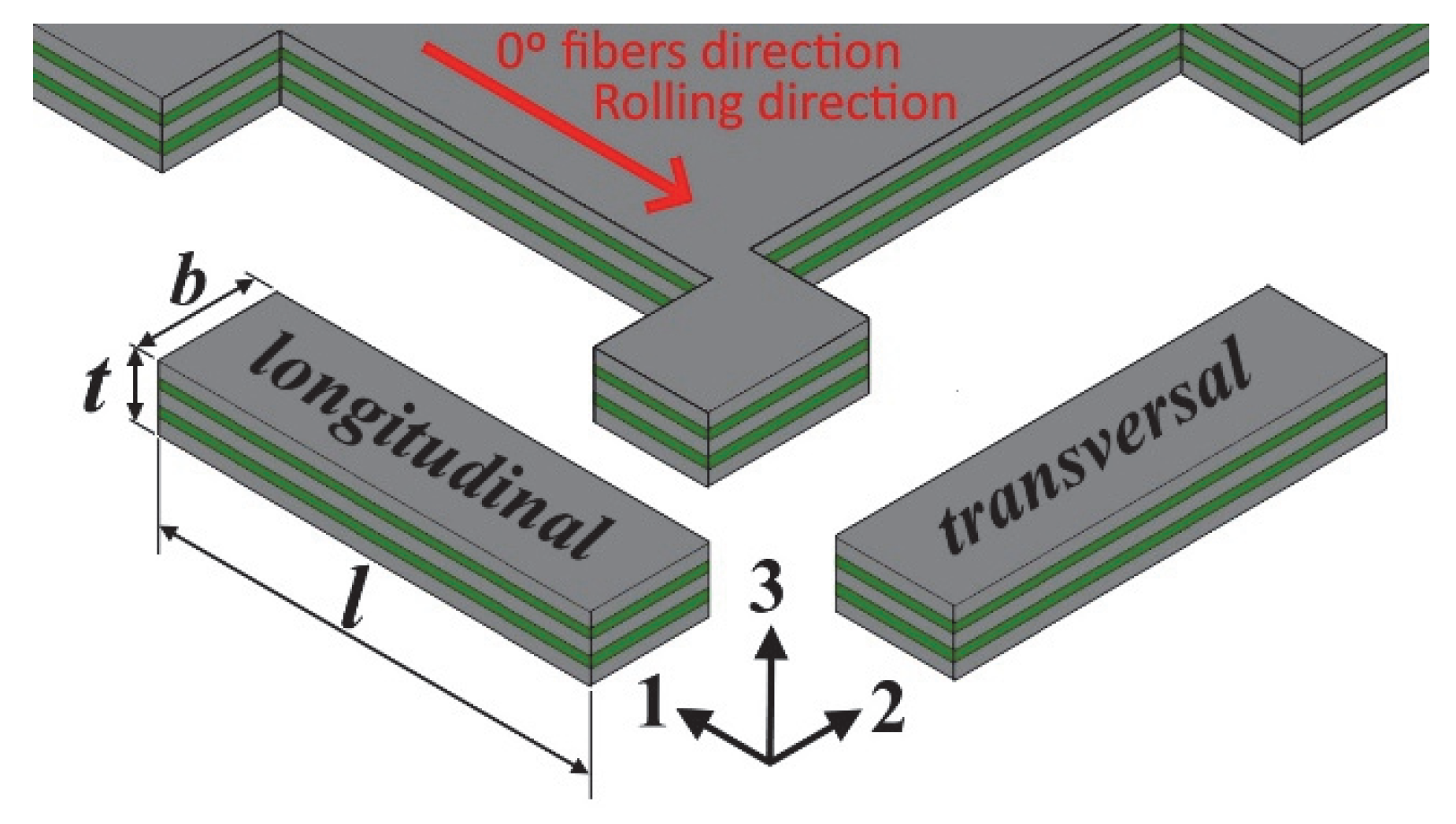

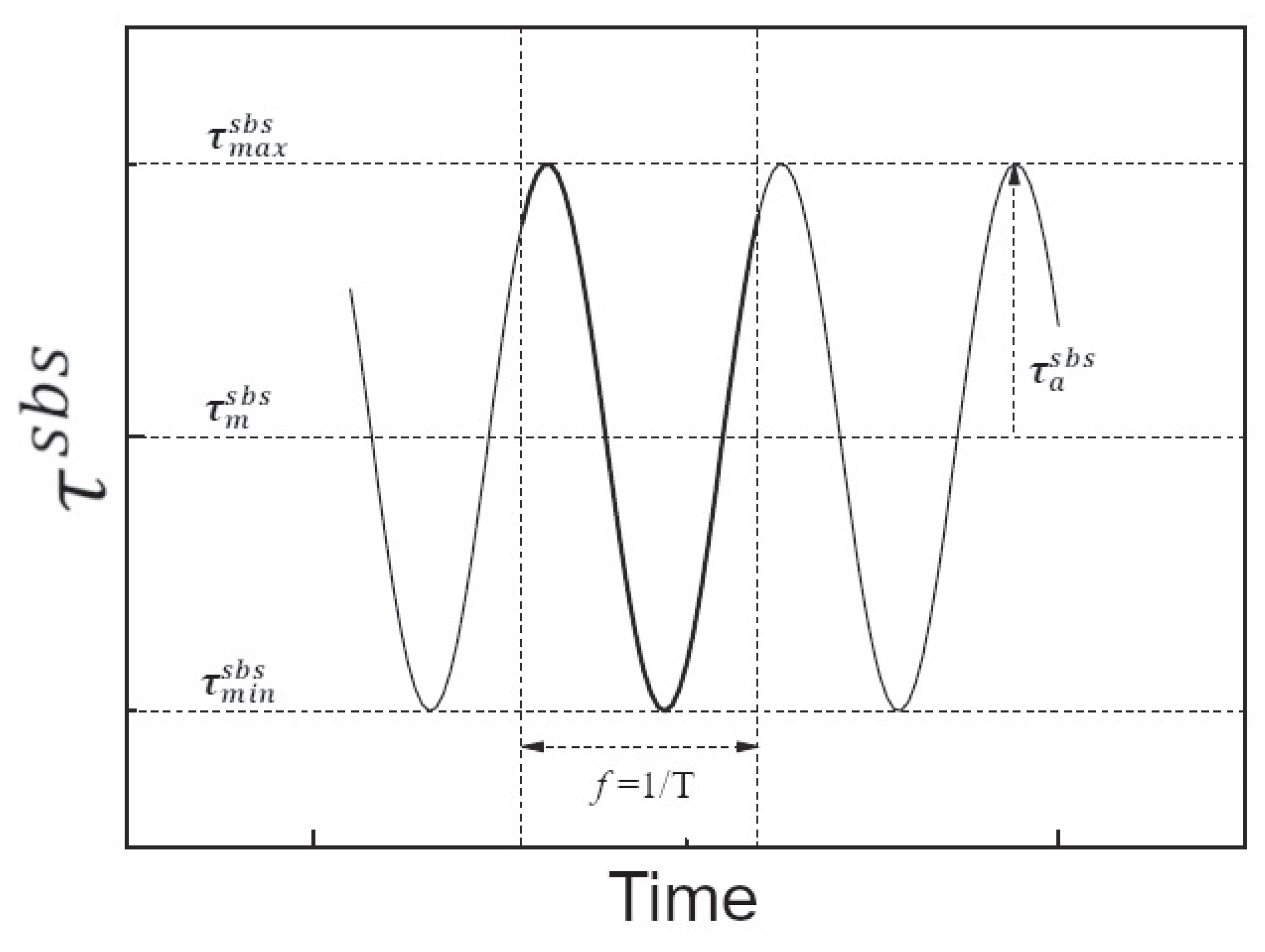

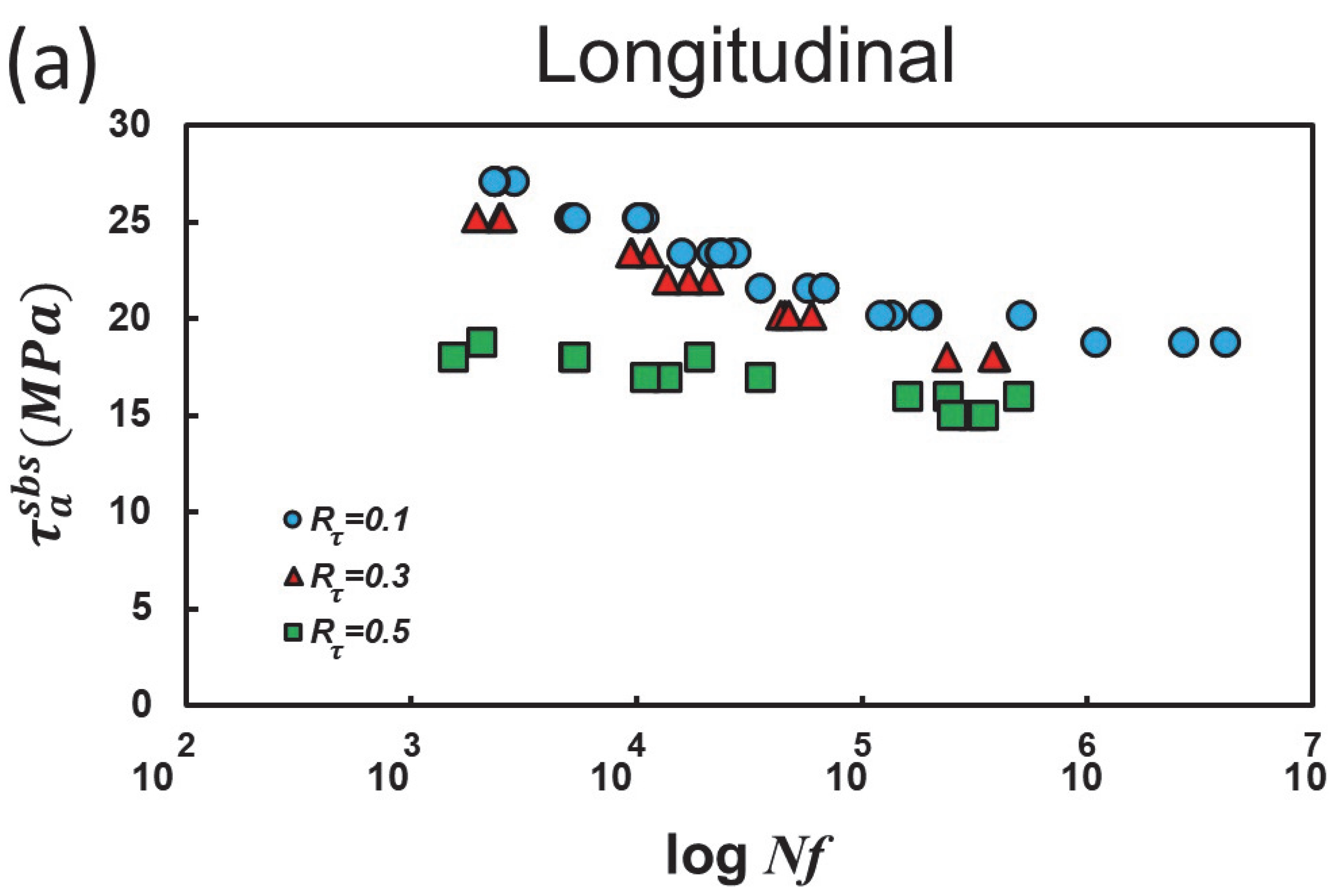
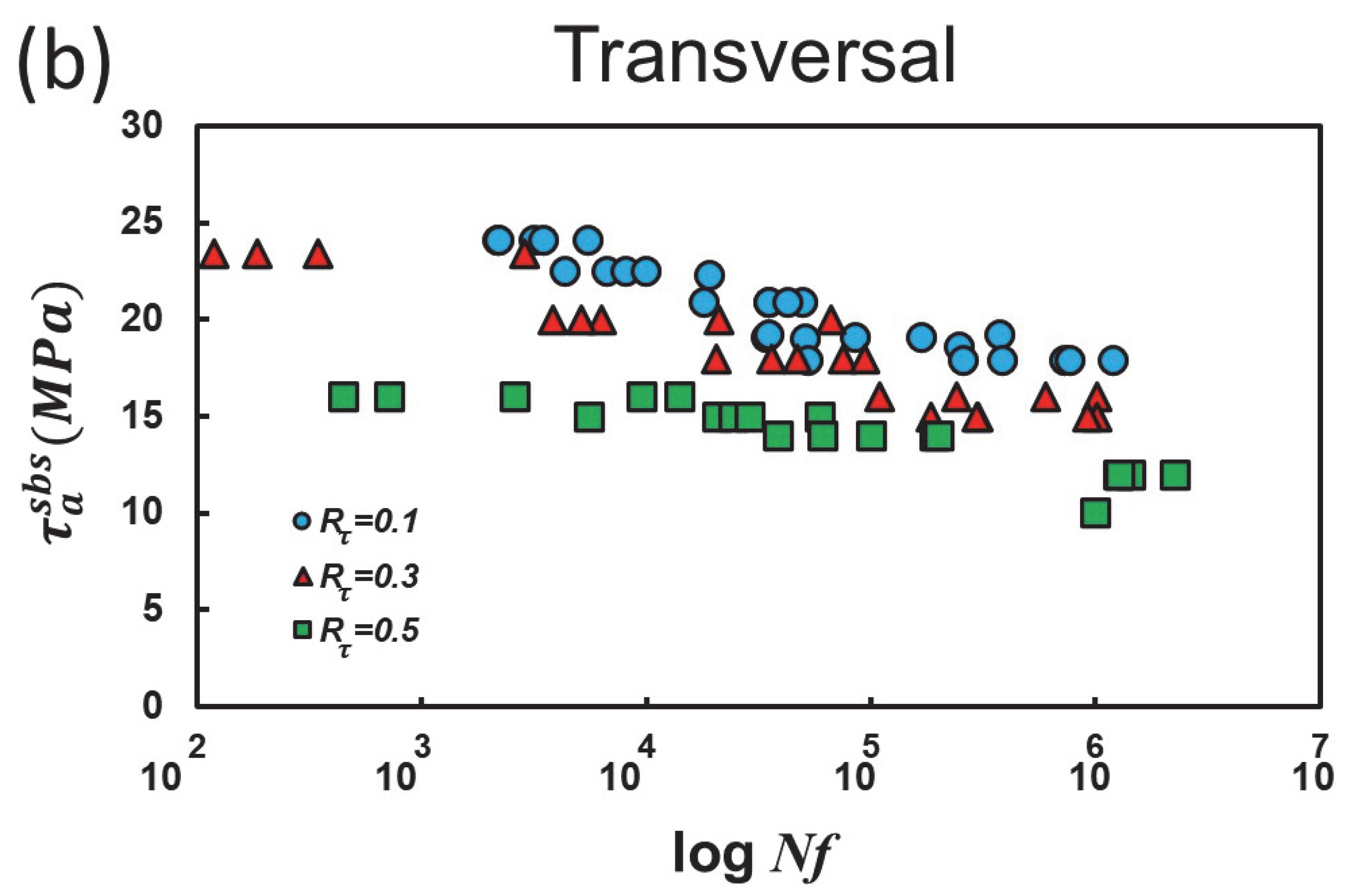





| Material | GLARE 1 |
|---|---|
| Lay-up (Al/prepreg) | 3/2 |
| Fibers | S-glass |
| Al alloy | 7475-T76 |
| Post-stretch (%) | 0.4 |
| ) (MPa) | 545 |
| ) (MPa) | 338 |
| Metallic percentage (Vol) | 67.9 |
| ) (MPa) | 1282 |
| ) (MPa) | 352 |
| Longitudinal Young’s modulus (E1) (GPa) | 64 |
| Transversal Young’s modulus (E2) (GPa) | 49 |
| Density (ρ) (kg/m3) | 2520 |
| Total thickness (t) (mm) | 1.42 |
| Orientation | (MPa) | Number of Replicates | Orientation | (MPa) | Number of Replicates | ||
|---|---|---|---|---|---|---|---|
| Longitudinal | 0.1 [34] | 60.2 | 4 | Transversal | 0.1 [34] | 53.6 | 5 |
| 56.0 | 6 | 50.0 | 4 | ||||
| 52.0 | 6 | 49.6 | 1 | ||||
| 48.0 | 5 | 46.4 | 5 | ||||
| 44.9 | 6 | 42.7 | 2 | ||||
| 41.8 | 3 | 42.4 | 3 | ||||
| 0.3 | 72.0 | 3 | 42.2 | 1 | |||
| 66.9 | 3 | 41.3 | 1 | ||||
| 62.9 | 3 | 39.8 | 6 | ||||
| 57.7 | 4 | 0.3 | 66.9 | 4 | |||
| 51.4 | 3 | 57.1 | 5 | ||||
| 0.5 | 72.0 | 4 | 51.4 | 5 | |||
| 68.0 | 3 | 45.7 | 4 | ||||
| 64.0 | 3 | 42.9 | 5 | ||||
| 60.0 | 4 | 0.5 | 64.0 | 5 | |||
| 60.0 | 5 | ||||||
| 56.0 | 5 | ||||||
| 48.0 | 4 |
| Basquin Curve Parameters | |||
|---|---|---|---|
| 1/k | |||
| Longitudinal | 0.1 | 93.7 | 0.06 |
| 0.3 | 124.2 | 0.07 | |
| 0.5 | 94.6 | 0.03 | |
| Transversal | 0.1 | 82.0 | 0.06 |
| 0.3 | 90.2 | 0.05 | |
| 0.5 | 84.7 | 0.04 | |
| Sendeckyj Curve Parameters | |||||
|---|---|---|---|---|---|
| αf | β (MPa) | C | G | ||
| Longitudinal | 0.1 | 28.5 | 84.8 | 0.485 | 0.052 |
| 0.3 | 30.0 | 85.1 | 0.004 | 0.071 | |
| 0.5 | 28.0 | 84.7 | 0.052 | 0.034 | |
| Transversal | 0.1 | 30.9 | 74.2 | 0.178 | 0.053 |
| 0.3 | 18.4 | 72.4 | 0.003 | 0.064 | |
| 0.5 | 29.0 | 73.8 | 0.002 | 0.050 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caetano, D.G.; Kotik, H.G.; Perez Ipiña, J.E.; Castrodeza, E.M. Short-Beam Shear Fatigue Behavior on Unidirectional GLARE: Mean Shear Stress Effect, Scatter, and Anisotropy. Fibers 2025, 13, 77. https://doi.org/10.3390/fib13060077
Caetano DG, Kotik HG, Perez Ipiña JE, Castrodeza EM. Short-Beam Shear Fatigue Behavior on Unidirectional GLARE: Mean Shear Stress Effect, Scatter, and Anisotropy. Fibers. 2025; 13(6):77. https://doi.org/10.3390/fib13060077
Chicago/Turabian StyleCaetano, Douglas G., Hector G. Kotik, Juan E. Perez Ipiña, and Enrique M. Castrodeza. 2025. "Short-Beam Shear Fatigue Behavior on Unidirectional GLARE: Mean Shear Stress Effect, Scatter, and Anisotropy" Fibers 13, no. 6: 77. https://doi.org/10.3390/fib13060077
APA StyleCaetano, D. G., Kotik, H. G., Perez Ipiña, J. E., & Castrodeza, E. M. (2025). Short-Beam Shear Fatigue Behavior on Unidirectional GLARE: Mean Shear Stress Effect, Scatter, and Anisotropy. Fibers, 13(6), 77. https://doi.org/10.3390/fib13060077







