Highlights
- What are the main findings?
- Defects and aging reduce flax fiber strength: Porosity, surface defects, (e.g., kink-bands, lumens), and degradation increase stress concentrations, weakening fibers. Aged fibers show more damage and lower stiffness than modern ones.
- Stable mechanical properties at 50 µm (REL): The elastic modulus stabilizes at this length, minimizing variability caused by microstructural defects in shorter segments.
- What are the implications of the main findings?
- Improved fiber design: Reducing defects in flax fibers enhances durability, making them more viable for sustainable composites and textiles.
- Conservation and predictive modeling: This study aids in preserving ancient flax textiles by quantifying aging effects and introduces a framework (REL) for predicting natural fiber behavior, benefiting research and industry.
Abstract
Flax fiber reinforcements weaken with aging and microstructural changes, limiting their applications. Here, we examine the effects of microstructure and aging on flax fiber elements’ performance by using 4000-year-old and modern Egyptian flax as references through multi-scale numerical modeling. This study introduces a novel investigation into the tensile stress distribution behavior of archaeological and modern flax yarns. The finite element (FE) model is derived from 3D volumes obtained via X-ray microtomography and tensile testing in the elastic domain. At the microscale, fibers exhibit higher axial stress concentrations around surface defects and pores, particularly in regions with kink bands and lumens. At the mesoscale, fiber bundles show increased stress concentrations at inter-fiber voids and lumen, with larger bundles exhibiting greater stress heterogeneity, especially around pores and surface roughness. At the macroscale, yarns display significant stress heterogeneity, especially around microstructural defects like pores and fiber–fiber cohesion points. Aged fibers from ancient Egyptian cultural heritage in particular demonstrate large fiber discontinuities due to long-term degradation or aging. These numerical observations highlight how porosity, surface imperfections, and structural degradation increase stress concentration, leading to fiber rupture and mechanical failure. This insight reveals how aging and defects impact flax fiber performance and durability.
1. Introduction
Composite materials are replacing traditional ones due to their superior performance, but they are costly, non-recyclable, non-biodegradable, and may pose health risks. With growing environmental concerns, there is a need to develop lightweight, cost-effective, and sustainable materials as alternatives to traditional ones. Recently, bio-fibers have gained popularity as replacements for glass fibers in polymer composites for various engineering applications [1,2,3,4,5]. Plant fibers are widely available, affordable, low-density, biodegradable, and renewable. Their mechanical properties are also comparable to synthetic glass fibers used in composite reinforcement [6,7,8,9]. Among plant fibers, flax stands out for its ideal combination of light weight and high strength and stiffness, making it suitable for structural applications in fields like civil engineering, automotive, and textiles [10,11,12]. Flax fibers are used at various scales, from individual fibers to yarns, particularly in composites. To effectively apply flax fiber-reinforced composites in engineering, it is crucial to thoroughly understand both the fiber’s mechanical properties and the impact of its structure on performance, which can be achieved through numerical simulations [13,14,15]. X-ray microtomography, combining with finite element simulation, serves as a great non-destructive technique [16,17], providing a true 3D representation of flax fiber elements in 3D images. This technology enables the creation of an accurate 3D finite element fiber model, which can then be utilized for numerical simulations to derive reliable solutions.
Flax fibers have a hierarchical structure across scales [18]. At the microscale, elementary fibers consist of cell walls, with the S2 layer, rich in aligned microfibrils, providing strength [19]. These fibers form bundles at the mesoscale, held together by the middle lamella [20]. At the macroscale, fibers and bundles are twisted into yarns, which can be single or ply types [21,22]. Voids exist at various levels, including within fibers (lumen) and between bundles and yarns [13,23,24,25,26,27]. This multi-scale structure significantly affects flax’s mechanical performance in textiles and composites, making it essential to understand for optimizing material use [18,28]. Flax fiber aging can lead to reduced strength and stiffness, influencing the durability and performance of composites [29,30]. Egypt’s long-standing textile history, spanning thousands of years, presents a unique opportunity to study the evolution of fiber usage and its influence on material durability [31,32]. Flax fiber aging involves the progressive degradation of non-cellulosic polymers (e.g., lignin and hemicellulose) in the cell wall, leading to reduced cohesion and increased porosity [33]. Synchrotron deep-UV fluorescence studies reveal that archaeological fibers exhibit significant depolymerization of parietal polymers, exacerbating microstructural defects like kink-bands and inducing a significant brittleness in the cell wall [33,34]. These chemical changes correlate with reduced crystallinity in cellulose Iβ [33] and increased sensitivity to environmental humidity [3], further compromising mechanical integrity. While our study focuses on microstructural and stress heterogeneity via non-destructive X-ray microtomography, the interplay of chemical degradation, crystallinity loss, and hygroscopic effects underscores the need for future multimodal characterization (e.g., FT-IR, XRD) to fully resolve aging mechanisms.
Studies on fiber aging investigate how structural changes due to degradation influence durability; however, there is a lack of knowledge on the impact of aging under tensile loading [31,35]. In this case, studying aging under tensile loading is essential, along with understanding the multiscale microstructure of flax fiber elements, to better optimize their properties. The motivation behind this work is rooted in advancing the understanding of how microstructure and aging affect the mechanical properties of flax fiber elements. The aged fibers examined in this study are naturally aged samples (~4000 year old) obtained from artifacts. While the 4000-year-old flax fibers examined here represent an extreme case of aging, their study provides a unique opportunity to investigate irreversible degradation mechanisms under uncontrolled environmental conditions. These insights are critical for understanding how modern flax fibers might degrade over shorter, industrially relevant lifespans (e.g., 10–50 years). For instance, studies on shorter-aged flax fibers exposed to humidity, UV radiation, or mechanical cycling [29,36,37] report similar microstructural changes (e.g., lumen collapse, microfibril misalignment) but at slower rates. By comparing ancient and modern fibers, this research bridges fundamental aging mechanisms with practical durability concerns in applications such as automotive composites or civil engineering reinforcements. Studying both naturally aged and modern flax fibers uncovers critical insights into how plant fibers degrade over time in uncontrolled aging processes and how these changes impact their performance. This knowledge is particularly valuable for optimizing the design and use of flax-based composites in modern engineering [37,38], particularly in sustainable materials and eco-friendly applications.
Numerical modeling enables a detailed analysis of the fiber’s internal structure by virtually slicing fibers in longitudinal and transverse cross-sections, an approach often challenging to achieve through experimental methods. Moreover, it allows for the prediction of how defects and microstructural variations influence mechanical performance. In particular, finite element (FE) modeling is essential for capturing stress heterogeneities that arise due to the complex structure of flax fibers, especially in the presence of kink band defects and varied geometry, where analytical approaches may fail to provide an accurate description. This is crucial for understanding how to improve modern flax-based composites by minimizing defects and optimizing fiber structures, ensuring better performance in engineering applications.
Interestingly, a concept called representative element length (REL) has been developed. REL aims to determine the smallest length of a fiber segment that accurately reflects the mechanical properties of the entire fiber. Flax fibers, due to their complex microstructures and inherent variability in porosity and morphology, exhibit significant variations in mechanical properties when subjected to different loading conditions [39,40,41]. Capturing the true mechanical behavior of fibers, especially in tensile simulations, often requires the use of smaller segments or sub-models derived from larger 3D reconstructions. However, when using smaller segments, variations in microstructural features—such as porosity, defects, and surface roughness—can lead to substantial scattering in calculated elastic moduli, rendering these smaller models unrepresentative of the entire fiber. To address this, we systematically investigated how fiber length influences the scatter in elastic modulus by introducing the REL approach. Starting from small sub-sections, we gradually increased the fiber length and evaluated the elastic modulus for each sub-section. This methodology enabled us to identify the minimum length at which the elastic modulus stabilizes, thus representing the overall fiber behavior. The REL concept not only provides accurate representation of the fiber’s mechanical properties but also offers valuable insights into how local microstructure affects fiber stiffness. The REL model’s validation involved conducting sensitivity analyses to understand the influence of microstructural variability on its predictions, assuring its robustness and accuracy. This process strengthens the theoretical framework and enhances the practical relevance of the REL concept in characterizing the mechanical behavior of flax fibers.
The objective of this study is to investigate the mechanical properties of aged (ancient) and recent (modern) flax fibers at microscale, mesoscale, and macroscale levels. By employing numerical simulations, REL is used to address the scatter in elastic modulus of elementary fibers.. Furthermore, this study aims to establish the correlations between porosity and elastic modulus, assess the effects of aging on fiber integrity, and analyze the heterogeneity in stress and strain distributions across elementary fibers, bundles, and yarns from finite element models.
2. Materials and Methods
2.1. Materials
Modern flax fibers were sourced from contemporary Egyptian fabric provided by the Institut Français d’Archéologie Orientale (IFAO) in Cairo, Egypt. In contrast, the ancient flax fibers were extracted from a textile preserved at the Louvre Museum in Paris (inv. E 13593G), which has been radiocarbon dated (SacA70167, CEA-Saclay, Paris, France) to between 4324 and 4053 BCE. The full details regarding the ancient materials are available in the literature [31]. The modern Egyptian flax fibers were cultivated in November 2022 and reached maturity by March 2023. Elementary and bundle fibers were manually extracted from the yarns. The modern elementary fibers are labeled MF1 and MF2, and the ancient ones as AF1 and AF2. Modern fiber bundles are referred to as BF1 and BF2, while modern and ancient yarns are denoted MY and AY, respectively. No chemical or mechanical pretreatments were applied to the fibers to preserve their native properties. The ancient flax fibers examined in this study represent a unique case of environmental aging under uncontrolled conditions over millennia. While their precise storage history (e.g., humidity, temperature fluctuations) remains unknown, their preservation in arid archaeological contexts provides valuable insights into long-term degradation patterns.
2.2. X-Ray Microtomography
Inline phase-contrast microtomography was performed at the ANATOMIX beamline of Synchrotron SOLEIL. The two different setups used are described in detail in previous studies [42,43]. In short, the first configuration gave an effective pixel size of 0.325 µm; it was used for measurements on static fibers and bundles. The second setup involved a tensile testing system [44] that allowed us to perform in situ microtomography during mechanical loading, with a gauge length of 10 mm, at an effective pixel size of 0.65 µm. The raw projection data were reconstructed into volume images using the standard processing pipeline at the beamline.
2.3. Finite-Element Computation
The static images obtained through X-ray microtomography were converted into numerical models using a method that combined surface tessellation with triangular elements and core propagation with tetrahedral elements. The volume mesh for elementary fiber, REL model, bundle, and yarn are shown in Figure 1. For elementary fibers, the total number of mesh elements ranged between 1.6 × 103 and 2 × 104, while for fiber bundles, the range was between 2 × 105 and 1 × 106 mesh elements. The yarns had approximately 1 × 106 mesh elements. In the REL models, the mesh element count varied between 1 × 103 and 1 × 105. The degrees of freedom (dof) for elementary fiber meshes ranged from 1 × 105 to 2 × 106, with the average element volume ranges between 1.2 × 10−9 mm3 and 4.7 × 10−11 mm3. For fiber bundles, dof values ranged from 1 × 106 to 7 × 106, with an average volume element of around 1.9 × 10−9 mm3. For yarns, the dof was between 6 × 106 and 7 × 106, with an average volume element ranging from 8.2 × 10−5 mm3 to 1.9 × 10−4 mm3. The mesh generation process was carried out using both FIJI (Version 1.54) and Simple ware ScanIP software (Version 2021.03). Quadratic tetrahedral elements, defined by 4 nodes with 3 degrees of freedom for structural displacement in 3D space, were used for meshing. The mechanical simulations were carried out in COMSOL software (Version 5.6). The computation time for elementary fiber models was only a few seconds, while for bundles, it took a few minutes. However, for yarns, it reached a maximum of approximately 5 h depicting the complexity in structure at this scale. The lengths used in the simulation are 160 µm for elementary fibers, 300 µm for bundles, and 600 µm for yarns. The yarn models are significantly larger, with more mesh elements, making them computationally intensive and complex to handle compared to elementary fibers and bundles. The porosity content for each cross-section obtained from X-ray microtomography images was calculated, with the mean porosity averaged along the fiber using Equation (1).
where Vp represents the voxel counts of porosities and Vf represents the voxel counts of the filled fiber.

Figure 1.
Mesh 3D volume of (a) modern elementary fiber, (b) example of REL models (length—30 µm and 10 µm), (c) modern bundle fiber, and (d) ancient yarn.
Four models were developed for elementary flax fibers: two representing aged fibers (AF1 and AF2) and two representing the modern fibers (MF1 and MF2). The lumens in these fibers were artificially filled, denoted as AFF and MFF for aged and modern fibers, respectively. An elliptical geometric model (GF) was created using measurements derived from the actual fiber models. Two models of modern flax fiber bundles were developed: BF1, which consists of three elementary fibers, and BF2, which contains multiple elementary fibers. A bundle model for ancient fibers was not included in this study due to difficulties in obtaining bundle fibers caused by degradation of the middle lamella, which can be partially affected by the water retting used in ancient fiber processing. Additionally, two models of flax yarn were created: one representing aged yarns (AY) and the other representing modern yarns (MY). The lengths of the models are approximately 160 µm for elementary fibers, 300 µm for bundles, and 600 µm for yarns. The representative element lengths were identified by analyzing the elementary fibers in both modern and ancient categories.
The concept of REL is performed by dividing the original fiber model into smaller segments and calculating the elastic modulus for each segment. The process started by selecting 10 µm lengths from the original 160 µm model. For each 10 µm length, we created multiple sub-models to capture the variation in fiber microstructure. Tensile simulations were performed under linear elastic conditions, with one end of the fiber fixed and a 1% strain applied at the other end. The 1% strain was chosen because it remains within the material’s linear elastic range, well below the elongation at break [45]. The elastic modulus was then calculated for each sub-model. If significant scattering in the elastic modulus was observed across the sub-models, indicating that the taken segments did not represent the behavior of the entire fiber, the segment length was incrementally increased. This process was repeated for various lengths with multiple sub-models generated at each length to ensure statistical robustness. The REL was defined as the smallest length at which the elastic modulus stabilized, showing minimal scatter and aligning closely with the elastic modulus of the original full-scale model. Sampling for each length was performed by selecting representative sub-segments from various regions along the fiber, ensuring that the heterogeneity of the fiber’s microstructure was captured. This approach was applied to both aged and modern fibers, and additional comparisons were made between different samples within each group (AF1 and AF2 for aged fibers, and MF1 and MF2 for modern fibers) to investigate the effect of defects on elastic modulus scattering.
The global properties used for the models are listed in Table 1, with details on their derivation explained in a previous study [45]. The material is treated as transversely isotropic, assuming MFA = 0°. Flax fibers have a hierarchical structure with cellulose microfibrils aligned along the fiber axis, embedded in a hemicellulose–lignin matrix. This results in high stiffness longitudinally and near-isotropic behavior transversely due to the more random microstructure [45]. Based on this, a transversely isotropic material model was used in the finite element simulations to capture the directional elastic response efficiently. While this simplifies local heterogeneities, it is appropriate for the study’s focus on global elastic behavior. Future work will address microstructural variability and nonlinear effects.

Table 1.
Global properties of flax fibers [45].
The lower fiber surface was clamped (displacement set to 0 in all directions), while the top surface was subjected to a displacement “d” in the z-direction according to Equations (2) and (3). Displacement values of 1.6 µm, 3 µm, and 6 µm were applied for elementary fibers, bundles, and yarns, corresponding to 1% strain over the length L. The average stress (σ) and strain (ε%) were determined using Equations (4) and (5), where FZ represents the total nodal reaction force, S is the filled fiber surface, and L is the length of the fiber. The resultant stress was computed as the average of reaction forces at the top and bottom surface of the fiber (Equation (4)). The heterogeneity in the displacement and stress distribution were calculated using Equations (6) and (7).
3. Results and Discussion
3.1. Microscale Elementary Fibers
Figure 2a presents the calculated overall elastic modulus from the numerical models, while Figure 2b highlights the relationship between porosity and elastic modulus in modern and aged elementary fibers. The results demonstrate a strong linear correlation between porosity and elastic modulus for modern fibers, indicating that as porosity increases, the stiffness of these fibers decreases predictably (Equation (8)). Similar observations can be found in the literature [45]. Aged fibers show an almost linear trend with a slightly lower correlation (R2 = 0.81 for aged fibers and R2 = 0.99 for modern fibers), suggesting that the relationship between porosity and elastic modulus is less consistent in aged fibers (Equation (9)), which may be due to a long-term alteration in structure creating random damages in the internal structure as well as in the surface. Both geometrical fibers (GF) and porosity-filled modern fibers (MFF) exhibit a similar elastic modulus, around 65 GPa, indicating that modern fibers, despite having porosity, maintain comparable stiffness to non-porous geometrical fibers. However, aged porosity-filled fibers (AFF) show a reduced elastic modulus, likely due to age-related morphological changes, such as increased surface roughness and internal structural heterogeneity. These changes may arise from long-term environmental exposure as well as changes in bio-chemical composition. Specifically, a major deterioration of non-cellulosic cell wall polymers was observed which is clearly described in other studies [33,34], contributing to the weakening of the fiber’s mechanical properties. The obtained elastic modulus for fiber models is in the range of 38 to 50 GPa, which is in agreement with experimental results [45]. Additionally, the analysis indicates that modern elementary fibers display a higher elastic modulus compared to their ancient counterparts, further emphasizing the effect of aging and degradation on fiber integrity over time.
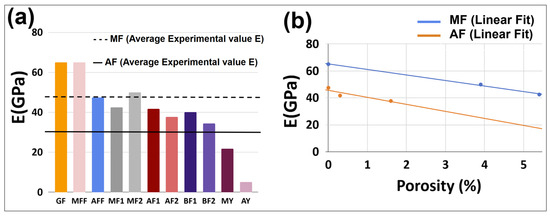
Figure 2.
(a) Elastic modulus (E) as a function of fibers. (b) Elastic modulus (E) as a function of porosity content for modern and aged elementary fibers.
Figure 3 shows the displacement plot in the z-direction and the axial stress distribution (σ33) for elementary fibers in the XZ plane. The z-direction displacement plot confirms the boundary conditions for tensile testing, where the bottom surface is fixed, and a maximum displacement of 1.6 µm for elementary fibers. The mean axial stress calculated for fiber models were in the range of 350 MPa to 500 MPa, which matches the average tensile strength of the experimental values [45]. The axial stress component shows homogenous stress distribution for geometrical fibers, and the stress heterogeneity in the surface of the fiber models can be observed; notably, higher stress concentration is observed in the surface, which may be due to surface roughness. Also, the higher stress can be observed in defective regions, which may be due to pores present at this region and also due to the deviations in the microfibril angle in this region. The homogenous distribution in the displacement plot can be observed in GF compared to the fiber models. In order to better understand the heterogeneity in the displacement and stress distribution on the surface of fiber models compared to the geometrical model, it is further quantified using Equations (5) and (6).
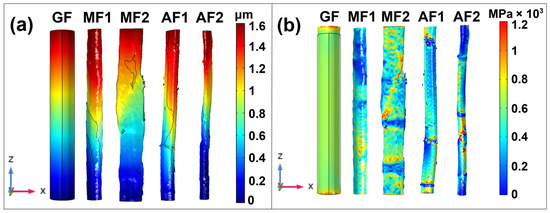
Figure 3.
(a) Displacement plot in z-direction. (b) Axial stress plot (σ33) in tensile direction.
Figure 4 provides the heterogeneity in the displacement and stress distribution between aged and modern elementary fibers. The displacement distribution analysis (Figure 4a) shows that MF2 exhibits greater heterogeneity than MF1, indicating a higher presence of defects in MF2. Interestingly, aged fibers display less heterogeneity compared to modern fibers. The stress distribution analysis (Figure 4b) further demonstrates that MF2 and AF2 have higher heterogeneity than MF1 and AF1, likely due to the increased number of defects. In particular, the outline of MF2 reveals lumens, defects, and voids concentrically aligned around the lumen at defect sites [46,47], with a wider fiber profile in these regions [48].
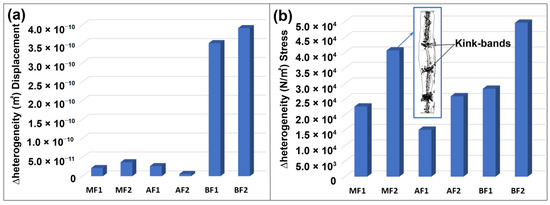
Figure 4.
Δheterogeneity as a function of modern and ancient elementary flax fibers and modern flax bundles: (a) strain; (b) stress.
The results obtained from REL are shown in Figure 5, which demonstrate that scattering in the elastic modulus is highly dependent on the segment length used in the finite element models. At the smallest length of 10 µm, the elastic modulus showed substantial variability, with different sub-models producing widely scattered results. This high level of scattering suggests that smaller-length segments do not capture the complete microstructure of the fiber, thus reflecting only localized mechanical behavior rather than the overall fiber properties. The variation in microstructure, such as porosity and surface defect, contributes to this scattering at smaller lengths. As the segment length increased to 20 µm, the degree of scattering decreased slightly, indicating that longer segments begin to encompass a more representative portion of the fiber’s microstructure. However, it was not until the segment length reached 30 µm and 40 µm that the elastic modulus started to stabilize, with much less scatter observed between the sub-models. At a length of 50 µm, the scattering was minimal, and the average elastic modulus closely matched that of the original full-scale 160 µm model, suggesting that the 50 µm segment length is an appropriate REL for both modern and aged flax fibers. This behavior was consistent across both modern and aged fibers. However, within the modern fibers, sample MF2 showed higher scattering at smaller lengths compared to MF1, likely due to the presence of more significant defects in MF2. Similarly, among the aged fibers, AF2 exhibited greater scattering than AF1, suggesting a higher degree of microstructural heterogeneity in AF2. The greater scattering in smaller segments may result from defects, where the length of kink-bands can range from 15 µm to 20 µm, leading to higher variability in shorter segments, such as 10 µm and 20 µm. Defected segments tend to display significantly lower modulus, while non-defected segments exhibit higher modulus. Additionally, it was observed that smaller-length models tended to exhibit higher stiffness, which decreased as the segment length increased, which is due to a higher presence of kink-bands (KB), and porosity increases the likelihood of early breakage, as the inter-KB length often falls below the critical length, a key parameter in composite design. In shorter segments, this effect is more pronounced, where defected regions exhibit lower modulus, while non-defected segments maintain higher stiffness, further emphasizing the impact of microstructural. This effect was particularly evident in MF1 and AF1. Overall, the REL of 50 µm was found to provide an accurate representation of the mechanical behavior of both modern and aged flax fibers, capturing the overall stiffness while minimizing scattering due to localized microstructural variations. While the 50 µm REL effectively stabilizes modulus variability in flax fibers, its applicability to other plant fibers (e.g., hemp, jute) may differ due to variations in microfibril orientation, defect distribution, and overall structural heterogeneity. Nevertheless, the same methodology can be applied to determine REL values for these materials individually.

Figure 5.
SEM elastic modulus (E) as a function of REL models for (a) modern fibers and (b) aged fibers.
To better understand the variability in stress, the maximum axial stress was calculated for both modern and aged fibers along their transverse cross-sections every 20 µm along the fiber length, as shown in Figure 6. The results indicate that the tensile direction (σ33) shows higher stress compared to other axial components (σ22 and σ11), with stress values reaching approximately 1700 MPa for modern fibers and aged fibers at specific locations, which matches with the experimental tensile strength [43]. These values highlight the critical role of stress concentration induced by defects, pores, and lumens [42,49]. This is further illustrated in the transverse cross-sections of fibers at higher-stress locations (Figure 6), where MF2 shows stress concentration around pores in kink-band areas, and similar behavior is observed in aged fibers, with higher stress around pores and lumens. These findings suggest that defects and lumens can act as initiation points for failure, with pores in defect areas potentially triggering fiber rupture. This type of behavior was observed for flax bundles and hemp fibers in the literature [42,45,49].
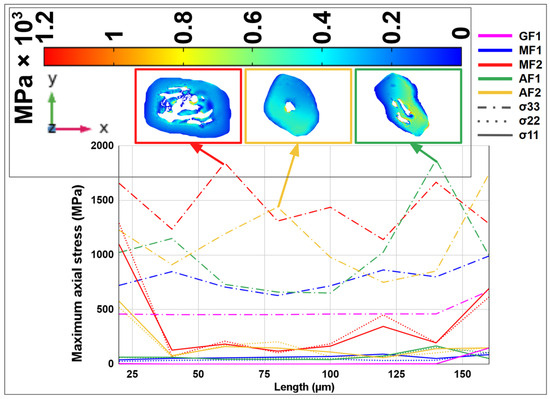
Figure 6.
Maximum axial stress (σ33, σ22, and σ11) as a function of length for elementary fibers.
3.2. Mesoscale Bundle Fibers
To understand the stress distribution, we observed the progression of stress in the fiber’s longitudinal cross-section. Bundles composed of three fibers exhibit a higher elastic modulus compared to larger bundles. This suggests that smaller bundles may maintain more mechanical integrity and stiffness, possibly due to reduced internal structural complexity and fewer inter-fiber defects or residues such as compound middle lamellae [20]. Larger bundles, on the other hand, likely introduce additional factors such as fiber misalignment, increased porosity between fibers, higher slippage, and more complex fiber interactions, which may reduce their overall stiffness. As observed in other research through experiments, flax fiber bundles in this study display a reduced elastic modulus compared to elementary fibers [50,51]. This reduction in stiffness could be due to the fiber–fiber interactions that introduce new sources of weakness, such as friction, slippage, and stress redistribution [51,52]. The displacement in the tensile z-direction is shown in Figure 7a, which corresponds to the applied boundary conditions in the simulation. With the bottom of the bundle clamped and a maximum displacement of 3 µm applied to the top, this result validates the model setup and the loading conditions. Axial stress distribution is shown in Figure 7b, exhibiting heterogenous stress distribution. The transverse displacements (in the x and y directions), seen in Figure 7c,d, show a shrinkage effect caused by the elongation in the axial direction (z). This shrinkage, however, is not uniform across all fibers. It can be attributed to the natural variation in fiber morphology, including differences in cross-sectional shape, porosity, and surface defects along the length of the fibers [3,53]. These factors create localized stress and strain differences, causing non-homogeneous deformation within the bundle.
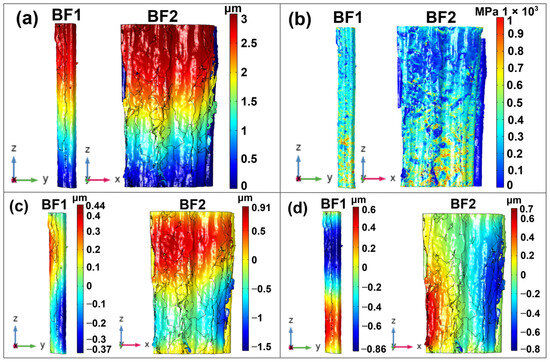
Figure 7.
(a) Displacement plot in z-direction. (b) Axial stress plot (σ33) in tensile direction (c) Displacement plot in y-direction. (d) Displacement in x-direction.
Stress (σ33) and strain distribution along the tensile direction further highlight the heterogeneity in the surface of the fiber bundles. To quantify this heterogeneity, an analysis was performed. Figure 4 shows that larger bundles containing more elementary fibers (BF2) exhibit higher heterogeneity compared to the smaller bundles with three fibers (BF1) due to themore complex internal structure in larger bundles. The fact that BF1 and BF2 are presented in the YZ and XZ planes, respectively, enhances the visual understanding of this heterogeneity. The mean axial stress values in the simulation range from 300 to 400 MPa, which is close to the experimental tensile strengths of flax fiber bundles reported in the literature. To better understand the stress distribution, an examination of the longitudinal cross-sections (Figure 8 and Figure 9) was conducted, revealing higher stress concentrations at areas of porosity and near the fiber surface. These high-stress regions are particularly prominent in BF2, and the porosity between fibers is more significant in BF2, likely due to the removal of the middle lamella during the extraction process [54]. The lumen in the elementary fibers in bundles and the surface roughness weakens the mechanical integrity of the bundle by acting as stress concentrators, contributing to localized failure [42,49,55]. Higher stress was observed in the axial components (σ33, σ22, σ11) than in the shear components (σ12, σ13, σ23). However, both exhibited heterogeneity in stress distribution along the longitudinal cross-section of the fiber, which can be seen in Figure 8 and Figure 9.
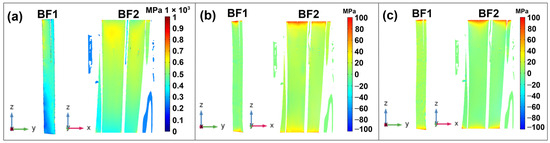
Figure 8.
Distribution of axial stress on longitudinal cross-section of fiber bundle in the YZ and XZ planes: (a) σ33; (b) σ22; (c) σ11.
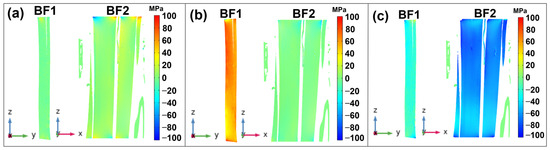
Figure 9.
Distribution of axial stress on longitudinal cross-section of fiber bundle in the YZ and XZ planes: (a) σ12; (b) σ13; (c) σ23.
To gain further insight into stress variability, the maximum axial and shear stress for fiber bundles was measured along their transverse cross-sections at 20 µm intervals along the fiber length, as shown in Figure 10. The maximum axial stress values in the tensile direction reach around 2200 MPa at specific points, which is approximately three times higher than the average tensile strength of flax fiber bundles reported in the literature. This sharp increase in stress is likely due to the influence of surface defects and lumen in elementary fiber, which are shown in the transverse cross-sections of both BF1 and BF2. Although the simulation model does not yet account for damage criteria or fiber–fiber bonding, such as the characteristics of the middle lamella, which will be incorporated in future studies to better align with experimental results, it emphasizes the significant influence of surface imperfections and porosity on stress concentration. The maximum stress points were observed on the surfaces of the bundles, suggesting a potential initiation of rupture due to surface irregularities and roughness. The stress distribution also shows that the axial stress components (σ33, σ22, σ11) are significantly higher than the shear components (σ12, σ13, σ23). This suggests that the primary mode of stress within the fiber bundles is tensile rather than shear, as expected in a tensile test scenario. However, within the shear stress components, σ13 and σ23 (related to shear along the fiber’s length in tensile direction) exhibit higher values compared to σ12, indicating that shear stresses along certain planes are more pronounced.
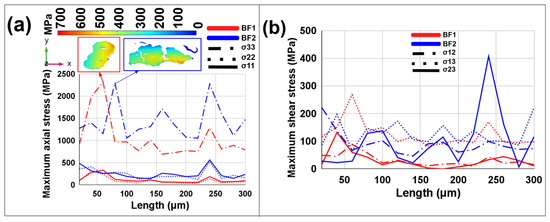
Figure 10.
(a) Maximum axial stress (σ33, σ22, σ11) as a function of length for bundle fibers. (b) Maximum shear stress (σ12, σ13, σ23) as a function of length for bundle fibers.
3.3. Macroscale Yarns
The obtained elastic moduli from the numerical models of modern and aged yarns are approximately 20 GPa and 5 GPa, respectively, which are lower than the moduli of individual elementary fibers and fiber bundles [50,51]. This discrepancy can be attributed to the complex structure of yarns, which includes factors such as inter-yarn porosity and the twisting of the yarns [11,22,56]. At the yarn scale, modern yarns exhibit a higher modulus than aged yarns, likely due to the degradation of fibers in the ancient yarns over time [33]. This mechanical behavior can be further understood through the stress distribution analysis discussed below.
Figure 11a shows the displacement in the z-direction for both modern and aged yarns, while Figure 11b illustrates the axial stress distribution (σ33). Similar to the behavior observed in elementary fibers and fiber bundles, the displacement in the z-direction aligns with the boundary conditions applied in the simulation and heterogeneity in displacement can be seen in both yarns reflecting the impact of morphological variations and aging [34]. The axial stress distribution plot reveals stress heterogeneity, particularly at the surface of the yarns, with higher concentrations in the internal structure. A more detailed analysis of the longitudinal and transverse cross-sections of the yarns was conducted to understand the stress distribution within the internal structure. The strain plot in the transverse directions (x and y), as shown in Figure 12, reveals some shrinkage behavior due to elongation in the axial z-direction. This lateral shrinkage is non-uniform for both modern and aged yarns, with aged yarns displaying higher shrinkage in the y-direction compared to modern yarns.
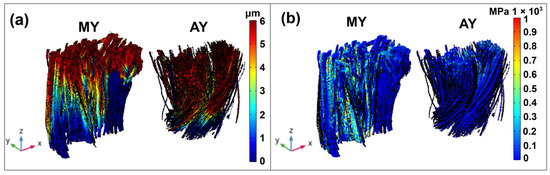
Figure 11.
(a) Displacement plot in the z-direction. (b) Axial stress plot (σ33) in the tensile direction for modern and aged yarns.
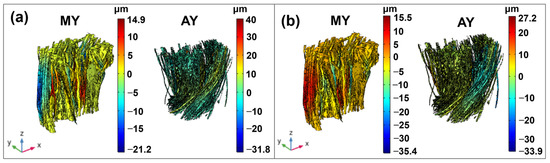
Figure 12.
Displacement plot for modern and aged yarns: (a) y-direction; (b) x-direction.
The mean axial strengths obtained are 140 MPa for modern yarns and 53 MPa for aged yarns, which are lower than the experimental values in the literature [57,58]. This discrepancy can be attributed to the assumptions of linear elasticity and the exclusion of frictional properties in the model, which will be addressed in future studies. Despite these limitations, the current model provides valuable insights into the stress distribution in both modern and aged yarns. Notably, aged yarns exhibit the structure of ply yarns, while modern yarns appear to be single yarns. In addition, a higher degree of fiber individualization is observed in aged yarns, likely due to long-term evolution and degradation over time [31,34]. The axial stress distribution (σ33) in the longitudinal cross-section of the yarns, presented in Figure 13, reaches up to 500 MPa, showing heterogeneous stress distribution within both the fibers and bundles. In Figure 13a, the stress in modern yarn appears to be concentrated near the surface, while in aged yarn, it is more fragmented and lower in intensity, likely due to increased defects and material degradation. In Figure 13b, modern yarn exhibits localized high-stress regions, particularly around fiber–fiber interfaces and voids, whereas aged yarn shows a more dispersed and lower-intensity stress distribution, indicating a weakened load-bearing capacity. There is also clear evidence of higher discontinuities in aged yarns compared to modern yarns, further indicating the degradation of fibers within the internal structure of aged yarns. The degradation patterns observed in ancient fibers (e.g., porosity increase, interfacial debonding) align qualitatively with those reported for modern flax fibers aged for short-term (1–10 years) under environmental stress. For example, flax/bio-epoxy composites exposed to 75% relative humidity for 24 months exhibited a 30% reduction in tensile strength, attributed to microfibril disorientation and middle lamella hydrolysis [37], mirroring the mechanisms observed here in ancient fibers but at an accelerated scale. Similarly, UV-exposed sisal fibers [29] showed lumen collapse and surface cracking within 5 years, paralleling our findings in archaeological flax. These comparisons suggest that the key aging mechanisms (e.g., polysaccharide depolymerization, defect propagation) are consistent across timescales, though their kinetics depend on environmental conditions. This underscores the importance of defect mitigation (e.g., coatings, hybridization) in extending the service life of modern flax composites.
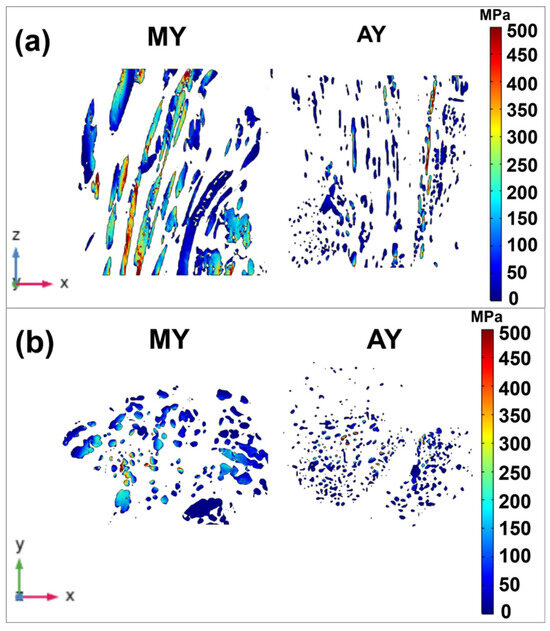
Figure 13.
Distribution of axial stress (σ33) on (a) a longitudinal cross-section of yarns in the XZ plane and (b) a transverse cross-section of yarns in the XY plane.
The contribution of fibers under tensile loading is non-uniform in both modern and aged yarns. In both cases, higher stress concentrations are observed in individual fibers within the yarns, particularly at the fiber surfaces and at pores within the fibers. This highlights the influence of microstructural features present at the microscale (elementary fibers) on the macroscale (yarns) [11]. Similar to the strain components (ε22 and ε11), the axial stress components (σ22, σ11) and shear stress components (σ12, σ13, σ23) fluctuate between negative and positive values, confirming shrinkage behavior in the fibers. This shrinkage is non-homogeneous in both yarns and can be attributed to the combined effects of tensile loading and shearing forces. The shearing is likely a result of cross-sectional variations along the yarn lengths and misalignment of fibers with respect to the tensile direction [13].
The transverse cross-section of aged yarns clearly shows two distinct yarns, resembling two bunches of fibers, which is not as evident in the longitudinal cross-section. This difference may be due to the uncoiling of fibers over time, which makes the yarns appear less twisted and more like single yarns in the longitudinal view. The stress distribution in the longitudinal cross-section reveals that the highest stresses occur in the tensile direction (σ33, σ13, and σ23) compared to other components (σ22, σ11, and σ12), which is shown in Figure 14. This is further quantified by calculating the maximum axial and shear stress in the transverse cross-sections of the yarns every 30 µm along their length, as displayed in Figure 15. The transverse stress plots confirm higher stress concentrations in the tensile direction compared to other stress components. Although the maximum axial stress (σ33) shows unrealistically high values (around 3500 MPa) at specific locations for both modern and aged yarns, likely due to the assumption of linear elastic models, the simulation effectively captures the stress concentration induced by microstructural features at the microscale. This influence is critical for understanding the failure behavior of yarns at the macroscale. The maximum stress in transverse cross-section shown in Figure 15 highlights the peaks at the 90 µm mark in the axial stress field (σ33). The maximum stress values are observed at the surface of elementary fibers where they connect with other fibers in the bundle, specifically at points of fiber–fiber cohesion. Additionally, higher stress concentrations are found at pores within both the elementary and bundled fibers, suggesting that these microstructural defects have the potential to initiate cracks, leading to fiber breakage and eventual yarn failure.
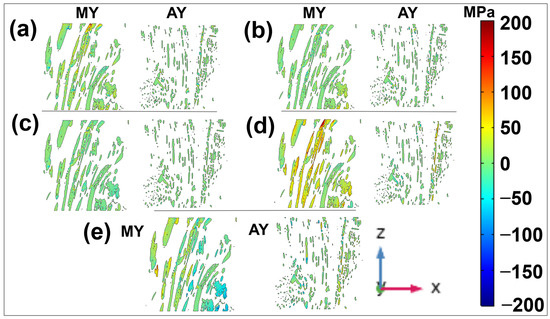
Figure 14.
(a,b) Distribution of axial stress on longitudinal cross-section of yarns in the XZ plane: σ22 and σ11. (c–e) Distribution of shear stress on longitudinal cross-section of yarns in the XZ plane: σ12, σ13, and σ23.
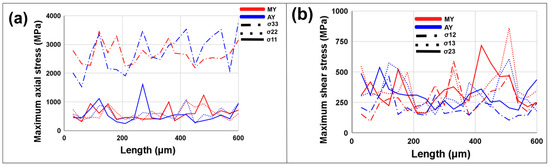
Figure 15.
(a) Maximum axial stress (σ33, σ22, σ11) as a function of length for yarns. (b) Maximum shear stress (σ12, σ13, σ23) as a function of length for yarns.
4. Conclusions
The effects of flax’s complex morphology and aging on its tensile properties were analyzed through a finite element model in the elastic domain using tomography volumes across multiple scales.
The key findings are as follows:
- The modulus decreases from elementary fibers to bundles and, further, to yarns due to increasing structural complexity, with larger bundles experiencing more slippage and defects, while smaller bundles retain better stiffness. Yarns exhibit the lowest modulus due to additional factors like twisting and interfacial behavior.
- High-stress regions were observed near defects, fiber–fiber interfaces, pores, and surface irregularities, with rupture initiation most likely occurring at kink-bands, bundle surfaces, and yarns due to high stress concentration at these points.
- From the REL approach, it can be observed that the elastic modulus varies significantly below 30 μm due to structural heterogeneity, particularly the microstructural defects, but stabilizes at ~50 μm, making it suitable for accurate mechanical characterization.
- Aging leads to increased porosity and surface roughness, weakening fiber integrity. Also, these fibers exhibit increased fiber discontinuities due to long-term degradation.
- Larger fiber bundles exhibit higher stress heterogeneity, likely due to its complex structural composition, increased porosity, and fiber misalignment.
- There is lower mechanical strength in aged yarns (~5 GPa vs. ~20 GPa for modern yarns). Higher stress concentrations in ancient fibers suggest increased rupture probability in these fibers.
- Effect of shearing: Shear stresses (σ12, σ13, σ23) fluctuate, contributing to fiber shrinkage. At larger fiber scales, such as the yarn scale, increased shear stress makes rupture more likely to occur perpendicularly to the loading direction.
- Aged yarns show higher shrinkage behavior, with more pronounced stress concentrations at fiber junctions.
This study aids the textile industry in designing durable flax composites and supports archaeologists in conserving ancient textiles by quantifying aging effects. In summary, this study highlights the importance of considering multiple scales and stress heterogeneity in optimizing flax fiber composites, ensuring improved mechanical performance and durability by addressing the effects of aging and microstructural defects.
To translate these findings into industrial practice, future research should systematically assess flax fibers aged between 10 and 50 years under controlled environmental conditions (e.g., temperature, humidity, and UV exposure). This would help quantify the acceleration factors comparing natural aging (as seen in archaeological samples) with real-world service conditions, facilitating the development of predictive models for composite durability. Further work should also integrate damage criteria into the model to improve accuracy, moving beyond the current linear elasticity assumption. Additionally, investigating the frictional properties of yarns and fiber bundles would provide deeper insights into interfacial interactions, further refining the model’s predictive performance.
Author Contributions
Conceptualization, V.R., S.G., J.B. and A.B.; methodology, A.M., V.R., M.S., J.P., H.P. and T.W.; software, S.G. and V.R.; validation, S.G., V.R., J.B. and A.B.; formal analysis, S.G., J.B. and V.R.; investigation, V.R. and S.G; resources, A.B.; data curation, S.G. and V.R; writing—original draft preparation, V.R.; writing—review and editing, S.G., V.R., J.B., T.W., A.M., M.S., J.P., H.P. and A.B.; supervision, S.G., J.B. and A.B.; project administration, A.B.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the French National Research Agency (ANR) through the Anubis project ANR-21-CE43-0010. ANATOMIX is an Equipment of Excellence (EQUIPEX) funded by the Investments for the Future program of the French National Research Agency (ANR), project NanoimagesX, grant no. ANR-11-EQPX-0031. Access to Anatomix was provided through SOLEIL beamtime proposal #20221519.
Data Availability Statement
Data supporting the findings of this study can be made available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Koronis, G.; Silva, A.; Fontul, M. Green composites: A review of adequate materials for automotive applications. Compos. Part B Eng. 2013, 44, 120–127. [Google Scholar] [CrossRef]
- Dittenber, D.B.; GangaRao, H.V. Critical review of recent publications on use of natural composites in infrastructure. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1419–1429. [Google Scholar] [CrossRef]
- Bourmaud, A.; Beaugrand, J.; Shah, D.U.; Placet, V.; Baley, C. Towards the design of high-performance plant fibre composites. Prog. Mater. Sci. 2018, 97, 347–408. [Google Scholar] [CrossRef]
- Yan, L.; Chouw, N.; Jayaraman, K. Lateral crushing of empty and polyurethane-foam filled natural flax fabric reinforced epoxy composite tubes. Compos. Part B Eng. 2014, 63, 15–26. [Google Scholar] [CrossRef]
- Richely, E.; Bourmaud, A.; Placet, V.; Guessasma, S.; Beaugrand, J. A critical review of the ultrastructure, mechanics and modelling of flax fibres and their defects. Prog. Mater. Sci. 2022, 124, 100851. [Google Scholar] [CrossRef]
- Guillou, E.; King, A.; Perrin, J.; Proudhon, H.; Weitkamp, T.; Shah, D.U.; Beigbeder, A.; Ouagne, P.; Bourmaud, A. Impact of flax fibre micro-structural features on composite damage observed through micro-CT characterisation. Compos. Part A Appl. Sci. Manuf. 2024, 181, 108118. [Google Scholar] [CrossRef]
- Madsen, B.; Hoffmeyer, P.; Lilholt, H. Hemp yarn reinforced composites–II. Tensile properties. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2204–2215. [Google Scholar] [CrossRef]
- Yan, L.; Su, S.; Chouw, N. Microstructure, flexural properties and durability of coir fibre reinforced concrete beams externally strengthened with flax FRP composites. Compos. Part B Eng. 2015, 80, 343–354. [Google Scholar] [CrossRef]
- Ku, H.; Wang, H.; Pattarachaiyakoop, N.; Trada, M. A review on the tensile properties of natural fiber reinforced polymer composites. Compos. Part B Eng. 2011, 42, 856–873. [Google Scholar] [CrossRef]
- Cevallos, O.; Olivito, R.S.; Codispoti, R.; Ombres, L. Flax and polyparaphenylene benzobisoxazole cementitious composites for the strengthening of masonry elements subjected to eccentric loading. Compos. Part B Eng. 2015, 71, 82–95. [Google Scholar] [CrossRef]
- Angelova, R.A. Failure of yarns in different textile applications. In Handbook of Materials Failure Analysis; Makhlouf, A.S.H., Aliofkhazraei, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 277–301. [Google Scholar]
- Hautala, M.; Pasila, A.; Pirilä, J. Use of hemp and flax in composite manufacture: A search for new production methods. Compos. Part A Appl. Sci. Manuf. 2004, 35, 11–16. [Google Scholar] [CrossRef]
- Aldroubi, S.; Kasal, B.; Yan, L.; Bachtiar, E.V. Multi-scale investigation of morphological, physical and tensile properties of flax single fiber, yarn and unidirectional fabric. Compos. Part B Eng. 2023, 259, 110732. [Google Scholar] [CrossRef]
- Abbey, B.; Eve, S.; Thuault, A.; Charlet, K.; Korsunsky, A. Synchrotron X-ray tomographic investigation of internal structure of individual flax fibres. In Proceedings of the 6th World Congress of Biomechanics (WCB 2010), Singapore, 1–6 August 2010. [Google Scholar]
- Chakrabarti, B.; Nodder, C. Some Effects of the Helical Fibrillar Structure of Vegetable Fibres. Nature 1949, 163, 19–20. [Google Scholar] [CrossRef]
- Guessasma, S.; Beaugrand, J. Damage kinetics at the sub-micrometric scale in bast fibers using finite element simulation and high-resolution X-Ray micro-tomography. Front. Plant Sci. 2019, 10, 194. [Google Scholar] [CrossRef] [PubMed]
- Ekaputri, T.S.; Tanaka, T. Quantitative analysis of commercial coating penetration into Fagus crenata wood using X-ray microtomography. Sci. Rep. 2024, 14, 13925. [Google Scholar] [CrossRef] [PubMed]
- Charlet, K.; Jernot, J.; Eve, S.; Gomina, M.; Bréard, J. Multi-scale morphological characterisation of flax: From the stem to the fibrils. Carbohydr. Polym. 2010, 82, 54–61. [Google Scholar] [CrossRef]
- Melelli, A.; Jamme, F.; Legland, D.; Beaugrand, J.; Bourmaud, A. Microfibril angle of elementary flax fibres investigated with polarised second harmonic generation microscopy. Ind. Crops Prod. 2020, 156, 112847. [Google Scholar] [CrossRef]
- Melelli, A.; Arnould, O.; Beaugrand, J.; Bourmaud, A. The middle lamella of plant fibers used as composite reinforcement: Investigation by atomic force microscopy. Molecules 2020, 25, 632. [Google Scholar] [CrossRef]
- Rask, M.; Madsen, B. Twisting of fibres in yarns for natural fibre composites. In Proceedings of the 18th International Conference on Composite Materials, Jeju Island, Republic of Korea, 21–26 August 2011. [Google Scholar]
- Elmogahzy, Y. Structure and mechanics of yarns. In Structure and Mechanics of Textile fibre Assemblies; Schwartz, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–25. [Google Scholar]
- Richely, E.; Durand, S.; Melelli, A.; Kao, A.; Magueresse, A.; Dhakal, H.; Gorshkova, T.; Callebert, F.; Bourmaud, A.; Beaugrand, J. Novel insight into the intricate shape of flax fibre lumen. Fibers 2021, 9, 24. [Google Scholar] [CrossRef]
- Baley, C.; Goudenhooft, C.; Perré, P.; Lu, P.; Pierre, F.; Bourmaud, A. Compressive strength of flax fibre bundles within the stem and comparison with unidirectional flax/epoxy composites. Ind. Crops Prod. 2019, 130, 25–33. [Google Scholar] [CrossRef]
- Haag, K.; Müssig, J. Scatter in tensile properties of flax fibre bundles: Influence of determination and calculation of the cross-sectional area. J. Mater. Sci. 2016, 51, 7907–7917. [Google Scholar] [CrossRef]
- Turan, R.B.; Okur, A.; Deveci, R.; Açikel, M. Predicting the intra-yarn porosity by image analysis method. Text. Res. J. 2012, 82, 1720–1728. [Google Scholar] [CrossRef]
- Havlová, M.; Špánková, J. Porosity of knitted fabrics in the aspect of air permeability-discussion of selected assumptions. Fibres Text. East. Eur. 2017, 25, 86–91. [Google Scholar] [CrossRef]
- Tumajer, P.; Ursíny, P.; Bílek, M.; Mouckova, E.; Pokorna, M. Influence of structure of the yarn on mechanical characteristics of yarns exposed to dynamic stress. Autex Res. J. 2012, 12, 44–49. [Google Scholar] [CrossRef]
- Zuccarello, B.; Militello, C.; Bongiorno, F. Environmental aging effects on high-performance biocomposites reinforced by sisal fibers. Polym. Degrad. Stab. 2023, 211, 110319. [Google Scholar] [CrossRef]
- Morgillo, L.; Melelli, A.; Scheel, M.; Wightman, R.; Weitkamp, T.; Goudenhooft, C.; Quiles, A.; Shah, D.U.; Abida, M.; Beaugrand, J. Inside the kink-bands of archaeological flax artefacts via sub-micrometer resolution micro-CT: A comprehensive microstructural analysis to better understand degradation mechanisms of fibres. Compos. Part B Eng. 2025, 298, 112347. [Google Scholar] [CrossRef]
- Melelli, A.; Shah, D.U.; Hapsari, G.; Cortopassi, R.; Durand, S.; Arnould, O.; Placet, V.; Benazeth, D.; Beaugrand, J.; Jamme, F. Lessons on textile history and fibre durability from a 4000-year-old Egyptian flax yarn. Nat. Plants 2021, 7, 1200–1206. [Google Scholar] [CrossRef] [PubMed]
- Gleba, M.; Boudin, M.; Di Pietro, G.A. Textiles from Zawaydah, Naqada, Upper Egypt. Archaeol. Text. Rev. 2019, 61, 14–23. [Google Scholar]
- Melelli, A.; Goudenhooft, C.; Durand, S.; Quiles, A.; Cortopassi, R.; Morgillo, L.; Magueresse, A.; Beaugrand, J.; Jamme, F.; Bourmaud, A. Revealing degradation mechanisms of archaeological flax textiles through the evolution of fibres’ parietal polymers by synchrotron deep-UV fluorescence. Polym. Degrad. Stab. 2024, 226, 110826. [Google Scholar] [CrossRef]
- Goudenhooft, C.; Melelli, A.; Durand, S.; Falourd, X.; Le-Bot, L.; Morgillo, L.; Gaballah, S.; Cortopassi, R.; Quiles, A.; Shah, D.U. Comparison of kink-band structures and specificities of cell wall polysaccharides in modern and ancient flax fibres. Carbohydr. Polym. 2024, 344, 122526. [Google Scholar] [CrossRef]
- Gleba, M.; Harris, S. The first plant bast fibre technology: Identifying splicing in archaeological textiles. Archaeol. Anthropol. Sci. 2019, 11, 2329–2346. [Google Scholar] [CrossRef]
- Hao, M.; Tang, M.; Wang, W.; Tian, M.; Zhang, L.; Lu, Y. Silver-nanoparticle-decorated multiwalled carbon nanotubes prepared by poly (dopamine) functionalization and ultraviolet irradiation. Compos. Part B Eng. 2016, 95, 395–403. [Google Scholar] [CrossRef]
- Moudood, A.; Rahman, A.; Khanlou, H.M.; Hall, W.; Öchsner, A.; Francucci, G. Environmental effects on the durability and the mechanical performance of flax fiber/bio-epoxy composites. Compos. Part B Eng. 2019, 171, 284–293. [Google Scholar] [CrossRef]
- Johnson, S.; Kang, L.; Akil, H.M. Mechanical behavior of jute hybrid bio-composites. Compos. Part B Eng. 2016, 91, 83–93. [Google Scholar] [CrossRef]
- Aslan, M.; Chinga-Carrasco, G.; Sørensen, B.F.; Madsen, B. Strength variability of single flax fibres. J. Mater. Sci. 2011, 46, 6344–6354. [Google Scholar] [CrossRef]
- Baley, C. Analysis of the flax fibres tensile behaviour and analysis of the tensile stiffness increase. Compos. Part A Appl. Sci. Manuf. 2002, 33, 939–948. [Google Scholar] [CrossRef]
- Baley, C.; Bourmaud, A. Average tensile properties of French elementary flax fibers. Mater. Lett. 2014, 122, 159–161. [Google Scholar] [CrossRef]
- Rajakumaran, V.; Melelli, A.; Quiles, A.; Weitkamp, T.; Perrin, J.; Proudhon, H.; Bourmaud, A.; Beaugrand, J.; Guessasma, S. Experimental and numerical approach to understand the role of defects in damage mechanisms of flax fibers at bundle scale. Ind. Crops Prod. 2024, 218, 119025. [Google Scholar] [CrossRef]
- Rajakumaran, V.; Guessasma, S.; D’Orlando, A.; Melelli, A.; Scheel, M.; Weitkamp, T.; Perrin, J.; Bourmaud, A.; Proudhon, H.; Beaugrand, J. Impact of Defects on Tensile Properties of Ancient and Modern Egyptian Flax Fibers: Multiscale X-Ray Microtomography and Numerical Modeling. Fibers 2024, 12, 111. [Google Scholar] [CrossRef]
- Pelerin, M.; King, A.; Laiarinandrasana, L.; Proudhon, H. Development of a versatile mechanical testing device for in situ synchrotron tomography and diffraction experiments. Integr. Mater. Manuf. Innov. 2019, 8, 378–387. [Google Scholar] [CrossRef]
- Richely, E.; Bourmaud, A.; Dhakal, H.; Zhang, Z.; Beaugrand, J.; Guessasma, S. Exploring the morphology of flax fibres by X-ray microtomography and the related mechanical response by numerical modelling. Compos. Part A Appl. Sci. Manuf. 2022, 160, 107052. [Google Scholar] [CrossRef]
- Quereilhac, D.; Pinsard, L.; Guillou, E.; Fazzini, M.; De Luycker, E.; Bourmaud, A.; Abida, M.; Perrin, J.; Weitkamp, T.; Ouagne, P. Exploiting synchrotron X-ray tomography for a novel insight into flax-fibre defects ultrastructure. Ind. Crops Prod. 2023, 198, 116655. [Google Scholar] [CrossRef]
- Morgillo, L.; Brionne, L.; Melelli, A.; Ouagne, P.; Scheel, M.; Weitkamp, T.; Shah, D.U.; Abida, M.; Beaugrand, J.; Bourmaud, A. Elucidating links between the mechanical performance of flax fibres and their structural defects. Ind. Crops Prod. 2023, 206, 117722. [Google Scholar] [CrossRef]
- Melelli, A.; Durand, S.; Arnould, O.; Richely, E.; Guessasma, S.; Jamme, F.; Beaugrand, J.; Bourmaud, A. Extensive investigation of the ultrastructure of kink-bands in flax fibres. Ind. Crops Prod. 2021, 164, 113368. [Google Scholar] [CrossRef]
- Beaugrand, J.; Guessasma, S.; Maigret, J. Damage mechanisms in defected natural fibers. Sci. Rep. 2017, 7, 14041. [Google Scholar] [CrossRef]
- Joffe, R.; Andersons, J.; Wallström, L. Strength and adhesion characteristics of elementary flax fibres with different surface treatments. Compos. Part A Appl. Sci. Manuf. 2003, 34, 603–612. [Google Scholar] [CrossRef]
- Charlet, K.; Beakou, A. Interfaces within flax fibre bundle: Experimental characterization and numerical modelling. J. Compos. Mater. 2014, 48, 3263–3269. [Google Scholar] [CrossRef]
- Ahmed, S.; Ulven, C.A. Dynamic in-situ observation on the failure mechanism of flax fiber through scanning electron microscopy. Fibers 2018, 6, 17. [Google Scholar] [CrossRef]
- Hänninen, T.; Thygesen, A.; Mehmood, S.; Madsen, B.; Hughes, M. Mechanical processing of bast fibres: The occurrence of damage and its effect on fibre structure. Ind. Crops Prod. 2012, 39, 7–11. [Google Scholar] [CrossRef]
- Gautreau, M.; Durand, S.; Paturel, A.; Le Gall, S.; Foucat, L.; Falourd, X.; Novales, B.; Ralet, M.-C.; Chevallier, S.; Kervoelen, A. Impact of cell wall non-cellulosic and cellulosic polymers on the mechanical properties of flax fibre bundles. Carbohydr. Polym. 2022, 291, 119599. [Google Scholar] [CrossRef]
- Beaugrand, J.; Guessasma, S. Scenarios of crack propagation in bast fibers: Combining experimental and finite element approaches. Compos. Struct. 2015, 133, 667–678. [Google Scholar] [CrossRef]
- Abida, M.; Baklouti, A.; Gehring, F.; Vivet, A.; Bouvet, C. Inverse approach for flax yarns mechanical properties identification from statistical mechanical characterization of the fabric. Mech. Mater. 2020, 151, 103638. [Google Scholar] [CrossRef]
- Codispoti, R.; Oliveira, D.V.; Olivito, R.S.; Lourenço, P.B.; Fangueiro, R. Mechanical performance of natural fiber-reinforced composites for the strengthening of masonry. Compos. Part B Eng. 2015, 77, 74–83. [Google Scholar] [CrossRef]
- Blanchard, J.; Sobey, A.; Blake, J. Multi-scale investigation into the mechanical behaviour of flax in yarn, cloth and laminate form. Compos. Part B Eng. 2016, 84, 228–235. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).