Influence of Geometric Non-Linearities on the Mixed-Mode Decomposition in Asymmetric DCB Samples
Abstract
1. Introduction
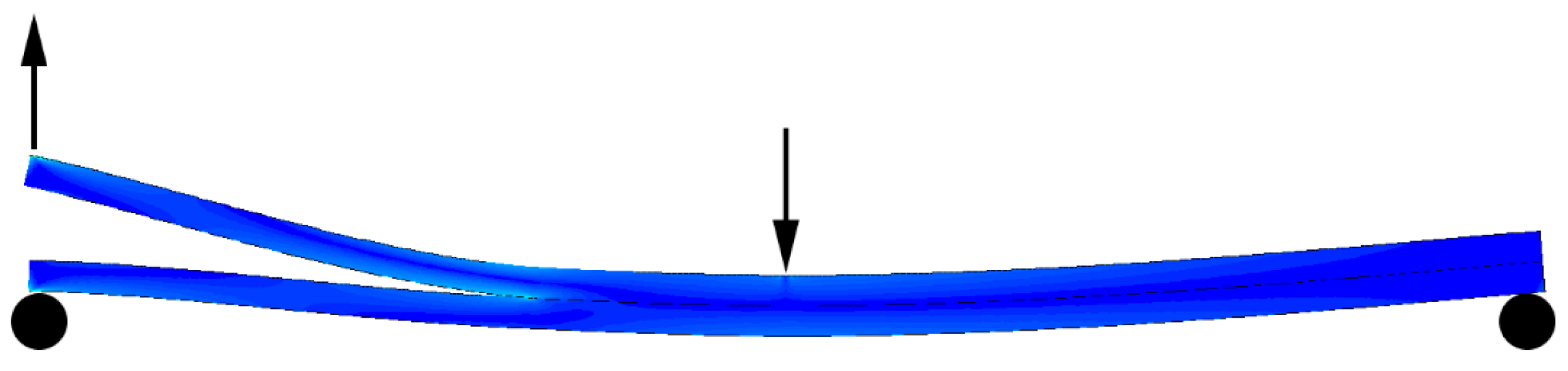
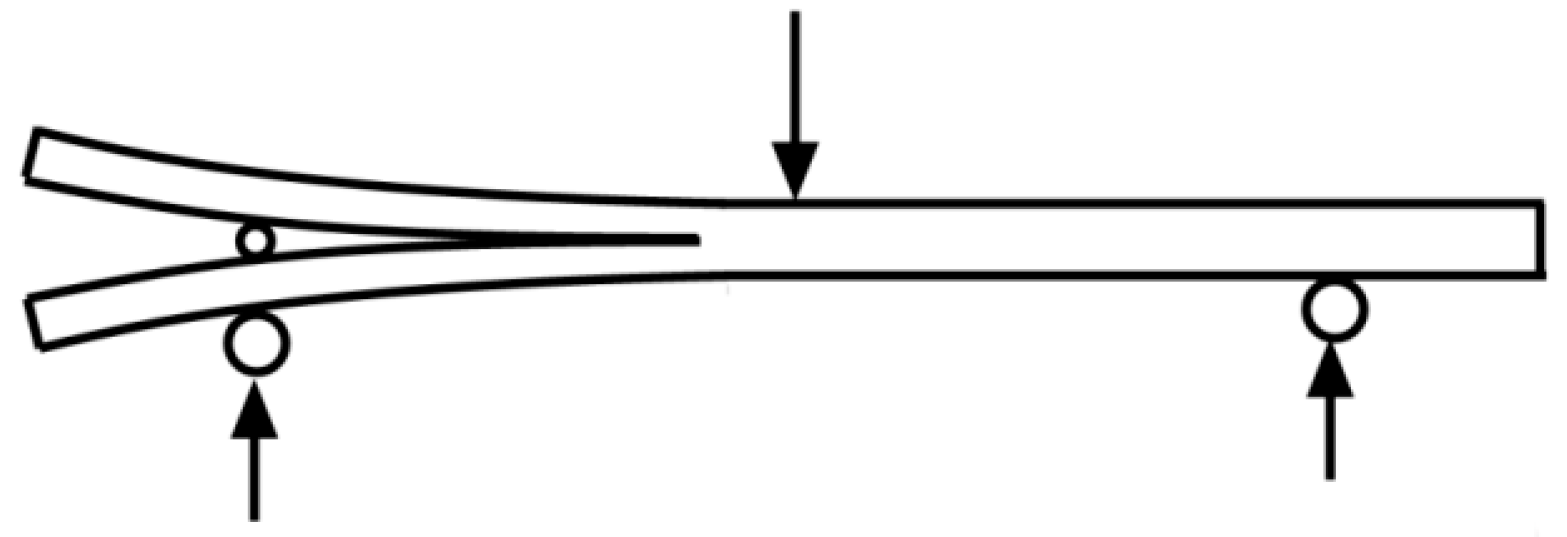
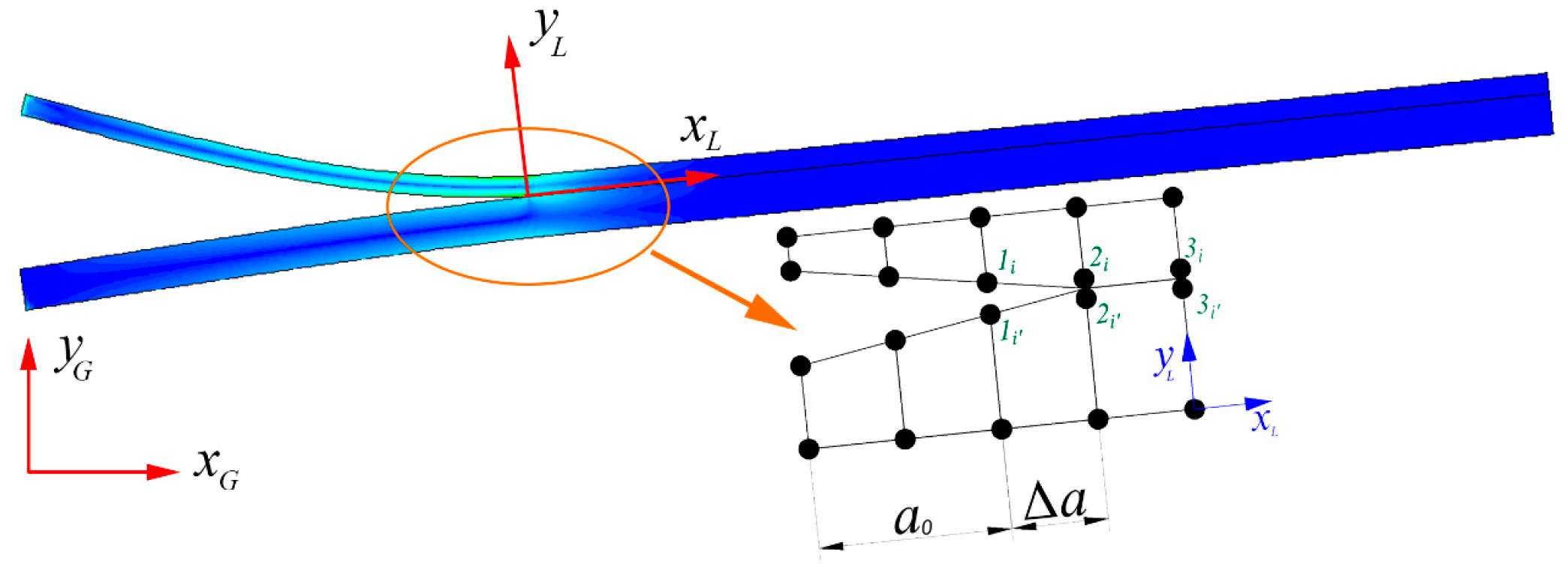
2. Materials and Methods
3. Model Calibration
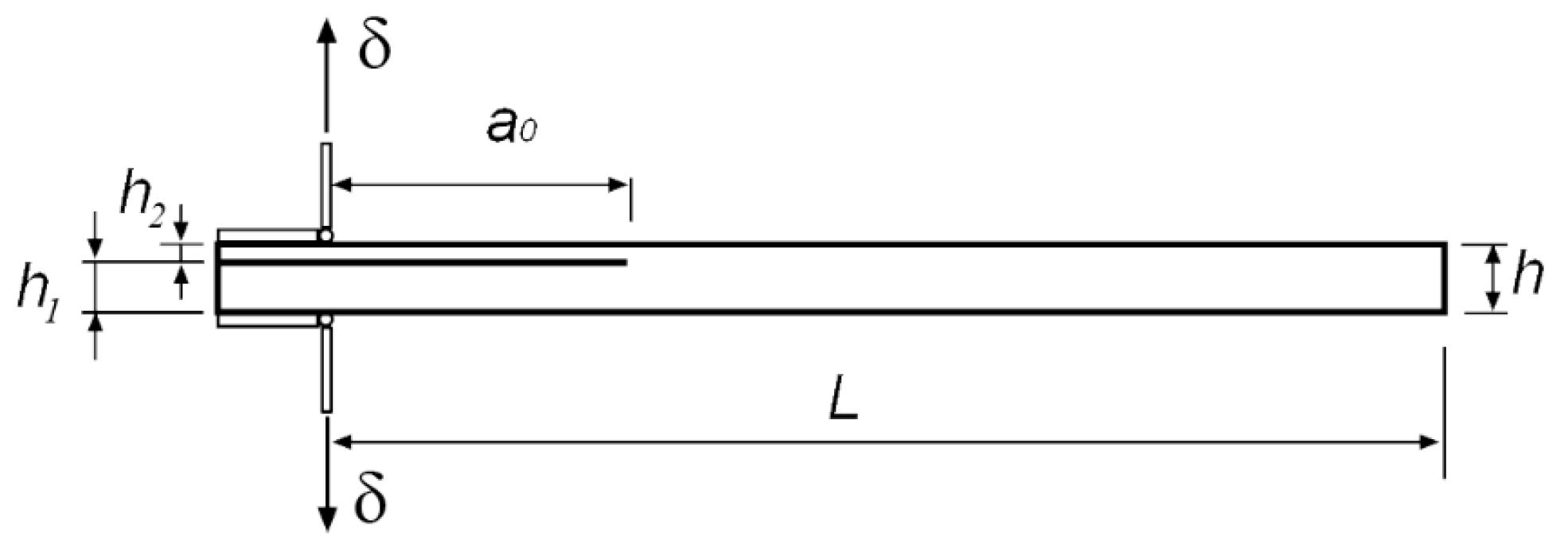
- L = 150 mm
- a0 = 50 mm
- h1 = 4.6 mm
- h2 = 1.4 mm
- uA = vA = 0
- uB =0, vB = δ
- P: applied load
- δ: applied displacement
- B: sample width
- a: crack length
- Δ: crack length correction
4. Influence of the Sample Rotation
4.1. Rotation Due to the Applied Displacement
4.2. Rotation Due to the Degree of Asymmetry
4.3. Crack Growth Calculations
- h1 = 5 mm
- h2 = 1 mm
- a0 = 50 mm
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Modelling |
| DCB | Double Cantilever Beam |
| ENF | End Notched Flexure |
| ADCB | Asymmetric Double Cantilever Beam |
| VCCT | Virtual Crack Closure Technique |
| TSEM | Two-Step Extension Method |
| GCS | Global Coordinate System |
| LCS | Local Coordinate System |
References
- ISO 15024; Fibre-Reinforced Plastic Composites-Determination of Mode I Interlaminar Fracture Toughness, GIC, for Unidirectionally Reinforced Materials. International Organization for Standardization: Geneva, Switzerland, 2023.
- ASTM D5528/D5528M-21; Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2021. [CrossRef]
- ASTM D7905/D7905M-19e1; Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2019. [CrossRef]
- ASTM D6671/D6671M–22; Standard Test Method for Mixed Mode I-Mode II Interlaminar Fracture Toughness of Unidirectional Fiber Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2022; pp. 1–15.
- Crews, J.H.; Reeder, J.R. A Mixed-Mode Bending Apparatus for Delamination Testing; NASA: Washington, DC, USA, 1988; NASA Technical Memorandum 100662.
- Ramírez, F.M.G.; de Moura, M.F.S.F.; Moreira, R.D.F.; Silva, F.G.A. Experimental and Numerical Mixed-Mode I + II Fracture Characterization of Carbon Fibre Reinforced Polymer Laminates Using a Novel Strategy. Compos. Struct. 2021, 263, 113683. [Google Scholar] [CrossRef]
- Szekrényes, A.; Uj, J. Comparison of Some Improved Solutions for Mixed-Mode Composite Delamination Coupons. Compos. Struct. 2006, 72, 321–329. [Google Scholar] [CrossRef]
- Szekrényes, A. Prestressed Fracture Specimen for Delamination Testing of Composites. Int. J. Fract. 2006, 139, 213–237. [Google Scholar] [CrossRef]
- Boyano, A.; Mollón, V.; Bonhomme, J.; De Gracia, J.; Arrese, A.; Mujika, F. Analytical and Numerical Approach of an End Notched Flexure Test Configuration with an Inserted Roller for Promoting Mixed Mode I/II. Eng. Fract. Mech. 2015, 143, 63–79. [Google Scholar] [CrossRef]
- Williams, M.L. The Stresses Around a Fault or Crack in Dissimilar Media; Seismological Society of America: Albany, CA, USA, 1959; Volume 49. [Google Scholar]
- Sundararaman, V.; Davidson, B.D. An Unsymmetric Double Cantilever Beam Test for Interfacial Fracture Toughness Determination. Int. J. Solids Struct. 1997, 34, 799–817. [Google Scholar] [CrossRef]
- Ducept, F.; Gamby, D.; Davies, P. A Mixed-Mode Failure Criterion Derived from Tests on Symmetric and Asymmetric Specimens. Compos. Sci. Technol. 1999, 59, 609–619. [Google Scholar] [CrossRef]
- Krueger, R. Virtual Crack Closure Technique: History, Approach, and Applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Girard, R.; Schaff, A. Numerical Analysis of Composite Systems by Using Interphase/Interface Models. Comput. Mech. 1997, 20, 3–11. [Google Scholar] [CrossRef]
- Chen, J.; Crisfield, M.; Kinloch, A.J.; Busso, E.P.; Matthews, F.L.; Qiu, Y. Predicting Progressive Delamination of Composite Material Specimens via Interface Elements. Mech. Compos. Mater. Struct. 1999, 6, 301–317. [Google Scholar] [CrossRef]
- Valvo, P.S. On the Calculation of Energy Release Rate and Mode Mixity in Delaminated Laminated Beams. Eng. Fract. Mech. 2016, 165, 114–139. [Google Scholar] [CrossRef]
- Williams, J.G. Observations on the Analysis of Mixed Mode Delamination in Composites. Procedia Eng. 2015, 114, 189–198. [Google Scholar] [CrossRef]
- Wang, S.; Harvey, C.M. Mixed Mode Partition Theories for One Dimensional Fracture. Eng. Fract. Mech. 2012, 79, 329–352. [Google Scholar] [CrossRef]
- VCCT-Based Crack Growth Simulation. ANSYS Release 2023R2. In Fracture Analysis Guide 3.5; ANSYS, Inc.: Canonsburg, PA, USA, 2023.
- Mollón, V.; Bonhomme, J.; Elmarakbi, A.M.; Argüelles, A.; Viña, J. Finite Element Modelling of Mode I Delamination Specimens by Means of Implicit and Explicit Solvers. Polym. Test. 2012, 31, 404–410. [Google Scholar] [CrossRef]
- Bonhomme, J.; Argüelles, A.; Viña, J.; Viña, I. Numerical and Experimental Validation of Computational Models for Mode I Composite Fracture Failure. Comput. Mater. Sci. 2009, 45, 993–998. [Google Scholar] [CrossRef]
- Bonhomme, J.; Mollón, V.; Viña, J.; Argüelles, A. Finite Element Analysis of the Longitudinal Half Fixed Beam Method for Mode III Characterization. Compos. Struct. 2020, 232, 111546. [Google Scholar] [CrossRef]
- Mollón, V.; Bonhomme, J.; Viña, J.; Argüelles, A. Mixed Mode Fracture Toughness: An Empirical Formulation for GI/GII Determination in Asymmetric DCB Specimens. Eng. Struct. 2010, 32, 3699–3703. [Google Scholar] [CrossRef]
- Wang, W.; Lopes Fernandes, R.; Teixeira De Freitas, S.; Zarouchas, D.; Benedictus, R. How Pure Mode I Can Be Obtained in Bi-Material Bonded DCB Joints: A Longitudinal Strain-Based Criterion. Compos. B Eng. 2018, 153, 137–148. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of Mixed-Mode Delamination Fracture Toughness of Unidirectional Glass/Epoxy Composites with Mixed-Mode Bending Apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Falcó, O.; Ávila, R.L.; Tijs, B.; Lopes, C.S. Modelling and Simulation Methodology for Unidirectional Composite Laminates in a Virtual Test Lab Framework. Compos. Struct. 2018, 190, 137–159. [Google Scholar] [CrossRef]
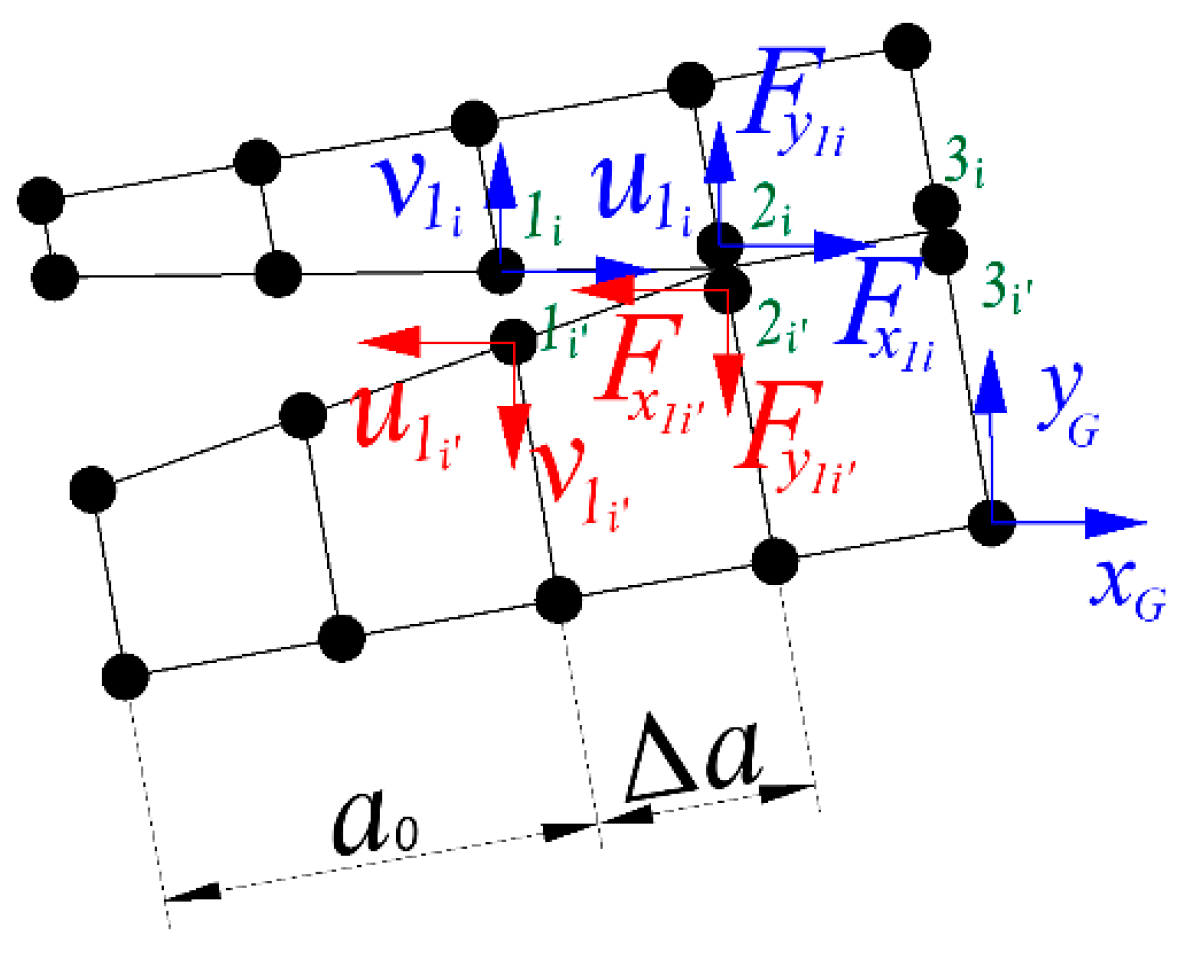
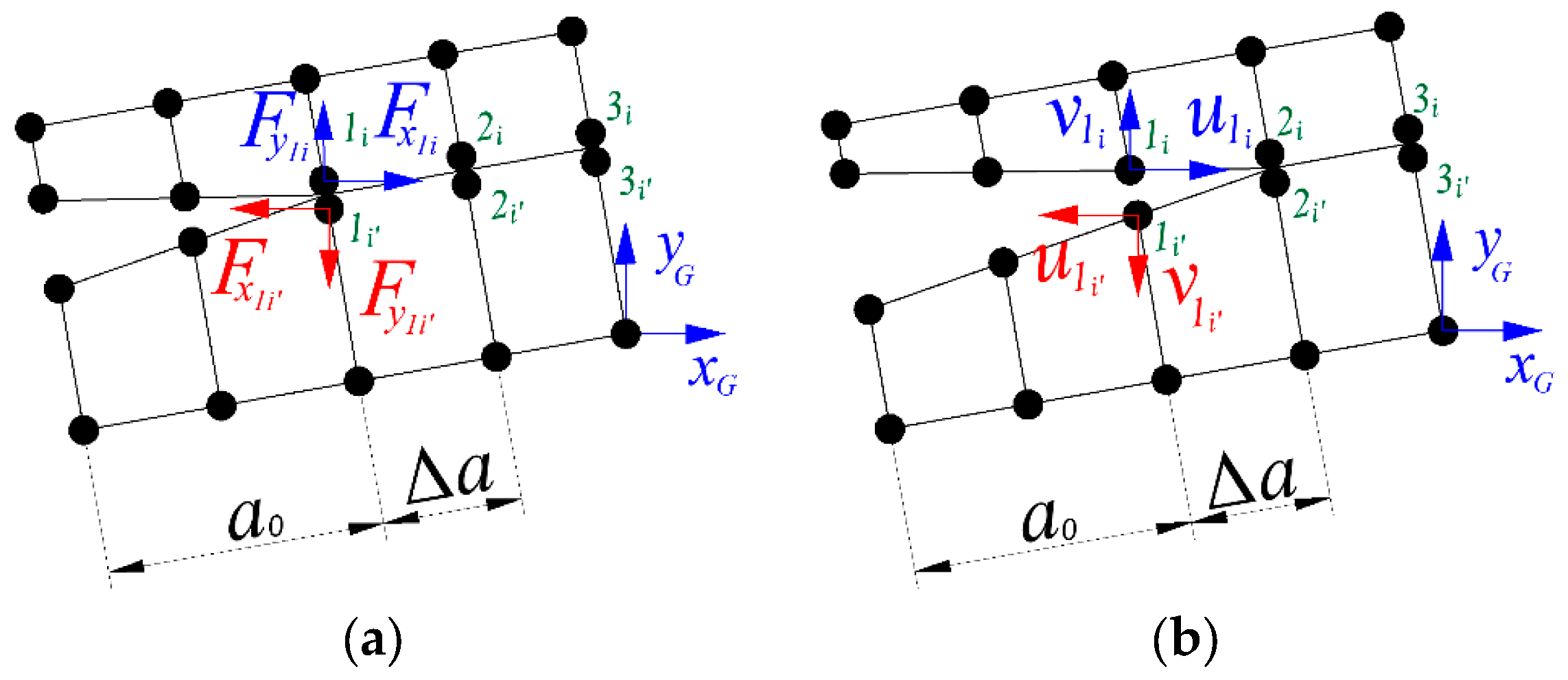

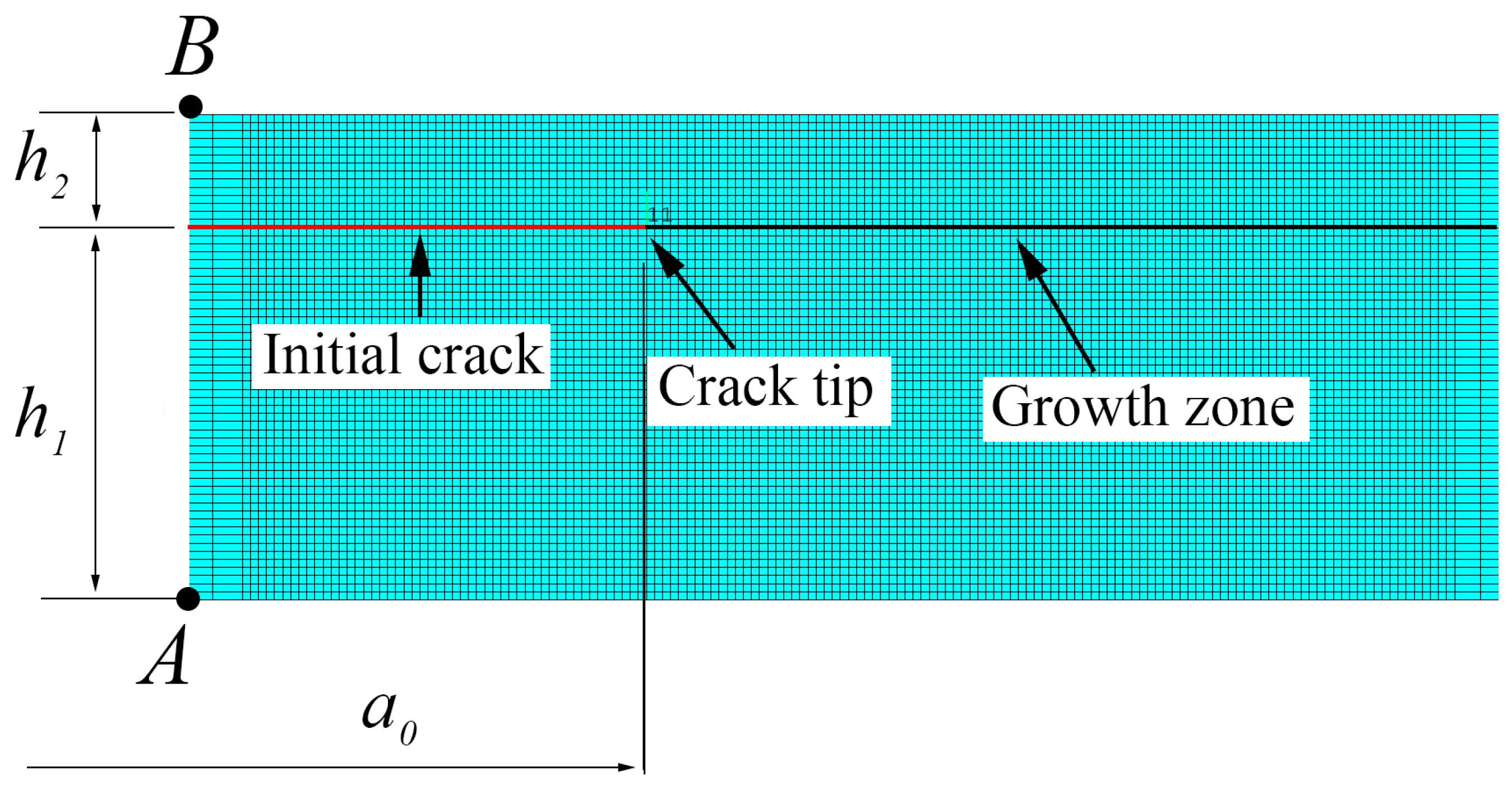

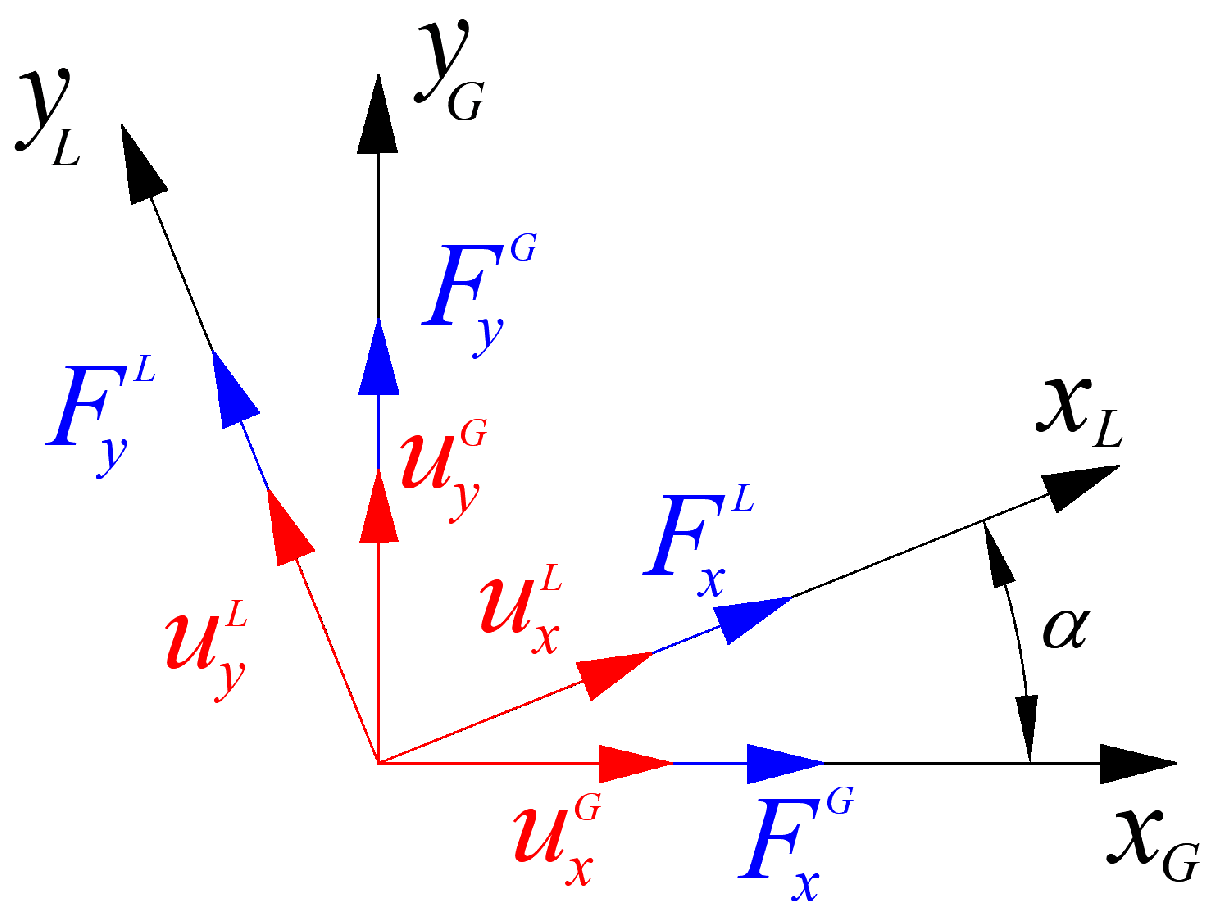
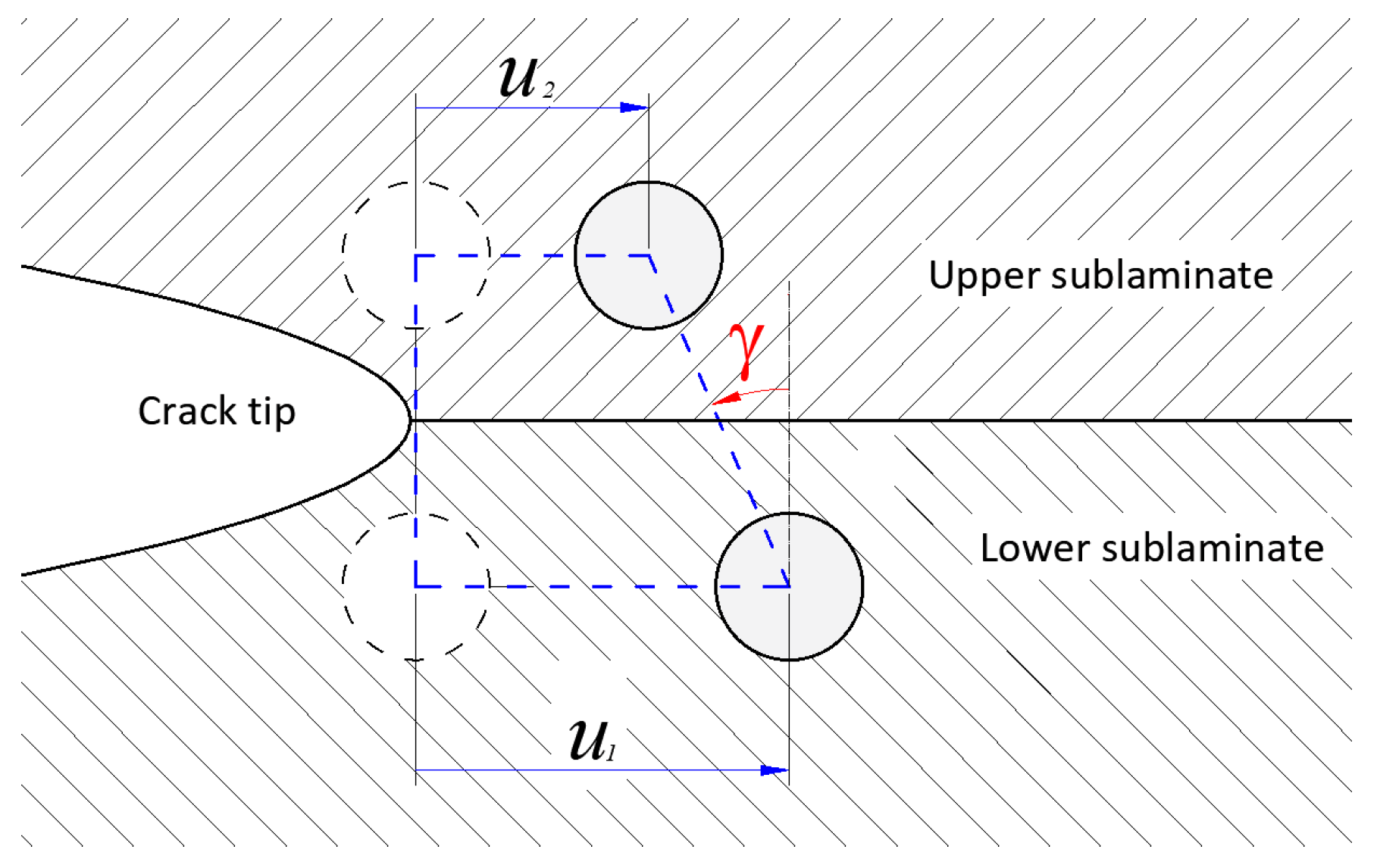
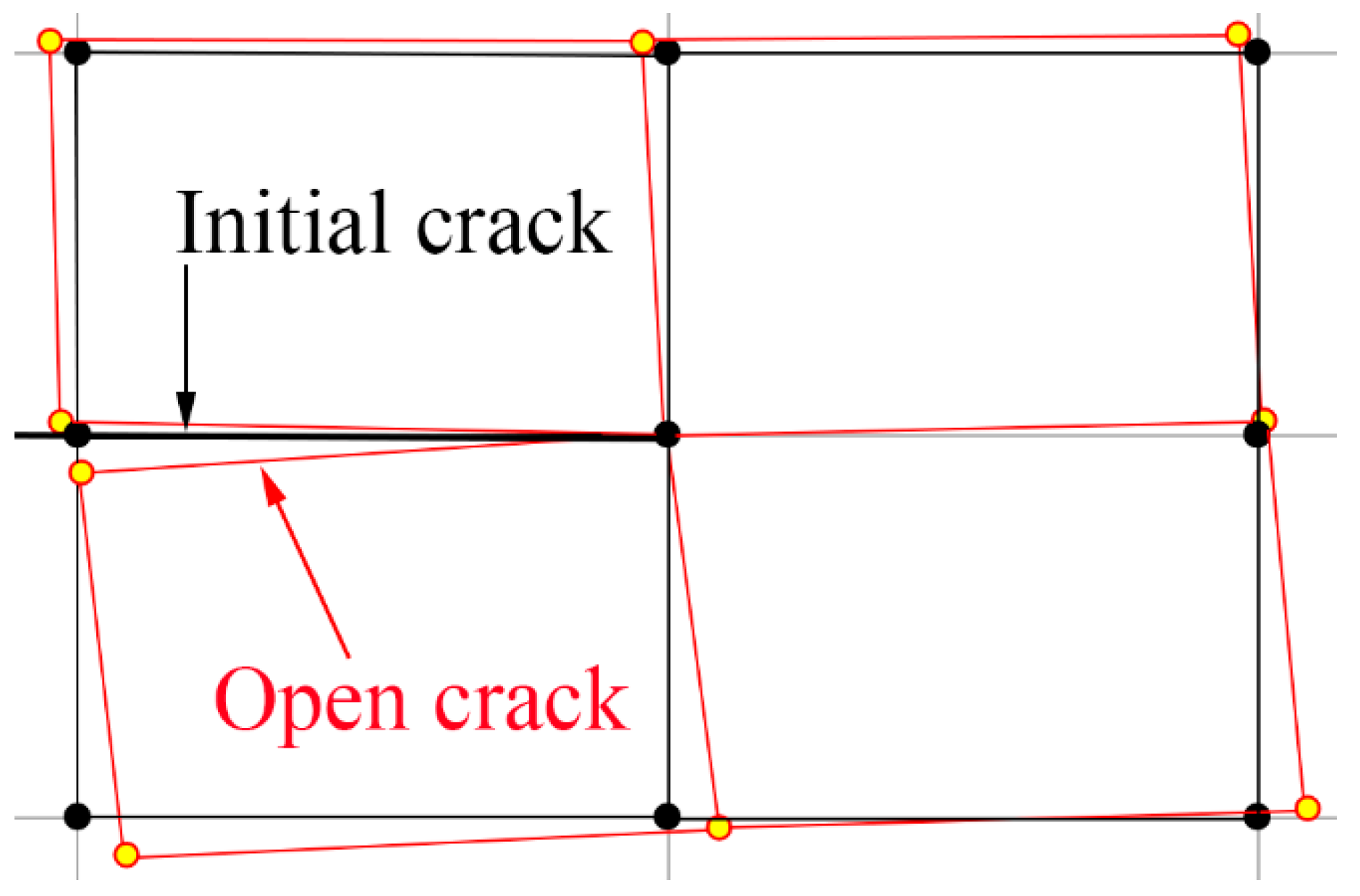

| Property | AS4/8552 |
|---|---|
| Ex (MPa) | 144,000 |
| Ey (MPa) | 10,600 |
| Ez (MPa) | 10,600 |
| Gxy (MPa) | 5360 |
| Gxz (MPa) | 5360 |
| Gyz (MPa) | 3786 |
| νxy | 0.34 |
| νxz | 0.34 |
| νyz | 0.40 |
| GIc (N/mm) | 0.250 |
| GIIc (N/mm) | 0.791 |
| Solution Procedure | P (N) | GI (N/mm) | GII (N/mm) | GT (=GI + GII) (N/mm) | GT (−dU/(Bda) (N/mm) | %GI | %GII |
|---|---|---|---|---|---|---|---|
| Linear | 2.985 | 0.288 | 0.093 | 0.382 | 0.382 | 76% | 24% |
| Non-linear | 3.008 | 0.282 | 0.102 | 0.384 | 0.385 | 74% | 26% |
| Calculation Procedure | GT (N/mm) TSEM (Equations (3) and (4)) | GT (N/mm) Analytical CBT Equation (Equation (6)) | Δ (mm) | Var. TSEM- Analytical |
|---|---|---|---|---|
| Linear | 0.382 | 0.385 | 3.04 | −0.4% |
| Non-linear | 0.384 | 0.382 | 2.12 | −0.2% |
| δ (mm) | P (N) | δ/P (mm/N) | GI (N/mm) | GII (N/mm) | GT (N/mm) | GI/GT | GII/GT |
|---|---|---|---|---|---|---|---|
| 1 | 0.664 | 1.506 | 0.014 | 0.005 | 0.019 | 75% | 25% |
| 5 | 3.347 | 1.494 | 0.348 | 0.127 | 0.476 | 73% | 27% |
| 10 | 6.802 | 1.470 | 1.332 | 0.586 | 1.919 | 69% | 31% |
| 15 | 10.404 | 1.442 | 2.854 | 1.523 | 4.376 | 65% | 35% |
| 20 | 14.254 | 1.403 | 4.825 | 3.117 | 7.942 | 61% | 39% |
| δ (mm) | P (N) | δ/P (mm/N) | GI (N/mm) | GII (N/mm) | GT (N/mm) | GI/GT | GII/GT |
|---|---|---|---|---|---|---|---|
| 1 | 0.664 | 1.506 | 0.014 | 0.005 | 0.019 | 75% | 25% |
| 5 | 3.347 | 1.494 | 0.347 | 0.127 | 0.474 | 73% | 27% |
| 10 | 6.802 | 1.470 | 1.335 | 0.587 | 1.922 | 69% | 31% |
| 15 | 10.404 | 1.442 | 2.866 | 1.528 | 4.394 | 65% | 35% |
| 20 | 14.254 | 1.403 | 4.856 | 3.135 | 7.991 | 61% | 39% |
| δ (mm) | P (N) | δ/P (mm/N) | GI (N/mm) | GII (N/mm) | GT (N/mm) | GI/GT | GII/GT |
|---|---|---|---|---|---|---|---|
| 1 | 0.664 | 1.506 | 0.014 | 0.005 | 0.019 | 76% | 24% |
| 5 | 3.347 | 1.494 | 0.363 | 0.112 | 0.474 | 76% | 24% |
| 10 | 6.802 | 1.470 | 1.486 | 0.436 | 1.922 | 77% | 23% |
| 15 | 10.404 | 1.442 | 3.431 | 0.963 | 4.394 | 78% | 22% |
| 20 | 14.254 | 1.403 | 6.297 | 1.694 | 7.991 | 79% | 21% |
| δ (mm) | Rotated Angle (Rad.) | Crack Tip Node ux Displacement (mm) | |||
|---|---|---|---|---|---|
| 1 | −1% | 2% | 0% | 0.0035 | −0.022 |
| 5 | −4% | 14% | 0% | 0.0292 | −0.196 |
| 10 | −10% | 35% | 0% | 0.0713 | −0.571 |
| 15 | −16% | 59% | 0% | 0.1172 | −1.116 |
| 20 | −23% | 85% | 0% | 0.1647 | −1.836 |
| Ex1(MPa) | Ex2/Ex1 | h2/h1 | GCS %GI | GCS %GII | LCS %GI | LCS %GII | Rotated Angle (Rad.) | |
|---|---|---|---|---|---|---|---|---|
| 144.000 | 1 | 1.000 | 1.000 | 100% | 0% | 100% | 0% | 0 |
| 144.000 | 1 | 0.714 | 0.510 | 95% | 5% | 97% | 3% | 0.0323 |
| 144,000 | 1 | 0.500 | 0.250 | 84% | 16% | 88% | 12% | 0.0563 |
| 144,000 | 1 | 0.333 | 0.111 | 72% | 28% | 79% | 21% | 0.0697 |
| 144,000 | 1 | 0.200 | 0.040 | 62% | 38% | 71% | 29% | 0.0751 |
| 144,000 | 0.25 | 0.200 | 0.010 | 43% | 57% | 52% | 48% | 0.0812 |
| 144,000 | 0.125 | 0.200 | 0.005 | 39% | 61% | 48% | 52% | 0.0822 |
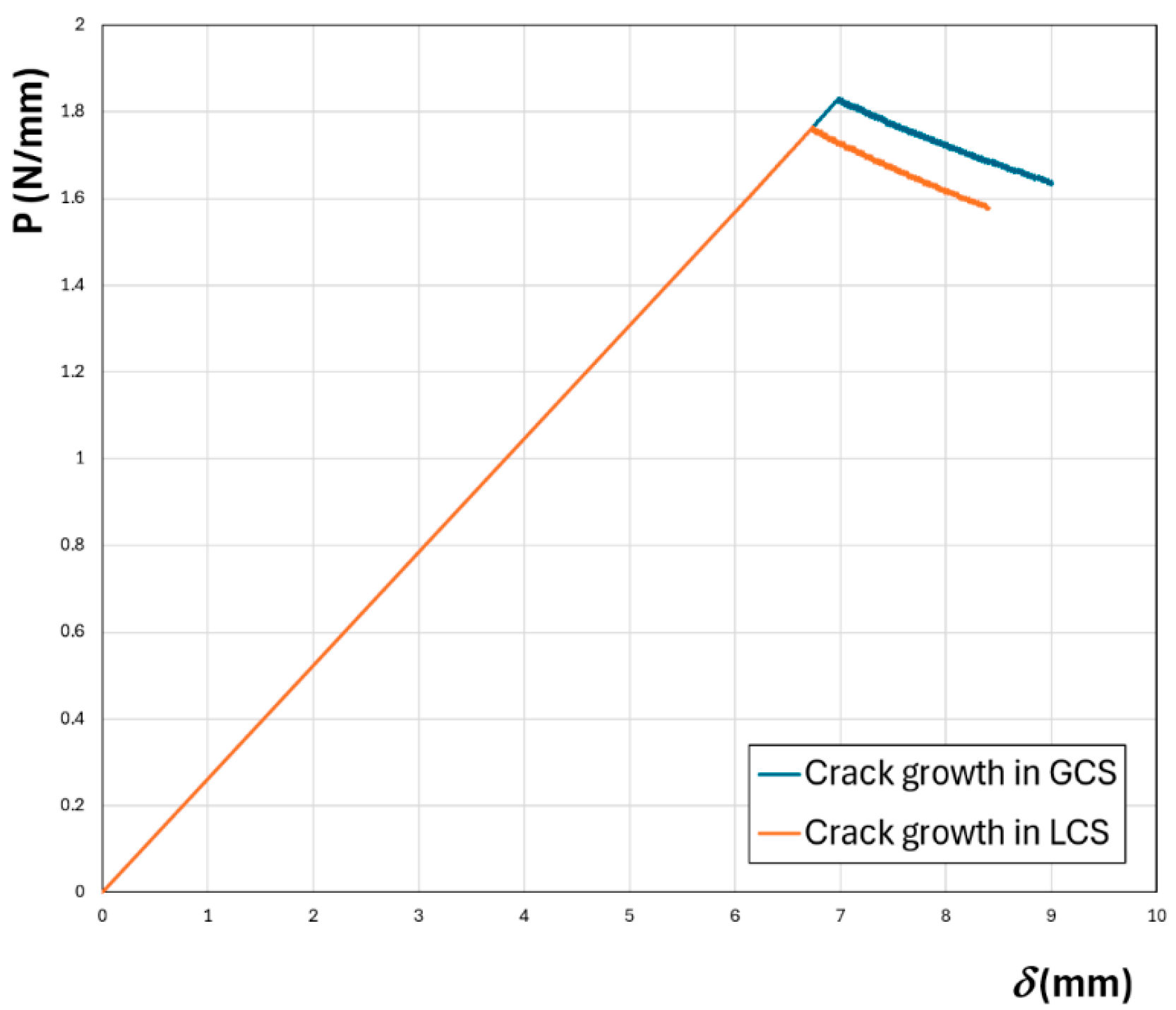
| δc (mm) | Pc (N/mm) | |
|---|---|---|
| GCS | 6.99 | 1.832 |
| LCS | 6.74 | 1.765 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonhomme, J.; Mollón, V.; Viña, J.; Argüelles, A. Influence of Geometric Non-Linearities on the Mixed-Mode Decomposition in Asymmetric DCB Samples. Fibers 2025, 13, 70. https://doi.org/10.3390/fib13060070
Bonhomme J, Mollón V, Viña J, Argüelles A. Influence of Geometric Non-Linearities on the Mixed-Mode Decomposition in Asymmetric DCB Samples. Fibers. 2025; 13(6):70. https://doi.org/10.3390/fib13060070
Chicago/Turabian StyleBonhomme, Jorge, Victoria Mollón, Jaime Viña, and Antonio Argüelles. 2025. "Influence of Geometric Non-Linearities on the Mixed-Mode Decomposition in Asymmetric DCB Samples" Fibers 13, no. 6: 70. https://doi.org/10.3390/fib13060070
APA StyleBonhomme, J., Mollón, V., Viña, J., & Argüelles, A. (2025). Influence of Geometric Non-Linearities on the Mixed-Mode Decomposition in Asymmetric DCB Samples. Fibers, 13(6), 70. https://doi.org/10.3390/fib13060070







