Effect of GFRP and CFPR Hybrid Confinement on the Compressive Performance of Concrete
Abstract
1. Introduction
2. Experimental Program
2.1. Test Specimens
2.2. Test Set-Up and Instrumentation
2.3. Material Properties
3. Experimental Results—Discussion
3.1. Failure Mode




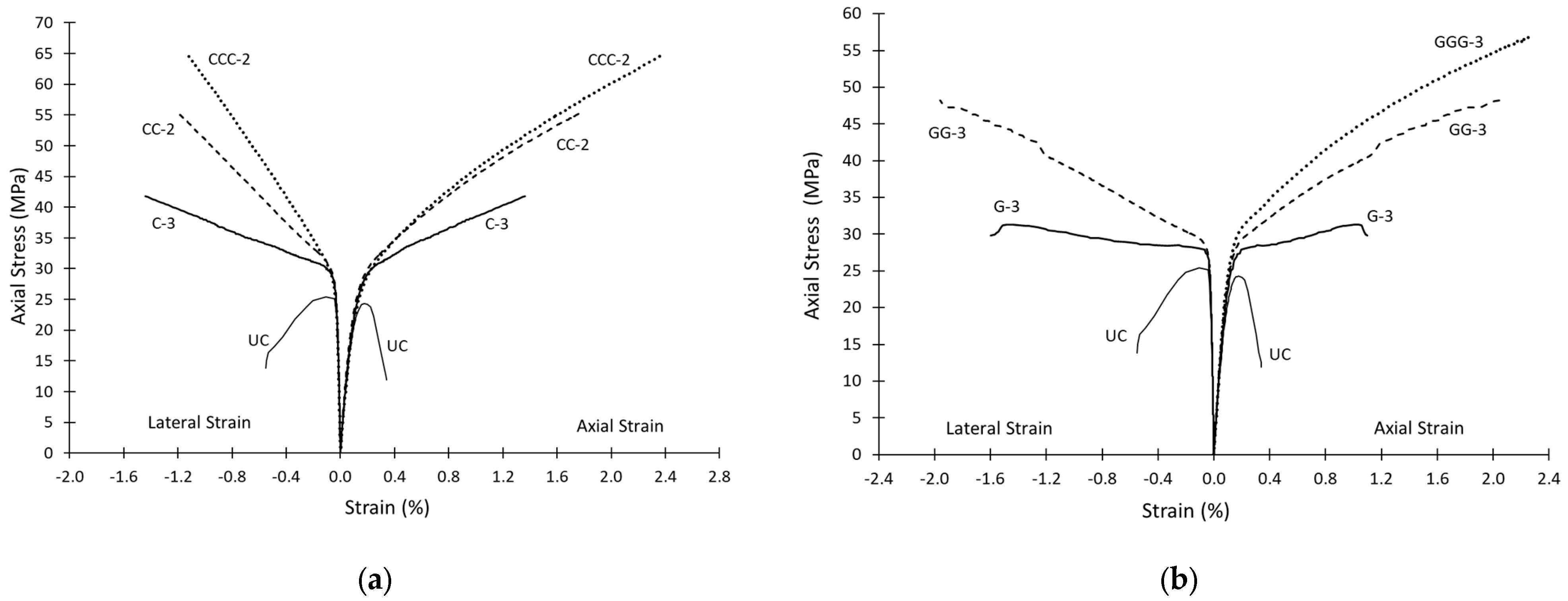
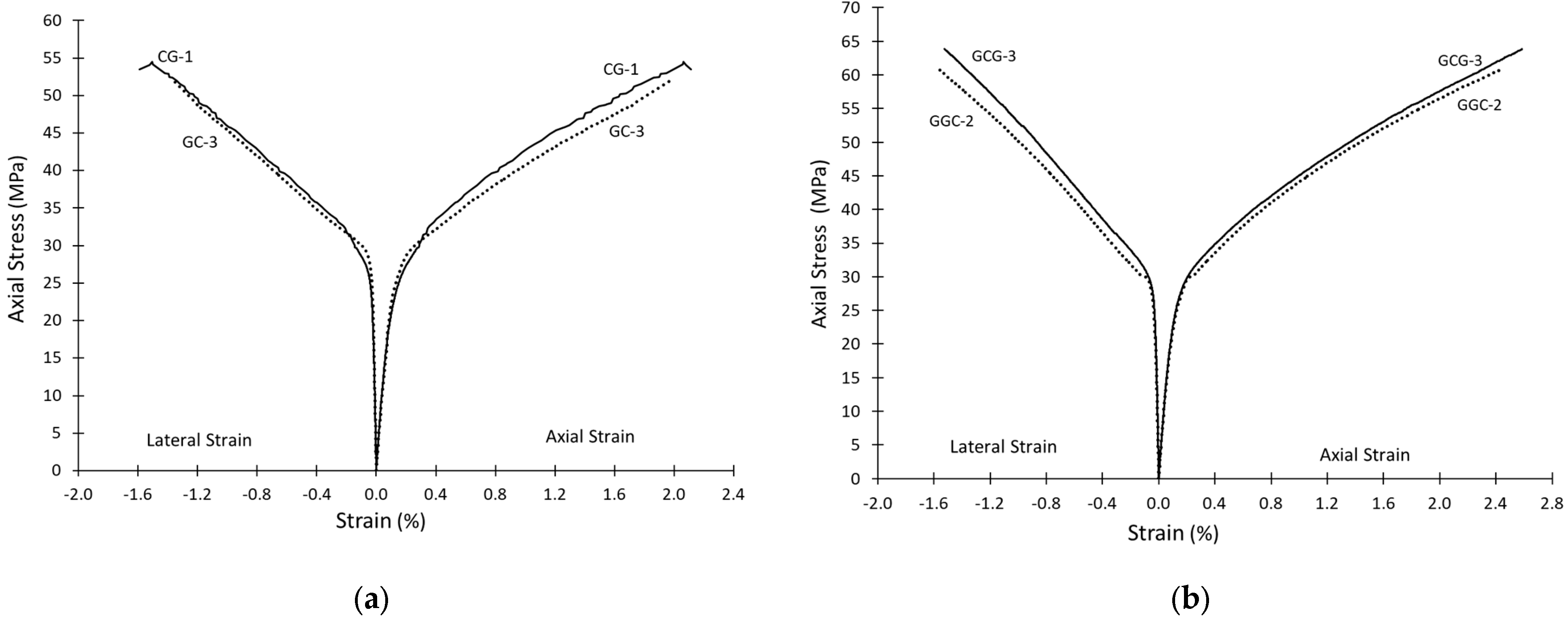
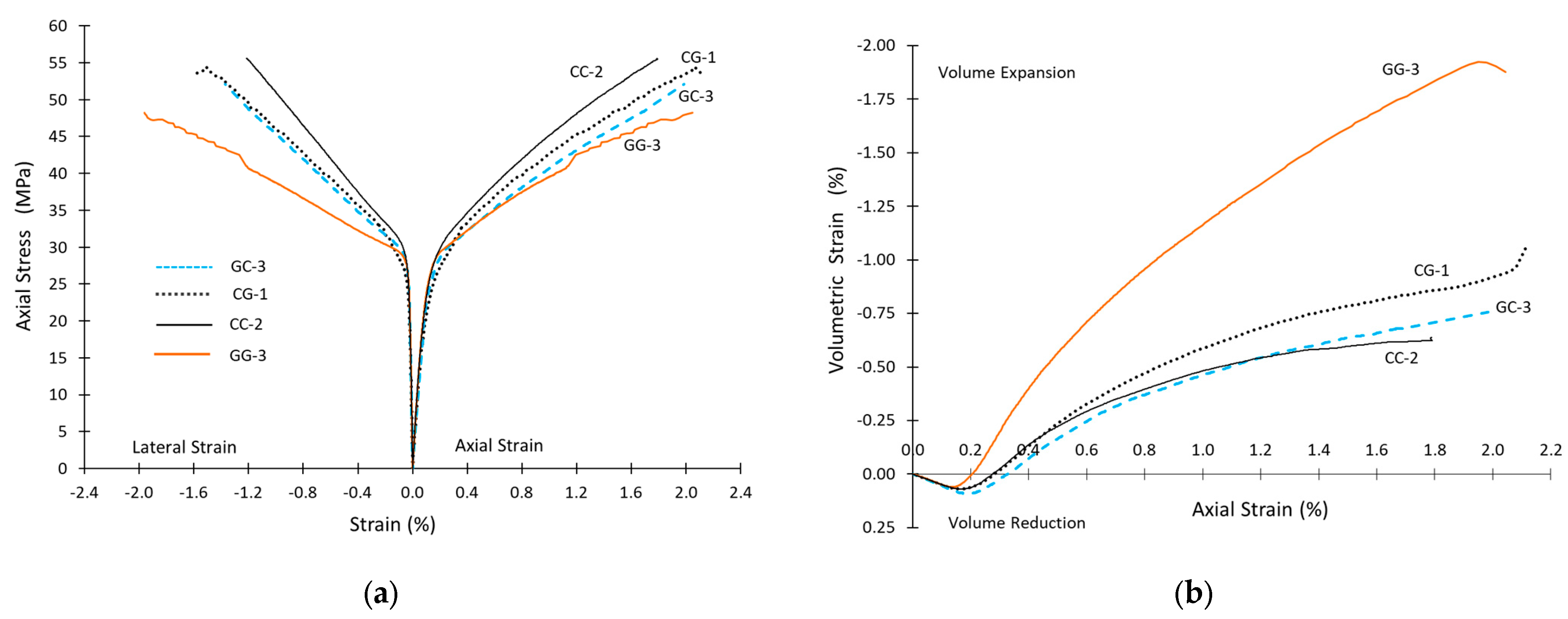
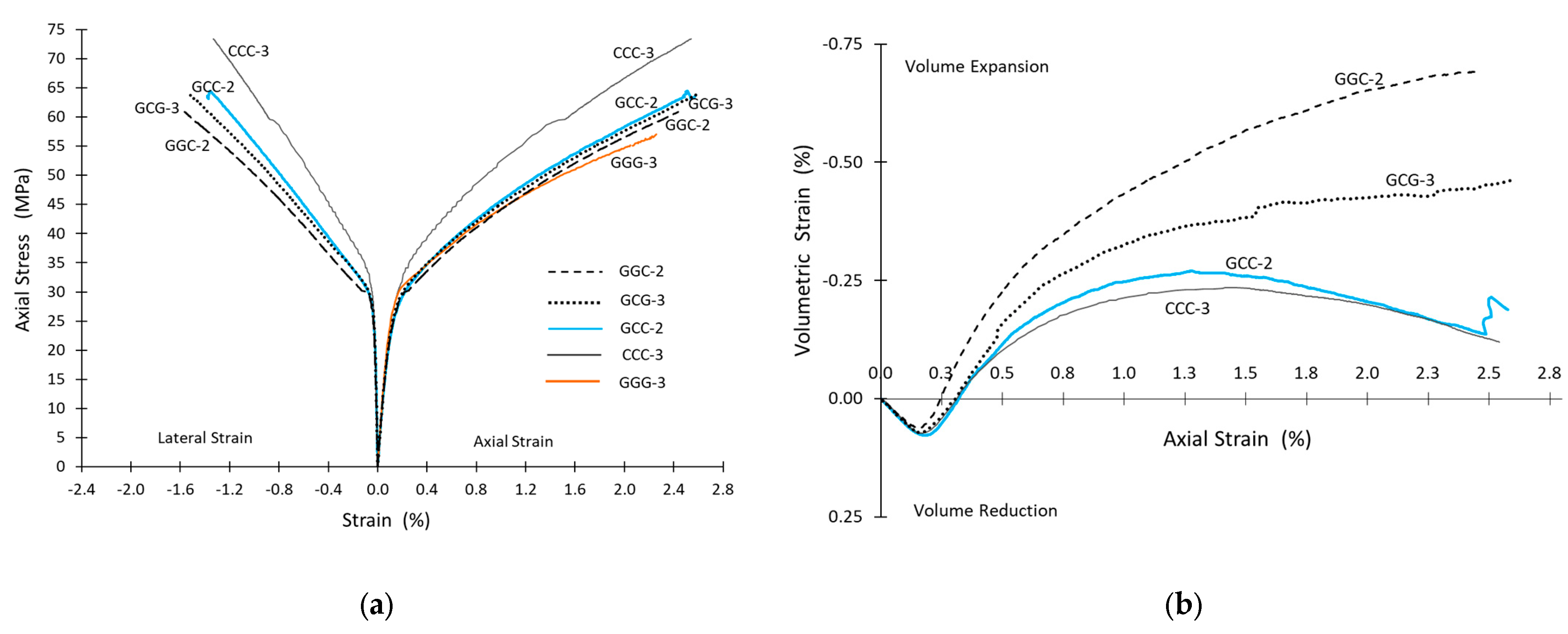
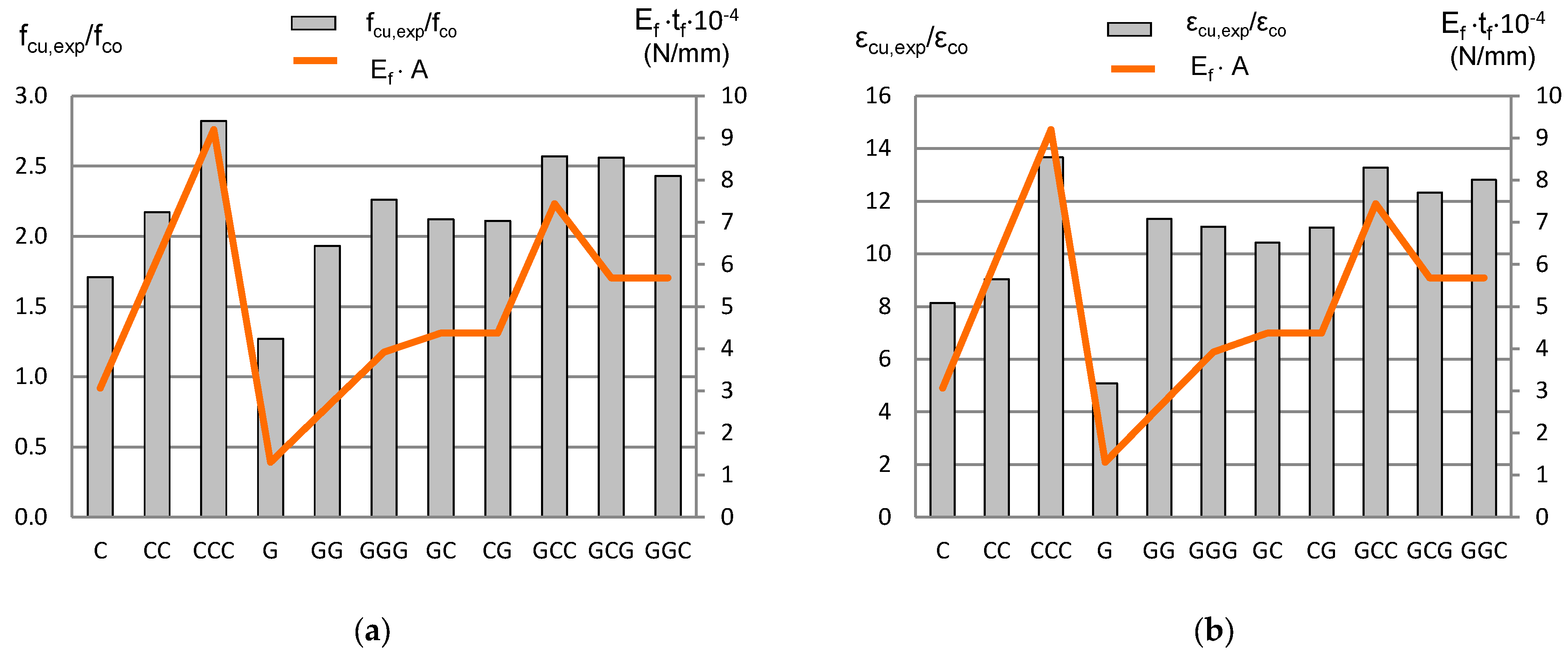
3.2. Axial Strength and Strain Relationships
3.3. Lateral Strain Efficiency Factor of the FRP Jackets Tested
4. Analytical Predictions—Discussion
Proposed Design Model
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, Y.; Wu, H. Compressive behavior of concrete confined by carbon fiber composite jackets. J. Mater. Civ. Eng. 2000, 12, 139–146. [Google Scholar] [CrossRef]
- Karabinis, A.I.; Rousakis, T.C. Concrete confined by FRP material a plasticity approach. Eng. Struct. 2002, 24, 923–932. [Google Scholar] [CrossRef]
- Tamuzs, V.; Tepfers, R.; Zile, E.; Ladnova, O. Behavior of concrete cylinders confined by a carbon composite: 3. Deformability and the ultimate axial strain. Mech. Compos. Mater. 2006, 42, 303–314. [Google Scholar] [CrossRef]
- Mirmiran, A.; Shahaway, M. Behavior of Concrete Columns Confined by Fiber Composites. J. Struct. Eng. 1997, 123, 583–590. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Saatcioglu, M. Seismic behavior of high-strength concrete columns confined by fiber reinforced polymer tubes. J. Compos. Constr. 2006, 10, 538–549. [Google Scholar] [CrossRef]
- Fam, A.Z.; Rizkalla, S.H. Flexural behavior of concrete-filled fiber reinforced polymer circular tubes. J. Compos. Constr. 2002, 6, 123–132. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Oehlers, D.J. Concrete-filled square and rectangular FRP tubes under axial compression. J. Compos. Constr. 2008, 12, 469–477. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Design-oriented stress–strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Bisby, L.A.; Dent, A.J.S.; Green, M.F. Comparison of confinement models for fiber-reinforced polymer-wrapped concrete. ACI Struct. J. 2005, 102, 62–72. [Google Scholar]
- Teng, J.G.; Huang, Y.L.; Lam, L.; Ye, L.P. Theoretical model for fiber-reinforced polymer-confined concrete. J. Compos. Constr. 2007, 11, 201–210. [Google Scholar] [CrossRef]
- Teng, J.G.; Jiang, T.; Lam, L.; Luo, Y.Z. Refinement of a design-oriented model for FRP-confined concrete. J. Compos. Constr. 2009, 13, 269–278. [Google Scholar] [CrossRef]
- Jiang, J.G.; Teng, J.G. Analysis-oriented stress-strain models for FRP-confined concrete. Eng. Struct. 2007, 29, 2968–2986. [Google Scholar] [CrossRef]
- Realfonzo, R.; Napoli, A. Concrete confined by FRP systems: Confinement efficiency and design strength models. Compos. Part B 2011, 42, 736–755. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Lim, J.C.; Vincent, T. FRP-confined concrete in circular sections: Review and assessment of stress–strain models. Eng. Struct. 2013, 49, 1068–1088. [Google Scholar] [CrossRef]
- Hayashi, T. On the improvement of mechanical properties of composites by hybrid composition. In Proceedings of the 8th International Reinforced Plastics Conference, Brighton, UK, 10–12 October 1972; paper 22. pp. 149–152. [Google Scholar]
- Bunsell, A.R.; Harris, B. Hybrid carbon and glass fibre composites. Composites 1974, 5, 157–164. [Google Scholar] [CrossRef]
- Manders, P.W.; Bader, M.G. The strength of hybrid glass/carbon fibre composites. J. Mater. Sci. 1981, 16, 2233–2245. [Google Scholar] [CrossRef]
- Bakis, C.E.; Nanni, A.; Terosky, J.A.; Koeler, S.W. Self-monitoring, pseudo-ductile, hybrid FRP reinforcement rods for concrete applications. Compos. Sci. Technol. 2001, 61, 815–823. [Google Scholar] [CrossRef]
- Ribeiro, F.; Sena-Cruz, J.; Branco, F.G.; Júlio, E. Hybrid effect and pseudo-ductile behaviour of unidirectional interlayer hybrid FRP composites for civil engineering applications. Constr. Build. Mater. 2018, 171, 871–890. [Google Scholar] [CrossRef]
- Summerscales, J.; Short, D. Carbon fibre and glass fibre hybrid reinforced plastics. Composites 1978, 9, 157–166. [Google Scholar] [CrossRef]
- Swolfs, Y.; Gorbatikh, L.; Verpoest, I. Fibre hybridisation in polymer composites: A review. Compos. Part A Appl. Sci. Manuf. 2014, 67, 181–200. [Google Scholar] [CrossRef]
- Lin, H.J.; Chen, C.T. Strength of concrete cylinder. J. Reinf. Plast. Compos. 2001, 20, 1577–1600. [Google Scholar] [CrossRef]
- Wu, G.; Wu, Z.S.; Lu, Z.T.; Ando, Y.B. Structural performance of concrete confined with hybrid FRP composites. J. Reinf. Plast. Compos. 2008, 27, 1323–1348. [Google Scholar] [CrossRef]
- Tang, W.; Liu, Z.; Lu, Y.; Li, S. Hybrid confinement mechanism of large-small rupture strain FRP on concrete cylinder. J. Build. Eng. 2022, 51, 104335. [Google Scholar] [CrossRef]
- Jalalvand, M.; Czél, G.; Wisnom, M.R. Damage analysis of pseudo-ductile thin-ply UD hybrid composites—A new analytical method. Compos. Part A 2015, 69, 83–93. [Google Scholar] [CrossRef]
- Czél, G.; Wisnom, M.R. Demonstration of pseudo-ductility in high performance glass/epoxy composites by hybridisation with thin-ply carbon prepreg. Compos. Part A 2013, 52, 23–30. [Google Scholar] [CrossRef]
- Pandya, K.S.; Veerraju, C.; Naik, N.K. Hybrid composites made of carbon and glass woven fabrics under quasi-static loading. Mater. Des. 2011, 32, 4094–4099. [Google Scholar] [CrossRef]
- Czél, G.; Jalalvand, M.; Wisnom, M.R. Design and characterisation of advanced pseudo-ductile unidirectional thin-ply carbon/epoxy–glass/epoxy hybrid composites. Compos. Struct. 2016, 143, 362–370. [Google Scholar] [CrossRef]
- Wisnom, M.R. Mechanisms to create high performance pseudo-ductile composites. IOP Conf. Ser. Mater. Sci. Eng. 2016, 139, 012010. [Google Scholar] [CrossRef]
- Rousakis, T.C. Hybrid confinement of concrete by fiber-reinforced polymer sheets and fiber ropes under cyclic axial compressive loading. J. Compos. Constr. 2013, 17, 732–743. [Google Scholar] [CrossRef]
- Rousakis, T.C. Reusable and recyclable nonbonded composite tapes and ropes for concrete columns confinement. Compos. Part B 2016, 103, 15–22. [Google Scholar] [CrossRef]
- Rousakis, T.C. Inherent seismic resistance of RC columns externally confined with nonbonded composite ropes. Compos. Part B 2018, 135, 142–148. [Google Scholar] [CrossRef]
- Saingam, P.; Hussain, Q.; Ejaz, A.; Nawaz, A.; Joklad, P.; Khan, K. Enhancing compressive behavior of concrete with novel low-cost hybrid passive confinement including large rupture strain cotton ropes: Experimental findings and a design-oriented model. Case Stud. Constr. Mater. 2024, 21, e03496. [Google Scholar] [CrossRef]
- Wahab, N.; Srinophakun, P.; Hussain, Q.; Chaimahawan, P. Performance of concrete confined with a jute–polyester hybrid fiber reinforced polymer composite: A novel strengthening technique. Fibers 2019, 7, 72. [Google Scholar] [CrossRef]
- Farokhi Nejad, A.; Bin Salim, M.Y.; Rahimian Koloor, S.S.; Petrik, S.; Yahya, M.Y.; Abu Hassan, S.; Mohd Shah, M.K. Hybrid and synthetic FRP composites under different strain rates: A review. Polymers 2021, 13, 3400. [Google Scholar] [CrossRef]
- Joyklad, P.; Saingam, P.; Ali, N.; Ejaz, A.; Hussain, Q.; Khan, K.; Chaiyasarn, K. Low-Cost Fiber Chopped Strand Mat Composites for Compressive Stress and Strain Enhancement of Concrete Made with Brick Waste Aggregates. Polymers 2022, 14, 4714. [Google Scholar] [CrossRef]
- Bai, Y.-L.; Liu, S.-Z.; Mei, S.J. Compressive behavior and modeling of concrete wrapped by hybrid low-high elongation capacities FRP. Eng. Struct. 2024, 300, 117155. [Google Scholar] [CrossRef]
- Ispir, M.; Dalgic, K.D.; Iki, A. Hybrid confinement of concrete through use of low and high rupture strain FRP. Compos. Part B 2018, 153, 154–196. [Google Scholar] [CrossRef]
- Garcia, R.; Hajirasouliha, I.; Pilakoutas, K. Seismic behaviour of deficient RC frames strengthened with CFRP composites. Eng. Struct. 2004, 32, 3075–3085. [Google Scholar] [CrossRef]
- Garcia, R.; Jemaa, Y.; Helal, Y.; Guadagnini, M.; Pilakoutas, K. Seismic strengthening of severely damaged beam-column RC joints using CFRP. J. Compos. Constr. 2013, 18, 3075–3085. [Google Scholar] [CrossRef]
- De Luca, A.; Nardone, F.; Matta, F.; Nanni, A.; Lingnola, G.P.; Prota, A. Structural Evaluation of Full-Scale FRP-Confined Reinforced Concrete Columns. J. Compos. Constr. 2011, 15, 112–123. [Google Scholar] [CrossRef]
- Dai, J.G.; Lam, L.; Ueda, T. Seismic retrofit of square RC columns with polyethylene terephthalate (PET) fibre reinforced polymer composites. Constr. Build. Mater. 2012, 27, 206–217. [Google Scholar] [CrossRef]
- Moretti, M.L. Rapid retrofit of substandard short RC columns with buckled longitudinal bars using CFRP jacketing. Earthq. Struct. 2023, 24, 97–109. [Google Scholar] [CrossRef]
- Bai, Y.L.; Dai, J.G.; Teng, J.G. Cyclic compressive behavior of concrete confined with large rupture strain FRP composites. J. Compos. Constr. 2014, 18, 04013025. [Google Scholar] [CrossRef]
- Moretti, Μ.L.; Arvanitopoulos, E. Overlap length for confinement of carbon and glass FRP-jacketed concrete columns. Compos. Struct. 2018, 195, 14–25. [Google Scholar] [CrossRef]
- Pessiki, S.; Harries, K.A.; Kestner, J.; Sause, R.; Ricles, J.M. The axial behavior of concrete confined with fiber reinforced composite jackets. ASCE J. Compos. Constr. 2001, 5, 237–245. [Google Scholar] [CrossRef]
- Wu, Y.F.; Jiang, J.F. Effective strain of FRP for confined circular concrete columns. Compos. Struct. 2013, 95, 479–491. [Google Scholar] [CrossRef]
- Shahawy, M.; Mirmiran, A.; Beitelman, A. Test and modelling of carbon-wrapped concrete columns. Compos. Part B Eng. 2000, 31, 471–480. [Google Scholar] [CrossRef]
- Moretti, M.L. Effectiveness of different confining configurations of FRP jackets for concrete columns. Struct. Eng. Mech. Int. J. 2019, 72, 155–168. [Google Scholar] [CrossRef]
- Vincent, T.; Ozbakkaloglu, T. Influence of overlap configuration on compressive behavior of CFRP-confined normal- and high-strength concrete. Mater. Struct. 2016, 49, 1245–1268. [Google Scholar] [CrossRef]
- Lim, J.C.; Ozbakkaloglu, T. Hoop strains in FRP-confined concrete columns: Experimental observations. Mater. Struct. 2015, 48, 2839–2854. [Google Scholar] [CrossRef]
- Moretti, M.L.; Miliokas, E.; Paparizos, I. Axial strength estimation of reinforced concrete columns confined through fiber reinforced polymer (FRP) jackets. J. Multidiscip. Eng. Sci. Technol. 2021, 8, 13804–13818. Available online: https://www.jmest.org/wp-content/uploads/JMESTN42353721.pdf (accessed on 30 April 2021).
- Wei, Y.-Y.; Wu, Y.-F. Unified stress-strain model of concrete for FRP-confined columns. Constr. Build. Mater. 2012, 26, 381–392. [Google Scholar] [CrossRef]
- Wu, Y.F.; Wei, Y. General stress-strain model for steel- and FRP-confined concrete. J. Compos. Constr. 2014, 19, 04014069. [Google Scholar] [CrossRef]
- Ilki, A.; Kumbasar, N. Compressive behaviour of carbon fibre composite jacketed concrete with circular and non-circular cross-sections. J. Earthq. Eng. 2003, 7, 381–406. [Google Scholar] [CrossRef]
- Ilki, A.; Kumbasar, N.; Koc, V. Low strength concrete members externally confined with FRP sheets. Struct. Eng. Mech. 2004, 18, 167–194. [Google Scholar] [CrossRef]

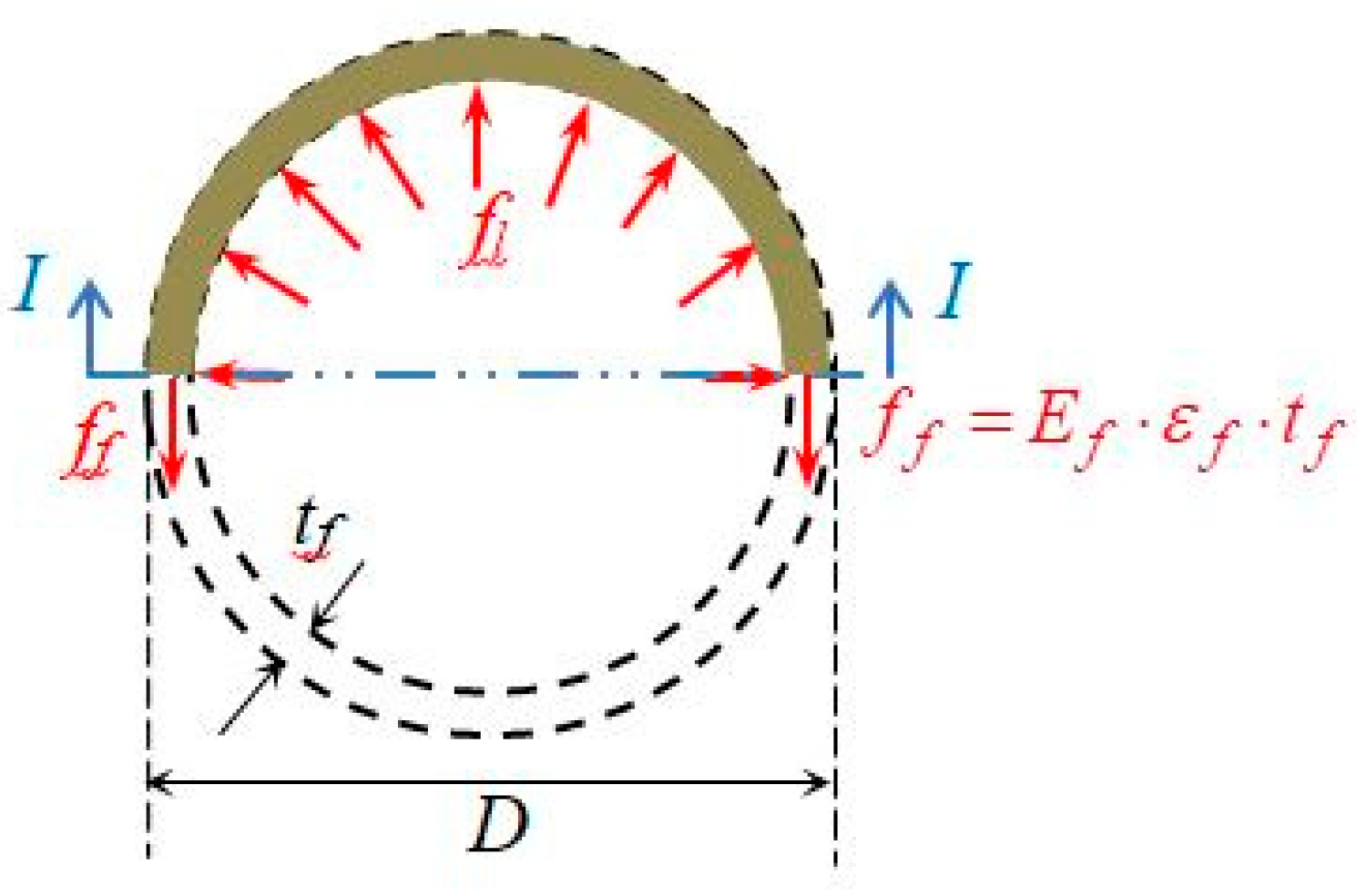


| FRP Type | Tensile Strength ffu (MPa) | Tensile Modulus of Elasticity Ef (GPa) | Fabric Design Thickness, tf (mm) | Ultimate Strain εfu (%) | Average Weight gr/m2 |
|---|---|---|---|---|---|
| carbon | 4300 MPa | 234 | 0.131 | 1.84 | 230 |
| glass | 2300 MPa | 76 | 0.172 | 3.03 | 445 |
| Specimen | fcu,exp (MPa) | εcu,exp (%) | εlu,exp (%) | εlu,exp/εfu2 |
|---|---|---|---|---|
| C-3 | 41.8 | 1.36 | 1.36 | 0.74 |
| C-4 | 42.1 | 1.57 | 1.57 | 0.85 |
| G-2 | 30.7 | 0.79 | N.A. 1 | N.A. 1 |
| G-3 | 31.3 | 1.04 | 1.60 | 0.53 |
| CC-2 | 55.6 | 1.79 | 1.21 | 0.66 |
| CC-3 | 50.6 | 1.46 | 1.11 | 0.60 |
| GG-1 | 46.6 | 1.85 | 1.83 | 0.60 |
| GG-2 | 47.2 | 2.08 | 2.20 | 0.73 |
| GG-3 | 48.2 | 2.04 | 1.96 | 0.65 |
| CCC-2 | 64.9 | 2.38 | 1.13 | 0.61 |
| CCC-3 | 73.4 | 2.54 | 1.33 | 0.72 |
| GGG-1 | 53.5 | 1.71 | N.A. 1 | N.A. 1 |
| GGG-3 | 57.1 | 2.26 | N.A. 1 | N.A. 1 |
| Specimen | fcu,exp (MPa) | εcu,exp (%) | εlu,exp (%) | εlu,exp/εfu2 |
|---|---|---|---|---|
| GC-2 | 52.0 | 1.77 | 1.29 | 0.70 |
| GC-3 | 52.1 | 1.98 | 1.37 | 0.74 |
| CG-1 | 53.5 | 2.12 | 1.59 | 0.86 |
| CG-3 | 49.7 | 1.84 | 1.51 | 0.82 |
| GCC-1 | 63.8 | N.A. 1 | N.A. 1 | N.A. 1 |
| GCC-2 | 63.6 | 2.58 | 1.38 | 0.75 |
| GCC-3 | 61.7 | 2.20 | 1.31 | 0.71 |
| GCG-1 | 61.2 | 2.16 | 1.61 | 0.88 |
| GCG-2 | 63.0 | 1.91 | N.A. 1 | N.A. 1 |
| CCG-3 | 63.8 | 2.59 | 1.52 | 0.83 |
| GGC-1 | 60.3 | 2.30 | 1.62 | 0.88 |
| GGC-2 | 60.9 | 2.44 | 1.56 | 0.85 |
| GGC-3 | 57.7 | 2.18 | 1.41 | 0.77 |
| Specimen | fcu,exp (MPa) | fcu,exp/fco | εcu,exp (%) | εcu,exp/εco | εlu,exp (%) | εlu,exp/εfu(2a.2b) | Εf · tf (N/mm) |
|---|---|---|---|---|---|---|---|
| C | 42.0 | 1.71 | 1.47 | 8.14 | 1.47 | 0.80 | 30,654 |
| G | 31.0 | 1.27 | 0.92 | 5.08 | 1.60 | 0.53 | 13,072 |
| CC | 53.1 | 2.17 | 1.63 | 9.03 | 1.16 | 0.63 | 61,308 |
| GG | 47.3 | 1.93 | 1.99 | 11.31 | 2.00 | 0.66 | 26,144 |
| CCC | 69.2 | 2.82 | 2.46 | 13.67 | 1.23 | 0.67 | 91,962 |
| GGG | 55.3 | 2.26 | 1.99 | 11.03 | N.A. 1 | N.A. 1 | 39,216 |
| GC | 52.1 | 2.12 | 1.88 | 10.42 | 1.33 | 0.72 | 43,726 |
| CG | 51.6 | 2.11 | 1.98 | 11.00 | 1.55 | 0.84 | 43,726 |
| GCC | 63.0 | 2.57 | 2.39 | 13.28 | 1.35 | 0.73 | 74,380 |
| GCG | 62.7 | 2.56 | 2.22 | 12.33 | 1.57 | 0.85 | 56,798 |
| GGC | 59.6 | 2.43 | 2.31 | 12.81 | 1.53 | 0.83 | 56,798 |
| Specimen | flu,anal (MPa) | fcu,anal (MPa) | fcu,anal/ fcu,exp | εcu,anal (%) | εcu,anal/ εcu,exp |
|---|---|---|---|---|---|
| C | 7.42 | 39.9 | 0.95 | 1.29 | 0.88 |
| G | 5.21 | 33.6 | 1.08 | 1.06 | 1.16 |
| CC | 14.84 | 58.1 | 1.09 | 1.95 | 1.20 |
| GG | 10.42 | 47.7 | 1.00 | 1.57 | 0.79 |
| CCC | 22.26 | 73.9 | 1.07 | 2.54 | 1.03 |
| GGG | 15.63 | 59.9 | 1.08 | 2.02 | 1.02 |
| GC | 10.58 | 48.1 | 0.92 | 1.58 | 0.84 |
| CG | 10.58 | 48.1 | 0.93 | 1.58 | 0.80 |
| GCC | 18.04 | 65.2 | 1.03 | 2.21 | 0.93 |
| GCG | 13.74 | 55.6 | 0.89 | 1.86 | 0.84 |
| GGC | 13.74 | 55.6 | 0.93 | 1.86 | 0.81 |
| Model keff = 0.85 (5) | Model keff = 1 | Wu and Wei (2014) [54] | Ilki–Kumbasar (2003) [55] | Lam and Teng (2003) [8] | |
|---|---|---|---|---|---|
| Average (1) (fcu,anal/fcu,exp)i | 0.97 | 1 | 1.04 | 1.07 | 0.94 |
| STDEV (2) [fcu,anal/fcu,exp] | 0.06 | 0.08 | 0.09 | 0.09 | 0.09 |
| MAE (3) Σ[abs(fcu,anal − fcu,exp)/n] | 2.89 | 3.65 | 4.40 | 4.25 | 4.46 |
| Δ (4) [(fcu,exp − fcu,anal)/fcu,exp] | 0.38 | 0 | −0.43 | −0.75 | 0.70 |
| Model keff = 0.85 (5) | Model keff = 1 | Wu and Wei (2014) [54] | Ilki–Kumbasar (2003) [55] | Lam and Teng (2003) [8] | |
|---|---|---|---|---|---|
| Average (1) (εcu,anal/εcu,exp)i | 0.90 | 0.94 | 2.80 | 0.94 | 0.98 |
| STDEV (2) [εcu,anal/εcu,exp] | 0.13 | 0.15 | 0.66 | 0.15 | 0.20 |
| MAE (3) Σ[abs(εcu,anal − εcu,exp)/n] | 0.28 | 0.26 | 3.46 | 0.26 | 0.33 |
| Δ (4) [(εcu,exp − εcu,anal)/εcu,exp] | 1.11 | 0.71 | −19.78 | 0.67 | 0.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moretti, M.L. Effect of GFRP and CFPR Hybrid Confinement on the Compressive Performance of Concrete. Fibers 2025, 13, 12. https://doi.org/10.3390/fib13020012
Moretti ML. Effect of GFRP and CFPR Hybrid Confinement on the Compressive Performance of Concrete. Fibers. 2025; 13(2):12. https://doi.org/10.3390/fib13020012
Chicago/Turabian StyleMoretti, Marina L. 2025. "Effect of GFRP and CFPR Hybrid Confinement on the Compressive Performance of Concrete" Fibers 13, no. 2: 12. https://doi.org/10.3390/fib13020012
APA StyleMoretti, M. L. (2025). Effect of GFRP and CFPR Hybrid Confinement on the Compressive Performance of Concrete. Fibers, 13(2), 12. https://doi.org/10.3390/fib13020012







