Optimizing Controlled-Resonance Acoustic Metamaterials with Perforated Plexiglass Disks, Honeycomb Structures, and Embedded Metallic Masses
Abstract
1. Introduction
- Design and fabricate a sandwich metamaterial configuration that exploits the principles of Helmholtz resonators and mass-spring resonances for selective sound absorption.
- Conduct experimental characterization of the metamaterial’s acoustic properties by measuring the Sound Absorption Coefficient (SAC) using an impedance tube (Kundt tube).
- Analyze the effect of design variables, such as hole size, metal mass distribution, and disk spacing, on the resonance frequencies and sound absorption effectiveness.
- Optimize the configuration to maximize sound absorption in specific frequency bands, through numerical simulations and comparison with experimental data.
- Evaluate the application potential of the optimized metamaterial in practical contexts such as industrial noise control, reduction in reverberation in enclosed spaces, and acoustic protection in critical environments.
2. State of the Art and Recent Innovations
3. Materials and Methods
3.1. Description of Materials
- f is the resonant frequency of the resonator (in Hz).
- c is the speed of sound in air (about 343 m/s at room temperature). This represents the speed at which sound waves travel through air and directly affects the resonant frequency.
- A is the area of the resonator opening (in m2). The larger the area of the opening, the more efficient the resonator is at absorbing sound waves.
- V is the volume of the resonator cavity (in m3). The volume of air inside the cavity affects the frequency at which the resonator resonates.
- L is the effective length of the mouth, which can be approximated by the length of the duct (in m). The length of the duct connecting the opening to the cavity modulates the resonant frequency.
- Room Acoustic Treatment: In spaces like theaters, recording studios, and concert halls, they help reduce unwanted frequencies, enhance sound quality, and create balanced acoustic environments by absorbing specific resonant frequencies.
- Industrial Noise Control: In industrial and automotive settings, they reduce noise from machines and vehicles, improving safety and comfort by attenuating disruptive noise frequencies.
- Acoustic Structure Design: Helmholtz resonators are integrated into noise barriers and sound-absorbing panels to optimize sound management in architectural and engineering projects.
- Advanced Technology Applications: In modern technologies, such as active noise reduction and intelligent acoustic devices, resonators enhance acoustic performance in dynamic environments.
- Geometry: Each hexagon is made up of six sides of equal length, in this case, 3 mm each. The internal angles of the hexagon are all 120°. The hexagons are arranged in a repeating grid and fit perfectly together with no gaps between them.
- Size and Area: The side length of each cell is 3 mm. The area of a single hexagonal cell can be calculated using the formula for the area of a regular hexagon:
- Thickness of the structure: When applied to a panel or material, the thickness of the honeycomb structure may vary depending on the application, with a depth of cells that can affect the stiffness and mechanical or acoustic properties of the material. In our case, the thickness of the structure is 13 mm.
- Material: The structure can be made of different materials, such as aluminum, plastic, or composites, which provide specific properties such as lightness, strength, and sound absorption or thermal insulation capacity. In this study, resinated aramid paper was used.
- Mechanical and Acoustic Properties: The hexagonal configuration distributes loads evenly, making the structure light but strong. In the acoustic context, this configuration can help dissipate sound waves, improving sound absorption and vibration reduction.
- High Mechanical Strength: Combines the tensile strength of aramid fibers with the compressive strength of resin, making it ideal for lightweight, rigid panels in sandwich structures and composites.
- Thermal Resistance: Withstands high temperatures without structural degradation, suitable for aerospace and electronic applications requiring thermal stability.
- Thermal and Electrical Insulation: Natural insulating properties enhanced by resin, widely used in transformers, cables, and electric motors for thermal and electrical insulation.
- Lightweight: Low density compared to metals like steel or aluminum, advantageous in aerospace, automotive, and high-performance industries focused on weight reduction.
- Chemical Resistance: Offers durability against acids, bases, and solvents, making it suitable for use in chemically aggressive environments.
- Vibration and Sound Absorption: Effectively dissipates energy from vibrations and sound waves, ideal for acoustic panels and noise reduction applications.
- Fire Resistance: Naturally flame-resistant aramid fibers combined with flame-retardant resin provide enhanced fire safety for public transport, building materials, and defense applications.
3.2. Measurement of Acoustic Properties of Metamaterial
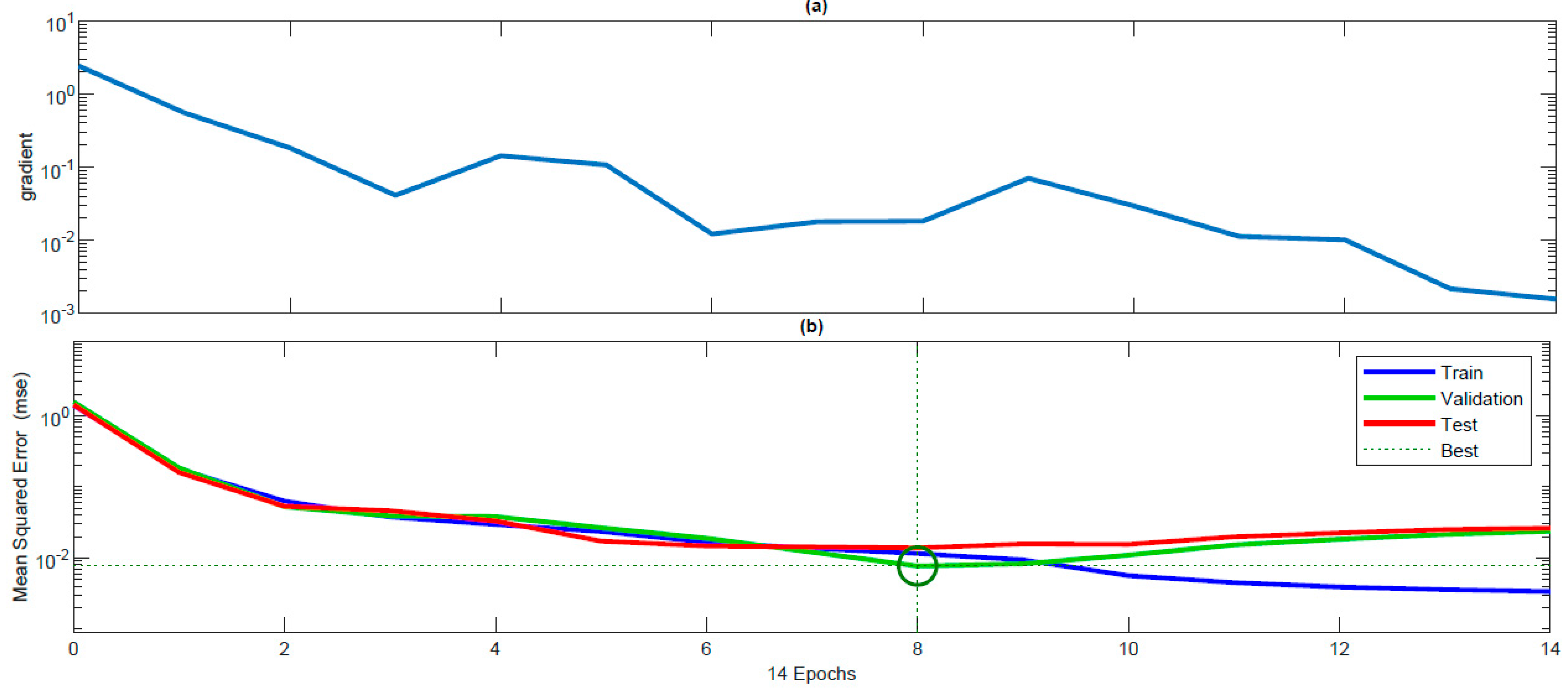
3.3. Artificial Neural Network (ANN) Based Modeling
- 1.
- Input Layer: This layer is responsible for accepting and standardizing input signals so they can be effectively processed by the neurons in the network.
- 2.
- Hidden Layers: These layers carry out the computational processing, with additional layers adding complexity and improving the network’s learning capability.
- 3.
- Output Layer: This layer compiles the outputs from the hidden layers and formats them for the network’s final response.
4. Results and Discussion
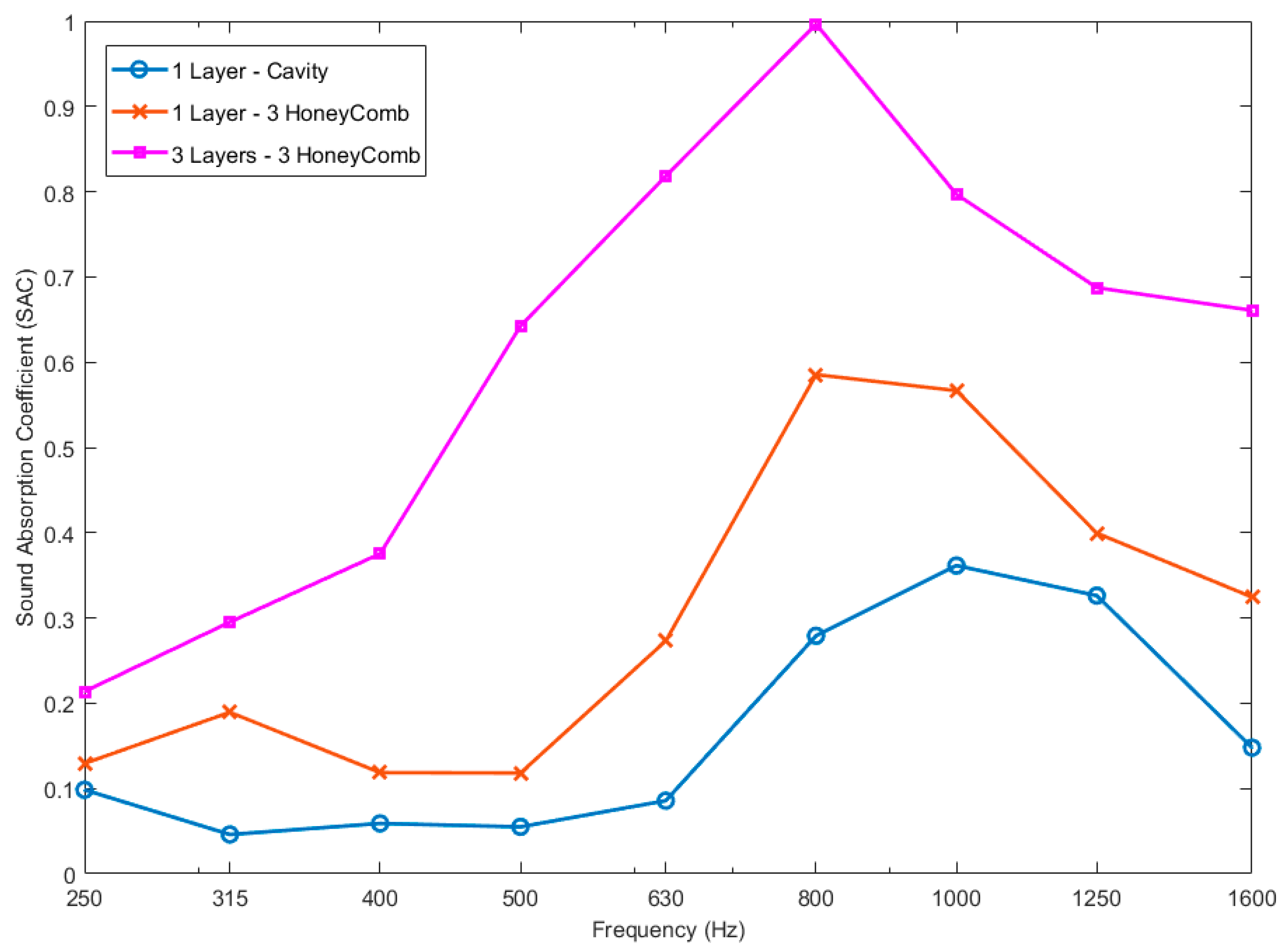
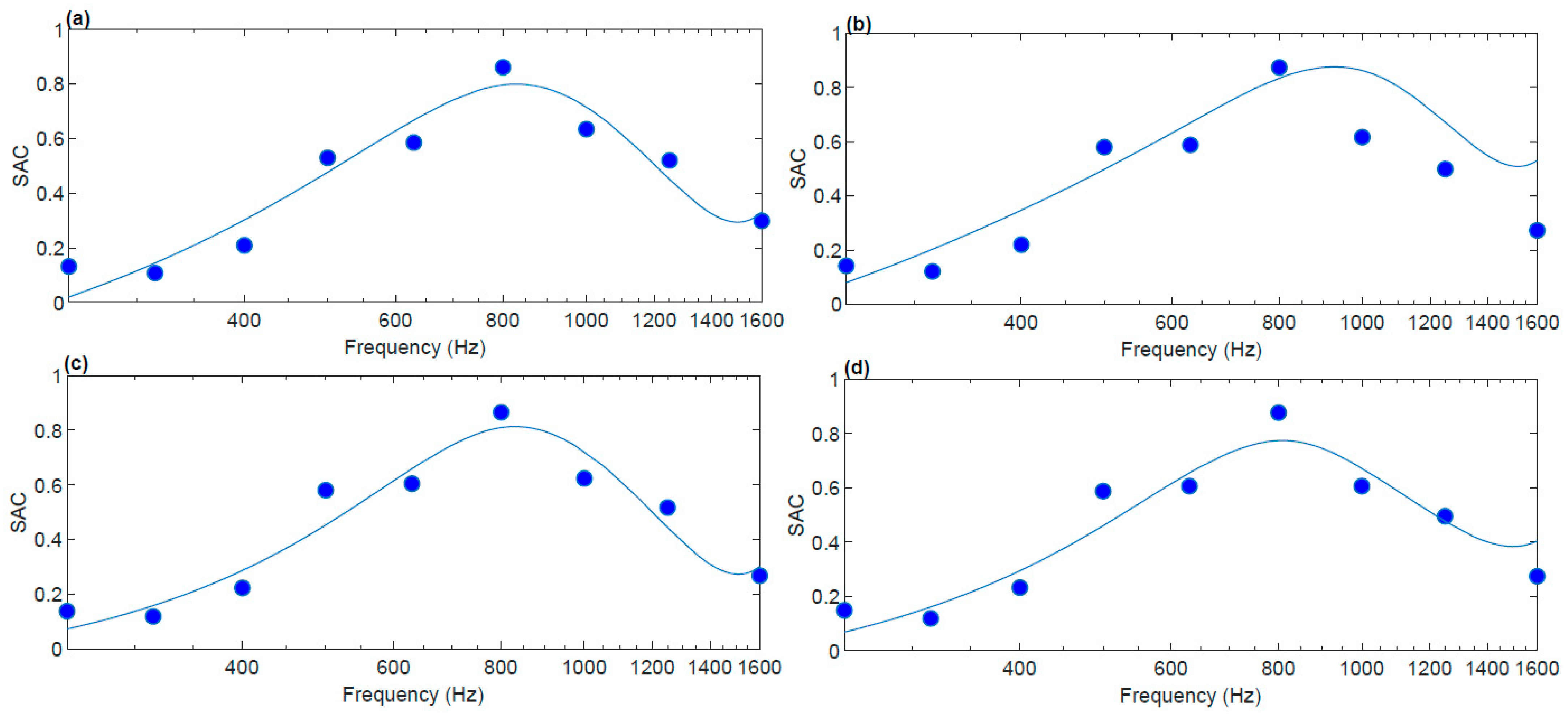
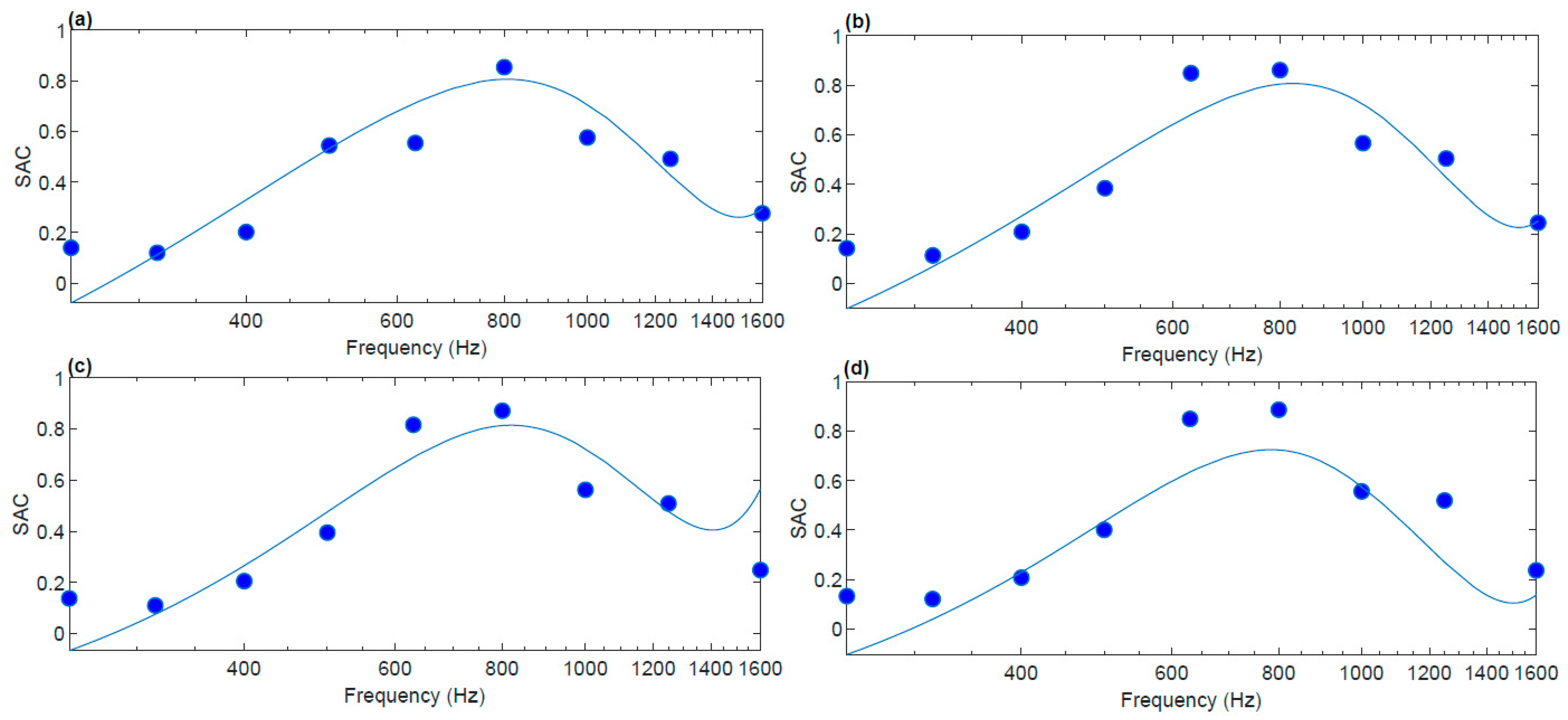
4.1. Analysis of Acoustic Characteristics of the Helmholtz Resonator-Based Metamaterial
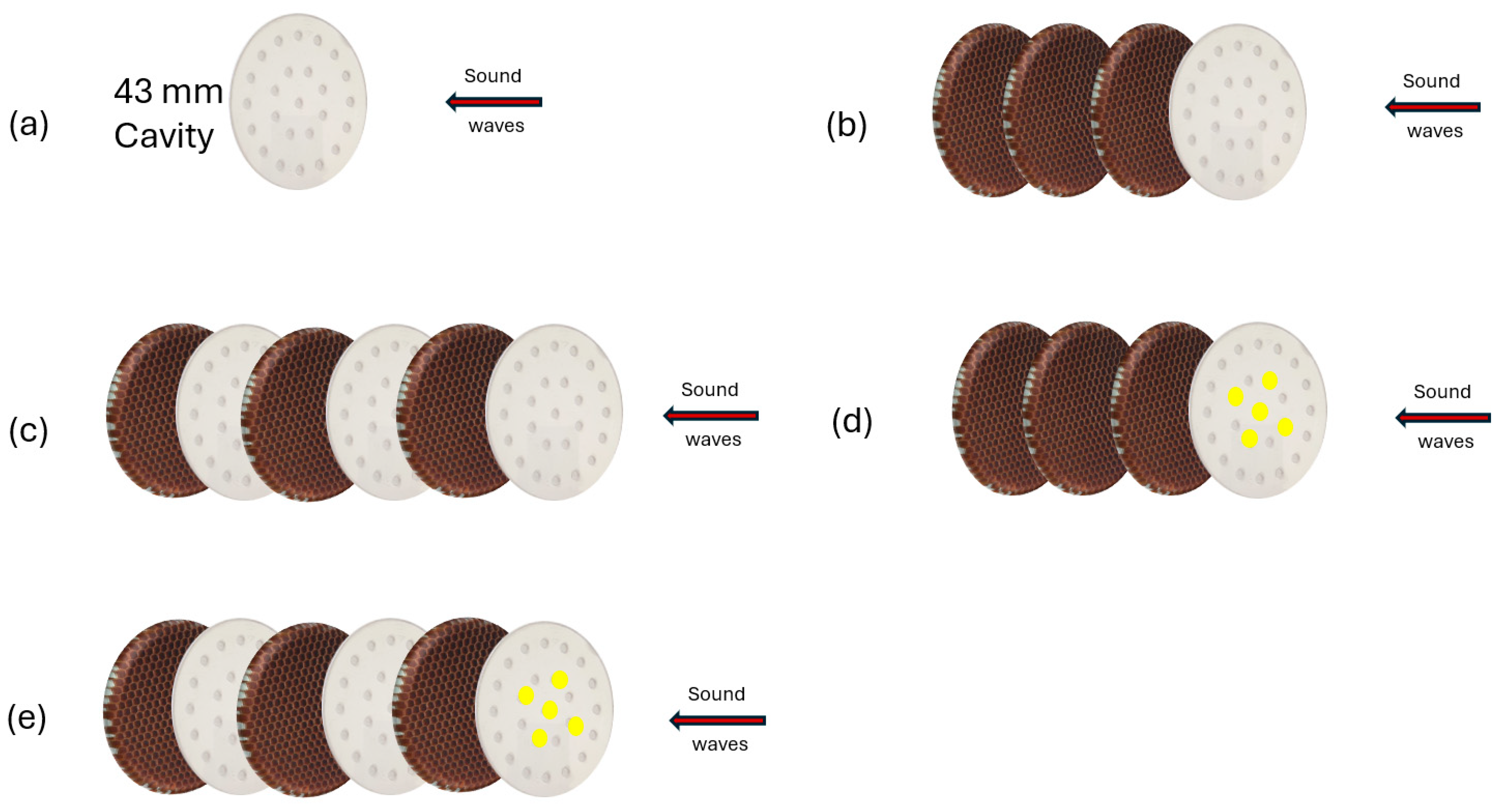
- (a)
- A perforated plexiglass disk and a 43 mm cavity;
- (b)
- A perforated plexiglass disk and three layers of honeycomb;
- (c)
- Three perforated plexiglass disks and three layers of honeycomb;
- (d)
- A perforated plexiglass disk, three layers of honeycomb and additional masses on the disk;
- (e)
- Three perforated plexiglass disks, three layers of honeycomb and additional masses on the first disk.
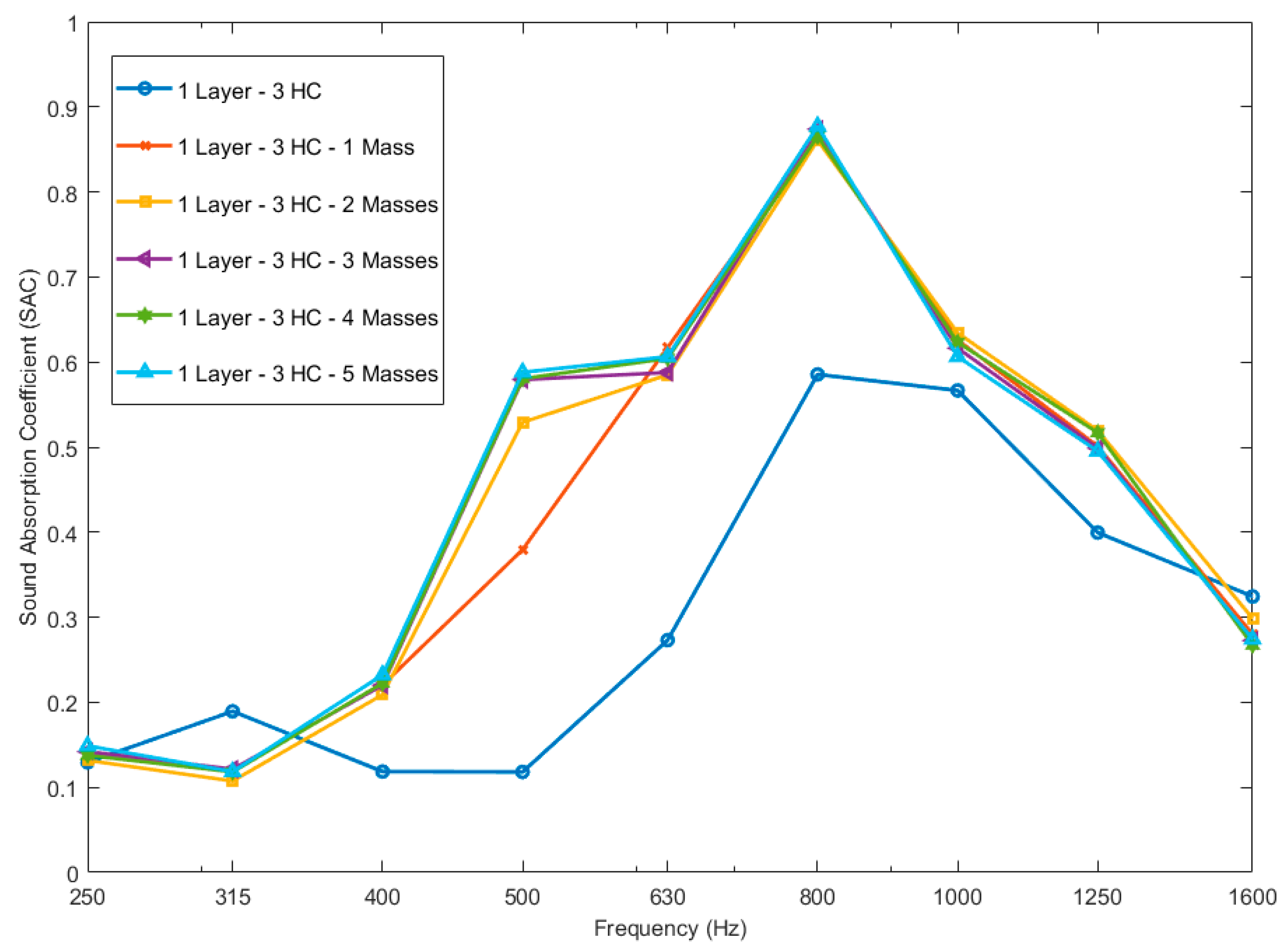
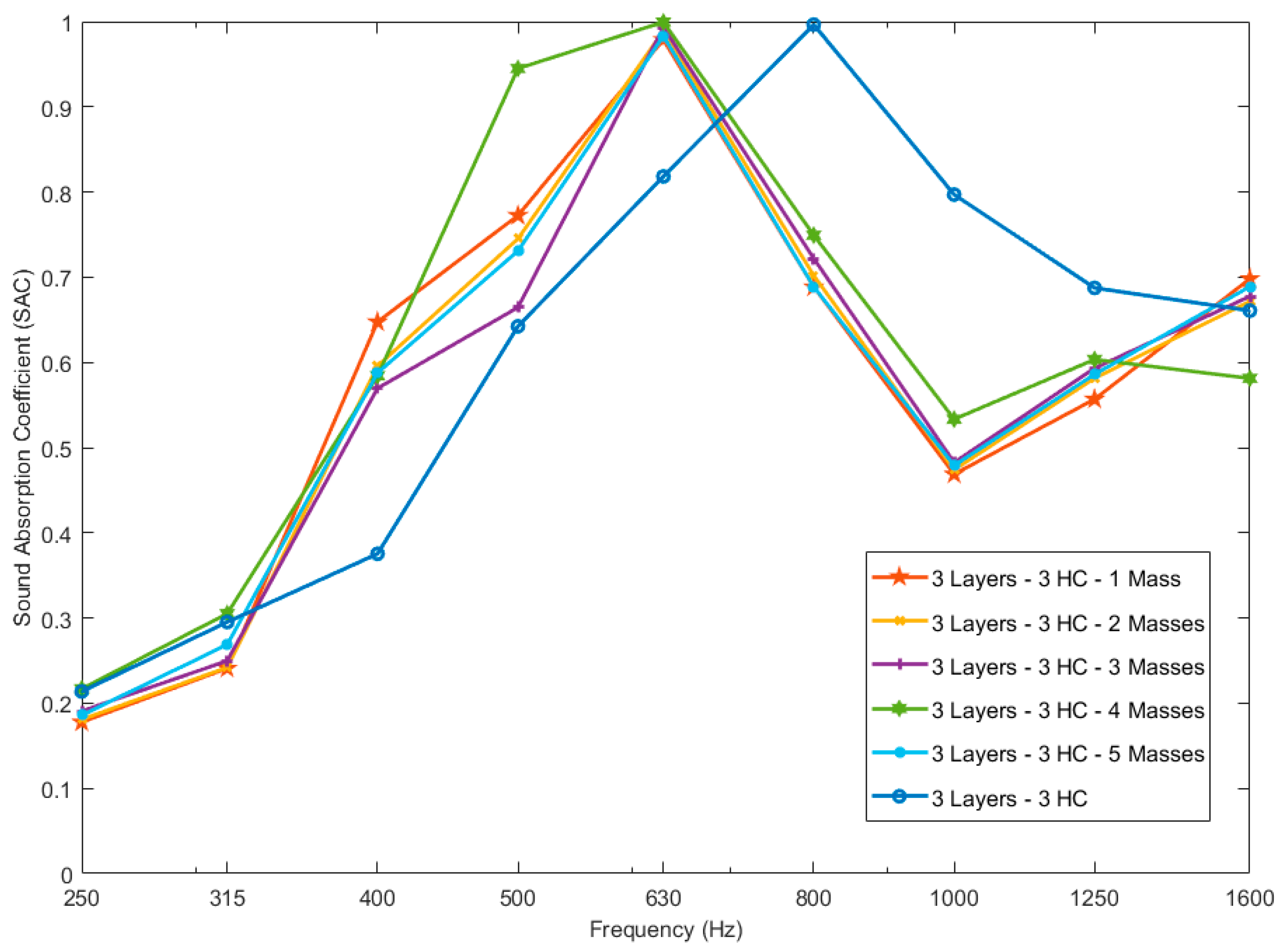
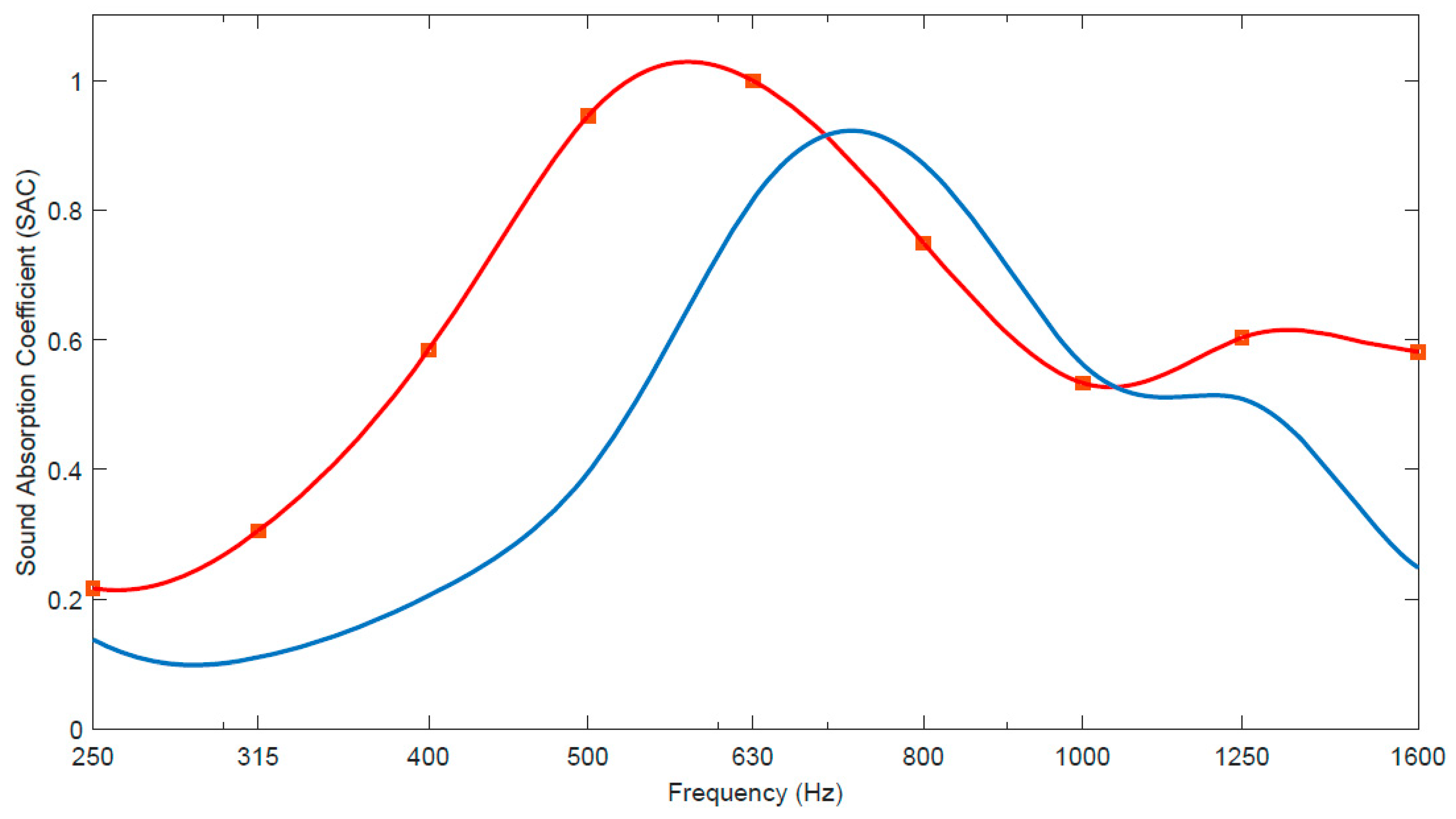
4.2. Optimization of the Metamaterial Configuration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Gao, N.; Zhang, Z.; Deng, J.; Guo, X.; Cheng, B.; Hou, H. Acoustic metamaterials for noise reduction: A review. Adv. Mater. Technol. 2022, 7, 2100698. [Google Scholar] [CrossRef]
- Haberman, M.R.; Guild, M.D. Acoustic metamaterials. Phys. Today 2016, 69, 42–48. [Google Scholar] [CrossRef]
- Ma, G.; Sheng, P. Acoustic metamaterials: From local resonances to broad horizons. Sci. Adv. 2016, 2, e1501595. [Google Scholar] [CrossRef]
- Li, J.; Wen, X.; Sheng, P. Acoustic metamaterials. J. Appl. Phys. 2021, 129, 171103. [Google Scholar] [CrossRef]
- Chen, S.; Fan, Y.; Fu, Q.; Wu, H.; Jin, Y.; Zheng, J.; Zhang, F. A review of tunable acoustic metamaterials. Appl. Sci. 2018, 8, 1480. [Google Scholar] [CrossRef]
- Ingard, U. On the theory and design of acoustic resonators. J. Acoust. Soc. Am. 1953, 25, 1037–1061. [Google Scholar] [CrossRef]
- Ciaburro, G.; Iannace, G. Numerical simulation for the sound absorption properties of ceramic resonators. Fibers 2020, 8, 77. [Google Scholar] [CrossRef]
- Liu, Y.; Cai, Y.; Zhang, Y.; Tovstopyat, A.; Liu, S.; Sun, C. Materials, design, and characteristics of bulk acoustic wave resonator: A review. Micromachines 2020, 11, 630. [Google Scholar] [CrossRef]
- Li, H.-Z.; Liu, X.-C.; Liu, Q.; Li, S.; Yang, J.-S.; Tong, L.-L.; Shi, S.-B.; Schmidt, R.; Schröder, K.-U. Sound insulation performance of double membrane-type acoustic metamaterials combined with a Helmholtz resonator. Appl. Acoust. 2023, 205, 109297. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Xie, S. A lightweight multilayer honeycomb membrane-type acoustic metamaterial. Appl. Acoust. 2020, 168, 107427. [Google Scholar] [CrossRef]
- Xing, T.; Gai, X.; Zhao, J.; Li, X.; Cai, Z.; Guan, X.; Wang, F. Low frequency sound absorption of adjustable membrane-type acoustic metamaterials. Appl. Acoust. 2022, 188, 108586. [Google Scholar] [CrossRef]
- Sun, Y.; Yuan, X.; Jin, Z.; Hong, G.; Chen, M.; Zhou, M.; Fang, D. An effective method to enhance the underwater sound absorption performance by constructing a membrane-type acoustic metamaterial. J. Phys. D Appl. Phys. 2022, 55, 435302. [Google Scholar] [CrossRef]
- Gao, N.; Hou, H.; Wu, J.H. A composite and deformable honeycomb acoustic metamaterial. Int. J. Mod. Phys. B 2018, 32, 1850204. [Google Scholar] [CrossRef]
- Sui, N.; Yan, X.; Huang, T.Y.; Xu, J.; Yuan, F.G.; Jing, Y. A lightweight yet sound-proof honeycomb acoustic metamaterial. Appl. Phys. Lett. 2015, 106, 171905. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Ma, L. Sound insulation performance of curved sandwich structure combined with acoustic metamaterials. J. Vib. Control 2024, 30, 2993–3005. [Google Scholar] [CrossRef]
- Xie, S.; Yang, S.; Yang, C.; Wang, D. Sound absorption performance of a filled honeycomb composite structure. Appl. Acoust. 2020, 162, 107202. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, X.; Li, P.; Huang, G.; Feng, S.; Shen, C.; Han, B.; Zhang, X.; Jin, F.; Xu, F.; et al. Bioinspired engineering of honeycomb structure–Using nature to inspire human innovation. Prog. Mater. Sci. 2015, 74, 332–400. [Google Scholar] [CrossRef]
- Yang, M.; Ma, G.; Wu, Y.; Yang, Z.; Sheng, P. Homogenization scheme for acoustic metamaterials. Phys. Rev. B 2014, 89, 064309. [Google Scholar] [CrossRef]
- Popa, B.I.; Cummer, S.A. Design and characterization of broadband acoustic composite metamaterials. Phys. Rev. B—Condens. Matter Mater. Phys. 2009, 80, 174303. [Google Scholar] [CrossRef]
- Nakayama, M.; Matsuoka, T.; Saito, Y.; Uchida, N.; Inoue, K.; Mitani, H.; Akasaka, S.; Koga, S. A practically designed acoustic metamaterial sheet with two-dimensional connection of local resonators for sound insulation applications. J. Appl. Phys. 2021, 129, 105106. [Google Scholar] [CrossRef]
- Ciaburro, G.; Parente, R.; Iannace, G.; Puyana-Romero, V. Design optimization of three-layered metamaterial acoustic absorbers based on PVC reused membrane and metal washers. Sustainability 2022, 14, 4218. [Google Scholar] [CrossRef]
- Ning, S.; Yang, F.; Luo, C.; Liu, Z.; Zhuang, Z. Low-frequency tunable locally resonant band gaps in acoustic metamaterials through large deformation. Extrem. Mech. Lett. 2020, 35, 100623. [Google Scholar] [CrossRef]
- Ciaburro, G.; Iannace, G. Membrane-type acoustic metamaterial using cork sheets and attached masses based on reused materials. Appl. Acoust. 2022, 189, 108605. [Google Scholar] [CrossRef]
- Mahesh, K.; Ranjith, S.K.; Mini, R.S. Recent advancements in helmholtz resonator based low-frequency acoustic absorbers: A critical review. Arch. Comput. Methods Eng. 2024, 31, 2079–2107. [Google Scholar] [CrossRef]
- Hoppen, H.; Langfeldt, F.; Gleine, W.; Von Estorff, O. Helmholtz resonator with two resonance frequencies by coupling with a mechanical resonator. J. Sound Vib. 2023, 559, 117747. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, D.; Liu, J.; Hu, B.; Wen, J. Transmission and bandgap characteristics of a duct mounted with multiple hybrid Helmholtz resonators. Appl. Acoust. 2021, 183, 108266. [Google Scholar] [CrossRef]
- Chen, J.-S.; Chen, Y.-B.; Cheng, Y.-H.; Chou, L.-C. A sound absorption panel containing coiled Helmholtz resonators. Phys. Lett. A 2020, 384, 126887. [Google Scholar] [CrossRef]
- Dogra, S.; Gupta, A. Design, manufacturing, and acoustical analysis of a Helmholtz resonator-based metamaterial plate. Acoustics 2021, 3, 630–641. [Google Scholar] [CrossRef]
- Rouxel, J.; Coutard, J.G.; Gidon, S.; Lartigue, O.; Nicoletti, S.; Parvitte, B.; Glière, A. Miniaturized differential Helmholtz resonators for photoacoustic trace gas detection. Sens. Actuators B Chem. 2016, 236, 1104–1110. [Google Scholar] [CrossRef]
- Romero-García, V.; Jimenez, N.; Theocharis, G.; Achilleos, V.; Merkel, A.; Richoux, O.; Pagneux, V. Design of acoustic metamaterials made of Helmholtz resonators for perfect absorption by using the complex frequency plane. Comptes Rendus Phys. 2020, 21, 713–749. [Google Scholar] [CrossRef]
- Koutserimpas, T.T.; Rivet, E.; Lissek, H.; Fleury, R. Active acoustic resonators with reconfigurable resonance frequency, absorption, and bandwidth. Phys. Rev. Appl. 2019, 12, 054064. [Google Scholar] [CrossRef]
- Komkin, A.I.; Mironov, M.A.; Bykov, A.I. Sound absorption by a Helmholtz resonator. Acoust. Phys. 2017, 63, 385–392. [Google Scholar] [CrossRef]
- Langfeldt, F.; Hoppen, H.; Gleine, W. Broadband low-frequency sound transmission loss improvement of double walls with Helmholtz resonators. J. Sound Vib. 2020, 476, 115309. [Google Scholar] [CrossRef]
- Neri, M.; Levi, E.; Cuerva, E.; Pardo-Bosch, F.; Zabaleta, A.G.; Pujadas, P. Sound absorbing and insulating low-cost panels from end-of-life household materials for the development of vulnerable contexts in circular economy perspective. Appl. Sci. 2021, 11, 5372. [Google Scholar] [CrossRef]
- Zhang, B.; Jia, L.; Tian, M.; Ning, N.; Zhang, L.; Wang, W. Surface and interface modification of aramid fiber and its reinforcement for polymer composites: A review. Eur. Polym. J. 2021, 147, 110352. [Google Scholar] [CrossRef]
- Du, X.; Kong, H.; Xu, Q.; Li, B.; Yu, M.; Li, Z. Effects of aramid nanofibers on the mechanical properties of epoxy resin and improved adhesion with aramid fiber. Polym. Compos. 2022, 43, 2103–2114. [Google Scholar] [CrossRef]
- Jing, W.; Zhang, F.; Chen, H. Comparative tribological performance and erosion resistance of epoxy resin composite coatings reinforced with aramid fiber and carbon fiber. Colloids Surf. A Physicochem. Eng. Asp. 2022, 648, 129354. [Google Scholar] [CrossRef]
- EN ISO 10534-2; Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes—Part 2: Transfer-Function Method. ISO: Geneva, Switzerland, 2023.
- Abdolrasol, M.G.M.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial neural networks based optimization techniques: A review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Ciaburro, G. Machine fault detection methods based on machine learning algorithms: A review. Math. Biosci. Eng. 2022, 19, 11453–11490. [Google Scholar] [CrossRef]
- Kumar, A.; Gandhi, C.P.; Zhou, Y.; Kumar, R.; Xiang, J. Improved deep convolution neural network (CNN) for the identification of defects in the centrifugal pump using acoustic images. Appl. Acoust. 2020, 167, 107399. [Google Scholar] [CrossRef]
- Mushtaq, Z.; Su, S.-F. Environmental sound classification using a regularized deep convolutional neural network with data augmentation. Appl. Acoust. 2020, 167, 107389. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Classification of underwater acoustical dataset using neural network trained by Chimp Optimization Algorithm. Appl. Acoust. 2020, 157, 107005. [Google Scholar] [CrossRef]
- Mushtaq, Z.; Su, S.F.; Tran, Q.V. Spectral images based environmental sound classification using CNN with meaningful data augmentation. Appl. Acoust. 2021, 172, 107581. [Google Scholar] [CrossRef]
- Liu, X.; Tian, S.; Tao, F.; Yu, W. A review of artificial neural networks in the constitutive modeling of composite materials. Compos. Part B Eng. 2021, 224, 109152. [Google Scholar] [CrossRef]
- Ciaburro, G.; Iannace, G. Modeling acoustic metamaterials based on reused buttons using data fitting with neural network. J. Acoust. Soc. Am. 2021, 150, 51–63. [Google Scholar] [CrossRef]
- Corredor-Bedoya, A.C.; Acuña, B.; Serpa, A.L.; Masiero, B. Effect of the excitation signal type on the absorption coefficient measurement using the impedance tube. Appl. Acoust. 2021, 171, 107659. [Google Scholar] [CrossRef]
- Bravo-Moncayo, L.; Puyana-Romero, V.; Argotti-Gómez, M.; Ciaburro, G. Enhanced Environmental Sustainability for the Acoustic Absorption Properties of Cabuya Fiber in Building Construction Using Machine Learning Predictive Model. Sustainability 2024, 16, 6204. [Google Scholar] [CrossRef]
- Ciaburro, G.; Romero, V.P.; Iannace, G.; Bravo Moncayo, L. Improving Acoustic Properties of Sandwich Structures Using Recycled Membrane and HoneyComb Composite (RMHCC). Buildings 2024, 14, 2878. [Google Scholar] [CrossRef]
- Ciaburro, G.; Puyana-Romero, V.; Iannace, G.; Jaramillo-Cevallos, W.A. Characterization and modeling of corn stalk fibers tied with clay using support vector regression algorithms. J. Nat. Fibers 2022, 19, 7141–7156. [Google Scholar] [CrossRef]
- Dong, C.; Liu, Z.; Pierce, R.; Liu, X.; Yi, X. Sound absorption performance of a micro perforated sandwich panel with honeycomb-hierarchical pore structure core. Appl. Acoust. 2023, 203, 109200. [Google Scholar] [CrossRef]
- Xie, S.; Wang, D.; Feng, Z.; Yang, S. Sound absorption performance of microperforated honeycomb metasurface panels with a combination of multiple orifice diameters. Appl. Acoust. 2020, 158, 107046. [Google Scholar] [CrossRef]
- Liao, G.; Luan, C.; Wang, Z.; Liu, J.; Yao, X.; Fu, J. Acoustic metamaterials: A review of theories, structures, fabrication approaches, and applications. Adv. Mater. Technol. 2021, 6, 2000787. [Google Scholar] [CrossRef]
- Banadkooki, F.B.; Ehteram, M.; Ahmed, A.N.; Teo, F.Y.; Ebrahimi, M.; Fai, C.M.; El-Shafie, A. Suspended sediment load prediction using artificial neural network and ant lion optimization algorithm. Environ. Sci. Pollut. Res. 2020, 27, 38094–38116. [Google Scholar] [CrossRef] [PubMed]
- Khan, I.; Raja, M.A.Z.; Shoaib, M.; Kumam, P.; Alrabaiah, H.; Shah, Z.; Islam, S. Design of neural network with Levenberg-Marquardt and Bayesian regularization backpropagation for solving pantograph delay differential equations. IEEE Access 2020, 8, 137918–137933. [Google Scholar] [CrossRef]
- Hodson, T.O. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Temizhan, E.; Mirtagioglu, H.; Mendes, M. Which correlation coefficient should be used for investigating relations between quantitative variables. Acad. Sci. Res. J. Eng. Technol. Sci. 2022, 85, 265–277. [Google Scholar]
- Yuan, M.; Zhang, W.; Tai, Y.; Yan, W.; Jiang, Y.; Zhang, S.; Xie, Y. Tympanic membrane metamaterial inspired multifunctional low-frequency acoustic triboelectric nanogenerator. Nano Energy 2024, 128, 109816. [Google Scholar] [CrossRef]
- Sun, K.; Fan, Y.; Chen, S.; Yang, F.; Li, J.; Fu, Q.; Zhang, F. Highly efficient transmissive wavefront steering with acoustic metagrating composed of Helmholtz-resonators. Mater. Des. 2022, 224, 111352. [Google Scholar] [CrossRef]
- Chen, S.; Fan, Y.; Yang, F.; Jin, Y.; Fu, Q.; Zheng, J.; Zhang, F. Engineering Coiling-Up space metasurfaces for broadband low-frequency acoustic absorption. Phys. Status Solidi (RRL)—Rapid Res. Lett. 2019, 13, 1900426. [Google Scholar] [CrossRef]
- Sun, K.; Fan, Y.; Chen, S.; Ye, Z.; Li, Z.; Zhang, Q.; Zhang, F. Rabi-Like Splitting in Acoustic Cavity Coupled with Membrane-Type Metasurface. Adv. Eng. Mater. 2024, 26, 2400340. [Google Scholar] [CrossRef]
- Yuan, M.; Cao, Z.; Luo, J.; Chou, X. Recent developments of acoustic energy harvesting: A review. Micromachines 2019, 10, 48. [Google Scholar] [CrossRef] [PubMed]

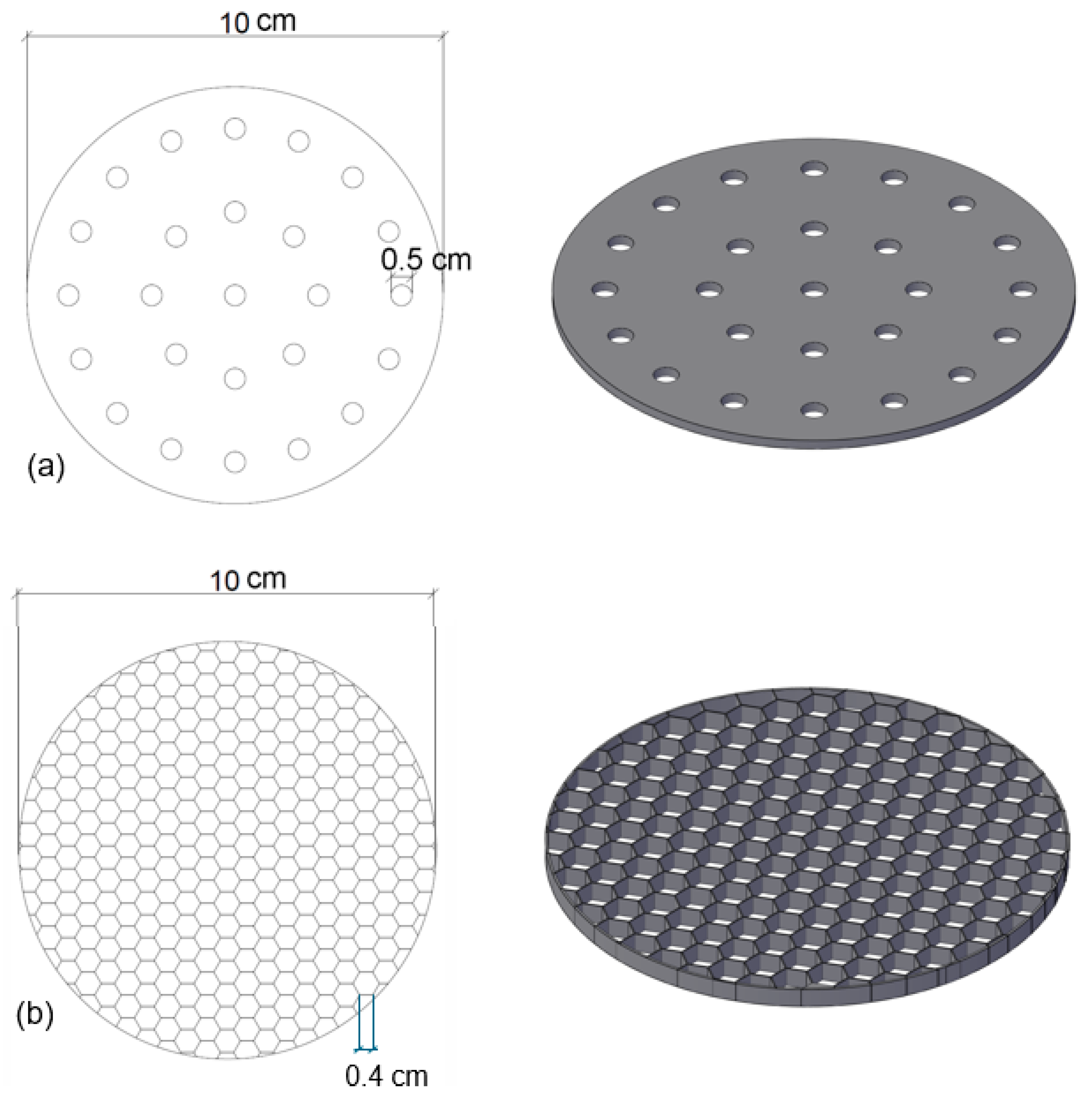



| Property | Value | Unit of Measure | Description |
|---|---|---|---|
| Density | 30–80 | kg/m3 | Varies based on the amount of resin used and the density of the aramid paper. |
| Compressive strength | 1.0–3.5 | MPa | Depends on the direction of compression (normal to the hexagonal cell) and the resin used. |
| Elastic modulus (compression) | 50–150 | MPa | Describes the stiffness of the structure in the direction of compression. |
| Shear strength (plane) | 0.5–1.5 | MPa | Ability of the structure to resist shear forces. |
| Shear modulus (plane) | 20–60 | MPa | Measure of the stiffness of the structure in response to shear forces. |
| Operating temperature | −60–180 | °C | Resistance to extreme temperatures due to the thermal stability of the aramid fibers and resin. |
| Flame resistance | Alta | - | Aramid fibers are flame retardant and the resin can be treated to further improve this property. |
| Water absorption | <1 | - | Low moisture absorption, useful in environments with high exposure to humidity or water. |
| Chemical resistance | Good | - | Resistant to oils, solvents and many chemicals, even in harsh conditions. |
| Dimensional stability | Excellent | - | Retains its shape even under thermal or mechanical stress. |
| Thermal insulation | Good | - | Due to the low thermal conductivity of the aramid fibers. |
| Sound insulation | Good | - | The honeycomb structure contributes to sound attenuation, useful in acoustic applications. |
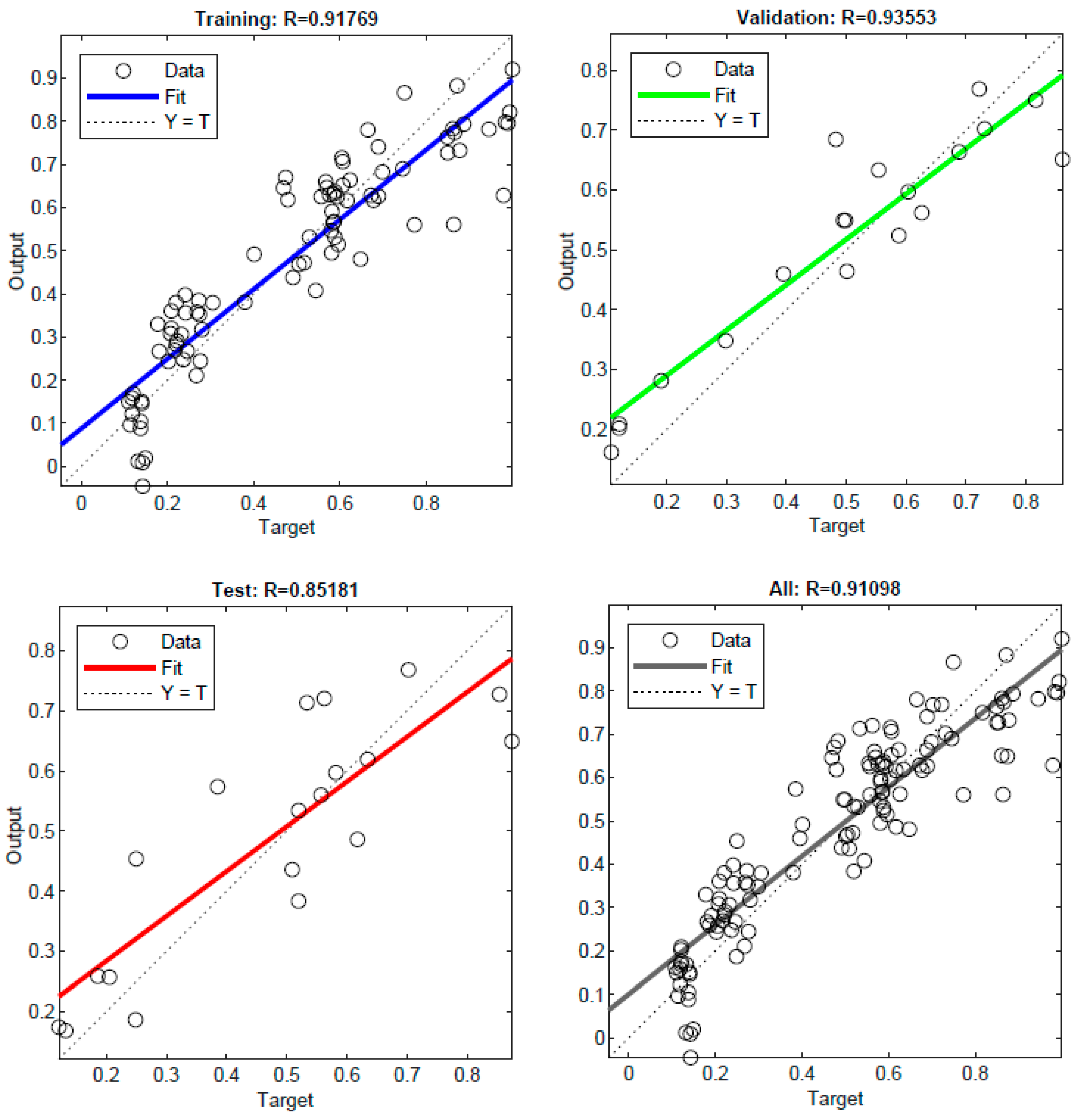
| MSE | R2 | |
|---|---|---|
| Training | 0.0115 | 0.9177 |
| Validation | 0.0077 | 0.9355 |
| Test | 0.0138 | 0.8518 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciaburro, G.; Iannace, G.; Romero, V.P. Optimizing Controlled-Resonance Acoustic Metamaterials with Perforated Plexiglass Disks, Honeycomb Structures, and Embedded Metallic Masses. Fibers 2025, 13, 11. https://doi.org/10.3390/fib13020011
Ciaburro G, Iannace G, Romero VP. Optimizing Controlled-Resonance Acoustic Metamaterials with Perforated Plexiglass Disks, Honeycomb Structures, and Embedded Metallic Masses. Fibers. 2025; 13(2):11. https://doi.org/10.3390/fib13020011
Chicago/Turabian StyleCiaburro, Giuseppe, Gino Iannace, and Virginia Puyana Romero. 2025. "Optimizing Controlled-Resonance Acoustic Metamaterials with Perforated Plexiglass Disks, Honeycomb Structures, and Embedded Metallic Masses" Fibers 13, no. 2: 11. https://doi.org/10.3390/fib13020011
APA StyleCiaburro, G., Iannace, G., & Romero, V. P. (2025). Optimizing Controlled-Resonance Acoustic Metamaterials with Perforated Plexiglass Disks, Honeycomb Structures, and Embedded Metallic Masses. Fibers, 13(2), 11. https://doi.org/10.3390/fib13020011








