Experimental Shear Behavior of Macro-Synthetic Fiber-Reinforced Concrete Panels
Abstract
1. Introduction
- Insufficient experimental data on the combined action of fibers and stirrups, particularly using macro-synthetic fibers at realistic volume fractions (<0.75%).
- Lack of studies employing pure shear loading, which is essential to decouple shear effects from flexure and more clearly isolate the fiber contribution.
- Absence of comparative assessments between experimental outcomes and existing shear strength prediction models or code provisions for hybrid fiber-stirrup systems.
2. Experimental Program
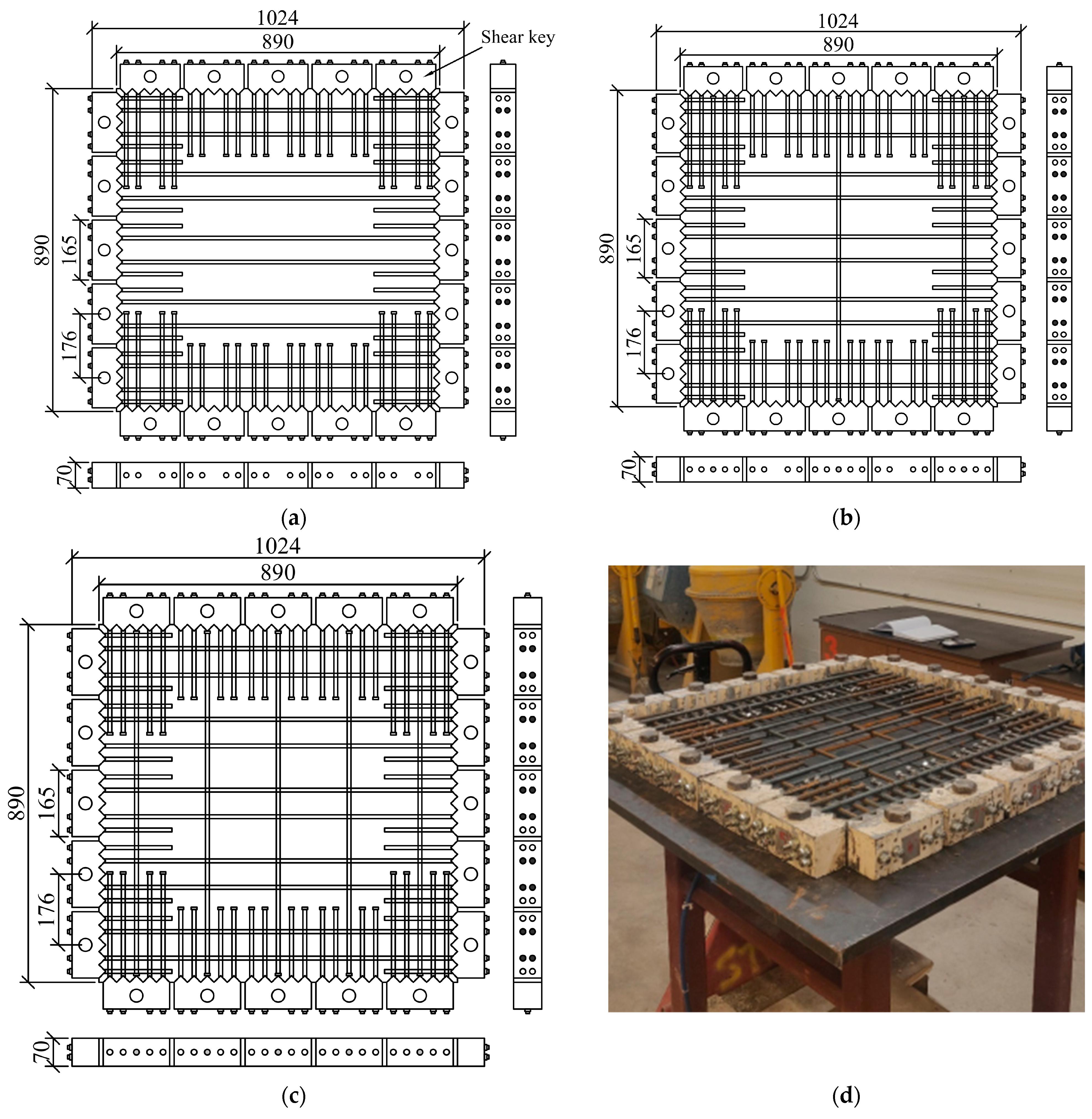
2.1. Specimen and Material Properties
2.2. Test Setup, Instrumentation and Loading
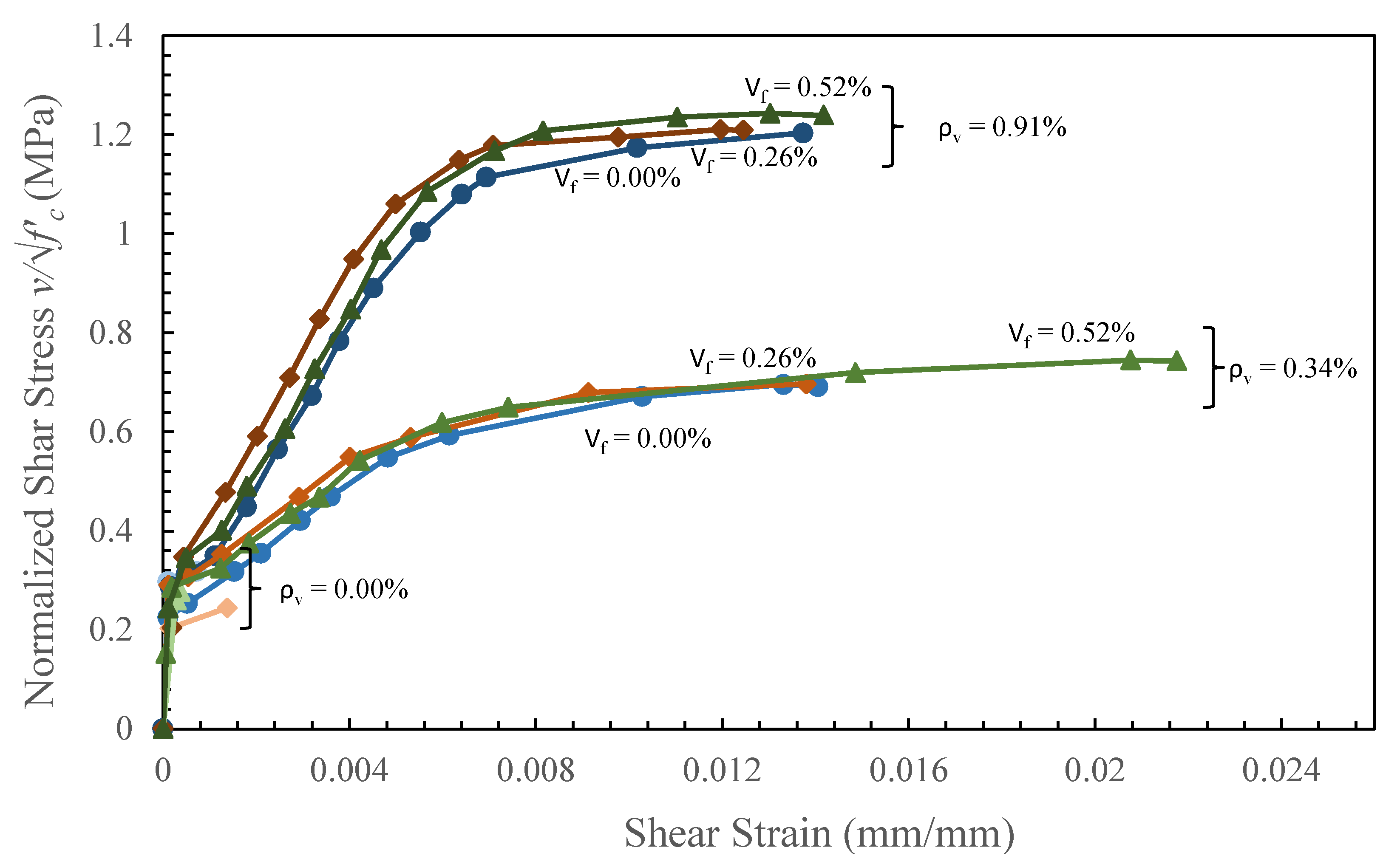
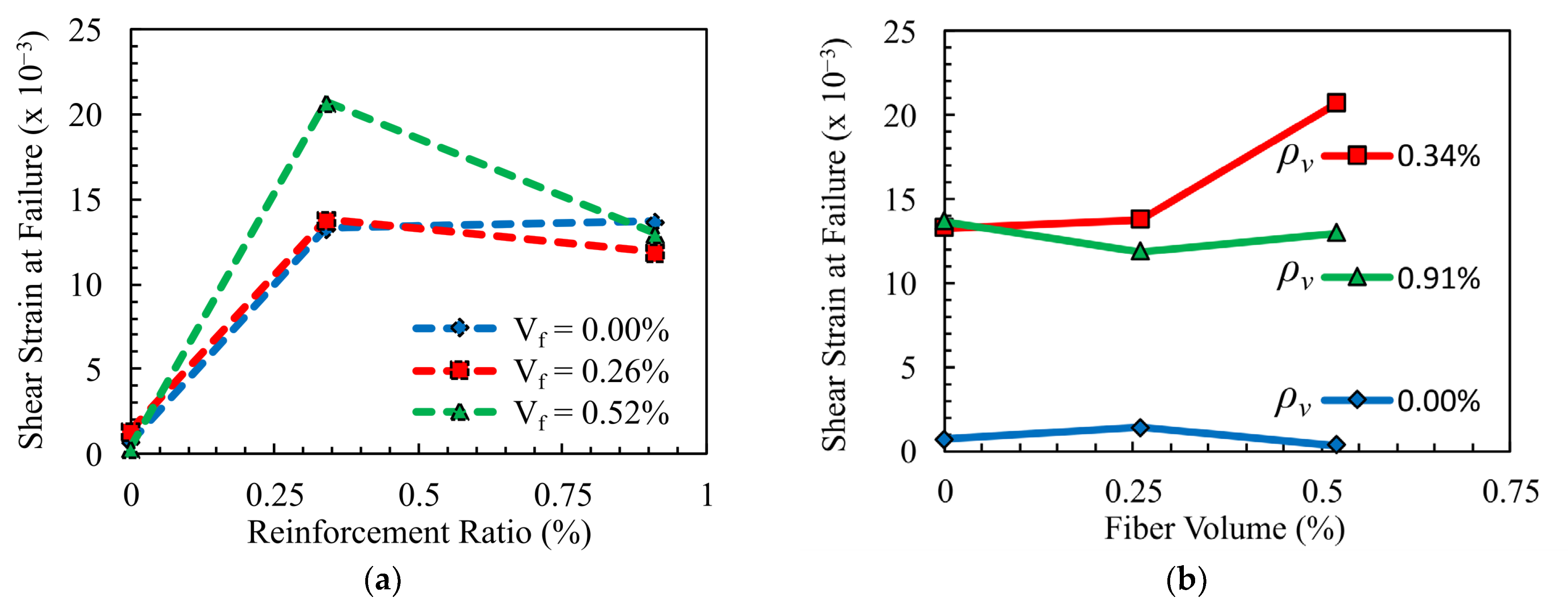
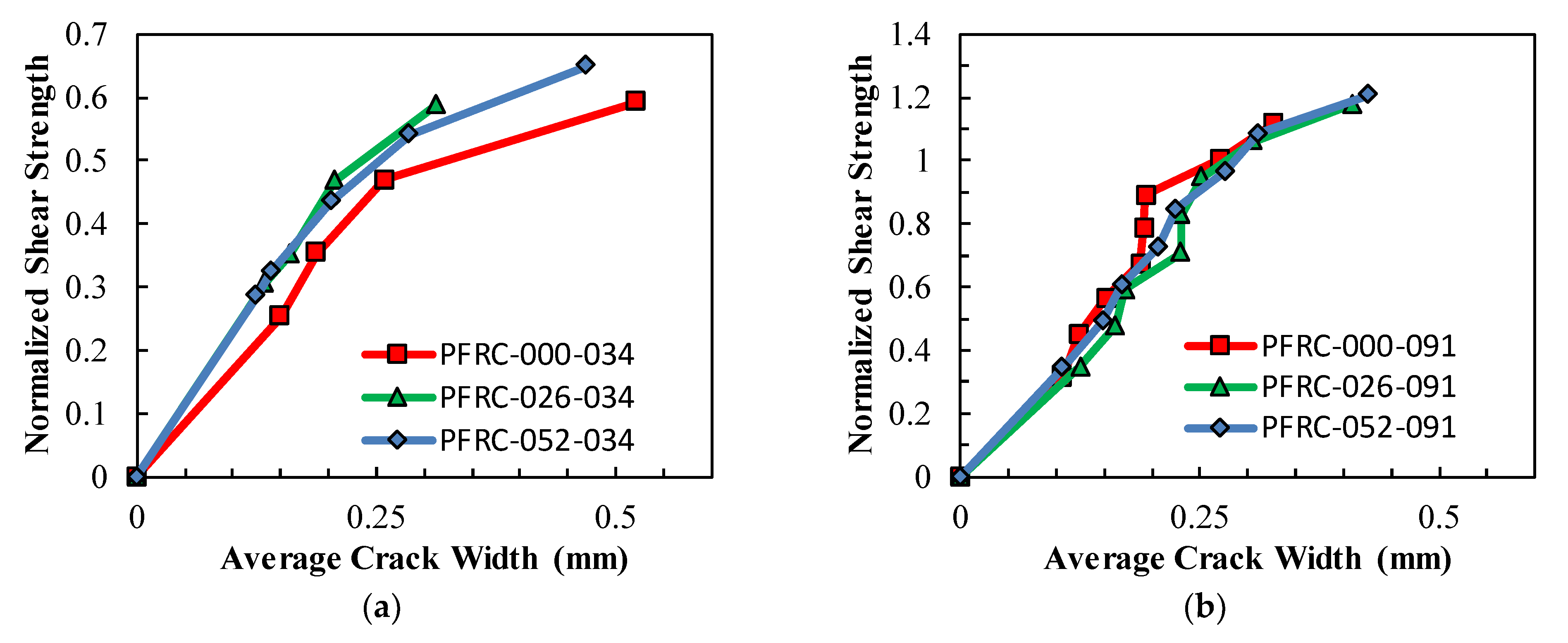
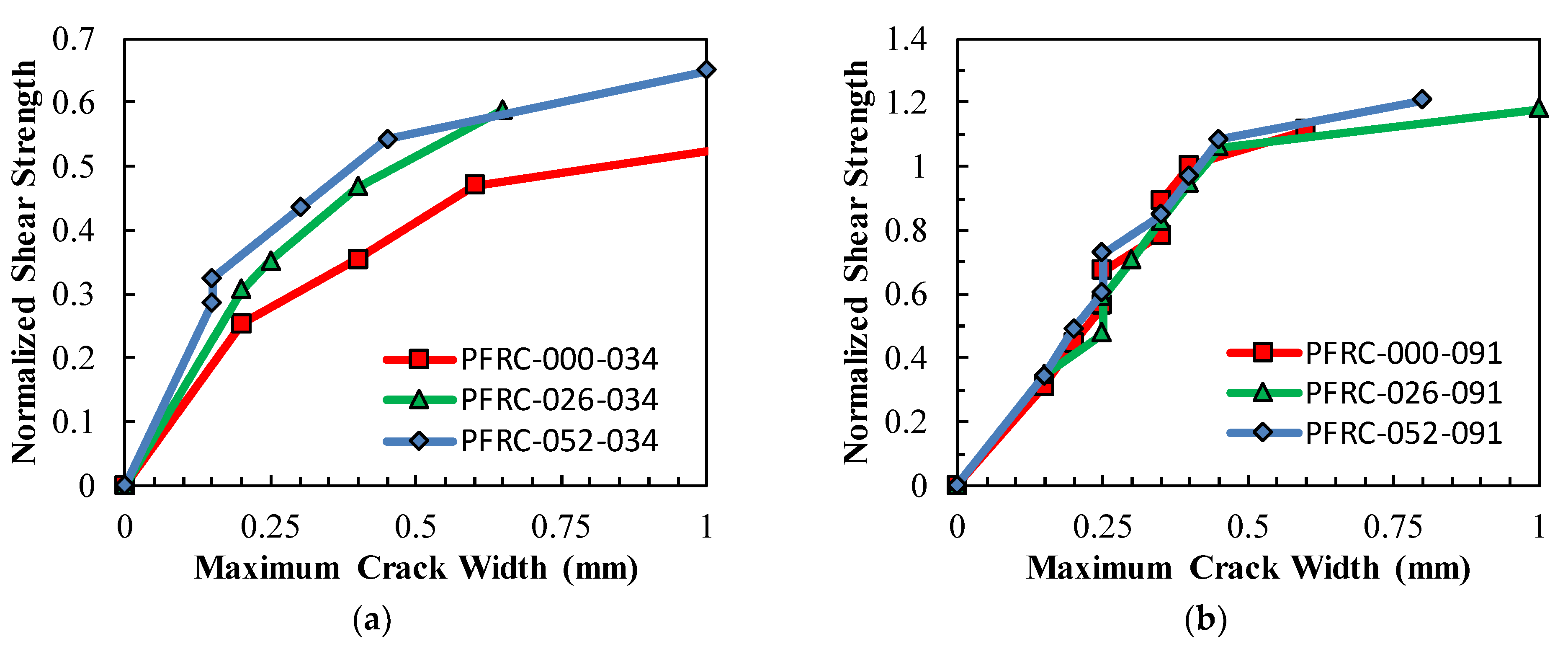
3. Experimental Results
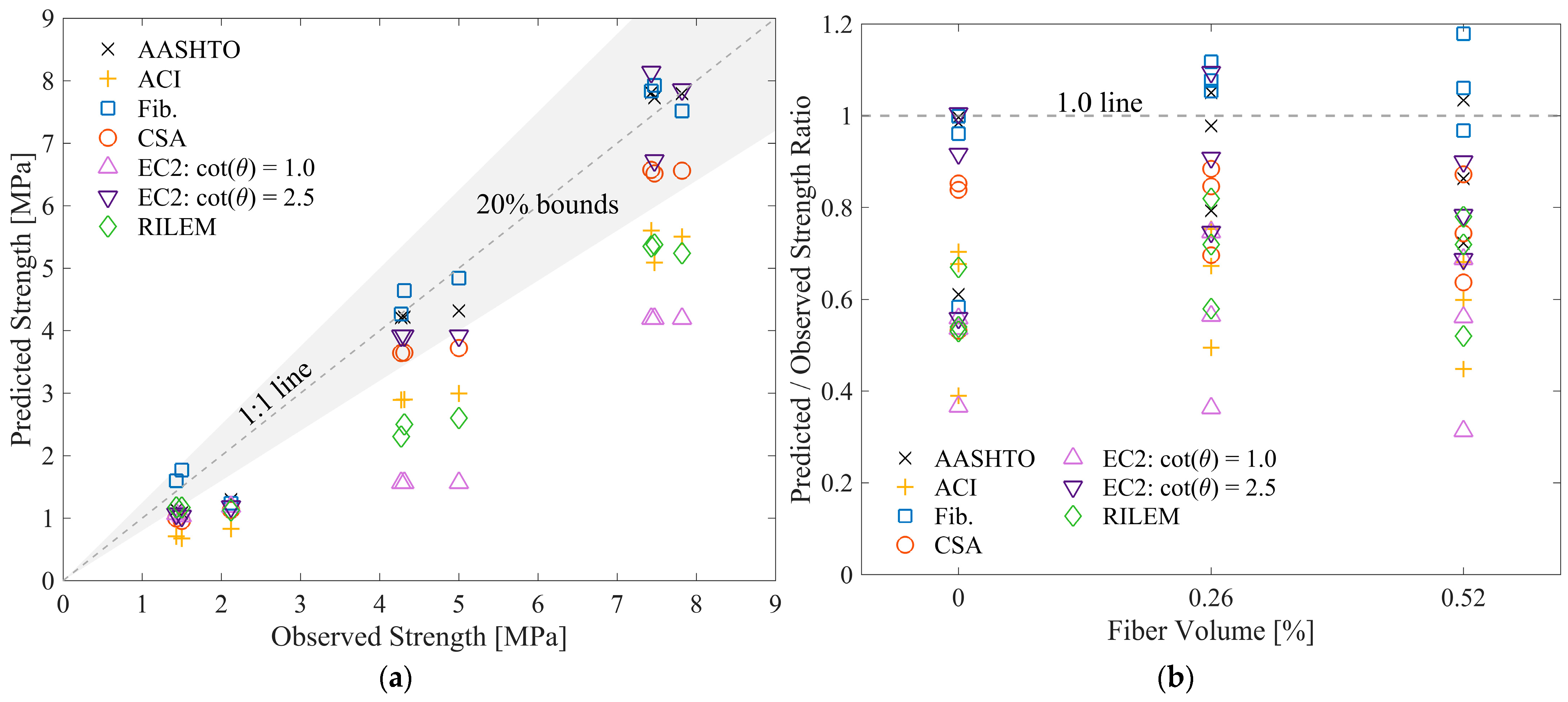
4. Comparison of Observed Strengths to Available Code Equations
5. Summary and Conclusions
- The addition of macro-synthetic fibers proved effective in reducing both maximum and average shear-induced crack widths in panels with a low transverse reinforcement ratio (ρv = 0.34%). At a shear stress corresponding to approximately 50% of specimen capacity, increasing the fiber volume fraction from 0% to 0.52% reduced the maximum crack width by 50% (from 0.6 mm to 0.3 mm) and the average crack width by 22% (from 0.32 mm to 0.25 mm). This benefit diminished in specimens with higher reinforcement, indicating that the effectiveness of fibers is influenced by the amount of transverse reinforcement present.
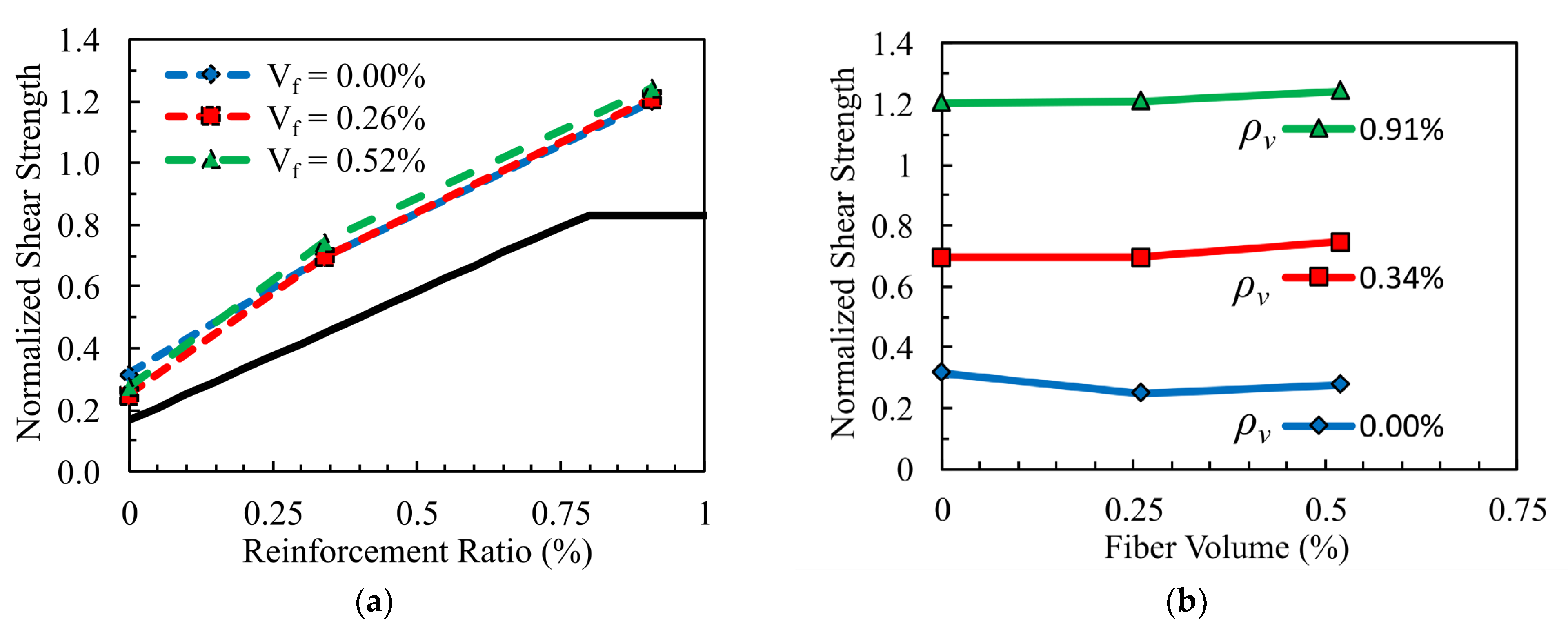
- The inclusion of macro-synthetic fibers, at the dosage rates tested, did not result in appreciable increases in shear strength for the PFRC panels tested as part of this study. However, prior beam-based studies (e.g., [6]), have reported shear strength improvements of approximately 20% with similar fiber volumes. These findings suggest that there is a potential strength benefit, or at least no strength penalty, for adding macro-synthetic fibers to control cracking and improve durability, especially for structural elements with low levels of transverse reinforcement.
- The discrepancy between the measured shear strength improvements for PFRC beams and panels likely stems from differences in specimen type and loading conditions (panels under in-plane shear under force control in this study versus beams experiencing combined shear and flexure under displacement control in previous work). It is anticipated that fibers may show greater benefit for improving the flexure-shear strength of beams, versus the web-shear strength. This would be consistent with the existing literature available and may explain the different behaviors observed in this and other testing series.
- The results suggest that the most promising benefits of macro-synthetic fibers occur in concrete panels with fiber volumes ≥ 0.5% and low transverse reinforcement ratios (ρv ≤ 0.5%). Future research should explore a broader range of fiber types (e.g., varying in shape, material, and coating) and concrete mixtures to evaluate the generalizability of these findings and further advance the structural application of PFRC (polymer fiber-reinforced concrete).
- With respect to determining shear strength, the fib MC2010 [36] demonstrated the best overall performance, while ACI 318 [24] and EC2 [40] with cot(θ) = 1.0 tended to significantly underestimate PFRC panel strength. These preliminary findings suggest that for design applications involving PFRC, fib MC2010 offer the most reliable predictions among the codes assessed. Additional work is recommended before definitive conclusions are drawn in this regard.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shah, S.P.; Rangan, B.V. Fiber reinforced concrete properties. ACI J. Proc. 1971, 68, 126–137. [Google Scholar] [CrossRef] [PubMed]
- Parra-Montesinos, G.J. Shear strength of beams with deformed steel fibers. Concord Int. 2006, 28, 57–66. [Google Scholar]
- Lantsoght, E.O.L. Database of shear experiments on steel fiber reinforced concrete beams without stirrups. Materials 2019, 12, 917. [Google Scholar] [CrossRef] [PubMed]
- Li, V.C.; Ward, R.; Hamza, A.M. Steel and Synthetic Fibers as Shear Reinforcement. ACI Mater. J. 1992, 89, 499–508. [Google Scholar]
- Greenough, T.; Nehdi, M. Shear behavior of fiber-reinforced self-consolidating concrete slender beams. ACI Mater. J. 2008, 105, 468. [Google Scholar]
- Altoubat, S.; Yazdanbakhsh, A.; Rieder, K.-A. Shear behavior of macro-synthetic fiber-reinforced concrete beams without stirrups. ACI Mater. J. 2009, 106, 381–389. [Google Scholar] [CrossRef]
- Parmentier, B.; Cauberg, N.; Vandewalle, L. Shear resistance of macro-synthetic and steel fibre reinforced concrete beams without stirrups. In Proceedings of the 8th RILEM International Symposium on Fibre Reinforced Concrete: Challenges and Opportunities, Guimaraes, Portugal, 19–21 September 2012. [Google Scholar]
- Sahoo, D.R.; Maran, K.; Kumar, A. Effect of steel and synthetic fibers on shear strength of RC beams without shear stirrups. Constr. Build. Mater. 2015, 83, 150–158. [Google Scholar] [CrossRef]
- Arslan, G.; Keskin, R.S.O.; Ozturk, M. Shear behaviour of polypropylene fibre-reinforced-concrete beams without stirrups. Proc. Inst. Civ. Eng. Struct. Build. 2017, 170, 190–198. [Google Scholar] [CrossRef]
- Murad, Y.; Abdel-Jabbar, H. Shear behavior of RC beams prepared with basalt and polypropylene fibers. Case Stud. Constr. Mater. 2022, 16, e00835. [Google Scholar] [CrossRef]
- Koura, M.M.; Tahwia, A.M.; Matthana, M.H. Influence of macro-synthetic fibers on the flexural behavior of high strength concrete beams reinforced with GFRP bars. Mansoura Eng. J. 2024, 49, 4. [Google Scholar] [CrossRef]
- Narayanan, R.; Darwish, I.Y.S. Use of steel fibers as shear reinforcement. ACI Struct. J. 1987, 84, 216–227. [Google Scholar] [CrossRef] [PubMed]
- Li, V.C.; Mishra, D.K.; Naaman, A.E.; Wight, J.K.; LaFave, J.M.; Wu, H.; Inada, Y. On the Shear Behavior of Engineered Cementitious Composites. Advn Cem. Bas Mater. 1994, 1994, 142–149. [Google Scholar] [CrossRef]
- Furlan, S.; Bento-de-Hanai, J.B. Shear behavior of fiber reinforced concrete beams. Cem. Concr. Comp. 1997, 19, 359–366. [Google Scholar] [CrossRef]
- Majdzadeh, F.; Soeimani, S.M.; Banthia, N. Shear strength of reinforced concrete beams with a fiber concrete matrix. Can. J. Civ. Eng. 2006, 33, 726–734. [Google Scholar] [CrossRef]
- Carnovale, D.; Vecchio, F. Effect of Fiber Material and Loading History on Shear Behavior of Fiber-Reinforced Concrete. ACI Struct. J. 2014, 111, 1235–1244. [Google Scholar] [CrossRef]
- Conforti, A.; Minelli, F.; Tinini, A.; Plizzari, G.A. Influence of polypropylene fibre reinforcement and width-to-effective depth ratio in wide-shallow beams. Eng. Struct. 2015, 88, 12–21. [Google Scholar] [CrossRef]
- Alhassan, M.; Al-Rousan, R.; Ababneh, A. Flexural behavior of lightweight concrete beams encompassing various dosages of macro synthetic fibers and steel ratios. Case Stud. Constr. Mater. 2017, 7, 280–293. [Google Scholar] [CrossRef]
- Navas, F.O.; Navarro-Gregori, J.; Herdocia, G.L.; Serna, P.; Cuenca, E. An experimental study on the shear behaviour of reinforced concrete beams with macro-synthetic fibres. Constr. Build. Mater. 2018, 169, 888–899. [Google Scholar] [CrossRef]
- Farag, B.F.; Thonstad, T.; Calvi, P.M. Numerical modeling of distributed macro-synthetic fiber and deformed bar reinforcement to resist shear. Buildings 2024, 14, 3247. [Google Scholar] [CrossRef]
- SDI. ANSI/SDI C; Standard for Composite Steel Floor Deck—Slabs. Steel Deck Institute: Glenshaw, PA, USA, 2017.
- Calvi, P.M.; Bentz, E.C.; Collins, M.P. Reversed Cyclic Experiments on Shear Stress Transfer across Cracks in Reinforced Concrete Elements. ACI Struct. J. 2016, 113, 851–859. [Google Scholar] [CrossRef]
- Zhang, H.; Calvi, P.M.; Lehman, D.; Kuder, K.; Roeder, C. Response of recycled coarse aggregate concrete subjected to pure shear. J. Struct. Eng. 2020, 146, 04020075. [Google Scholar] [CrossRef]
- ACI; Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary, Committee 318. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- ASTM. A706/A706M; Standard Specification for Deformed and Plain Low-Alloy Steel Bars for Concrete Reinforcement. ASTM International: West Conshohocken, PA, USA, 2022.
- ASTM. C33/C33M; Standard Specification for Concrete Aggregates. ASTM International: West Conshohocken, PA, USA, 2023.
- ASTM. C39/C39M; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2023.
- ASTM. C469/C469M; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. ASTM International: West Conshohocken, PA, USA, 2022.
- ASTM. C1609/C1609M; Standard Test Method for Flexural Performance of Fiber-Reinforced Concrete (Using Beam With Third-Point Loading. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM. C78/C78M; Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading). ASTM International: West Conshohocken, PA, USA, 2022.
- Bažant, Z.P.; Novák, D. Proposal for standard test of modulus of rupture of concrete with its size dependence. ACI Mater. J. 2001, 98, 79–87. [Google Scholar]
- Gaston, J.P. Shear Behavior of Macro-Synthetic Fiber-Reinforced Concrete Panels. Master’s Thesis, University of Washington, Seattle, WA, USA, 2023. [Google Scholar]
- ASTM. D7508/D7508M; Standard Specification for Polyolefin Chopped Strands for Use in Concrete. ASTM International: West Conshohocken, PA, USA, 2020.
- Vecchio, F.J. Reinforced Concrete Membrane Element Formulations. J. Struct. Eng. 1990, 116, 730–750. [Google Scholar] [CrossRef]
- Vecchio, F.J.; Collins, M.P. The modified compression-field theory for reinforced concrete elements subjected to shear. ACI J. Proc. 1986, 83, 219–231. [Google Scholar] [CrossRef]
- FIB. Model Code 2010 for Concrete Structures; International Federation for Structural Concrete (fib): Lausanne, Switzerland, 2010. [Google Scholar]
- AASHTO. LRFD Bridge Design Specifications, 10th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2024. [Google Scholar]
- CSA; Design of Concrete Structures (CSA A23.3). Canadian Standards Association: Mississauga, Canada, 2014.
- Bentz, E.C.; Vecchio, F.J.; Collins, M.P. Simplified modified compression field theory for calculating shear strength of reinforced concrete elements. ACI Struct. J. 2006, 103, 614. [Google Scholar] [CrossRef]
- CEN. EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2015.
- RILEM. RILEM TC 162-TDF: Test and design methods for steel fibre reinforced concrete sigma-epsilon-design method. Mater. Struct. 2003, 36, 560–567. [Google Scholar] [CrossRef]





| Vf (%) | Transverse Reinforcement Ratio, ρv (%) | ||
|---|---|---|---|
| 0 | 0.34 | 0.91 | |
| 0 | PFRC-000-000 | PFRC-000-034 | PFRC-000-091 |
| 0.26 | PFRC-026-000 | PFRC-026-034 | PFRC-026-091 |
| 0.52 | PFRC-052-000 | PFRC-052-034 | PFRC-052-091 |
| Constituent | Absorption | Specific Gravity | M1 1 0% Fiber | M2 1 0.26% Fibers | M3 1 0.52% Fibers |
|---|---|---|---|---|---|
| (%) | SSD Mass (kg/m3) | ||||
| Cement (IL) | 3.15 | 317 | 317 | 317 | |
| Fine Aggregate | 2.10 | 2.65 | 858 | 838 | 819 |
| Coarse Aggregate | 1.12 | 2.68 | 1077 | 1090 | 1103 |
| Water | 158 | 158 | 158 | ||
| Air (1.5%) | |||||
| Fibers | 0.92 | 0 | 2.4 | 4.7 | |
| Total | 2410 | 2403 | 2403 | ||
| Panel Specimen | fc (MPa) | Ec (GPa) | ff (MPa) |
|---|---|---|---|
| PFRC-000-000 | 44.5 | 32.1 | 5.17 |
| PFRC-000-034 | 37.7 | 28.2 | 5.83 |
| PFRC-000-091 | 42.2 | 32.3 | 5.29 |
| PFRC-026-000 | 32.6 | 26.0 | 5.93 |
| PFRC-026-034 | 38.3 | 30.4 | 4.38 |
| PFRC-026-091 | 37.7 | 31.7 | 3.86 |
| PFRC-052-000 | 29.4 | –* | 3.69 |
| PFRC-052-034 | 45.0 | 29.7 | 4.34 |
| PFRC-052-091 | 36.1 | 28.6 | 3.45 |
| Property (Nominal) | Value |
|---|---|
| Specific gravity | 0.92 |
| Modulus of elasticity | 9.5 GPa |
| Tensile strength | 620 MPa |
| Length | 40 mm |
| Width | 1.4 mm |
| Thickness | 0.105 mm |
| Equivalent Diameter | 0.43 mm |
| Aspect Ratio 1 | 90 |
| Fiber Count | 187,000 per kg |
| Specimen | νcr | γcr | νu | γxy | εx | εy | fc1 | fc2 | ε1 | ε2 | fsx | fsy | wm | sm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (MPa) | (×10−3) | (MPa) | (×10−3) | (×10−3) | (×10−3) | (MPa) | (MPa) | (×10−3) | (×10−3) | (MPa) | (MPa) | (mm) | (mm) | |
| PFRC-000-000 | 1.99 | 0.12 | 2.12 | 0.71 | 0.11 | 0.42 | 1.92 | −2.35 | 0.65 | −0.13 | 19 | 0 | - | - |
| PFRC-000-034 | 1.39 | 0.09 | 4.27 | 13.3 | 2.04 | 13.7 | 0.34 | −10.5 | 16.7 | −0.97 | 367 | 513 | 0.52 | 109 |
| PFRC-000-091 | 1.92 | 0.22 | 7.82 | 13.7 | 4.21 | 8.35 | 0.00 | −17.1 | 13.4 | −0.89 | 512 | 512 | 0.33 | 64 |
| PFRC-026-000 | 1.20 | 0.13 | 1.43 | 1.37 | 0.96 | 0.37 | 0.46 | −4.40 | 1.41 | −0.08 | 173 | 0 | - | - |
| PFRC-026-034 | 1.78 | 0.08 | 4.31 | 13.8 | 1.60 | 11.0 | 0.77 | −9.10 | 14.7 | −2.03 | 289 | 512 | 0.31 | 69 |
| PFRC-026-091 | 1.81 | 0.37 | 7.43 | 11.9 | 2.26 | 7.92 | 0.08 | −15.2 | 11.7 | −1.52 | 407 | 512 | 0.41 | 69 |
| PFRC-052-000 | 1.38 | 0.24 | 1.50 | 0.36 | 0.07 | 0.18 | 1.36 | −1.66 | 0.31 | −0.06 | 13 | 0 | - | - |
| PFRC-052-034 | 1.79 | 0.31 | 5.00 | 20.7 | 2.38 | 19.7 | 0.63 | −12.2 | 24.6 | −2.46 | 429 | 520 | 0.47 | 64 |
| PFRC-052-091 | 1.84 | 0.47 | 7.47 | 13.0 | 2.54 | 8.52 | 0.00 | −15.9 | 12.7 | −1.63 | 458 | 512 | 0.43 | 64 |
| Code | Concrete Shear Strength (MPa) |
|---|---|
| AASHTO [37] | = parameter that accounts for concrete’s ability to transmit tensile stresses transverse reinforcement contribution of the shear strength = angle of inclination of compressive struts = prestress contribution of the shear strength |
| ACI 318 [24] | = lightweight concrete factor = size effect factor = design axial force = cross-sectional area. transverse reinforcement contribution of the shear strength = transverse reinforcement ratio |
| fib MC2010 [36] | = size effect parameter = calibration factor for the design shear capacity = concrete material factor = characteristic value of post cracking strength characteristic tensile strength of concrete (assuming ≤ C50) = characteristic concrete cylinder compressive strength. transverse reinforcement contribution of the shear strength |
| CSA [38] | = parameter that accounts for concrete’s ability to transmit tensile stresses |
| EC2 [40] | is a size effect factor is an axial stress from prestressing is the minimum shear resistance resistance from transverse reinforcement is the maximum shear resistance = 1.0 for non-prestressed members = strength reduction factor for concrete |
| RILEM TC162-TDF [41] | fiber contribution of the shear strength = factor for flange contributions in T-sections (1.0 for rectangular sections) bond strength between fibers and matrix = residual flexural strength at a CMOD of 3.5 mm transverse reinforcement contribution of the shear strength |
| Specimen | AASHTO [37] | ACI 318 [24] | fib MC2010 [36] | CSA [38] | EC2 [40] cot(θ) = 1.0 | EC2 [40] cot(θ) = 2.5 | RILEM TC162-TDF [41] |
|---|---|---|---|---|---|---|---|
| PFRC-000-000 | 0.61 | 0.39 | 0.58 | 0.53 | 0.56 | 0.56 | 0.53 |
| PFRC-000-034 | 0.99 | 0.68 | 1.00 | 0.85 | 0.37 | 0.92 | 0.54 |
| PFRC-000-091 | 1.00 | 0.70 | 0.96 | 0.84 | 0.54 | 1.00 | 0.67 |
| PFRC-026-000 | 0.79 | 0.49 | 1.12 | 0.70 | 0.75 | 0.75 | 0.82 |
| PFRC-026-034 | 0.98 | 0.67 | 1.08 | 0.85 | 0.36 | 0.91 | 0.58 |
| PFRC-026-091 | 1.05 | 0.75 | 1.05 | 0.88 | 0.56 | 1.10 | 0.72 |
| PFRC-052-000 | 0.72 | 0.45 | 1.18 | 0.64 | 0.69 | 0.69 | 0.78 |
| PFRC-052-034 | 0.86 | 0.60 | 0.97 | 0.74 | 0.31 | 0.78 | 0.52 |
| PFRC-052-091 | 1.03 | 0.68 | 1.06 | 0.87 | 0.56 | 0.90 | 0.72 |
| Average | 0.89 | 0.60 | 1.00 | 0.77 | 0.52 | 0.85 | 0.65 |
| Standard Dev. | 0.16 | 0.13 | 0.17 | 0.12 | 0.15 | 0.17 | 0.11 |
| COV (%) | 17.4 | 21.1 | 17.3 | 16.0 | 28.7 | 19.6 | 17.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaston, J.P.; Farag, B.F.; Thonstad, T.; Calvi, P.M. Experimental Shear Behavior of Macro-Synthetic Fiber-Reinforced Concrete Panels. Fibers 2025, 13, 136. https://doi.org/10.3390/fib13100136
Gaston JP, Farag BF, Thonstad T, Calvi PM. Experimental Shear Behavior of Macro-Synthetic Fiber-Reinforced Concrete Panels. Fibers. 2025; 13(10):136. https://doi.org/10.3390/fib13100136
Chicago/Turabian StyleGaston, John P., Benedikt F. Farag, Travis Thonstad, and Paolo M. Calvi. 2025. "Experimental Shear Behavior of Macro-Synthetic Fiber-Reinforced Concrete Panels" Fibers 13, no. 10: 136. https://doi.org/10.3390/fib13100136
APA StyleGaston, J. P., Farag, B. F., Thonstad, T., & Calvi, P. M. (2025). Experimental Shear Behavior of Macro-Synthetic Fiber-Reinforced Concrete Panels. Fibers, 13(10), 136. https://doi.org/10.3390/fib13100136







