Analysis and Modeling of the System Boundaries of a High-Speed Direct-Yarn-Placement System for In Situ Impregnation of Carbon Fibre Heavy Tows as Textile Reinforcements for Concrete Parts

Abstract

This study investigates a novel approach in modeling the system limits of a braked, high-speed yarn-laying process with in situ impregnation. Special attention is paid to the investigation of the yarn spool overrun after the robot has come to a standstill. This phenomenon occurs at low yarn tensions in combination with high traversing speed and/or acceleration. The modeling of the yarn spool overrun is carried out using physical equations, taking into account the travel speed, acceleration of the robot, and braking force of the spool brake. Previous research has confirmed various operating points of the yarn-laying process, but a comprehensive and complete analysis of the system limits at different operating points and speeds up to 2 m/s is missing. The result of the study is a novel model that describes the system boundaries of the direct-yarn-placement. Furthermore, models for robot braking time, carbon spool diameter, and spool mass are developed. The proposed models have an $R^2$ > 0.9674. Regarding the system stability boundaries, the calculations reveal that, as acceleration rises, the minimum tension requirement also increases. The same trend is found for system velocity. At $a=12.5$%, a minimum tension of 16 N suffices, compared to 23 N and 32 N at $a=25$% and 50%, respectively. The impact on tension of quadrupling the speed outweighs that of acceleration, with tension increasing by factors of up to 22.5 and 2, respectively.

1. Introduction

The current developments of population growth and global warming pose major challenges for the construction industry. To reduce CO₂ emissions in building construction, reinforcements based on textile materials offer possible solutions. Direct-yarn-placement technology using an industrial robot is proving to be a promising method for the automated production of individual reinforcements. Here, typically a carbon yarn is unwound and impregnated in situ with the resin matrix directly within the placement head.

High efficiency and quality are required for an economically efficient automated process. The efficiency of the process can be achieved primarily by increasing the production speed. In addition to good impregnation, a key factor with regard to quality is a continuous yarn tension during yarn placement. Modeling of the yarn-placement system limits is an important challenge, especially for fiber placement with high speed. They require a precise knowledge of the yarn spool overrun after the stoppage of a robot movement.

The focus of this scientific article is the detailed investigation of a specific yarn-placement process, which is characterized by the simultaneous application of low yarn tensions, high travel speeds, and an exclusively braked placement. Previous studies have demonstrated setups for selected operating points of up to $0.5$ m/s, whereby systems with braked and driven bobbins were considered. However, to the best of the author’s knowledge, a comprehensive analysis of the system boundaries at different operating points in conjunction with a braked spool has not yet been carried out.

Since the fabrication of a single textile reinforcement requires the laying of multiple strands in vertical and horizontal directions, achieving short cycle times is highly dependent on production speed. To be competitive with warp knitting machines, it is essential to reduce production time. Consequently, the authors investigate system limits at speeds of up to 2 m/s, a fourfold increase from the currently proposed $0.5$ m/s.

The aim of this research is to address this gap by systematically analyzing the interactions between the aforementioned variables of speed, acceleration, and braking force. Through modeling of the system limits, knowledge can be gained that will contribute to the optimization of the investigated yarn-placement process. These furthermore form the basis for the subsequent design of the in situ impregnation unit in terms of the yarn tension to be tolerated.

2. State of the Research

The method of direct-yarn-placement (DYP) involves the precise deposition of continuous filaments with in situ impregnation onto a base frame. This technique offers advantages such as enhanced control over fiber placement and the ability to create intricate structures with varying fiber orientations.

A key feature is that, unlike textile reinforcements fabricated with conventional textile technologies such as weaving or knitting, no subsequent trimming of the grid reinforcement is necessary. As a result, no waste or scrap is generated, and the necessary finishing steps are eliminated. This makes DYP resource- and cost-efficient compared to traditional manufacturing technologies [1].

Currently, only small literature entries are found for DYP, but the technology is comparable to yarn-laying advancements in additive manufacturing, fiber placement, and filament winding. This paper aims to provide a overview on recently developed technologies, exploring different mechanical builds and their process variables, such as speed, acceleration, and yarn tension.

2.1. Search Criteria

To explore the state of research, a comprehensive search was conducted using Google Scholar, focusing on papers published since 2020. The search encompassed a wide range of topics related to carbon fiber composite production, with specific emphasis on filament winding, fiber placement, and spool overrun. Different combinations of keywords extracted from the paper’s keyword section were used (

Table A1. Search entries used.

Direct-Yarn-Placement with In Situ Impregnation

Spool Overrun

carbon textile reinforcement production direct yarn laying textile reinforcement though carbon impregnation during direct yarn laying in situ impregnation of textiles carbon filament winding in situ impregnation carbon fiber placement in situ impregnation carbon fiber robotic automated fiber placement in situ impregnation carbon robotic automated filament winding in situ impregnation carbon filament winding pin-assisted impregnation

carbon filament winding spool overrun analysis carbon filament winding spool tension control carbon filament winding spool unwinding analysis carbon filament winding process stability carbon filament winding spinning conditions carbon filament winding spooling optimization carbon filament winding spooling dynamics carbon filament winding spool overrun compensation carbon filament winding spool overshoot compensation carbon yarn placement in situ impregnation

).

2.2. Additive Manufacturing

2.2.1. Typical Builds of the Laying Head

The research landscape in the realm of additive manufacturing for continuous fiber-reinforced composites (CFRCs) is diverse, reflecting a range of methodologies and designs aimed at optimizing the yarn-laying head. Terekhina et al. [2] explore in-nozzle impregnation during fused filament fabrication (FFF), employing a modified nozzle combining a brake and motor for yarn and polymer filaments. Mosleh et al. [3] also leverage modified FFF nozzles, utilizing a single port nozzle for CFRTC manufacturing. An et al. [4] adopt an in situ pin-assisted melt impregnation approach, utilizing a heating block with pins for impregnation. Wang et al. [5] focus on melt impregnation, employing an impregnation mold designed for optimal impregnation pressure and filament shaping. Additionally, Zhi et al. [6] utilize hot-melt impregnation for direct 3D printing, incorporating heating rods and a shaping die. Elderfield et al. [7] introduce discrete in situ consolidation (DISC) using a conical stainless steel tool, whereas Parmar et al. [8] discuss various designs tailored for prepregs, including preimpregnation with subsequent additive manufacturing. Cheng et al. [9] provide a comprehensive review, encompassing various impregnation methods, such as in-nozzle and in-line impregnation. Furthermore, Tao et al. [10] and Hu et al. [11] offer extensive reviews covering a spectrum of impregnation techniques and designs, including dual-channel extruder heads and specialized FDM nozzles. Kipping et al. [12] focus on path planning for reinforcement rather than impregnation specifics, utilizing multi-axis additive manufacturing for carbon fiber reinforcement. Lastly, Wang et al. [13] employ a specific nozzle design for carbon fiber impregnation in conjunction with low-energy electron beam curing. These studies collectively contribute to advancing the state of the art in yarn-laying head design for CFRC additive manufacturing.

2.2.2. Investigated Speeds, Acceleration, and Tension Settings

In examining the state of research concerning laying speed, acceleration, and tension in additive manufacturing for continuous fiber-reinforced composites (CFRCs), a variety of methodologies and designs have been explored across different studies. Terekhina et al. [2] focused on in-nozzle impregnation during fused filament fabrication (FFF) with a laying speed of 0.01 m/s. Elderfield et al. [7] explored discrete in situ consolidation (DISC), with a laying speed of 0.004 m/s. An et al. [4] adopted an in situ pin-assisted melt impregnation approach with a laying speed of 0.00167 m/s. Wang et al. [5] investigated melt impregnation with an optimal speed of 0.067 m/s. Mosleh et al. [3] studied solution impregnation for fiber prepreg with a laying speed of 0.001 m/s. Chen et al. [14] examined melt impregnation with a speed of 0.0167 m/s. Wang et al. [13] combined EB curing with FFF printing with a speed of 0.01 m/s. Notably, laying acceleration and yarn tension were not explicitly specified in these documents.

2.3. Fiber Placement

2.3.1. Typical Builds of the Laying Head

In the landscape of advanced composite manufacturing, the design and functionality of yarn-laying effectors are recognized as critical factors for achieving high-quality output and operational efficiency. Donough et al. ([15]) emphasize the importance of heat sources and roller configurations in their review of in situ consolidation processes, offering valuable insights into effector considerations. Ji et al. ([16]) focus on laser irradiation, utilizing a semiconductor laser with adjustable power settings, showcasing a specific effector configuration tailored to their process. Parmar et al. ([8]) provide a comprehensive overview of various manufacturing techniques, which indirectly underscores the significance of effector design in composite manufacturing. Raps et al. ([17]) employ heated tooling for in situ consolidation, contributing to the understanding of effector functionalities, although specific details about effector design remain undisclosed. These studies collectively highlight the importance of further research to explore and refine effector design, thereby advancing composite manufacturing practices.

2.3.2. Investigated Speeds, Acceleration, and Tension Settings

The yarn-laying speed, acceleration, and tension results from the studies are summarized as follows: Donough et al. [15] did not provide specific values but discussed speeds of up to 0.35 m/s. Ji et al. [16] reported movement speeds ranging from 0.02 m/s to 0.08 m/s during the laser-assisted in situ consolidation additive manufacturing process. Parmar et al. [8] highlighted a maximum yarn-laying speed of 0.1 m/s in their review. Raps et al. [17] specified a layup speed of 0.125 m/s, but detailed information on acceleration and tension was not provided beyond the use of heated tooling for in situ consolidation.

2.4. Filament Winding

2.4.1. Typical Builds of the Laying Head

Research on yarn-laying head design [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44] showcases a diverse array of effector builds catering to specific impregnation needs. Traditional wet impregnation baths with multiple pins remain prevalent [21,30,31,32,33,35,38,39,40,41,43,44], offering versatility in impregnation.

Moreover, some studies explore specialized setups optimized for specific processes, including robotic coreless filament winding systems [23,24,41]. These systems often integrate tension control mechanisms within the effector, ensuring uniform impregnation and winding. Another notable trend is the incorporation of tension sensors directly into end-effectors for real-time monitoring [41].

In addition to practical implementations, digital approaches such as Bayesian optimization are gaining traction for fine-tuning impregnation machine parameters [34]. These methods offer increased efficiency and accuracy in impregnation, contributing to advancements in yarn-laying head technology.

2.4.2. Investigated Speeds, Acceleration, and Tension Settings

The laying speed, acceleration, and tension settings in the various papers exhibit a wide range of variables and values, showcasing the diverse approaches in filament winding and related processes [19,20,24,33,35,36,37]. Usun et al. (2021) focused on 3D printed composites, utilizing a laying speed of 0.01 m/s [19]. Shi et al. (2022) optimized winding parameters with a laying speed of 1 m/s, and tensions varied from 5 N to 25 N [20]. Bodea et al. (2022) developed a cyber-physical manufacturing process for large coreless filament wound composite elements, achieving an average laying speed of up to 0.148 m/s, with tensions ranging from 190 N to 320 N during traveling [24]. Sinha et al. (2024) studied the effect of fiber tension on carbon/epoxy composite specimens, with a processing speed of 0.056 m/s during impregnation [33]. Sieira et al. (2021) explored the impact of spinning conditions on the diameter and tensile properties of mesophase petroleum pitch carbon fibers, achieving a winding speed of up to 0.57 m/s [36]. Hopmann et al. (2021) detected and evaluated fiber deposition parameters during wet filament winding, with winding speeds ranging from 0.28 to 0.96 m/s and resin bath temperatures from 40 to 60 °C [37]. Siegl et al. (2024) examined the winding process of fiber-reinforced thermoplastic tubes, achieving an impregnation line speed of up to 1 m/s [35].

Further information regarding acceleration was not provided in the reviewed papers. The focus primarily remained on laying speed and tension settings, with little mention of acceleration values.

2.5. Winding Models

In the realm of winding dynamics research, several models have been proposed to elucidate various facets of the process. Pušnik et al., in their study [45], explored the effect of winding angle on yarn unwinding, emphasizing the optimization of boundary conditions influencing balloon formation. They developed a mathematical model describing yarn motion during unwinding, incorporating balloon theory, Coriolis force, and the effects of gravity and tangential air drag. Through theoretical modeling and computer simulations, they demonstrated the significance of winding angle and apex angle on yarn angular velocity, thereby impacting tension reduction during unwinding.

Kevac et al. delved into the dynamics of sudden jumps during rope winding processes [46]. Their investigation centered on analyzing the nonlinear and pulsed nature of these dynamics, with a test matrix incorporating variables such as the rotational speed of the winch and rope tension. The employed methods include the analysis of nonlinear dynamics through simulation and experimental validation. The results encompassed the identification of cyclicality in the rope winding (unwinding) process and demonstrated the nonlinear and pulsed nature of the dynamic variables. However, specific details regarding the interaction of tension, velocity, and acceleration on spool overrun were not discussed in their study.

The study by Zhang et al. (2023) endeavored to comprehend yarn tension and vibration dynamics during carbon fiber bobbin unwinding [47]. Employing a test matrix with variables including spring preload and unwinding speed, the researchers developed a dynamic model grounded in an axially moving strings theory, utilizing MATLAB simulations for analysis. Their study showed a close relation between yarn tension during unwinding and spring preload. To avoid damage to the carbon fiber yarn, the speed and tension should be controlled.

2.6. Research Gap

While the given studies contribute valuable insights into winding processes, there remains a gap in the comprehensive examination of acceleration, velocity, and tension dynamics simultaneously, along with the analysis of spool overrun in degrees. Existing literature lacks detailed analyses in these areas, particularly across a broad speed range. While previous studies have explored single work points in additive manufacturing and fiber placement, they often lack specifics on tension, acceleration, and drive-train dynamics. Similarly, in filament winding, research primarily focuses on limited speed ranges and lacks comprehensive tension and acceleration data. In most cases, the system is optimized with regard to a single work point. The proposed model aims to bridge this gap by providing a holistic framework for understanding and optimizing laying processes across a wider range of work points for different combinations of the parameters laying speed, yarn tension, and robot acceleration.

3. Modeling the Carbon Spool Overrun

Efficient filament winding processes rely on precise control of the carbon spool to prevent overrun during robot movements. As the robot accelerates and decelerates while laying yarn, the inertia of the rotating spool fluctuates, potentially leading to overrun if not properly managed. To mitigate this issue, it is essential to accurately model the carbon spool overrun dynamics. The deceleration curve of the robot is modeled as illustrated in Figure 1.

At time $t_1$, the robot begins decelerating from a constant speed, v. This deceleration is characterized by a linear decrease between the starting time, $t_1$, and the ending time, $t_2$. The duration of this deceleration, denoted by the variable t, represents the time delta from start to finish.

The speed progression of the spool is encapsulated within t. The constant speed, n, of the carbon spool before $t_1$ is assumed to be based on the speed, v, of the robot according to Equation (5). The deceleration behavior of the spool is influenced by the spool brake torque, M, and the combined inertia of the spool and brake shaft, J. The required time for the carbon spool to come to a stop is modeled as follows. Equations (1), (4), (8) and (10) are derived from the work of Heinemann et al. [48].

$$M=J\dot{\omega }=2\pi J\dot{n}$$

(1)

$${\int }_{t_1}^{t_2}\dot{n}={\int }_{t_1}^{t_2}\frac{M}{J\ast 2\pi }dt={\int }_0^t\frac{M}{J2\pi }dt,$$

(2)

$$t=\frac{-nJ2\pi }{M},$$

(3)

where the rotational speed, n, as a factor of the yarn speed, v, is given by:

$$v=\omega \ast r$$

(4)

$$n=\frac{v}{\pi d_o}.$$

(5)

To calculate their inertia, the brake shaft and carbon spool are defined as cylindrical tubes with an inner diameter, $d_i$, outer diameter, $d_o$, and mass, m.

$$J_{brake,spool}=\frac{1}{2}m\left({\left(\frac{d_o}{2}\right)}^2+{\left(\frac{d_i}{2}\right)}^2\right)$$

(6)

$$J=k_1(J_{brake}+J_{spool})$$

(7)

The total inertia is represented by the sum of the two individual components. Additionally, a calibration factor, $k_1$, is introduced to account for potential variations between the assumed inertia values based on supplier data and the actual system. The torque applied to the carbon spool during unwinding depends on the carbon spool’s outer diameter, $d_o$ (Figure 2).

$$M=F{d}_o/2$$

(8)

Based on the spool stopping time, t, and the robot deceleration time, $t_f$, the time for spool overrun, $\Delta t$, can be determined.

$$\Delta t=t_{-}{t}_f$$

(9)

In setups where the robot deceleration time is shorter than the necessary spool stopping time, an overrun will occur. The overrun is represented in degrees of spool rotations, denoted as $\alpha$.

$$\omega =\frac{d\alpha }{dt}$$

(10)

$$\alpha =\omega \Delta t=\frac{v\ast \Delta t}{r}\left[rad\right]$$

(11)

In the event of a spool overrun, the spool rotation speed is lower than that at the beginning of the deceleration process. The prevailing speed at the time of the overrun, referred to as $\Delta v$ (immediately after the robot has stopped), is modeled by downscaling the original speed with a constant factor, $k_2$.

$$\Delta v=v\ast k_2$$

(12)

4. Materials and Methods

4.1. Investigation of the Spool Overrun

A passive yarn feeding mechanism has been selected for yarn laying, where the yarn is exclusively tensioned by braking forces acting on the spool. This was chosen over an active feed mechanism because it would have required frequency converters combined with high torque motors, which increase the weight and cost of the laying head. Should any slack be present within the setup, the laying head must traverse to eliminate it, as back-winding of the spool is not possible. The presence of slack could result in yarn guiding failures within the feeding apparatus, potentially causing the yarn to slip out of the guiding rollers, leading to severe system damage. To maintain high process stability, it is imperative to ensure that no slack occurs.

During yarn laying, the electro-mechanical systems of the robot and laying head interact. An industrial robot, KUKA KR150, is utilized for yarn placement, programmed in KUKA Robot Language with a soft linear velocity profile (SLIN). The robot’s code incorporates velocities and accelerations as per the test matrix.

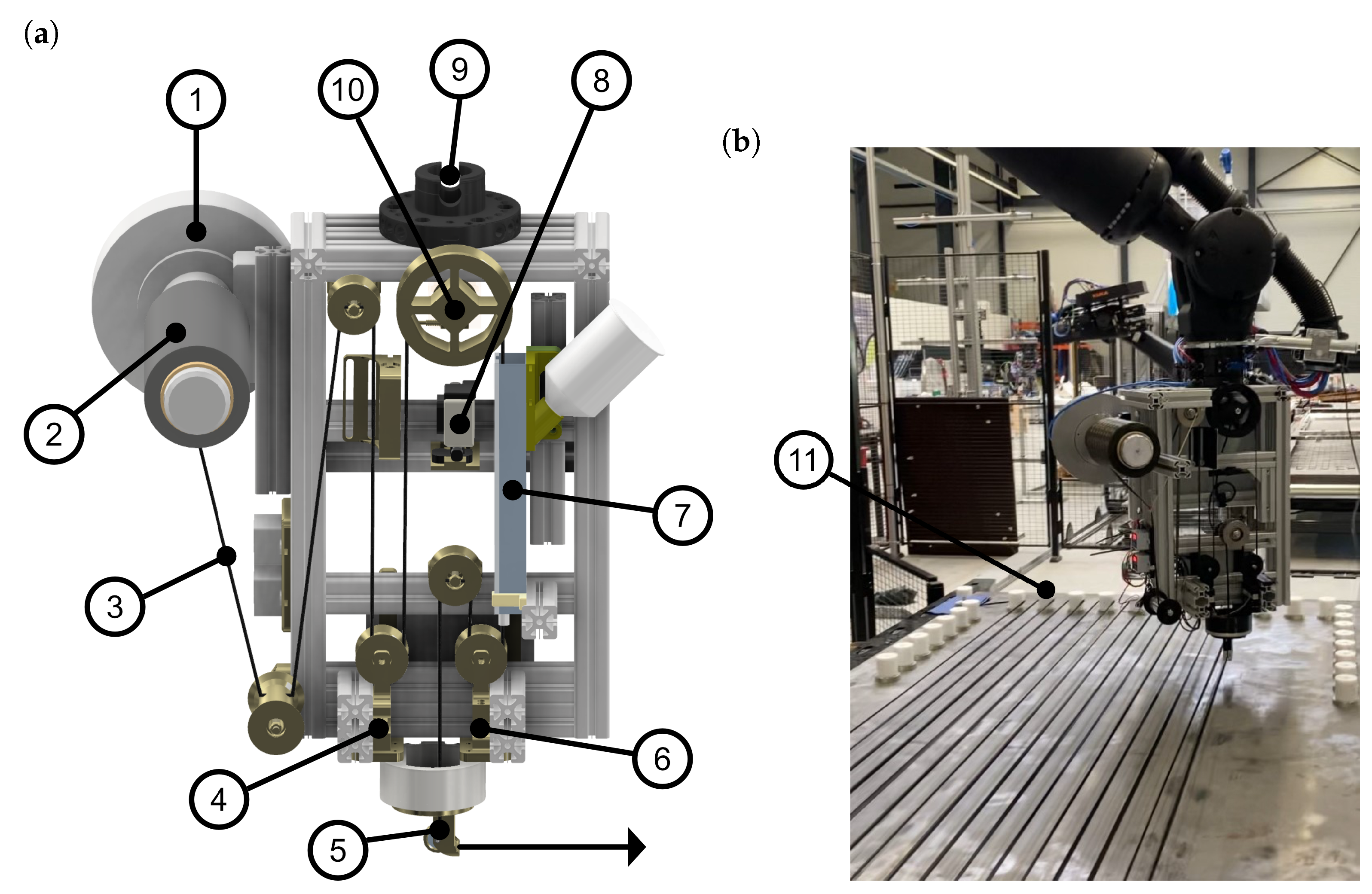
In the process of yarn laying, a specially developed robot effector (laying head) is utilized (Figure 3a). The carbon filament spool is mounted on a magnetic powder brake (IBD Wickeltechnik GmbH, type B.0351.V24), featuring an expansion clamping shaft of length $l=300$ mm and a mass of approximately 6 kg. Multiple sensors on the laying head monitor process variables such as input tension, output tension, filament speed, yarn width, ambient temperature, ambient humidity, and impregnation unit filling degree. These sensors are calibrated and managed by an Adafruit Feather STM32 Express programmed in Python, while yarn tension control is executed by an Industrial Shields ARDBOX 20 I/Os Analog HF Plus programmed in C. Yarn exits the laying effector via a 360-degree rotatable, ball-bearing-mounted deflection head.

The carbon fiber yarn material used is TENAX-E STS40 F13 3200 tex [49]. The spools used weigh approximately 2 kg. The spool clamping diameter is $d_i=$77 mm. The outer diameter is initially $d_o=145$ mm and changes throughout the process.

To monitor spool overrun, a grid pattern with 45° angles has been affixed to the outer end of the brake shaft. Optical tracking of the overrun is conducted using an Apple iPhone SE 2020 using its slow-motion recording capabilities. Subsequently, overrun values are manually extracted from the recorded videos based on the 45° gridding.

The impregnated yarn is positioned by the robot onto a worktable equipped with magnetic deflection points. These points are automatically positioned using a robot equipped with suitable fixtures for the deflection elements, according to the required size and mesh width of the desired textile reinforcement (Figure 3b). For yarn laying, a horizontal grid comprising 20 strands was selected. The laying distance spans $3.3$ m, with the overall width of the reinforcement measuring $1.2$ m. The diameter of the deflection rollers is 50 mm.

To assess the influence of the robot, brake system, and spool properties on spool overrun, the key variables outlined in

Table 1. Identified variables of the experiment.

Primary Variables	Unmanaged Variables
velocity v	spool diameter $d_o$
acceleration a	spool mass m
brake value

were identified. The primary variables, actively manipulated during the trials, are the focus of the experiment. Meanwhile, the secondary variables remain unmanaged throughout the experiment. With regard to the spool properties, such as diameter and weight, this implies that, due to carbon yarn consumption throughout the experiment, its values will alter over the course of the trial.

The primary variables were tested in a full factorial matrix, as shown in

Table 2. Overrun test settings to determine system stability.

Laying Acceleration (%)	Brake Value (%)	Laying Speed (mm/s)
12.5, 25, 50	12, 20, 28	250, 1000, 2000

. Three stages were tested for each variable, resulting in $3\times 3\times 3=27$ trials. For each trial, six samples were tested, totaling 162 samples in all. Each sample is represented by one horizontal strand (refer to Figure 3b for illustration).

To construct the spool overrun model, the following measurements are required: spool overrun, robot deceleration time, spool properties (diameter and mass), and yarn tension. Spool overrun is measured through video recording. The speed velocity profile is directly logged by the robot output via a Python script. The spool circumference is determined using a tape measure, allowing back calculation of spool diameter and mass for the model construction. Yarn tension is measured by the input force sensor. The data is then extracted using a Python code, which calculates the mean values in the robot’s constant speed zone.

The variable settings are controlled as follows: the acceleration value is set in the KUKA software KSS 8.5.8 as a percentage. The brake value is adjusted to various constant percentages of the maximum brake torque of 35 Nm. Based on the authors previous work, these selected values are known to be compatible with the in situ impregnation device, ranging from approximately 5 N to 25 N. The speed is configured in the KUKA software, utilizing an SLIN movement.

4.2. Carbon Spool Properties

The characteristics of the carbon spool play a critical role in the overrun model. Equations (5) and (8) demonstrate that the outer diameter of the spool serves as an important input parameter. For determining $d_o$, a methodology relying on circumference measurement was adopted. A tape measure marked at 1 mm intervals was wrapped around the spool to determine its circumference, U.

With the values obtained through circumference measurements and the manufacturer’s data, it is possible to first calculate the outer diameter and second determine mass based on the outer diameter. To achieve this, it is essential to compute the outer spool diameter from the measured variable, U. For determining the spool weight, a conversion function based on the manufacturer data is selected (

Table 3. Manufacturer data of mass to outer diameter ratio [49].

Outer Diameter ${\mathit{d}}_{\mathit{o}}$ (mm)	Net Weight m (kg)
105	0.5
120	1
145	2
180	4
205	6
225	8
245	10

).

$$d_o=\frac{U}{\pi }$$

(13)

4.3. Robot Speed Ramp

Characterizing the robot speed ramp involves key variables: rising time, constant speed, and falling time, all logged in the experiment as previously stated. Data extraction from the KUKA speed log follows a specific procedure. Initially, the maximum value of the robot speed signal, $v_{max}$, is determined. Subsequently, the timestamps where the signal enters and exits the tolerance goal of 90% $v_{max}$ is ascertained. Based on these values, the rising and falling times of the robot speed curve is calculated. The rising time signifies the duration of the acceleration ramp from $v=0$ mm/s to 90% $v_{max}$. In contrast, for the falling time, it represents the period from leaving the 90% $v_{max}$ tolerance band until reaching a minimum speed value. These configurations were found to effectively filter the complex speed behavior at different acceleration settings of the robot, as depicted in Figure 6d. Due to the robot’s continuous movement during the laying process, the minimum speed value is 50 mm/s.

4.4. Spool Overrun Model Development

For the development of the spool overrun model, equations from the literature are employed, with solutions calculated separately for each trial. The process involves multiple steps conducted using Excel.

Firstly, rotational speed, n, is computed using Equation (5). Subsequently, the inertias of the carbon spool ($J_{\mathrm{spool}}$) and the magnetic powder brake shaft ($J_{\mathrm{brake}}$) are determined with Equation (6). For the carbon spool, parameters, including a diameter ($d_i$) of 77 mm and model values for outer diameter ($d_o$) and mass (m), are employed. For the brake shaft, a mass $m=6$ kg and an outer diameter $d_o=77$ mm are employed. The inner diameter is set to $d_i=50$ mm.

The momentum is then calculated by multiplying the measured tension, T, with the outer diameter of the carbon spool. The estimated time for spool stopping is derived from Equation (2), while spool overrun time is determined using Equation (9), with a measured values of $t_f$.

Before computing the overrun angle, the remaining overrun speed ($\Delta v$) is computed with Equation (12). For determining the values of the constants $k_1$ and $k_2$, a python code for a curvefit based on the library scipy/optimize/curve_fit is used. The code numerically solves the overrun model for different values of $k_1$ and $k_2$, in combination with the measured variables of each trial. It then returns the values of the constants that showed the strongest model fit to the experimental data.

4.5. Simulation of System Boundaries

In exploring the system boundaries, the previously developed overrun model is tailored to the following framework conditions. To ensure system stability, it is imperative to eliminate any spool overrun, implying that the maximum tolerated overrun time, $\Delta t$, must be zero. Consequently, it follows that constant $k_2$ becomes unnecessary for predicting system stability. Furthermore, from Equations (3) and (9) with $\Delta t=0$, it can be deduced that $t=t_f$. With this representation, the model for predicting the system boundaries is established.

$$t_f=\frac{-nJ2\pi }{M}$$

(14)

In achieving high productivity, production speed plays a key factor and should be as high as possible. Furthermore, different accelerations can be given to the system in order to reach long constant speed times. Assuming the latter are fixed, the remaining factor to transfer the system into a stable state is the yarn tension. This is, however, limited by the requirement of the impregnation unit in respect to a low input tension.

Based on the illustrated conditions, the lowest possible input tension is simulated in respect to different speed and acceleration inputs.

With $M=F\ast r$:

$$F=\frac{-nJ2\pi }{t_f\ast r}$$

(15)

To calculate the falling time, the regression model derived from the robot speed analysis is utilized. To ensure a conservative estimate of system boundaries, a worst-case scenario approach is adopted. Here, the model prediction $t_{f_{wc}}$ is downscaled based on the identified errors of the falling time model. This is due to the representation of a worst-case scenario by short robot deceleration time, $t_f$.

$$t_{f_{wc}}=t_f\ast t_{e2}-t_{e1}$$

(16)

The selected error values, based on the results of the previous section, are set to $t_{e1}=0.218$ s and $t_{e2}\approx 10$%. Concerning the carbon fiber spool properties, it is assumed that a weight of 2 kg is consistent across all simulations. An unused spool is expected to exhibit the highest overshoot, given that its mass and outer diameter are at maximum compared to an already unwound spool. Utilizing manufacturer data, $d_o=2r=145$ mm and $m=2$ kg are employed for the simulation. The speed range is interpolated from 250 to 2000 mm/s in increments of 50 mm/s, with three accelerations of $12.5$%, 25%, and 50% employed for the simulation.

5. Results

5.1. Experiment on the Spool Overrun

The experiment results indicate the significant influences of the primary variables on the system. Both robot acceleration (a) and robot speed (v) demonstrate direct influences, while the magnetic powder brake value exhibits an indirectly proportional effect. Additionally, the secondary variable, spool circumference, U, experiences significant fluctuations throughout the experiment. Raw data are presented in

Table 4. Results of the overrun experiment.

Trial	a (%)	Brake Value (%)	v (mm/s)	U (cm)	${\mathit{t}}_{\mathit{f}}$ (s)	${\mathit{T}}_{\mathit{in}}$ (N)	$\mathit{\alpha }$ (°)
1	25	12	250	41.0	2.37	3.5	0
2	25	12	1000		0.84	3.5	285
3	25	12	2000		0.52	5.5	1380
4	25	20	250	39.8	2.39	4.5	0
5	25	20	1000		0.91	5.0	83
6	25	20	2000		0.62	5.5	1110
7	25	27	250	38.6	2.4	17.0	0
8	25	27	1000		0.91	18.0	3
9	25	27	2000		0.6	14.0	183
10	50	12	250	37.2	1.42	5.5	0
11	50	12	1000		0.58	6.0	170
12	50	12	2000		0.35	7.0	1080
13	50	20	250	36.1	1.41	6.5	0
14	50	20	1000		0.55	7.5	113
15	50	20	2000		0.39	8.5	848
16	50	27	250	34.8	1.45	18.0	0
17	50	27	1000		0.58	17.5	0
18	50	27	2000		0.36	15.0	244
19	12.5	12	250	33.5	3.62	7.0	0
20	12.5	12	1000		1.40	7.5	0
21	12.5	12	2000		0.99	8.0	473
22	12.5	20	250	32.0	3.63	8.0	0
23	12.5	20	1000		1.45	8.0	0
24	12.5	20	2000		0.9	10.0	263
25	12.5	27	250	30.6	3.64	20.8	0
26	12.5	27	1000		1.43	20.5	0
27	12.5	27	2000	29.4	0.94	20.0	0

, detailing the determined target values: carbon spool circumference, U, robot deceleration time, $t_f$, yarn tension, $T_{in}$, and spool overrun, $\alpha$. These values are obtained by calculating the means of the six samples in each trial, with circumference measurements conducted every three trials. The standard deviations are available in

Table A2. Standard Deviations in the overrun experiment.

Trial	${\mathit{t}}_{\mathit{f}}$ (s)	${\mathit{T}}_{\mathit{in}}$ (N)	$\mathit{\alpha }$ (°)
1	2.37 ± 0.05 s	3.5 ± 0.1 N	0 ± 0°
2	0.84 ± 0.05 s	3.5 ± 0.2 N	285 ± 65°
3	0.52 ± 0.03 s	5.5 ± 0.6 N	1380 ± 90°
4	2.39 ± 0.07 s	4.5 ± 0 N	0 ± 0°
5	0.91 ± 0.05 s	5 ± 0.3 N	83 ± 13°
6	0.62 ± 0.06 s	5.5 ± 0.3 N	1110 ± 40°
7	2.4 ± 0.07 s	17 ± 0.9 N	0 ± 0°
8	0.91 ± 0.06 s	18 ± 1.4 N	3 ± 3°
9	0.6 ± 0.06 s	14 ± 1.1 N	183 ± 3°
10	1.42 ± 0.05 s	5.5 ± 0.3 N	0 ± 0°
11	0.58 ± 0.06 s	6 ± 1 N	170 ± 12°
12	0.35 ± 0.04 s	7 ± 0.8 N	1080 ± 36°
13	1.41 ± 0.06 s	6.5 ± 0.1 N	0 ± 0°
14	0.55 ± 0.02 s	7.5 ± 0.3 N	113 ± 18°
15	0.39 ± 0.05 s	8.5 ± 0.9 N	848 ± 68°
16	1.45 ± 0.05 s	18 ± 0.4 N	0 ± 0°
17	0.58 ± 0.04 s	17.5 ± 0.3 N	0 ± 0°
18	0.36 ± 0.04 s	15 ± 0.9 N	244 ± 41°
19	3.62 ± 0.16 s	7 ± 0.3 N	0 ± 0°
20	1.4 ± 0.08 s	7.5 ± 0.1 N	0 ± 0°
21	0.99 ± 0.05 s	8 ± 0.6 N	473 ± 68°
22	3.63 ± 0.15 s	8 ± 0.2 N	0 ± 0°
23	1.45 ± 0.08 s	8 ± 0.2 N	0 ± 0°
24	0.9 ± 0.04 s	10 ± 0.5 N	263 ± 60°
25	3.64 ± 0.18 s	20.8 ± 0.4 N	0 ± 0°
26	1.43 ± 0.11 s	20.5 ± 0.6 N	0 ± 0°
27	0.94 ± 0.05 s	20 ± 1.3 N	0 ± 0°

, located in Appendix A.

The raw data illustrates the general relationship between the settings. It is observed that, as the speed increases, the spool overshoot rises sharply; for example, from 0 to 1380° from trial 1 to trial 3. Additionally, an increase in the brake value corresponds to a lower spool overshoot. Regarding acceleration, it is observed that only at the lowest setting ($a=12$%) is a stable condition of zero overrun consistently maintained across all speeds (trials 25–27).

5.2. Carbon Spool Properties

5.2.1. Spool Diameter $d_o$

The calculated values are depicted in Figure 4, revealing a linear relationship between the number of trials and the spool diameter. To allow subsequent solving of the overrun model for each trial, a linear regression analysis is performed using the following equation. The resulting linear regression exhibits an $R^2$ value of $0.9978$ and a maximum error of $1.1$%. This demonstrates a strong fit to the experimental data and is utilized for further analysis and processing.

5.2.2. Spool Mass m

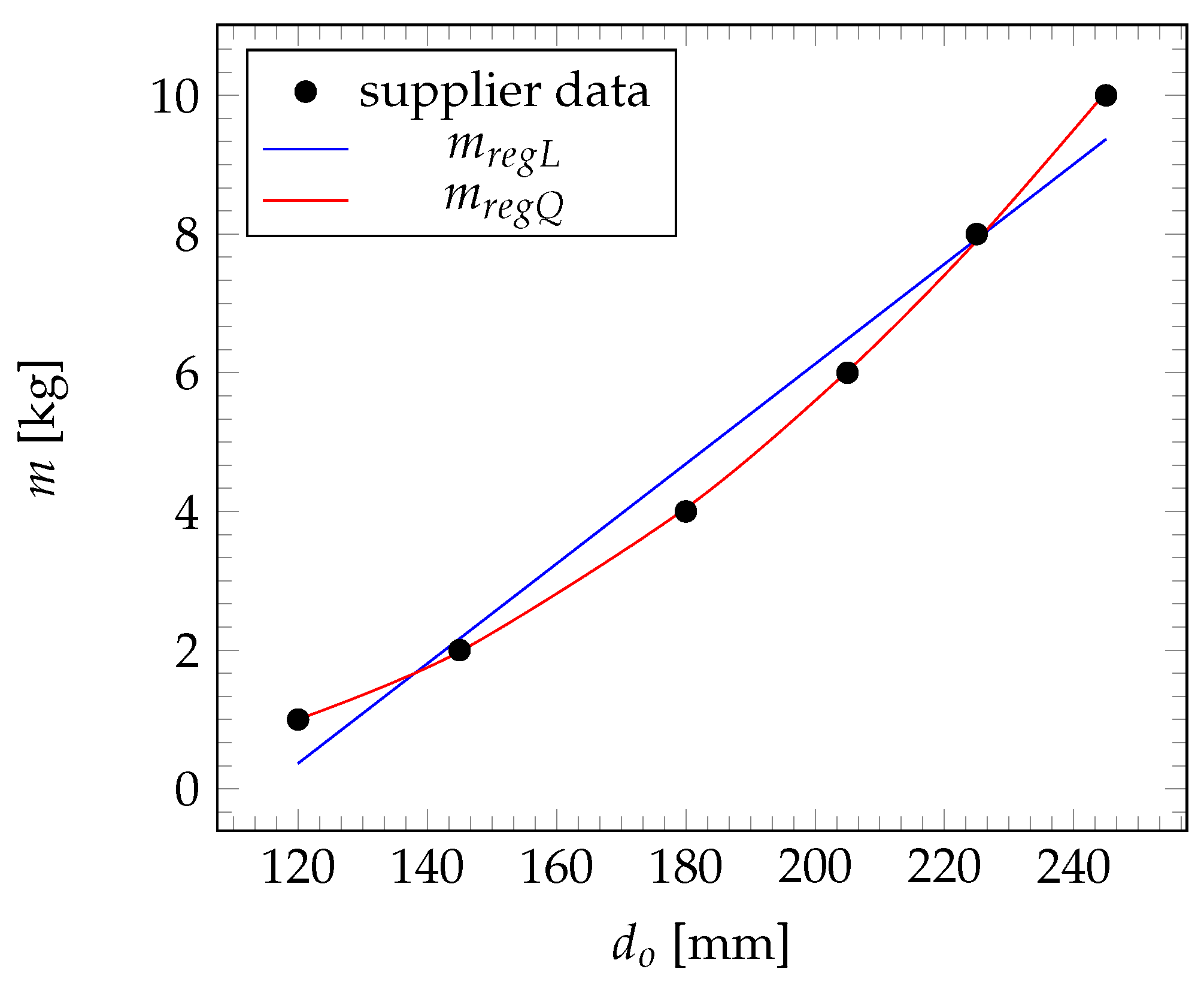
To obtain a function describing the net weight in relation to $d_o$, both linear and quadratic regression functions, denoted as $m_{regL}$ and $m_{regQ}$, respectively, are evaluated. The results, depicted in Figure 5, reveal that, within the available range of spool masses from $0.5$ kg to 10 kg, an exponential relationship exists. Consequently, the quadratic function closely aligns with the manufacturer data compared to the linear regression and is thus chosen for further analysis. The $R^2$ values obtained are $0.9746$ and $0.9998$, respectively, with maximum errors of 63% and $1.1$%.

$$m_{regL}=0.0720\ast d_o-8.2755$$

(17)

$$m_{regQ}=3.3266\ast {10}^{-4}\ast x^2-4.9041\ast {10}^{-2}\ast x+2.0957$$

(18)

5.3. Robot Speed Ramp

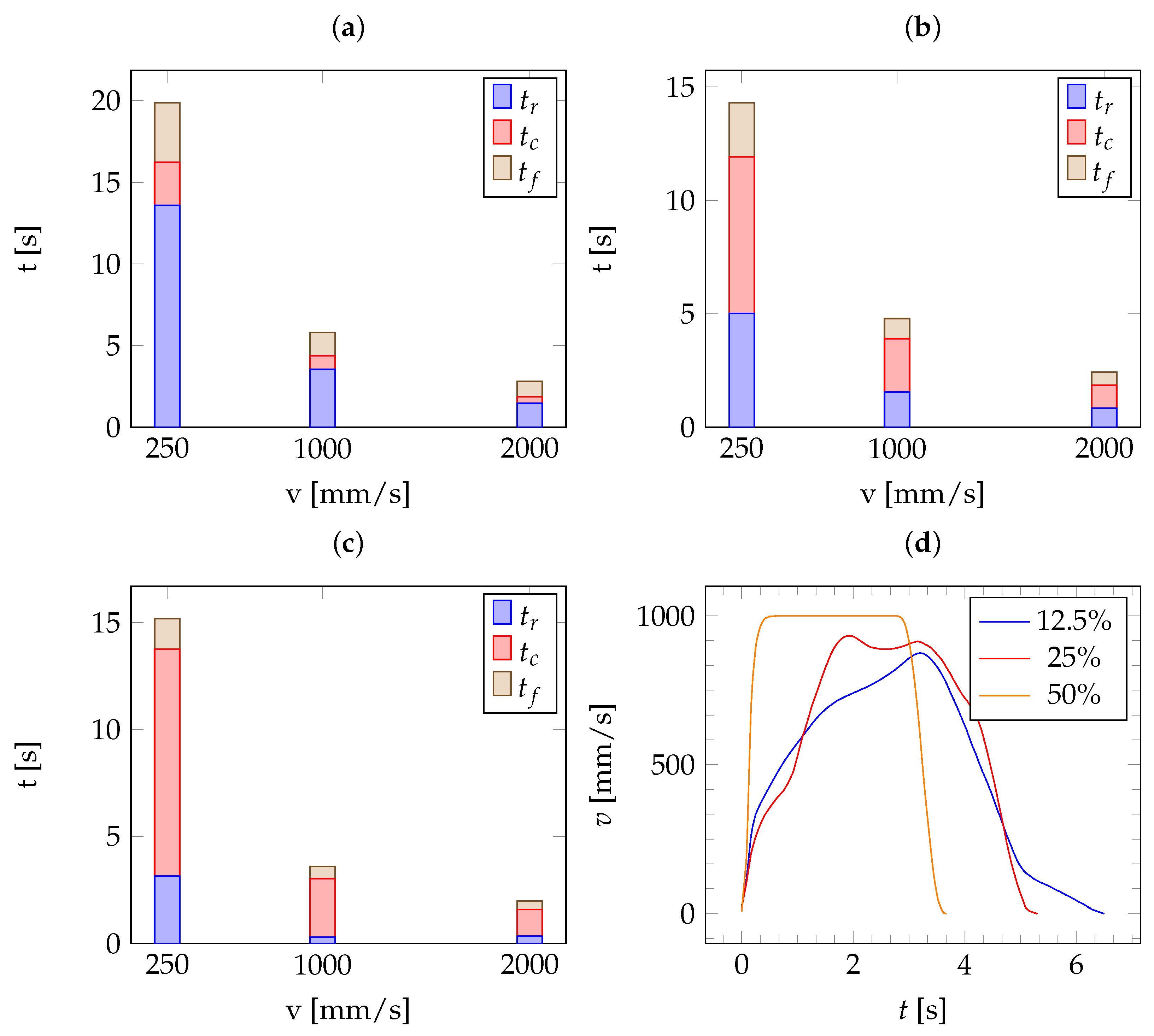
5.3.1. Data Overview

The analysis indicates that the robot signal times remain consistent across varying brake values. To consolidate common data points for the robot timing (brake values are equal), mean calculation is employed. This process yields values for the robot signal times based on 18 samples each. The summarized results are presented in

Table A3. Results from the robot speed ramp analysis.

a (%)	v (mm/s)	${\mathit{t}}_{\mathit{rise}}$ (s)	${\mathit{t}}_{\mathit{constant}}$ (s)	${\mathit{t}}_{\mathit{fall}}$ (s)
12.5	250	13.58 ± 0.12	2.65 ± 0.01	3.63 ± 0.01
12.5	1000	3.55 ± 0.51	0.83 ± 0.0	1.42 ± 0.02
12.5	2000	1.47 ± 0.03	0.4 ± 0.03	0.94 ± 0.04
25	250	5.01 ± 0.1	6.9 ± 5.13	2.39 ± 0.01
25	1000	1.55 ± 0.09	2.35 ± 0.13	0.89 ± 0.04
25	2000	0.85 ± 0.15	1.01 ± 0.05	0.58 ± 0.05
50	250	3.13 ± 0.03	10.62 ± 0.01	1.42 ± 0.02
50	1000	0.3 ± 0.03	2.72 ± 0.01	0.57 ± 0.02
50	2000	0.34 ± 0.0	1.25 ± 0.03	0.37 ± 0.02

and visually depicted in an overview plot shown in Figure 6.

The experimental data further demonstrates the dependence of robot traveling times on both speed and acceleration. Rising and falling times decrease with increasing speed or acceleration. However, an asymmetry is observed, with rising times being generally longer than falling times. This asymmetry increases with lower acceleration values. This trend is illustrated in Figure 6d through mean curves interpolated from six samples of trials 2, 11, and 20, driven at a constant speed of 1000 mm/s at varying accelerations. The average standard deviation of the robot speed was $2.3$%, $1.2$%, and $0.6$% for 250, 1000, and 2000 m/s, respectively.

Moreover, the size of the constant speed zone is directly proportional to acceleration. The maximum speed of the robot also varies with a, notably reaching a plateau at $a=25$% that is not equal to the target speed of 1000 mm/s.

This behavior suggests potential areas for future research, particularly in addressing the non-stable speed curve behavior observed in trials with SLIN movement.

5.3.2. Model Development

Based on the behavior observed in the robot SLIN movement, a model for the falling time, $t_f$, is developed. This is done due to $t_f$ being one of the main influencing factors for later calculation of the spool overrun. Through trials, it is observed that increasing speed or acceleration leads to a decrease in $t_f$. An empirical model is thus selected to represent this relationship, with constants $c_1$ and $c_2$ calibrated based on experimental data.

$$t_f=\frac{c_1}{v\ast a}+c_2$$

(19)

The values for acceleration (a) are input as percentages and for velocity (v) in m/s. Utilizing a Python code for curve fitting from the library scipy/optimize/curve_fit, the following constants are obtained: $c_1=0.1046$ and $c_2=0.4618$. The model exhibits a fit to the data with an $R^2$ value of 0.978 and a maximum time error of 0.22 s. Experimental and model predictions are visually compared in Figure 7. For $t_f>0.8$ s, the model predicts the experiment with a maximum error of $10.9$%, while for values below $0.8$ s the maximum error is $\Delta t=0.218$ s (27%).

5.4. Modeling the Spool Overrun

Based on the measurements of $t_f$, $T_{in}$, and $\alpha$, combined with the models for the spool outer diameter, $d_o$, and mass, m, the overrun model is calibrated. This calibration involves calculating values for the constants. The model solutions are calculated for each trial separately and are displayed in

Table A4. Overview of the calculated variables for the computation of the overrun per trial.

Trial	a (%)	$\mathit{brakeVal}$ (%)	v (mm/s)	${\mathit{\alpha }}_{\mathit{exp}}$ (°)	n ($1/\mathbf{s}$)	${\mathit{J}}_{\mathit{spool}}$ (kgm2)	${\mathit{J}}_{\mathit{brake}}$ (kgm2)	M ($\mathbf{Nm}$)	${\mathit{\alpha }}_{\mathit{model}}$ (°)
1	25	12.5	250	0	0.6098	0.0039	0.0077	0.2284	0
2	25	12.5	1000	285	2.4651	0.0037	0.0077	0.2260	232
3	25	12.5	2000	1380	4.9834	0.0035	0.0077	0.3513	1140
4	25	20	250	0	0.6297	0.0033	0.0077	0.2843	0
5	25	20	1000	83	2.5467	0.0031	0.0077	0.3125	10
6	25	20	2000	1110	5.1502	0.0030	0.0077	0.3399	1107
7	25	27	250	0	0.6510	0.0028	0.0077	1.0390	0
8	25	27	1000	0	2.6339	0.0026	0.0077	1.0877	0
9	25	27	2000	183	5.3286	0.0025	0.0077	0.8363	93
10	50	12.5	250	0	0.6739	0.0023	0.0077	0.3248	0
11	50	12.5	1000	170	2.7273	0.0022	0.0077	0.3501	126
12	50	12.5	2000	1080	5.5198	0.0021	0.0077	0.4037	1163
13	50	20	250	0	0.6983	0.0020	0.0077	0.3704	0
14	50	20	1000	113	2.8275	0.0018	0.0077	0.4222	70
15	50	20	2000	848	5.7252	0.0017	0.0077	0.4726	930
16	50	27	250	0	0.7246	0.0016	0.0077	0.9884	0
17	50	27	1000	0	2.9354	0.0015	0.0077	0.9488	0
18	50	27	2000	244	5.9465	0.0014	0.0077	0.8029	411
19	12.5	12.5	250	0	0.7530	0.0013	0.0077	0.3699	0
20	12.5	12.5	1000	0	3.0519	0.0013	0.0077	0.3911	0
21	12.5	12.5	2000	473	6.1856	0.0012	0.0077	0.4117	517
22	12.5	20	250	0	0.7837	0.0011	0.0077	0.4062	0
23	12.5	20	1000	0	3.1780	0.0010	0.0077	0.4006	0
24	12.5	20	2000	263	6.4447	0.0010	0.0077	0.4939	374
25	12.5	27	250	0	0.8170	0.0009	0.0077	1.0106	0
26	12.5	27	1000	0	3.3149	0.0009	0.0077	0.9842	0
27	12.5	27	2000	0	6.7265	0.0008	0.0077	0.9464	0

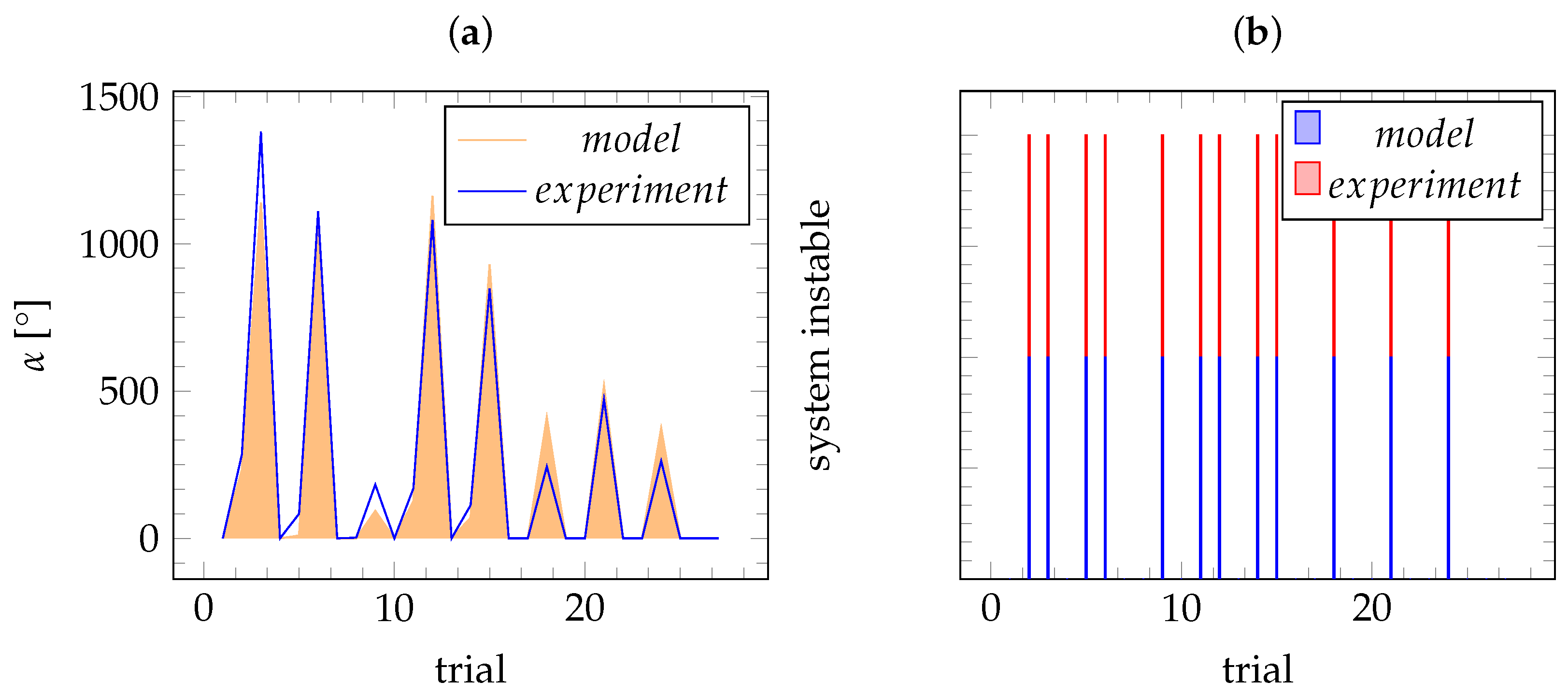
. A comparison of the experimental and model behavior per trial is presented in Figure 8a.

The model demonstrates the ability to predict both large and small overrun angles, $\alpha$, while also following the reduction of spool weight and outer diameter during the trials. Notably, large overruns ($\alpha >$ 400°) are reliably detected, although error percentages increase for smaller angles. The maximum angle errors are 191° and 176° for angles of $\alpha \le$ 400° and $\alpha >$ 400°, respectively. However, for predicting system boundaries, a precise modeling of experimental angles to the degree is unnecessary. Instead, the focus is on detecting the presence or absence of overrun (Boolean True or False detection), where True indicates $\alpha >0$ and False indicates $\alpha =0$. Intermediate calculations are summarized in Table A4.

A comparison of Boolean overrun detection is depicted in Figure 8b, demonstrating the model’s ability to accurately predict instability due to overrun without false detections across all trials. All instances of overrun are accurately anticipated, demonstrating the model’s proficiency in capturing the influence of speed, brake value, acceleration, and spool properties. The rate of detection is 100%.

Parameter values for constants $k_1$ and $k_2$ are obtained via curve fitting with Python code, yielding $k_1=1.68$ and $k_2=0.58$. The model’s strong fit to experimental data is reflected in an $R^2$ value of $0.9674$.

5.5. Modeling System Boundaries Based on Overrun Model

The adjusted overrun model enables the prediction of crucial minimum tension values for system stability in respect to a worst-case scenario. While there is potential for full overrun compensation at slightly lower values in practical scenarios, the study primarily aims to reliably estimate values where system stability is thought to be assured.

The calculations, illustrated in Figure 9a, show that, with rising acceleration, the necessary minimum tension increases, showing a similar trend concerning system velocity. For high velocities with low tension, a minimum acceleration is recommended. For instance, at $a=12.5$%, only 16 N is required, compared to 23 N and 32 N at $a=25$% and 50%, respectively.

The influence of speed on tension is significantly greater than that of acceleration. This is evident from the observation that the necessary tension increases by factors of 45, 35, and 26 for accelerations of $12.5$%, 25%, and 50%, respectively, over a speed range increase of a factor of 8. Conversely, when the acceleration is increased by a factor of 4, the maximum tension increase only rises by a factor of 2.

A comparison of the boundary model results with the experiment are displayed in Figure 9b. It demonstrates that the model predicts higher tension values than those observed in the experiment, suggesting an average tension increase of 2.9 times to avoid overrun.

Based on the evaluated curves, it is possible to predict necessary minimum tensions, which are a key factor for impregnation unit development. In scenarios where the system demands high-speed yarn laying, optimizing the impregnation unit to accommodate greater input forces becomes imperative. Therefore, future research will delve into developing a modeling approach tailored to addressing this aspect.

6. Discussion

6.1. Spool Diameter Model

A linear regression model, developed based on the experiments, demonstrates a good fit with a low maximum error. However, its validity is limited to the current experimental background, as the yarn usage per trial depends on the total laying distance and the number of samples. Further research is necessary to create a more comprehensive model, considering variations in laying length and sample size. Alternatively, a mathematical approach involving back calculation of the spool trial number relative to laying path length and sample number could be explored. Despite its limitations, the model proves valid within the proposed experimental context.

6.2. Spool Mass Model

A model was constructed to establish a relationship between spool diameter and mass using manufacturer data. Both linear and quadratic models were examined, revealing an exponential behavior in the manufacturer data. However, as the spool was not weighed during or after each trial in the experiment, fluctuations to the estimated model may occur in reality. While these influences could not be validated for the selected model, a sufficient fit is estimated based on the manufacturer data. Combining the mass model with the overrun model compensates for fluctuations between reality and experiment by using calibration factors.

6.3. Robot Speed Ramp Model

To the authors’ knowledge, recent yarn-laying experiments combined with in situ impregnation have not yielded any models concerning a robot movement model for calculating deceleration time (falling time, $t_f$). Hence, a model was devised based on the acceleration and velocity settings combined with an SLIN movement type.

Experimental findings showed a complex interplay between acceleration and velocity settings concerning the falling time. Despite minor discrepancies in dimension estimation, the selected model captures the interaction of these settings on falling times. To refine the model, falling times were adjusted downwards using error values derived from maximum fluctuations between reality and model. Consequently, the speed ramp model allows for practical application through worst-case scenario calculations. This worst-case scenario is defined by the possibility that the calculated minimum yarn tension may exceed the actual requirement in practice.

Future research should concentrate on enhancing the model by exploring additional settings and various motion types affecting the resulting robot falling time. Despite its fluctuations, within the chosen experimental parameters the model reliably predicts values with essential accuracy.

6.4. Modeling the Spool Overrun

Although overrun prediction relied on mechanical equations, two fitting constants were required to achieve a good match between reality and experiment. Subsequent calibration improved the model’s accuracy in predicting spool overrun across varying speed, acceleration, and brake values, effectively accounting for changes in spool properties. However, the model exhibits weaknesses in precisely calculating the overrun angle, resulting in both over- and underpredictions during experimentation. Nevertheless, for system stability analysis, estimating the occurrence of overrun suffices, obviating the need for precise angle measurements. Analysis of the model in a Boolean manner demonstrated its capability to predict situations of system instability with a 100% success rate, indicating its suitability for delineating system boundaries. While acknowledging the potential for slight deviations in reality, this highlights the potential for further investigation, especially in cases where the model predicts small overrun angles (<15°). Here, predictive accuracy may be refined through targeted research efforts.

6.5. Modeling System Boundaries Based on Overrun Model

The evaluation of the model for system boundaries involves utilizing the calibrated overrun model to predict situations where no overrun occurs initially, representing stable system conditions. By incorporating known errors into the model prediction, they serve as a safety coefficient to ensure stability of the evaluated behavior in reality. The model, acting as an initial prediction tool, can be used to develop subsequent components of the laying head based on worst-case assumptions. Additionally, it is noted that, in reality, the final laying head may potentially be stable at lower values as estimated, although this adjustment is not obligatory if the system is already stable.

Regarding the comparison between model predictions and experimental outcomes, it is evident that the model consistently recommends an increasing tension to compensate the spool overrun that occurred in the experiments. This observation underscores the model’s capability to accurately approximate the necessary data points.

6.6. Area of Application of the Models

In the development of a direct-yarn-laying effector, the proposed model serves as the initial step, offering valuable insights. Once the specifics of yarn spool weights, materials, process speeds, and acceleration are determined, it is possible to approximate the minimum yarn tension required based on the model. This estimated tension becomes crucial for designing the impregnation unit. Within the impregnation unit, tension on the yarn increases due to shear and friction, potentially leading to fiber breakage. Therefore, based on the estimated input tension values, the impregnation unit can be optimized to ensure that tension increases remain within the tolerable process window for the textile yarn.

7. Conclusions

Based on the comprehensive analysis conducted, it is evident that this research has made significant strides in understanding the dynamics of the direct-yarn-laying process and its associated parameters. The experiments conducted on spool overrun, carbon spool properties, robot speed ramp modeling, spool overrun modeling, and system boundary modeling have provided valuable insights into the intricate relationships between various process variables.

The results of the experiment on spool overrun highlighted the direct influences of robot acceleration and speed, as well as the indirect influence of the magnetic powder brake value on the system. Additionally, the fluctuations in spool circumference were observed throughout the experiment, further emphasizing the complex nature of the process.

The models developed for spool diameter and mass exhibited strong fits to the experimental data, providing valuable tools for further analysis and processing. Similarly, the robot speed ramp model successfully captured the interplay between acceleration and velocity settings, allowing for practical applications in approximate calculations.

The spool overrun model, despite its reliance on fitting constants, demonstrated a high degree of accuracy in predicting system instability across varying parameters. While precise angle measurements proved challenging, the model’s ability to anticipate overrun situations with a 100% success rate underscores its utility in delineating system boundaries. Furthermore, the evaluation of system boundaries based on the overrun model highlighted the model’s effectiveness in recommending minimum tension values for stable system conditions.

Overall, the models developed in this research hold immense potential for practical applications in the development of direct-yarn-laying effectors. By providing insights into minimum tension requirements, these models pave the way for optimizing the impregnation unit to ensure stable process conditions while minimizing the risk of fiber breakage. Future research endeavors could focus on refining these models and exploring additional variables to further enhance their predictive capabilities in real-world scenarios.