Relaxation Modeling of Unidirectional Carbon Fiber Reinforced Polymer Composites Before and After UV-C Exposure
Abstract
:1. Introduction
2. Materials
Resin-Only Specimen Preparation and Conditioning
3. Matrix Experimental Characterization
3.1. Resin-Only Specimen Characterization
3.2. Fitting to Viscoelastic Model
4. Composite Material Finite Element Modeling
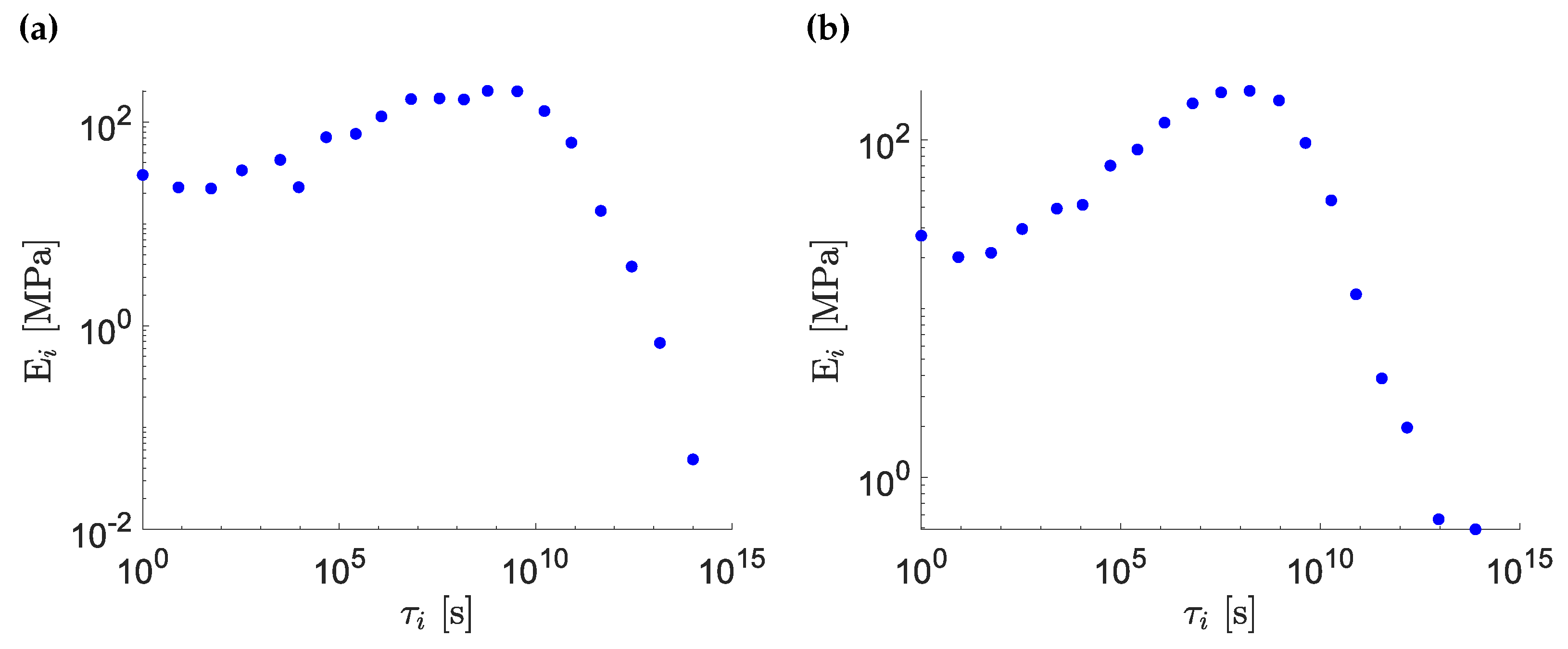
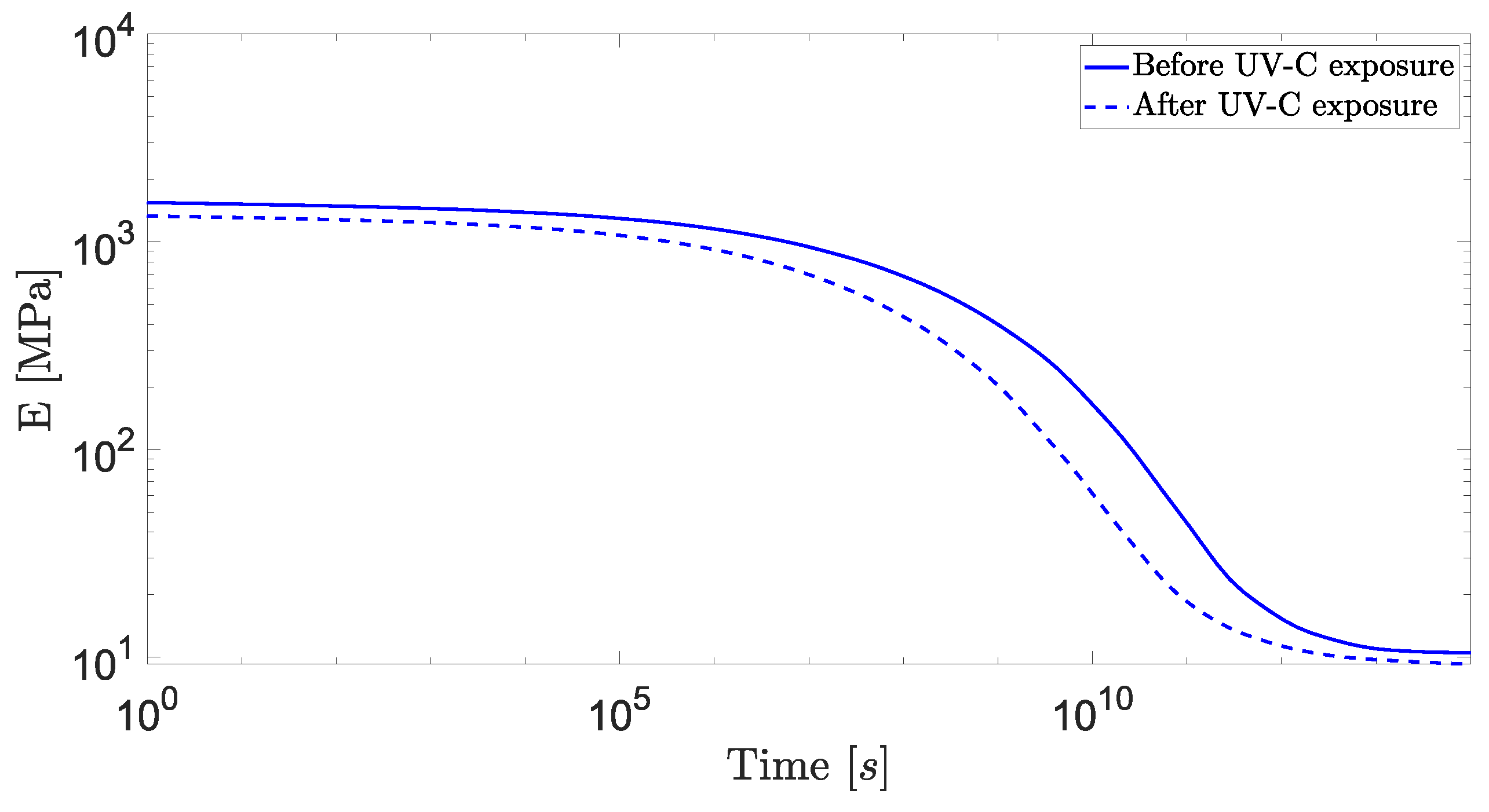
5. Matrix Experimental Characterization Results
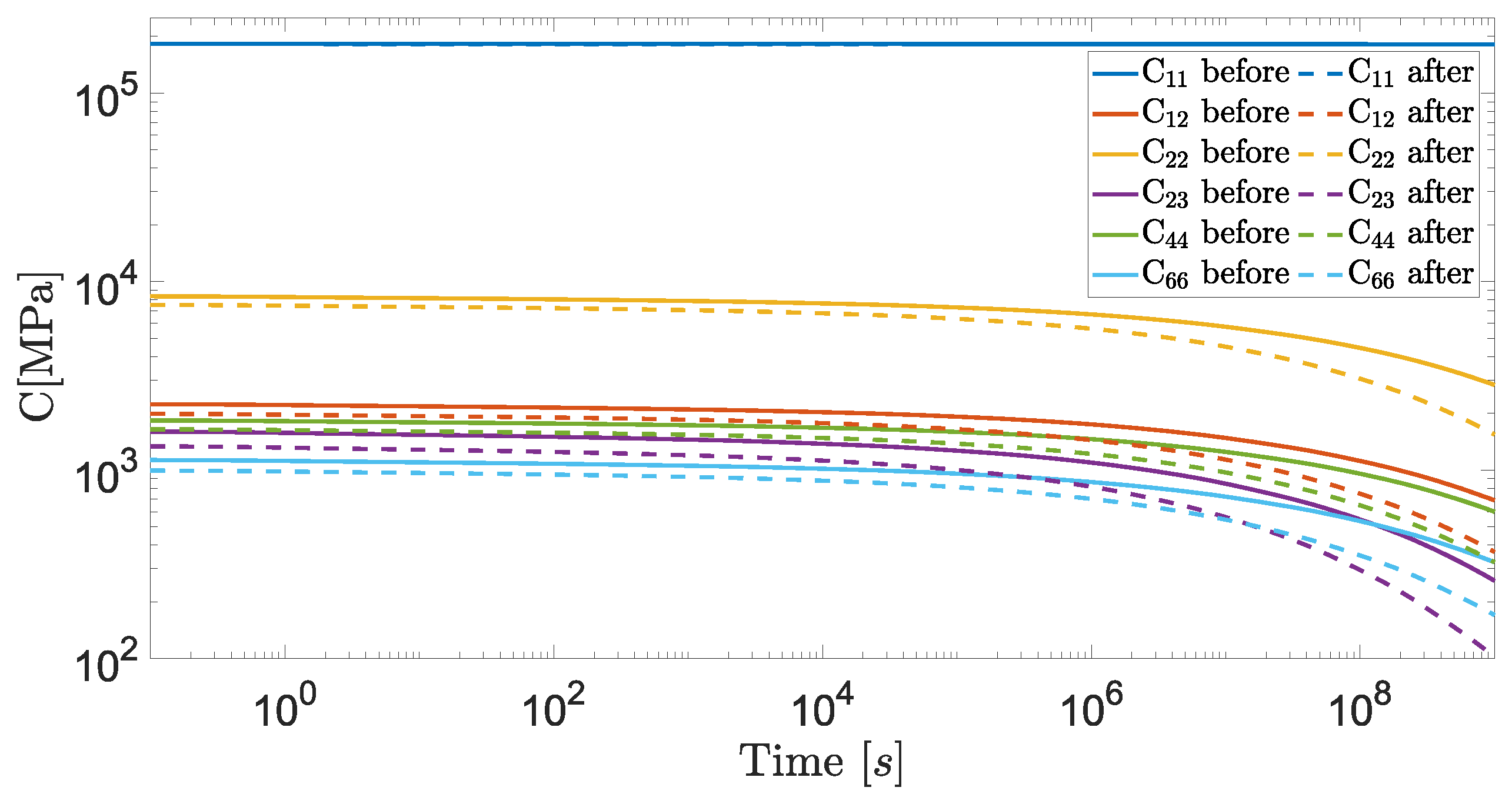
6. Composite Material Finite Element Modeling Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AO | Atomic Oxygen |
| CFRP | Carbon fiber-reinforced polymer |
| DMA | Dynamic mechanical analysis |
| FEM | Finite element method |
| LEO | Low Earth orbit |
| LLSS | Linear least squares solvers |
| MWNTs | Multi walled nanotubes |
| PBC | Periodic boundary condition |
| PMCs | Polymer matrix composites |
| PSO | Particle swarm optimization |
| RVE | Representative volume element |
| TTSP | Time–temperature superposition principle |
| UD | Unidirectional |
References
- Tribble, A.C. The Space Environment: Implications for Spacecraft Design-Revised and Expanded Edition; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Grossman, E.; Gouzman, I. Space environment effects on polymers in low earth orbit. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2003, 208, 48–57. [Google Scholar] [CrossRef]
- Han, J.H.; Kim, C.G. Low earth orbit space environment simulation and its effects on graphite/epoxy composites. Compos. Struct. 2006, 72, 218–226. [Google Scholar] [CrossRef]
- Deev, I.; Nikishin, E. Effect of long-term exposure in the space environment on the microstructure of fibre-reinforced polymers. Compos. Sci. Technol. 1997, 57, 1391–1401. [Google Scholar] [CrossRef]
- Schwam, D.; Litt, M. Evaluation of atomic oxygen resistant coatings for space structures. Adv. Perform. Mater. 1996, 3, 153–169. [Google Scholar] [CrossRef]
- Golub, M.A.; Cormia, R.D. ESCA study of poly (vinylidene fluoride), tetrafluoroethylene-ethylene copolymer and polyethylene exposed to atomic oxygen. Polymer 1989, 30, 1576–1581. [Google Scholar] [CrossRef]
- Scialdone, J.J. Characterization of the outgassing of spacecraft materials. In Proceedings of the Shuttle Optical Environment, Washington, DC, USA, 23–24 April 1981; Volume 287, pp. 2–9. [Google Scholar]
- Rånby, B. Photodegradation and photo-oxidation of synthetic polymers. J. Anal. Appl. Pyrolysis 1989, 15, 237–247. [Google Scholar] [CrossRef]
- Mahmoud, W.; Elfiky, D.; Robaa, S.; Elnawawy, M.; Yousef, S. Effect of atomic oxygen on LEO CubeSat. Int. J. Aeronaut. Space Sci. 2021, 22, 726–733. [Google Scholar] [CrossRef]
- Tan, Q.; Li, F.; Liu, L.; Chu, H.; Liu, Y.; Leng, J. Effects of atomic oxygen on epoxy-based shape memory polymer in low earth orbit. J. Intell. Mater. Syst. Struct. 2018, 29, 1081–1087. [Google Scholar] [CrossRef]
- Tagawa, M.; Yokota, K. Atomic oxygen-induced polymer degradation phenomena in simulated LEO space environments: How do polymers react in a complicated space environment? Acta Astronaut. 2008, 62, 203–211. [Google Scholar] [CrossRef]
- Shin, K.B.; Kim, C.G.; Hong, C.S.; Lee, H.H. Prediction of failure thermal cycles in graphite/epoxy composite materials under simulated low earth orbit environments. Compos. Part B Eng. 2000, 31, 223–235. [Google Scholar] [CrossRef]
- Lu, T.; Solis-Ramos, E.; Yi, Y.; Kumosa, M. UV degradation model for polymers and polymer matrix composites. Polym. Degrad. Stab. 2018, 154, 203–210. [Google Scholar] [CrossRef]
- Singh, B.; Sharma, N. Mechanistic implications of plastic degradation. Polym. Degrad. Stab. 2008, 93, 561–584. [Google Scholar] [CrossRef]
- Larché, J.F.; Bussière, P.O.; Therias, S.; Gardette, J.L. Photooxidation of polymers: Relating material properties to chemical changes. Polym. Degrad. Stab. 2012, 97, 25–34. [Google Scholar] [CrossRef]
- Ding, J.; Cheng, L. Experimental study on ultrasonic three-point bending fatigue of CFRP under ultraviolet radiation. Eng. Fract. Mech. 2021, 242, 107435. [Google Scholar] [CrossRef]
- Shi, Z.; Zou, C.; Zhou, F.; Zhao, J. Analysis of the mechanical properties and damage mechanism of carbon fiber/epoxy composites under UV aging. Materials 2022, 15, 2919. [Google Scholar] [CrossRef] [PubMed]
- Tortorici, D.; Toto, E.; Santonicola, M.G.; Laurenzi, S. Effects of UV-C exposure on composite materials made of recycled carbon fibers. Acta Astronaut. 2024, 220, 367–373. [Google Scholar] [CrossRef]
- Moon, J.B.; Kim, M.G.; Kim, C.G.; Bhowmik, S. Improvement of tensile properties of CFRP composites under LEO space environment by applying MWNTs and thin-ply. Compos. Part A Appl. Sci. Manuf. 2011, 42, 694–701. [Google Scholar] [CrossRef]
- Jang, J.H.; Hong, S.B.; Kim, J.G.; Goo, N.S.; Lee, H.; Yu, W.R. Long-term properties of carbon fiber-reinforced shape memory epoxy/polymer composites exposed to vacuum and ultraviolet radiation. Smart Mater. Struct. 2019, 28, 115013. [Google Scholar] [CrossRef]
- Jang, J.H.; Hong, S.B.; Kim, J.G.; Goo, N.S.; Yu, W.R. Accelerated testing method for predicting long-term properties of carbon fiber-reinforced shape memory polymer composites in a low earth orbit environment. Polymers 2021, 13, 1628. [Google Scholar] [CrossRef]
- Zarrelli, M.; Skordos, A.A.; Partridge, I.K. Thermomechanical analysis of a toughened thermosetting system. Mech. Compos. Mater. 2008, 44, 181–190. [Google Scholar] [CrossRef]
- Lange, J.; Månson, J.A.E.; Hult, A. Build-up of structure and viscoelastic properties in epoxy and acrylate resins cured below their ultimate glass transition temperature. Polymer 1996, 37, 5859–5868. [Google Scholar] [CrossRef]
- Müller-Pabel, M.; Agudo, J.A.R.; Gude, M. Measuring and understanding cure-dependent viscoelastic properties of epoxy resin: A review. Polym. Test. 2022, 114, 107701. [Google Scholar] [CrossRef]
- Woo, E.; Seferis, J.; Schaffnit, R. Viscoelastic characterization of high performance epoxy matrix composites. Polym. Compos. 1991, 12, 273–280. [Google Scholar] [CrossRef]
- Saseendran, S.; Wysocki, M.; Varna, J. Evolution of viscoelastic behaviour of a curing LY5052 epoxy resin in the rubbery state. Adv. Compos. Mater. 2017, 26, 553–567. [Google Scholar] [CrossRef]
- Cost, T.L.; Becker, E.B. A multidata method of approximate Laplace transform inversion. Int. J. Numer. Methods Eng. 1970, 2, 207–219. [Google Scholar] [CrossRef]
- Baumgaertel, M.; Winter, H. Determination of discrete relaxation and retardation time spectra from dynamic mechanical data. Rheol. Acta 1989, 28, 511–519. [Google Scholar] [CrossRef]
- Davies, A.; Anderssen, R.S. Sampling localization in determining the relaxation spectrum. J. Non-Newton. Fluid Mech. 1997, 73, 163–179. [Google Scholar] [CrossRef]
- Honerkamp, J.; Weese, J. Determination of the relaxation spectrum by a regularization method. Macromolecules 1989, 22, 4372–4377. [Google Scholar] [CrossRef]
- Mustapha, S.S.; Phillips, T. A dynamic nonlinear regression method for the determination of the discrete relaxation spectrum. J. Phys. D Appl. Phys. 2000, 33, 1219. [Google Scholar] [CrossRef]
- Jiang, B.; Kamerkar, P.; Keffer, D.J.; Edwards, B. Using multiple-mode models for fitting and predicting rheological properties of polymeric melts. J. Appl. Polym. Sci. 2006, 99, 405–423. [Google Scholar] [CrossRef]
- Suchocki, C.; Pawlikowski, M.; Skalski, K.; Jasiński, C.; Morawiński, Ł. Determination of material parameters of quasi-linear viscoelastic rheological model for thermoplastics and resins. J. Theor. Appl. Mech. 2013, 51, 569–580. [Google Scholar]
- Simhambhatla, M.; Leonov, A. The extended Padé-Laplace method for efficient discretization of linear viscoelastic spectra. Rheol. Acta 1993, 32, 589–600. [Google Scholar] [CrossRef]
- Selivanov, M.F.; Chernoivan, Y.A. A combined approach of the Laplace transform and Pade approximation solving viscoelasticity problems. Int. J. Solids Struct. 2007, 44, 66–76. [Google Scholar] [CrossRef]
- Rekik, A.; Brenner, R. Optimization of the collocation inversion method for the linear viscoelastic homogenization. Mech. Res. Commun. 2011, 38, 305–308. [Google Scholar] [CrossRef]
- Emri, I.; Tschoegl, N. Determination of mechanical spectra from experimental responses. Int. J. Solids Struct. 1995, 32, 817–826. [Google Scholar] [CrossRef]
- Bradshaw, R.D.; Brinson, L. A sign control method for fitting and interconverting material functions for linearly viscoelastic solids. Mech. Time-Depend. Mater. 1997, 1, 85–108. [Google Scholar] [CrossRef]
- Carrot, C.; Verney, V. Determination of a discrete relaxation spectrum from dynamic experimental data using the Pade-Laplace method. Eur. Polym. J. 1996, 32, 69–77. [Google Scholar] [CrossRef]
- Cho, K.S. A simple method for determination of discrete relaxation time spectrum. Macromol. Res. 2010, 18, 363–371. [Google Scholar] [CrossRef]
- Fernanda, M.; Costa, P.; Ribeiro, C. Parameter estimation of viscoelastic materials: A test case with different optimization strategies. AIP Conf. Proc. Am. Inst. Phys. 2011, 1389, 771–774. [Google Scholar]
- Gerlach, S.; Matzenmiller, A. Comparison of numerical methods for identification of viscoelastic line spectra from static test data. Int. J. Numer. Methods Eng. 2005, 63, 428–454. [Google Scholar] [CrossRef]
- Costa, M.F.P.; Ribeiro, C. Generalized fractional Maxwell model: Parameter estimation of a viscoelastic material. AIP Conf. Proc. Am. Inst. Phys. 2012, 1479, 790–793. [Google Scholar]
- Cui, Z.; Brinson, L.C. A combination optimisation method for the estimation of material parameters for viscoelastic solids. Int. J. Comput. Sci. Math. 2014, 5, 325–335. [Google Scholar] [CrossRef]
- Sun, C.T.; Vaidya, R.S. Prediction of composite properties from a representative volume element. Compos. Sci. Technol. 1996, 56, 171–179. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, K.K.; Ha, S.K. Effects of fiber arrangement on mechanical behavior of unidirectional composites. J. Compos. Mater. 2008, 42, 1851–1871. [Google Scholar] [CrossRef]
- Ye, F.; Wang, H. A simple Python code for computing effective properties of 2D and 3D representative volume element under periodic boundary conditions. arXiv 2017, arXiv:1703.03930. [Google Scholar]
- Liu, X.; Tang, T.; Yu, W.; Pipes, R.B. Multiscale modeling of viscoelastic behaviors of textile composites. Int. J. Eng. Sci. 2018, 130, 175–186. [Google Scholar] [CrossRef]
- Palmeri, F.; Lambertini, L.; Laurenzi, S. Numerical relaxation analysis of carbon fiber reinforced polymers. Macromol. Symp. 2024, 413, 2400038. [Google Scholar] [CrossRef]
- An, N.; Jia, Q.; Jin, H.; Ma, X.; Zhou, J. Multiscale modeling of viscoelastic behavior of unidirectional composite laminates and deployable structures. Mater. Des. 2022, 219, 110754. [Google Scholar] [CrossRef]
- Kwok, K.; Pellegrino, S. Micromechanics models for viscoelastic plain-weave composite tape springs. Aiaa J. 2017, 55, 309–321. [Google Scholar] [CrossRef]
- Pathan, M.; Tagarielli, V.; Patsias, S. Numerical predictions of the anisotropic viscoelastic response of uni-directional fibre composites. Compos. Part A Appl. Sci. Manuf. 2017, 93, 18–32. [Google Scholar] [CrossRef]
- Kemnitz, R.A.; Cobb, G.R.; Singh, A.K.; Hartsfield, C.R. Characterization of simulated low earth orbit space environment effects on acid-spun carbon nanotube yarns. Mater. Des. 2019, 184, 108178. [Google Scholar] [CrossRef]
- Anderson, B.J.; Smith, R.E. Natural Orbital Environment Definition Guidelines for Use in Aerospace Vehicle Development; Technical Memorandum 4527; NASA Marshall Space Flight Center: Huntsville, AL, USA, 1994. [Google Scholar]
- Ward, I.M.; Sweeney, J. Mechanical Properties of Solid Polymers; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wong, T.T.; Lau, K.T.; Tam, W.Y.; Leng, J.; Wang, W.; Li, W.; Wei, H. Degradation of nano-ZnO particles filled styrene-based and epoxy-based SMPs under UVA exposure. Compos. Struct. 2015, 132, 1056–1064. [Google Scholar] [CrossRef]
- Brinson, H.F.; Brinson, L.C. Polymer engineering science and viscoelasticity. Introduction 2008, 99, 157. [Google Scholar]
- Al Azzawi, W.; Epaarachchi, J.; Leng, J. Investigation of ultraviolet radiation effects on thermomechanical properties and shape memory behaviour of styrene-based shape memory polymers and its composite. Compos. Sci. Technol. 2018, 165, 266–273. [Google Scholar] [CrossRef]
- Yan, L.; Chouw, N.; Jayaraman, K. Effect of UV and water spraying on the mechanical properties of flax fabric reinforced polymer composites used for civil engineering applications. Mater. Des. 2015, 71, 17–25. [Google Scholar] [CrossRef]
- Tan, Q.; Li, F.; Liu, L.; Liu, Y.; Leng, J. Effects of vacuum thermal cycling, ultraviolet radiation and atomic oxygen on the mechanical properties of carbon fiber/epoxy shape memory polymer composite. Polym. Test. 2023, 118, 107915. [Google Scholar] [CrossRef]
- Tan, Q.; Li, F.; Liu, L.; Liu, Y.; Yan, X.; Leng, J. Study of low earth orbit ultraviolet radiation and vacuum thermal cycling environment effects on epoxy-based shape memory polymer. J. Intell. Mater. Syst. Struct. 2019, 30, 2688–2696. [Google Scholar] [CrossRef]
- Dexter, H.B. Long-Term Environmental Effects and Flight Service Evaluation of Composite Materials; NASA Langley Research Center: Hampton, VA, USA, 1987; Volume 89067. [Google Scholar]

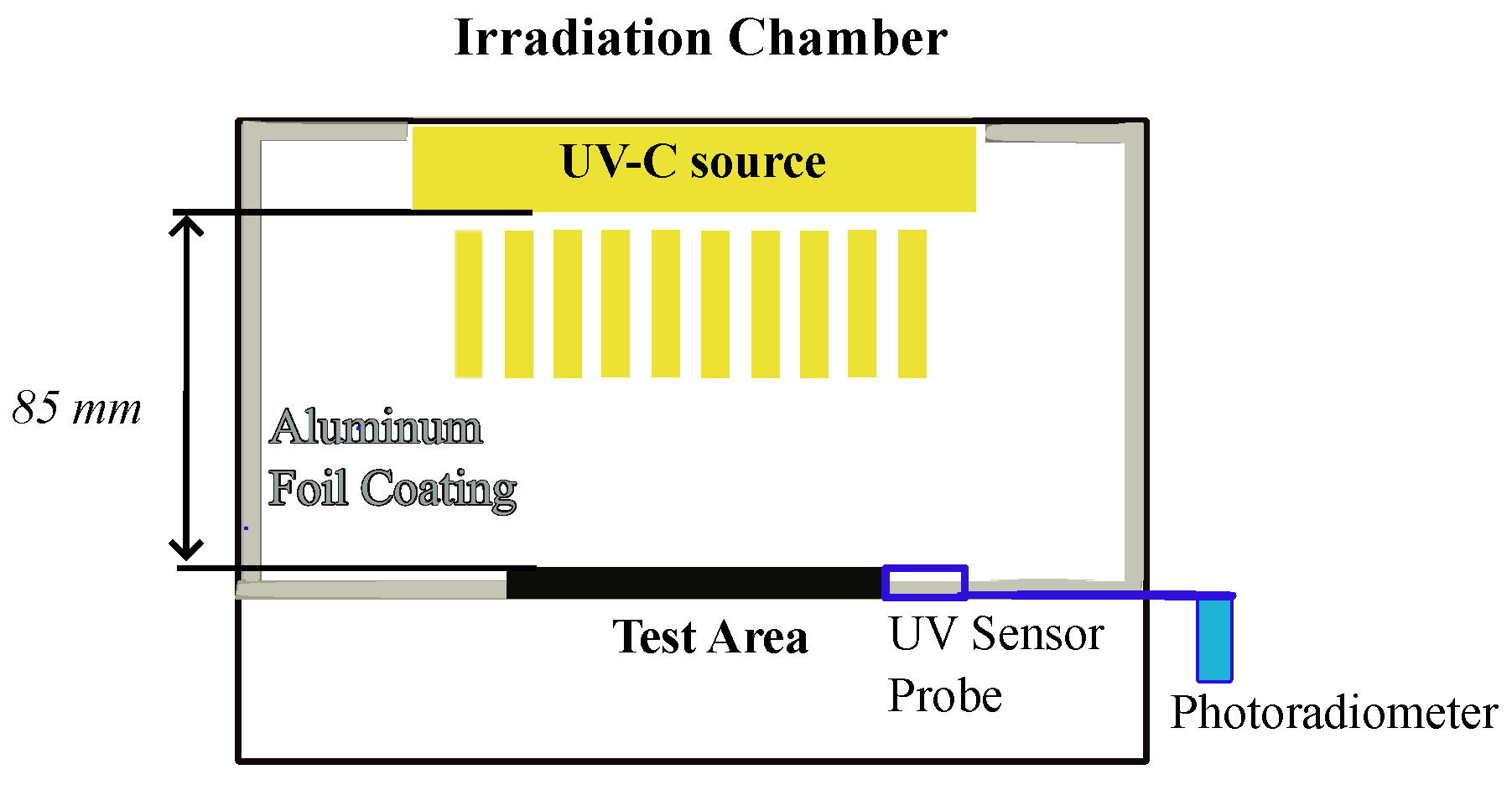

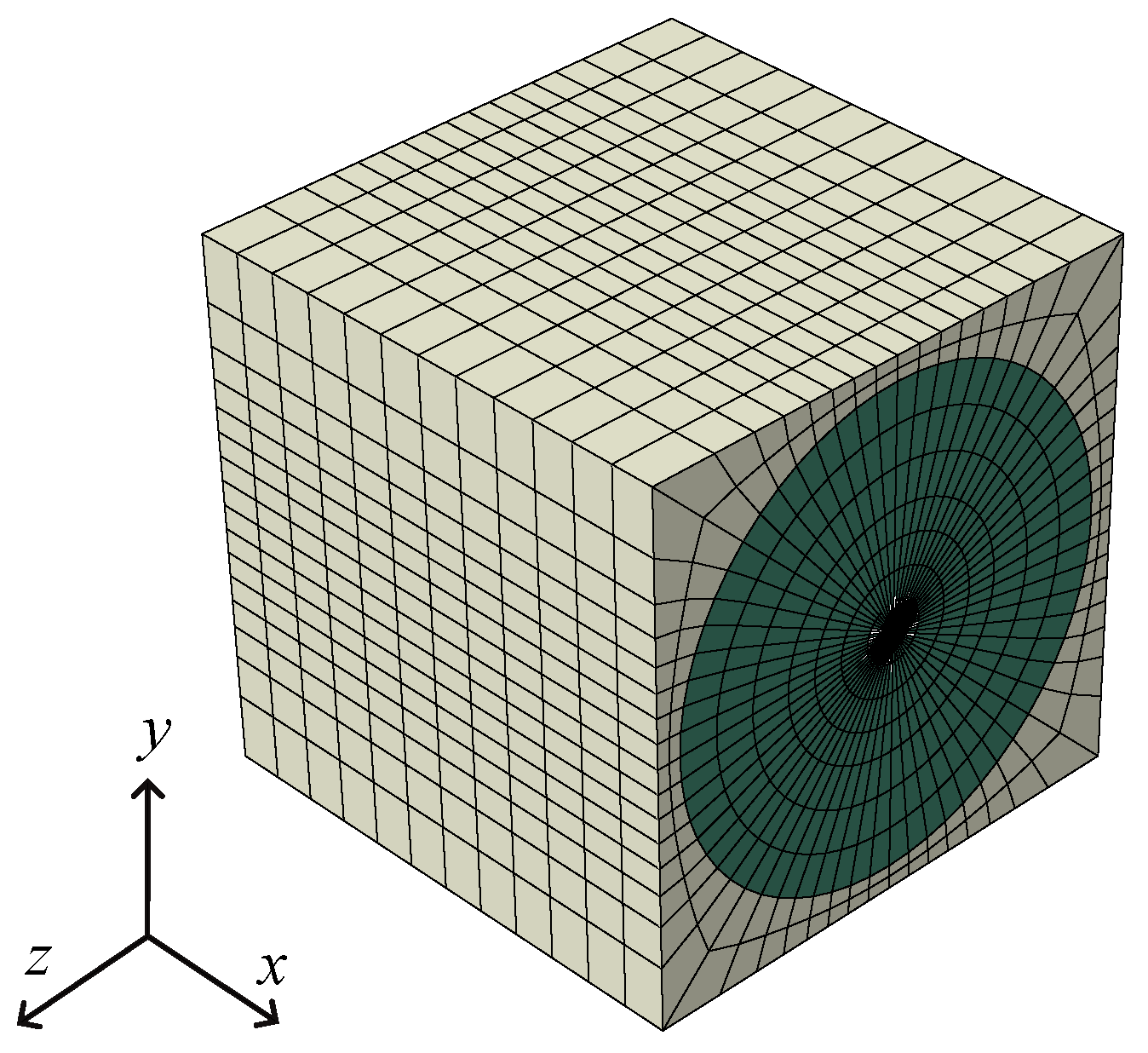
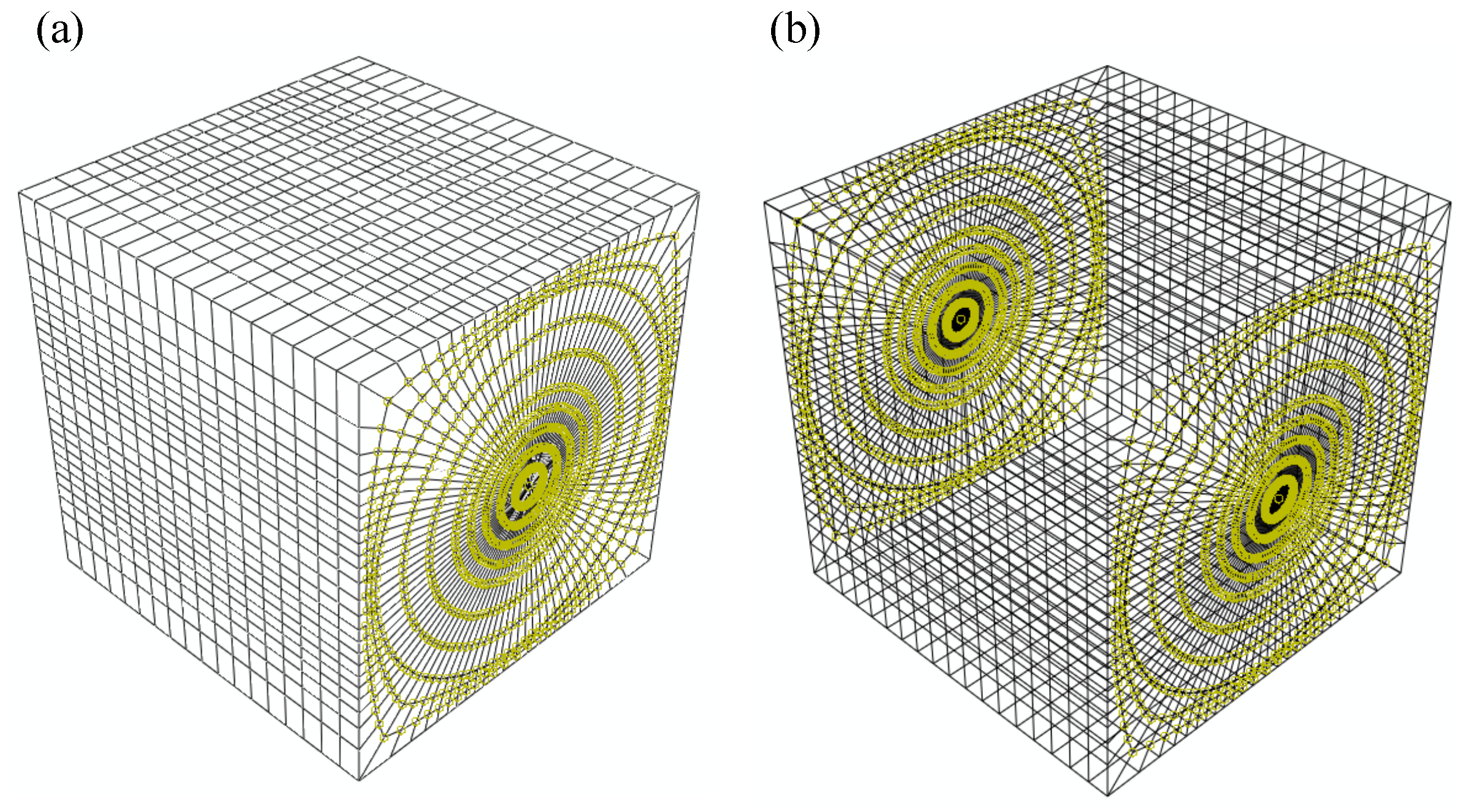
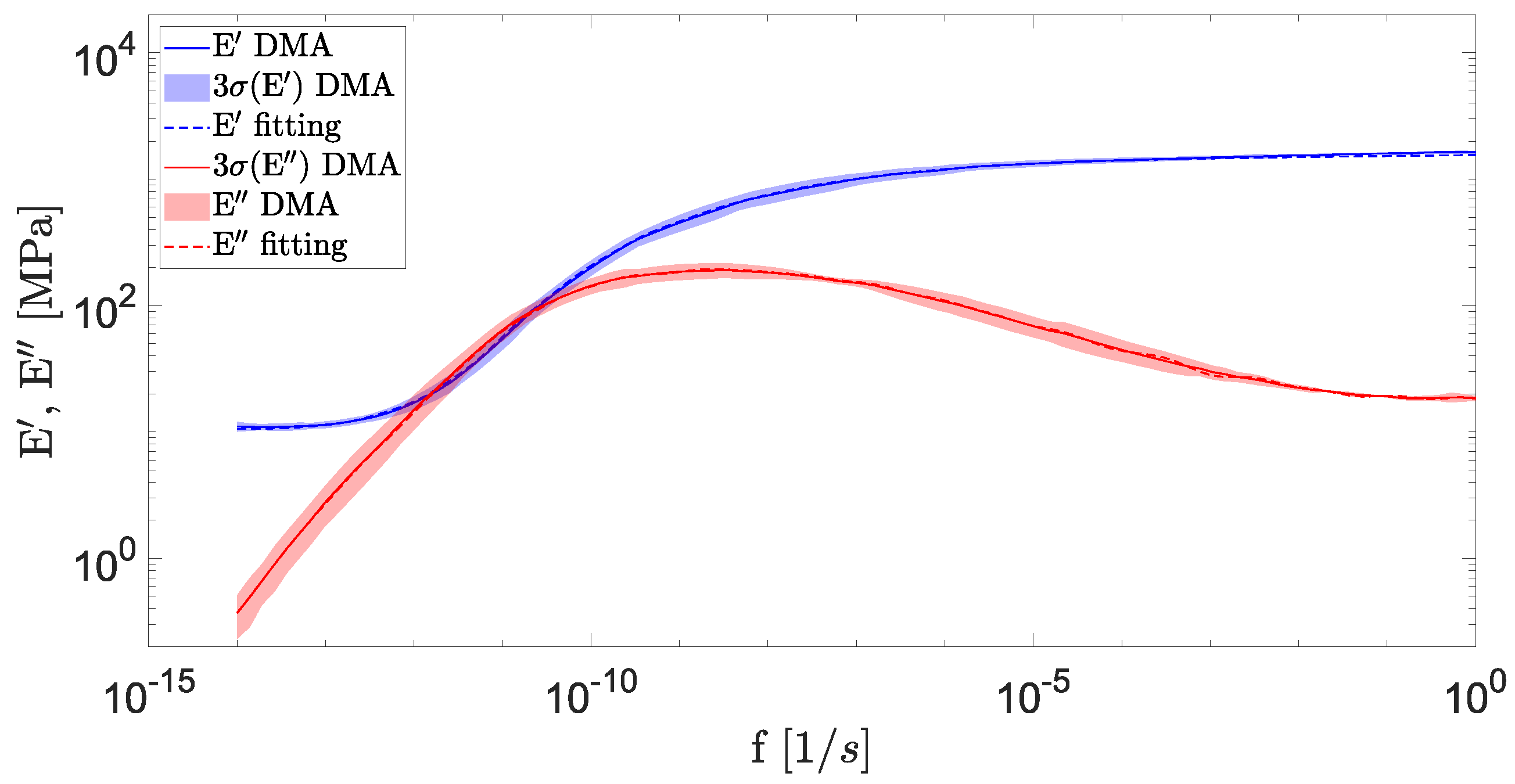

| Properties | Value |
|---|---|
| Longitudinal Modulus [GPa] | 233 |
| Transverse Modulus [GPa] | 23.1 |
| Shear Modulus [GPa] | 8.693 |
| Longitudinal Poisson’s Ratio | 0.2 |
| Index | Before UV-C Exposure | After UV-C Exposure | ||
|---|---|---|---|---|
| [MPa] | [s] | [MPa] | [s] | |
| 0 | 1568.94 | – | 1352.82 | – |
| 1 | 30.33 | 1.00 | 27.03 | 1.00 |
| 2 | 22.91 | 8.11 | 20.16 | 8.49 |
| 3 | 22.31 | 5.48 | 21.40 | 5.62 |
| 4 | 33.64 | 3.34 | 29.62 | 3.38 |
| 5 | 42.64 | 3.16 | 39.10 | 2.50 |
| 6 | 22.97 | 9.31 | 41.19 | 1.10 |
| 7 | 71.15 | 4.66 | 70.36 | 5.49 |
| 8 | 76.83 | 2.64 | 87.60 | 2.62 |
| 9 | 113.97 | 1.18 | 126.42 | 1.25 |
| 10 | 168.69 | 6.73 | 164.57 | 6.30 |
| 11 | 171.35 | 3.56 | 191.08 | 3.26 |
| 12 | 167.29 | 1.49 | 195.25 | 1.70 |
| 13 | 203.33 | 5.95 | 171.21 | 9.24 |
| 14 | 201.21 | 3.39 | 95.89 | 4.25 |
| 15 | 128.81 | 1.66 | 43.79 | 1.88 |
| 16 | 63.00 | 8.06 | 12.14 | 7.86 |
| 17 | 13.47 | 4.53 | 3.85 | 3.46 |
| 18 | 3.81 | 2.76 | 1.97 | 1.50 |
| 19 | 0.68 | 1.45 | 0.56 | 9.25 |
| 20 | 0.05 | 1.00 | 0.49 | 7.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palmeri, F.; Laurenzi, S. Relaxation Modeling of Unidirectional Carbon Fiber Reinforced Polymer Composites Before and After UV-C Exposure. Fibers 2024, 12, 110. https://doi.org/10.3390/fib12120110
Palmeri F, Laurenzi S. Relaxation Modeling of Unidirectional Carbon Fiber Reinforced Polymer Composites Before and After UV-C Exposure. Fibers. 2024; 12(12):110. https://doi.org/10.3390/fib12120110
Chicago/Turabian StylePalmeri, Flavia, and Susanna Laurenzi. 2024. "Relaxation Modeling of Unidirectional Carbon Fiber Reinforced Polymer Composites Before and After UV-C Exposure" Fibers 12, no. 12: 110. https://doi.org/10.3390/fib12120110
APA StylePalmeri, F., & Laurenzi, S. (2024). Relaxation Modeling of Unidirectional Carbon Fiber Reinforced Polymer Composites Before and After UV-C Exposure. Fibers, 12(12), 110. https://doi.org/10.3390/fib12120110







