Abstract
The paper presents the results of experimental research on unstrengthened and strengthened laminated veneer beams subjected to 4-point bending. Aramid, glass and carbon sheets with high tensile strength (HS) and ultra-high modulus of elasticity (UHM) glued to external surfaces with an epoxy resin adhesive were used as reinforcement. Two reinforcement layouts were used: (1) sheets glued along the bottom surface and (2) sheets glued to the bottom and side surfaces. Based on the test results, the flexural strength, flexural ductility and stiffness were estimated. Compared to the reference beams, the maximum bending moment was higher by 15%, 20%, 30% and by 16%, 22% and 35% for the Aramid Fiber Reinforced Polymers (AFRP), Glass Fiber Reinforced Polymers (GFRP) and Carbon Fiber Reinforced Polymers (CFRP) HS sheets, respectively. There was no significant increase in the flexural bending capacity for beams reinforced with UHM CFRP sheets. Similar values of bending ductility indices based on deflection and energy absorption were obtained. Higher increases in ductility were observed for AFRP, GFRP and CFRP HS sheets in “U” reinforcement layout. The average increase in bending stiffness coefficient ranged from 8% for AFRP sheets to 33% for UHM CFRP sheets compared to the reference beams.
1. Introduction
Bending strengthening of timber beams is required, inter alia, due to increasing load values (resulting, for example, from a change in the way of use), compensation for degradation of the mechanical properties of wood (decreasing their strength and stiffness with crack extension [1]) or the need to reduce excessive deflections. In the case of reinforced elements made of glued laminated timber, they can be made of lower-grade timber or with a smaller cross-section and thus lighter timber. It is also reasonable to commercially use lower-grade, faster-growing species of trees. Strengthened elements are characterized by a higher uniformity of properties, and thus greater repeatability in the process of production.
A common method of strengthening bending members to increase load bearing capacity, stiffness and ductility parameters is the incorporation of additional elements to strengthen the existing beam. Several reinforcement layouts have been tested in 3- and 4-point bending tests. Reinforcement inserts can take the form of sheets [2,3], bars [4,5,6], laminates, plates or other structural shapes (T-sections, C-sections, I-sections, etc.) connected to the reinforced element by means of mechanical fasteners or structural adhesives. The reinforcement can be placed outside or inside the cross-section, in the tension and/or compression zone of the beam. Elements made of solid timber, glued laminated timber or engineering wood products can be strengthened. Conventional reinforcement of such elements is made of steel or aluminum. Composite materials are currently gaining popularity though. In addition to design requirements, the choice of reinforcement measurements is also constrained by other factors such as aesthetic aspects, cost, access to the reinforced element or fire protection requirements.
Figure 1 shows strengthening layouts examples. Configurations marked with a.1 correspond to the external reinforcement, whereas a.2 to the internal reinforcement. Layouts “b” present the reinforcement techniques used at the stage of production [7].
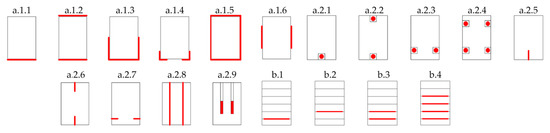
Figure 1.
Strengthening layouts of timber beams [7].
Since bent wooden beams normally fail due to brittle fracture in the tensile zone, placing the reinforcement on the tensile surfaces is an effective way to increase the flexural capacity. The application of the reinforcement shifts the position of the neutral axis towards the bottom surface of the element. As a result, an increase in the value of strains in the compression zone is observed in relation to the strains in the tension zone.
For many years, the basic material used to strengthen structural timber elements was steel and other metals. The analysis of the validity of using steel profiles of the S275J0 class (U-shaped) for strengthening solid, laminated and old ceiling beams was presented by González-Bravo et al. [8]. The sections were screwed to the upper surfaces, resulting in a 45% to 98% increase in stiffness and a 27% to 58% increase in flexural capacity in comparison to the reference structural elements. The increase in load capacity and stiffness was also obtained by using aluminum facings glued to the lower and upper surfaces of the bent beam [9]. Plasticization in the compression zone occurred before failure in the tension zone for beams reinforced with steel bars [10]. A 48% increase in the maximum load capacity and a 28% increase in stiffness were obtained for spruce beams reinforced with steel bars—the reinforcement ratio was 0.82% [11]. Soriano et al. [12] obtained a significant increase in stiffness at a symmetrical layout of steel bars both in the compression and tension zone. The use of punched metal plate fasteners did not bring favorable results in strengthening the bent timber beams [13]. An overview of techniques for repairing and strengthening timber structures in historical buildings using stainless steel components is presented in [14].
Tapes, sheets and bars made of synthetic resin reinforced with Aramid, basalt [15,16,17], glass or carbon fibers [18] have been the subject of numerous research papers aimed at strengthening solid [19] or laminated timber beams. The first papers started to appear in the 1960s [20]. Hybrid [21], natural (flax, hemp) fibers [22] or a combination of materials reinforced with various fibers within one element were used less frequently. Carbon fibers (due to the effectiveness of reinforcement [23,24,25,26,27,28,29,30,31]) and glass fibers [32,33,34,35,36,37] (for economic reasons) were commonly used as external and internal reinforcement. CFRP composites are characterized by high tensile strength and modulus of elasticity—depending on the mechanical properties of the reinforced beam, it is possible to achieve an increase in load capacity and stiffness by over 100%. Elements made of lower grade timber can be reinforced with GFRP materials that should provide the required increase in flexural bending capacity but may not be sufficient in terms of stiffness. Increasing the flexural bending capacity of the elements can cause failure due to the shear forces involved. In such cases, reinforcement against bending and shear may be required. The strength and stiffness of strengthened element may be enhanced by increasing reinforcement ratio [38]. The application of CFRP laminates to strengthen full-size bent LVL beams, glued into pre-drilled grooves along the bottom surface and applied to the underside of the beams, is described in [39,40]. Experimental investigation of timber beams strengthened with U-shape steel sections and carbon fiber-reinforced plastic is presented in [41].
General comments on ductility in the design of timber structures were provided by Jorissen and Fragiacomo [30]. According to them, the main reasons for designing the ductile structures are as follows:
- failure occurs after large deformations that will alert users in the event of unforeseen loads (e.g., increased snow loads);
- the load capacity of the structure is increased in relation to the values estimated based on elastic analysis (by redistributing stresses and forces);
- reliability of the structure is increased. Ductility is a way of ensuring the possibility of transferring increased displacements and rotations in the event of failure of one of the system’s elements;
- energy dissipation under seismic loads is ensured.
Shekarchi et al. [42] used the µΔ index to assess the ductility of timber beams reinforced with GFRP profiles. The beam displacement for the point uu in the middle of the span was assumed at the load equal to 0.8 Fmax for the descending part of the load versus deflection curve (after exceeding the peak load). Point at yield was considered according to the elastic-plastic equivalent of plasticisation while maintaining the original stiffness and load-bearing capacity of the system. Depending on the adopted reinforcement layout, the observed increase in deflection ductility was from 25% to 79%. The energy absorption of the reinforced elements increased by a maximum of 209.32%.
Nadir et al. [43] achieved a 44.37% and 46.36% increase in the ductility index µE for glued laminated timber beams reinforced with one and two layers of GFRP sheet, for which the degree of reinforcement in the tension zone was 2.5% and 5%. Slightly higher values were observed when using CFRP sheets. The tests were carried out on elements on a laboratory scale.
The effectiveness of reinforcement of timber beams reinforced with CFRP bands was the subject of the study [44]. The tests were carried out on a laboratory scale, using beams subjected to 4-point bending. It was found that the ductility (determined using the index µE) increases with the increase of the degree of reinforcement in the tension zone. The greatest increase was noticed when the value reached the level of 0.59%.
The Naaman and Jeong [45] formula was also used to assess the ductility of T-beams with a laminated timber web with a reinforced concrete flange, reinforced against bending with GFRP sheets [46].
Yusof [47] analysed the ductility of bent timber beams reinforced with bars and carbon laminates using indices based on energy absorption and deflection values. Higher percentages of increment were recorded using indices based on energy absorption.
A detailed review of the principles of designing timber joints concerning ductility, taking into account a discussion on several ductility indices and the determination of characteristic points, was presented by Ottenhaus et al. in [48]. Experimental ductility tests of the reinforced joints are discussed in [49].
Analysis of the global and local value of the bending stiffness coefficient EI for glued laminated timber beams reinforced with FRP composites are presented in [5,36], and for the repaired elements in publication [50]. Application of Basalt Fiber Reinforced Polymer (BFRP) bars with a diameter of 12 mm bonded into the grooves cut in the lowest layer allowed to obtain an increase in stiffness and maximum bending moment by 10% and 23%, respectively [5]. Comparable gains were achieved using 1.2 mm thick GFRP laminates glued to the bottom of the beam and between the two bottom layers [36]. Renovation of cracked laminated beams that were bent to failure and then repaired by gluing glass fiber reinforced bars did not allow to recover the original global and local value of flexural stiffness [50]. The percentage value of the restored stiffness increased with the increase of the degree of the cross-section reinforcement. A greater percentage increase in global versus local stiffness was also very characteristic.
The quotient of the global stiffness coefficients kg for load values of 1/3Fmax and Fmax was used in [51] as an index describing the effect of high strength steel cords reinforcement on the behaviour of bent timber beams. A slight influence of the reinforcement on the increase of stiffness and load-bearing capacity in the elastic range was observed, with a satisfactory increase in the load-bearing capacity and ductility. The authors, Corradi and Borri, used this parameter also when assessing the stiffness of solid timber beams reinforced with GFRPs made in the process of pultrusion [52]. The analysis of static behaviour of timber beams, supported by experimental and numerical studies, taking into account the assessment of the impact of the number of reinforcement layers (GFRP flat bars), fixed with mechanical fasteners on the on the beams’ stiffness is presented in [33].
Significant increase in the average value of stiffness kg in bending and reduction in scatter of standard deviation values were observed for solid timber beams (fir and oak), reinforced with CFRP and GFRP sheets [53]. Stiffness was estimated as the quotient of the load increment and the corresponding deflection increment for the loads 0.1 and 0.5 Fmax. The slope of the linear part of the load-deflection graph, covering the loading force range from 30% to 60%, was used to assess the stiffness of laminated beams reinforced with CFRP sheets in [54].
Comparison of the values of experimental and numerical changes of the total stiffness coefficient kg in the linear-elastic range for beams reinforced with composite sheets are described in paper [55].
2. Materials and Methods
The subject of the research was the analysis of the static work of laminated veneer lumber (LVL) beams strengthened with composites and reference beams. Four types of polyester matrix composite sheets were used in the research: Aramid Fiber Reinforced Polymer (AFRP), Glass Fiber Reinforced Polymer (GFRP), High Strength Carbon Fiber Reinforced Polymer (HS CFRP) and Ultra-High Modulus Carbon Fiber Reinforced Polymer (UHM CFRP).
The scope of tests included the preparation of nine series (3 beams for each series) in the following configurations (Figure 2):
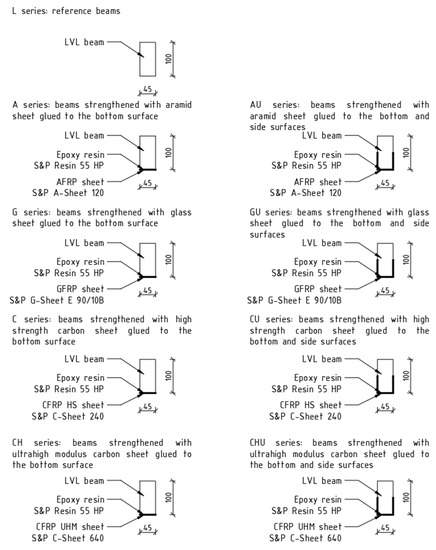
Figure 2.
Strengthening schemes of laminated veneer lumber beams.
- LVL series—reference beams;
- LVLC series—beams strengthened with 4.5 cm wide high strength carbon sheet glued to the bottom surface (reinforcement ratio, ρt = 0.33%);
- LVLCU series—beams strengthened with 14.5 cm wide high strength carbon sheet glued to the bottom and side surfaces (reinforcement ratio, ρt = 1.07%);
- LVLCH series—beams strengthened with 4.5 cm wide ultra-high modulus carbon sheet glued to the bottom surface (reinforcement ratio, ρt = 0.19%);
- LVLCHU series—beams strengthened with 14.5 cm wide ultra-high modulus carbon sheet glued to the bottom and side surfaces, ρt = 0.61%);
- LVLA series—beams strengthened with 4.5 cm wide aramid sheet glued to the bottom surface itki (reinforcement ratio, ρt = 0.20%);
- LVLAU series—beams strengthened with 14.5 cm wide aramid sheet glued to the bottom and side surfaces (reinforcement ratio, ρt = 0.64%);
- LVLG series—beams strengthened with 4.5 cm wide glass sheet glued to the bottom surface (reinforcement ratio, ρt = 0.31%);
- LVLGU series—beams strengthened with 14.5 cm wide glass sheet glued to the bottom and side surfaces (reinforcement ratio, ρt = 0.99%).
2.1. Materials
The pilot tests were carried out on laboratory scale beams. The nominal dimension of the beams were 45 × 100 × 1700 mm. Each beam consisted of fifteen 3 mm thick veneer layers with a generally unidirectional grain arrangement. The beams were tested in the edge-wise orientation. The direction of the veneer fibers coincided with the longitudinal axis. Selected mechanical and physical properties of laminated veneer lumber are presented in Table 1.

Table 1.
Mechanical and physical properties of laminated veneer lumber (exposed by manufacturer) [56].
CFRP sheets have a fabric-like structure with carbon fibers arranged in layers, rectilinearly and unidirectionally. The fibers laid in the main direction are stabilized (bonded) with transverse polyester fibers. UHM CFRP sheet is characterized by much greater stiffness, which makes it less flexible for shaping. AFRP sheet has a structure similar to the CFRP sheet—aramid fibers are arranged in one direction and are bound with polyester fibers. In GFRP sheets (made of E fibers), the fibers are arranged in layers, in a wavy way (they pass in the form of a wave between the transverse and longitudinal directions) and bidirectionally with a fiber content of 90% and 10% in the main direction and transverse direction, respectively. The fabrics were cut to the assumed sizes with the use of scissors. The specification of the composite sheets used is presented in Table 2.

Table 2.
Technical data of composite sheets (exposed by manufacturer) [57].
The sheets were glued with a two-component, solvent-free adhesive, based on epoxy resin with the amine hardener. The technical data of the adhesive is presented in Table 3. In the case of CFRP and GFRP sheets (with a more compact structure and higher basis weight), a wet application was used with the simultaneous impregnation of the veneer surface. AFRP sheets were applied dry by pressing against the surface of the veneer covered with glue. Lamination was carried out with the use of a brush and a rubber trowel. The sheets were placed by hand, with the load bearing fibers in the required direction. After laying the fabric, the adhesive between the sheet and the application surface was spread with the rubber trowel from the centre towards the outer edges—along the fibers only. The excess adhesive was removed and applied to the outer surface of the sheet. Particular attention was paid to the proper coating of the composite material edges. Adhesive consumption was approximately one kilogram of the adhesive compound for each square meter of the sheet.

Table 3.
Technical data of epoxy resin (exposed by manufacturer) [57].
Before starting the reinforcement application, the surface of the beams was sanded with a belt grinder (using 120-grade sandpaper) and cleaned. The corners of the reinforced elements (for the U-type reinforcement layout) were rounded using a milling machine—the curve radius was 6.25 mm. There were no cavities or cracks in the areas of reinforcement application. After the reinforcement was applied, the beams were stored in the laboratory until the test was performed.
2.2. Methods
The test were conducted at the Laboratory for Strength of Materials of the Kielce University of Technology (Kielce, Poland). An MTS-320 universal testing machine (MTS Systems GmbH, Berlin, Germany) was used to carry out the 4-point bending test. The tests were carried out following the guidelines given in standards [58,59]. The loading rate was assumed at 7 mm/min, so that the failure of the unreinforced beams took place within the recommended time interval of 300 s ± 120 s. Regardless of the reinforced beams test length, the previously established kinematic conditions were not changed. The first significant decrease in the loading force was assumed as the moment of failure.
The diagram of the static test setup is shown in Figure 3, and its view presented in Figure 4. The beams were loaded symmetrically with two concentrated forces. The concentrated force supplied by actuator of the testing machine was divided into components using a steel I-bar. The total length of the beams was seventeen-fold height of the cross section. They were oriented in such a way as to ensure that the length of the support span was equal to 16-fold height of the cross-section. The distance between the point at which the concentrated force was applied and the nearest support was five-fold height of the cross-section. Steel guide plates were used in order to distribute the load over a larger area and prevent local indentations on the supports and at the point of the concentrated force application.
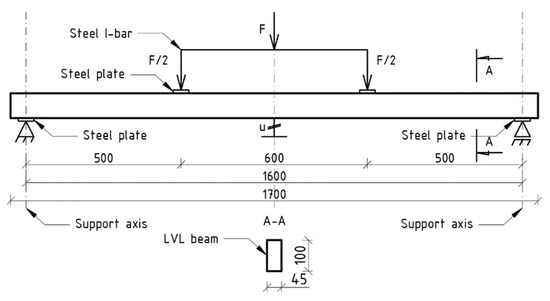
Figure 3.
Static scheme.

Figure 4.
View of the test bench.
During the research, the following parameters were recorded:
- the loading force value F [N], displacement of the hydraulic actuator head us [mm] (which can be equated with the displacement of the beam at the points of application of the concentrated load) and test time t [s]—with the use of a computer set connected to the universal testing machine MTS-320;
- deflection in the center of the beam at the extreme lower fibers under tension u [mm]—measurement performed using an inductive sensor of the Hottinger Baldwin Messtechnik system;
- failure mode—description and photographic documentation.
The data recording frequency was 5 Hz.
After the tests, the moisture content of the elements was checked using a Tanel WRD-100 resistance hygrometer. The value of the average moisture content of the laminated veneer timber at the time of the test is presented in Table 4.

Table 4.
Average moisture content value of laminated veneer lumber in each series.
3. Results
3.1. Bending Strength
The analytical model of the reinforced beams was created using the equivalent cross-section method, in which the reinforcement is taken into account by a proportional increase of the geometrical dimensions of the timber beam cross-section [60,61]. Modulus of Rupture (MOR) determines the maximum normal stress occurring in the outermost fibers subjected to compression or tension, determined for the maximum value of the bending moment recorded in the 4-point bending test. The calculations were made for the reinforced beams, using the geometric characteristics of the equivalent cross-section, assuming a linear stress distribution over the depth of the cross section. The maximum normal stress was estimated on the basis of the experimental data according to the formula (based on [60]):
where: Mmax—maximum bending moment; zf—distance between neutral axis and outermost fibers subjected to compression or tension; Iy,zast—moment of inertia of equivalent cross-section about y axis.
Figure 5 shows the average values of the maximum bending moment, loading force and modulus of rupture. The percentages of the increment in relation to the reference beams are shown in brackets. Extreme (maximum) values are marked with red fill pattern.
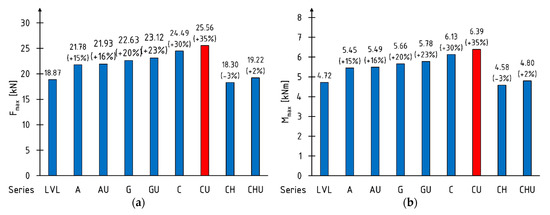
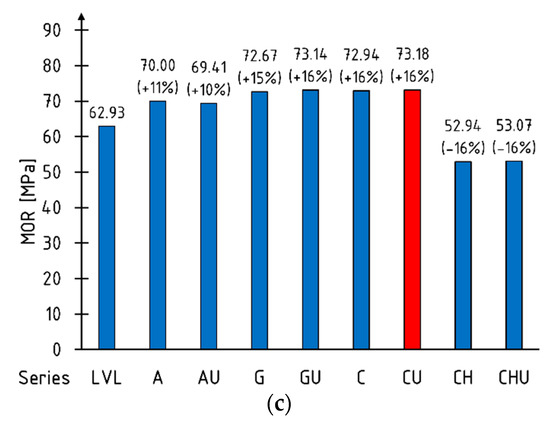
Figure 5.
Load bearing capacity: (a) maximum loading force; (b) maximum bending moment; (c) modulus of rupture.
Figure 6 shows the relationship between the loading force and the deflection for selected tested beams. As can be seen, the value of deflection and loading force increases with increasing reinforcement ratio and coverage value of side surface with composite material.
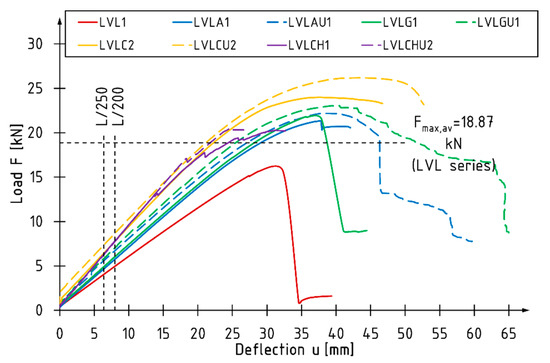
Figure 6.
Force versus deflection curves for selected beams.
3.2. Ductility
Ductility is defined as the ability to withstand plastic deformation while maintaining the required level of load bearing capacity until failure. Element deformation can be considered in terms of deflection, curvature or strain [62,63]. Based on this definition, ductility can be expressed in terms of deformation measures (dimensionless deformation rates) or energy absorption (dimensionless energy rates). In the case of beams reinforced with steel bars, for which plastic deformations can be unequivocally determined, the ductility can be determined as the ratio of the limit value of the deformation to the value at the yield point. For the elements reinforced with FRP materials, determining the yield point may be difficult or even impossible.
The ductility analysis was carried out with the use of three indicators, hereinafter referred to as D, µΔ, and µE.
The simplest measure of ductility, marked with the symbol D, of a timber beam reinforced with FRP material, is based on a comparison of the unreinforced element deflection value with the reinforced element deflection, according to the following formula [22]:
where: uFmax,w—deflection at maximum load of strengthened beam; uFmax,nw—deflection at maximum load of unstrengthened beam.
As defined in the index above, “D” of the reference elements is equal to 1.
The deflection ductility index µΔ is defined as the ratio of the ultimate deflection to the deflection at yield point, according to the following formula [64]:
where: uu—ultimate deflection; uy—deflection at yield point.
Ductility index µE is expressed as the quotient of the total and elastic energy as follows [45]:
where: Wtot—total energy; We—elastic energy.
The elastic energy can be estimated based on the area of a triangle, one of the vertices of which is at the point of failure of the beam. The remaining corners of the triangle rest on the horizontal axis. Their positions are determined by leading two straight lines through the point of destruction: vertical and the inclined one, which is parallel to the linear-elastic part of the load-deflection plot [62,65]. An alternative method used in many studies to determine the areas under the curve is the integration of a polynomial approximating the bending behaviour in the range defined by the characteristic points, such as the beginning of the test, the limit of the proportionality, plasticity or element failure [47].
The yield point of the elements was determined according to the guidelines given in the study [66]. The maximum deflection value was taken at the point of significant load drop. The energy was determined by integrating fifth-degree polynomials from the beginning of the test to the characteristic point. Figure 7 shows the average values of ductility indices. Extreme (maximum) values are marked with red fill pattern.
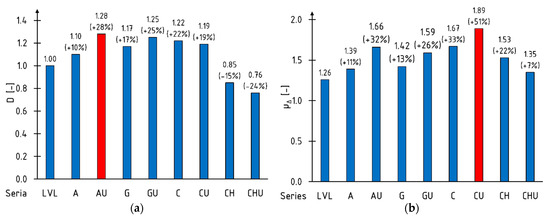
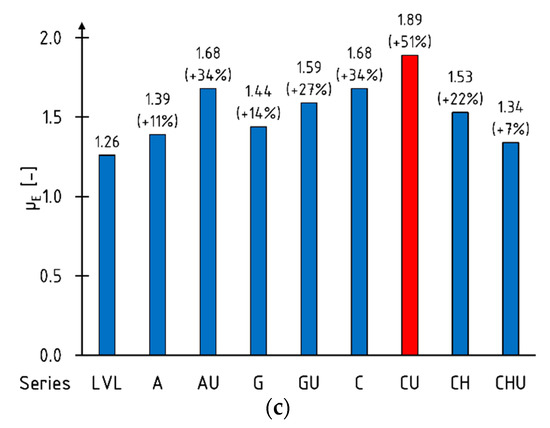
Figure 7.
Ductility indices: (a) D; (b) µΔ; (c) µE.
Almost identical values of the bending ductility of beams on a laboratory scale were obtained using indices µΔ and µE. The highest percentage increase in ductility was achieved with the use of HS CFRP sheets, amounting to more than 30% when applying the reinforcement to the bottom of the beam (LVLC series) and over 50% for the U-type reinforcement (LVLCU series). A negative value of the D index percentage increase for the beams reinforced with UHM CFRP sheets resulted from lower deflection at maximum load compared to reference beams.
3.3. Stiffness
Global stiffness coefficient kg for beams on a laboratory scale was determined based on the deflection of the beam measured at the level of the outermost tensile fibers in the middle of the span of the element and the corresponding load. On the sections of the “load-deflection” dependence graph, the limit deflection values for the serviceability limit state, adopted according to [67], and the equation of the trend lines were marked (Figure 8). The analysis was performed using the slope of the regression line. The results of the statistical analysis are presented in Table 5.
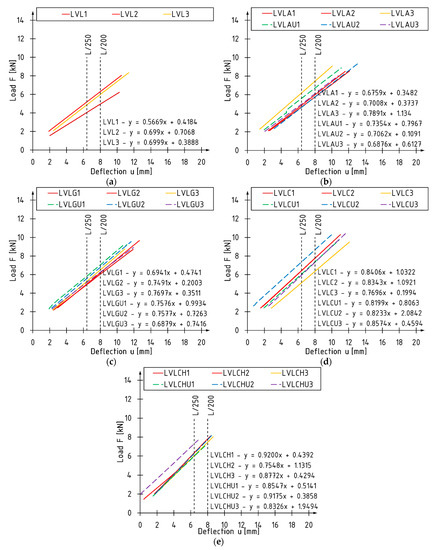
Figure 8.
Section of load-deflection graphs between 0.1 Fmax and 0.4 Fmax: (a) LVL series; (b) LVLA/AU series; (c) LVLG/GU series; (d) LVLC/CU series; (e) LVLCH/CHU series.

Table 5.
Stiffness analysis.
The smallest increases in the average value of the global stiffness coefficient, amounting to about 10%, were recorded for beams reinforced with aramid and glass sheets characterized by lower values of the modulus of elasticity compared to carbon sheets. The percentage increase for beams reinforced with carbon sheets of high tensile strength was over 20%, and for sheets with ultra-high modulus of elasticity—over 30%. With the increase of the composite sheet modulus of elasticity, the percentage increase grew. A higher increase of kg coefficient when using CFRP sheets was obtained for the U-type reinforcement layout. This phenomenon was not observed in the case of beams reinforced with AFRP and GFRP sheets.
3.4. Failure Modes
The reference beams (LVL series) failed at the maximum bending moment zone in brittle fashion. The failure of these beams resulted from the exceed of strength in the tension zone. Figure 9a shows typical failure of a reference beam.


Figure 9.
Failure modes: (a) brittle fracture in tension zone; (b) tensile failure of composite sheet and LVL; (c) tensile failure of LVL; (d) shear failure of LVL; (e) splitting failure—extensive rupture; (f) compressive failure of LVL; (g) compressive failure of LVL and tensile failure of LVL and composite.
Greater variation of strengthened beams was recorded. Failure modes of strengthened beams:
- Rupture of composite reinforcement with failure of timber in tension zone (Figure 9b)—typical failure mode for beams strengthened with AFRP and CFRP sheet bonded to the underside;
- Brittle fracture of timber beam in tension zone, with no rupture of composite reinforcement (Figure 9c)—typical failure mode for beams strengthened with GFRP bonded to the underside;
- Shear failure (Figure 9d)—single example recorded for beam strengthened with one layer of CFRP sheet bonded to the underside;
- Sudden rupture of composite fibers which caused splitting the beam—single example (Figure 9e);
- Failure of timber in compression zone (kink-bands), with no rupture of composite reinforcement (Figure 9f)—typical failure for beams strengthened with GFRP sheets in U-configuration;
- Failure of timber in compression zone (kink-bands), with rupture of composite reinforcement (Figure 9g)—typical failure for beams strengthened with AFRP and CFRP sheets in U-configuration.
4. Conclusions
The subject of the research were laminated veneer lumber beams strengthened with AFRP, GFRP, HS CFRP and UHM CFRP sheets, glued to the external surfaces of the structural elements with an structural adhesives based on epoxy resin. Two reinforcement layouts were used: reinforcement with sheets glued to the bottom of the beam and U-type reinforcement. The following conclusions can be put forth:
- The time to failure and loading force increases with increasing reinforcement ratio and coverage value of side surface with composite material.
- The higher the modulus of elasticity of composite sheet was, the greater increase of bending stiffness was obtained. The largest percentage increase in the bending stiffness coefficient kg, over 30% in comparison with reference beams, was obtained for the LVLCH and LVLCHU series.
- Generally, the higher the tensile strength of composite sheet was, the greater increase in load bearing capacity was achieved. It is not applicable for composite materials with low value of elongation at rupture, as in the case of UHM CFRP.
- Similar values of the flexural ductility of unreinforced and reinforced beams were obtained when using ductility indices based on plastic deformation—an index based on deflection µΔ and energy absorption µE.
- The ductility, based on comparison of deflection values—index D, of beams strengthened with ultra-high modulus carbon sheets decreased.
- The highest ductility was found in the beams strengthened with HS CFRP sheet which is characterized by high tensile strength, high modulus of elasticity and sufficient elongation at rupture—to withstand elongation of fibers corresponding to the increasing deflection.
Author Contributions
Conceptualization, M.M.B.; methodology, M.M.B. and P.G.K.; software, M.M.B.; validation, M.M.B.; formal analysis, M.M.B.; investigation, M.M.B.; writing—original draft preparation, M.M.B.; writing—review and editing, M.M.B. and P.G.K.; supervision, P.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
The tests were implemented thanks to the financial support of the Kielce University of Technology within the framework of the statutory work No. 02.0.12.00/2.01.01.00.0000, SUBB.BKWM.21.002.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors would also like to thank S&P Polska Sp. z o.o. for providing the research materials.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Kossakowski, P.G. Influence of anisotropy on the energy release rate G(i) for highly orthotropic materials. J. Theor. Appl. Mech. 2007, 45, 739–752. [Google Scholar]
- Nabati, A.; Ghanbari-Ghazijahani, T.; Valipour, H.R. Innovative flitch sandwich beams with steel core under four-point bending. Eng. Struct. 2021, 233, 111724. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Y.; Peng, D.; Zhao, K.; Hu, Y. Experimental investigation of timber beams strengthened by bamboo scrimber with anchorage structure. Structures 2021, 33, 1–11. [Google Scholar] [CrossRef]
- Micelli, F.; Scialpi, V.; La Tegola, A. Flexural reinforcement of glulam timber beams and joints with carbon fiber-reinforced polymer rods. J. Compos. Constr. 2005, 9, 337–347. [Google Scholar] [CrossRef]
- Raftery, G.M.; Kelly, F. Basalt FRP rods for reinforcement and repair of timber. Compos. Part B Eng. 2015, 70, 9–19. [Google Scholar] [CrossRef]
- Yeboah, D.; Gkantou, M. Investigation of flexural behaviour of structural timber beams strengthened with NSM basalt and glass FRP bars. Structures 2021, 33, 390–405. [Google Scholar] [CrossRef]
- Rescalvo, F.J.; Valverde-Palacios, J.; Suarez, E.; Gallego, A. Experimental Comparison of Different Carbon Fiber Composites in Reinforcement Layouts for Wooden Beams of Historical Buildings. Materials 2017, 10, 1113. [Google Scholar] [CrossRef] [Green Version]
- González-Bravo, C.; Arriaga-Martitegui, F.; Maldonado-Ramos, L.; Díez-Barra, R. Bending reinforcement of timber beams with steel cross sections on the upper face. Mater. Constr. 2010, 60, 123–135. [Google Scholar] [CrossRef]
- Mark, R. Wood-aluminium beams within and beyond the elastic range. Part 1: Rectangular sections. For. Prod. J. 1961, 11, 115–119. [Google Scholar]
- Dziuba, T. The ultimate strength of wooden beams with tension reinforcement. Holzforsch. Holzverwert. 1985, 37, 115–119. [Google Scholar]
- De Luca, V.; Marano, C. A comparison of un-reinforced and reinforced timber glulam with steel bars. Eur. J. Technol. Adv. Eng. Res. 2011, 2, 45–54. [Google Scholar]
- Soriano, J.; Pellis, B.P.; Mascia, N.T. Mechanical performance of glued-laminated timber beams symmetrically reinforced with steel bars. Compos. Struct. 2016, 150, 200–207. [Google Scholar] [CrossRef]
- Nielsen, J.; Ellegaard, P. Moment Capacity of Timber Reinforced with Punched Metal Plate Fasteners. In Proceedings of the 1st RILEM Symposium on Timber Engineering, Stockholm, Sweden, 13–15 September 1999; Boström, L., Ed.; RILEM Publications: Lyon, France, 1999; pp. 129–137. [Google Scholar]
- Corradi, M.; Osofer, A.I.; Borri, A. Repair and Reinforcement of Historic Timber Structures with Stainless Steel—A Review. Metals 2019, 9, 106. [Google Scholar] [CrossRef] [Green Version]
- Pengyi, Z.; Shijie, S.; Chunmei, M. Strengthening mechanical properties of glulam with basalt fiber. Adv. Nat. Sci. 2011, 4, 130–133. [Google Scholar]
- Wdowiak-Postulak, A. Basalt Fiber Reinforcement of Bent Heterogeneous Glued Laminated Beam. Materials 2021, 14, 51. [Google Scholar] [CrossRef] [PubMed]
- Wdowiak-Postulak, A. Natural Fiber as Reinforcement for Vintage Wood. Materials 2020, 13, 4799. [Google Scholar] [CrossRef]
- Wdowiak-Postulak, A.; Brol, J. Ductility of the Tensile Zone in Bent Wooden Beams Strengthened with CFRP Materials. Materials 2020, 13, 5451. [Google Scholar] [CrossRef]
- Burawska, I.; Jachowicz, P.; Zbieć, M.; Grześkiewicz, M. Local reinforcement of naturally defected structural lumber. Ann. Wars. Univ. Life Sci. SGGW. For. Wood Technol. 2014, 87, 25–34. [Google Scholar]
- Theakston, F.H. A feasibility study for strengthening timber beams with fiberglass. Can. Agric. Eng. 1965, 7, 17–19. [Google Scholar]
- Brol, J. Wzmacnianie zginanych belek z drewna klejonego taśmami GARP na etapie produkcji (Strengthening of bent glued laminated (glulam) beams with GARP tapes at the stage of production). Wiadomości Konserw. 2009, 26, 345–353. [Google Scholar]
- Borri, A.; Corradi, M.; Speranzini, E. Bending Tests on Natural Fiber Reinforced Fir Wooden Elements. Adv. Mat. Res. 2013, 778, 537–544. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Grazini, A.A. A method for flexural reinforcement of old wood beams with CFRP materials. Compos. Part B Eng. 2005, 36, 143–153. [Google Scholar] [CrossRef]
- Brol, J. Wzmacnianie elementów drewnianych taśmami lub matami z włókien węglowych. Zesz. Nauk. Politech. Śląskiej Ser. Bud. 2001, 93, 67–76. [Google Scholar]
- Brol, J. Wzmacnianie zespolonych stropów drewniano-żelbetowych polimerami zbrojonymi włóknami węglowymi. Zesz. Nauk. Politech. Śląskiej Ser. Bud. 2002, 95, 105–113. [Google Scholar]
- Glišović, I.; Stevanović, B.; Todorović, M.; Stevanović, T. Glulam beams externally reinforced with CFRP plates. Wood Res. 2016, 61, 141–154. [Google Scholar]
- Kliger, R.; Johansson, M.; Crocetti, R.; Al.-Emrani, M. Strengthening timber with CFRP or steel plates—short and long-term performance. In Proceedings of the World Conference on Timber Engineering (WCTE08), Miyazaki, Japan, 2–5 June 2008; Engineered Wood Products Association: Tacoma, WA, USA, 2009; pp. 414–421. [Google Scholar]
- Li, Y.-F.; Xie, Y.-M.; Tsai, M.-J. Enhancement of the flexural performance of retrofitted wood beams using CFRP composite sheets. Constr. Build. Mater. 2009, 23, 411–422. [Google Scholar] [CrossRef]
- Nowak, T.P.; Jasieńko, J.; Czepiżak, D. Experimental tests and numerical analysis of historic bent timber elements reinforced with CFRP strips. Constr. Build. Mater. 2013, 40, 197–206. [Google Scholar] [CrossRef]
- Jorissen, A.; Fragiacomo, M. General notes on ductility in timber structures. Eng. Struct. 2011, 33, 2987–2997. [Google Scholar] [CrossRef]
- Schober, K.-U.; Rautenstrauch, K. Post-strengthening of timber structures with CFRPs. Mater. Struct. 2006, 40, 27–35. [Google Scholar] [CrossRef]
- Basterra, L.A.; Balmori, J.A.; Morillas, L.; Acuña, L.; Casado, M. Internal reinforcement of laminated duo beams of low-grade timber with GFRP sheets. Constr. Build. Mater. 2017, 154, 914–920. [Google Scholar] [CrossRef]
- Corradi, M.; Vo, T.P.; Poologanathan, K.; Osofero, A.I. Flexural behaviour of hardwood and softwood beams with mechanically connected GFRP plates. Compos. Struct. 2018, 206, 610–620. [Google Scholar] [CrossRef] [Green Version]
- Gentile, C.; Svecova, D.; Rizkalla, S.H. Timber beams strengthened with GFRP bars: Development and applications. J. Compos. Constr. 2002, 6, 11–20. [Google Scholar] [CrossRef]
- Hernandez, R.; Davalos, J.F.; Sonti, S.S.; Kim, Y.; Moody, R.C. Strength and Stiffness of Reinforced Yellow-Poplar Glued-Laminated Beams; Research Paper FPL-RP-554; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1997. [Google Scholar]
- Raftery, G.M.; Harte, A.M. Low-grade glued laminated timber reinforced with FRP plate. Compos. Part B Eng. 2011, 42, 724–735. [Google Scholar] [CrossRef]
- Raftery, G.M.; Whelan, C.; Harte, A.M. Bonded-in GFRP rods for the repair of glued laminated timber. In Proceeding of the World Conference on Timber Engineering (WCTE12), Auckland, New Zealand, 16–19 July 2012. [Google Scholar]
- Ye, L.; Wang, B.; Shao, P. Experimental and Numerical Analysis of a Reinforced Wood Lap Joint. Materials 2020, 13, 4117. [Google Scholar] [CrossRef]
- Bakalarz, M. Load bearing capacity of laminated veneer lumber beams strengthened with CFRP strips. Arch. Civ. Eng. 2021, 67, 139–155. [Google Scholar]
- Bakalarz, M.M.; Kossakowski, P.G.; Tworzewski, P. Strengthening of Bent LVL Beams with Near-Surface Mounted (NSM) FRP Reinforcement. Materials 2020, 13, 2350. [Google Scholar] [CrossRef] [PubMed]
- Ghazijahani, T.G.; Holloway, D. Composite Timber Beams Strengthened by Steel and CFRP. J. Compos. Constr. 2017, 21, 04016059. [Google Scholar] [CrossRef]
- Shekarchi, M.; Oskouei, A.V.; Raftery, G.M. Flexural behavior of timber beams strengthened with pultruded glass fiber reinforced polymer profiles. Compos. Struct. 2020, 241, 112062. [Google Scholar] [CrossRef]
- Nadir, Y.; Nagarajan, P.; Mohammed, A.; Arif, M.M. Flexural stiffness and strength enhancement of horizontally glued laminated wood beams with GFRP and CFRP composite sheets. Constr. Build. Mater. 2016, 112, 547–555. [Google Scholar] [CrossRef]
- Bhat, J.A. Effect of CFRP-Reinforcement variation on the strength parameters of different timber beams. Mater. Today Proc. 2021, 44, 2785–2791. [Google Scholar] [CrossRef]
- Naaman, A.E.; Jeong, S.M. Structural Ductility of Concrete Beams Prestressed with FRP Tendons. In Proceedings of the 2nd International RILEM Symposium (FRPRXS-2), Non-Metallic (FRP) Reinforcement for Concrete Structures, Ghent, Belgium, 23–25 August 1995; Taerwe, L., Ed.; RILEM: Bagneus, France, 1995; pp. 379–386. [Google Scholar]
- Ali, Y.A.Z. Flexural behavior of FRP strengthened concrete-wood composite beams. Ain Shams Eng. J. 2018, 9, 3419–3424. [Google Scholar] [CrossRef]
- Yusof, A. Bending Behavior of Timber Beams Strengthened Using Fiber Reinforced Polymer Bars and Plates. Ph.D. Thesis, Universiti Teknologi, Johor, Malaysia, 2010. [Google Scholar]
- Ottenhaus, L.-M.; Jockwer, R.; Drimmelen, D.; Crews, K. Designing timber connections for ductility—A review and discussion. Constr. Build. Mater. 2021, 304, 124621. [Google Scholar] [CrossRef]
- Brühl, F.; Kuhlmann, U.; Jorissen, A. Consideration of plasticity within the design of timber structures due to connection ductility. Eng. Struct. 2011, 33, 3007–3017. [Google Scholar] [CrossRef]
- Raftery, G.M.; Harte, A.M. Repair of glulam beams using GFRP rods. Structural Studies, Repairs and Maintenance of Heritage Architecture. WIT Trans. Built Environ. 2009, 109, 417–427. [Google Scholar]
- Borri, A.; Corradi, M. Strengthening of timber beams with high strength steel cords. Compos. Part B Eng. 2011, 42, 1480–1491. [Google Scholar] [CrossRef]
- Corradi, M.; Borri, A. Fir and chestnut timber beams reinforced with GFRP pultruded elements. Compos. Part B Eng. 2007, 38, 172–181. [Google Scholar] [CrossRef]
- Corradi, M.; Borri, A.; Righetti, L.; Speranzini, E. Uncertainty analysis of FRP reinforced timber beams. Compos. Part B Eng. 2017, 113, 174–184. [Google Scholar] [CrossRef]
- Subhani, M.; Globa, A.; Al-Ameri, R.; Moloney, J. Flexural strengthening of LVL beam using CFRP. Constr. Build. Mater. 2017, 150, 480–489. [Google Scholar] [CrossRef]
- Kossakowski, P.; Ordysiński, G. Numeryczne szacowanie sztywności zginanych elementów drewnianych wzmacnianych matami kompozytowymi. Zesz. Nauk. Politech. Rzesz. 2012, 59, 373–380. [Google Scholar]
- Zeszyt Konstrukcyjny STEICO. Fornir Klejony Warstwowo. Available online: https://www.steico.com/fileadmin/steico/content/pdf/Marketing/Polska/Foldery_produktow/LVL/STEICOlvl_pl_i.pdf (accessed on 1 April 2021).
- Technical Data Sheets of Composite Materials. Available online: http://www.sp-reinforcement.pl/pl-PL (accessed on 1 April 2021).
- Polski Komitet Normalizacyjny. Konstrukcje Drewniane—Drewno Konstrukcyjne Lite i Klejone Warstwowo. Oznaczanie Niektórych Właściwości Mechanicznych; PN-EN 408+A1:2012; Polski Komitet Normalizacyjny: Warszawa, Poland, 2012. [Google Scholar]
- Polski Komitet Normalizacyjny. Konstrukcje Drewniane. Fornir Klejony Warstwowo (LVL). Wymagania; PN-EN 14374:2005; Polski Komitet Normalizacyjny: Warszawa, Poland, 2005. [Google Scholar]
- Rudziński, L. Konstrukcje Drewniane. Naprawy, Wzmocnienia, Przykłady Obliczeń; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2010. [Google Scholar]
- Masłowski, E.; Spiżewska, D. Wzmacnianie Konstrukcji Budowlanych; Wydawnictwo Arkady: Warszawa, Poland, 2000. [Google Scholar]
- Grace, N.F.; Soliman, A.K.; Abdel-Sayed, G.; Saleh, K.R. Behaviour and Ductility of Simple and Continuous FRP Reinforced Beams. J. Compos. Constr. 1998, 2, 186–194. [Google Scholar] [CrossRef]
- Mirmiran, A.; Shahawy, M.; Samaan, M. Strength and Ductility of Hybrid FRP-Concrete Beam-Columns. J. Struct. Eng. 1999, 125, 1085–1093. [Google Scholar] [CrossRef]
- Park, R. Evaluation of ductility of structures and structural assemblages for laboratory testing. Bull. N. Z. Soc. Earthq. Eng. 1989, 22, 155–166. [Google Scholar] [CrossRef]
- Wang, H.; Belarbi, A. Flexural behavior of fiber-reinforced-concrete beams reinforced with FRP rebars. ACI Struct. J. 2005, 51, 895–914. [Google Scholar]
- Tomasi, R.; Parisi, M.A.; Piazza, M. Ductile design of glued-laminated timber beams. Pract. Period. Struct. Des. 2009, 14, 113–122. [Google Scholar] [CrossRef]
- Polski Komitet Normalizacyjny. Projektowanie Konstrukcji Drewnianych. Część 1-1: Postanowienia Ogólne. Reguły Ogólne i Reguły Dotyczące Budynków PN-EN 1995-1-1:2010. Eurokod 5; Polski Komitet Normalizacyjny: Warszawa, Poland, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).