Ultrashort Pulse Retrieval from Experimental Spectra Transformed in Chalcogenide and Silica Fibers
Abstract
1. Introduction
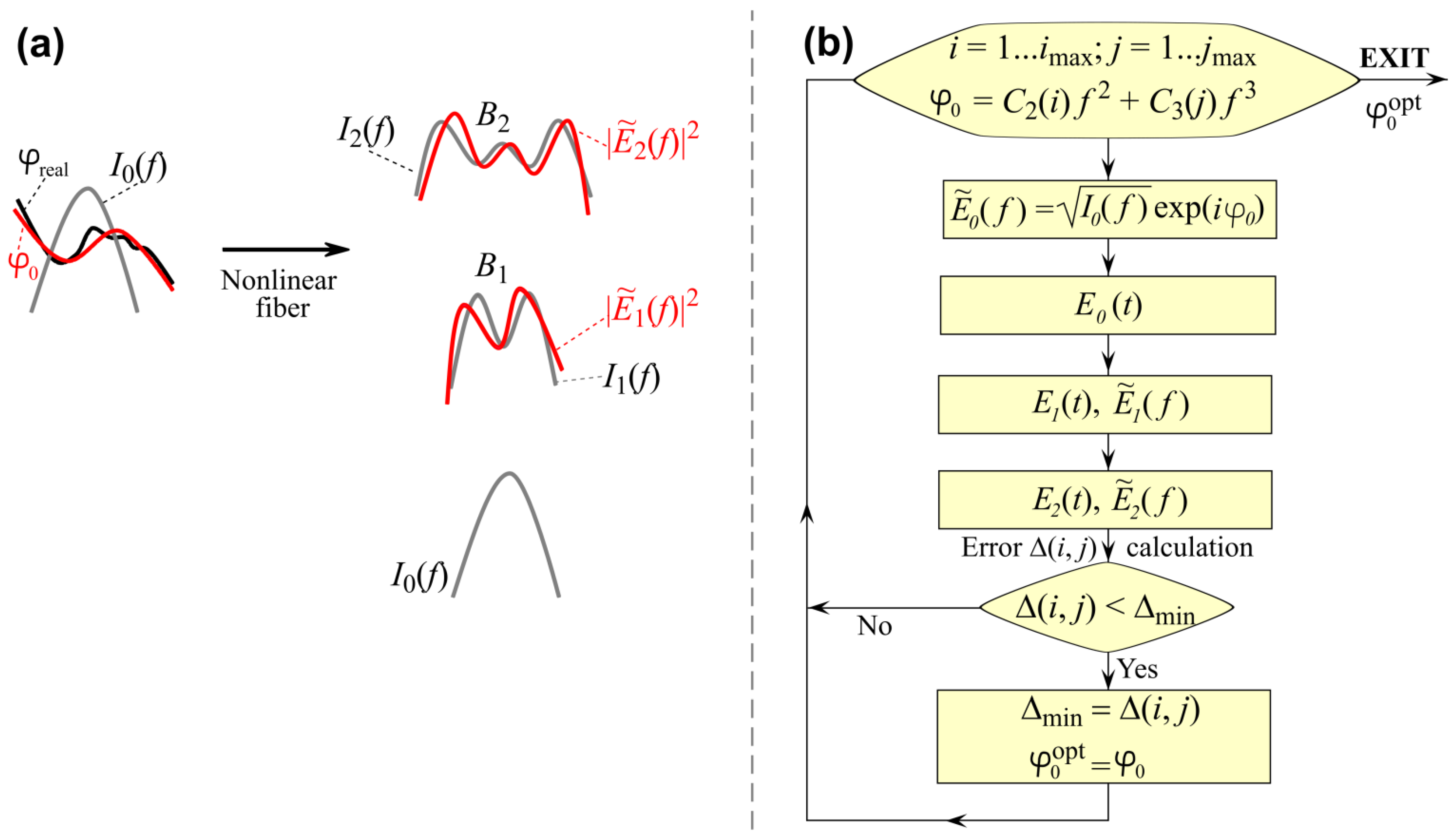
2. Methods
2.1. Numerical Algorithm
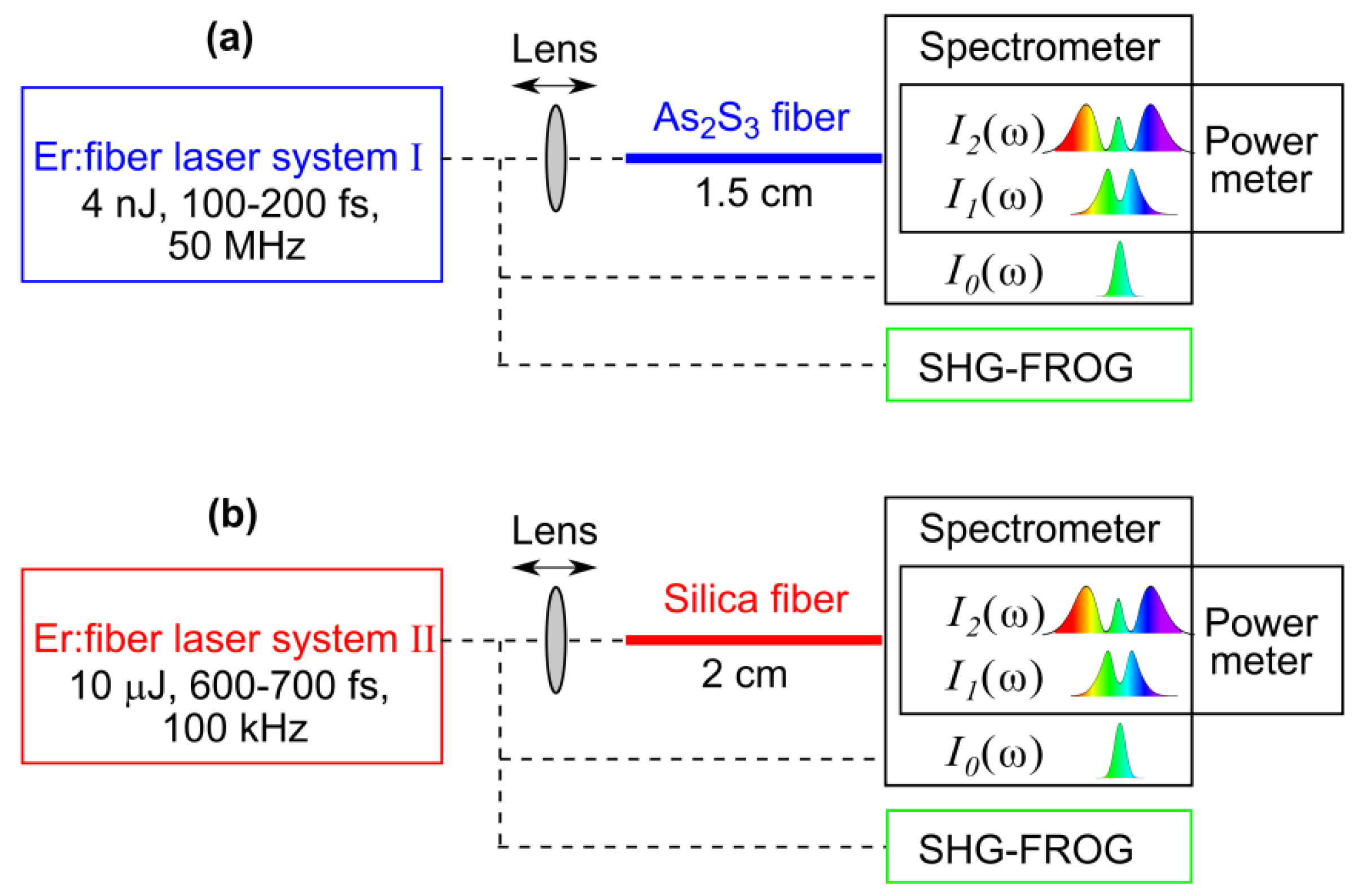
2.2. Experimental Schemes
3. Results
3.1. Pulse Retrieval from Measurements Using Chalcogenide Fiber
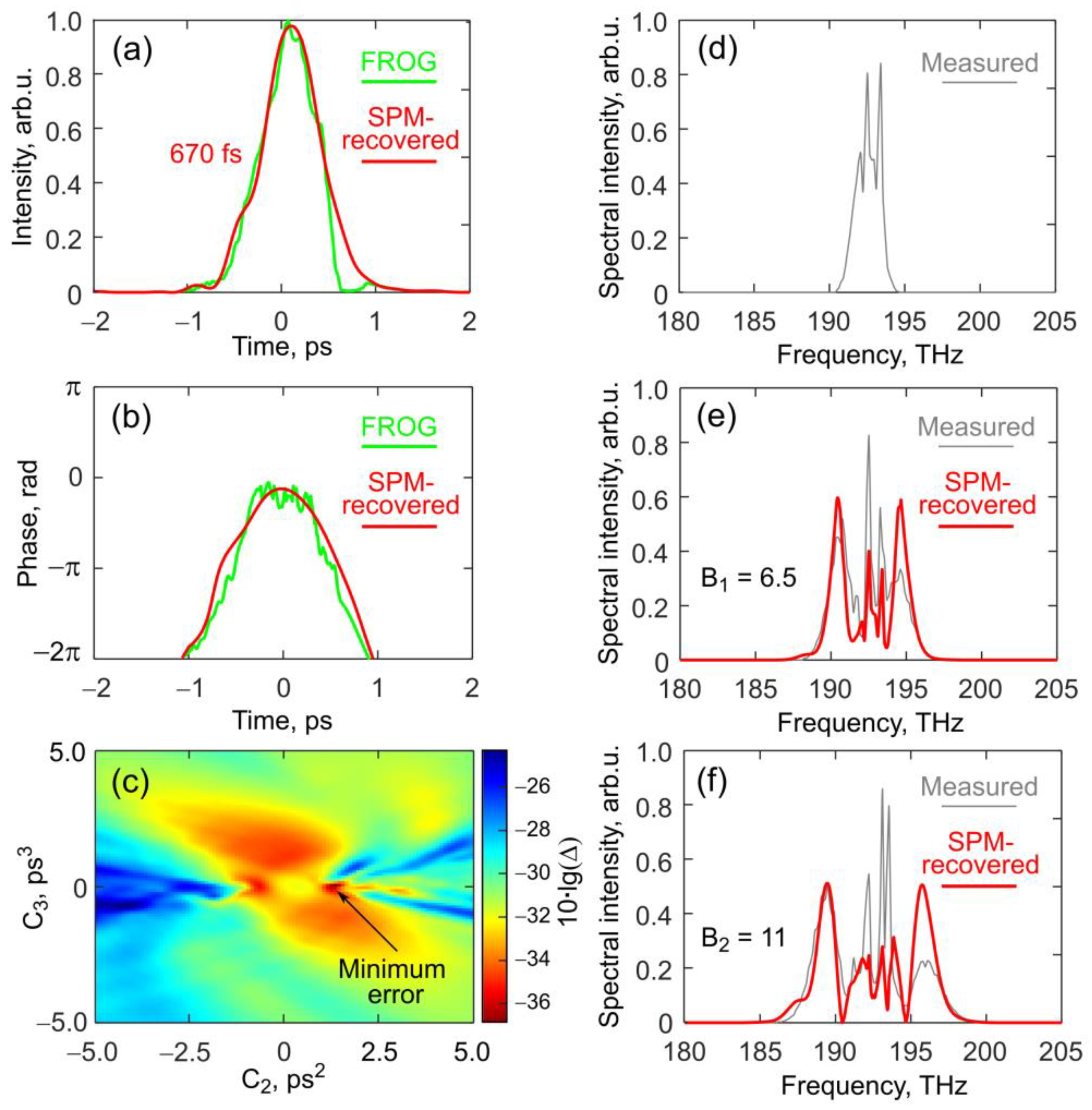
3.2. Pulse Retrieval from Measurements Using a Silica Fiber
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Trebino, R. Frequency-Resolved Optical Gating: The Measurement of Ultrashort Laser Pulses; Kluwer Academic Publishers: Boston, MA, USA, 2002. [Google Scholar]
- Walmsley, I.A.; Dorrer, C. Characterization of Ultrashort Electromagnetic Pulses. Adv. Opt. Photonics 2009, 1, 308–437. [Google Scholar] [CrossRef]
- Trebino, R.; Jafari, R.; Akturk, S.A.; Bowlan, P.; Guang, Z.; Zhu, P.; Escoto, E.; Steinmeyer, G. Highly Reliable Measurement of Ultrashort Laser Pulses. J. Appl. Phys. 2020, 128, 171103. [Google Scholar] [CrossRef]
- Miranda, M.; Arnold, C.L.; Fordell, T.; Silva, F.; Alonso, B.; Weigand, R.; L’Huillier, A.; Crespo, H. Characterization of Broadband Few-Cycle Laser Pulses with the d-Scan Technique. Opt. Express 2012, 20, 18732–18743. [Google Scholar] [CrossRef]
- Goda, K.; Jalali, B. Dispersive Fourier Transformation for Fast Continuous Single-Shot Measurements. Nat. Photonics 2013, 7, 102–112. [Google Scholar] [CrossRef]
- Sugavanam, S.; Fabbri, S.; Le, S.T.; Lobach, I.; Kablukov, S.; Khorev, S.; Churkin, D. Real-Time High-Resolution Heterodyne-Based Measurements of Spectral Dynamics in Fibre Lasers. Sci. Rep. 2016, 6, 23152. [Google Scholar] [CrossRef] [PubMed]
- Zahavy, T.; Dikopoltsev, A.; Moss, D.; Haham, G.I.; Cohen, O.; Mannor, S.; Segev, M. Deep Learning Reconstruction of Ultrashort Pulses. Optica 2018, 5, 666–673. [Google Scholar] [CrossRef]
- Lapre, C.; Billet, C.; Meng, F.; Ryczkowski, P.; Sylvestre, T.; Finot, C.; Genty, G.; Dudley, J.M. Real-Time Characterization of Spectral Instabilities in a Mode-Locked Fibre Laser Exhibiting Soliton-Similariton Dynamics. Sci. Rep. 2019, 9, 13950. [Google Scholar] [CrossRef] [PubMed]
- Anashkina, E.A.; Ginzburg, V.N.; Kochetkov, A.A.; Yakovlev, I.V.; Kim, A.V.; Khazanov, E.A. Single-Shot Laser Pulse Reconstruction Based on Self-Phase Modulated Spectra Measurements. Sci. Rep. 2016, 6, 33749. [Google Scholar] [CrossRef] [PubMed]
- Anashkina, E.A.; Andrianov, A.V.; Koptev, M.Y.; Kim, A.V. Complete Field Characterization of Ultrashort Pulses in Fiber Photonics. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 8700107. [Google Scholar] [CrossRef]
- Baudin, K.; Audo, F.; Finot, C. Fiber-Based Measurement of Temporal Intensity and Phase Profiles of an Optical Telecommunication Pulse through Self-Phase Modulation. Microw. Opt. Technol. Lett. 2018, 60, 882–886. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Koptev, M.Y.; Andrianov, A.V.; Dorofeev, V.V.; Singh, S.; Leuchs, G.; Kim, A.V. Reconstruction of Optical Pulse Intensity and Phase Based on SPM Spectra Measurements in Microstructured Tellurite Fiber in Telecommunication Range. J. Lightw. Technol. 2019, 37, 4375–4381. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Andrianov, A.V.; Leuchs, G. Single-Shot Reconstruction of a Subpicosecond Pulse from a Fiber Laser System via Processing Strongly Self-Phase Modulated Spectra. Results Phys. 2020, 16, 102848. [Google Scholar] [CrossRef]
- Sorokin, A.A.; Andrianov, A.V.; Anashkina, E.A. Numerical Study of Mid-IR Ultrashort Pulse Reconstruction Based on Processing of Spectra Converted in Chalcogenide Fibers with High Kerr Nonlinearity. Fibers 2022, 10, 81. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Anashkina, E.A.; Andrianov, A.V.; Muravyev, S.V.; Kim, A.V. All-Fiber Design of Erbium-Doped Laser System for Tunable Two-Cycle Pulse Generation. Opt. Express 2011, 19, 20141–20150. [Google Scholar] [CrossRef] [PubMed]
- Andrianov, A.V.; Koptev, M.Y.; Anashkina, E.A.; Muravyev, S.V.; Kim, A.V.; Lipatov, D.S.; Velmiskin, V.V.; Levchenko, A.E.; Bubnov, M.M.; Likhachev, M.E. Tapered Erbium-Doped Fibre Laser System Delivering 10 MW of Peak Power. Quantum Electron. 2019, 49, 1093–1099. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anashkina, E.A.; Sorokin, A.A.; Andrianov, A.V. Ultrashort Pulse Retrieval from Experimental Spectra Transformed in Chalcogenide and Silica Fibers. Fibers 2022, 10, 98. https://doi.org/10.3390/fib10110098
Anashkina EA, Sorokin AA, Andrianov AV. Ultrashort Pulse Retrieval from Experimental Spectra Transformed in Chalcogenide and Silica Fibers. Fibers. 2022; 10(11):98. https://doi.org/10.3390/fib10110098
Chicago/Turabian StyleAnashkina, Elena A., Arseny A. Sorokin, and Alexey V. Andrianov. 2022. "Ultrashort Pulse Retrieval from Experimental Spectra Transformed in Chalcogenide and Silica Fibers" Fibers 10, no. 11: 98. https://doi.org/10.3390/fib10110098
APA StyleAnashkina, E. A., Sorokin, A. A., & Andrianov, A. V. (2022). Ultrashort Pulse Retrieval from Experimental Spectra Transformed in Chalcogenide and Silica Fibers. Fibers, 10(11), 98. https://doi.org/10.3390/fib10110098







