Two-Dimensional SiP, SiAs, GeP and GeAs as Promising Candidates for Photocatalytic Applications
Abstract
1. Introduction
2. Computational Method
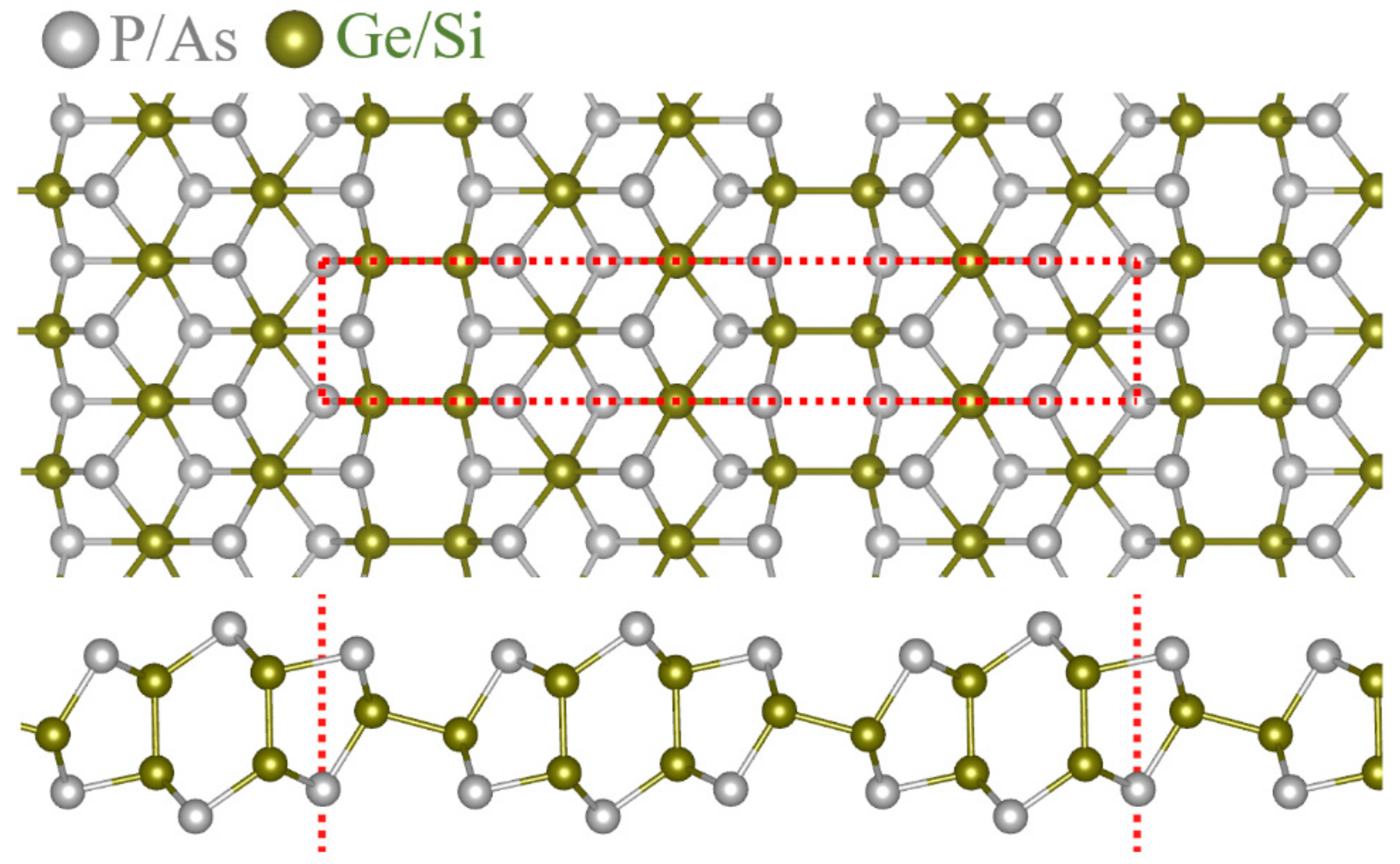
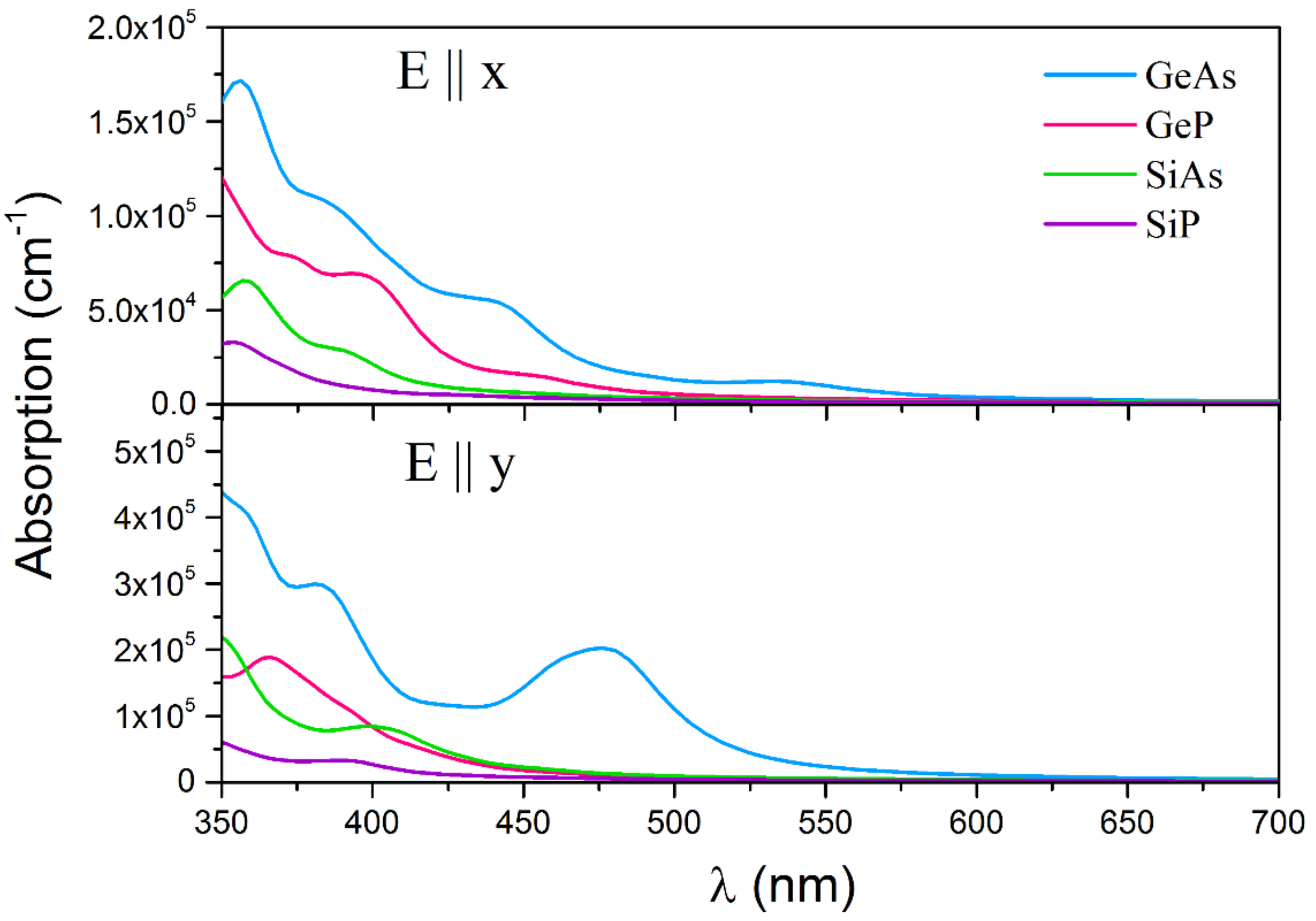
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Novoselov, K.; Geim, A.K.; Morozov, S.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Kubota, Y.; Watanabe, K.; Tsuda, O.; Taniguchi, T. Deep ultraviolet light-emitting hexagonal boron nitride synthesized at atmospheric pressure. Science 2007, 317, 932–934. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Ci, L.; Lu, H.; Sorokin, P.B.; Jin, C.; Ni, J.; Kvashnin, A.G.; Kvashnin, D.G.; Lou, J.; Yakobson, B.I.; et al. Large scale growth and characterization of atomic hexagonal boron nitride layers. Nano Lett. 2010, 10, 3209–3215. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ding, Y. Strain-induced self-doping in silicene and germanene from first-principles. Solid State Commun. 2013, 155, 6–11. [Google Scholar] [CrossRef]
- Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 2011, 6, 147–150. [Google Scholar] [CrossRef]
- Watts, M.C.; Picco, L.; Russell-Pavier, F.S.; Cullen, P.L.; Miller, T.S.; Bartuś, S.P.; Payton, O.D.; Skipper, N.T.; Tileli, V.; Howard, C.A. Production of phosphorene nanoribbons. Nature 2019, 568, 216–220. [Google Scholar] [CrossRef]
- Gusmão, R.; Sofer, Z.; Pumera, M. Functional protection of exfoliated black phosphorus by noncovalent modification with anthraquinone. ACS Nano 2018, 12, 5666–5673. [Google Scholar] [CrossRef]
- Sturala, J.; Sofer, Z.; Pumera, M. Chemistry of layered pnictogens: Phosphorus, arsenic, antimony, and bismuth. Angew. Chem. Int. Ed. 2019, 131, 7551–7557. [Google Scholar] [CrossRef]
- Ares, P.; Palacios, J.J.; Abellán, G.; Gómez-Herrero, J.; Zamora, F. Recent progress on antimonene: A new bidimensional material. Adv. Mater. 2018, 30, 1703771. [Google Scholar] [CrossRef]
- Jariwala, D.; Sangwan, V.K.; Lauhon, L.; Marks, T.J.; Hersam, M.C. Emerging device applications for semiconducting two-dimensional transition metal dichalcogenides. ACS Nano 2014, 8, 1102–1120. [Google Scholar] [CrossRef] [PubMed]
- Mohammad, R.; Kenneth, D.; Shi-Zhang, Q. Advent of 2D rhenium disulfide (ReS2): Fundamentals to applications. Adv. Funct. Mater. 2017, 27, 1606129. [Google Scholar] [CrossRef]
- Shengxue, Y.; Yanhan, Y.; Minghui, W.; Chunguang, H.; Wanfu, S.; Yongji, G.; Li, H.; Chengbao, J.; Yongzhe, Z. Highly in-plane optical and electrical anisotropy of 2D germanium arsenide. Adv. Funct. Mater. 2018, 28, 1707379. [Google Scholar] [CrossRef]
- Liu, E.; Fu, Y.; Wang, Y.; Feng, Y.; Liu, H.; Wan, X.; Zhou, W.; Wang, B.; Shao, L.; Ho, C.H.; et al. Integrated digital inverters based on two-dimensional anisotropic ReS2 field-effect transistors. Nat. Commun. 2015, 6, 6991. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Hu, M.; Li, D.; He, Y.; Zhao, R.; Jiang, X.; Song, S.; Wang, L.; Fan, C. A nano and micro-integrated protein chip based on quantum dot probes and a microfluidic network. Nano Res. 2008, 1, 490–496. [Google Scholar] [CrossRef]
- Yang, H.; Jussila, H.; Autere, A.; Komsa, H.P.; Ye, G.; Chen, X.; Hasan, T.; Sun, Z. Optical waveplates based on birefringence of anisotropic two-dimensional layered materials. ACS Photonics 2017, 4, 3023–3030. [Google Scholar] [CrossRef]
- Beck, C.G. Crystallography of SiP and SiAs single crystals and of SiP precipitates in Si. J. Appl. Phys. 1966, 37, 4683. [Google Scholar] [CrossRef]
- Donohue, P.C.; Young, H.S. Synthesis, structure, and superconductivity of new high pressure phases in the systems GeP and GeAs. J. Solid State Chem. 1970, 1, 143–149. [Google Scholar] [CrossRef]
- Ashton, M.; Sinnott, S.B.; Hennig, R.G. Computational discovery and characterization of polymorphic two-dimensional IV–V materials. Appl. Phys. Lett. 2016, 109, 192103. [Google Scholar] [CrossRef]
- Liang, L.; Weike, W.; Penglai, G.; Xiangde, Z.; Bei, D.; Xingqiang, S.; Guoying, G.; Huiqiao, L.; Tianyou, Z. 2D GeP: An unexploited low-symmetry semiconductor with strong in-plane anisotropy. Adv. Mater. 2018, 30, 1706771. [Google Scholar] [CrossRef]
- Cheng, A.Q.; He, Z.; Zhao, J.; Zeng, H.; Chen, R.S. Monolayered silicon and germanium monopnictide semiconductors: Excellent stability, high absorbance, and strain engineering of electronic properties. ACS Appl. Mater. Interfaces 2018, 10, 5133–5139. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B.; Rabczuk, T. Anisotropic mechanical properties and strain tuneable band-gap in single-layer SiP, SiAs, GeP and GeAs. Phys. E Low Dimens. Syst. Nanostruct. 2018, 103, 273–278. [Google Scholar] [CrossRef]
- Chen, Q.Y.; Cao, C.; He, Y. Optical anisotropy and strain tunable optical, electronic and structural properties in monolayer GeP: A computational study. Phys. E Low Dimens. Syst. Nanostruct. 2019, 113, 172–180. [Google Scholar] [CrossRef]
- Wang, X.; Deng, G.; Yu, W.; Wang, B.; Li, X.; Liu, Y.; Zhao, Y.; Wang, Q.; Zhang, L.; Cai, X. A class of two-dimensional SiAs monolayers with novel electronic and optical properties from ab initio investigations. Eur. Phys. J. Plus 2019, 134, 287. [Google Scholar] [CrossRef]
- Shi, L.B.; Cao, S.; Yang, M. Strain behavior and carrier mobility for novel two-dimensional semiconductor of GeP: First principles calculations. Phys. E Low Dimens. Syst. Nanostruct. 2019, 107, 124–130. [Google Scholar] [CrossRef]
- Shojaei, F.; Hahn, J.R.; Kang, H.S. Electronic structure and photocatalytic band offset of few-layer GeP2. J. Mater. Chem. A 2017, 5, 22146–22155. [Google Scholar] [CrossRef]
- Mortazavi, H. Could art therapy reduce the death anxiety of patients with advanced cancer? An interesting question that deserves to be investigated. Indian J. Palliat. Care 2018, 24, 387–388. [Google Scholar] [CrossRef]
- Shojaei, F.; Kang, H.S. Electronic structures and Li-diffusion properties of group IV-V layered materials: Hexagonal germanium phosphide and germanium arsenide. J. Phys. Chem. C 2016, 120, 23842–23850. [Google Scholar] [CrossRef]
- Tabatabaeichehr, M.; Mortazavi, H.; Abadi, M.H.; Moayed, L. Sexual desire and related factors in middle-aged and elderly married women: A cross-sectional study in Iran. Open Access Maced. J. Med Sci. 2018, 6, 1906–1911. [Google Scholar] [CrossRef]
- Tagani, M.B. Electrical and mechanical properties of a fully hydrogenated two-dimensional polyaniline sheet. Comput. Mater. Sci. 2018, 153, 126–133. [Google Scholar] [CrossRef]
- Tagani, M.B.; Vishkayi, S.I. Polyaniline (C3N) nanoribbons: Magnetic metal, semiconductor, and half-metal. J. Appl. Phys. 2018, 124, 84304. [Google Scholar] [CrossRef]
- Vishkayi, S.I.; Tagani, M.B. Current-voltage characteristics of borophene and borophane sheets. Phys. Chem. Chem. Phys. 2017, 19, 21461–21466. [Google Scholar] [CrossRef]
- Bafekry, A.; Shayesteh, S.F.; Peeters, F.M. C3N monolayer: Exploring the emerging of novel electronic and magnetic properties with adatom adsorption, functionalizations, electric field, charging, and strain. J. Phys. Chem. C 2019, 123, 12485–12499. [Google Scholar] [CrossRef]
- Peng, Y.; Li, J.; Tang, X.; Yang, W.; Chen, X.; Fan, C.; Wang, K. Molecular dynamics study on the tribological properties of phosphorene/polyethylene composites. Coatings 2019, 9, 342. [Google Scholar] [CrossRef]
- Liu, T.; Qin, H.; Yang, D.; Zhang, G. First principles study of gas molecules adsorption on monolayered β-SnSe. Coatings 2019, 9, 390. [Google Scholar] [CrossRef]
- Bafekry, A.; Ghergherehchi, M.; Shayesteh, S.F.; Peeters, F. Adsorption of molecules on C3N nanosheet: A first-principle calculations. Chem. Phys. 2019, 526, 110442. [Google Scholar] [CrossRef]
- Shi, L.B.; Yang, M.; Cao, S.; You, Q.; Niu, Y.Y.; Wang, Y.Z. Elastic behavior and intrinsic carrier mobility for monolayer SnS and SnSe: First-principles calculations. Appl. Surf. Sci. 2019, 492, 435–448. [Google Scholar] [CrossRef]
- Makaremi, M.; Grixti, S.; Butler, K.T.; Ozin, G.A.; Singh, C.V. Band engineering of carbon nitride monolayers by N-Type, P-Type, and isoelectronic doping for photocatalytic applications. ACS Appl. Mater. Interfaces 2018, 10, 11143–11151. [Google Scholar] [CrossRef]
- Bafekry, A.; Ghergherehchi, M.; Shayesteh, S.F. Tuning the electronic and magnetic properties of antimonene nanosheets via point defects and external fields: First-principles calculations. Phys. Chem. Chem. Phys. 2019, 21, 10552–10566. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Shahrokhi, M. Quasi-particle energies and optical excitations of ZnS monolayer honeycomb structure. Appl. Surf. Sci. 2016, 390, 377–384. [Google Scholar] [CrossRef]
- Tachibana, Y.; Vayssieres, L.; Durrant, J.R. Artificial photosynthesis for solar water-splitting. Nat. Photonics 2012, 6, 511–518. [Google Scholar] [CrossRef]
- Lewis, N.S.; Nocera, D.G. Powering the planet: Chemical challenges in solar energy utilization. Proc. Natl. Acad. Sci. USA 2006, 103, 15729–15735. [Google Scholar] [CrossRef] [PubMed]
- Kreher, K. Fundamentals of semiconductors—physics and materials properties. Z. Phys. Chem. 1997, 198, 275. [Google Scholar] [CrossRef]
- Seitz, L.C.; Chen, Z.; Forman, A.J.; Pinaud, B.A.; Benck, J.D.; Jaramillo, T.F. Modeling practical performance limits of photoelectrochemical water splitting based on the current state of materials research. ChemSusChem 2014, 7, 1372–1385. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.K.; Zhou, L.; Shinde, A.; Suram, S.K.; Montoya, J.H.; Winston, D.; Gregoire, J.M.; Persson, K.A. Electrochemical stability of metastable materials. Chem. Mater. 2017, 29, 10159–10167. [Google Scholar] [CrossRef]
- Jain, A.; Wang, Z.; Nørskov, J.K. Stable two-dimensional materials for oxygen reduction and oxygen evolution reactions. ACS Energy Lett. 2019, 4, 1410–1411. [Google Scholar] [CrossRef]
- Gubaev, K.; Podryabinkin, E.V.; Hart, G.L.; Shapeev, A.V. Accelerating high-throughput searches for new alloys with active learning of interatomic potentials. Comput. Mater. Sci. 2019, 156, 148–156. [Google Scholar] [CrossRef]
- Kostiuchenko, T.; Körmann, F.; Neugebauer, J.; Shapeev, A. Impact of lattice relaxations on phase transitions in a high-entropy alloy studied by machine-learning potentials. Npj Comput. Mater. 2019, 5, 55. [Google Scholar] [CrossRef]
- Podryabinkin, E.V.; Tikhonov, E.V.; Shapeev, A.V.; Oganov, A.R. Accelerating crystal structure prediction by machine-learning interatomic potentials with active learning. Phys. Rev. B 2019, 99, 064114. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mortazavi, B.; Shahrokhi, M.; Cuniberti, G.; Zhuang, X. Two-Dimensional SiP, SiAs, GeP and GeAs as Promising Candidates for Photocatalytic Applications. Coatings 2019, 9, 522. https://doi.org/10.3390/coatings9080522
Mortazavi B, Shahrokhi M, Cuniberti G, Zhuang X. Two-Dimensional SiP, SiAs, GeP and GeAs as Promising Candidates for Photocatalytic Applications. Coatings. 2019; 9(8):522. https://doi.org/10.3390/coatings9080522
Chicago/Turabian StyleMortazavi, Bohayra, Masoud Shahrokhi, Gianaurelio Cuniberti, and Xiaoying Zhuang. 2019. "Two-Dimensional SiP, SiAs, GeP and GeAs as Promising Candidates for Photocatalytic Applications" Coatings 9, no. 8: 522. https://doi.org/10.3390/coatings9080522
APA StyleMortazavi, B., Shahrokhi, M., Cuniberti, G., & Zhuang, X. (2019). Two-Dimensional SiP, SiAs, GeP and GeAs as Promising Candidates for Photocatalytic Applications. Coatings, 9(8), 522. https://doi.org/10.3390/coatings9080522






