Mathematical Analysis of the Coating Process over a Porous Web Lubricated with Upper-Convected Maxwell Fluid
Abstract
:1. Introduction
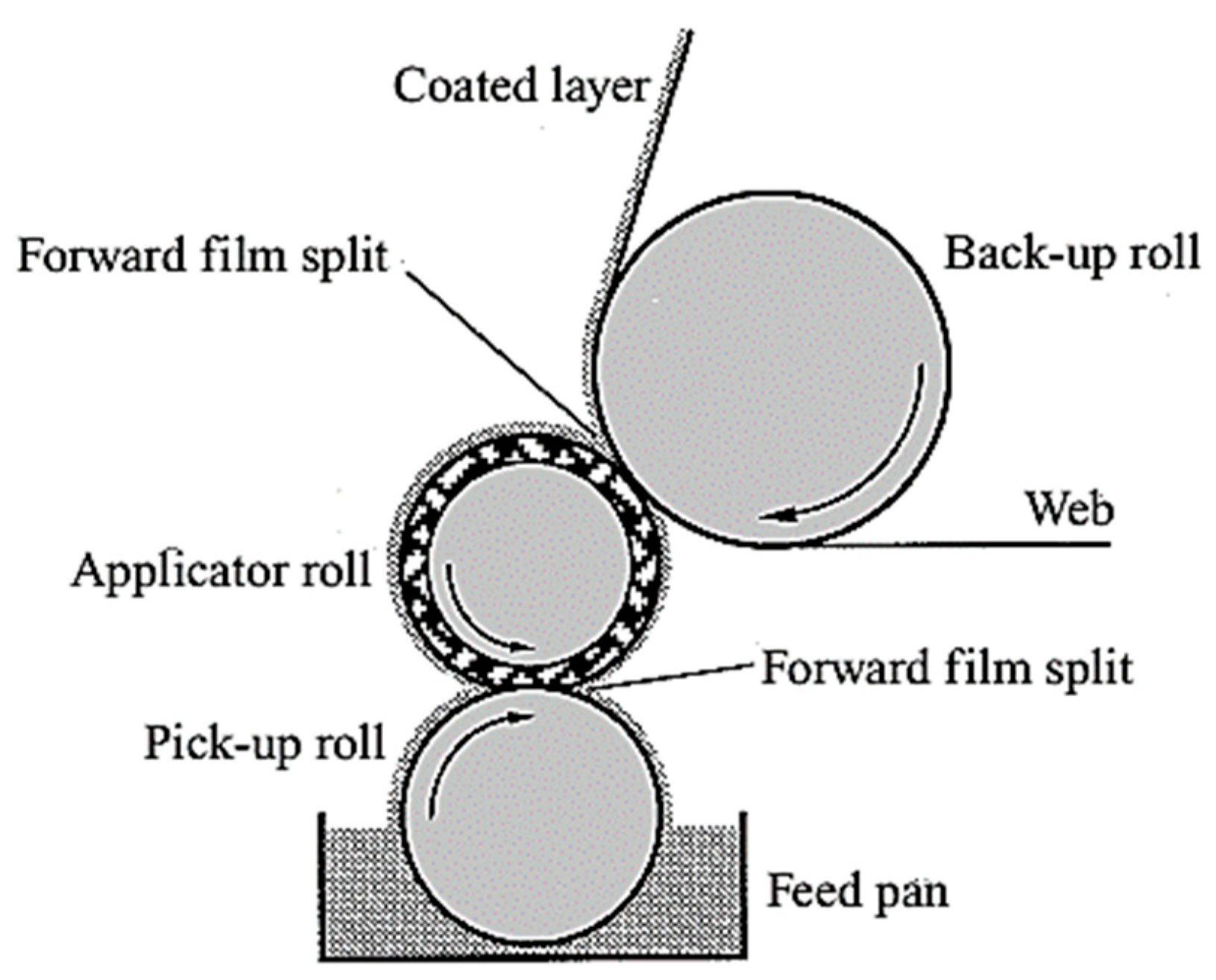
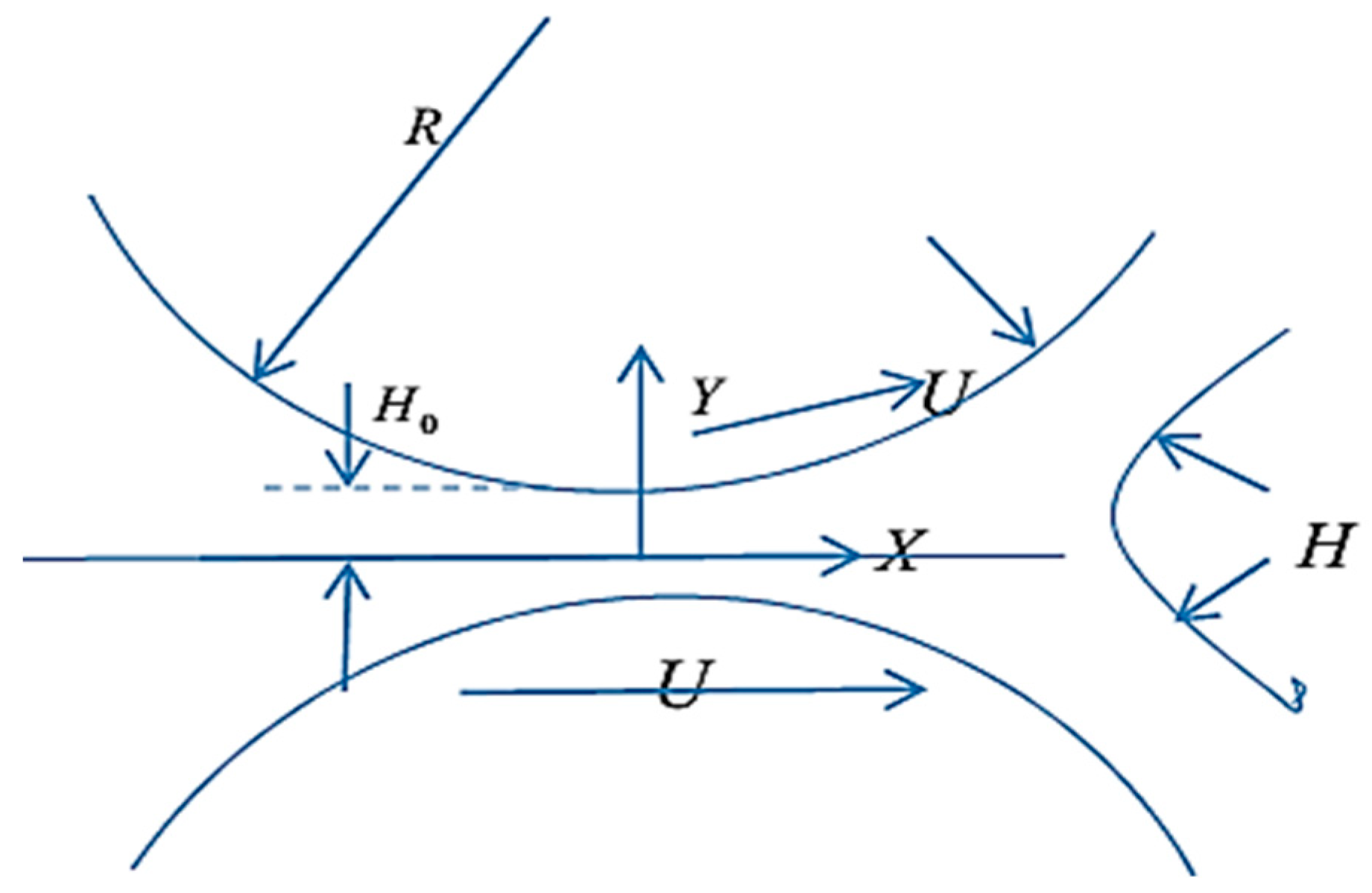
2. Mathematical Formulation
3. Solution of the Problem
4. Operating Variables
4.1. Separating Force
4.2. Power Input
4.3. Adiabatic Temperature
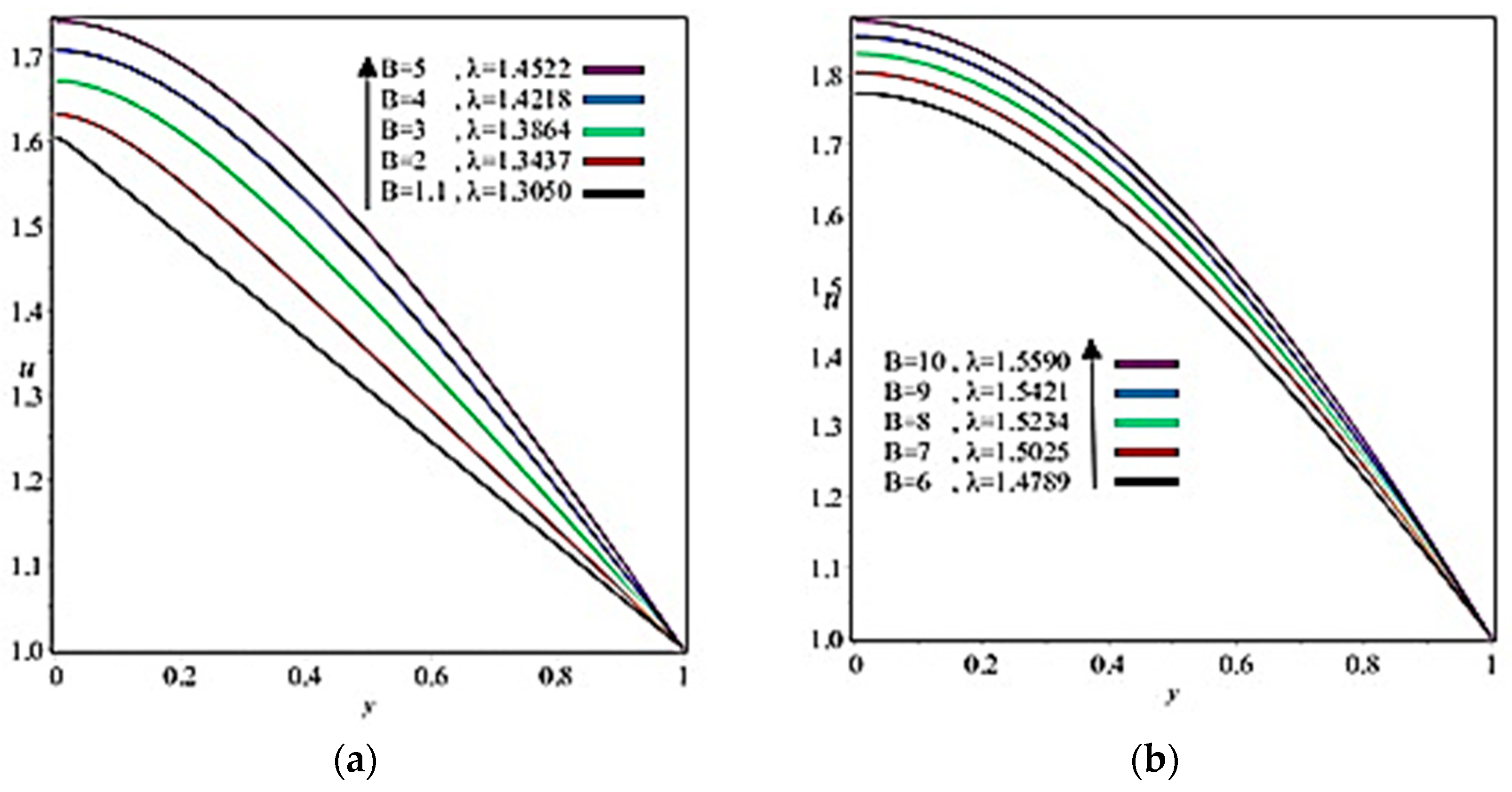
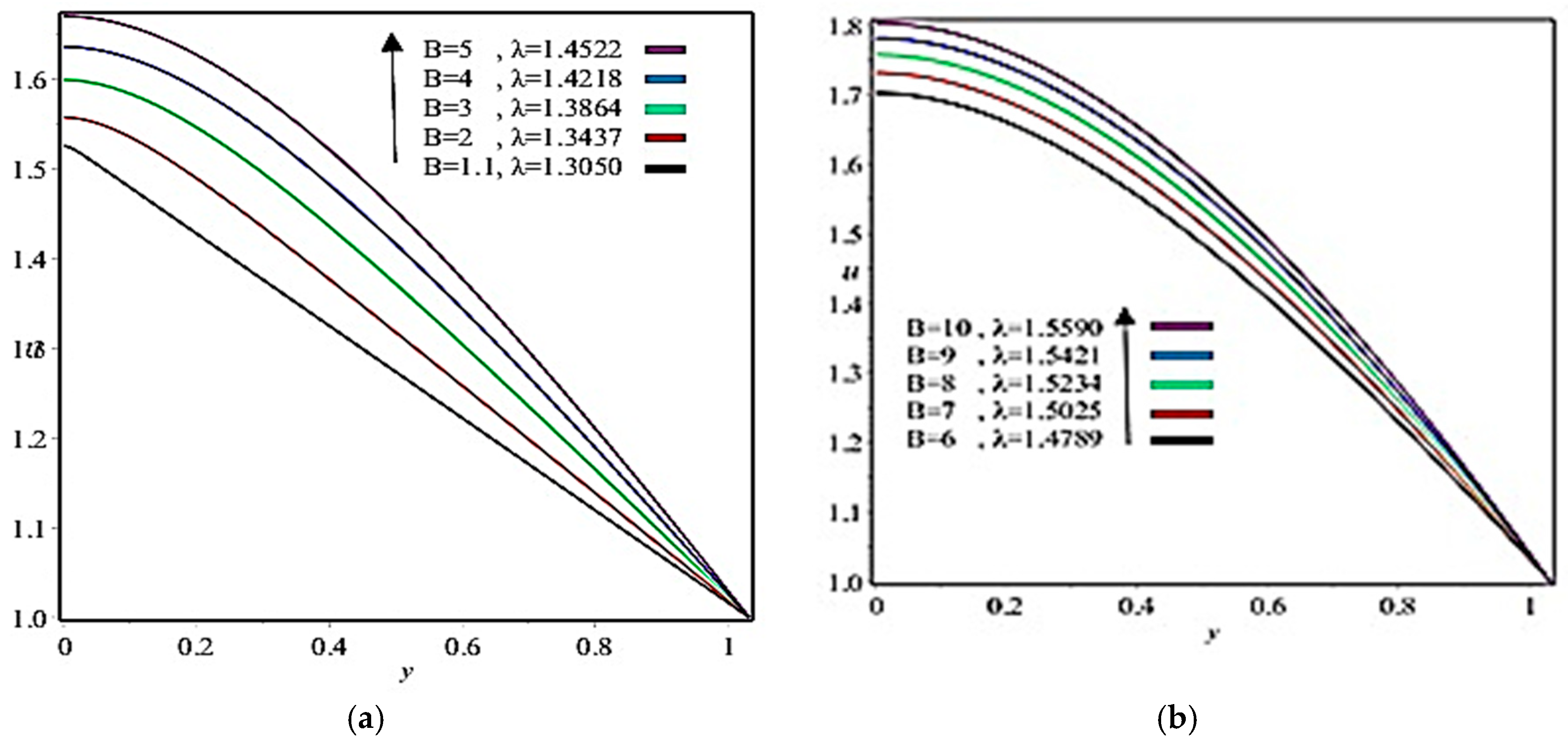
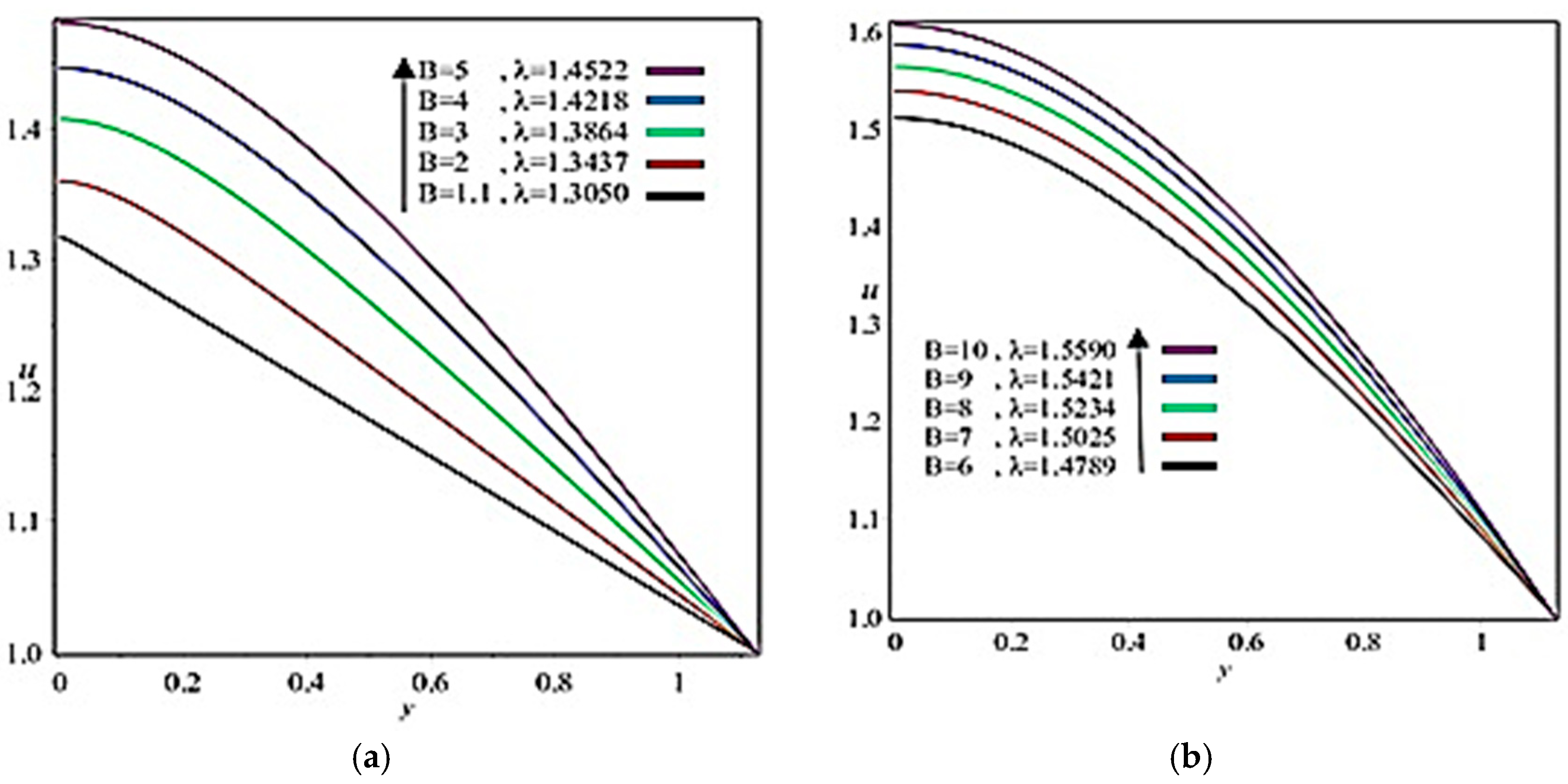
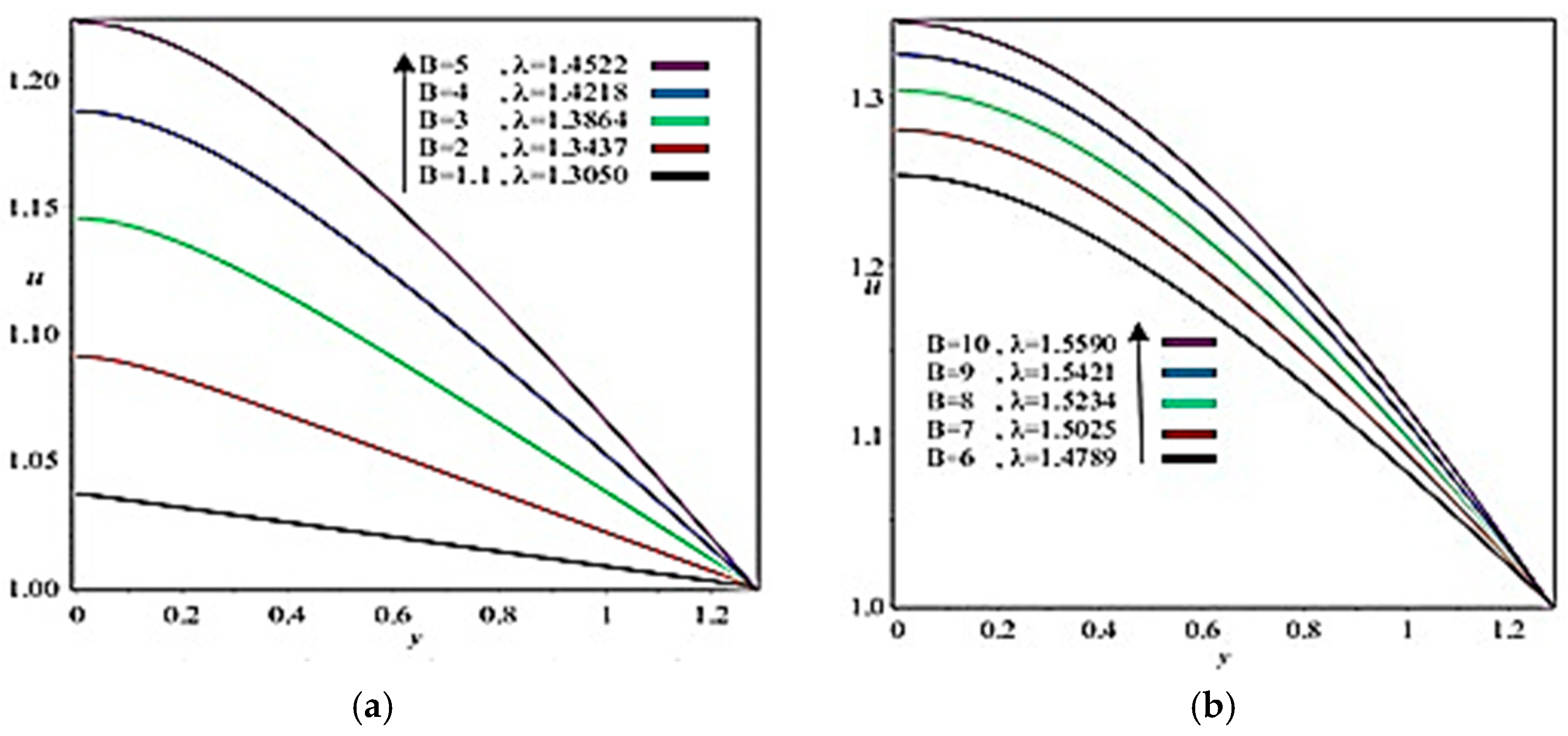
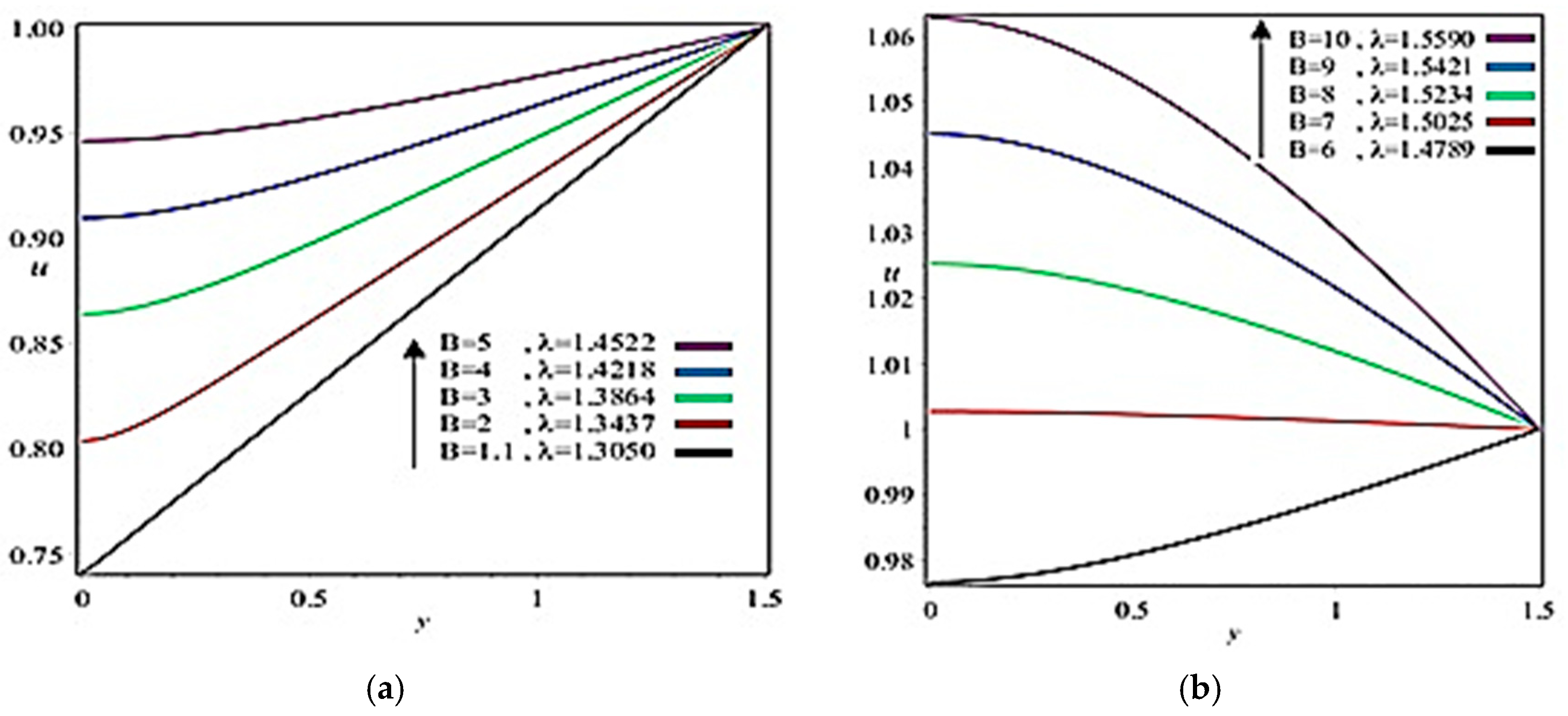
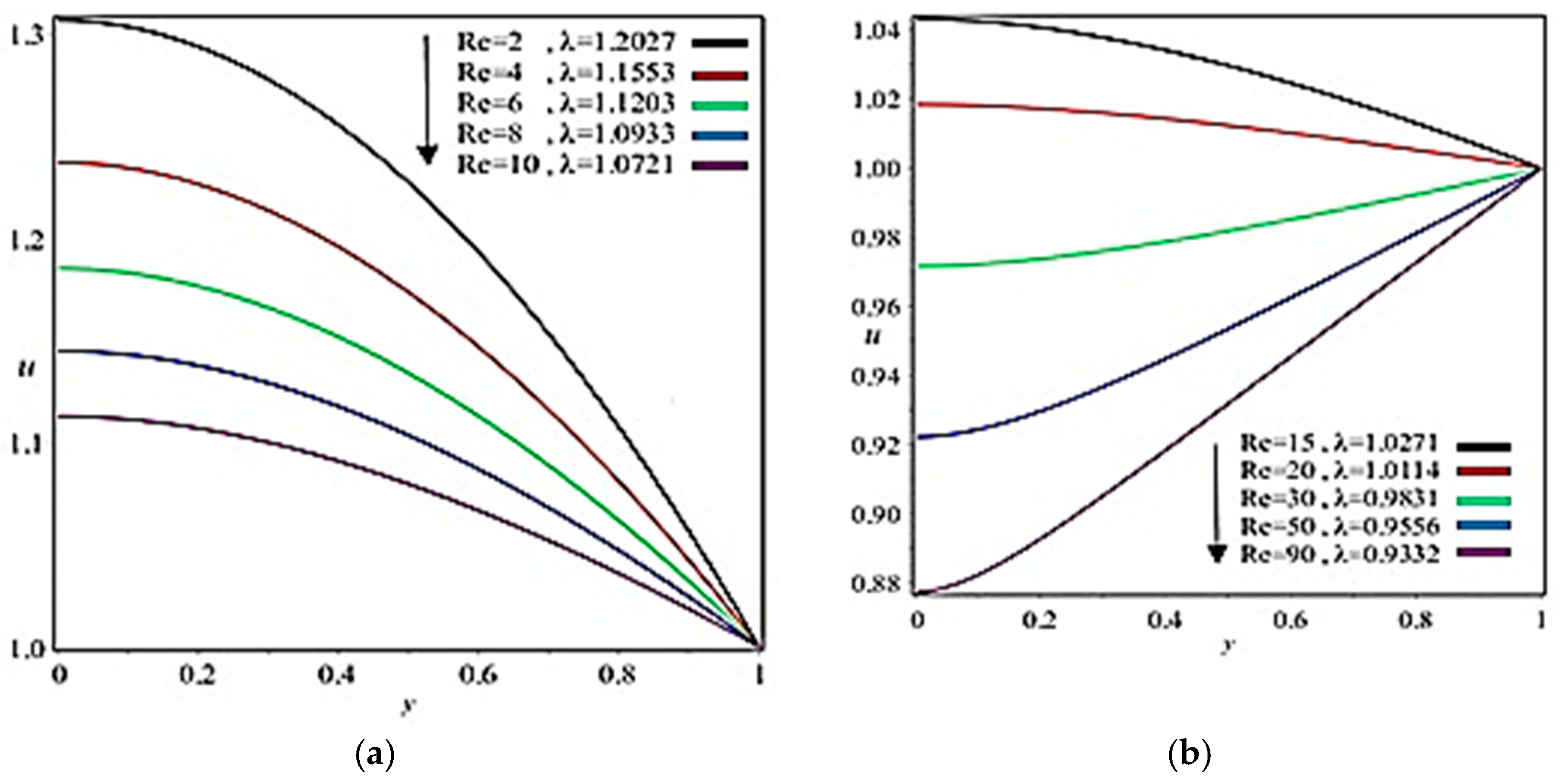
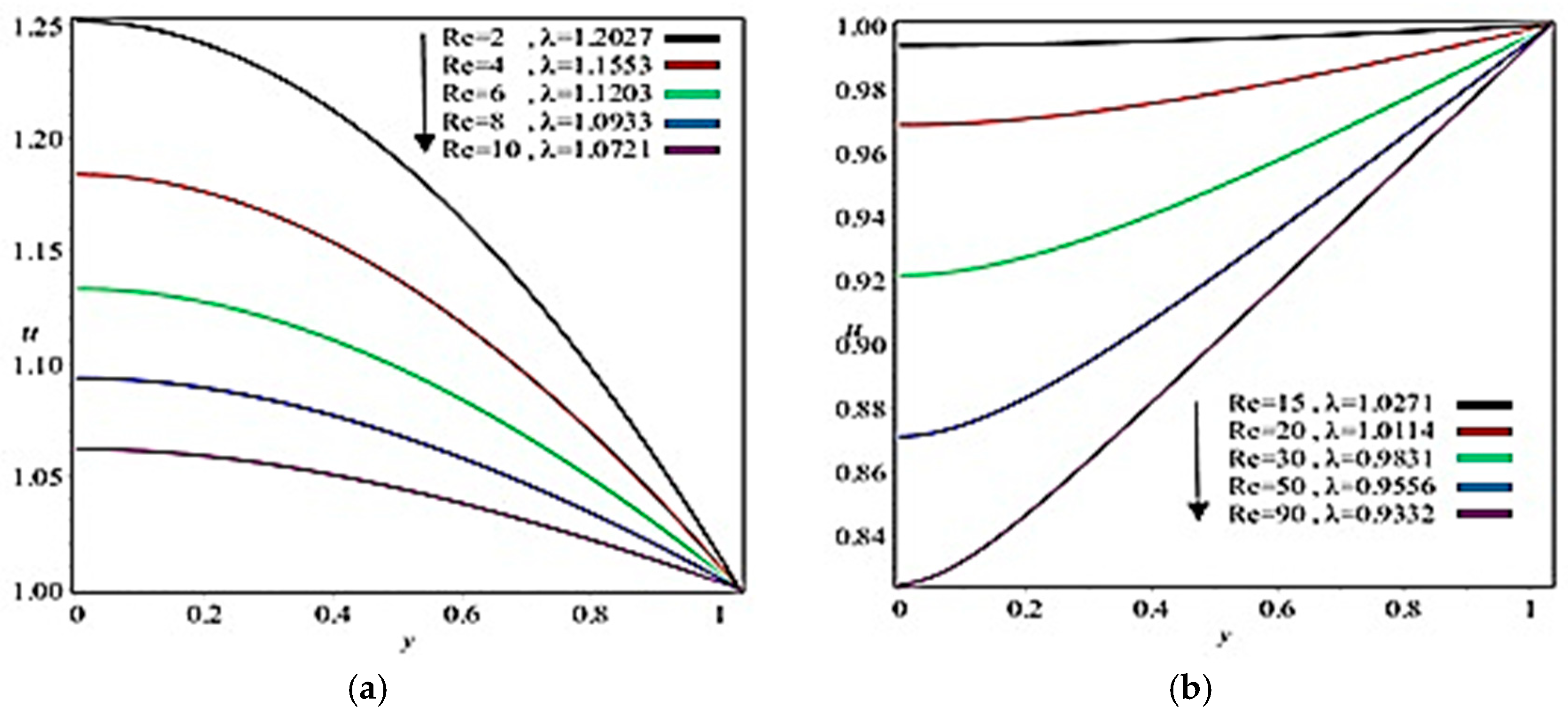
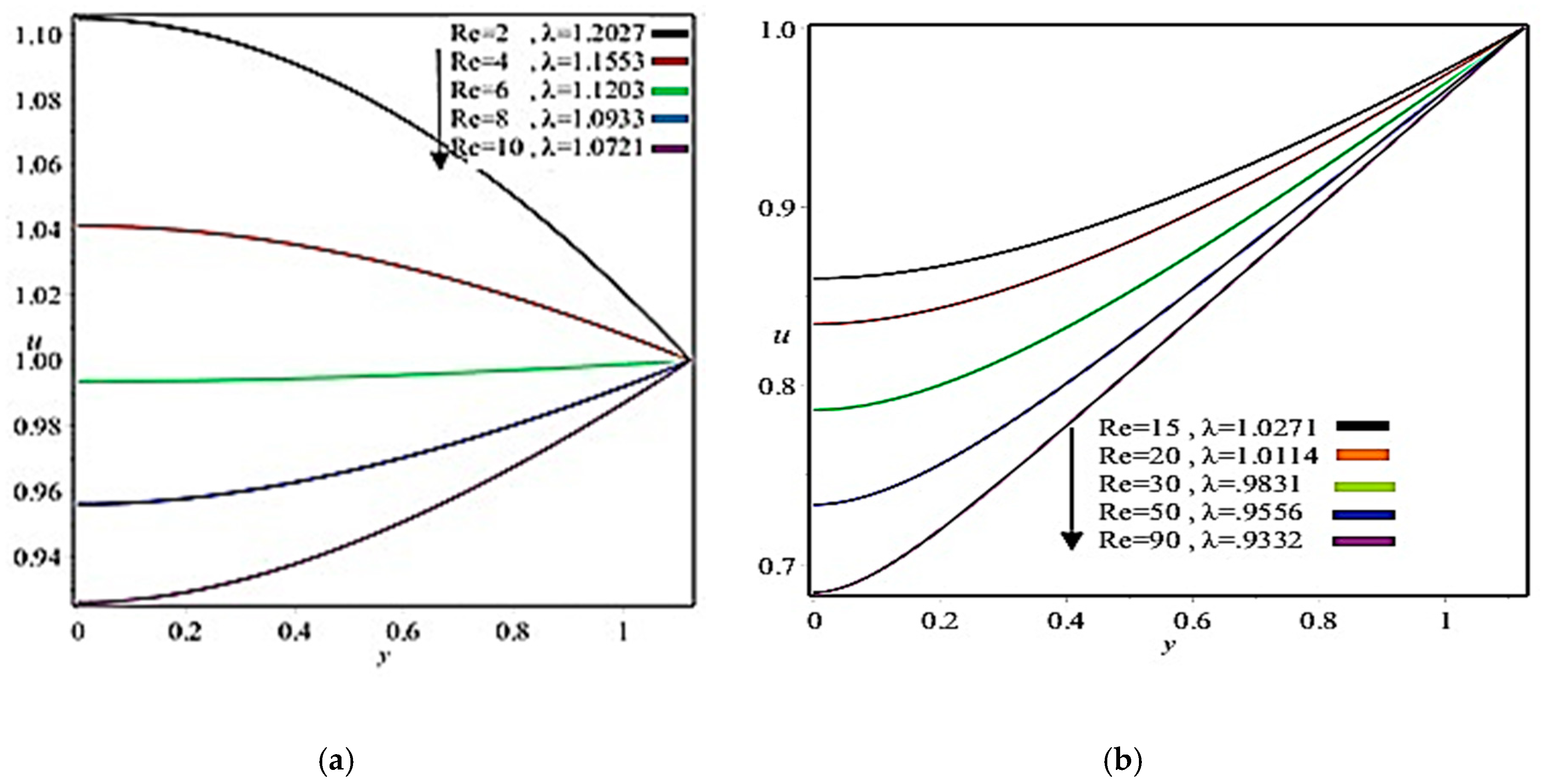
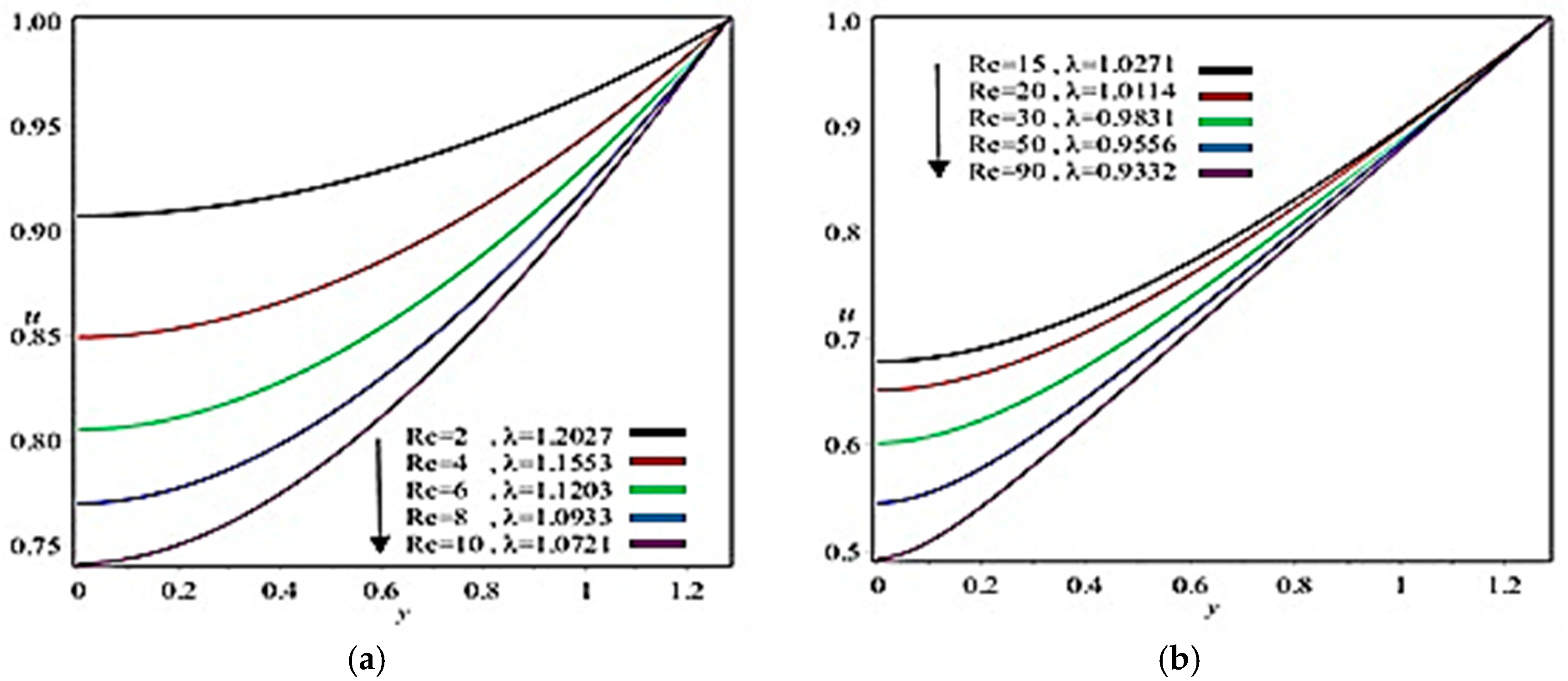
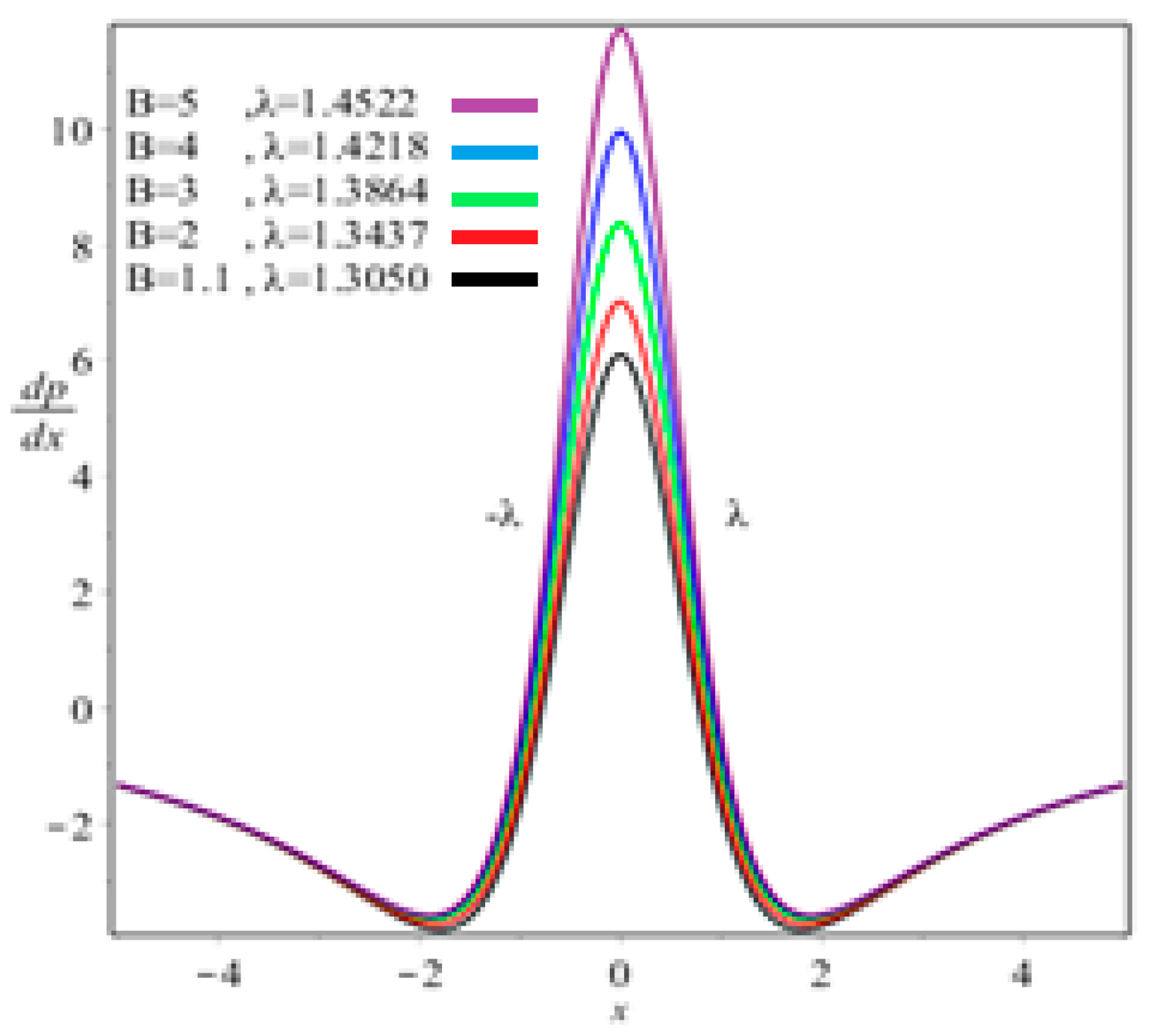
5. Results and Discussion
6. Conclusions
- In the case of the upper-convected Maxwell fluid model, which is a class of viscoelastic material, a theoretical study was carried out, as most of the material in the coating industry is viscoelastic. Hence the theoretical results for these industries are presented in this study so that they can set their engineering quantities numerically according to the theoretical findings listed in Table 1, Table 2 and Table 3;
- Coating thickness, separation region/separation point, roll separation force, power input, and pressure can be controlled through Reynolds number and fluid parameter ;
- Separating point and coating thickness increases by increasing Capillary number;
- Viscous force has a dominant role on coating thickness, separation force, and power input;
- The outcomes of Middleman [5] are obtained when B → 0 and Re → 0;
- The nip region demonstrates the highest velocity and pressure gradient.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| τ | Extra stress tensor |
| ρ | Density |
| B | Viscoelastic parameter |
| μ | Viscosity |
| v | Kinematic viscosity |
| Re | Reynolds number |
| γ | Surface tension |
| λ | Coating thickness |
| NCa₂ | Modified capillary number |
References
- Rajagopal, K.R. A note on unsteady unidirectional flows of a non-Newtonian fluid. Int. J. Non-Linear Mech. 1982, 17, 369–373. [Google Scholar] [CrossRef]
- Benharbit, A.M.; Siddiqui, A.M. Certain solution of the equations of the planar motion of a second grade fluid for steady and unsteady cases. Acta Mech. 1992, 94, 85–96. [Google Scholar] [CrossRef]
- Taylor, J.H.; Zeltlemoyer, A.C. Hypothesis on the mechanism of ink splitting during printing. Tappi J. 1958, 41, 749–757. [Google Scholar]
- Hintermaier, J.C.; White, R.E. The splitting of a water film between rotating rolls. Tappi J. 1965, 48, 617–625. [Google Scholar]
- Greener, J.; Middleman, S. A theory of roll coating viscous and viscoelastic fluids. Polym. Eng. Sci. 1975, 15, 1–10. [Google Scholar] [CrossRef]
- Benkreira, H.; Edwards, M.F.; Wilkinson, W.L. A semi-empirical model of the forward roll coating flow of Newtonian fluids. Chem. Eng. Sci. 1981, 42, 423–437. [Google Scholar] [CrossRef]
- Souzanna, S.; Mitsoulis, E. Roll-over-web coating of pseudoplastic and viscoplastic sheets using the lubrication approximation. J. Plast. Film Sh. 2005, 21, 307–333. [Google Scholar]
- Wang, Z.; Jin, X.; Keer, L.M.; Wang, Q. A numerical approach for analyzing three-dimensional steady-state rolling contact including creep using a fast semianalytical method. Tribol. Trans. 2012, 55, 446–457. [Google Scholar] [CrossRef]
- Zahid, M.; Haroon, T.; Rana, M.A.; Siddiqui, A.M. Roll coating analysis of a third grade fluid. J. Plast. Film Sh. 2017, 33, 72–91. [Google Scholar] [CrossRef]
- Zahid, M.; Rana, M.A.; Siddiqui, A.M. Roll coating analysis of a second-grade material. J. Plast. Film Sh. 2018, 34, 141–164. [Google Scholar] [CrossRef]
- Sun, J.; Hui, S.; Liu, P.; Sun, R.; Wang, M. Investigations on forming ether coated iron nanoparticle materials by first-principle calculations and molecular dynamic simulations. Coatings 2019, 9, 395. [Google Scholar] [CrossRef]
- Liu, C.; Li, S.; Zhang, Z.; Zeng, M.; Wang, F.; Wang, J.; Guo, Y. Numerical simulation of thermal evolution and solidification behavior of laser cladding AlSiTiNi composite coatings. Coatings 2019, 9, 391. [Google Scholar] [CrossRef]


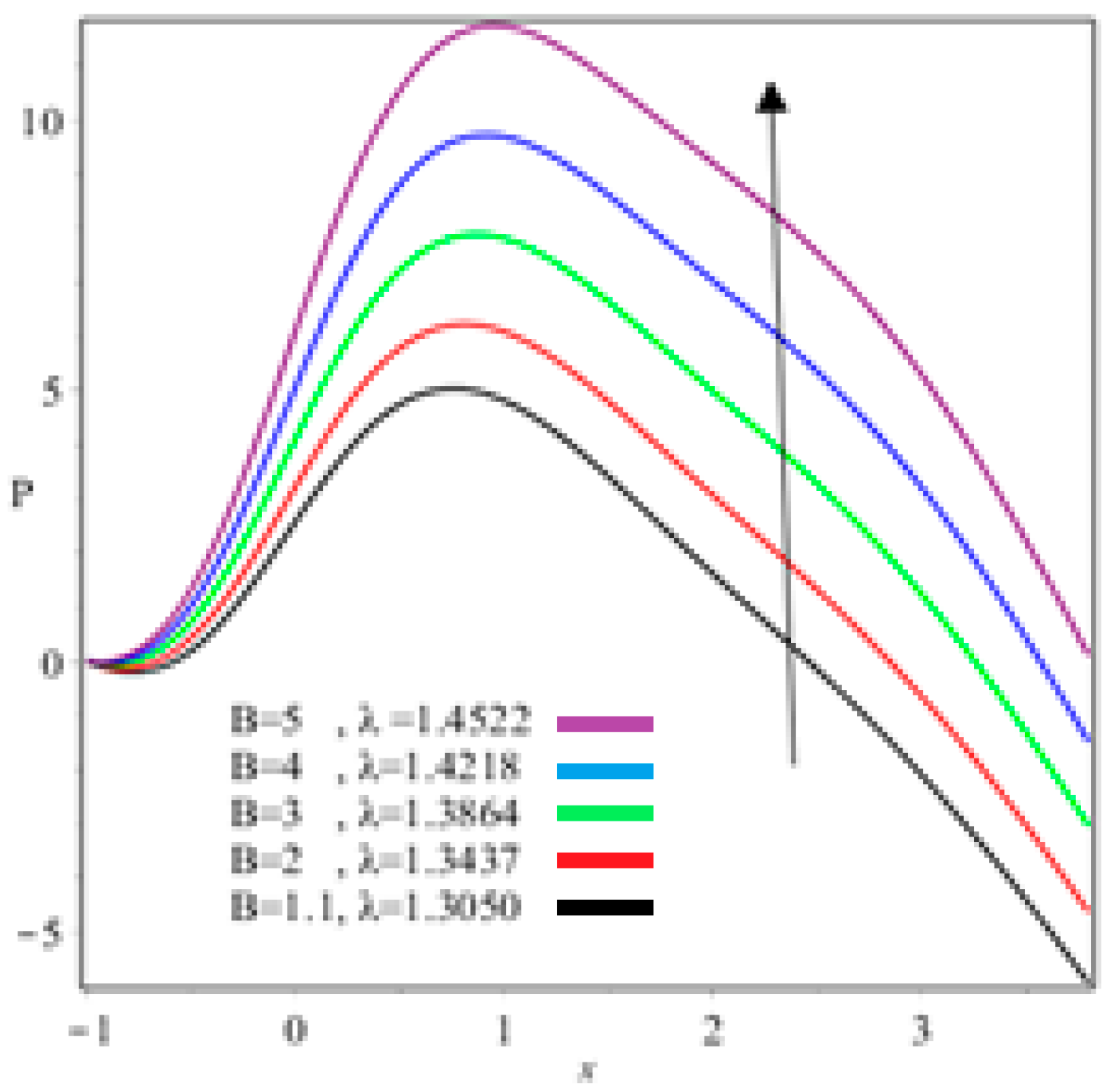
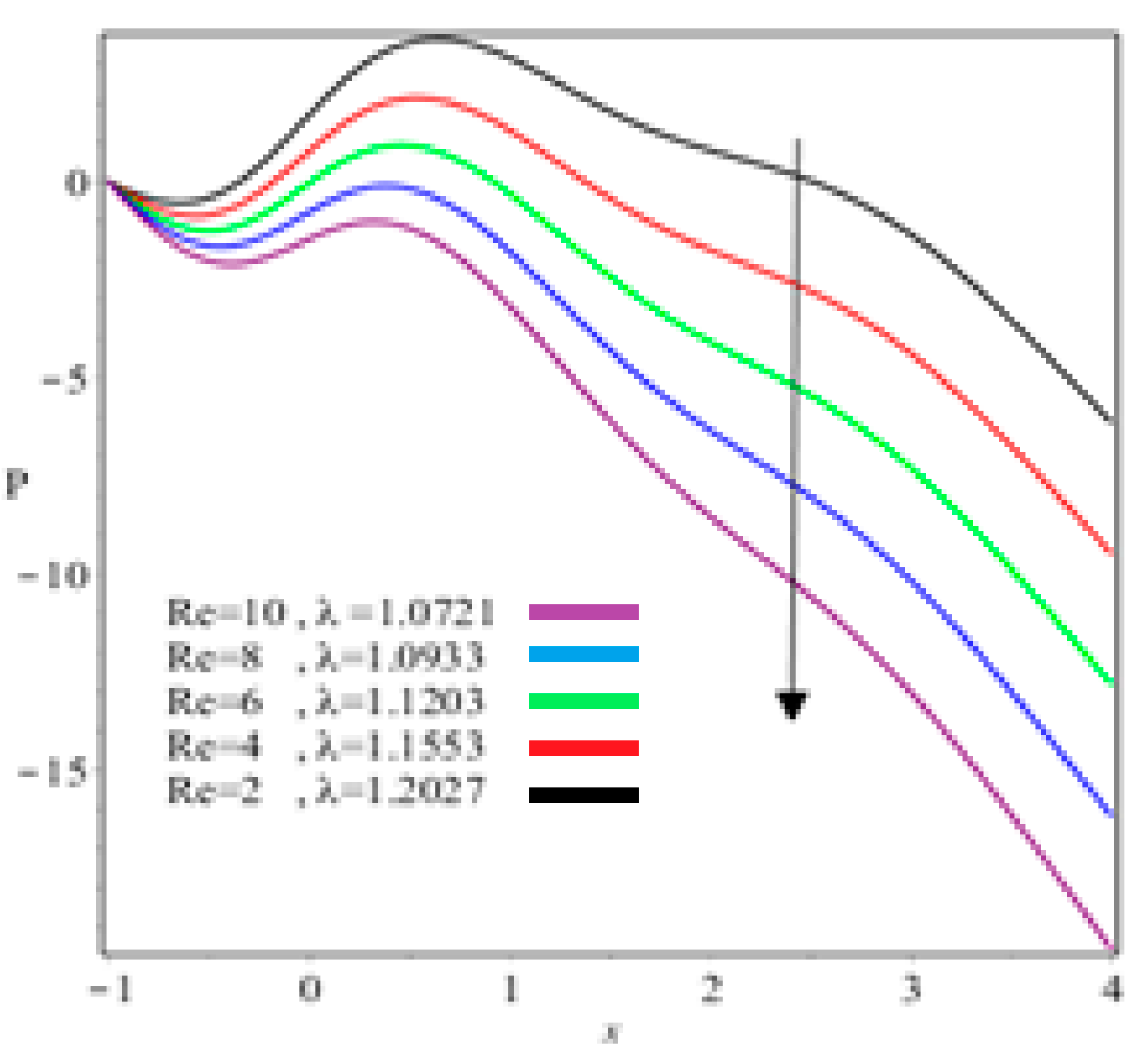
| B | xs | λ | F | Pw |
|---|---|---|---|---|
| 1.1 | 1.8000 | 1.3050 | 7.8107 | −0.2335 |
| 2 | 1.8425 | 1.3437 | 10.3295 | −0.3614 |
| 3 | 1.8883 | 1.3864 | 13.8451 | −0.5327 |
| 4 | 1.9254 | 1.4218 | 17.7476 | −0.7010 |
| 5 | 1.9567 | 1.4522 | 22.0537 | −0.8803 |
| 6 | 1.9838 | 1.4789 | 26.7183 | −0.9980 |
| 7 | 2.0075 | 1.5025 | 31.6752 | −1.1240 |
| 8 | 2.0282 | 1.5234 | 36.8622 | −1.2360 |
| 9 | 2.0466 | 1.5421 | 42.2522 | −1.3367 |
| 10 | 2.0630 | 1.5590 | 47.8226 | −1.4263 |
| Re | xs | λ | F | Pw |
|---|---|---|---|---|
| 2 | 2.2351 | 1.2027 | 5.1937 | −0.0433 |
| 4 | 2.1744 | 1.1553 | 0.8853 | 0.1910 |
| 6 | 2.1282 | 1.1203 | −2.9233 | 0.3726 |
| 8 | 2.0919 | 1.0933 | −6.3312 | 0.4912 |
| 10 | 2.0630 | 1.0721 | −9.4709 | 0.5914 |
| 15 | 1.9999 | 1.0271 | −17.6440 | 0.7867 |
| 20 | 1.9774 | 1.0114 | −23.5755 | 0.8553 |
| 30 | 1.9362 | 0.9831 | −37.1632 | 0.9527 |
| 50 | 1.8952 | 0.9556 | −65.0365 | 1.0213 |
| 90 | 1.8612 | 0.9332 | −122.8755 | 1.0673 |
| NCa₂ | xs | λ |
|---|---|---|
| 1 | 2.2474 | 1.2303 |
| 2 | 2.2563 | 1.2376 |
| 3 | 2.2592 | 1.2400 |
| 4 | 2.2607 | 1.2412 |
| 5 | 2.2615 | 1.2418 |
| 6 | 2.2619 | 1.2422 |
| 7 | 2.2625 | 1.2427 |
| 8 | 2.2629 | 1.2430 |
| 9 | 2.2631 | 1.2432 |
| 10 | 2.2633 | 1.2433 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zafar, M.; A. Rana, M.; Zahid, M.; Ahmad, B. Mathematical Analysis of the Coating Process over a Porous Web Lubricated with Upper-Convected Maxwell Fluid. Coatings 2019, 9, 458. https://doi.org/10.3390/coatings9070458
Zafar M, A. Rana M, Zahid M, Ahmad B. Mathematical Analysis of the Coating Process over a Porous Web Lubricated with Upper-Convected Maxwell Fluid. Coatings. 2019; 9(7):458. https://doi.org/10.3390/coatings9070458
Chicago/Turabian StyleZafar, Muhammad, Muhammad A. Rana, Muhammad Zahid, and Babar Ahmad. 2019. "Mathematical Analysis of the Coating Process over a Porous Web Lubricated with Upper-Convected Maxwell Fluid" Coatings 9, no. 7: 458. https://doi.org/10.3390/coatings9070458
APA StyleZafar, M., A. Rana, M., Zahid, M., & Ahmad, B. (2019). Mathematical Analysis of the Coating Process over a Porous Web Lubricated with Upper-Convected Maxwell Fluid. Coatings, 9(7), 458. https://doi.org/10.3390/coatings9070458




