Optimizing Processing Parameters for Multi-Track Laser Cladding Utilizing Multi-Response Grey Relational Analysis

Abstract

Multi-track laser cladding is the primary technology used in industrial applications for surface reinforcement and remanufacturing of broken parts. In this study, the influence of processing parameters on multi-track laser cladding was investigated using a Taguchi orthogonal experimental design. A multi-response grey relational analysis (GRA) was employed to identify laser cladding processing parameters that simultaneously optimize the flatness ratio of the coating and the cladding efficiency. The optimal parameters setting found by GRA were validated experimentally. Results showed that the flatness ratio and cladding efficiency were closely correlated to the overlap rate and laser power, where the overlap rate shows the most significant impact on the flatness ratio and the laser power shows the most significant impact on cladding efficiency. Results from the validation experiment were within one percent (0.97% error) of the predicted value. This demonstrates the benefits of utilizing GRA in laser cladding process optimization. The methods presented in this paper can be used to identify ideal processing parameters for multi-response multi-track laser cladding processes or other industrial applications.

1. Introduction

Laser cladding is an advanced technology used for surface reinforcement and restoration. It creates a condensed coating on the substrate surface, forming a metallurgical bond that improves the substrate properties, such as wear resistance, corrosion resistance, and oxidation resistance [1,2,3,4,5,6,7]. Laser cladding is a complex process, and the quality of the cladding coating is primarily affected by several parameters including laser power, gas flow, and powder feeding rate [7]. A long-term goal for researchers is to develop a system to predict and control the coating quality obtained by laser cladding through the manipulation of different processing parameters. Over the years, various methods have been developed to investigate and analyze these interrelations during the laser cladding process.

Nabhani et al. studied the influence of laser power, scanning rate, and powder feeding rate on the clad height, clad width, penetration depth, wetting angle, and dilution in single-track cladding of Ti-6Al-4V powder alloy deposited on Ti-6Al-4V substrate. The optimal processing parameter combination was obtained by a linear regression analysis of each response [8]. Liu et al. investigated how laser power, pre-placed powder depth, and scanning speed affected the clad width, height, area, and wetting angle using a full factorial design with single-track laser cladding. A mathematical model was proposed to explain the relationship between processing parameters and the aforementioned geometrical characteristics [9]. Kumar et al. researched the influence of laser power, scanning speed, and aluminum nitride composition percentage on the clad width and micro-hardness. A mathematical model was developed to relate the responses and processing parameters. Experimental results indicated that clad width increased with the increasing scanning speed [10]. Bourahima et al. utilized central composite design to study Ni-based powder laser cladding on a Cu–Ni–Al alloy substrate. They evaluated the influence of the processing parameters (laser power, scanning speed, powder feeding rate) on bonding quality and coating geometry (clad width and height). A mathematical model was developed to explain these interrelationships. Results illustrated that coating geometry was negatively correlated with scanning speed and bonding quality was improved with increased scanning speed and decreased powder feeding rate [11]. A high accuracy predictive model was developed by Alam et al. to explain how the clad characteristics (hardness, bead aspect ratio, and wetting angle) were affected by the processing parameters (powder feed rate, laser power, focal length of lens, laser speed, and contact tip to workpiece distance) [12].

Most of these studies were focusing on predicting the optimal processing parameters in single-track laser cladding, which limits the cladding area to a narrow track. Although single track cladding is useful in understanding properties that affect the cladding process, the ability to process a larger area is needed for actual industrial application such as restoration or remanufacturing. For these applications, multi-track cladding is necessary. In multi-track cladding, individual tracks are laid adjacent to one another covering the surface of a component with clads. This process forms an irregular surface with a high region in the center of each track and a lower region between track centers. The goal of this research is to understand the processing parameters that control surface irregularity and to finding processing parameters that produce a cladded surface with minimal irregularity while maintaining cladding efficiency, a crucial requirement for industrial application.

2. Materials and Methods

AISI/SAE 1045 steel was selected as the substrate with a size of 40 mm × 20 mm × 5 mm. The laser beam diameter was set to 3 mm during the cladding process. The cladding powder was high-speed steel powder (W6Mo5Cr4V2) produced by Chengdu Huayin Powder Technology CO., LTD (Chengdu, China) with a particle size ranging from 48 to 106 μm, which met the powder feed specifications in the laser cladding system. The elemental composition of W6Mo5Cr4V2 high-speed steel powder is listed in

Table 1. Elemental composition (wt.%) of W6Mo5Cr4V2 high-speed steel powder.

C	Si	Mn	Cr	Mo	V	W	Fe
0.8–0.9	0.15–0.4	0.2–0.45	3.8–4.4	4.5–5.5	1.75–2.2	5.5–6.75	Rest

.

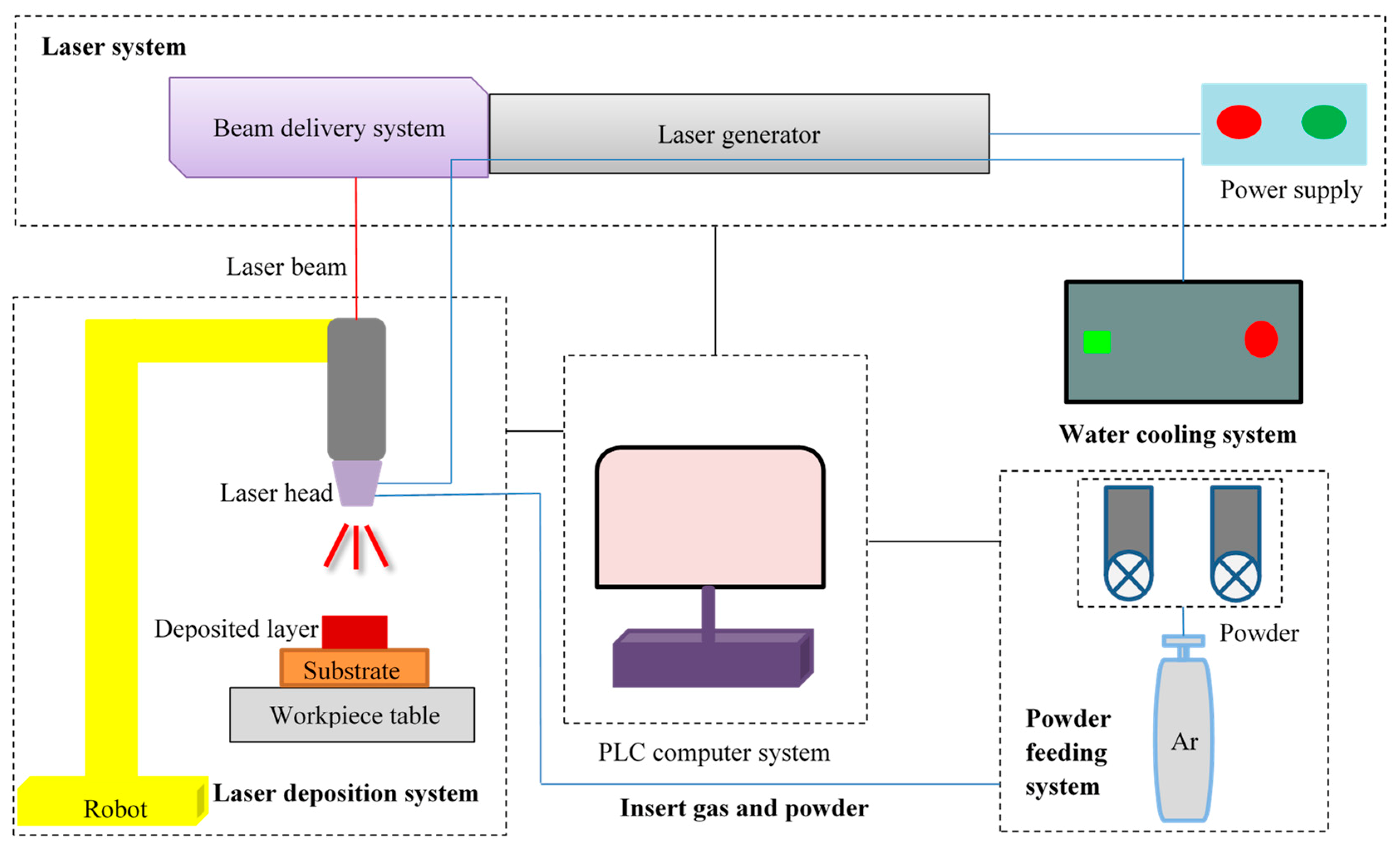
The laser cladding system is shown in Figure 1, which includes a laser system (YLS-3000, IPG, Burbach, Germany), laser cladding nozzle with 300 mm focal length (FDH0273, Lasermech, Novi, MI, USA), industrial robot (M-710iC/50, FANUC, Yamanashi, Japan), water cooling system (TFLW-4000WDR-01-3385, Sanhe Tongfei, Sanhe, China), powder feeding system (CR-PGF-D-2, Songxing, Fuzhou, China), control system (PLC, Mitsubishi, Japan), and laser pulse control system (SX14-012PULSE, IPG, Burbach, Germany). The material was protected by argon gas during the cladding process.

Before cladding, the surface of the 1045 steel substrate was cleaned with acetone, rinsed with alcohol, and dried. The cladding powder was dried in a vacuum dryer for 30 min at a temperature of 120 °C prior to use. After laser cladding, the sample was prepared for evaluation by cutting, setting, grinding, and polishing. The sample was immersed in a 4% nitric acid and alcohol mixture for 30 s. Geometric characteristics of the clad sample were measured with a KH-1300 3D microscope (Hirox Co Ltd., Tokyo, Japan).

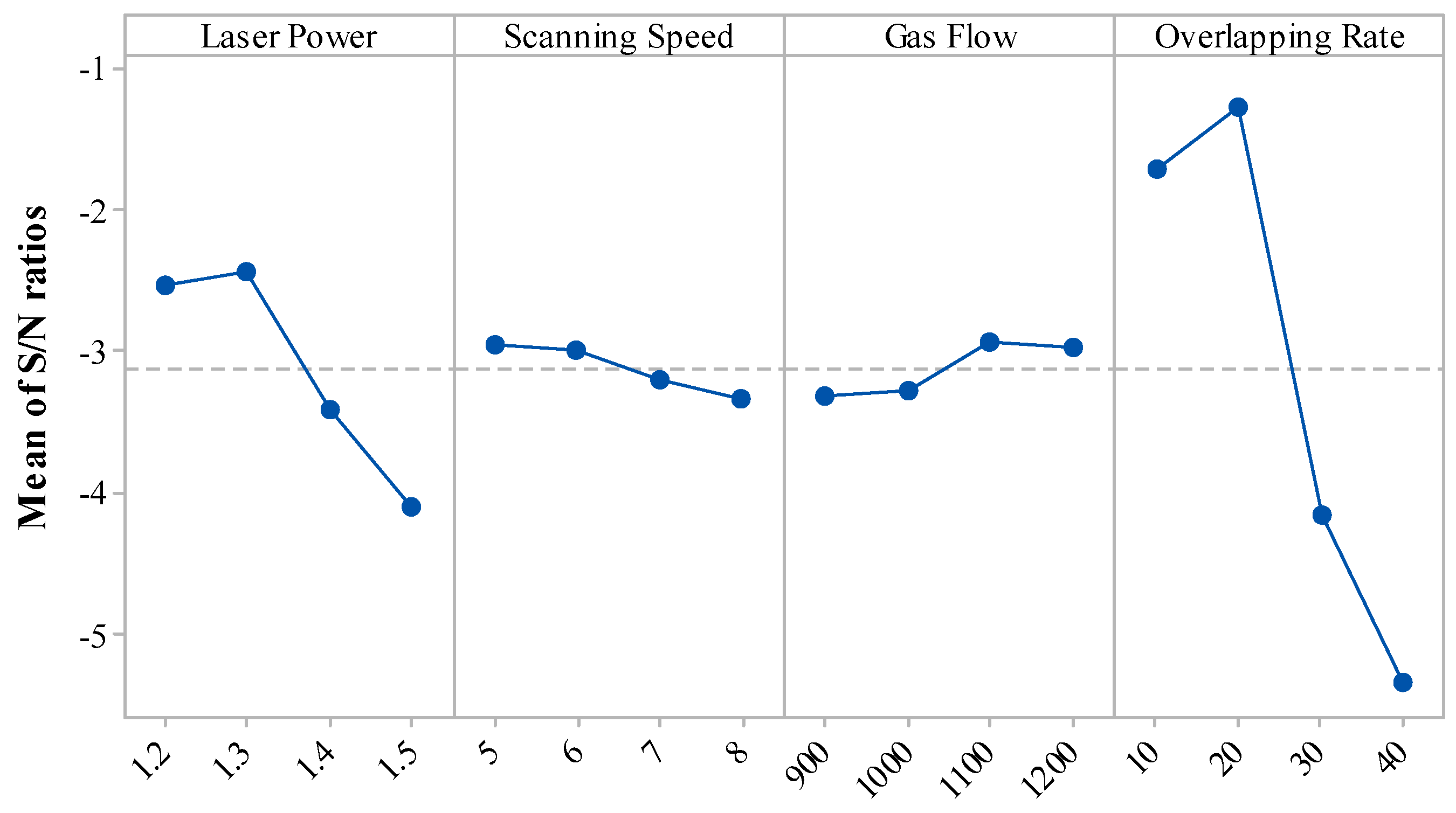
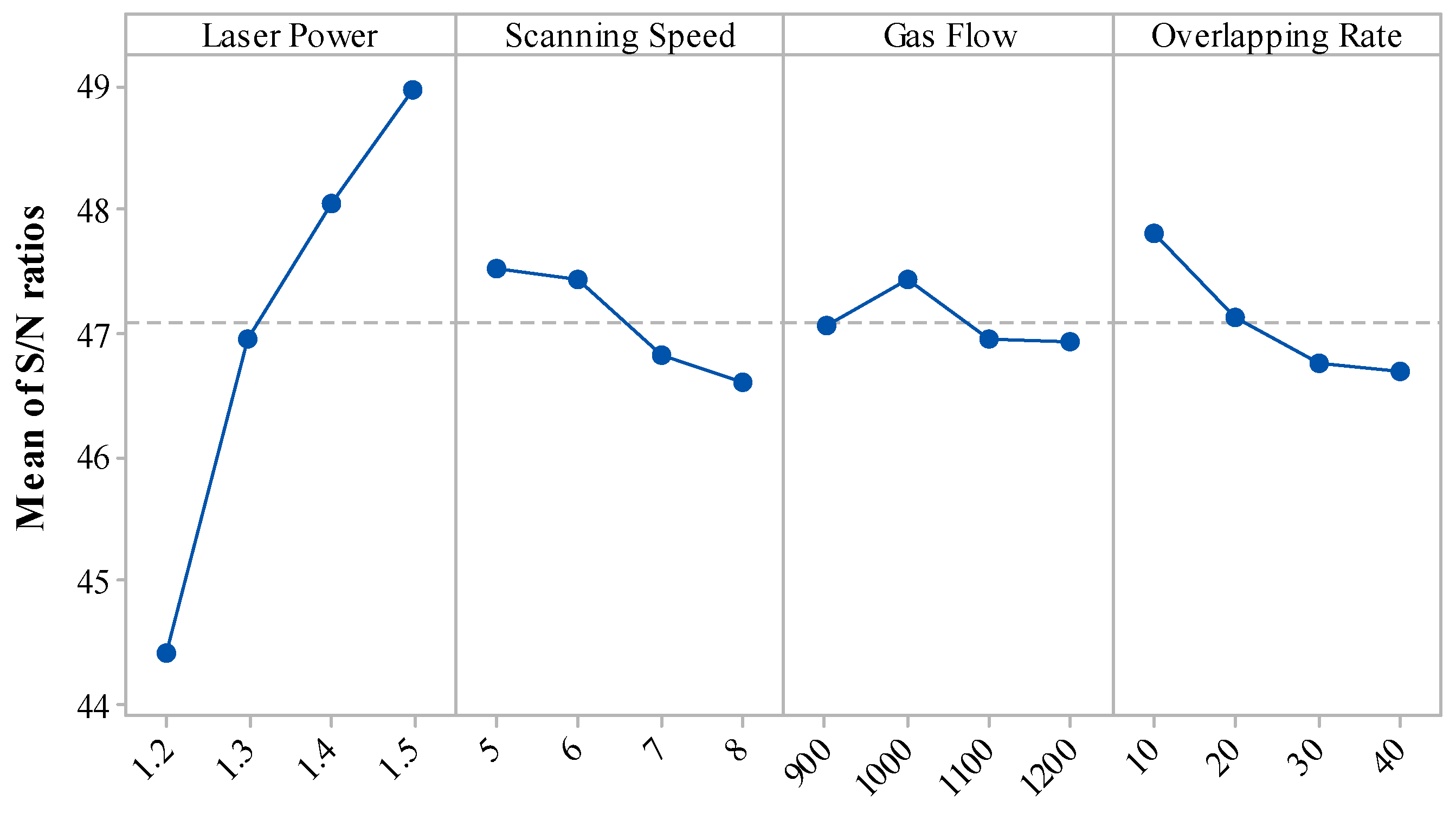
This study utilized Taguchi orthogonal methodology to design the multi-track laser cladding experiment. Four factors were evaluated (laser power, scanning speed, gas flow, overlapping rate). A full factorial experiment would have required 4⁴ = 256 different combinations since there were 4 levels for each factor. By using a Taguchi orthogonal L₁₆ (4⁴) design, only 16 runs were needed, substantially reducing the number of runs over a full factorial experiment [13]. The Taguchi orthogonal array is a balanced design with each factor level weighted equally, so each factor can be evaluated independently.

Table 2. Orthogonal experimental design.

Processing Parameter	Notation	Unit	Levels
			1	2	3	4
Laser Power	A	kW	1.2	1.3	1.4	1.5
Scanning Speed	B	mm/s	5	6	7	8
Gas Flow	C	L/h	900	1000	1100	1200
Overlapping Rate	D	%	10	20	30	40

shows the factors and their corresponding levels in the Taguchi orthogonal experimental design.

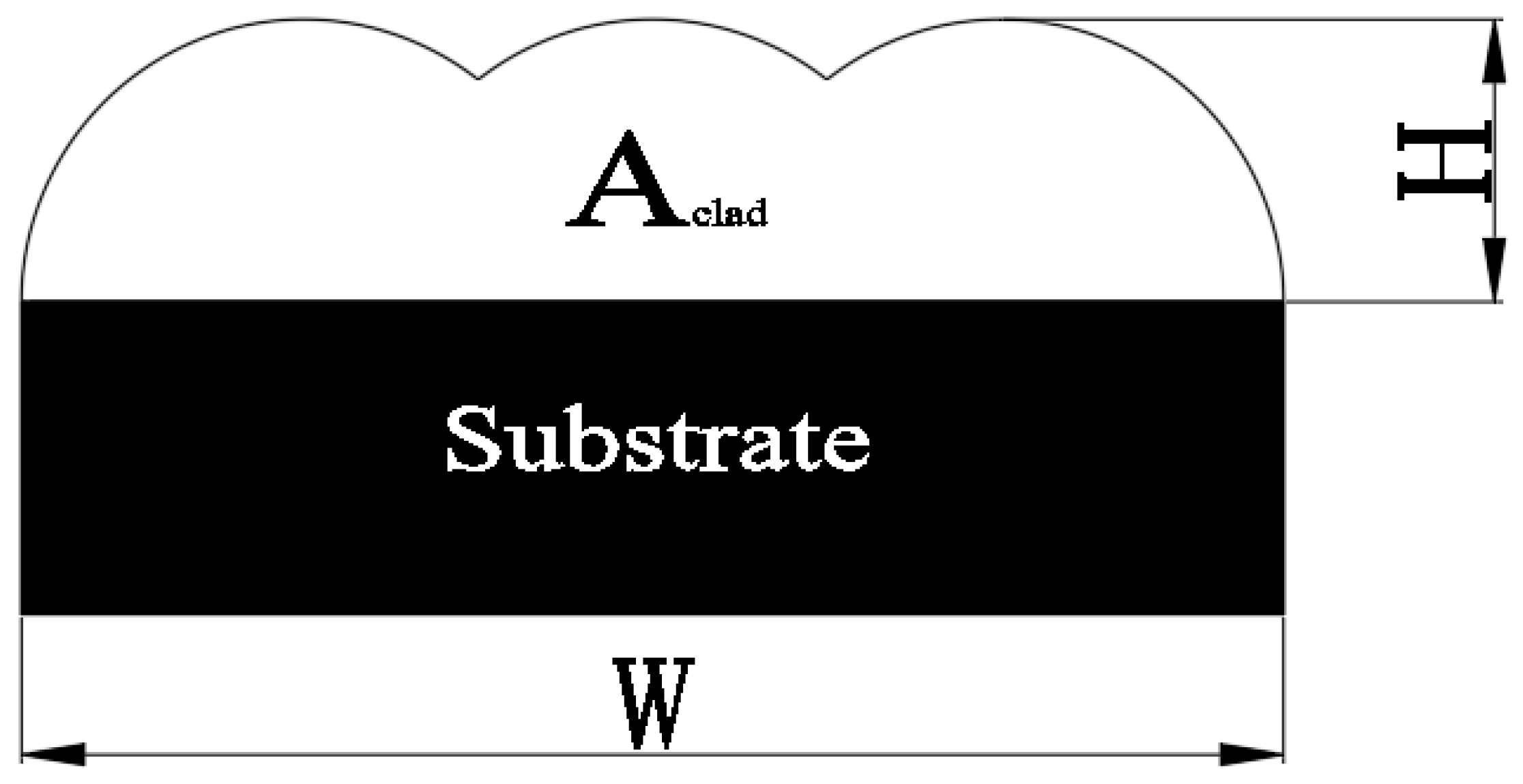
Important responses in this study are the flatness ratio (θ) and cladding efficiency (η). These parameters are expressed by Equations (1) and (2), respectively [14].

$$\mathsf{\theta }=\frac{A_{\mathrm{clad}}}{W\times H}$$

(1)

$$\mathsf{\eta }=A_{\mathrm{clad}}\times B$$

(2)

where A_clad is the cross-sectional area of clad on the substrate; W is the width of the total clad layer; H is the maximal height of the clad layer; B represents the scanning speed (Figure 2).

Calculating the signal–to–noise ratio (S/N) is a useful technique in data analysis for predicting optimized results [13,15,16]. S/N is a measure of the error between the actual response and the expected value [17,18]. Because S/N quantifies the quality of response based on the interaction between the noise and the signal, S/N is a measurement that can be used to identify controllable factors. Through analysis of the S/N, the aimed parameters can be obtained [19].

Converting the experimental results to their corresponding S/N is an effective process to simultaneously improve the flatness ratio and cladding efficiency [17,18]. A larger S/N value indicates a better quality of flatness ratio and cladding efficiency. Equation (3) is used to conduct the S/N conversion for flatness ratio and cladding efficiency,

$$\frac{S}{N}=-10\log \left(\frac{1}{n}{\displaystyle \sum }_{i=1}^n\frac{1}{Y_i^2}\right)$$

(3)

where n is the number of replicates in the experiment; Y_i is the experimental result [16,20]. After the S/N conversion of flatness ratio and cladding efficiency, analysis of variance (ANOVA) was used to investigate the relation between processing parameters and responses. The significance level, α was set at 0.05.

3. Results and Discussion

Table 3. Parameter settings in orthogonal experimental design, responses, and corresponding signal–to–noise (S/N) conversion of each run.

Run	A (kW)	B (mm/s)	C (L/h)	D (%)	Parameter Combination	θ: Flatness Ratio	η: Cladding Efficiency (mm3/s)	S/N
								θ	η
1	1.2	5	900	10	A1B1C1D1	0.892	192.052	−0.99270	45.66840
2	1.2	6	1000	20	A1B2C2D2	0.912	175.705	−0.80010	44.89570
3	1.2	7	1100	30	A1B3C3D3	0.682	153.434	−3.32431	43.71840
4	1.2	8	1200	40	A1B4C4D4	0.562	147.635	−5.00527	43.38380
5	1.3	5	1100	40	A2B1C3D4	0.603	213.336	−4.39365	46.58130
6	1.3	6	1200	30	A2B2C4D3	0.704	221.583	−3.04855	46.91070
7	1.3	7	900	20	A2B3C1D2	0.886	216.448	−1.05133	46.70710
8	1.3	8	1000	10	A2B4C2D1	0.864	238.899	−1.26973	47.56430
9	1.4	5	1200	20	A3B1C4D2	0.881	262.787	−1.10048	48.39210
10	1.4	6	1100	10	A3B2C3D1	0.806	281.659	−1.87330	48.99450
11	1.4	7	1000	40	A3B3C2D4	0.518	247.254	−5.71340	47.86290
12	1.4	8	900	30	A3B4C1D3	0.566	222.415	−4.94367	46.94330
13	1.5	5	1000	30	A4B1C2D3	0.541	295.395	−5.33605	49.40820
14	1.5	6	900	40	A4B2C1D4	0.487	279.107	−6.24942	48.91540
15	1.5	7	1200	10	A4B3C4D1	0.732	282.874	−2.70978	49.03190
16	1.5	8	1100	20	A4B4C3D2	0.783	267.139	−2.12476	48.53470

shows the 16 runs from the Taguchi orthogonal experimental design, with their corresponding processing parameter settings. The response of the flatness ratio (θ) and cladding efficiency (η) in this study is also shown in Table 3, as well as their corresponding signal–to–noise ratio conversion.

3.1. Analysis of Flatness Ratio

Out of the 16 runs, the best result for flatness ratio occurred in the second run, whose processing parameter setting was A₁B₂C₂D₂ (1.2 kW laser power; 6 mm/s scanning speed; 1000 L/h gas flow; 20% overlapping rate).

Table 4. ANOVA on S/N of flatness ratio.

Source	Sum of Squares	Degree of Freedom	Mean Square	F-Value	p-Value Prob > F
A	7.45	3	2.48	21.27	0.0159
B	0.38	3	0.13	1.10	0.4703
C	0.49	3	0.16	1.39	0.3969
D	45.71	3	15.24	130.56	0.0011
Residual	0.35	3	0.12	–	–
Cor Total	54.38	15	–	–	–

shows the ANOVA analysis result of the flatness ratio S/N data in Table 3. As indicated by the p-value, laser power (A) and overlapping rate (D) had a significant impact on the flatness ratio, while scanning speed (B) and gas flow (C) were not statistically significant.

Figure 3 illustrates the main effects plot for S/N of θ. This plot was generated by plotting the means for each value of each categorical variable using Minitab software (17.1.0.0). Solid lines connect each mean value within each category and the dashed reference line indicates the overall mean. The main effect for each categorical variable is evaluated by comparing the solid plotted line to the dashed reference line. A horizontal solid line indicates that there is no main effect for this parameter. Otherwise, a main effect for the parameter exists. A steeper slope denotes that the parameter has a stronger influence on the results.

Figure 3 shows that the overlapping rate has the most significant influence on the flatness ratio, which is consistent with the results in Table 4. The best flatness ratio occurred at an overlapping rate of 20%. The flatness ratio was lower at an overlapping rate of 10%. This was because the shared area between overlapping tracks was smaller, causing a greater height difference than at a 20% overlapping rate. With overlapping rates higher than 20%, there was a buildup of cladding material in the area between the adjacent tracks, a phenomenon known as “slope cladding”. This also caused the flatness ratio to decrease. Similar results were observed for the laser power. The flatness ratio displayed a small increase then decrease with increasing laser power. Since the laser power determined the amount of energy received by the molten pool during laser cladding, a relatively low laser power limited the energy absorbed by the molten pool, leading to insufficient melting of the cladding powder. This resulted in a narrower cladding track on the substrate. As laser power increased, the convection effect in the molten pool increased, which increased the width of the total clad layer, resulting in an increase in the flatness ratio. A further increase in the laser power resulted in lower flatness ratios. This effect can be explained by Equation (1). Increasing laser power flattened the molten pool and increased the width at a faster rate than the total clad area was increased [21].

The main effects plot shows scanning speed and gas flow to be close to the reference dash line indicating that their impact on the flatness ratio is not significant. These results are consistent with the data presented in the ANOVA analysis in Table 4. Based on these results, when only the flatness ratio was considered, the best processing parameters were a 1.3 kW laser power and 20% overlapping rate.

3.2. Analysis of Cladding Efficiency

The best result of cladding efficiency was achieved in the 13th run, whose processing parameter setting was A₄B₁C₂D₃ (1.5 kW laser power; 5 mm/s scanning speed; 1000 L/h gas flow; 30% overlapping rate). An ANOVA analysis of the cladding efficiency S/N data in Table 3 is shown in

Table 5. ANOVA on S/N of cladding efficiency.

Source	Sum of Squares	Degree of Freedom	Mean Square	F-Value	p-Value Prob > F
A	46.53	3	15.51	146.09	0.0009
B	2.38	3	0.79	7.47	0.0664
C	0.65	3	0.22	2.03	0.2876
D	3.24	3	1.08	10.16	0.0443
Residual	0.32	3	0.11	–	–
Cor Total	53.11	15	–	–	–

. Laser power (A) and overlapping rate (D) had significant impact on the cladding efficiency, with p-values being 0.0009 and 0.0443, respectively. Scanning speed (B) and gas flow (C) were not statistically significant at the predetermined value of α equal to 0.05. Although not significant in this experiment, the scanning speed showed a trend toward significance (p = 0.0664) and should be investigated further.

The main effects plot (Figure 4) showed that laser power had the most significant influence on cladding efficiency. Cladding efficiency increased dramatically with increasing laser power. Since laser power controlled the energy absorbed during the cladding process, higher laser power resulted in more energy being absorbed by the cladding powder. These higher energy levels increased the width of the cladding track and the cross-sectional area of clad (A_clad) [21]. As expected, increasing the overlapping rate decreased cladding efficiency. During multi-track laser cladding, a larger overlapping rate requires more passes to cover the same cladding area, thus reducing cladding efficiency.

According to Equation (2), the cladding efficiency is directly proportional to the scanning speed, however, experimental results show the cladding efficiency to decrease with scanning speed. The reason for this behavior is that a faster scanning speed shortened the laser energy exposure duration on the cladding powder and the molten pool. This decrease in energy resulted in a smaller area of clad because the powder did not receive sufficient laser energy to melt during the cladding process [22,23]. From these data, the best processing parameters were a laser power of 1.5 kW, a 5 mm/s scanning speed, and a 10% overlapping rate when only cladding efficiency was considered.

3.3. Multi-Response Grey Relational Analysis

The goal of this study was to simultaneously achieve both a high flatness ratio and suitable cladding efficiency. Since the best result of the flatness ratio and cladding efficiency occurred on different runs (i.e., different processing parameter settings), additional investigation is needed to achieve a multi-response optimization. To determine the optimal processing parameters while taking both flatness ratio and cladding efficiency into consideration, this paper applied grey relational analysis to achieve multi-response optimization [17]. Grey relational analysis was conceived by Julong Deng in the 1980s. This theory effectively combines multiple objectives into a “single” objective, thus solving the complex multi-response question. Grey relational analysis provides an effective way to optimize multiple parameters to attain the optimal solution that satisfies multiple objectives [24,25].

There are three steps to complete the grey relational analysis [19,26,27,28]. The first step is to normalize the data. This process accounts for the differences in units and the range of the original data. Normalized data is expressed as a value between 0 and 1. In this study, Equation (4) was selected to conduct normalization,

$$X_i\left(k\right)=\frac{Y_i\left(k\right)-min{Y}_i\left(k\right)}{max{Y}_i\left(k\right)-min{Y}_i\left(k\right)}$$

(4)

where k is the kth response (k = 1,2) for the two responses in this paper; i is the ith experimental data (i = 1, 2, 3, …, 16); $X_i\left(k\right)$ is the response data after normalization; $Y_i\left(k\right)$ stands for the original response data; $min{Y}_i\left(k\right)$ and $max{Y}_i\left(k\right)$ represent the minimum and maximum value of $Y_i\left(k\right)$. The second step is to calculate the grey relational coefficient for each response using Equation (5).

$${\mathrm{GRC}}_i\left(k\right)=\frac{{\Delta }_{min}+{\mathsf{\psi }\mathsf{\Delta }}_{max}}{{\Delta }_i\left(k\right)+{\mathsf{\psi }\mathsf{\Delta }}_{max}}$$

(5)

where ${\mathrm{GRC}}_i\left(k\right)$ is the grey relational coefficient (GRC) of the kth response in the ith run; ${\Delta }_i\left(k\right)$ represents the deviation between the normalized value and the reference sequence $\left\{X_0\right\}=\left\{1,1\right\}$. The deviation is obtained through ${\Delta }_i\left(k\right)=\left|X_0\left(k\right)-X_i\left(k\right)\right|$; ${\Delta }_{min}$ and ${\mathsf{\Delta }}_{max}$ denote the minimum and maximum value of ${\Delta }_i\left(k\right)$; $\mathsf{\psi }$ is the distinguishing coefficient with $\mathsf{\psi }\in \left[0,1\right]$. Normally 0.5 is selected for $\mathsf{\psi }$ since it gives a moderate distinguishing effect and stability [29]. After normalization of the original data for the flatness ratio and cladding efficiency, the result after grey relational generation (X) and their corresponding deviation (Δ) are shown in

Table 6. Original experimental data after normalization and the corresponding deviation.

Run	X(θ)	Δ(θ)	X(η)	Δ(η)
1	0.96466	0.03534	0.37922	0.62078
2	1	0	0.25096	0.74904
3	0.53678	0.46322	0.05554	0.94446
4	0.22831	0.77169	0	1
5	0.34055	0.65945	0.53076	0.46924
6	0.58739	0.41261	0.58544	0.41456
7	0.95390	0.04610	0.55164	0.44836
8	0.91382	0.08618	0.69393	0.30607
9	0.94488	0.05512	0.83134	0.16866
10	0.80306	0.19694	0.93133	0.06867
11	0.09836	0.90164	0.74349	0.25651
12	0.23962	0.76038	0.59085	0.40915
13	0.16761	0.83239	1	0
14	0	1	0.91820	0.08180
15	0.64956	0.35044	0.93754	0.06246
16	0.75691	0.24309	0.85501	0.14499

. The last step is to perform the grey relational calculation on multi-responses using Equation (6),

$${\mathrm{GRG}}_i=\frac{1}{n}{\displaystyle \sum }_{k=1}^n{\mathrm{GRC}}_i\left(k\right)$$

(6)

where GRG_i is the grey relational grade (GRG) for the ith run; n is the number of responses, which is two in this study.

In this paper, the goal of achieving a good flatness ratio and high cladding efficiency were determined to be equally important. Therefore, the same weight was given to both the flatness ratio and cladding efficiency for the grey relational grade (GRG) calculation. The GRCs, GRG, and S/N conversion of GRG for each run are shown in

Table 7. Grey relational coefficient (GRC) of flatness ratio and cladding efficiency, grey relational grade (GRG), S/N conversion of GRG for each run.

Run	GRC(θ)	GRC(η)	GRG	S/N (GRG)	Rank
1	0.93398	0.44612	0.69005	−3.22240	8
2	1	0.40031	0.70015	−3.09613	7
3	0.51909	0.34615	0.43262	−7.27782	15
4	0.39318	0.33333	0.36326	−8.79575	16
5	0.43124	0.51587	0.47355	−6.49262	13
6	0.54788	0.54671	0.54729	−5.23559	11
7	0.91558	0.52723	0.72140	−2.83645	6
8	0.85298	0.62029	0.73664	−2.65495	4
9	0.90070	0.74776	0.82423	−1.67902	1
10	0.71742	0.87924	0.79833	−1.95633	2
11	0.35673	0.66093	0.50883	−5.86856	12
12	0.39670	0.54996	0.47333	−6.49665	14
13	0.37527	1	0.68763	−3.25287	9
14	0.33333	0.85940	0.59637	−4.48973	10
15	0.58793	0.88895	0.73844	−2.63372	3
16	0.67287	0.77520	0.72403	−2.80481	5

, with larger values being more desirable. The 9th run setting (A₃B₁C₄D₂) was determined to be the preferred processing parameters (1.4 kW laser power; 5 mm/s scanning speed; 1200 L/h gas flow; 20% overlapping rate), with a GRG value of 0.82423.

The results of ANOVA on the S/N of the grey relational grade are shown in

Table 8. ANOVA on S/N of GRG.

Source	Sum of Squares	Degree of Freedom	Mean Square	F-Value	p-Value Prob > F
A	11.31	3	3.77	12.27	0.0343
B	7.19	3	2.40	7.80	0.0628
C	1.92	3	0.64	2.09	0.2807
D	47.74	3	15.91	51.78	0.0044
Residual	0.92	3	0.31	–	–
Cor Total	69.08	15	–	–	–

. Based on the obtained p-values, the overlapping rate (D) and laser power (A) were statistically significant and had an impact on the flatness ratio and cladding efficiency. The scanning speed (B) showed a trend toward significance (p = 0.0628).

Analysis of GRG S/N data in

Table 9. Mean of S/N (GRG) for each processing parameter.

Processing Parameter	Notation	Levels				Absolute Value Difference	Rank
		1	2	3	4
Laser Power	A	−5.59802	−4.28774	−3.93094	−3.29528	2.30274	2
Scanning Speed	B	−3.64456	−3.62525	−4.65414	−5.18804	1.56279	3
Gas Flow	C	−4.26131	−3.71838	−4.54653	−4.58602	1.02268	4
Overlapping Rate	D	−2.54765	−2.60410	−5.56573	−6.39449	3.84684	1

shows the maximum absolute value difference to occur in the overlapping rate. This indicates that the overlapping rate had the most significant influence on both the flatness ratio and cladding efficiency. Table 9 was used to determine the optimal processing parameter settings by selecting the level in each category with the highest value. The optimal setpoint was determined to be A₄B₂C₂D₁ (1.5 kW laser power; 6 mm/s scanning speed; 1000 L/h gas flow; 10% overlapping rate). Since this processing parameter setting was not one of the settings in the 16 original runs, a validation experiment was needed to confirm this processing parameters prediction.

3.4. Processing Parameters Optimization and Experimental Validation

The GRG prediction was used to estimate the outcome of the parameter setpoint (A₄B₂C₂D₁) prior to conducting the experiment. The GRG prediction was calculated by [26],

$${\mathrm{GRG}}_{\mathrm{prediction}}=\overline{{\mathrm{GRG}}_{\mathrm{total}}}+{\displaystyle \sum }_{j=1}^q\left(\overline{{\mathrm{GRG}}_j}-\overline{{\mathrm{GRG}}_{\mathrm{total}}}\right)$$

(7)

where ${\mathrm{GRG}}_{\mathrm{prediction}}$ is the predicted value of GRG from the selected set; $\overline{{\mathrm{GRG}}_{\mathrm{total}}}$ represents the total mean of the GRG; q is the number of processing parameters, which is four in this study; $\overline{{\mathrm{GRG}}_j}$ stands for the average GRG value at the selected level for the jth processing parameter.

The best results from the 16 orthogonal runs, the grey relational analysis (GRA) prediction, and the validation experiment are compared in

Table 10. Optimization and experimental validation result comparison.

Output	Best Parameter set from Orthogonal Design	GRA Prediction	Validation on GRA Prediction
Parameter Set	A3B1C4D2	A4B2C2D1	A4B2C2D1
Flatness Ratio	0.881	–	0.889
Cladding Efficiency	253.336	–	260.786
GRG	0.82423	0.87663	0.88510

. When the best results from orthogonal experimental design (A₃B₁C₄D₂) were compared with the optimal parameters setting derived from GRA (A₄B₂C₂D₁), the flatness ratio increased from 0.881 to 0.889 and the cladding efficiency increased from 253.336 to 260.786 mm³/s. Although the increase of the flatness ratio was only 0.91%, the increase of the cladding efficiency was 2.94%. These differences may not seem significant, but even a small improvement in processing parameters can have a large impact on the overall quality of the product and substantial financial gains. In addition, the optimal parameters setting derived from GRA increased the two responses simultaneously, indicating that the optimal parameters setting was better than the best run in the Taguchi orthogonal array.

Furthermore, the grey relational grade prediction derived from Equation (7) and the experimental validation differed by less than one percent (0.97%). It shows the high accuracy of multi-response optimization using grey relational analysis. The methods developed in this paper can also be used to evaluate uneven weighting distributions for the flatness ratio and cladding efficiency, for example, if flatness ratio was deemed to be a higher priority, the weighing factor in the GRA could be set to 75% for the flatness ration and only 25% for the cladding efficiency. In addition, this multi-response optimization method with GRA could be used to guide the design of a large-scale experiment. This is important because actual experiments can be expensive and time-consuming. It could be used to evaluate different responses such as wetting angle, penetration depth, and dilution instead of flatness ratio and cladding efficiency. Moreover, because GRA was designed to optimize multiple responses, it could also be used to optimize three or four of the above responses simultaneously.

Figure 5 below shows the clad morphology and cross-section comparison of multi-track laser clad derived by the best parameter set from the orthogonal design experiment and the optimal GRA parameter set, respectively. Figure 5d elucidates that incomplete fusion was significantly avoided in the optimal GRA parameter set, compared with the best parameter set found in the orthogonal design experiment (Figure 5b). The morphology of the clad made with the optimal parameters (A₄B₂C₂D₁) found using the GRA is shown in Figure 5c. No excessive powder adhesion was observed, and it had better cladding efficiency than the best run in the orthogonal design experiment. These results demonstrate the remarkable quality of the cladding layer when produced using the optimal processing parameters obtained from grey relational analysis.

4. Conclusions

This paper utilized an orthogonal experimental design to study the influence of laser power, scanning speed, gas flow, and overlapping rate on clad flatness ratio and cladding efficiency in multi-track laser cladding. Signal–to–noise ratio conversion and grey relational analysis was used to find the optimal processing parameters. Once the optimal processing parameters were determined, a validation experiment was conducted to verify the results. Based on this investigation, the following conclusions were made:

• Analysis of the flatness ratio as the single response showed that the overlapping rate and laser power affected the flatness ratio. The flatness ratio increased then decreased with increasing overlapping rate and laser power over the range of values studied.
• Analysis of the cladding efficiency as the single response revealed that the cladding efficiency was influenced by laser power, overlapping rate, and scanning speed. The cladding efficiency increased dramatically with the increased laser power. Increased scanning speed and overlapping rate caused a relatively small reduction in cladding efficiency.
• Grey relational analysis was effective in finding processing parameters that optimized the flatness ratio and cladding efficiency simultaneously. When these two objectives were weighted equally, the optimal processing parameters were determined to be 1.5 kW laser power, 6 mm/s scanning speed, 1000 L/h gas flow over, and 10% overlapping rate. This optimal parameter setting generated a better flatness ratio and cladding efficiency than best run in the orthogonal design experiment.
• The validation experiment using the optimal parameter setting found by grey relational analysis were within one percent (0.97% error) of the predicted value. This demonstrates the potential that GRA perform as a tool for identifying optimal laser cladding processing parameters. The methods presented in this paper can be used as a guide to developing optimal multi-track laser cladding processes for industrial applications.