Fracture Mechanics Solutions for Interfacial Cracks between Compressible Thin Layers and Substrates
Abstract
1. Introduction
2. Materials and Methods
2.1. Analytical Model: Materials with
2.2. Computational Model
2.3. Semi-Analytical Model—General Material Mismatch
3. Results
3.1. Finite Element Results for Materials with
3.2. Tabulated Coefficients for the Semi-Analytic Solutions in Equation (13)—Materials with
3.3. Explicit Solutions for Soft/Stiff Material Substrates and Nearly Homogeneous Systems—
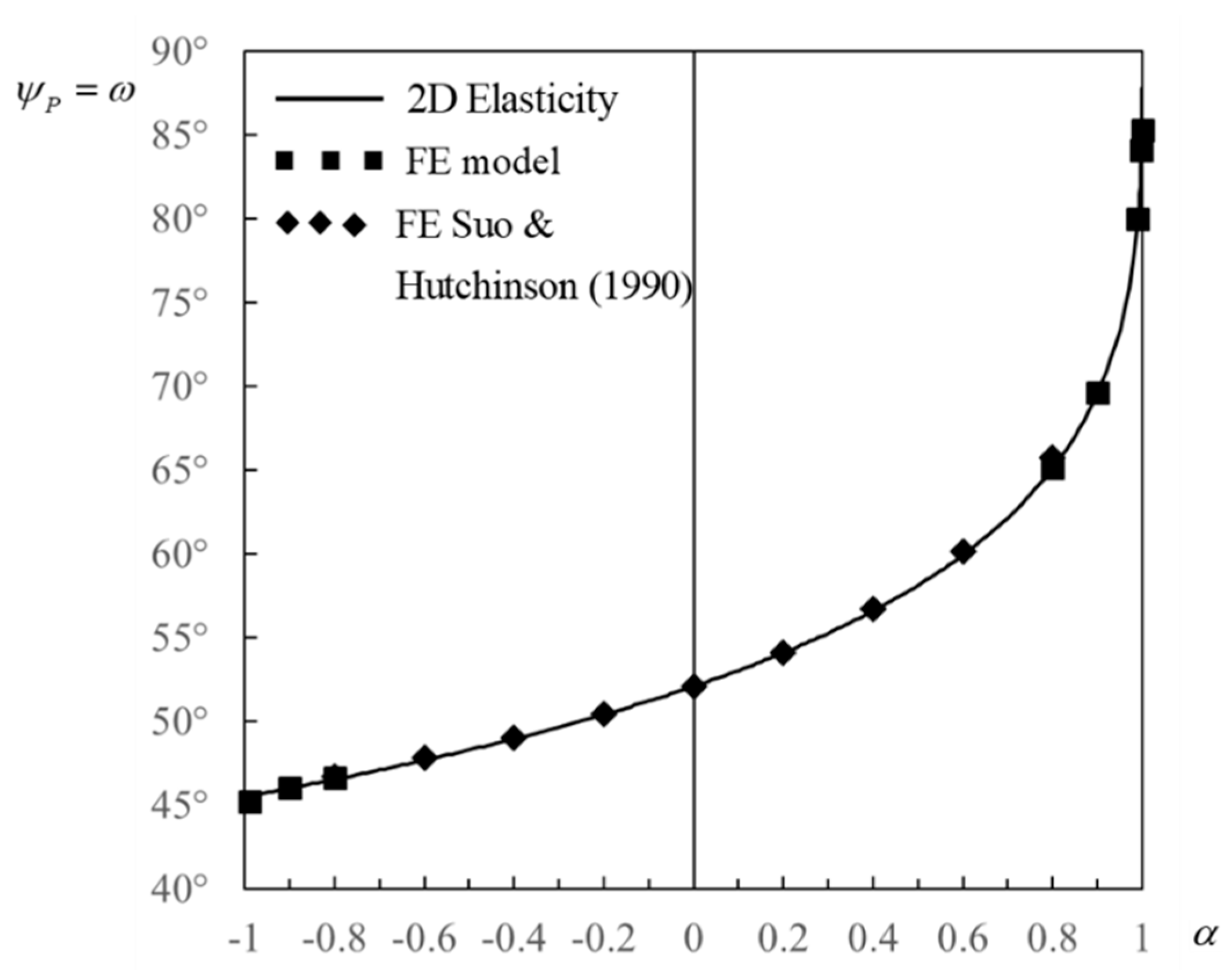
- Phase angle associated with the axial force, (in radians) [28]:The uncertainties are below for () in Equation (14), for in Equation (15), and for () in Equation (16). These uncertainties imply a relative percent error always lower than 0.4%. The equations can be used with confidence for all values of outside the interval where the exact analytical solutions in Equation (A1) or interpolation of the results in Table 3 and Figure 2 should be applied.
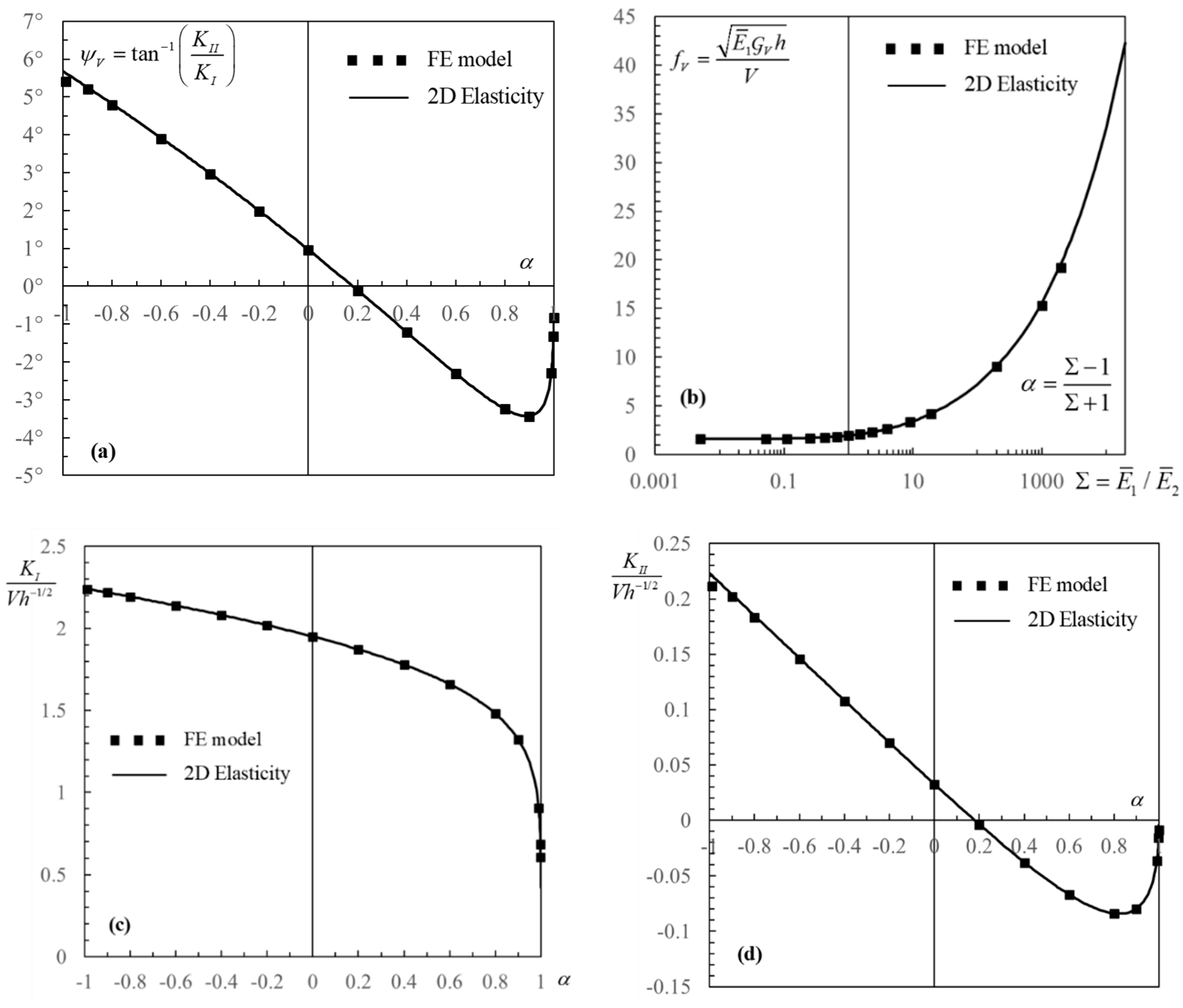
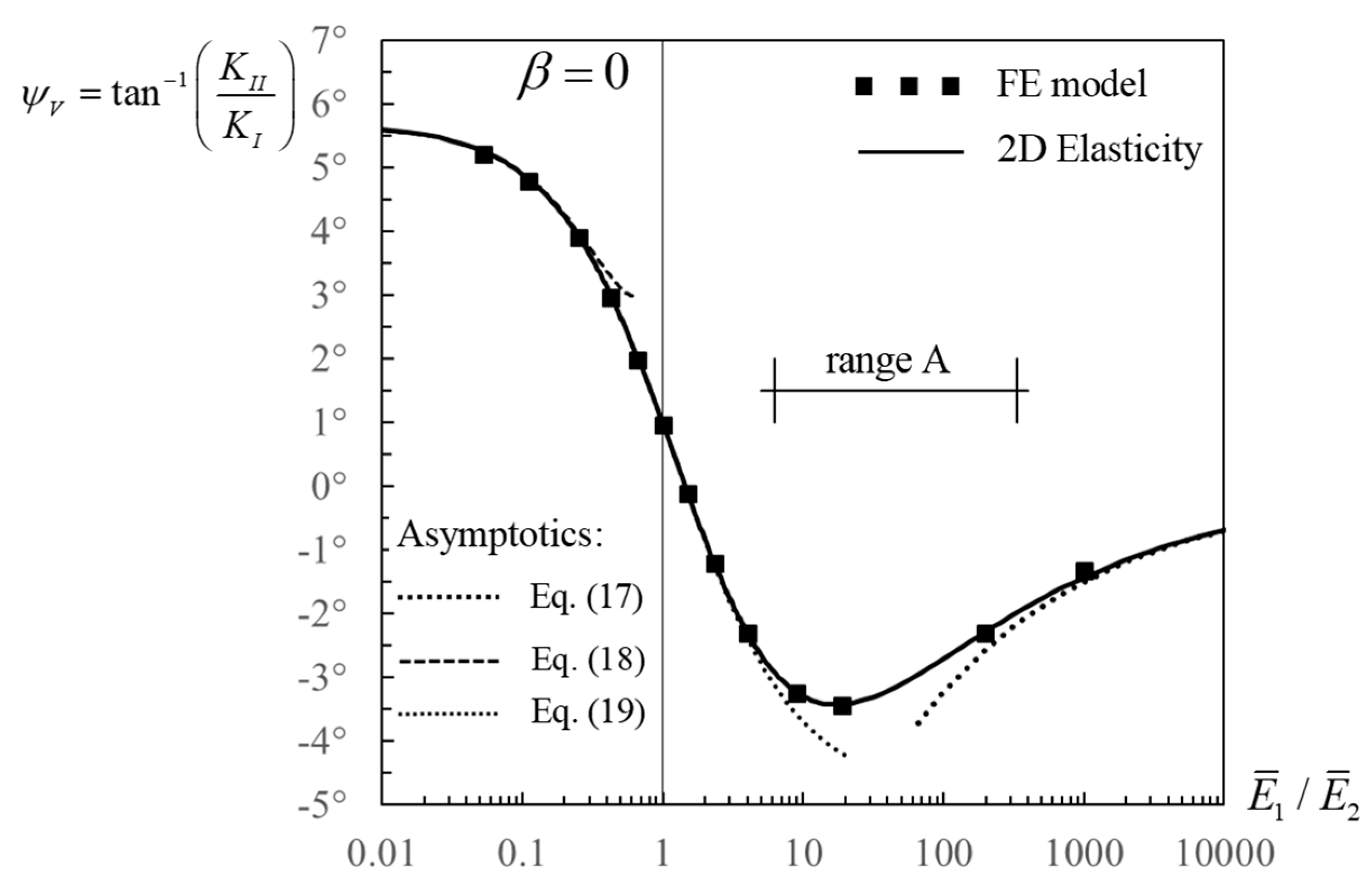
- Phase angle associated with shear, (in radians):The uncertainties are below for () in Equation (17), for in Equation (18), and for () in Equation (19). These uncertainties imply a relative percent error higher than that on , since is much smaller, which can be as high as 9% (Figure 2 and Figure 3). However, this occurs when is closed to zero, and the problem is essentially mode I, and the error is therefore irrelevant for engineering applications. The equations can be used with confidence for all values of outside the interval , where the exact analytical solutions in Equations (9) and (A2), or interpolation of the results in Table 4, should be applied.
- The dimensionless function which defines the energy release rate associated with shear, :
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
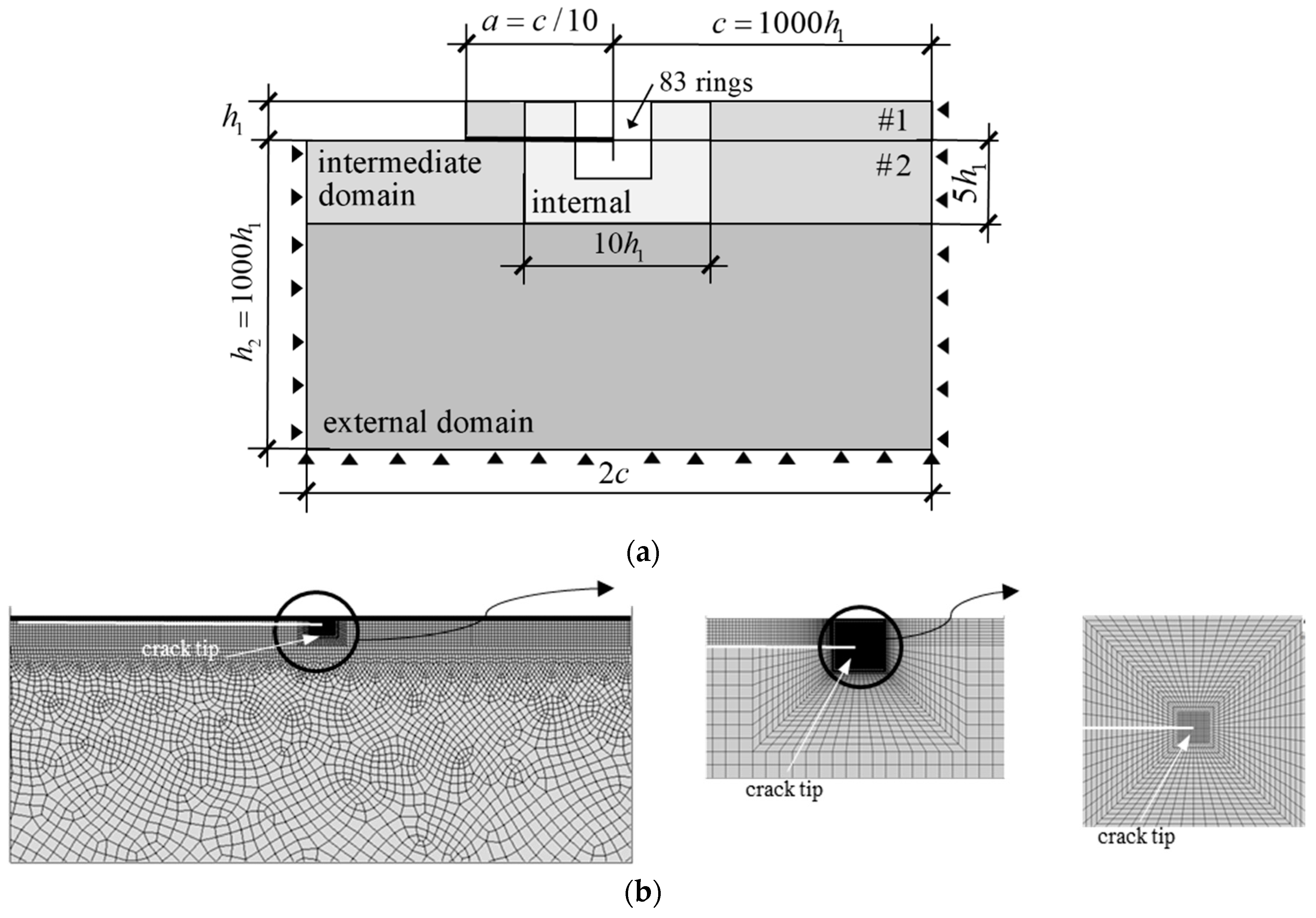
Appendix B. Finite Element Model
References
- Hutchinson, J.W.; Suo, Z. Mixed Mode Cracking in Layered Materials. Adv. Appl. Mech. 1991, 29, 63–191. [Google Scholar]
- Begley, M.R.; Hutchinson, J.W. The Mechanics and Reliability of Films, Multilayers and Coatings; Cambridge University Press: Cambridge, UK, 2017; ISBN 9781316443606. [Google Scholar]
- Freund, L.B.; Suresh, S. Thin Film Materials: Stress, Defect Formation, and Surface Evolution; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780511165658. [Google Scholar]
- Carlsson, L.A.; Kardomateas, G.A. Structural and Failure Mechanics of Sandwich Composites; Springer: Dordrecht, The Netherlands, 2011; ISBN 9781402032240. [Google Scholar]
- Rinker, M.; Krueger, R.; Ratcliffe, J. Analysis of an Aircraft Honeycomb Sandwich Panel with Circular Face Sheet/Core Disbond Subjected to Ground-Air Pressurization; NASA/CR-2013-217974; NASA Center for AeroSpace Information: Hanover, MD, USA, 2013. [Google Scholar]
- Chen, Z.M.; Krueger, R.; Rinker, M. Face Sheet/Core Disbond Growth in Honeycomb Sandwich Panels Subjected to Ground-Air-Ground Pressurization and In-Plane Loading. In Proceedings of the NAFEMS World Congress 2015, San Diego, CA, USA, 21–24 June 2015. NF1676L-19962. [Google Scholar]
- Farshidi, A.; Berggreen, C. Analysis of disbonded aircraft sandwich panels with unvented honeycomb cores. Int. J. Rev. 2018. under review. [Google Scholar]
- Østergaard, R.C.; Sørensen, B.F. Interface crack in sandwich specimen. Int. J. Fract. 2007, 143, 301–316. [Google Scholar] [CrossRef]
- Balaguru, P.N.; Nanni, A.; Giancaspro, J. FRP Composites for Reinforced and Prestressed Concrete Structures: A Guide to Fundamentals and Design for Repair and Retrofit; Taylor & Francis: Abingdon, UK, 2009; ISBN 9780415448543. [Google Scholar]
- Yu, H.; Bai, Y.-L.; Dai, J.-G.; Gao, W.-Y. Finite element modeling for debonding of FRP-to-concrete interfaces subjected to mixed-mode loading. Polymers 2017, 9, 438. [Google Scholar] [CrossRef]
- Vaunois, J.-R.; Poulain, M.; Kanouté, P.; Chaboche, J.-L. Development of bending tests for near shear mode interfacial toughness measurement of EB-PVD thermal barrier coatings. Eng. Fract. Mech. 2017, 171, 110–134. [Google Scholar] [CrossRef]
- Hutchinson, R.G.; Hutchinson, J.W. Lifetime assessment for thermal barrier coatings: Tests for measuring mixed mode delamination toughness. J. Am. Ceram. Soc. 2011, 94, S85–S98. [Google Scholar] [CrossRef]
- Evans, A.G.; Mumm, D.R.; Hutchinson, J.W.; Meier, G.H.; Pettit, F.S. Mechanisms controlling the durability of thermal barrier coatings. Prog. Mater. Sci. 2001, 46, 505–553. [Google Scholar] [CrossRef]
- Di Leo, C.V.; Luk-Cyr, J.; Liu, H.; Loeffel, K.; Al-Athel, K.; Anand, L. A new methodology for characterizing traction-separation relations for interfacial delamination of thermal barrier coatings. Acta Mater. 2014, 71, 306–318. [Google Scholar] [CrossRef]
- Cotterell, B.; Chen, Z. Buckling and cracking of thin films on compliant substrates under compression. Int. J. Fract. 2000, 104, 169–179. [Google Scholar] [CrossRef]
- Yu, H.-H.; Hutchinson, J.W. Influence of substrate compliance on buckling delamination of thin films. Int. J. Fract. 2002, 113, 39–55. [Google Scholar] [CrossRef]
- Volinsky, A.A.; Moody, N.R.; Gerberich, W.W. Interfacial toughness measurements for thin films on substrates. Acta Mater. 2002, 50, 441–466. [Google Scholar] [CrossRef]
- Pelassa, M.; Massabò, R. Explicit solutions for multi-layered wide plates and beams with perfect and imperfect bonding and delaminations under thermo-mechanical loading. Meccanica 2015, 50, 2497–2524. [Google Scholar] [CrossRef]
- Thouless, M.D.; Evans, A.G.; Ashby, M.F.; Hutchinson, J.W. The edge cracking and spalling of brittle plates. Acta Metall. 1987, 35, 1333–1341. [Google Scholar] [CrossRef]
- van den Bosch, M.J.; Schreurs, P.J.G.; Geers, M.G.D. Identification and characterization of delamination in polymer coated metal sheet. J. Mech. Phys. Solids 2008, 56, 3259–3276. [Google Scholar] [CrossRef]
- Jiménez-Pardo, I.; van der Ven, L.; van Benthem, R.; de With, G.; Esteves, A. Hydrophilic self-replenishing coatings with long-term water stability for anti-fouling applications. Coatings 2018, 8, 184. [Google Scholar] [CrossRef]
- Xiao, J.; Gong, C.; Qi, M.; Jiag, A.; Wang, Z.; Li, M.; Ma, J. Effect of TiN/C microstructure composite layer on the adhesion of FDLC film onto silicon substrate. Coatings 2018, 8, 18. [Google Scholar] [CrossRef]
- Rao, J.; Sharma, A.; Rose, T. Titanium aluminium nitride and titanium boride multilayer coatings designed to combat tool wear. Coatings 2018, 8, 12. [Google Scholar] [CrossRef]
- Collino, R.R.; Philips, N.R.; Rossol, M.N.; McMeeking, R.M.; Begley, M.R. Detachment of compliant films adhered to stiff substrates via van der Waals interactions: Role of frictional sliding during peeling. J. R. Soc. Interface 2014, 11. [Google Scholar] [CrossRef] [PubMed]
- Suo, Z.; Hutchinson, J.W. Interface crack between two elastic layers. Int. J. Fract. 1990, 43, 1–18. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.; Thouless, M.D. The effects of shear on delamination in layered materials. J. Mech. Phys. Solids 2004, 52, 193–214. [Google Scholar] [CrossRef]
- Andrews, M.G.; Massabò, R. The effects of shear and near tip deformations on energy release rate and mode mixity of edge-cracked orthotropic layers. Eng. Fract. Mech. 2007, 74, 2700–2720. [Google Scholar] [CrossRef]
- Ustinov, K. On separation of a layer from the half-plane: Elastic fixation conditions for a plate equivalent to the layer. Mech. Solids 2015, 50, 62–80. [Google Scholar] [CrossRef]
- Obreimoff, J.W. The splitting strength of mica. Proc. R. Soc. A Math. Phys. Eng. Sci. 1930. [Google Scholar] [CrossRef]
- Zlatin, A.N.; Khrapkov, A.A. Semi-infinite crack parallel to the boundary of an elastic half-plane. Sov. Phys. Dokl. 1986, 31, 1009. [Google Scholar]
- Jensen, H.M.; Thouless, M.D. Effects of residual stresses in the blister test. Int. J. Solids Struct. 1993, 30, 779–795. [Google Scholar] [CrossRef]
- Sundaram, S.; Lipkin, D.M.; Johnson, C.A.; Hutchinson, J.W. The influence of transient thermal gradients and substrate constraint on delamination of thermal barrier coatings. J. Appl. Mech. Trans. ASME 2013, 80. [Google Scholar] [CrossRef]
- Parry, G.; Colin, J.; Coupeau, C.; Foucher, F.; Cimetière, A.; Grilhé, J. Effect of substrate compliance on the global unilateral post-buckling of coatings: AFM observations and finite element calculations. Acta Mater. 2005, 53, 441–447. [Google Scholar] [CrossRef]
- Suga, T.; Elssner, G.; Schmauder, S. Composite parameters and mechanical compatibility of material joints. J. Compos. Mater. 1988, 22, 917–934. [Google Scholar] [CrossRef]
- Liechti, K.M.; Chai, Y.S. Asymmetric shielding in interfacial fracture under in-plane shear. J. Appl. Mech. Trans. ASME 1992, 59, 295–304. [Google Scholar] [CrossRef]
- Ratcliffe, J.G.; Reeder, J.R. Sizing a single cantilever beam specimen for characterizing facesheet-core debonding in sandwich structure. J. Compos. Mater. 2011, 45, 2669–2684. [Google Scholar] [CrossRef]
- Dundurs, J. Discussion: Edge-bonded dissimilar orthogonal elastic wedges under normal and shear loading. J. Appl. Mech. Trans. ASME 1969, 36, 650–651. [Google Scholar] [CrossRef]
- Williams, M.L. The stresses around a fault or crack in dissimilar media. Bull. Seismol. Soc. Am. 1959, 49, 199–204. [Google Scholar]
- Salganik, R.L. The brittle fracture of cemented bodies. J. Appl. Math. Mech. 1963, 27, 1468–1478. [Google Scholar] [CrossRef]
- Rice, J.R. Elastic fracture mechanics concepts for interfacial cracks. J. Appl. Mech. 1988, 55, 98–103. [Google Scholar] [CrossRef]
- Malyshev, B.M.; Salganik, R.L. The strength of adhesive joints using the theory of cracks. Int. J. Fract. Mech. 1965, 1, 114–128. [Google Scholar] [CrossRef]
- Banks-Sills, L. Interface fracture mechanics: Theory and experiment. Int. J. Fract. 2015, 191, 131–146. [Google Scholar] [CrossRef]
- Suo, Z. Delamination specimens for orthotropic materials. J. Appl. Mech. 1990, 57, 627–634. [Google Scholar] [CrossRef]
- Brandinelli, L.; Massabò, R. Mode II weight functions for isotropic and orthotropic double cantilever beams. Int. J. Fract. 2006, 139, 1–25. [Google Scholar] [CrossRef]
- Massabò, R.; Brandinelli, L.; Cox, B.N. Mode I weight functions for an orthotropic double cantilever beam. Int. J. Eng. Sci. 2003, 41, 1497–1518. [Google Scholar] [CrossRef]
- Gakhov, F.D. Boundary Value Problems; Pergamon Press: Oxford, UK, 1966; Volume 85. [Google Scholar]
- Rogosin, S.; Mishuris, G. Constructive methods for factorization of matrix-functions. IMA J. Appl. Math. 2016, 81, 365–391. [Google Scholar] [CrossRef]
- Berggreen, C.; Simonsen, B.C.; Borum, K.K. Experimental and numerical study of interface crack propagation in foam-cored sandwich beams. J. Compos. Mater. 2007, 41. [Google Scholar] [CrossRef]
- Beuth, J.L. Separation of crack extension modes in orthotropic delamination models. Int. J. Fract. 1996, 77, 305–321. [Google Scholar] [CrossRef]
- Rybicki, E.F.; Kanninen, M.F. A finite element calculation of stress intensity factors by a modified crack closure integral. Eng. Fract. Mech. 1977, 9, 931–938. [Google Scholar] [CrossRef]
- Berggreen, C. Damage Tolerance of Debonded Sandwich Structures. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2004. [Google Scholar]
- Salganik, R.L.; Ustinov, K.B. Deformation problem for an elastically fixed plate modeling a coating partially delaminated from the substrate (Plane Strain). Mech. Solids 2012, 47, 415–425. [Google Scholar] [CrossRef]
- Shield, T.W.; Kim, K.S. Beam theory models for thin film segments cohesively bonded to an elastic half space. Int. J. Solids Struct. 1992, 29, 1085–1103. [Google Scholar] [CrossRef]
- Ustinov, K.B. On influence of substrate compliance on delamination and buckling of coatings. Eng. Fail. Anal. 2015, 47, 338–344. [Google Scholar] [CrossRef]
- Barbieri, L.; Massabò, R.; Berggreen, C. The effects of shear and near tip deformations on interface fracture of symmetric sandwich beams. Eng. Fract. Mech. 2018, 201, 298–321. [Google Scholar] [CrossRef]
- Thouless, M.D. Shear forces, root rotations, phase angles and delamination of layered materials. Eng. Fract. Mech. 2018, 191, 153–167. [Google Scholar] [CrossRef]
- Andrews, M.G.; Massabò, R. Delamination in flat sheet geometries with material imperfections and thickness variations. Compos. Part B Eng. 2008, 39, 139–150. [Google Scholar] [CrossRef]
- Kardomateas, G.A.; Berggreen, C.; Carlsson, L.A. Energy-release rate and mode mixity of face/core debonds in sandwich beams. AIAA J. 2013, 51, 885–892. [Google Scholar] [CrossRef]
- Yu, H.-H.; He, M.Y.; Hutchinson, J.W. Edge effects in thin film delamination. Acta Mater. 2001, 49, 93–107. [Google Scholar] [CrossRef]
- Suo, Z.; Bao, G.; Fan, B.; Wang, T.C. Orthotropy rescaling and implications for fracture in composites. Int. J. Solids Struct. 1991, 28, 235–248. [Google Scholar] [CrossRef]
- Ustinov, K. On semi-infinite interface crack in bi-material elastic layer. Eur. J. Mech. A Solids 2019, 75, 56–69. [Google Scholar] [CrossRef]
- Massabó, R. (University of Genoa, Genova, Italy); Barbieri, L. (University of Genoa, Genova, Italy); Berggreen, C. (Technical University of Denmark, Lyngby, Denmark). The influence of shear on an interface crack between two elastic layers: Large mismatch of the elastic constants. Personal communication, 2019. [Google Scholar]

| Dundurs’ Parameters | ||
|---|---|---|
| Glass-epoxy/polymer foam | 0.99 | 0.28 |
| Glass/epoxy | 0.94 | 0.19 |
| Al/PMMA. | 0.91 | 0.23 |
| ITO/PET. | 0.97 | 0.2 |
| Ni/Polycarbonate | 0.975 | 0.2 |
| Al/Alfoam. | 0.82 | 0.23 |
| Y2O3-ZrO2/β-(Ni,Pt)Al. | 0.63 | 0.31 |
| Au/PDMS | ≈1 | ≈0 |
| SiO2/Epoxy | 0.89 | 0.21 |
| SiC/SiO2 | 0.72 | 0.38 |
| −1 | −0.999 | −0.99 | −0.9 | −0.8 | −0.6 | −0.4 | −0.2 | 0 | |
| 0.794183 | 0.794268 | 0.795042 | 0.802955 | 0.812157 | 0.832039 | 0.854295 | 0.879592 | 0.908934 | |
| 0.416984 | 0.417119 | 0.418335 | 0.430885 | 0.445719 | 0.478693 | 0.517208 | 0.563241 | 0.619981 | |
| 0.2 | 0.4 | 0.6 | 0.8 | 0.9 | 0.99 | 0.998 | 0.999 | 1 | |
| 0.943943 | 0.987518 | 1.045755 | 1.136137 | 1.214548 | 1.395760 | 1.466932 | 1.48809 | π/2 | |
| 0.693045 | 0.793630 | 0.949054 | 1.258612 | 1.637033 | 3.676521 | 6.33202 | 7.98856 | – |
| β = −0.4 | β = −0.3 | β = −0.2 | β = −0.1 | β = 0 | β = 0.1 | β = 0.2 | β = 0.3 | β = 0.4 | |
|---|---|---|---|---|---|---|---|---|---|
| α = −0.99 | 64.0° | 59.0° | 54.3° | 49.8° | 45.2° (45.553°) | ||||
| α = −0.9 | 64.7° | 59.8° | 55.2° | 50.6° | 46° (46.006°) | ||||
| α = −0.8 | 64.4° | 60.2° | 55.5° | 51.0° | 46.7° (46.533°) | ||||
| α = 0.8 | 65.7° (65.096°) | 62.0° | 57.0° | 54.9° | 50.3° | ||||
| α = 0.9 | 69.6° (69.588°) | 66.1° | 62.6° | 58.9° | 55.1° | ||||
| α = 0.99 | 80° (79.971°) | 77.7° | 75.4° | 73.1° | 70.7° | ||||
| α = 0.998 | 84.1° (84.049°) | 82.7° | 81.4° | 80.1° | 78.8° | ||||
| α = 0.999 | 85.3° (85.261°) | 84.3° | 83.4° | 82.6° | 81.8° | ||||
| β = −0.4 | β = −0.3 | β = −0.2 | β = −0.1 | β = 0 | β = 0.1 | β = 0.2 | β = 0.3 | β = 0.4 | |
|---|---|---|---|---|---|---|---|---|---|
| α = −0.99 | 18.4° | 15.0° | 11.7° | 8.6° | 5.4° (5.634°) | ||||
| α = −0.9 | 17.9° | 14.6° | 11.4° | 8.3° | 5.2° (5.252°) | ||||
| α = −0.8 | 17.2° | 14.0° | 10.9° | 7.8° | 4.8° (4.818°) | ||||
| α = −0.6 | 12.7° | 9.7° | 6.8° | 3.9° (3.920°) | |||||
| α = −0.4 | 11.3° | 8.5° | 5.7° | 3.0° (2.978°) | 0.2° | ||||
| α = −0.2 | 7.2° | 4.6° | 2.0° (1.993°) | −0.7° | |||||
| α = 0 | 5.8° | 3.4° | 1.0° (0.963°) | −1.5° | −4.1° | ||||
| α = 0.2 | 2.1° | −0.1° (−0.107°) | −2.4° | −4.8° | |||||
| α = 0.4 | 0.7° | −1.2° (−1.208°) | −3.2° | −5.4° | −7.6° | ||||
| α = 0.6 | −2.3° (−2.301°) | −4.0° | −5.8° | −7.7° | |||||
| α = 0.8 | −3.2° (−3.238°) | −4.4° | −5.7° | −7.0° | −8.5° | ||||
| α = 0.9 | −3.4° (−3.427°) | −4.1° | −4.8° | −5.7° | −6.6° | ||||
| α = 0.99 | −2.3° (−2.284°) | −1.5° | −0.7° | 0.2° | 1.0° | ||||
| α = 0.998 | −1.3° (−1.436°) | 0.4° | 2.2° | 4.1° | 6.0° | ||||
| β = −0.4 | β = −0.3 | β = −0.2 | β = −0.1 | β = 0 | β = 0.1 | β = 0.2 | β = 0.3 | β = 0.4 | |
|---|---|---|---|---|---|---|---|---|---|
| α = −0.99 | 1.444 | 1.489 | 1.528 | 1.563 | 1.593 (1.597) | ||||
| α = −0.9 | 1.465 | 1.510 | 1.550 | 1.585 | 1.616 (1.617) | ||||
| α = −0.8 | 1.487 | 1.533 | 1.573 | 1.609 | 1.640 (1.641) | ||||
| α = −0.6 | 1.586 | 1.627 | 1.663 | 1.695 (1.696) | |||||
| α = −0.4 | 1.650 | 1.692 | 1.729 | 1.762 (1.762) | 1.791 | ||||
| α = −0.2 | 1.773 | 1.811 | 1.844 (1.845) | 1.874 | |||||
| α = 0 | 1.878 | 1.916 | 1.951 (1.951) | 1.981 | 2.007 | ||||
| α = 0.2 | 2.058 | 2.093 (2.093) | 2.123 | 2.150 | |||||
| α = 0.4 | 2.261 | 2.297 (2.298) | 2.328 | 2.355 | 2.378 | ||||
| α = 0.6 | 2.627 (2.628) | 2.658 | 2.685 | 2.708 | |||||
| α = 0.8 | 3.316 (3.317) | 3.347 | 3.374 | 3.395 | 3.411 | ||||
| α = 0.9 | 4.190 (4.193) | 4.222 | 4.247 | 4.266 | 4.279 | ||||
| α = 0.99 | 9.1 (9.089) | 9.1 | 9.1 | 9.1 | 9.1 | ||||
| α = 0.998 | 15.3 (15.559) | 15.6 | 15.6 | 15.5 | 15.5 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massabò, R.; Ustinov, K.; Barbieri, L.; Berggreen, C. Fracture Mechanics Solutions for Interfacial Cracks between Compressible Thin Layers and Substrates. Coatings 2019, 9, 152. https://doi.org/10.3390/coatings9030152
Massabò R, Ustinov K, Barbieri L, Berggreen C. Fracture Mechanics Solutions for Interfacial Cracks between Compressible Thin Layers and Substrates. Coatings. 2019; 9(3):152. https://doi.org/10.3390/coatings9030152
Chicago/Turabian StyleMassabò, Roberta, Konstantin Ustinov, Luca Barbieri, and Christian Berggreen. 2019. "Fracture Mechanics Solutions for Interfacial Cracks between Compressible Thin Layers and Substrates" Coatings 9, no. 3: 152. https://doi.org/10.3390/coatings9030152
APA StyleMassabò, R., Ustinov, K., Barbieri, L., & Berggreen, C. (2019). Fracture Mechanics Solutions for Interfacial Cracks between Compressible Thin Layers and Substrates. Coatings, 9(3), 152. https://doi.org/10.3390/coatings9030152





