1. Introduction
Multi-coated thin-walled composite mechanical components, such as beams, plates, and shells, can be considered as an application of the Functionally Graded Material (FGM) technology, making it possible to obtain specific mechanical properties, such as high strength and stiffness, light inertia, and high damping. In most modern industrial applications, damping behaviour can be critical and may greatly affect design activities. In the aerospace field, high stiffness and high strength slender shell components, such as turbine blades, are required to show a limited free vibrational behaviour in standard operating conditions in order to increase the system life, to reduce the generated noise, and to maximize the machine efficiency. In this specific field, recent applications were explored, mainly based on experimental approaches. The influence of thin ceramic, polymeric, and metallic coatings, in some cases reinforced by carbon nanotubes, deposed on thin-walled components, on the damping behaviour of the obtained multi-layer composite systems was experimentally studied by some researchers [
1,
2,
3,
4,
5]. In all of these works, it was found that the deposition of thin coatings can improve the damping behaviour of the composite system. Moreover, it was experimentally found in [
6,
7,
8,
9,
10] that the dissipative actions in multi-layer architectures can be assumed as localized at the interfaces of the layers.
A global modelling approach of FGM composite components is given in [
11], in which an experimental identification procedure of the mechanical properties of nonstandard composite materials by means of frequency domain measurements is reported. However, the global constitutive model of a specific composite material experimentally obtained cannot be used to obtain the model related to a different composite material solution, so that virtual prototyping of new solutions is de facto not allowed in principle. On the other hand, several works on multi-layer composite structure modelling can be found in the literature, but no attempt was made to investigate the dissipative mechanism acting at the interface between any two layers. In [
12,
13,
14,
15,
16,
17], multi-layer beam models, assuming polynomial first and higher order longitudinal displacement component, were proposed and validated by numerical comparisons with exact analytical solutions. Nevertheless, dissipation effects were not taken into account. A dynamical model that was able to deal with the dissipative actions influencing the damping properties of the system response and with the specific multilayer coating architecture was not proposed, to the authors’ knowledge.
The damping behaviour of multi-layer composite beams is taken into account in this work and introduced in a beam model. The local dissipations, acting at the interface between any two layers of the composite beam, are investigated. The dissipation mechanism in a multi-layer structure is described by means of distributed viscous linear shear actions acting at the interface between two layers. The shear-strain local constitutive behaviour is described by defining continuous dissipation functions depending on the thickness and the viscosity at the interface. These parameters can be assumed to model the layer interface coupling actions, which mainly originated by chemical or mechanical coupling phenomena, and are associated with the different technologies employed to depose the layer coatings [
18].
Although distributed viscous modelling of the internal shear dissipative actions was already published in known scientific literature, it must be taken into account that such an assumption can lead to misleading results, since while polymer-based materials may follow this behaviour, most metal and ceramic materials do not exhibit internal dissipative actions depending on strain velocity. Moreover, since a proportional damping model follows from this assumption, the theoretical modal damping ratio of a homogeneous component made of a viscoelastic material following the Kelvin-Voigt model linearly increases with respect to frequency, and this result is not supported by experimental findings [
11,
19]. Since it can be experimentally found that the free vibration modal damping ratio
ξk tends to slowly vary with respect to the mode natural frequency
ωk and order
k for homogeneous, uniform beam specimens made of viscoelastic material, high order material viscoelastic constitutive relationships [
11] or fractional derivative order model-based viscoelastic relationships [
20,
21,
22,
23] were proposed in the past to overcome the limits of a simple Kelvin viscoelastic model.
In the approach proposed in this paper, viscous shear actions are mainly localized at the interface between any two different layers; they are defined by a C1 function only depending on two parameters, and they are not distributed on the whole layer domain, making it possible to properly model and experimentally validate the modal damping ratio with respect to the modal natural frequency value. Multi-layer prismatic beams with distributed visco-elastic constraints that are subjected to distributed, dynamic load are considered, and a discrete dynamical beam model is introduced. The contribution of aerodynamic drag dissipative actions can be taken into account by means of modelling viscous constraint actions distributed along the whole beam length.
Some examples, consisting of multi-layer composite beams composed by a thick metal-based substrate with high strength and stiffness, and thin coatings, are considered. By varying the coating parameters, such as the number, thickness, and material properties of the layers, the interlaminar dissipation layer thickness, and the viscosity, the effect on the system damping estimate in the frequency range under interest is analysed by means of numerical simulations from within the proposed model. The sensitivity of the layer parameters on the damping behaviour of the structure is outlined. Some effective multilayer configurations associated with a relevant increase of the damping ratio with respect to the single layer solution are illustrated, and a critical discussion follows.
2. Multi-Layer Beam Modelling
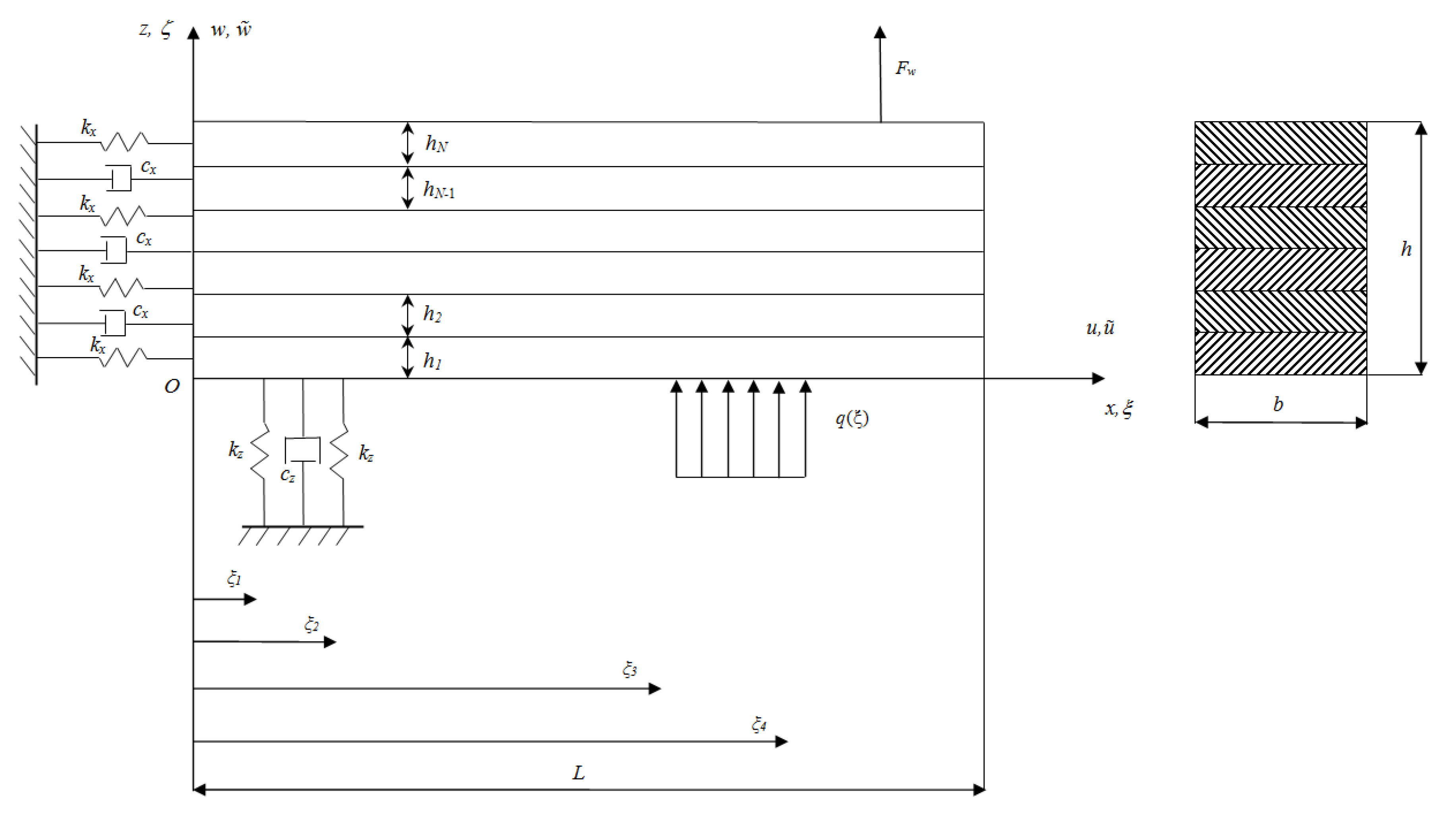
In
Figure 1, a scheme of a uniform, rectangular section, multi-layer composite beam is shown. Geometrical parameters are the beam length
L, depth
b, and thickness
h;
N is the number of layers,
hk is the
k-th layer thickness,
x is the longitudinal, and
z is the transversal coordinate;
zk is the
k-th layer coordinate with respect to the bottom surface,
ξ and
ζ are the dimensionless coordinates, defined by the relationships:
Kinematical parameters are the axial ũ and transversal beam displacement components, kx,z is the stiffness of the longitudinal and transversal distributed elastic constraints, cx,z is the viscosity of the longitudinal and transversal distributed viscous constraints, q and Fw are the distributed and concentrated external transversal loads, ρk, Ek, and Gk are the material, k-th layer, mass density, axial and shear moduli, and t is the time coordinate.
The displacement field is defined in dimensionless form, i.e.,
,
; by assuming
w to be independent of coordinate
ζ, this assumption is mainly valid in the low to medium excitation frequency range [
24] taken into account in this work, and by assuming that
u varies with respect to
ζ following a cubic polynomial function, whose linear parameter components vary in each layer in the form:
the following
unknown, (2·
N + 3) state variables result, where
.
Starting from Equation (2), in the hypothesis of small deformations, the axial normal strain for the
k-th layer,
k = 1…
N, is:
with:
and the transverse shear strain for the
k-th layer is:
The transverse normal stress is neglected (σzz = 0), assuming the plane stress hypothesis.
The constitutive equation for the
k-th layer of the beam, in the case of isotropic material, is:
From Equations (3), (5) and (6):
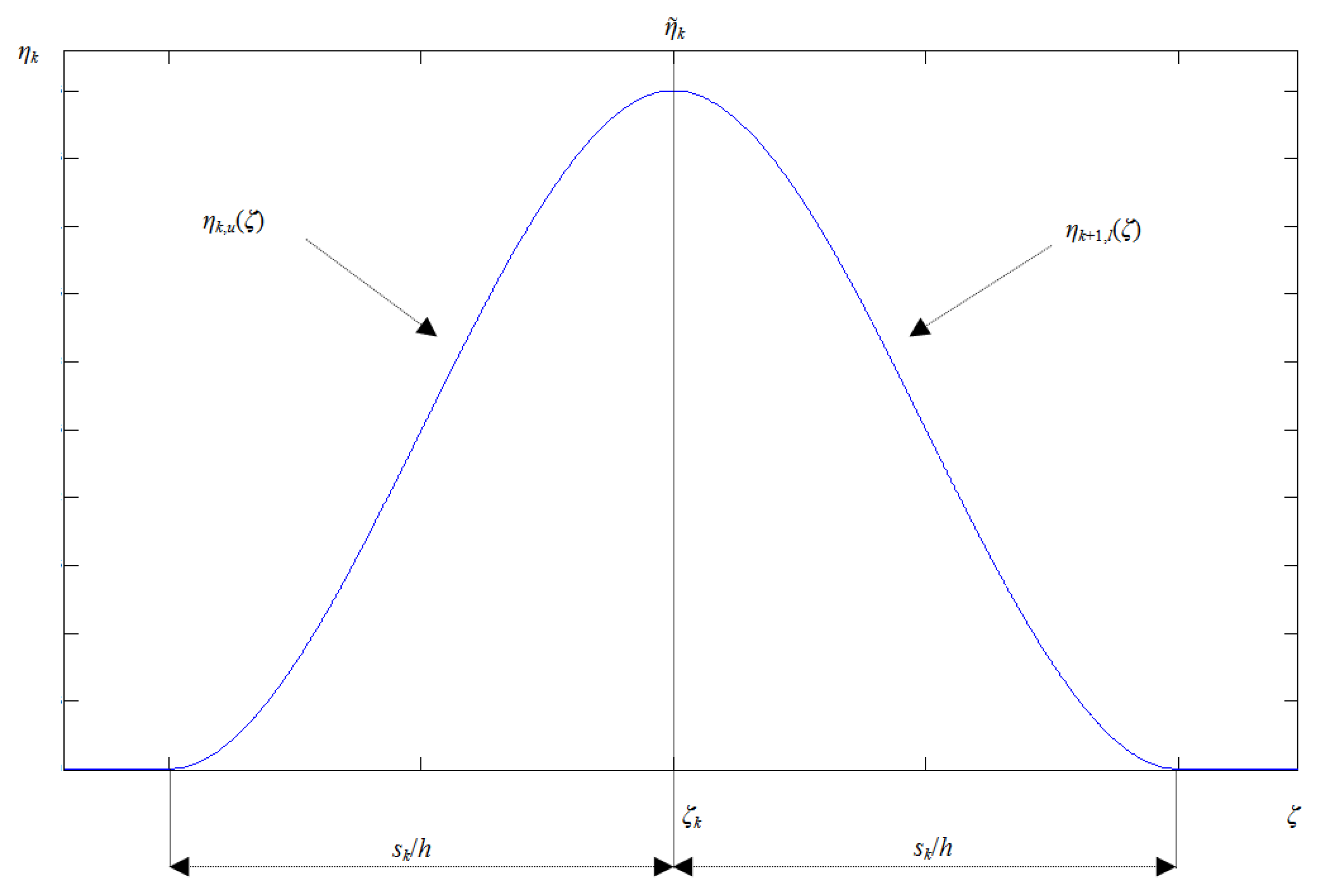
in which
, plotted in
Figure 2, is assumed to model the viscous behaviour localized at the
k-th interface:
in which
sk is the interlaminar dissipation layer thickness at the
k-th interface.
The upper
ηk,u(
ζ) and lower
ηk+1,l(
ζ) contributions are given by means of interpolating polynomials:
satisfying the following conditions,
k = 1,…,
N − 1:
By imposing the continuity of the shear stress at the bottom surface (
ζ =
ζ0 = 0):
giving:
Substituting Equation (12) into Equation (7):
By imposing the continuity of the shear stress at the top surface (
ζ =
ζN = 1):
giving:
By imposing the continuity of the shear stress at the
k-th interface,
, where
:
In the static case
, Equation (16) can be arranged as follows:
By equating the sum of Equation (17) left side to the sum of the right side:
and the following iterative formula is obtained as well:
It can be easily found that this result, collected in Equations (18) and (19), is also valid in the general dynamic case, since evaluating
, Equation (16) is still validated:
By imposing the continuity of the axial displacement at the
k-th interface:
the following iterative formula is obtained:
From Equations (12), (15), (18), (19) and (22):
The strain components are:
and the stress components are:
Three independent model state scalar variables result and are collected: φ(ξ,t) = [α w δ]T.
The axial displacement, and the normal and shear strains, can be expressed as a function of
φ(
ξ,
t):
The equations of motion can be obtained by minimizing the total potential Π, given by the sum of the elastic deformation energy
Uel, the interlaminar dissipation energy
Udiss, the inertial force work
Win, the external force work
Wext, and the potential associated with the visco-elastic constraints ΔΠ:
3. Numerical Discretization
Since the system Equation (27) is expressed by means of integro-differential equations that cannot be generally solved in closed form, then a model discretization is proposed, by means of the following hypothesis:
in which
Y(
t) is unknown and
N(
ξ) is assumed to be known, and expressed by means of harmonic shape functions in the variable
ξ having argument
:
Equation (34) makes it possible to model three plane beam rigid body motions, so that the total number
ntot of system discrete degrees of freedom is:
From Equations (26), (32), and (33):
The elastic deformation energy is:
The dissipation energy contribution is:
The contribution of the inertial forces is:
The contribution of the external forces is:
The potential energy associated with the visco-elastic constraints is:
From Equations (27) and (37)–(41):
4. Damping Behaviour Estimate
From Equation (42), the following eigenproblem can be obtained:
in which 2 ·
ntot complex conjugate
λr eigenvalues and
Δr eigenvectors are expected to result.
From
λr r-th eigenvalue, natural circular frequency
fr and damping ratio
ζr can be evaluated as follows:
The ζr values may be considered as a useful system damping estimate in a local frequency range close to r-th natural frequency fr.
A better damping estimate, depending on the input-output coordinate choice and on a frequency range [fmin,fmax], may be obtained from within the evaluation of the system frequency response function H(j∙2πf) related to input in xforce and output in xresponse.
From Equation (40), by defining a discrete vector of equivalent force
F related to unitary excitation
at
xforce coordinate:
Ys s-th response component of vector
Y may be easily evaluated by means of the modal approach [
25]:
and the complex frequency response function related to
xforce and
xresponse is:
Since the imaginary part of
H is mainly responsible of the damping behaviour, a normalized scalar function may be defined as:
in which
is defined for every frequency value and can be plotted in a limited frequency range related to a specific engineering field of interest.
It can be easily found that except at resonance, if dissipation actions are null, and d is also expected to increase the higher the dissipative contribution is.
5. Application Examples
The damping behaviour of some multi-layer composite beam architectures with distributed visco-elastic constraints is simulated by means of the previously introduced model. Since the effect of aerohydrodynamic damping is not negligible in free and forced vibrations of large specimens [
26], drag dissipative actions are linearized and modeled by means of viscous constraint actions that are distributed along the whole beam length.
Some multi-layer architectures are taken into account by considering different substrate and layer parameters (substrate geometry and material, N, hk, Gk, Ek, ρk, sk, k).
Tables 1 and 12 refer to two different beam substrate choices, while Tables 3, 4, 6, 7, 9, 10, 14, 15, 17, 18, 20, and 21 refer to different beam multi-layer solutions.
Damping estimates are evaluated with respect to the different configurations and results are shown in Tables 2, 5, 8, 11, 13, 16, 19, and 22, and Figures 3–10.
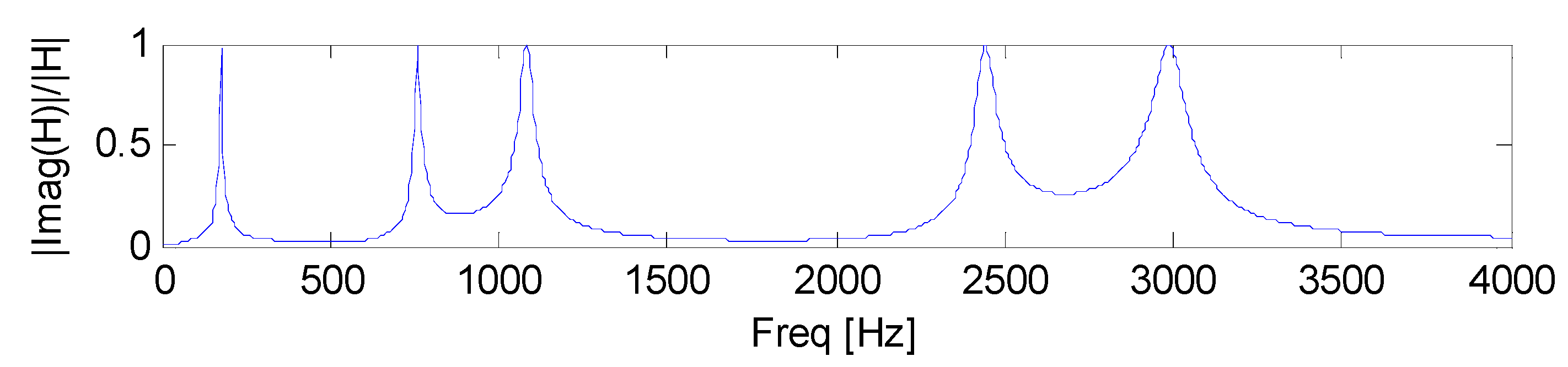
5.1. Configuration 1
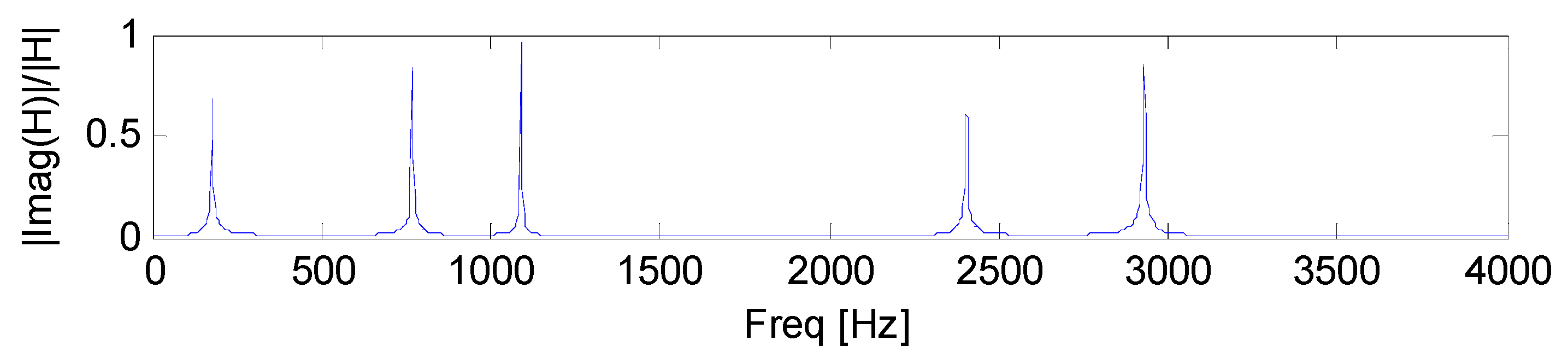
Configuration 1 is given by a homogeneous, uniform, rectangular section single-layer beam subjected to distributed visco-elastic constraints. The mechanical parameters are given in
Table 1, the first natural frequencies and damping ratios in
Table 2,
d parameter with
xforce =
xresponse =
L is plotted in
Figure 3.
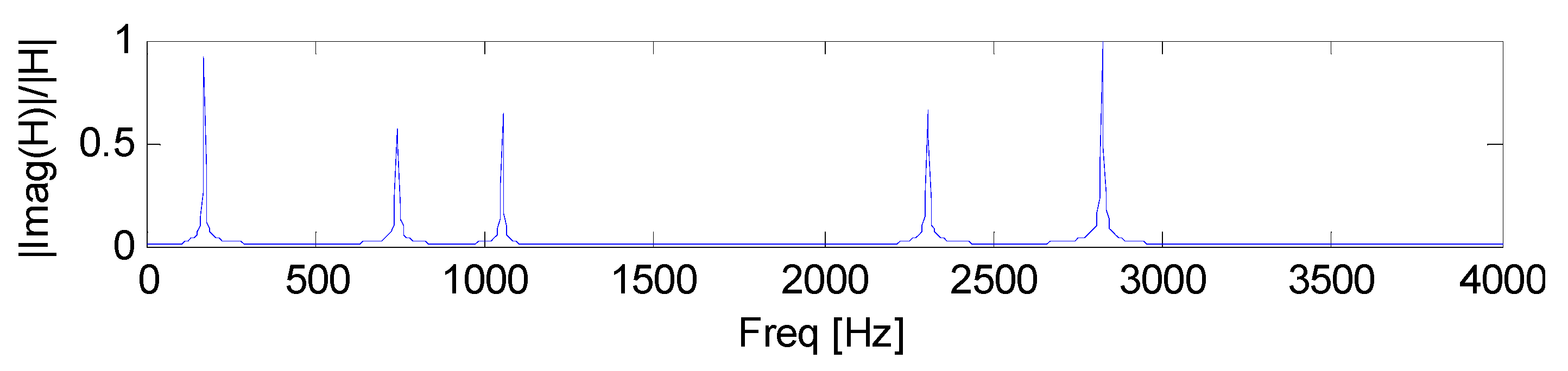
5.1.1. Configuration 1, Four Coating Layers, First Case
A multi-layer architecture is studied,
N = 5, i.e., substrate + 4 coating layers. Beam length
L, width
b, viscoelatic stiffness constraints are reported in
Table 1, and in
Table 3 and
Table 4 the remaining mechanical parameters are listed. In
Table 5, the first natural frequencies and damping ratios are given. The
d value with
xforce =
xresponse =
L is plotted in
Figure 4.
5.1.2. Configuration 1, Four Coating Layers, Second Case
A multi-layer architecture is analysed,
N = 5, i.e., substrate + 4 coating layers. Beam length
L, width
b, viscoelatic stiffness constraints are reported in
Table 1, and in
Table 6 and
Table 7 the remaining mechanical parameters are listed. The first natural frequencies and damping ratios are reported in
Table 8. The
d damping estimator with
xforce =
xresponse =
L is plotted in
Figure 5.
5.1.3. Configuration 1, Eight Coating Layers
A multi-layer architecture is considered,
N = 9, i.e., substrate + 8 coating layers. Beam length
L, width
b, and viscoelatic stiffness constraints are reported in
Table 1, and in
Table 9 and
Table 10 the remaining mechanical parameters are listed. In
Table 11, the first natural frequencies and damping ratios are reported. The
d estimate with
xforce =
xresponse =
L is plotted in
Figure 6.
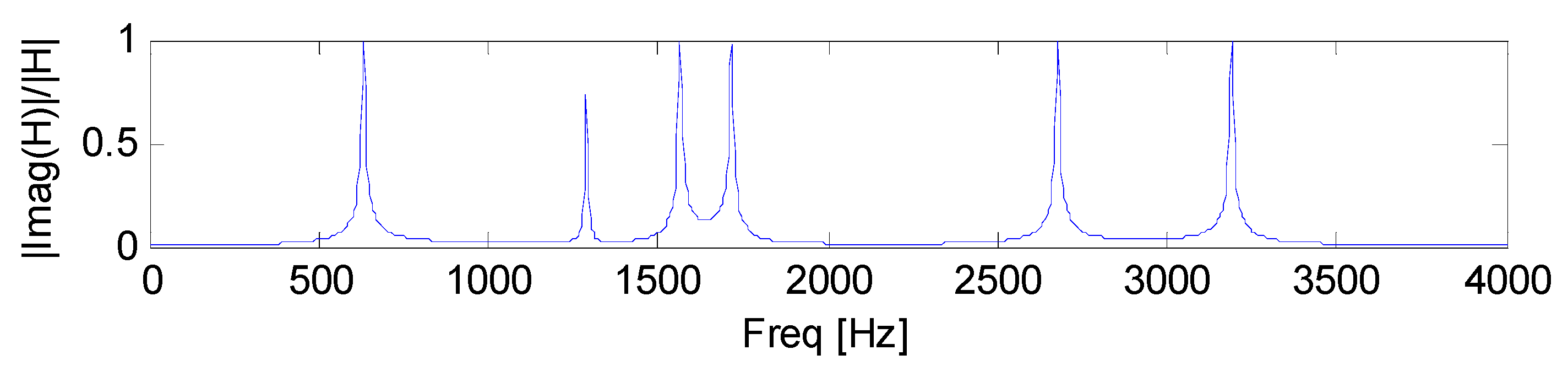
5.2. Configuration 2
Configuration 2 is associated with a homogeneous, uniform, rectangular section beam subjected to distributed visco-elastic constraints. The mechanical parameters are reported in
Table 12, natural frequencies and damping ratios in
Table 13;
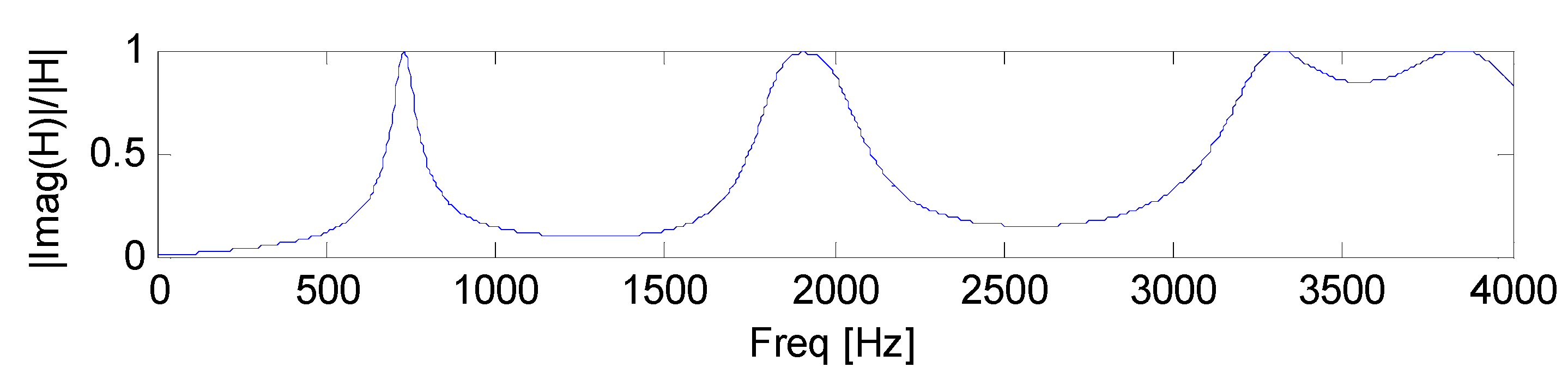
d damping estimator for
xforce =
xresponse = 0.3 m is plotted in
Figure 7.
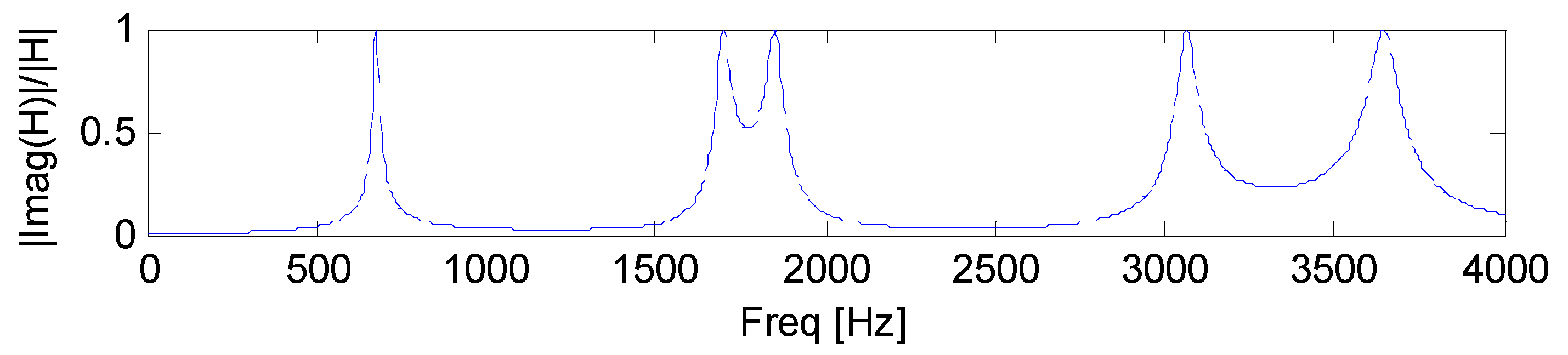
5.2.1. Configuration 2, Eight Coating Layers, First Case
A multi-layer architecture is considered,
N = 9, i.e., substrate + 8 coating layers. Beam length
L, width
b, and viscoelatic stiffness constraints are reported in
Table 12, and in
Table 14 and
Table 15 the remaining mechanical parameters are listed. In
Table 16, the first natural frequencies and damping ratios are given. The
d estimate,
xforce =
xresponse = 0.3 m, is plotted in
Figure 8.
5.2.2. Configuration 2, Eight Coating Layers, Second Case
Table 17 and
Table 18 report the mechanical parameters of a
N = 9, i.e., substrate + 8 coating layers, composite beam example, beam length
L, width
b, viscoelatic stiffness constraints being reported in
Table 12.
Table 19 lists the first natural frequencies and damping ratios.
d damping estimator,
xforce =
xresponse = 0.3 m, is plotted in
Figure 9.
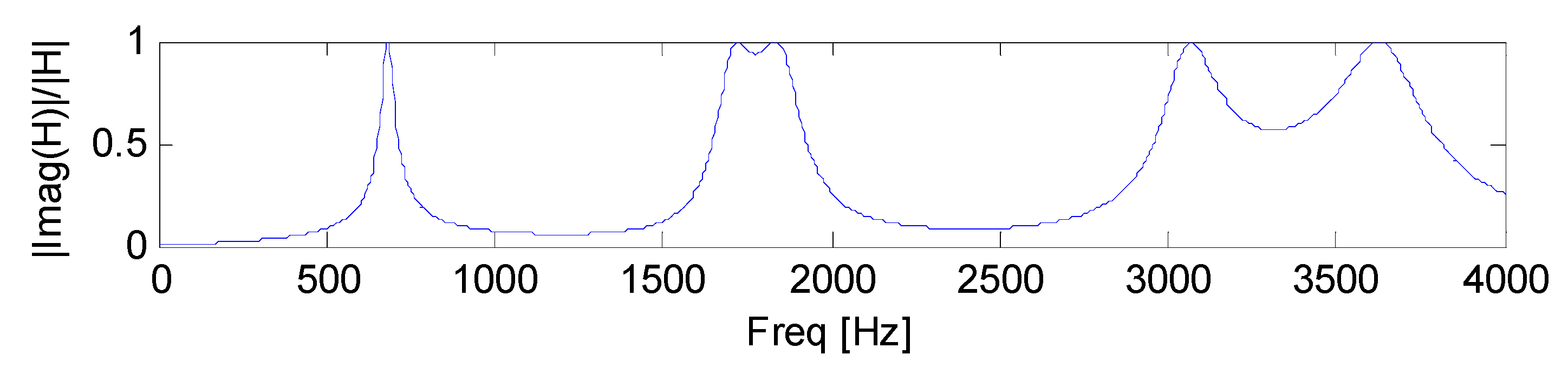
5.2.3. Configuration 2, Sixteen Coating Layers
Table 20 and
Table 21 report the mechanical parameters of a
N = 17, i.e., substrate + 16 coating layers, composite beam example, and
Table 22 the first natural frequencies and damping ratios. Beam length
L, width
b, viscoelatic stiffness constraints are reported in
Table 12. The
d estimate with
xforce =
xresponse = 0.3 m is plotted in
Figure 10.
6. Discussion
The application examples presented in the previous section showed that the damping behaviour of a uniform, rectangular section beam, vibrating in flexural-axial plane conditions, may be influenced by a multi-layer coating surface treatment that is local enough to not modify the structure main geometry, strength, and stiffness.
Example 5.1.1 consists of a four coating layer surface treatment, with 2 mm upper and lower total thickness. It is shown that the damping behaviour exhibits little change with respect to the one obtained from the uncoated specimen (Example 5.1), making this specific solution not effective. As a matter of fact, the constrained layer damping (CLD) contribution [
1,
9], exhibited when the material shear modulus of two close layer coatings is highly different, is low in this example case. To increase the CLD contribution, in Example 5.1.2 a different, stiffer material was adopted in layers
k = 2, 4, letting all of the remaining parameters unchanged with respect to previous Example 5.1.1. Both the first evaluated damping ratios and the damping estimator
d(j·
ω) showed an increase, making the solution related to Example 5.1.2 effective. Example 5.1.3 shows the effect of increasing the number of coating layers, by using the same layer material parameters and architecture, by doubling the number of upper and lower coating layers, and by maintaining the same coating resulting thickness. This solution is even more effective from the damping standpoint than the previously discussed architecture (Example 5.1.2).
Example 5.2 refers to a new beam substrate solution, 4 mm upper total thickness and 12 mm lower total thickness, differing from the one reported in example 5.1 by means of the material, geometry, and boundary conditions. Example 5.2.1 refers to an eight-coating layers unsymmetrical architecture, trying to maximize the CLD contribution: results are poor with respect to damping behaviour, and this solution has not been shown to be effective. Example 5.2.2 refers to the same architecture reported in Example 5.2.1, but a different, softer material was adopted in layers k = 2, 4, 6, and 8, leaving all of the remaining parameters unchanged with respect to previous Example 5.2.1. An effective architecture results from the damping behaviour standpoint, since the first damping ratios and the damping functional d(j·ω) increase, although the material shear modulus difference between any two alternating coating layers is lower than in Example 5.2.1. Example 5.2.3 shows that, by doubling the number of coating layers while maintaining the same architecture, same upper and lower coating thickness, the specimen damping behaviour is increased since, as expected, the contribution of the frictional actions at the layer interfaces is increased as well, so that confirming the same result obtained in Example 5.1.3.
The aim of the model-oriented approach presented in this paper is to obtain, at the design stage, an effective multi-layer coating architecture able to increase the damping behaviour of a mechanical component operating in flexural conditions without altering too much the starting geometrical, inertial, strength, and stiffness properties. Since finding a general, analytical model able to deal with any geometrical and mechanical configuration is a complex task, which requires a high number of degrees of freedom in order to be ineffective at the design stage for iteratively solving the problem at hand, a simple multi-layer beam model is proposed here.
Starting from a given uniform beam configuration, any boundary conditions and new, sub-optimal multi-layer solutions with respect to the damping behaviour may be iteratively and effectively investigated in order to be later applied to real mechanical components. Moreover, starting from the results of the present work, identification tools based on experimental dynamical measurements of simple specimens must also be developed to estimate most of the unknown layer parameters associated with the manufacturing technology, i.e., the ones related to inter-layer coupling, making it possible to extend the design optimization research stage. An experimental dynamical measurement test activity made on bi-layer specimens, mainly differing by means of the PVD, CVD, or hot melting deposition technology adopted, the substrate material, the surface finish texture, and the coating thickness, can be performed by properly designing an experimental test apparatus, following the indications reported in [
27,
28,
29,
30,
31]. Test data can be used to evaluate the unknown interlaminar dissipation viscosity and thickness values by means of a robust, numerical identification technique, since only two unknown parameters have to be identified, following the approach developed by our research group in [
11]. The multi-layer beam model may then be validated by means of new measurements related to multi-layer beam specimens and by adopting the interlaminar dissipation parameters experimentally identied in the bi-layer configuration.
Interlaminar local dissipative actions were modelled by means of a symmetrical, C1 formulation reported in Equation (8), which only depended on two parameters: namely, sk and . Since the formulation η(ζ) is polynomial, the evaluation of the integral in Equation (38) along ζ variable is de facto performed in closed form, because the integrand function Bk∙η(ζ) that appears in Equation (38) is still a polynomial function, thus making this evaluation easy and effective from a computational standpoint. It should be outlined that a non-symmetrical η(ζ) formulation could be easily taken into account by assuming a different upper and lower interlaminar dissipation thickness, but that an ill-defined numerical problem is expected to result when dealing with the experimental identification of the interlaminar dissipation parameters, since the number of optimization variables increases and multiple equivalent minima are also expected to result.
Results obtained by means of the multilayer beam model, consisting of the number of coating layers to be applied, coating thickness, deposition technology, and coating materials, are expected to be also effective with respect to the application to thin-walled mechanical components such as turbine blades, engine rods, and mechanism shafts among all.
7. Conclusions
Experimental works recently made by one of these authors and by other researchers outlined that coating layer surface treatments may increase the damping behaviour of thin-walled mechanical components vibrating in flexural conditions. Nevertheless, it was also experimentally found that most of these coating surface treatments gave a negligible or null effect with respect to the vibrational damped response in testing or operating conditions.
In order to investigate how different solutions in a free and forced flexural vibration response perform, a simple model, based on a multi-layer, zig-zag, beam assumption, which also locally models the dissipative actions at the interface between the layers, is proposed, and some virtual prototyping application examples are reported.
Numerical examples show that the beam damping behaviour can be increased by both maximizing the CLD behaviour, i.e., the relative difference of the material coating stiffness at any interface and by properly choosing the local interface dissipation parameters. A negligible effect on the damping behaviour is expected to result even if a high value of the viscous dissipation parameters at any interface between the layers is chosen, but coating material stiffness does not vary to a great extent. While the CLD behaviour is already known in principle from previous works, it appears from the reported numerical simulations that the system damping behaviour does not always generally increase by making the difference of the shear modulus of two contiguous coating layers as large as possible, but that an optimal material coating choice has to be found, so that justifying the adoption of this specific model approach. The contribution of the interaction of the layer material stiffness and the interface dissipative actions on the component damping is generally unknown at the design stage, but it can be found by means of the proposed modeling tool.
New multi-layer coating architectures may be investigated in principle by applying this modelling tool, and optimal solutions may then be applied on thin-walled mechanical components at the design stage, to reduce unwanted vibrational behaviour in high speed operating conditions.
Future research will be dedicated towards the experimental identification of the interface dissipative action parameters related to any layer deposition technology under study by testing and modelling simple dual layer beam specimen. Numerical identification techniques, based on the approach reported in [
11], are currently under development by these authors. The implementation of some techniques for automatic, optimal generation of a multi-layer coating solution will also be considered and developed in future work.