Frost Resistance and Life Prediction of Waste Polypropylene Fibre-Reinforced Recycled Aggregate Concrete
Abstract
1. Introduction
2. Experimental Materials and Methods
2.1. Raw Materials
2.2. Mix Proportion Design
2.3. Specimen Preparation
2.4. Testing Methods
2.4.1. Freeze–Thaw Cycle Test
2.4.2. Mass Loss Rate Test
2.4.3. RDEM Test
2.4.4. Compressive Strength Test
2.4.5. Scanning Electron Microscopy (SEM) Test
3. Results and Analysis
3.1. Evolution of Apparent Damage
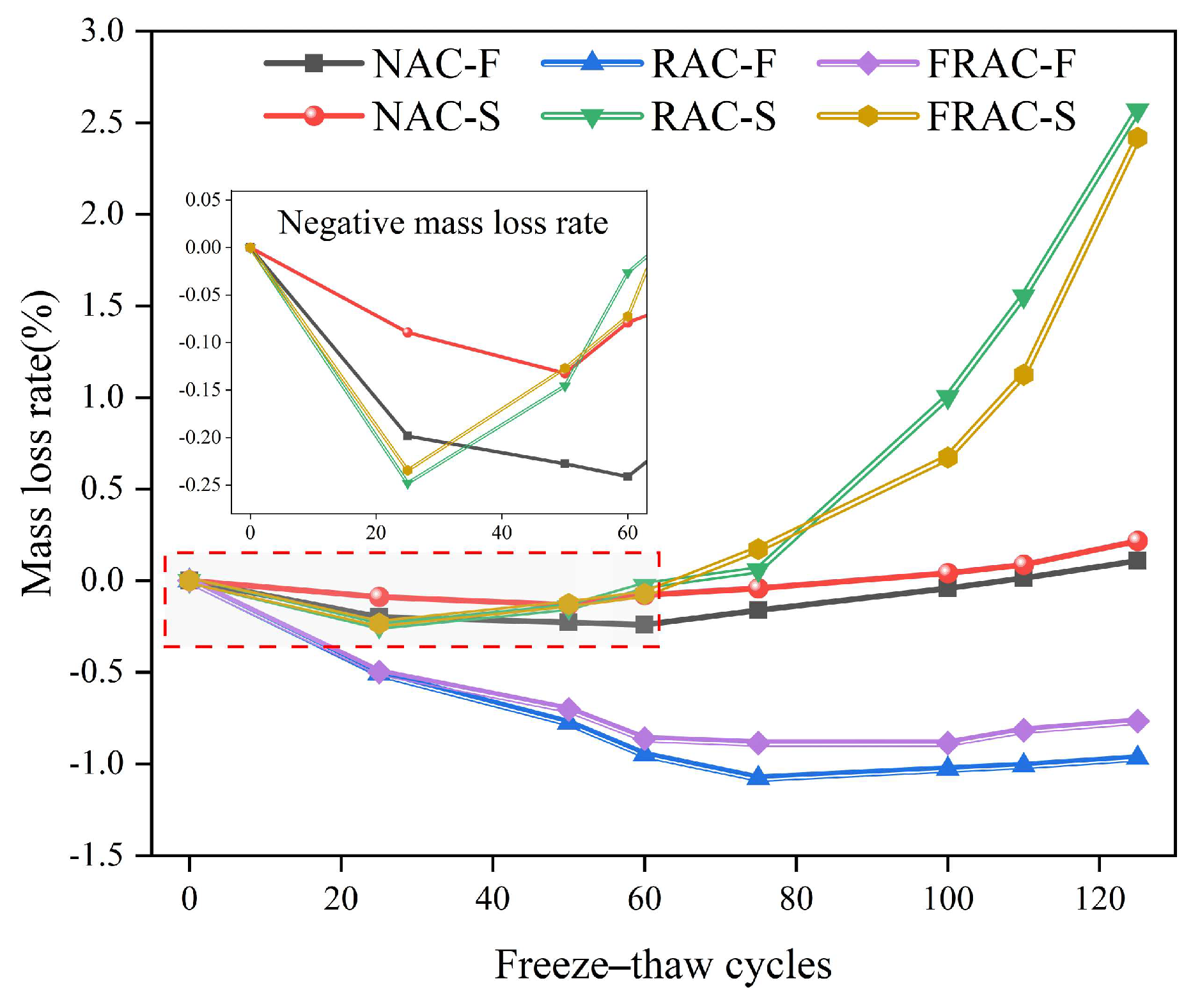
3.2. Mass Loss Rate
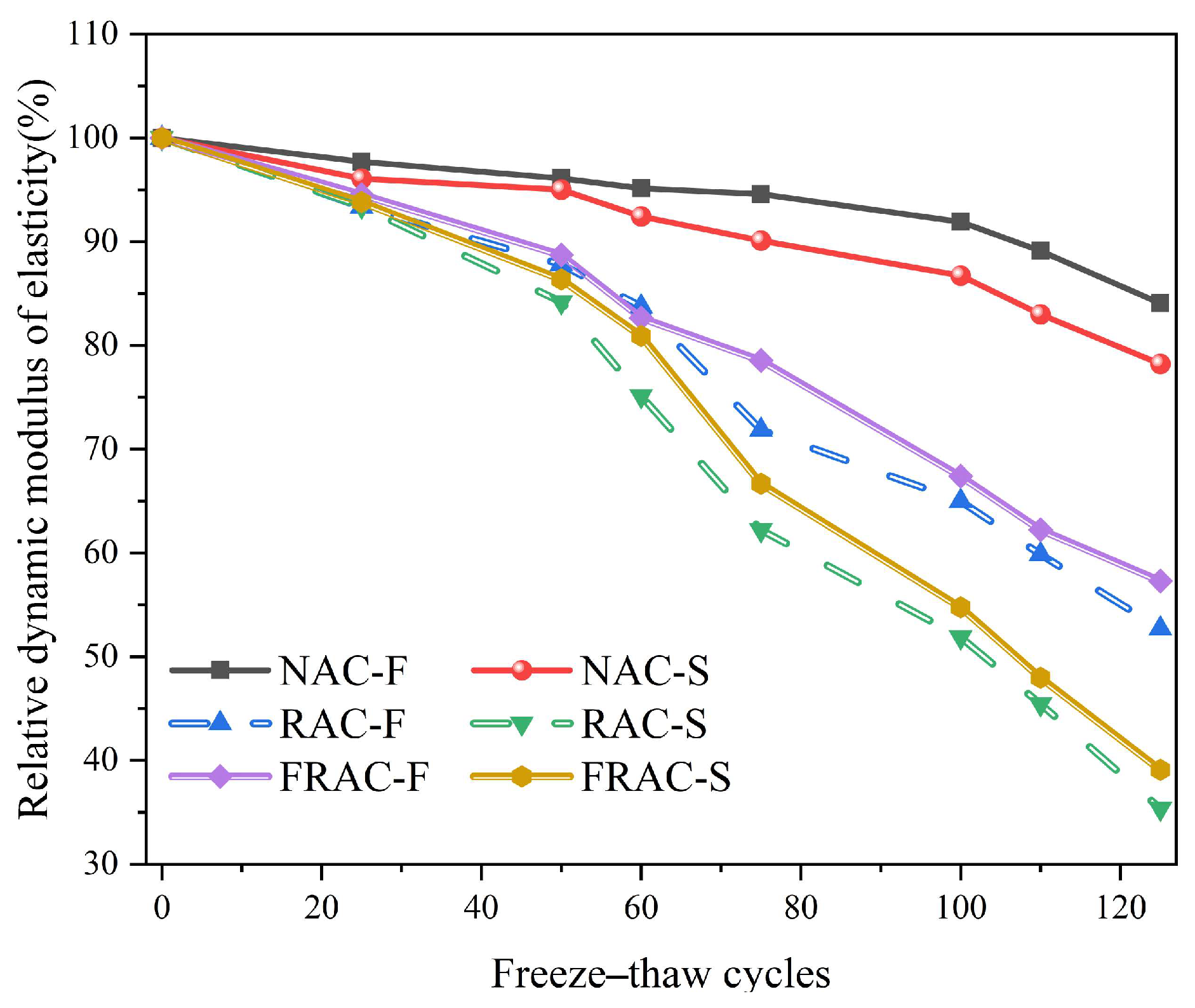
3.3. RDEM Attenuation
3.4. Compressive Strength
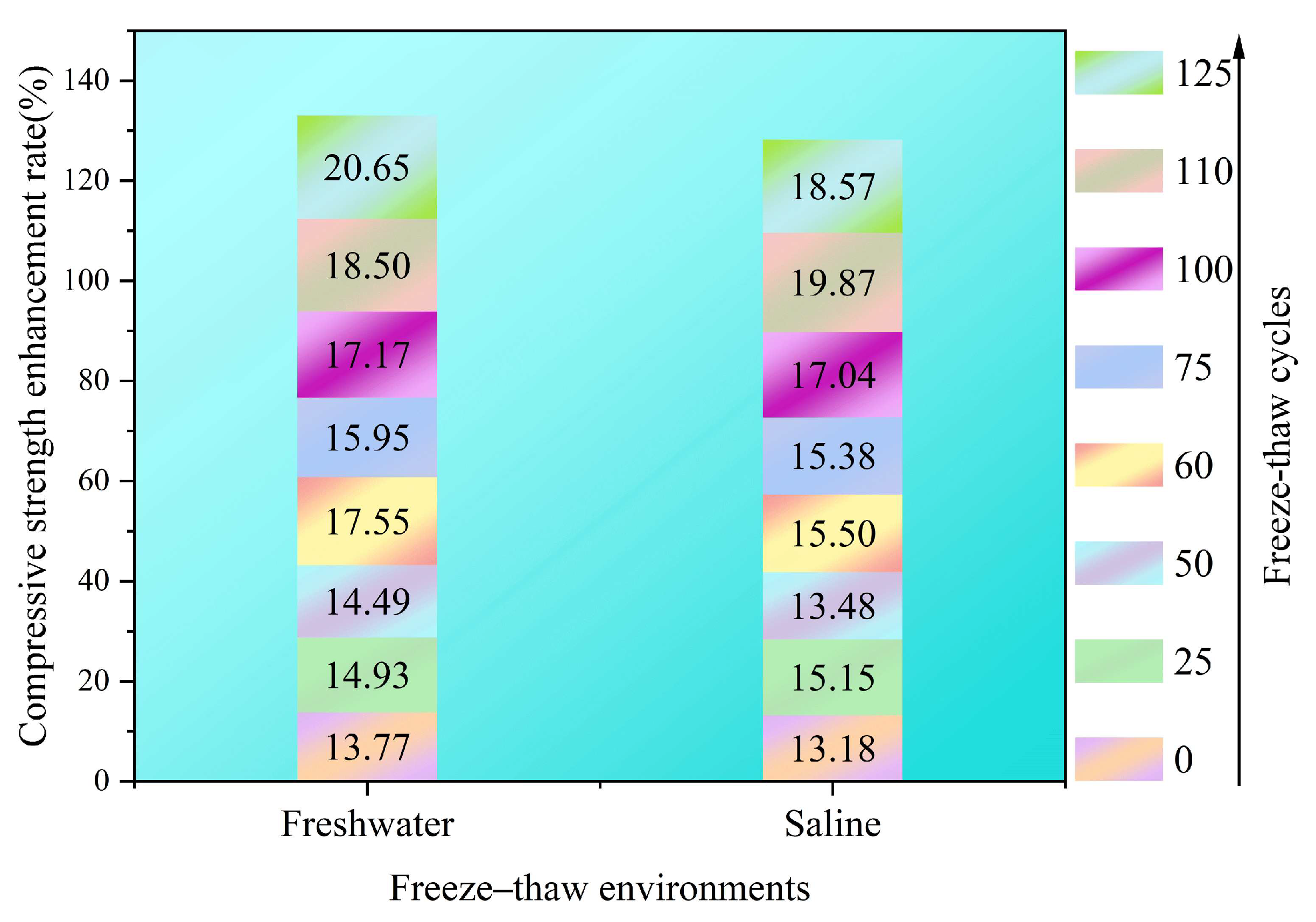
3.4.1. Compressive Strength Loss Rate
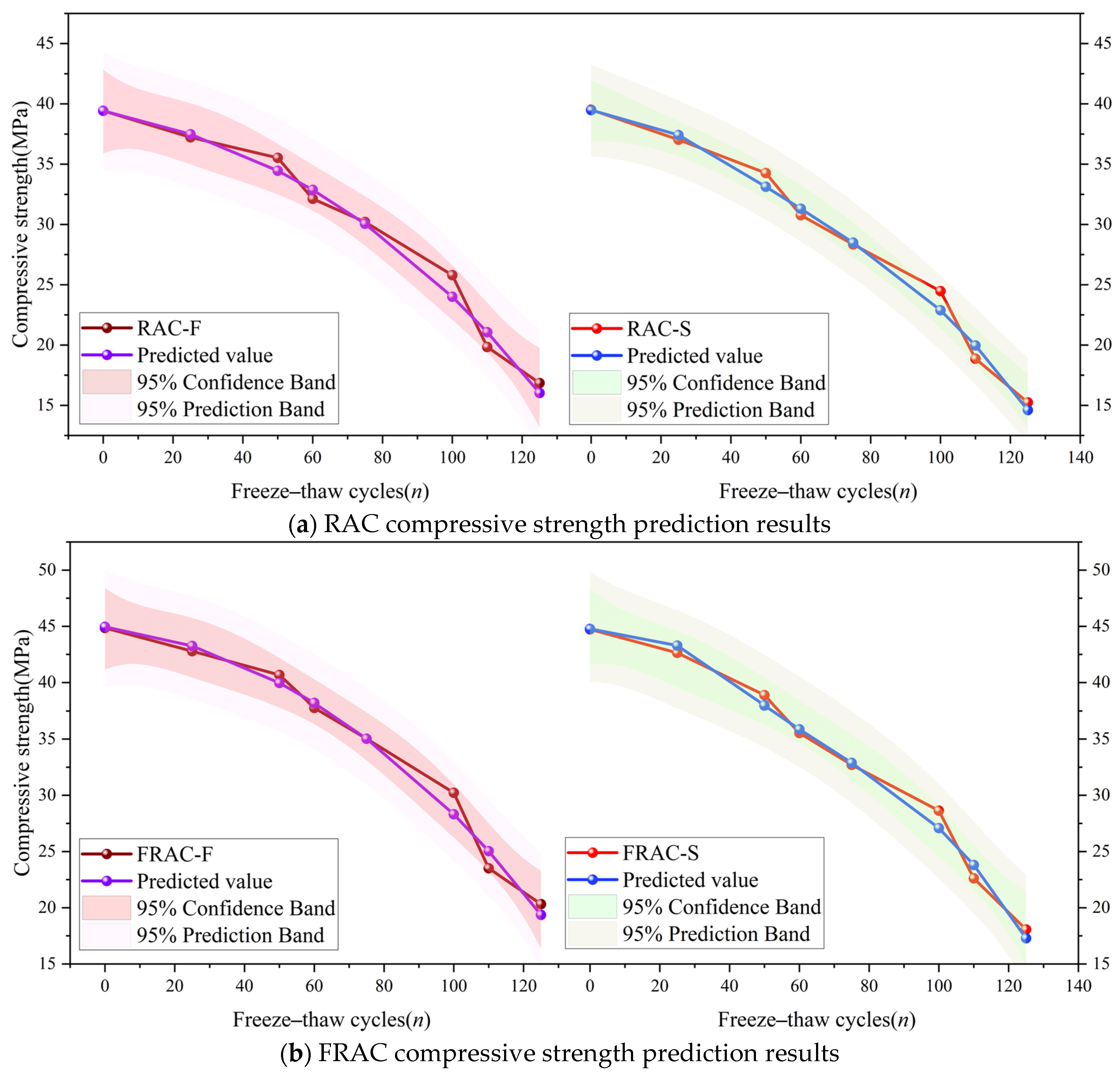
3.4.2. Compressive Strength Prediction Model
3.5. Systematic Quantitative Comparison of Frost Resistance
3.6. Dual-Damage Parameter Life Prediction
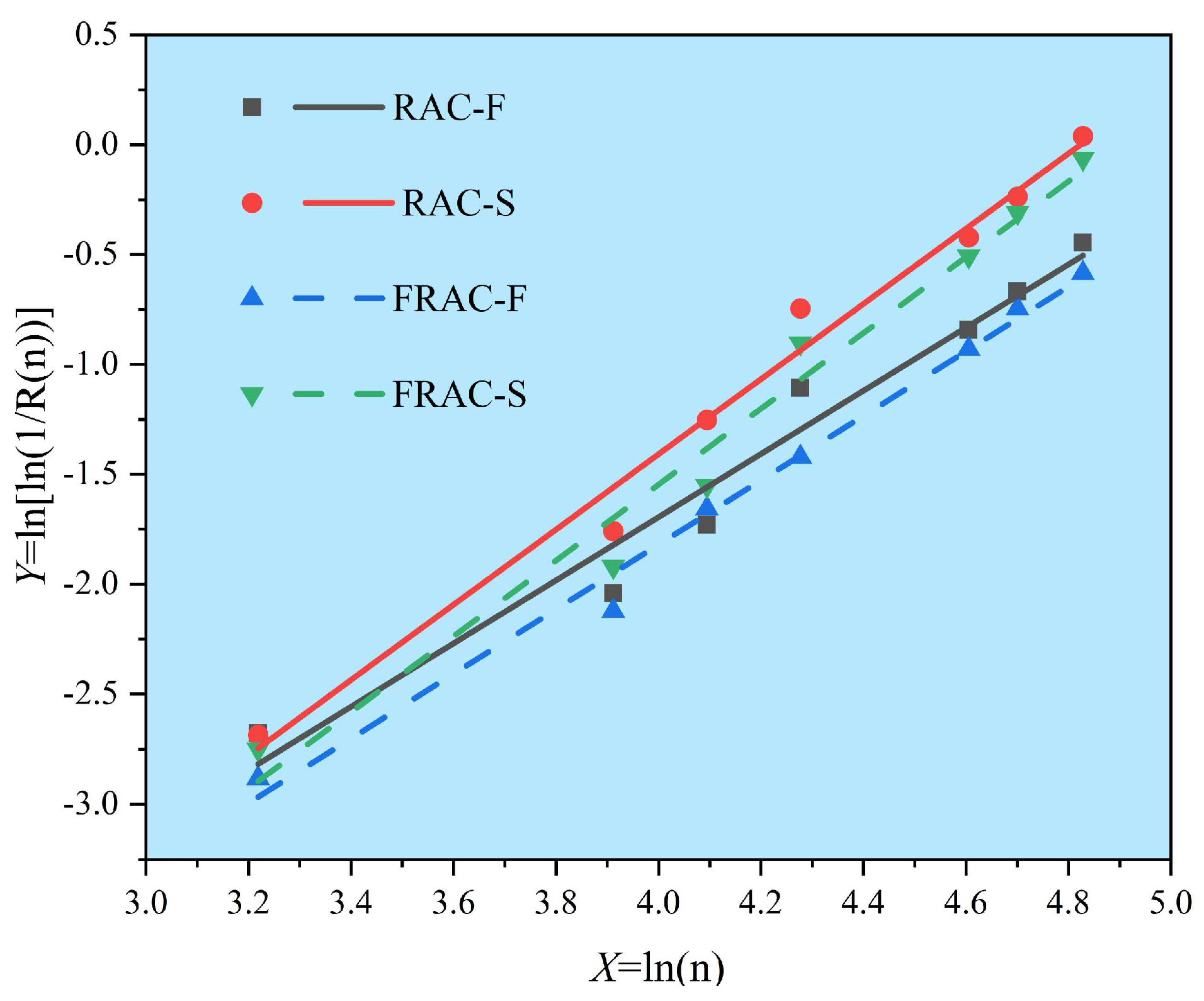
3.6.1. Life Prediction Based on RDEM Threshold
3.6.2. Life Prediction Based on Compressive Strength Loss Rate Threshold
3.6.3. Sensitivity Analysis and Engineering Failure Thresholds
3.7. Microstructure Analysis
3.8. Mechanism Analysis
4. Conclusions
- (1)
- With increasing freeze–thaw cycles, the mass loss rate of concrete first decreased and then increased, while the compressive strength and RDEM continuously decreased. Freeze–thaw in salt solution exacerbated the structural damage of RAC, and the frost resistance of RAC was significantly lower than that of NAC.
- (2)
- WPF effectively enhanced the frost resistance of RAC. The improvement was more pronounced in freshwater. After 125 freeze–thaw cycles, the RDEM attenuation amplitude of FRAC decreased by 9.69% (freshwater) and 5.77% (salt solution) compared to RAC. The compressive strength increased by 20.65% and 18.57%, respectively. The negative mass growth rate in freshwater decreased by 20.62%, and the mass loss rate in salt solution decreased by 5.84%.
- (3)
- WPF optimized the pore structure of RAC and enhanced the density of the matrix by bridging microcracks and dividing connected pores, effectively inhibiting the penetration of water and salt, delaying the debonding failure and crack propagation of the ITZ, and thereby improving the frost resistance of RAC.
- (4)
- Life prediction demonstrated that WPF increased the service life of RAC. The RDEM-based model predicted longer lives (119/90 cycles for FRAC-F/FRAC-S) but corresponded to higher strength loss rates (34%–52%). Conversely, the strength-based model predicted shorter lives (89/84 cycles) but more stable residual strength (30%–31% loss rate). A comprehensive analysis using both models is recommended for accurate life assessment.
5. Limitations and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RCA | Recycled coarse aggregate |
| RAC | Recycled aggregate concrete |
| NCA | Natural coarse aggregate |
| NAC | Natural aggregate concrete |
| SEM | Scanning electron microscopy |
| WPF | Waste polypropylene fibre |
| FRAC | Waste polypropylene fibre-reinforced recycled aggregate concrete |
| RDEM | Relative dynamic elastic modulus |
| ITZ | Interface transition zone |
| CDW | Construction and demolition waste |
References
- Pandey, B.; Brelsford, C.; Seto, K.C. Rising infrastructure inequalities accompany urbanization and economic development. Nat. Commun. 2025, 16, 1193. [Google Scholar] [CrossRef]
- Bai, G.; Zhu, C.; Liu, C.; Liu, B. An evaluation of the recycled aggregate characteristics and the recycled aggregate concrete mechanical properties. Constr. Build. Mater. 2020, 240, 117978. [Google Scholar] [CrossRef]
- Wu, L.; Sun, Z.; Cao, Y. Modification of recycled aggregate and conservation and application of recycled aggregate concrete: A review. Constr. Build. Mater. 2024, 431, 136567. [Google Scholar] [CrossRef]
- Cho, N.; El Asmar, M.; Aldaaja, M. An analysis of the impact of the circular economy application on construction and demolition waste in the United States of America. Sustainability 2022, 14, 10034. [Google Scholar] [CrossRef]
- Liu, H.; Guo, D.; Xu, H. Pathway selection to achieving synergistic benefits of pollution and carbon reduction through solid waste resource utilization based on system dynamics. Environ. Impact Assess. Rev. 2025, 115, 108053. [Google Scholar] [CrossRef]
- Salgado, F.D.A.; Silva, F.D.A. Recycled aggregates from construction and demolition waste towards an application on structural concrete: A review. J. Build. Eng. 2022, 52, 104452. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, K.; Ding, T.; Zhang, Q.; Xiao, X. Fundamental issues towards unified design theory of recycled and natural aggregate concrete components. Engineering 2023, 29, 188–197. [Google Scholar] [CrossRef]
- Hao, L.; Liu, Y.; Wang, W.; Zhang, J.; Zhang, Y. Effect of salty freeze-thaw cycles on durability of thermal insulation concrete with recycled aggregates. Constr. Build. Mater. 2018, 189, 478–486. [Google Scholar] [CrossRef]
- Luan, H.; Wu, J.; Xu, C.; Hu, J.; Guo, S.; Wang, Y.; Geng, F.; Li, Z. Freeze-thaw deterioration development characterization and mechanism investigation of recycled coarse aggregate concrete under deicing salt exposure. Constr. Build. Mater. 2025, 489, 142232. [Google Scholar] [CrossRef]
- Huda, S.B.; Alam, M.S. Mechanical and freeze-thaw durability properties of recycled aggregate concrete made with recycled coarse aggregate. J. Mater. Civ. Eng. 2015, 27, 04015003. [Google Scholar] [CrossRef]
- Yuan, C.; Qu, S.; Bai, W.; Guan, J.; Xie, Y. Study on the mechanical properties and mesoscopic damage mechanism of recycled aggregate concrete under different dynamic strain rates after freeze-thaw cycles. Case Stud. Constr. Mater. 2025, 22, e04182. [Google Scholar] [CrossRef]
- Bogas, J.A.; Gomes, A. Non-steady-state accelerated chloride penetration resistance of structural lightweight aggregate concrete. Cem. Concr. Compos. 2015, 60, 111–122. [Google Scholar] [CrossRef]
- Hu, J.; Wu, J. Mechanical properties and uni-axial compression stress-strain relation of recycled coarse aggregate concrete subjected to salt-frost cycles. Constr. Build. Mater. 2019, 197, 652–666. [Google Scholar] [CrossRef]
- Su, T.; Wu, J.; Yang, G.; Zou, Z. Bond behavior between recycled coarse aggregate concrete and steel bar after salt-frost cycles. Constr. Build. Mater. 2019, 226, 673–685. [Google Scholar] [CrossRef]
- Su, T.; Wang, T.; Wang, C.; Yi, H. The influence of salt-frost cycles on the bond behavior distribution between rebar and recycled coarse aggregate concrete. J. Build. Eng. 2022, 45, 103568. [Google Scholar] [CrossRef]
- Thaulow, N.; Sahu, S. Mechanism of concrete deterioration due to salt crystallization. Mater. Charact. 2004, 53, 123–127. [Google Scholar] [CrossRef]
- Du, X.; Li, G.; Cao, A.; Wang, A.; Zhou, Y. Study of transport and binding behavior of chloride ions in concrete under single-sided salt-freezing cycle. Constr. Build. Mater. 2025, 471, 140749. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, K.; Yin, Z.; Zhou, J. Deterioration performance of recycled aggregate Pervious concrete under freezing-thawing cycle and chloride environment. Buildings 2023, 13, 645. [Google Scholar] [CrossRef]
- Chen, S.; Ren, J.; Li, Y.; Ren, X.; Song, Y.; Sun, J. Macroscopic and mesoscopic deterioration behaviors of concrete under the coupling effect of chlorine salt erosion and freezing-thawing cycle. Materials 2021, 14, 6471. [Google Scholar] [CrossRef]
- Zhu, H.; Li, X. Experiment on freezing and thawing durability characteristics of recycled aggregate concrete. Key Eng. Mater. 2009, 400–402, 447–452. [Google Scholar] [CrossRef]
- Richardson, A.; Coventry, K.; Bacon, J. Freeze/thaw durability of concrete with recycled demolition aggregate compared to virgin aggregate concrete. J. Clean. Prod. 2011, 19, 272–277. [Google Scholar] [CrossRef]
- Atasham ul haq, M.; Wang, P.; Wang, Y.; Cui, H.; Tahir, M.; Gong, F.; Li, W. Optimization and utilization of air-entrained recycled brick aggregate concrete under freeze-thaw environment. Case Stud. Constr. Mater. 2025, 23, e04941. [Google Scholar] [CrossRef]
- GivKashi, M.R.; Tohidloo, M. The effect of freeze-thaw cycles and sulfuric acid attack separately on the compressive strength and microstructure of 3D-printed air-entrained concrete. Constr. Build. Mater. 2024, 440, 137411. [Google Scholar] [CrossRef]
- Gao, D.; Zhang, L.; Zhao, J.; You, P. Durability of steel fibre-reinforced recycled coarse aggregate concrete. Constr. Build. Mater. 2020, 232, 117119. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, Y.; Wang, J.; Hu, S.; Jiao, M.; Ling, Y. Mechanical properties and durability of polypropylene and steel fiber-reinforced recycled aggregates concrete (FRRAC): A review. Sustainability 2020, 12, 9509. [Google Scholar] [CrossRef]
- Fan, X.; Wu, D.; Chen, H. Experimental research on the freeze-thaw resistance of basalt fiber reinforced concrete. Adv. Mater. Res. 2014, 919–921, 1912–1915. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, S.; Liu, R. Study on antifreeze properties and pore structure of basalt fiber reinforced concrete. J. Phys. Conf. Ser. 2020, 1605, 012151. [Google Scholar] [CrossRef]
- Moceikis, R.; Kičaitė, A.; Sahmenko, G.; Selsekienė, A. Durability characterisation of glass fibre reinforced concrete by resistance to freezing and thawing. J. Sustain. Archit. Civ. Eng. 2020, 26, 98–109. [Google Scholar] [CrossRef]
- Al-Lebban, M.F.; Khazaly, A.I.; Shabbar, R.; Jabal, Q.A.; Asadi, L.A.R.A.I. Effect of polypropylene fibers on some mechanical properties of concrete and durability against freezing and thawing cycles. Key Eng. Mater. 2021, 895, 130–138. [Google Scholar] [CrossRef]
- Wang, C.; Chen, F. Durability of polypropylene fiber concrete exposed to freeze-thaw cycles with deicing salts. In Proceedings of the 2019 International Conference on Electronical, Mechanical and Materials Engineering, Wuhan, China, 20–21 January 2019; pp. 203–206. [Google Scholar] [CrossRef]
- Richardson, A. Polypropylene fibres in concrete with regard to durability. Struct. Surv. 2003, 21, 87–94. [Google Scholar] [CrossRef]
- Idrees, M.; Saeed, F.; Farooq, Z.; Köksal, F.; Shi, J. Production of waste carpet fiber-reinforced concrete as sustainable material. J. Build. Eng. 2023, 77, 107499. [Google Scholar] [CrossRef]
- Cui, S.; Wang, T.; Zhang, Z.; Sun, X.; Li, J.; Li, B.; Zhang, W.; Su, T.; Cao, F. Frost resistance and life prediction of recycled brick aggregate concrete with waste polypropylene fiber. Rev. Adv. Mater. Sci. 2023, 62, 20230154. [Google Scholar] [CrossRef]
- Han, F.; Lang, C.; Qiu, Y. Cleaning behavior based on waste textile before resource conversion and its challenges in China–A comprehensive review. J. Clean. Prod. 2022, 370, 133509. [Google Scholar] [CrossRef]
- JGJ 522006; Standard for Quality and Test Methods of Ordinary Concrete Sand and Stone. China Architecture & Building Press: Beijing, China, 2006. (In Chinese)
- JGJ 632006; Standard for Water of Concrete. China Architecture & Building Press: Beijing, China, 2006. (In Chinese)
- Zhang, W.; Wang, T.; Cao, F.; Wang, C.; Mei, X.; Shao, J.; Su, T. Improvement effect assessment of waste fibre on the comprehensive performance of mixed recycled aggregate concrete. Constr. Build. Mater. 2025, 491, 142633. [Google Scholar] [CrossRef]
- GB/T 50082-2024; Standard for Test Methods of Long-Term Performance and Durability of Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2024. (In Chinese)
- JGJ 552011; Specification for Mix Proportion Design of Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2011. (In Chinese)
- Ferreira, L.; Brito, J.D.; Barra, M. Influence of the pre-saturation of recycled coarse concrete aggregates on concrete properties. Mag. Concr. Res. 2011, 63, 617–627. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, J.; Wu, D.; Kang, T.; Liu, A. Bond behavior of recycled fiber recycled concrete with reinforcement after freeze-thaw cycles. Crystals 2021, 11, 1506. [Google Scholar] [CrossRef]
- Zhou, J.; Kang, T.; Wang, F. Study on mesostructure of recycled concrete with waste fiber. Concrete 2019, 11, 78–82. [Google Scholar] [CrossRef]
- GB/T 50476-2019; Code for Durability Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2019. (In Chinese)
- Duan, M.; Qin, Y.; Li, Y.; Zhou, H. Durability and damage model of polyacrylonitrile fiber reinforced concrete under freeze-thaw and erosion. Constr. Build. Mater. 2023, 29, 132238. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Standard for Test Methods of Physical and Mechanical Properties of Concrete. China Architecture & Building Press: Beijing, China, 2019. (In Chinese)
- Wang, J.; Dai, Q.; Si, R.; Guo, S. Mechanical; durability, and microstructural properties of macro synthetic polypropylene (PP) fiber-reinforced rubber concrete. J. Clean. Prod. 2019, 234, 1351–1364. [Google Scholar] [CrossRef]
- Lu, J.; Liu, J.; Yang, H.; Wan, X.; Gao, J.; Zhang, J.; Li, P. Experimental investigation on the mechanical properties and pore structure deterioration of fiber-reinforced concrete in different freeze-thaw media. Constr. Build. Mater. 2022, 350, 128887. [Google Scholar] [CrossRef]
- Ren, J.; Lai, Y. Study on the durability and failure mechanism of concrete modified with nanoparticles and polypropylene fiber under freeze-thaw cycles and sulfate attack. Cold Reg. Sci. Technol. 2021, 188, 103301. [Google Scholar] [CrossRef]
- Zhang, W.; Pi, Y.; Kong, W.; Zhang, Y.; Wu, P.; Zeng, W.; Yang, F. Influence of damage degree on the degradation of concrete under freezing-thawing cycles. Constr. Build. Mater. 2020, 260, 119903. [Google Scholar] [CrossRef]
- Wu, C.; Jierula, A.; Fu, Z.; Chen, Y.; Kuang, Y.; Xia, J. Study on the mechanism of anti sulfate freeze-thaw, dry wet cycle of polypropylene fiber foam concrete. Constr. Build. Mater. 2025, 463, 140144. [Google Scholar] [CrossRef]
- Feng, Z.; Wu, J.; Hu, D.; Zhao, L. Uniaxial compressive behavior and unified damage constritutive model of various types of recycled coarse aggregate concrete under freeze-thaw action. Mater. Today Commun. 2024, 41, 110976. [Google Scholar] [CrossRef]
- Yang, W.; Tang, Z.; Wu, W.; Zhang, K.; Yuan, J.; Li, H.; Feng, Z. Effect of different fibers on impermeability of steam cured recycled concrete. Constr. Build. Mater. 2022, 328, 127063. [Google Scholar] [CrossRef]
- Li, S.; Yin, S.; Gao, Y. Analysis of interface properties between TRC and concrete under chloride attack based on fracture energy. Int. J. Concr. Struct. Mater. 2020, 14, 28. [Google Scholar] [CrossRef]
- Xiao, Q.; Wu, Z.; Qiu, J.; Dong, Z.; Shi, S. Capillary water absorption performance and damage constitutive model of recycled concrete under freeze-thaw action. Constr. Build. Mater. 2022, 353, 129120. [Google Scholar] [CrossRef]
- Valenza, J.J.; Scherer, G.W. A review of salt scaling: II. Mechanisms. Cem. Concr. Res. 2007, 37, 1022–1034. [Google Scholar] [CrossRef]
- Gong, S.; Bai, L.; Tan, Z.; Xu, L.; Bai, X.; Huang, Z. Mechanical properties of polypropylene fiber recycled brick aggregate concrete and its influencing factors by gray correlation analysis. Sustainability 2023, 15, 11135. [Google Scholar] [CrossRef]
- Xu, F.; Li, T.; Li, C.; Li, Z.; Wang, S.; Zhao, N. Compressive behavior, microstructural properties, and freeze-thaw behavior of tailing recycled aggregate concrete with waste polypropylene fiber addition. Materials 2021, 14, 6712. [Google Scholar] [CrossRef]
- Dong, W.; Ji, Y.; Zhou, M. Microstructure and service-life prediction models of aeolian sand concrete under freeze-thaw damage. Int. J. Pavement Res. Technol. 2024, 17, 908–917. [Google Scholar] [CrossRef]
- Wiyanto, H.; Makarim, C.A.; Gondokusumo, O.; Siregar, J.P.; Irawan, A.P.; Cionita, T.; Najid, N. Determining concrete structure condition rating based on concrete compressive strength. Buildings 2022, 12, 776. [Google Scholar] [CrossRef]
- Ma, S.; Wu, Y.; Bao, P. Study on damage mechanism and residual life of clay brick in central plains of China under freeze-thaw environment. Arab. J. Sci. Eng. 2022, 47, 13317–13331. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, N.; Xu, H.; Yang, Q. Evaluation of ZIF-67 particle size and dosage on cement paste strength, microstructural development and calcium hydroxide morphology. Powder Technol. 2025, 464, 121271. [Google Scholar] [CrossRef]
- Liu, H.; Liu, C.; Wu, J.; Gao, Y.; Shao, J.; Wang, C.; Su, T.; Cao, F.; Zhang, W.; Yang, Q.; et al. Preparation of high-belite calcium sulfoaluminate cement and calcium sulfoaluminate cement from industrial solid waste: A Review. Sustainability 2025, 17, 4269. [Google Scholar] [CrossRef]
- Yuan, Z.; Jia, Y. Mechanical properties and microstructure of glass fiber and polypropylene fiber reinforced concrete: An experimental study. Constr. Build. Mater. 2021, 266, 121048. [Google Scholar] [CrossRef]
- Tang, Z.; He, X.; Wei, B.; Wang, H.; Zhou, M.; Wu, C. Flexural capacity of concrete beams reinforced by different types of polypropylene fibers and FRP bars. J. Build. Eng. 2025, 106, 112650. [Google Scholar] [CrossRef]
- Wu, J.; Liu, K.; Wang, S.; Quan, X.; Tian, P.; Tian, Z.; Ying, H. Evaluation of hybrid steel-polyethylene fiber-reinforced aggregated solid waste cementitious composites subjected to seawater freeze-thaw cycles attack: Durability, 3D pore structure, and microstructure. Constr. Build. Mater. 2025, 493, 143069. [Google Scholar] [CrossRef]
- Huang, D.; Wang, X.; Li, X.; Su, L.; Tian, J. Advanced nuclear magnetic resonance technology analysis of hybrid fiber reinforced concrete for optimized pore structure and strength. Constr. Build. Mater. 2025, 467, 140383. [Google Scholar] [CrossRef]
- Gokce, A.; Nagataki, S.; Saeki, T.; Hisada, M. Freezing and thawing resistance of air-entrained concrete incorporating recycled coarse aggregate: The role of air content in demolished concrete. Cem. Concr. Res. 2004, 34, 799–806. [Google Scholar] [CrossRef]
- Fu, K.; Sang, Y.; Chen, C.; Liu, K. Frost resistance of recycled aggregate concrete subjected to coupling sustained compressive load and freeze-thaw cycles. Constr. Build. Mater. 2024, 448, 138219. [Google Scholar] [CrossRef]
- Liang, N.; Geng, S.; Mao, J.; Liu, X.; Zhou, X. Investigation on cracking resistance mechanism of basalt-polypropylene fiber reinforced concrete based on SEM test. Constr. Build. Mater. 2024, 411, 134102. [Google Scholar] [CrossRef]
- Liang, N.; You, X.; Yan, R.; Miao, Q.; Liu, X. Experimental investigation on the mechanical properties of polypropylene hybrid fiber-reinforced roller-compacted concrete pavements. Int. J. Concr. Struct. Mater. 2022, 16, 3. [Google Scholar] [CrossRef]

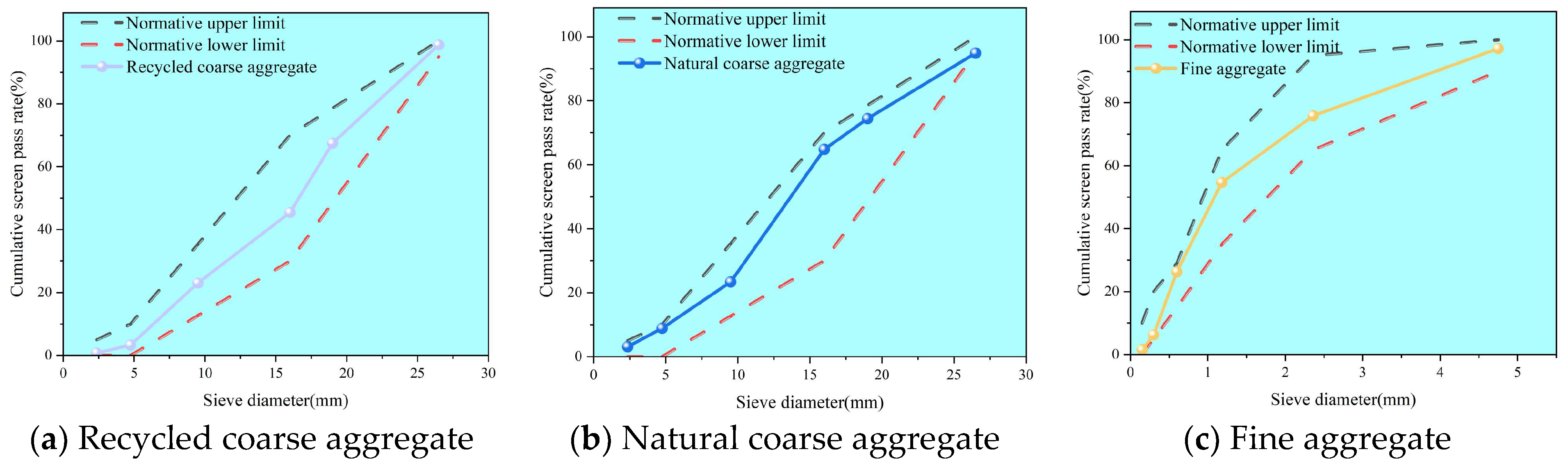

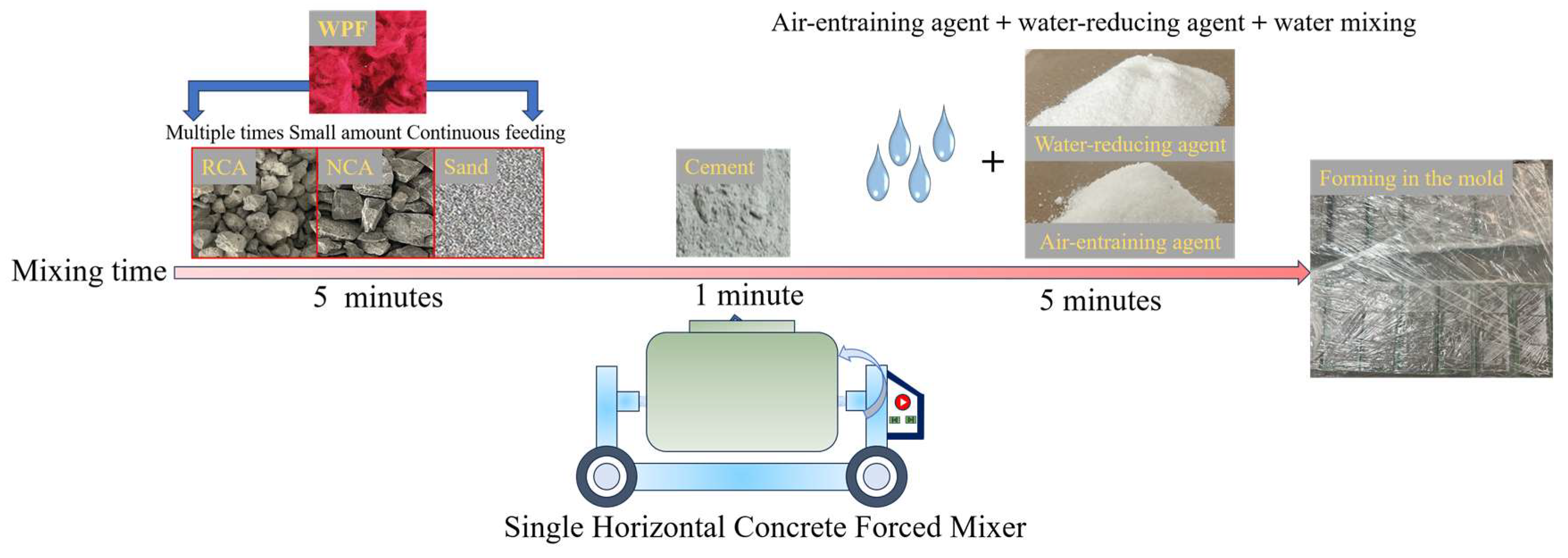






| Type of Coarse Aggregates | Apparent Density (kg/m3) | Crushing Index (%) | Water Absorption (%) | Mud Content (%) |
|---|---|---|---|---|
| RCA | 2541 | 16 | 3.5 | 1.5 |
| NCA | 2635 | 7.5 | 1.3 | 0.5 |
| Cement Grade | Density (g/cm3) | Specific Surface Area (m2/kg) | Initial/Final Condensation Time (min) | 3d/28d Compressive Strength (MPa) |
|---|---|---|---|---|
| P O 42.5 | 3.21 | 312 | 195/259 | 24.6/45.2 |
| Monofilament Diameter (mm) | Elastic Modulus (MPa) | Tensile Strength (MPa) | Water Absorption (%) | Ultimate Elongation (%) | Density (g/cm3) |
|---|---|---|---|---|---|
| 0.043 | 3.67 × 103 | 380 | <0.10 | 1.81 | 0.91 |
| Specimens | NAC | RAC | FRAC |
|---|---|---|---|
| Cement (kg/m3) | 485 | 485 | 485 |
| Sand (kg/m3) | 540 | 540 | 540 |
| Water (kg/m3) | 184 | 184 | 184 |
| RCA (kg/m3) | - | 1150 | 1150 |
| NCA (kg/m3) | 1150 | - | - |
| Additional water (%) | - | 34 | 34 |
| WPF volume fraction (%) | - | - | 0.12 |
| Water-reducing agent (%) | 0.11 | 0.11 | 0.11 |
| Air-entraining agent (%) | 0.11 | 0.11 | 0.11 |
| Air content (%) | 4.3 | 4.5 | 4.6 |
| Specimen Grouping | Medium | Specimen Size (mm3) | Number of Freeze–Thaw Cycles |
|---|---|---|---|
| NAC-F | freshwater | 100 × 100 × 100 100 × 100 × 400 | 0, 25, 50, 60, 75, 100, 110, 125 |
| NAC-S | salt solution | 100 × 100 × 100 100 × 100 × 400 | 0, 25, 50, 60, 75, 100, 110, 125 |
| RAC-F | freshwater | 100 × 100 × 100 100 × 100 × 400 | 0, 25, 50, 60, 75, 100, 110, 125 |
| RAC-S | salt solution | 100 × 100 × 100 100 × 100 × 400 | 0, 25, 50, 60, 75, 100, 110, 125 |
| FRAC-F | freshwater | 100 × 100 × 100 100 × 100 × 400 | 0, 25, 50, 60, 75, 100, 110, 125 |
| FRAC-S | salt solution | 100 × 100 × 100 100 × 100 × 400 | 0, 25, 50, 60, 75, 100, 110, 125 |
| Freeze–Thaw Cycles | NAC-F | NAC-S | RAC-F | RAC-S | FRAC-F | FRAC-S | |
|---|---|---|---|---|---|---|---|
| Mass loss rate (%) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 75 | −0.16 | −0.04 | −1.08 | 0.06 | −0.89 | 0.17 | |
| 125 | 0.11 | 0.22 | −0.97 | 2.57 | −0.77 | 2.42 | |
| RDEM attenuation (%) | 0 | 100 | 100 | 100 | 100 | 100 | 100 |
| 75 | 94.58 | 90.11 | 71.85 | 62.21 | 78.55 | 66.67 | |
| 125 | 84.05 | 78.21 | 52.71 | 35.36 | 57.29 | 39.09 | |
| Compressive strength loss rate (%) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 75 | 10.34 | 10.91 | 23.38 | 28.26 | 21.91 | 26.87 | |
| 125 | 18.91 | 24.56 | 57.27 | 61.44 | 54.68 | 59.6 |
| Specimen Grouping | Freeze–Thaw Cycle | 1/R(n) | X = ln(n) | Y = ln[ln(1/R(n))] | Specimen Grouping | Freeze–Thaw Cycle | 1/R(n) | X = ln(n) | Y = ln[ln(1/R(n))] |
|---|---|---|---|---|---|---|---|---|---|
| RAC-F | 25 | 1.071 | 3.219 | −2.678 | RAC-S | 25 | 1.071 | 3.219 | −2.686 |
| 50 | 1.139 | 3.912 | −2.041 | 50 | 1.188 | 3.912 | −1.759 | ||
| 60 | 1.194 | 4.094 | −1.730 | 60 | 1.331 | 4.094 | −1.252 | ||
| 75 | 1.392 | 4.277 | −1.107 | 75 | 1.607 | 4.277 | −0.745 | ||
| 100 | 1.538 | 4.605 | −0.842 | 100 | 1.927 | 4.605 | −0.422 | ||
| 110 | 1.670 | 4.700 | −0.667 | 110 | 2.201 | 4.700 | −0.237 | ||
| 125 | 1.897 | 4.828 | −0.446 | 125 | 2.828 | 4.828 | 0.039 | ||
| FRAC-F | 25 | 1.058 | 3.219 | −2.882 | FRAC-S | 25 | 1.066 | 3.219 | −2.750 |
| 50 | 1.127 | 3.912 | −2.123 | 50 | 1.158 | 3.912 | −1.920 | ||
| 60 | 1.210 | 4.094 | −1.657 | 60 | 1.236 | 4.094 | −1.551 | ||
| 75 | 1.273 | 4.277 | −1.421 | 75 | 1.500 | 4.277 | −0.903 | ||
| 100 | 1.484 | 4.605 | −0.930 | 100 | 1.826 | 4.605 | −0.507 | ||
| 110 | 1.607 | 4.700 | −0.746 | 110 | 2.084 | 4.700 | −0.309 | ||
| 125 | 1.746 | 4.828 | −0.585 | 125 | 2.558 | 4.828 | −0.063 |
| Specimen Grouping | A | B | R2 | Specimen Grouping | A | B | R2 |
|---|---|---|---|---|---|---|---|
| RAC-F | 1.43677 | −7.44156 | 0.96556 | RAC-S | 1.71116 | −8.25331 | 0.98491 |
| FRAC-F | 1.46745 | −7.69048 | 0.99001 | FRAC-S | 1.72544 | −8.44831 | 0.97722 |
| Specimen Grouping | RAC-F | RAC-S | FRAC-F | FRAC-S |
|---|---|---|---|---|
| Service life | 111 | 83 | 119 | 90 |
| Predicted compressive strength (MPa) | 20.75 | 26.89 | 21.76 | 29.70 |
| Loss rate of maximum strength (%) | 47.37 | 31.90 | 51.59 | 33.67 |
| Specimen Grouping | Freeze–Thaw Cycle | 1/R(n) | X = ln(n) | Y = ln[ln(1/R(n))] | Specimen Grouping | Freeze–Thaw Cycle | 1/R(n) | X = ln(n) | Y = ln[ln(1/R(n))] |
|---|---|---|---|---|---|---|---|---|---|
| RAC-F | 25 | 20.255 | 3.219 | 1.101 | RAC-S | 25 | 19.086 | 3.219 | 1.081 |
| 50 | 7.924 | 3.912 | 0.727 | 50 | 6.210 | 3.912 | 0.602 | ||
| 60 | 6.015 | 4.094 | 0.585 | 60 | 4.826 | 4.094 | 0.454 | ||
| 75 | 4.207 | 4.277 | 0.362 | 75 | 3.593 | 4.277 | 0.246 | ||
| 100 | 2.557 | 4.605 | −0.063 | 100 | 2.379 | 4.605 | −0.143 | ||
| 110 | 2.147 | 4.700 | −0.269 | 110 | 2.023 | 4.700 | −0.350 | ||
| 125 | 1.685 | 4.828 | −0.651 | 125 | 1.587 | 4.828 | −0.772 | ||
| FRAC-F | 25 | 26.542 | 3.219 | 1.187 | FRAC-S | 25 | 30.048 | 3.219 | 1.225 |
| 50 | 9.014 | 3.912 | 0.788 | 50 | 6.585 | 3.912 | 0.634 | ||
| 60 | 6.653 | 4.094 | 0.639 | 60 | 5.028 | 4.094 | 0.479 | ||
| 75 | 4.534 | 4.277 | 0.413 | 75 | 3.766 | 4.277 | 0.282 | ||
| 100 | 2.702 | 4.605 | −0.006 | 100 | 2.531 | 4.605 | −0.074 | ||
| 110 | 2.258 | 4.700 | −0.205 | 110 | 2.135 | 4.700 | −0.277 | ||
| 125 | 1.758 | 4.828 | −0.573 | 125 | 1.629 | 4.828 | −0.717 |
| Specimen Grouping | A | B | R2 | Specimen Grouping | A | B | R2 |
|---|---|---|---|---|---|---|---|
| RAC-F | −1.04803 | 4.69317 | 0.90758 | RAC-S | −1.08344 | 4.74667 | 0.92739 |
| FRAC-F | −1.05605 | 4.79154 | 0.91925 | FRAC-S | −1.11818 | 4.95578 | 0.94631 |
| Specimen Grouping | RAC-F | RAC-S | FRAC-F | FRAC-S |
|---|---|---|---|---|
| Service life | 84 | 76 | 89 | 84 |
| Predicted compressive strength (MPa) | 28.09 | 28.30 | 31.51 | 31.04 |
| Loss rate of maximum strength (%) | 28.77 | 28.32 | 29.89 | 30.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, Z.; Tai, H.-W.; Li, B.; Li, J.; Zhang, W.; Su, T.; Liu, J. Frost Resistance and Life Prediction of Waste Polypropylene Fibre-Reinforced Recycled Aggregate Concrete. Coatings 2025, 15, 1070. https://doi.org/10.3390/coatings15091070
Yang X, Zhang Z, Tai H-W, Li B, Li J, Zhang W, Su T, Liu J. Frost Resistance and Life Prediction of Waste Polypropylene Fibre-Reinforced Recycled Aggregate Concrete. Coatings. 2025; 15(9):1070. https://doi.org/10.3390/coatings15091070
Chicago/Turabian StyleYang, Xuechao, Zehui Zhang, Hsing-Wei Tai, Bangxiang Li, Jiahui Li, Weishen Zhang, Tian Su, and Jianping Liu. 2025. "Frost Resistance and Life Prediction of Waste Polypropylene Fibre-Reinforced Recycled Aggregate Concrete" Coatings 15, no. 9: 1070. https://doi.org/10.3390/coatings15091070
APA StyleYang, X., Zhang, Z., Tai, H.-W., Li, B., Li, J., Zhang, W., Su, T., & Liu, J. (2025). Frost Resistance and Life Prediction of Waste Polypropylene Fibre-Reinforced Recycled Aggregate Concrete. Coatings, 15(9), 1070. https://doi.org/10.3390/coatings15091070






