Self-Repairing Polyurethane–Urea Coating for Wind Turbine Blades: Modeling and Analysis
Abstract
1. Introduction
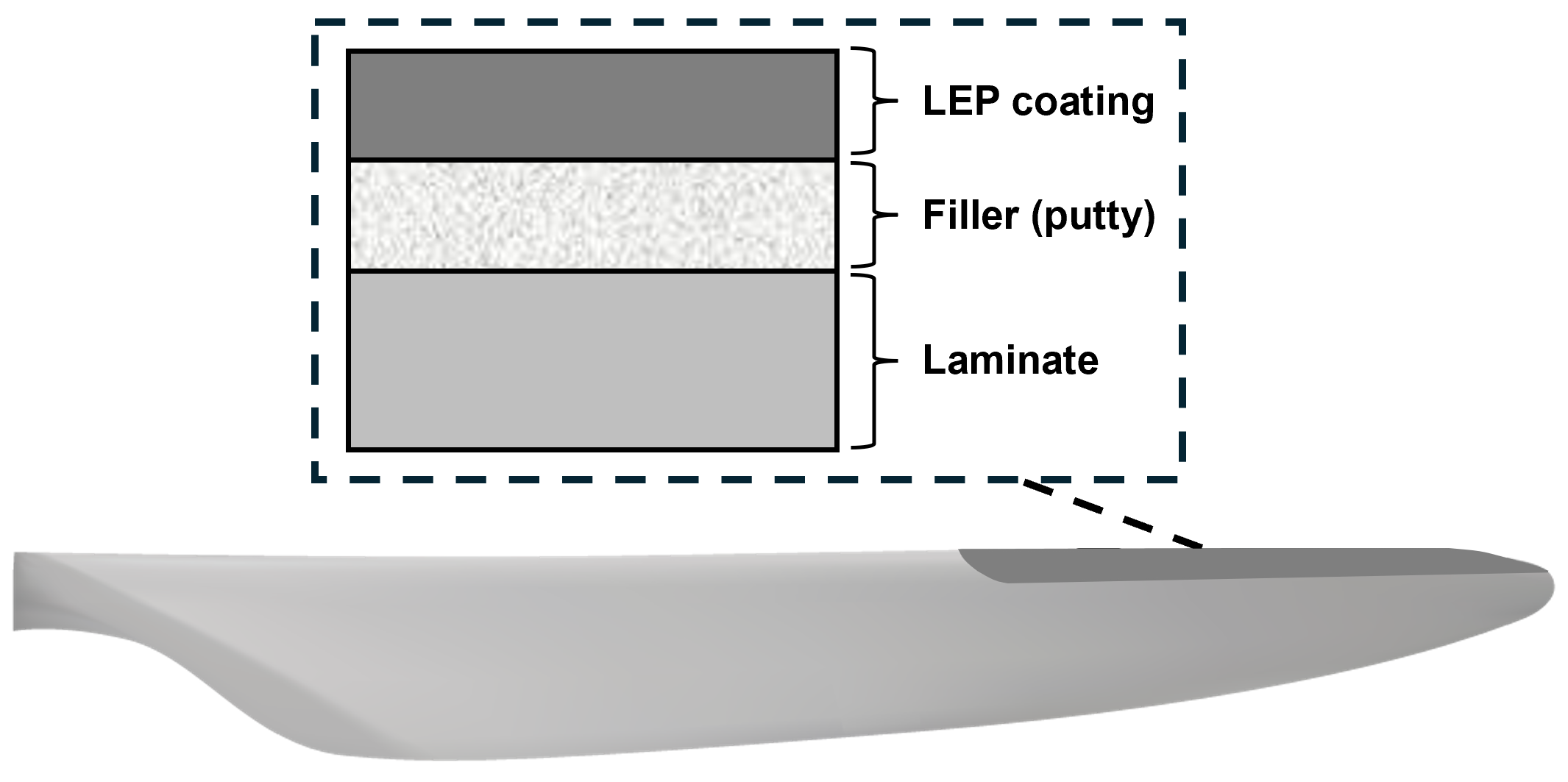
2. Materials
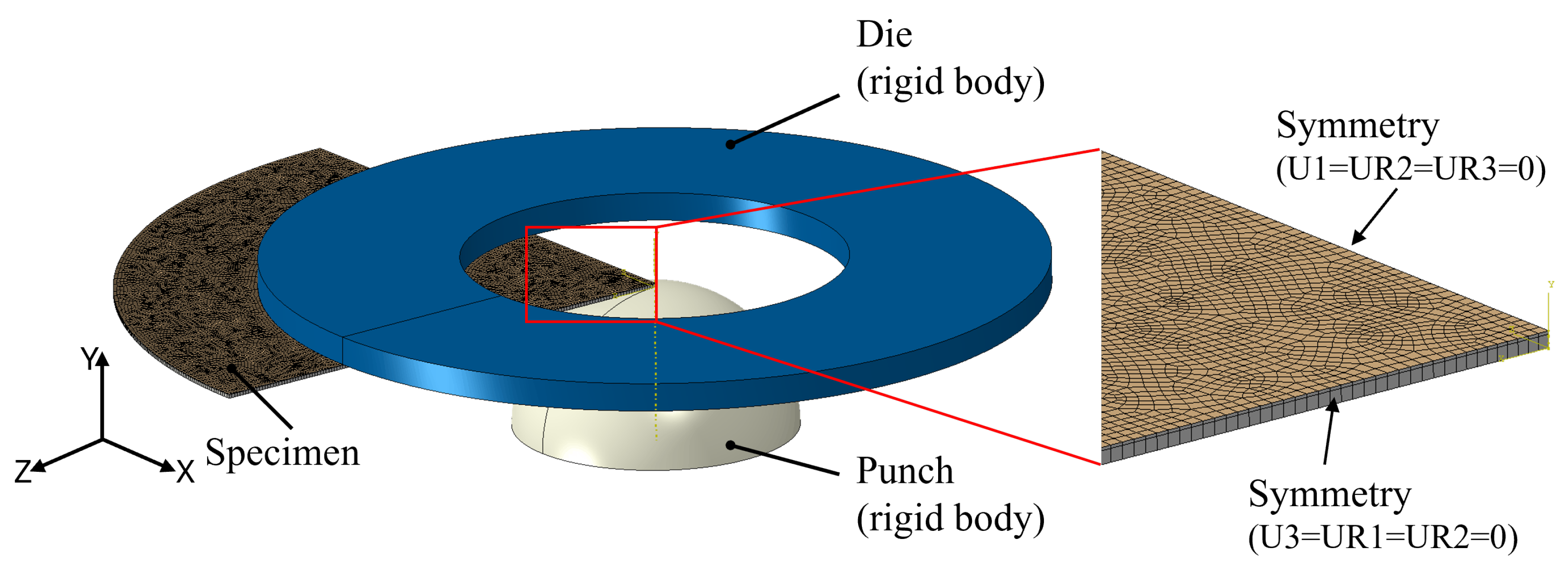
3. Methodology
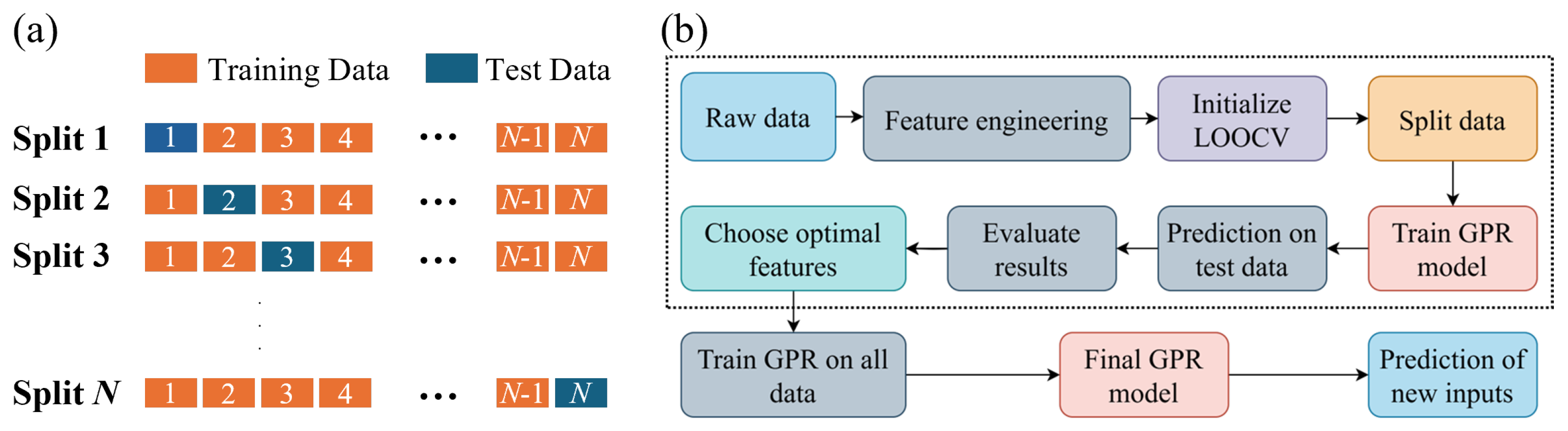
3.1. Prediction of Mobile Fraction by Gaussian Process Regression
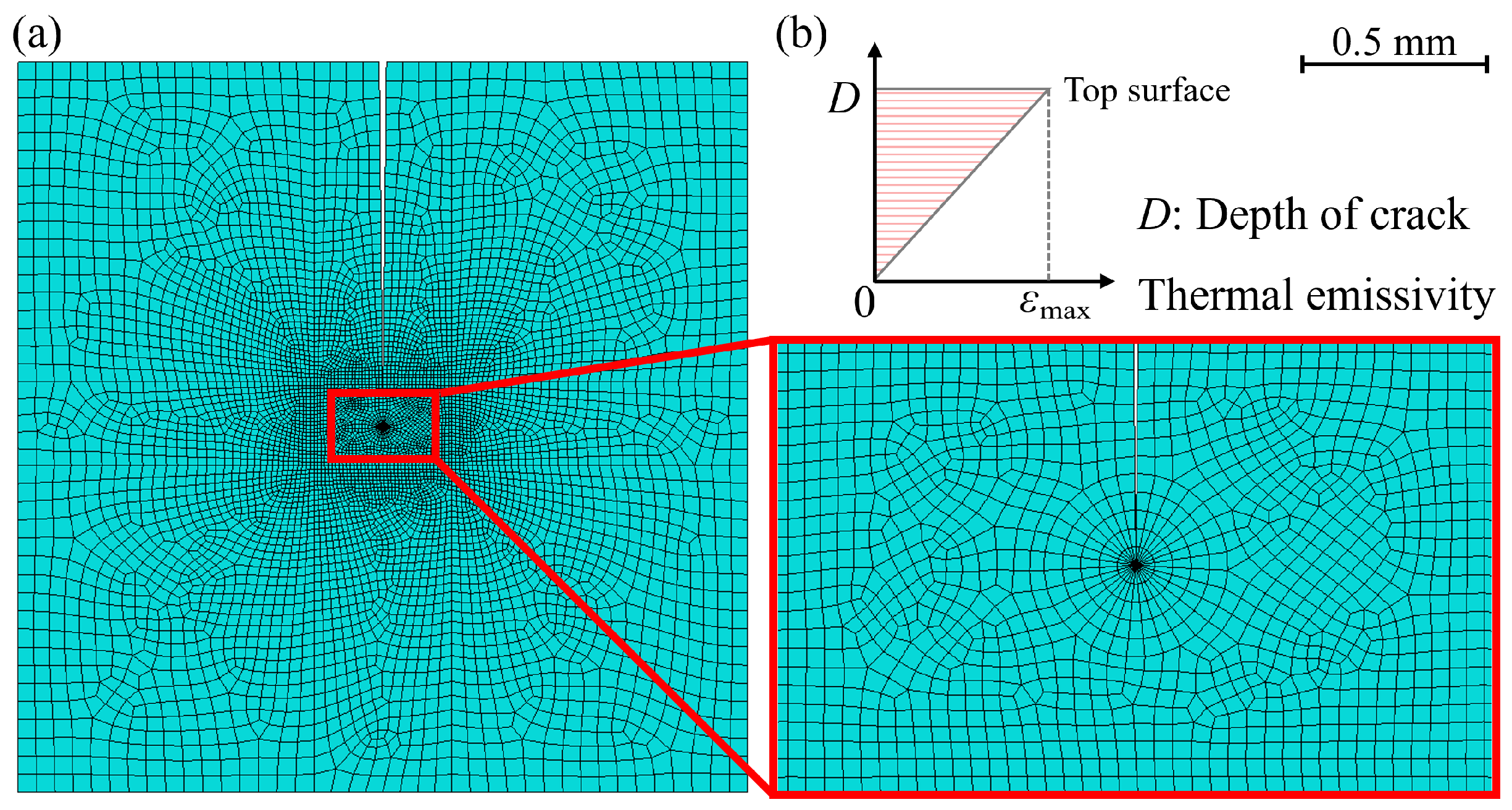
3.2. Single-Crack Model
3.2.1. Temperature Effects
3.2.2. Moisture Effects
3.3. Damage Model for Dehydrated Coating
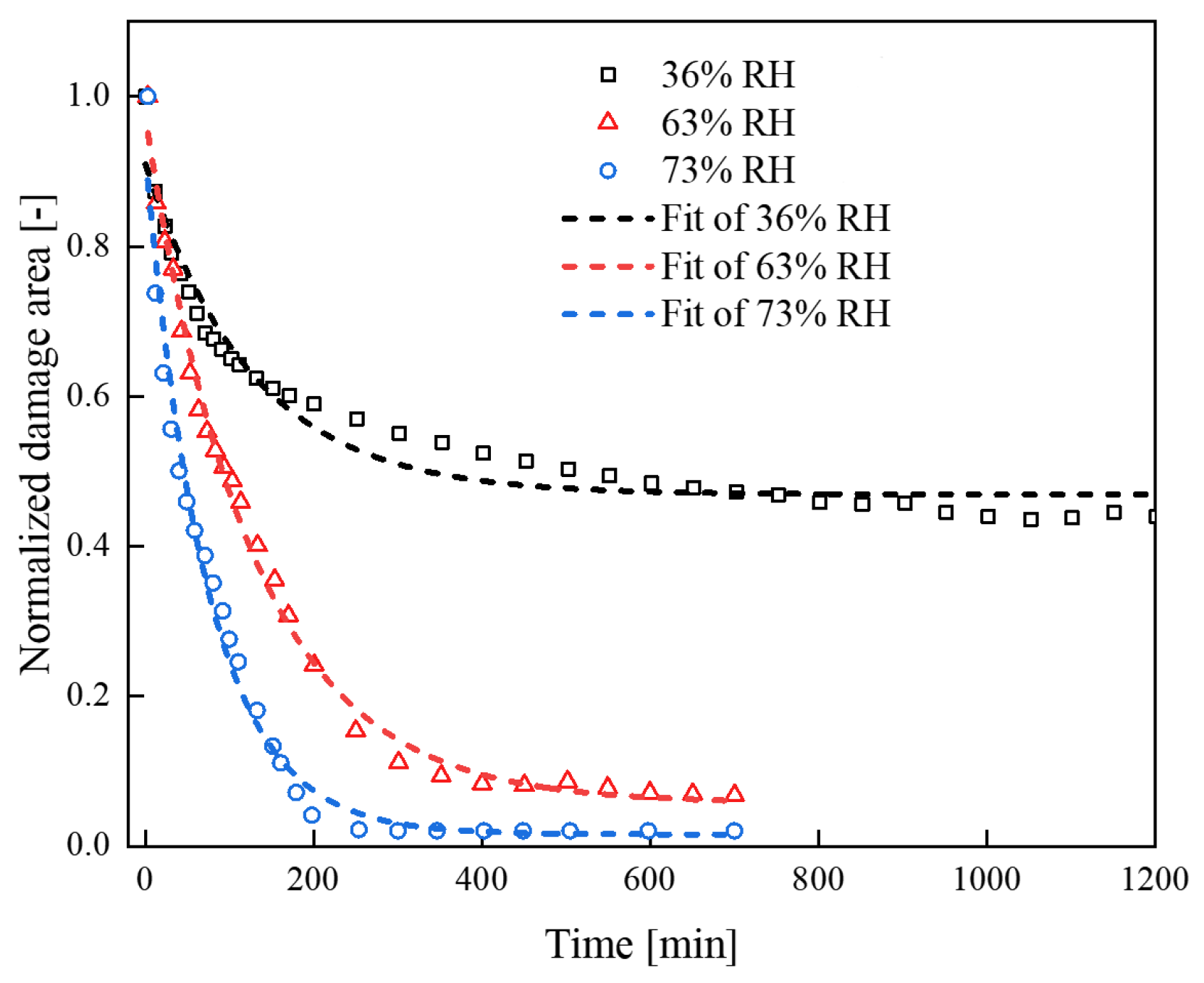
3.4. Self-Healing Kinetics of UDETA-Based PUU Polymers
4. Results and Discussion
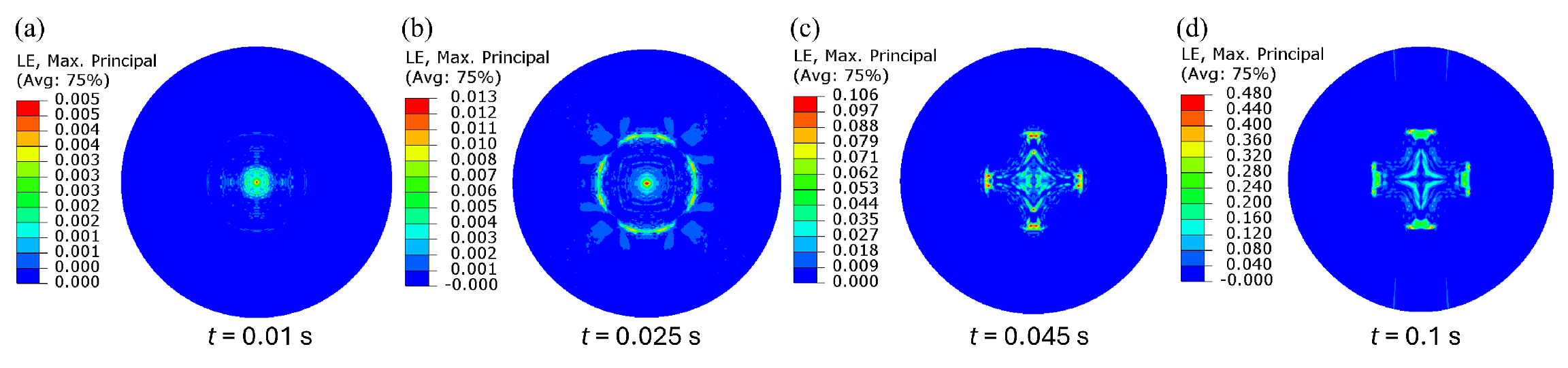
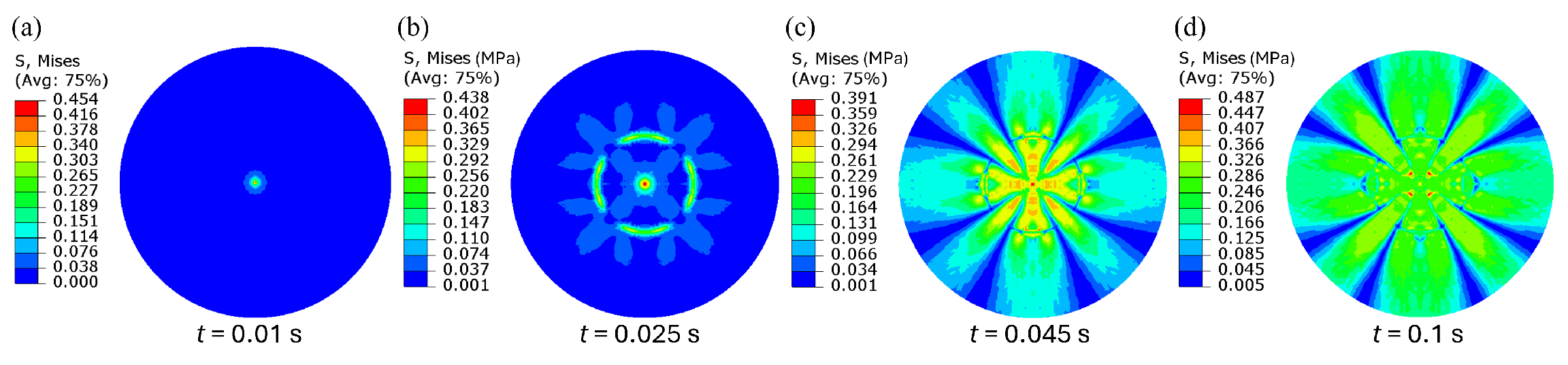
4.1. Single-Crack Model
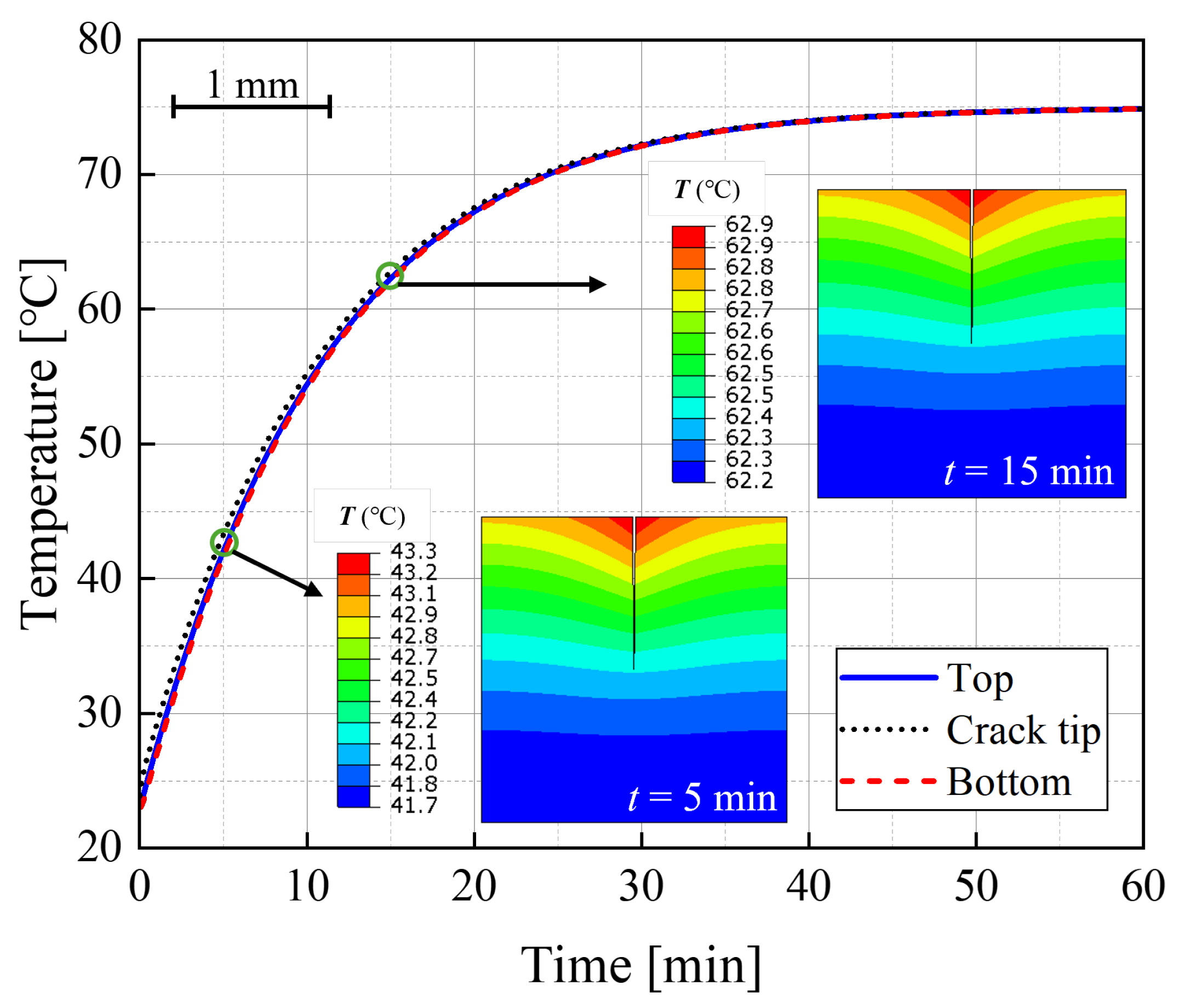
4.1.1. Interplay of Temperature and Thermal Stress
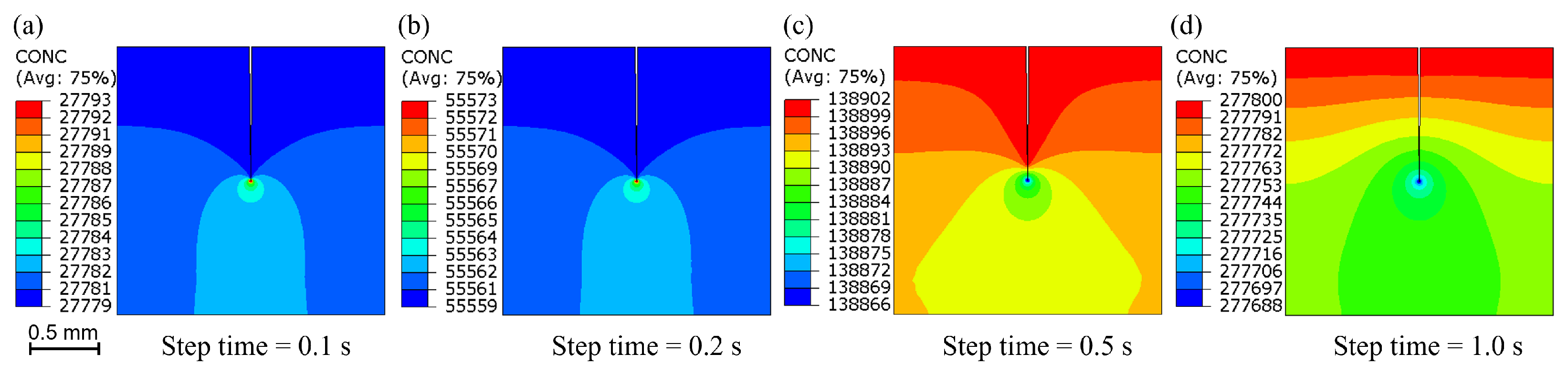
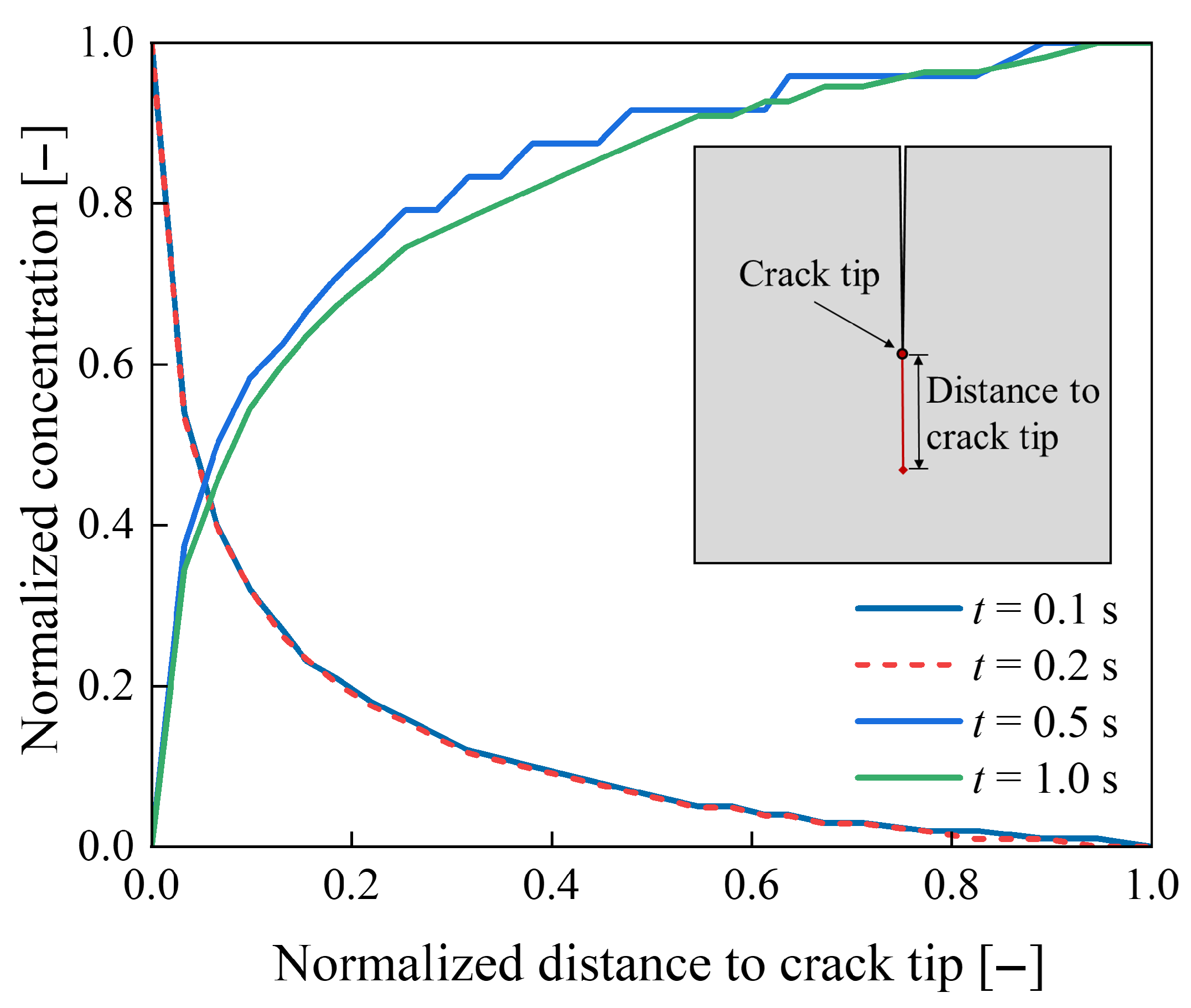
4.1.2. Influence of Pressure Stress on Moisture Distribution
4.2. Damage Model of the Self-Healing Coating
4.3. Healing Model of the Self-Healing Coating
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Predicted Mobile Fraction Using the GPR Model
Appendix A.1. Feature Engineering
Appendix A.2. Model Validation
| No. | Temperature | Amount of UDETA | RH | Mobile Fraction | |
|---|---|---|---|---|---|
| (°C) | (mol%) | (%) | Experiment | Predicted | |
| 1 | 40 | 0 | 0 | 0.000 | |
| 2 | 40 | 11 | 0 | 0.144 | |
| 3 | 40 | 22 | 0 | 0.207 | |
| 4 | 40 | 34 | 0 | 0.322 | |
| 5 | 40 | 0 | 36 | 0.102 | |
| 6 | 40 | 11 | 36 | 0.298 | |
| 7 | 40 | 22 | 36 | 0.330 | |
| 8 | 40 | 34 | 36 | 0.378 | |
| 9 | 40 | 0 | 73 | 0.216 | |
| 10 | 40 | 11 | 73 | 0.304 | |
| 11 | 40 | 22 | 73 | 0.635 | |
| 12 | 40 | 34 | 73 | 0.609 | |
| 13 | 75 | 0 | 0 | 0.001 | |
| 14 | 75 | 6 | 0 | 0.298 | |
| 15 | 75 | 11 | 0 | 0.320 | |
| 16 | 75 | 22 | 0 | 0.313 | |
| 17 | 75 | 34 | 0 | 0.369 | |
| 18 | 75 | 0 | 18 | 0.049 | |
| 19 | 75 | 6 | 18 | 0.324 | |
| 20 | 75 | 11 | 18 | 0.348 | |
| 21 | 75 | 34 | 18 | 0.539 | |
| 22 | 75 | 0 | 36 | 0.289 | |
| 23 | 75 | 6 | 36 | 0.323 | |
| 24 | 75 | 11 | 36 | 0.342 | |
| 25 | 75 | 22 | 36 | 0.361 | |
| 26 | 75 | 34 | 36 | 0.482 | |
| 27 | 75 | 0 | 63 | 0.251 | |
| 28 | 75 | 6 | 63 | 0.378 | |
| 29 | 75 | 11 | 63 | 0.400 | |
| 30 | 75 | 34 | 63 | 0.692 | |
| 31 | 75 | 0 | 73 | 0.284 | |
| 32 | 75 | 6 | 73 | 0.340 | |
| 33 | 75 | 11 | 73 | 0.366 | |
| 34 | 75 | 22 | 73 | 0.590 | |
| 35 | 75 | 34 | 73 | 0.653 | |
Appendix B. Self-Healing Kinetics of UDETA-Based PUU Polymers
References
- Mishnaevsky, L. Root Causes and Mechanisms of Failure of Wind Turbine Blades: Overview. Materials 2022, 15, 2959. [Google Scholar] [CrossRef]
- Mishnaevsky, L., Jr.; Thomsen, K. Costs of Repair of Wind Turbine Blades: Influence of Technology Aspects. Wind Energy 2020, 23, 2247–2255. [Google Scholar] [CrossRef]
- Jones, S.M.; Rehfeld, N.; Schreiner, C.; Dyer, K. The Development of a Novel Thin Film Test Method to Evaluate the Rain Erosion Resistance of Polyaspartate-Based Leading Edge Protection Coatings. Coatings 2023, 13, 1849. [Google Scholar] [CrossRef]
- Mishnaevsky, L.; Hasager, C.B.; Bak, C.; Tilg, A.M.; Bech, J.I.; Doagou Rad, S.; Fæster, S. Leading Edge Erosion of Wind Turbine Blades: Understanding, Prevention and Protection. Renew. Energy 2021, 169, 953–969. [Google Scholar] [CrossRef]
- Cortés, E.; Sánchez, F.; O’Carroll, A.; Madramany, B.; Hardiman, M.; Young, T.M. On the Material Characterisation of Wind Turbine Blade Coatings: The Effect of Interphase Coating–Laminate Adhesion on Rain Erosion Performance. Materials 2017, 10, 1146. [Google Scholar] [CrossRef] [PubMed]
- Hoksbergen, T.H.; Akkerman, R.; Baran, I. Fatigue Lifetime Prediction Model for Leading Edge Protection Coating Systems of Wind Turbine Blades. Tribol. Int. 2023, 189, 108901. [Google Scholar] [CrossRef]
- Bera, P.; Lakshmi, R.V.; Pathak, S.M.; Bonu, V.; Mishnaevsky, L., Jr.; Barshilia, H.C. Recent Progress in the Development and Evaluation of Rain and Solid Particle Erosion Resistant Coatings for Leading Edge Protection of Wind Turbine Blades. Polym. Rev. 2024, 64, 639–689. [Google Scholar] [CrossRef]
- Bech, J.I.; Hasager, C.B.; Bak, C. Extending the Life of Wind Turbine Blade Leading Edges by Reducing the Tip Speed during Extreme Precipitation Events. Wind Energy Sci. 2018, 3, 729–748. [Google Scholar] [CrossRef]
- Eling, B.; Tomović, Ž.; Schädler, V. Current and Future Trends in Polyurethanes: An Industrial Perspective. Macromol. Chem. Phys. 2020, 221, 2000114. [Google Scholar] [CrossRef]
- Finnegan, W.; Flanagan, M.; Ó Coistealbha, R.; Dasan Keeryadath, P.; Meier, P.; Chi Hung, L.; Flanagan, T.; Goggins, J. A Novel Solution for Preventing Leading Edge Erosion in Wind Turbine Blades. J. Struct. Integr. Maint. 2021, 6, 136–147. [Google Scholar] [CrossRef]
- Yu, K.; Zhang, Y.; OuYang, H.; Ahmad, H.A.; Ren, Z.H.; Guan, Z.H. Degradable, Self-Healing, Humidity-Driven Poly(Urethane-Urea) Film. Polymer 2024, 308, 127358. [Google Scholar] [CrossRef]
- Engels, H.W.; Pirkl, H.G.; Albers, R.; Albach, R.W.; Krause, J.; Hoffmann, A.; Casselmann, H.; Dormish, J. Polyurethanes: Versatile Materials and Sustainable Problem Solvers for Today’s Challenges. Angew. Chem. Int. Ed. 2013, 52, 9422–9441. [Google Scholar] [CrossRef]
- Hia, I.L.; Vahedi, V.; Pasbakhsh, P. Self-Healing Polymer Composites: Prospects, Challenges, and Applications. Polym. Rev. 2016, 56, 225–261. [Google Scholar] [CrossRef]
- Nik Md Noordin Kahar, N.N.F.; Osman, A.F.; Alosime, E.; Arsat, N.; Mohammad Azman, N.A.; Syamsir, A.; Itam, Z.; Abdul Hamid, Z.A. The Versatility of Polymeric Materials as Self-Healing Agents for Various Types of Applications: A Review. Polymers 2021, 13, 1194. [Google Scholar] [CrossRef]
- Shen, R.; Amano, R.S.; Lewinski, G.; Matt, A.K.K. A New Vascular System Highly Efficient in the Storage and Transport of Healing Agent for Self-Healing Wind Turbine Blades. J. Energy Resour. Technol. 2019, 141, 051212. [Google Scholar] [CrossRef]
- Choi, K.; Noh, A.; Kim, J.; Hong, P.H.; Ko, M.J.; Hong, S.W. Properties and Applications of Self-Healing Polymeric Materials: A Review. Polymers 2023, 15, 4408. [Google Scholar] [CrossRef] [PubMed]
- Wan, P.; Wu, S.; Liu, Q.; Wang, H.; Gong, X.; Zhao, Z.; Xu, S.; Jiang, J.; Fan, L.; Tu, L. Extrinsic Self-Healing Asphalt Materials: A Mini Review. J. Clean. Prod. 2023, 425, 138910. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, R.; Tang, J.; Zou, X.; Wan, W.; Guo, H. Optimizing Mechanical Properties and Corrosion Resistance in Core-Shell Nanofiber Epoxy Self-Healing Coatings: Impact of Shell Material Variation. Polym. Eng. Sci. 2024, 64, 1770–1785. [Google Scholar] [CrossRef]
- Li, B.; Cao, P.F.; Saito, T.; Sokolov, A.P. Intrinsically Self-Healing Polymers: From Mechanistic Insight to Current Challenges. Chem. Rev. 2023, 123, 701–735. [Google Scholar] [CrossRef]
- Mohd Sani, N.F.; Yee, H.J.; Othman, N.; Talib, A.A.; Shuib, R.K. Intrinsic Self-Healing Rubber: A Review and Perspective of Material and Reinforcement. Polym. Test. 2022, 111, 107598. [Google Scholar] [CrossRef]
- Jin, H.; Mangun, C.L.; Griffin, A.S.; Moore, J.S.; Sottos, N.R.; White, S.R. Thermally stable autonomic healing in epoxy using a dual-microcapsule system. Adv. Mater. 2014, 26, 282–287. [Google Scholar] [CrossRef]
- Cohades, A.; Manfredi, E.; Plummer, C.J.G.; Michaud, V. Thermal Mending in Immiscible Poly(ε-Caprolactone)/Epoxy Blends. Eur. Polym. J. 2016, 81, 114–128. [Google Scholar] [CrossRef]
- Cordier, P.; Tournilhac, F.; Soulié-Ziakovic, C.; Leibler, L. Self-Healing and Thermoreversible Rubber from Supramolecular Assembly. Nature 2008, 451, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Eom, Y.; Kim, S.M.; Lee, M.; Jeon, H.; Park, J.; Lee, E.S.; Hwang, S.Y.; Park, J.; Oh, D.X. Mechano-Responsive Hydrogen-Bonding Array of Thermoplastic Polyurethane Elastomer Captures Both Strength and Self-Healing. Nat. Commun. 2021, 12, 621. [Google Scholar] [CrossRef]
- Wei, Y.; Ma, X. The Self-healing Cross-linked Polyurethane by Diels–Alder Polymerization. Adv. Polym. Technol. 2018, 37, 1987–1993. [Google Scholar] [CrossRef]
- Wittmer, A.; Brinkmann, A.; Stenzel, V.; Hartwig, A.; Koschek, K. Moisture-Mediated Intrinsic Self-Healing of Modified Polyurethane Urea Polymers. J. Polym. Sci. Part A Polym. Chem. 2018, 56, 537–548. [Google Scholar] [CrossRef]
- Chen, X.; Shen, Z.; Jia, H.; Gao, Y.; Zhang, M.; Luo, Y.; Luo, Z. Understanding the Self-Healing Mechanism of Polyurethane Elastomer Based on Hydrogen Bonding Interactions through Molecular Dynamics Simulation. Macromol. Theory Simulations 2022, 31, 2100051. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, J.; Luo, Y.; Chen, J.; Ma, X.; Bukhvalov, D.; Liu, H.; Zhang, M.; Luo, Z. Molecular Dynamics Simulation Insight into the Temperature Dependence and Healing Mechanism of an Intrinsic Self-Healing Polyurethane Elastomer. Phys. Chem. Chem. Phys. 2020, 22, 17620–17631. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, H.; Sun, Y.; Zhang, Y.; Guo, Y. A Molecular Dynamics Simulation on Self-Healing Behavior Based on Disulfide Bond Exchange Reactions. Polymer 2021, 212, 123111. [Google Scholar] [CrossRef]
- Casillas, G.E.; Vazquez, A.E.; Gomez, F.J.R.; Vásquez, A.P.; Mata, R.; Miralrio, A.; Castro, M.; Martínez, R.G.; Cruz, R.O. Corrosion inhibition with a perezone-impregnated Mg/Al hydrotalcite coating in AS21 alloy. Electrochim. Acta 2023, 456, 142428. [Google Scholar] [CrossRef]
- Wu, S.; Wang, J.; Liu, T.; Guo, X.; Ma, L. Sulfosalicylic acid modified carbon dots as effective corrosion inhibitor and fluorescent corrosion indicator for carbon steel in HCl solution. Colloids Surfaces A: Physicochem. Eng. Asp. 2023, 661, 130951. [Google Scholar] [CrossRef]
- Fang, Y.; Yue, T.; Li, S.; Zhang, Z.; Liu, J.; Zhang, L. Molecular dynamics simulations of self-healing topological copolymers with a comblike structure. Macromolecules 2021, 54, 1095–1105. [Google Scholar] [CrossRef]
- Tang, J.; Wang, H. Compatibility and Self-Healing Properties of Asphalt Binder with Polyethylene Plastics: Observations from Coarse-Grained Molecular Simulation. J. Mater. Civ. Eng. 2023, 35, 04023412. [Google Scholar] [CrossRef]
- Wen, J.; Xu, G.; Liang, Z.; Li, S.; Wang, Y.; Yang, J.; Nie, Y. Combing experimental methods and molecular simulations to study self-healing behaviors of polyurethane elastomers containing multiple hydrogen bond networks and flexible blocks. Phys. Chem. Chem. Phys. 2023, 25, 28162–28179. [Google Scholar] [CrossRef]
- Sun, Y.; Simonini, L.; Xing, C.; Mishnaevsky, L. Self-Healing Interfaces in Fiber Reinforced Polymers: Computational Modeling. Compos. Sci. Technol. 2025, 270, 111269. [Google Scholar] [CrossRef]
- Sun, Y.; Mishnaevsky, L., Jr. Healable polymer blends: Computational analysis of damage and healing mechanisms. Int. J. Mech. Sci. 2025, 287, 109938. [Google Scholar] [CrossRef]
- Wittmer, A.; Wellen, R.; Saalwächter, K.; Koschek, K. Moisture-Mediated Self-Healing Kinetics and Molecular Dynamics in Modified Polyurethane Urea Polymers. Polymer 2018, 151, 125–135. [Google Scholar] [CrossRef]
- Stetsyshyn, Y.; Ohar, H.; Budkowski, A.; Lazzara, G. Molecular Design and Role of the Dynamic Hydrogen Bonds and Hydrophobic Interactions in Temperature-Switchable Polymers: From Understanding to Applications. Polymers 2025, 17, 1580. [Google Scholar] [CrossRef]
- Lepot, M.; Aubin, J.B.; Clemens, F.H.L.R. Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment. Water 2017, 9, 796. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning, 3rd print ed.; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Esmaeilbeigi, M.; Chatrabgoun, O.; Cavoretto, R.; De Rossi, A.; Shafa, M. Sparse Gaussian Process Regression via Compactly Supported Kernels: A Trade-off between Accuracy and Computational Efficiency. Inf. Sci. 2025, 717, 122306. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. (Eds.) Principles of Heat and Mass Transfer, 7th ed.; International Student Version ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Fick, A. Ueber Diffusion. Ann. Der Phys. 1855, 170, 59–86. [Google Scholar] [CrossRef]
- De Nevers, N. Physical and Chemical Equilibrium for Chemical Engineers, 2nd ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kurumatani, M.; Terada, K.; Kato, J.; Kyoya, T.; Kashiyama, K. An Isotropic Damage Model Based on Fracture Mechanics for Concrete. Eng. Fract. Mech. 2016, 155, 49–66. [Google Scholar] [CrossRef]
- Bian, X.; He, J.; He, M.; Liu, B.; Zhang, Y. Study on the Properties of Polyurethane–Urea Elastomers Prepared by TDI/MDI Mixture. Int. J. Polym. Sci. 2024, 2024, 9248135. [Google Scholar] [CrossRef]
- Karpiesiuk, J. Young’s Modulus and Poisson’s Ratio of Polyurethane Adhesive in Lightweight Floor System. Mod. Approaches Mater. Sci. 2020, 2, 251–255. [Google Scholar] [CrossRef]
- Pugar, J.A.; Gang, C.; Huang, C.; Haider, K.W.; Washburn, N.R. Predicting Young’s Modulus of Linear Polyurethane and Polyurethane–Polyurea Elastomers: Bridging Length Scales with Physicochemical Modeling and Machine Learning. ACS Appl. Mater. Interfaces 2022, 14, 16568–16581. [Google Scholar] [CrossRef]
- Wittchen, S.; Kahl, H.; Waltschew, D.; Shahzad, I.; Beiner, M.; Cepus, V. Diffusion Coefficients of Polyurethane Coatings by Swelling Experiments Using Dielectric Spectroscopy. J. Appl. Polym. Sci. 2020, 137, 49174. [Google Scholar] [CrossRef]
- Thomson, G.W. The Antoine Equation for Vapor-pressure Data. Chem. Rev. 1946, 38, 1–39. [Google Scholar] [CrossRef] [PubMed]
- Zaoui-Djelloul-Daouadji, M.; Negadi, A.; Mokbel, I.; Negadi, L. (Vapor-liquid) Equilibria and Excess Gibbs Free Energy Functions of (Ethanol + Glycerol), or (Water + Glycerol) Binary Mixtures at Several Temperatures. J. Chem. Thermodyn. 2014, 69, 165–171. [Google Scholar] [CrossRef]
- Sorce, F.S.; Ngo, S.; Lowe, C.; Taylor, A.C. Quantification of Coating Surface Strains in Erichsen Cupping Tests. J. Mater. Sci. 2019, 54, 7997–8009. [Google Scholar] [CrossRef]
- Eom, J.H.; Jeon, H.J.; Babu, J.S.S.; Kang, N.S.; Lim, O.D.; Kim, C.; Lee, M.S. Experimental and Simulation Studies of Erichsen Cupping Test on Aluminum(7075) Sheet Using Damage Theory. Int. J. Precis. Eng. Manuf. 2024, 25, 1639–1649. [Google Scholar] [CrossRef]
- Sun, Y.; Xing, C.; Zhang, C.; Tao, C.; Ji, H.; Qiu, J. A 3D Homogenized Model for Nonlinear Wave Interaction with Randomly Distributed Microcracks. Acta Mech. Solida Sin. 2022, 35, 961–971. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Z.; Ng, T.Y.; Sharma, P. The Effect of Water Content on the Elastic Modulus and Fracture Energy of Hydrogel. Extrem. Mech. Lett. 2020, 35, 100617. [Google Scholar] [CrossRef]
- Vásquez, J.C.G.; Kumral, M. Artificial Neural Networks and Support Vector Machines for More Accurate Cost Estimation in Underground Mining: A Contractor’s Viewpoint. Mach. Learn. Appl. 2025, 21, 100689. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A Survey of Cross-Validation Procedures for Model Selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Ramachandran, K.M.; Tsokos, C.P. (Eds.) Chapter 7—Linear Regression Models. In Mathematical Statistics with Applications in R, 3rd ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 301–341. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Mishnaevsky, L., Jr.; Koschek, K.; Sayer, F. Self-Repairing Polyurethane–Urea Coating for Wind Turbine Blades: Modeling and Analysis. Coatings 2025, 15, 1059. https://doi.org/10.3390/coatings15091059
Sun Y, Mishnaevsky L Jr., Koschek K, Sayer F. Self-Repairing Polyurethane–Urea Coating for Wind Turbine Blades: Modeling and Analysis. Coatings. 2025; 15(9):1059. https://doi.org/10.3390/coatings15091059
Chicago/Turabian StyleSun, Yulin, Leon Mishnaevsky, Jr., Katharina Koschek, and Florian Sayer. 2025. "Self-Repairing Polyurethane–Urea Coating for Wind Turbine Blades: Modeling and Analysis" Coatings 15, no. 9: 1059. https://doi.org/10.3390/coatings15091059
APA StyleSun, Y., Mishnaevsky, L., Jr., Koschek, K., & Sayer, F. (2025). Self-Repairing Polyurethane–Urea Coating for Wind Turbine Blades: Modeling and Analysis. Coatings, 15(9), 1059. https://doi.org/10.3390/coatings15091059







