First-Order Structural Modal Damping Ratio Identification by Withdrawing Amplitudes of Free Decaying Responses
Abstract
1. Introduction
2. Establishment of Numerical Model
2.1. Global Mass Matrix, Stiffness Matrix, and Damping Matrix
2.2. State Space Theory
2.3. Identification Model of First-Order Modal Damping Ratio
3. Analysis of Numerical Simulation
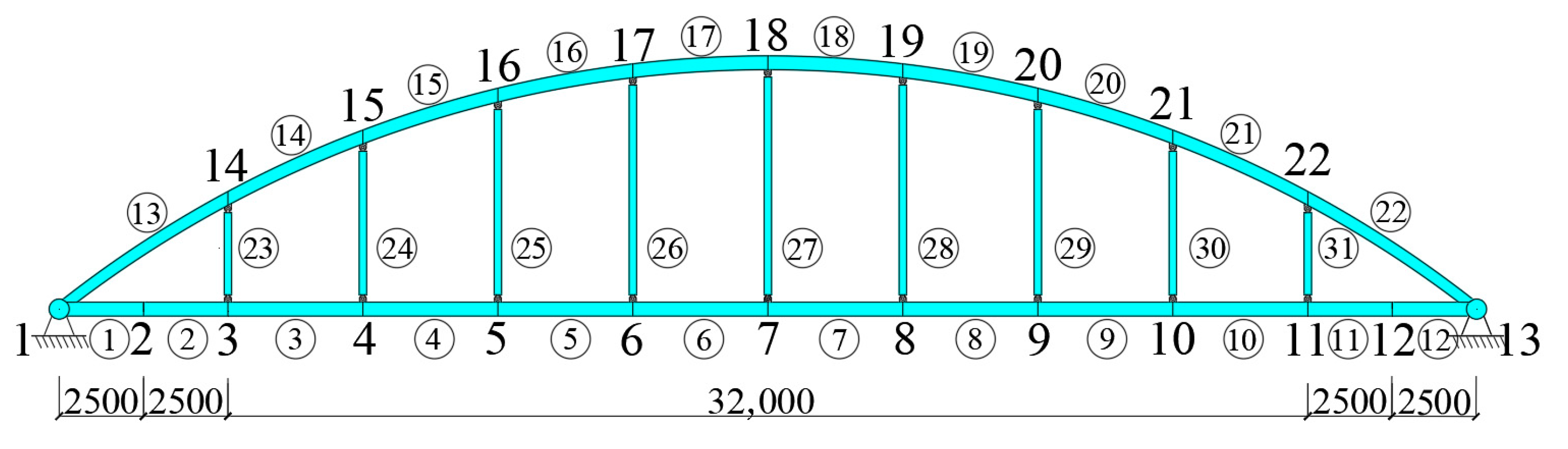
3.1. Profile of Simulation
3.2. Proposition of Set Modal Damping Ratios
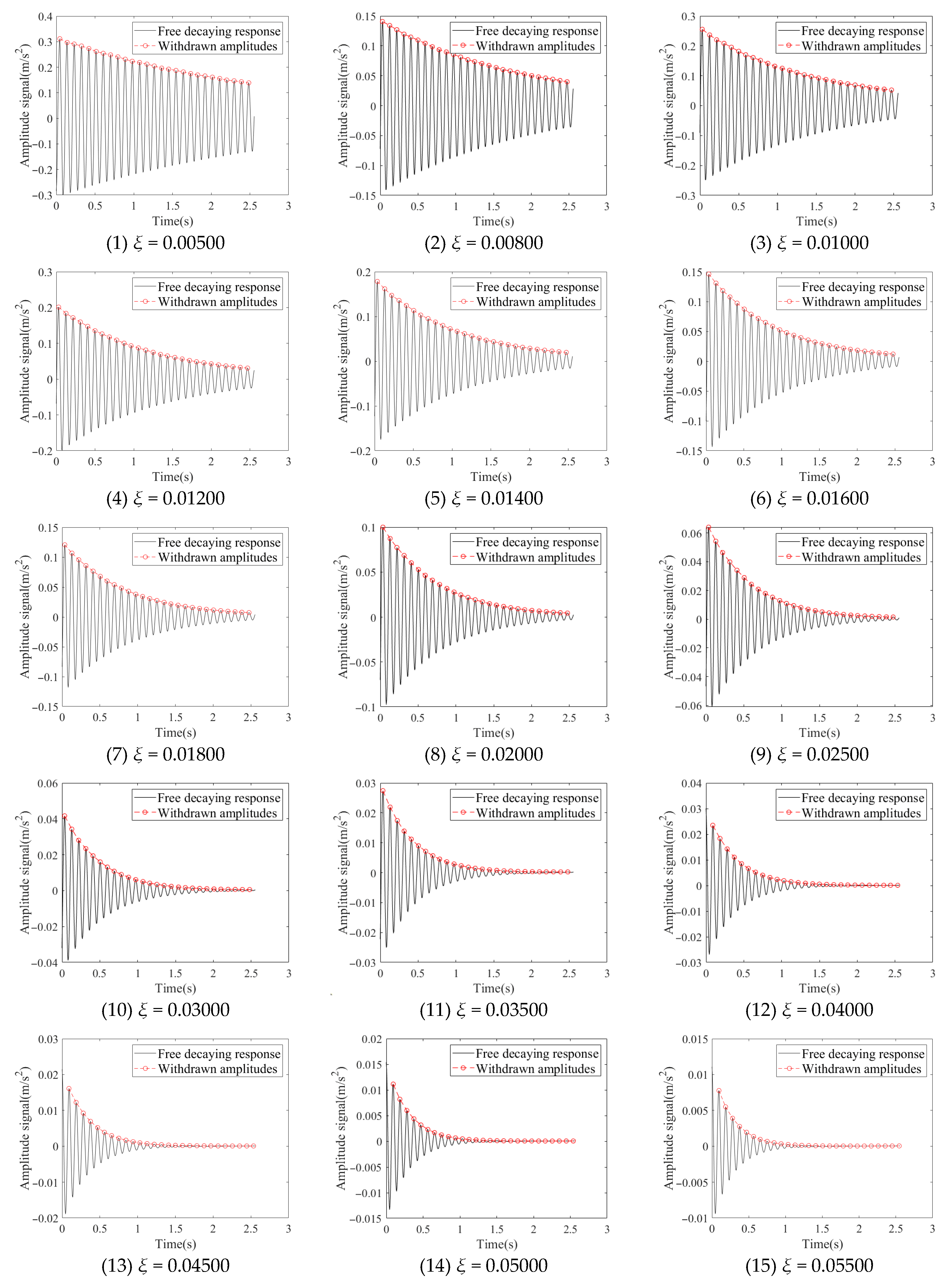
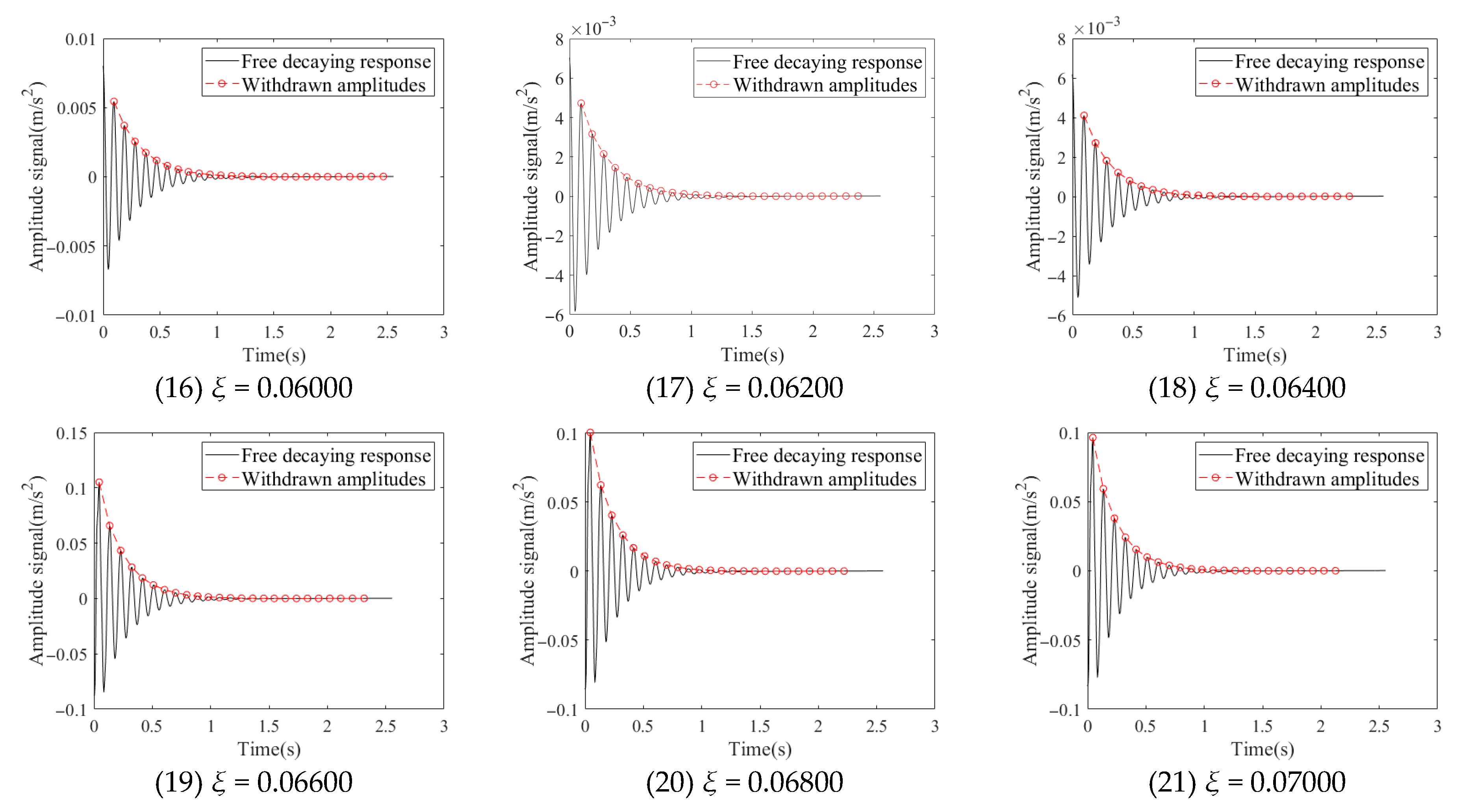
3.3. Withdrawing Amplitudes of Free Decaying Responses and Calculation of Natural Frequency
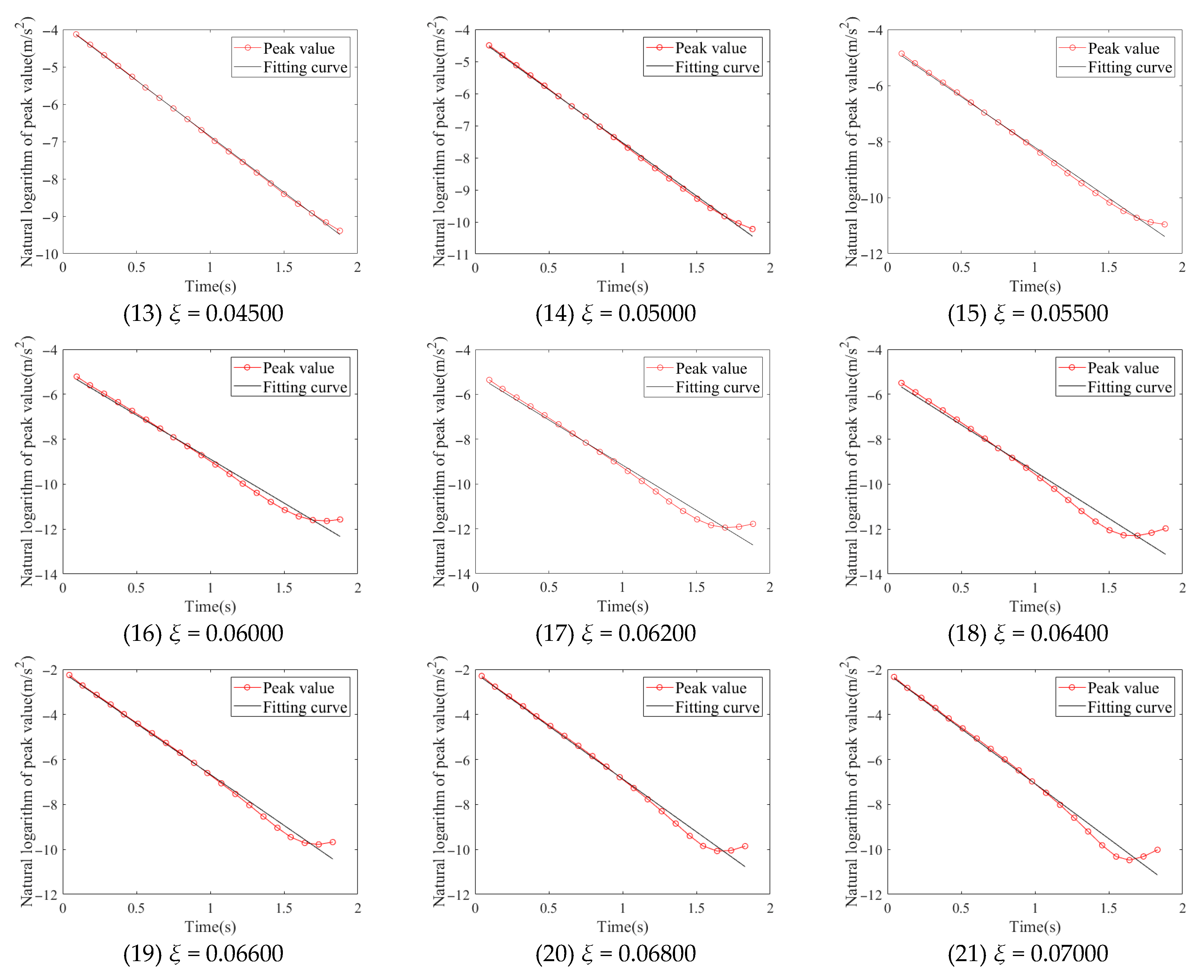
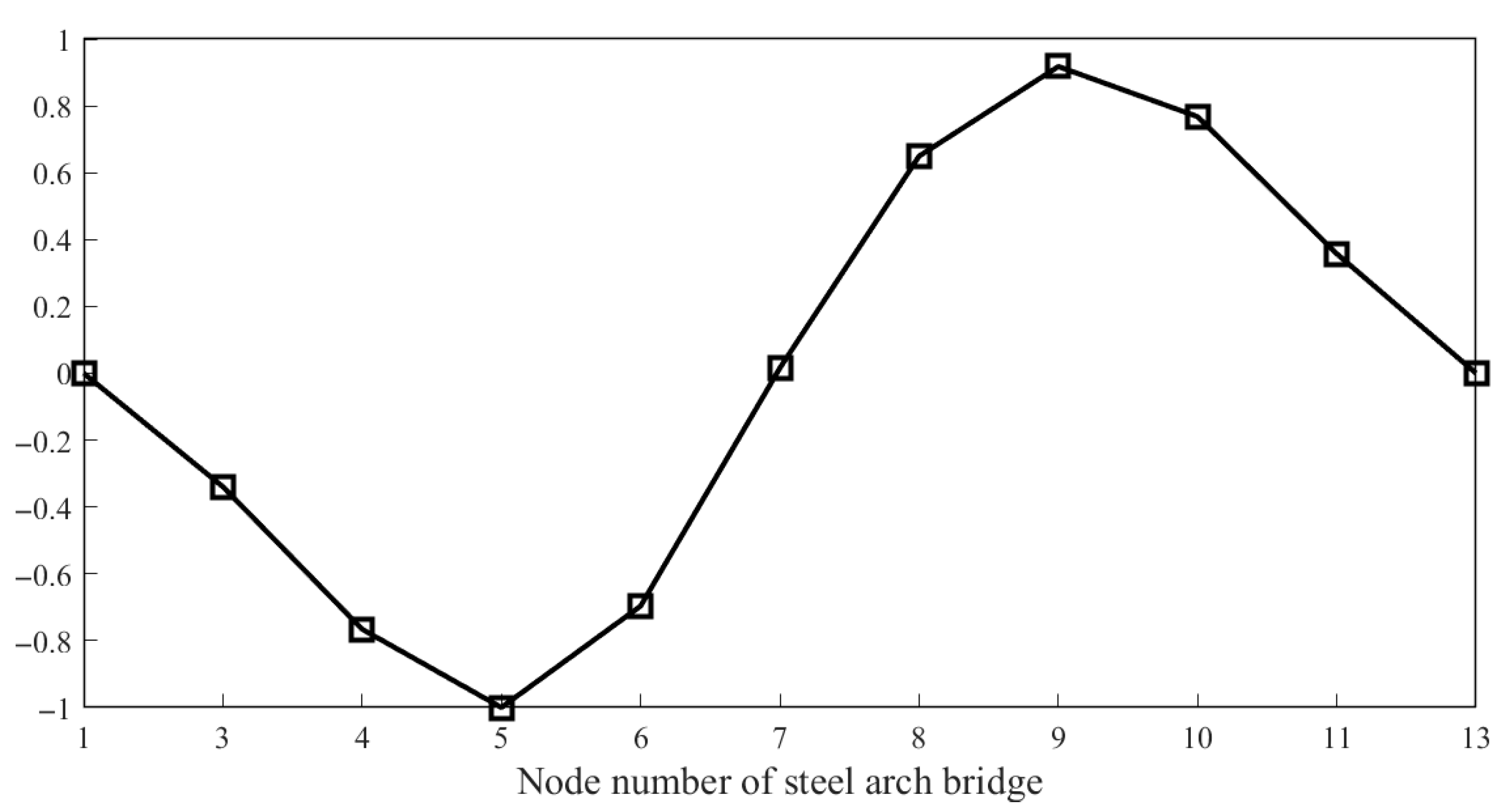
3.4. Identification of Modal Damping Ratio
3.5. Analysis of Identification Error of Damping Ratio
4. Case Analysis of Steel Arch Bridges
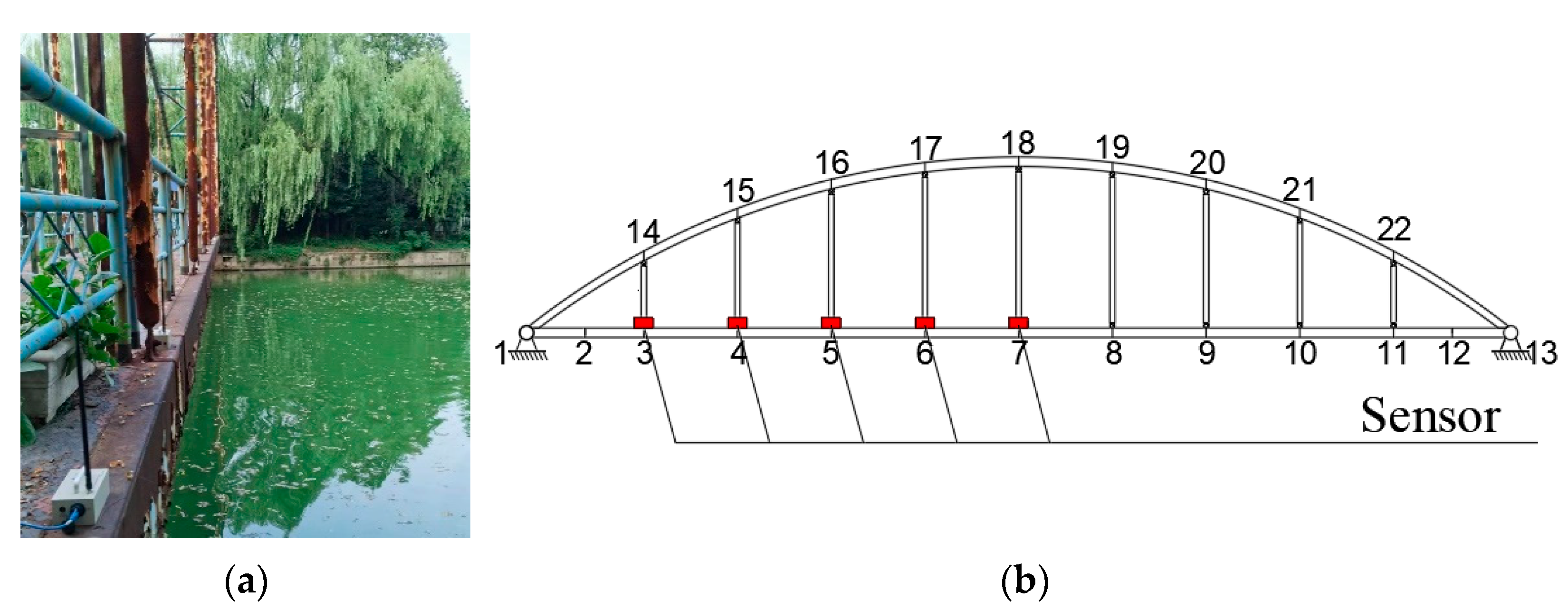
4.1. Overview of Steel Arch Bridge Project
4.2. Identification of Modal Damping Ratio of Steel Arch Bridge
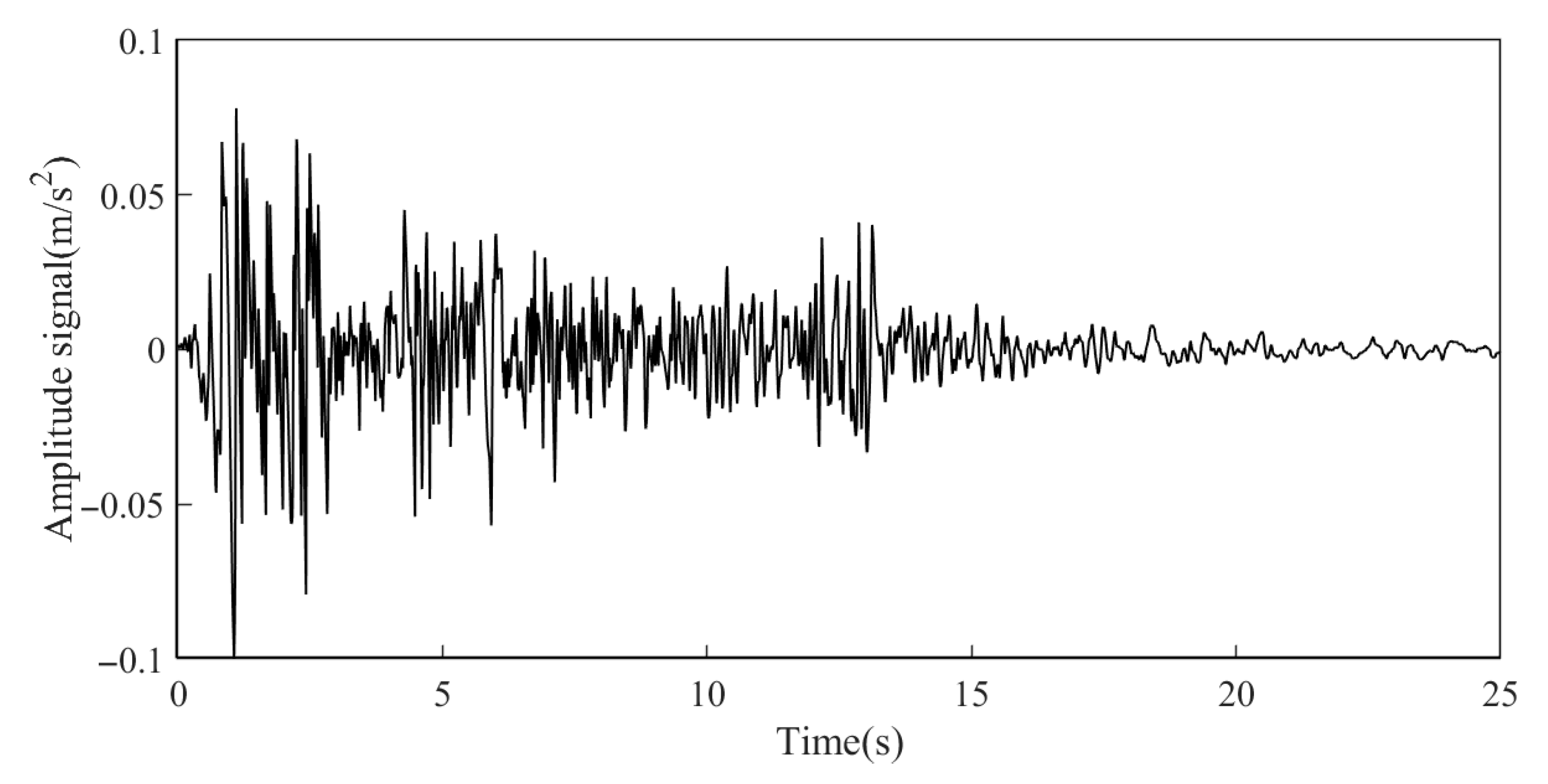
4.2.1. Measurement of Acceleration Time History
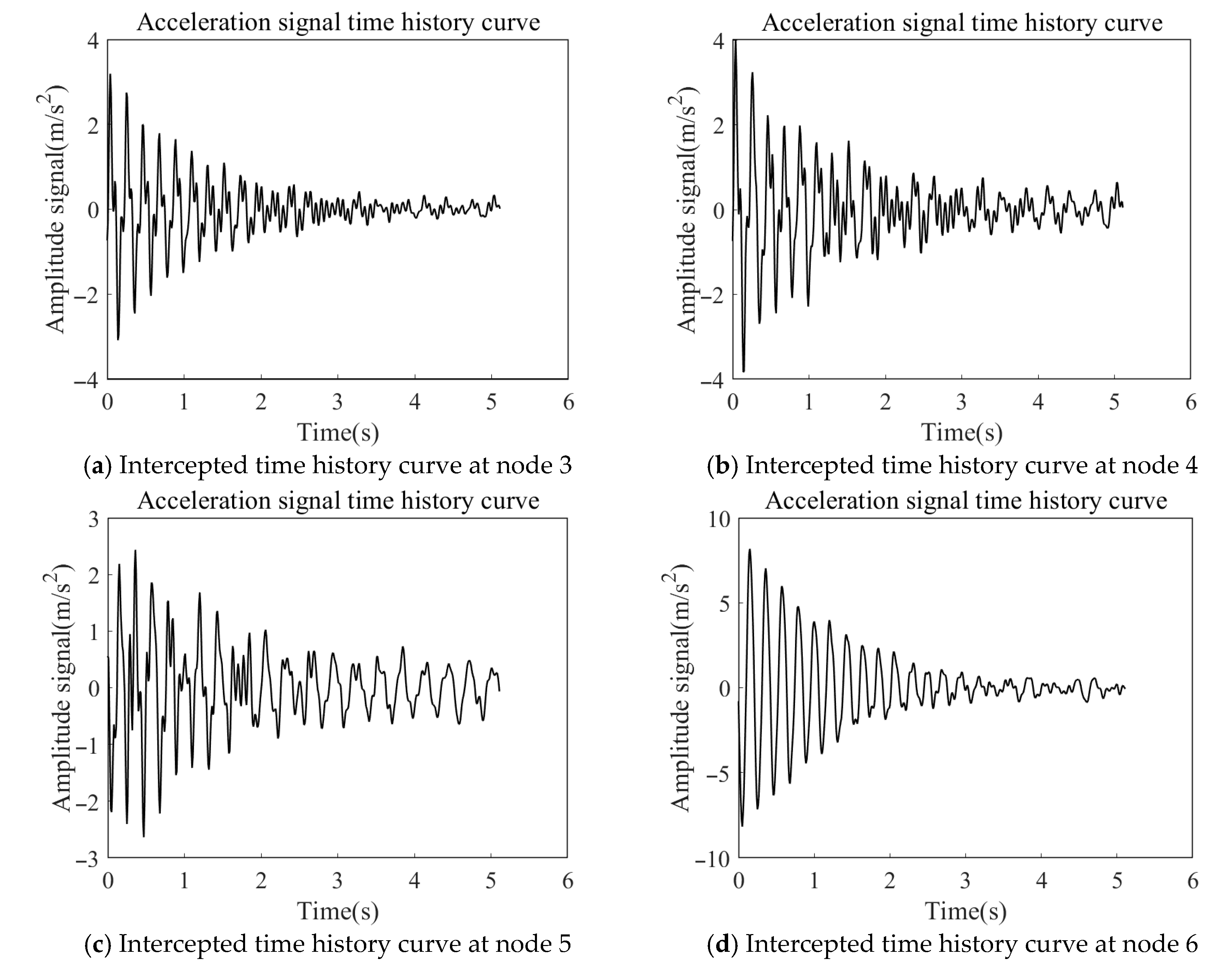
4.2.2. Selection of Data
4.2.3. Identification of First-Order Modal Damping Ratio
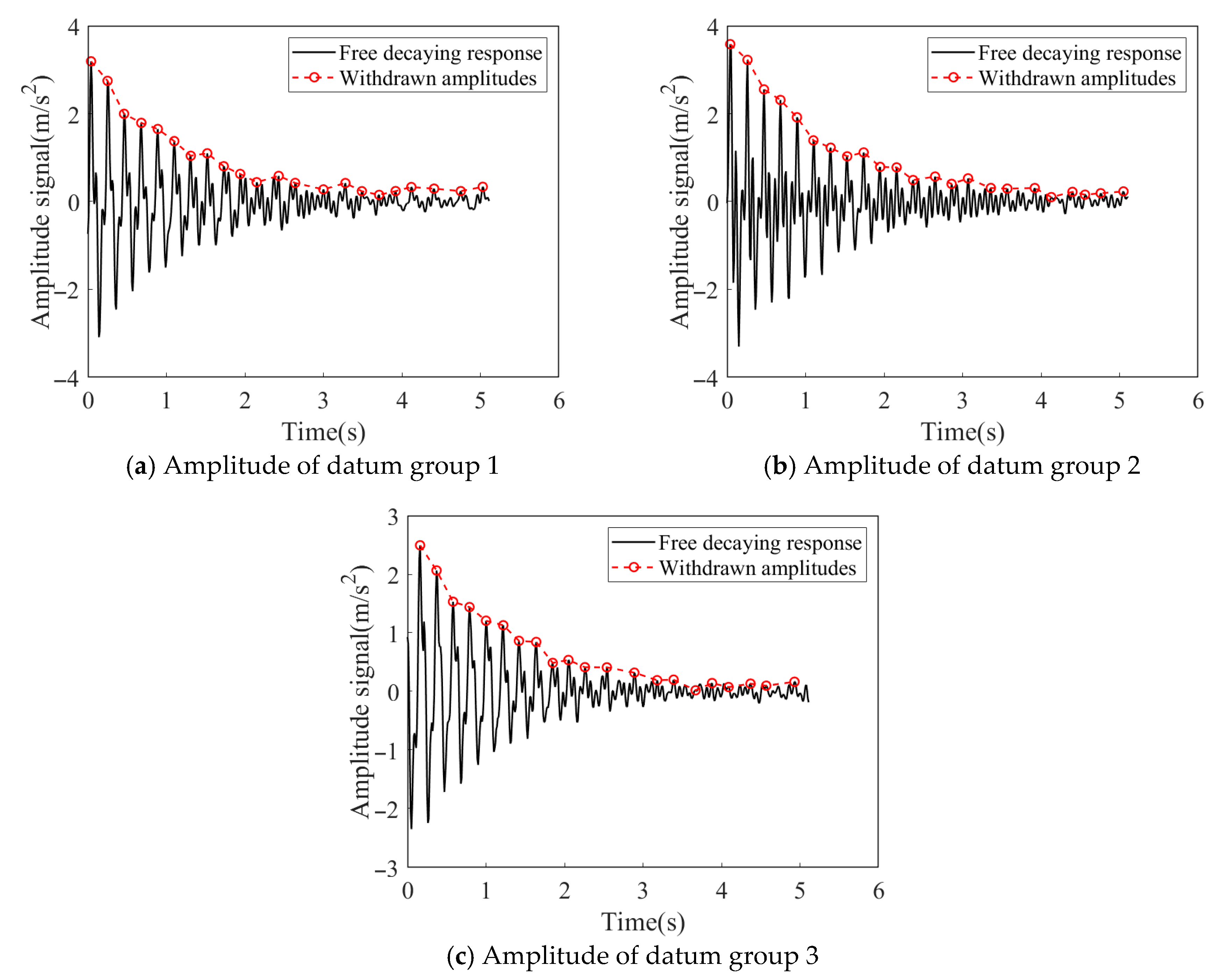
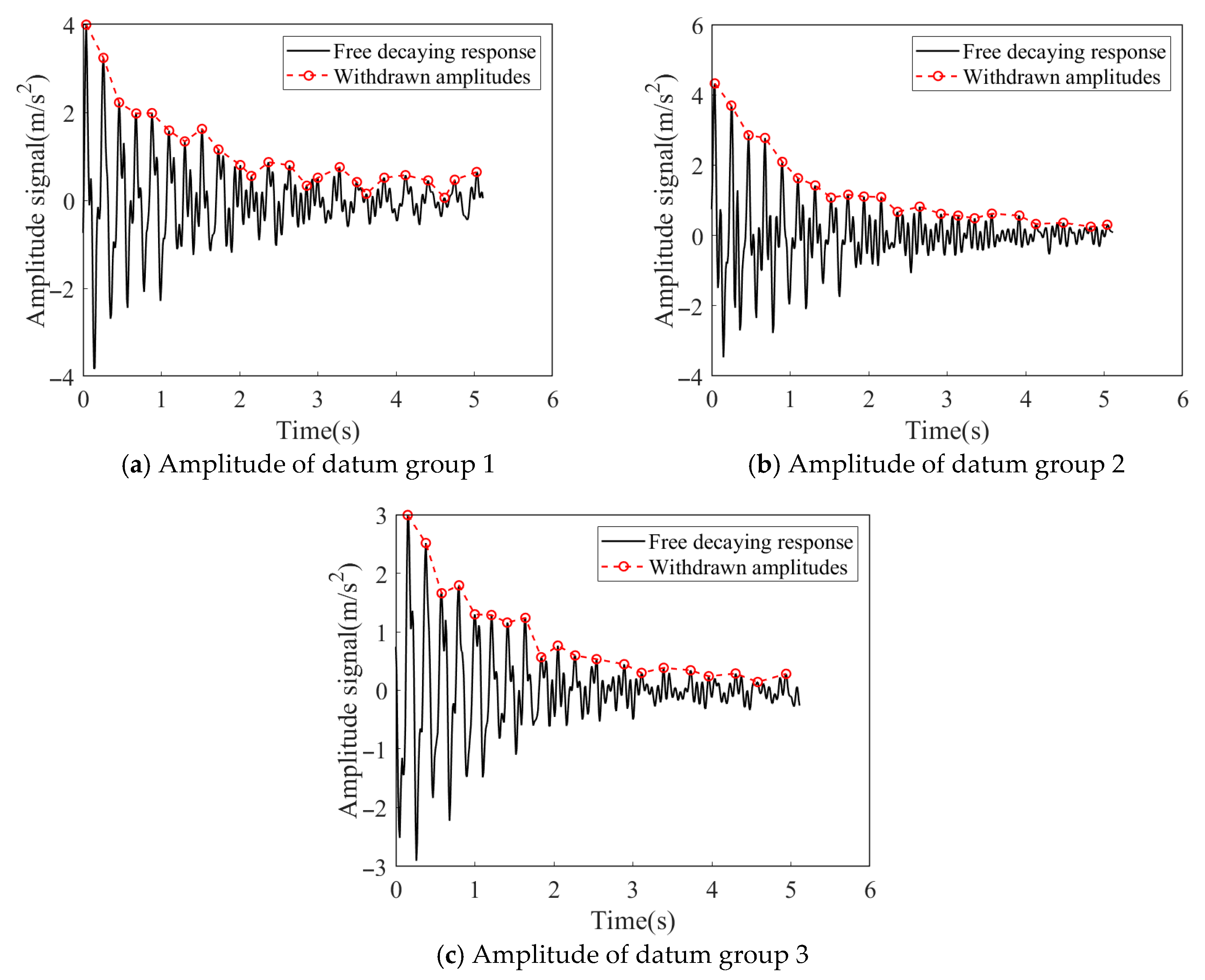
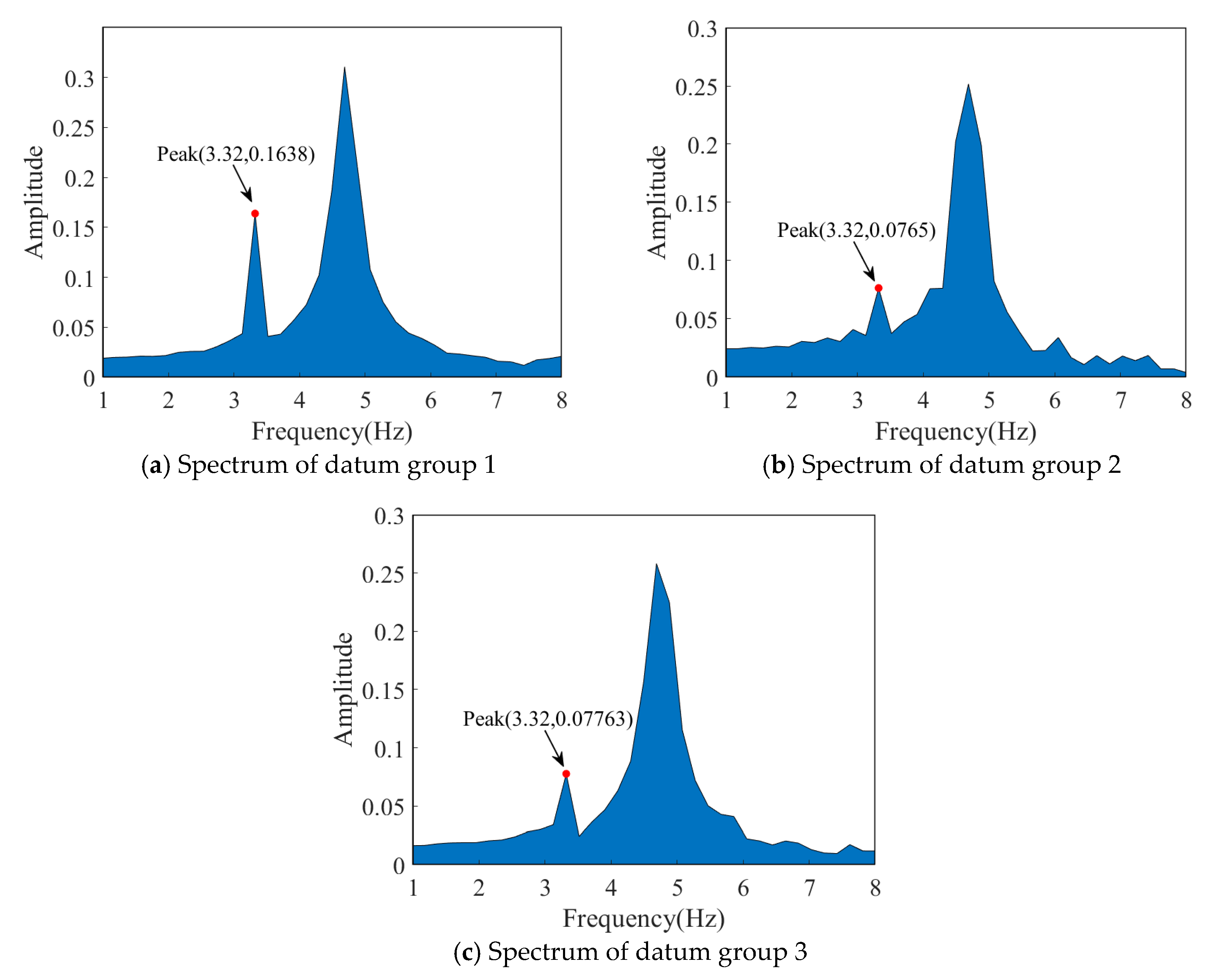
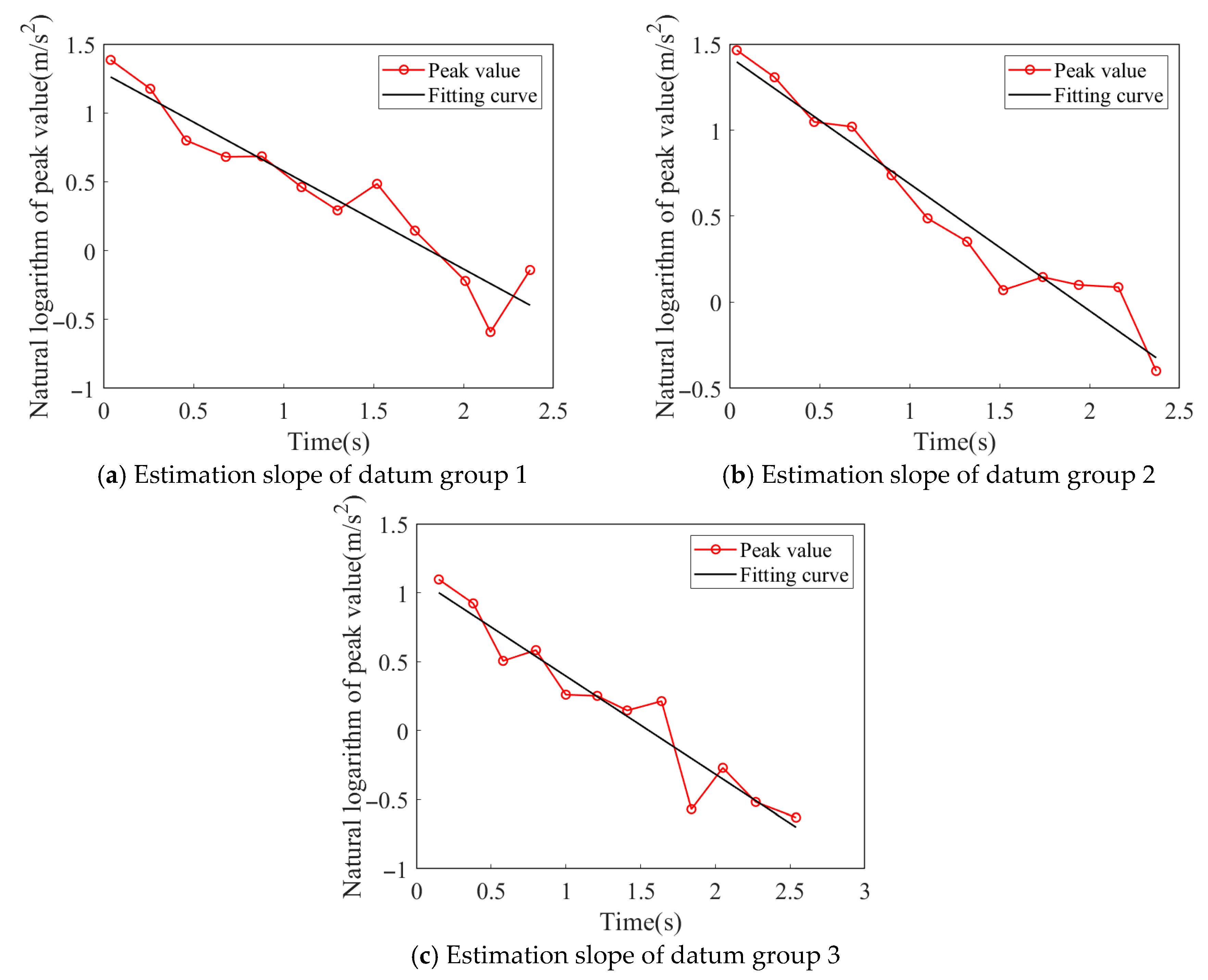
Identification of Damping Ratio at Node 3
Identification of Damping Ratio at Node 4
4.3. Dynamic Response Analysis of Steel Arch Bridge
4.3.1. Dynamic Response Analysis Under Random Excitation
4.3.2. Dynamic Response Analysis Under El Centro Seismic Wave Excitation
4.4. The Universality Analysis of Application
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bartilson, D.T.; Jang, J.; Smyth, A.W. Symmetry Properties of Natural Frequency and Mode Shape Sensitivities in Symmetric Structures. Mech. Syst. Signal Process. 2020, 143, 106797. [Google Scholar] [CrossRef]
- Bertrand, D.; Grange, S. Progressive Collapse Analysis of RC Frame Building Based on Pseudo-Dynamic (PsD) Testing with Sub-Structuring. J. Build. Eng. 2022, 52, 104420. [Google Scholar] [CrossRef]
- Huang, F.L.; Wang, X.M.; Chen, Z.Q.; He, X.H.; Ni, Y.Q. A New Approach to Identification of Structural Damping Ratios. J. Sound Vib. 2007, 303, 144–153. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Shen, J. Coarse-Grained Evaluation of the First Mode Damping Ratios in Buildings. J. Wind Eng. Ind. Aerodyn. 2022, 223, 104944. [Google Scholar] [CrossRef]
- Nejad, A.Z.B.; Sahebi, M.M. An Investigation on the Capability of Proper Orthogonal Modes in Determining the Natural Frequencies and Damping Ratios of Linear Structural Systems. Eng. Struct. 2021, 243, 112691. [Google Scholar] [CrossRef]
- Williams, K.R.; Lesser, T.H.J. A Finite Element Analysis of the Natural Frequencies of Vibration of the Human Tympanic Membrane. Part I. Br. J. Audiol. 1990, 24, 319–327. [Google Scholar] [CrossRef]
- Nandan, H.; Singh, M.P. Effects of Thermal Environment on Structural Frequencies. II: A System Identification Model. Eng. Struct. 2014, 81, 491–498. [Google Scholar] [CrossRef]
- Huang, M.S.; Gul, M.; Zhu, H.P. Vibration-Based Structural Damage Identification under Varying Temperature Effects. J. Aerosp. Eng. 2018, 31, 04018014. [Google Scholar] [CrossRef]
- Ji, X.; Xu, X.; Huang, K. Damage Detection of Frame Structure Using a Novel Time-Domain Regression Method. Discover Appl. Sci. 2024, 6, 359. [Google Scholar] [CrossRef]
- Khatami, S.; Naderpour, H.; Barros, R.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Effective Formula for Impact Damping Ratio for Simulation of Earthquake-Induced Structural Pounding. Geosciences 2019, 9, 347. [Google Scholar] [CrossRef]
- Gong, F.; Pan, C.; Xia, Y. Experimental Study on the Damping Ratio Evaluation of a Cable-Stayed Bridge Based on Damping Dissipation Function. Struct. Control Health Monit. 2025, 2025, 5810450. [Google Scholar] [CrossRef]
- De Risi, M.T.; Scala, S.A.; Del Gaudio, C.; Verderame, G.M. Seismic Retrofit of Italian Pre-‘70 Case-Study RC Buildings by Solving Shear Failures: Code-Compliant Assessment and Economic Effort. Int. J. Disaster Risk Reduct. 2023, 97, 104007. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á.; Caetano, E.; Brincker, R. Damping Estimation Using Free Decays and Ambient Vibration Tests. Mech. Syst. Signal Process. 2010, 24, 1274–1290. [Google Scholar] [CrossRef]
- Torvik, P.J. On Estimating System Damping from Frequency Response Bandwidths. J. Sound Vib. 2011, 330, 6088–6097. [Google Scholar] [CrossRef]
- Lee, S.H.; Min, K.W.; Hwang, J.S.; Kim, J. Evaluation of Equivalent Damping Ratio of a Structure with Added Dampers. Eng. Struct. 2004, 26, 335–346. [Google Scholar] [CrossRef]
- Avci, O. Amplitude-Dependent Damping in Vibration Serviceability: Case of a Laboratory Footbridge. J. Archit. Eng. 2016, 22, 04016005. [Google Scholar] [CrossRef]
- Zou, D.J.; Liu, T.J.; Qiao, G.F. Experimental Investigation on the Dynamic Properties of RC Structures Affected by the Reinforcement Corrosion. Adv. Struct. Eng. 2014, 17, 851–860. [Google Scholar] [CrossRef]
- Dai, K.; Lu, D.; Zhang, S.; Shi, Y.; Meng, J.; Huang, Z. Study on the Damping Ratios of Reinforced Concrete Structures from Seismic Response Records. Eng. Struct. 2020, 223, 111143. [Google Scholar] [CrossRef]
- Ha, T.; Shin, S.H.; Kim, H. Damping and Natural Period Evaluation of Tall RC Buildings Using Full-Scale Data in Korea. Appl. Sci. 2020, 10, 1568. [Google Scholar] [CrossRef]
- Khosravi, M.R.; Mohammadizadeh, M.R.; Saffari, H.; Torkzadeh, P. A Study of Progressive Collapse in Moment-Resisting Reinforced Concrete Structures Considering Damping Ratio. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 48, 3323–3337. [Google Scholar] [CrossRef]
- Guo, Z.; Sheng, M.; Ma, J.; Zhang, W. Damping Identification in Frequency Domain Using Integral Method. J. Sound Vib. 2015, 338, 237–249. [Google Scholar] [CrossRef]
- Brumat, M.; Slavič, J.; Boltežar, M. Spatial Damping Identification in the Frequency Domain—A Theoretical and Experimental Comparison. J. Sound Vib. 2016, 376, 182–193. [Google Scholar] [CrossRef]
- Zhou, R.; Yang, M.; Shang, C.; Zeng, Q. A Frequency Domain Identification Method of General Mechanical Drive System. In Proceedings of the 2023 IEEE 4th China International Youth Conference On Electrical Engineering (CIYCEE), Chengdu, China, 8–10 December 2023; pp. 1–7. [Google Scholar]
- Qu, C.-X.; Liu, Y.-F.; Yi, T.-H.; Li, H.-N. Structural Damping Ratio Identification through Iterative Frequency Domain Decomposition. J. Struct. Eng. 2023, 149, 5. [Google Scholar] [CrossRef]
- Kerschen, G.; Golinval, J. Frequency Domain Approaches for the Identification of an Experimental Beam with a Local Nonlinearity. In Proceedings of the 20th International Modal Analysis Conference, Los Angeles, CA, USA, 4–7 February 2002. [Google Scholar]
- Karaağaçlı, T.; Özgüven, H.N. A Frequency Domain Nonparametric Identification Method for Nonlinear Structures: Describing Surface Method. Mech. Syst. Signal Process. 2020, 144, 106872. [Google Scholar] [CrossRef]
- Gründel, L.; Reiners, C.; Lienenlüke, L.; Storms, S.; Brecher, C.; Bitterolf, D. Frequency-Based Identification of the Inertial Parameters of an Industrial Robot. In Lecture Notes in Production Engineering; Springer: Berlin/Heidelberg, Germany, 2020; pp. 429–438. [Google Scholar]
- Álvarez, R.; Borbor, E.; Grijalva, F. Comparison of methods for signal analysis in the time-frequency domain. In Proceedings of the 2019 IEEE Fourth Ecuador Technical Chapters Meeting (ETCM), Guayaquil, Ecuador, 11–15 November 2019; pp. 1–6. [Google Scholar]
- Ying, H.; Liu, J.; Shen, S. Half-Power Band Width Method and INV Damping Ratio Solver Study. Noise Vib. Control 2006, 2006, 4–6. [Google Scholar]
- Sun, W.P.; Sun, Y.H.; Yu, Y.P.; Wu, B.S. A Comparison of the Improved and Classic Half-Power Bandwidth Methods in Estimating Damping for Multi-DOF Systems. J. Vib. Eng. Technol. 2018, 6, 219–225. [Google Scholar] [CrossRef]
- Vu, D.H.; Ta, D.-T. Viscous damping estimation of structures using extreme frequency bandwidth method. Vietnam Inst. Build. Sci. Technol. 2024, 3, 22–30. [Google Scholar] [CrossRef]
- Sun, P.; Wang, D. Comparison of Damping Parameters Based on the Half-Power Bandwidth Methods of Viscous and Hysteretic Damping Models. J. Vib. Control 2021, 29, 968–979. [Google Scholar] [CrossRef]
- Wang, J.-T.; Jin, F.; Zhang, C.-H. Estimation Error of the Half-Power Bandwidth Method in Identifying Damping for Multi-DOF Systems. Soil Dyn. Earthq. Eng. 2012, 39, 138–142. [Google Scholar] [CrossRef]
- Papagiannopoulos, G.A.; Hatzigeorgiou, G.D. On the Use of the Half-Power Bandwidth Method to Estimate Damping in Building Structures. Soil Dyn. Earthq. Eng. 2011, 31, 1075–1079. [Google Scholar] [CrossRef]
- Wu, B. A Correction of the Half-Power Bandwidth Method for Estimating Damping. Arch. Appl. Mech. 2015, 85, 315–320. [Google Scholar] [CrossRef]
- Treszkai, M.F.; Sipos, D.; Feszty, D. Damping Determination by Half-Power Bandwidth Method for a Slightly Damped Rectangular Steel Plate in the Mid-Frequency Range. Acta Tech. Jaurinensis 2020, 13, 177–196. [Google Scholar] [CrossRef]
- Wang, X.; Liu, K.; Liu, H.; He, Y. Damping Identification with Acceleration Measurements Based on Sensitivity Enhancement Method. Shock Vib. 2018, 2018, 6476783. [Google Scholar] [CrossRef]
- Zhang, G.; Tang, B.; Chen, Z. Operational Modal Parameter Identification Based on PCA-CWT. Measurement 2019, 139, 334–345. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, X.; Li, Y.; Sun, H.; Zhang, J.; Huang, B. Improved Continuous Wavelet Transforms for Modal Parameter Identification of Long-Span Bridges. Shock Vib. 2020, 2020, 4360184. [Google Scholar] [CrossRef]
- Dou, H.; Hua, Y.; Qi, A.; Xu, J.; Zhao, J. A Transient Response Domain Time Analysis Method of Transmission Lines. In Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2019; pp. 869–873. [Google Scholar]
- Ge, C.; Sutherland, S. Application of Experimental Modal Analysis to Determine Damping Properties for Stacked Corrugated Boxes. Math. Probl. Eng. 2013, 2013, 651348. [Google Scholar] [CrossRef]
- López-Aragón, J.A.; Puchol, V.; Astiz, M.A. Influence of the Modal Damping Ratio Calculation Method in the Analysis of Dynamic Events Obtained in Structural Health Monitoring of Bridges. J. Civil Struct. Health Monit. 2024, 14, 1191–1213. [Google Scholar] [CrossRef]
- Yang, P.; Ying, L.; Chen, M.; Wang, J.; Wang, G. The Processing Method of Background Noise in Secondary Path Identification of ANC System. In Electrical Measurement and Instrumentation; Atlantis Press: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Koruk, H.; Rajagopal, S. A Comprehensive Review on the Viscoelastic Parameters Used for Engineering Materials, Including Soft Materials, and the Relationships between Different Damping Parameters. Sensors 2024, 24, 6137. [Google Scholar] [CrossRef]
- Dziedziech, K.; Staszewski, W.J.; Uhl, T. Wavelet-Based Modal Analysis for Time-Variant Systems. Mech. Syst. Signal Process. 2015, 50–51, 323–337. [Google Scholar] [CrossRef]
- Xi, Y.; Zhang, X.; Pan, J.; Sun, L.; Li, H.; Wang, Z. Assessment of Damping in Monopile-Supported Offshore Wind Turbines: Integrating Operational Modal Analysis with Regression Techniques. Structures 2025, 75, 108702. [Google Scholar] [CrossRef]
- Bernal, D. Analytical Minimization of Synchronicity Errors in Stochastic Identification. Mech. Syst. Signal Process. 2018, 98, 415–424. [Google Scholar] [CrossRef]
- Stachiw, T.; Ricciardi, J.; Crain, A. Combined Time- and Frequency-Domain Aircraft System Identification Using Pareto Optimization. In Volume 4: Advances in Aerospace Technology, Proceedings of the ASME 2021 International Mechanical Engineering Congress and Exposition, Virtual, 1–5 November 2021; ASME: New York, NY, USA, 2021. [Google Scholar]
- Stollwitzer, A.; Bettinelli, L.; Loidl, S.; Schellander, J.; Vospernig, M.; Fink, J. Novel Evaluation Methods for Data-Based Determination of Damping Factors in the Frequency and Time Domains with Application on Railway Bridges. Railw. Eng. Sci. 2025; in press. [Google Scholar] [CrossRef]
- Zhang, X.; Luo, R.; He, J.; Hua, X.; Yang, L.; Peng, X.; Yang, C.; Chen, Z. Identification of Damping Ratios of Long-Span Bridges Using Adaptive Modal Extended Kalman Filter. Struct. Control Health Monit. 2025, 2025, 1493319. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Q.; Zhang, Q.; Wang, X.; Du, Y. Bayesian Continuous Wavelet Transform for Time-Varying Damping Identification of Cables Using Full-Field Measurement. Autom. Constr. 2024, 168, 105791. [Google Scholar] [CrossRef]
- Gong, F.; Xia, Y.; Komarizadehasl, S.; He, T. Bridge Damping Ratio Identification and Variation Analysis Based on Two-Year Monitoring Data Considering Operational Environment Effects. Struct. Control Health Monit. 2025, 2025, 9191209. [Google Scholar] [CrossRef]
- Zhou, J.; Li, H.W.; Wang, Y.W.; Ni, Y.Q. Operational Modal Damping Identification Based on Compressive Sensing. J. Civ. Struct. Health Monit. 2025; in press. [Google Scholar] [CrossRef]
- Shang, X.-Q.; Huang, T.-L.; He, Y.-B.; Chen, H.-P. Operational Modal Analysis of Civil Engineering Structures with Closely Spaced Modes Based on Improved Hilbert–Huang Transform. Sensors 2024, 24, 7600. [Google Scholar] [CrossRef]
- Wang, Q.-G.; Zhang, L. System Identification in the Network Era: A Survey of Data Issues and Innovative Approaches. IEEE/CAA J. Autom. Sin. 2025, 12, 1305–1319. [Google Scholar] [CrossRef]
- Burdzik, R.; Khan, D. An Overview of the Current State of Knowledge and Technology on Techniques and Procedures for Signal Processing, Analysis, and Accurate Inference for Transportation Noise and Vibration. Measurement 2025, 252, 117314. [Google Scholar] [CrossRef]
- Felippa, C.A.; Guo, Q.; Park, K.C. Mass Matrix Templates: General Description and 1D Examples. Arch. Comput. Methods Eng. 2015, 22, 1–65. [Google Scholar] [CrossRef]
- Luo, S.; Liu, W. Coordinate Transformation Method of Finite Element Model for Frame Structures. Sichuan Build. Sci. 2016, 36, 17–23. [Google Scholar]
- Luo, S.; Zhu, J.; Liang, C.; Liu, W. Assembling Global Stiffness Matrix for Finite Element Model. J. Shenzhen Univ. Sci. Eng. 2018, 35, 467–472. [Google Scholar] [CrossRef]
- Hu, C.-B.; Wang, Y.-G.; Ling, D.-S. Physical Essence and Influence of Model Parameters on Dynamic Response of Rayleigh Damping. J. Zhejiang Univ. (Eng. Sci.) 2017, 51, 1284–1290. [Google Scholar]
- Zand, H.; Akbari, J. Selection of Viscous Damping Model for Evaluation of Seismic Responses of Buildings. KSCE J. Civ. Eng. 2018, 22, 4414–4421. [Google Scholar] [CrossRef]
- Swindlehurst, A.; Roy, R.; Ottersten, B.; Kailath, T. A Subspace Fitting Method for Identification of Linear State-Space Models. IEEE Trans. Autom. Control 1995, 40, 311–316. [Google Scholar] [CrossRef]
- Bernal, D.; Döhler, M.; Kojidi, S.M.; Kwan, K.; Yang, L. First Mode Damping Ratios for Buildings. Earthq. Spectra 2015, 31, 367–381. [Google Scholar] [CrossRef]
- Wu, X.; He, H.; Chen, G. A New State-Space Method for Exponentially Damped Linear Systems. Comput. Struct. 2019, 212, 137–144. [Google Scholar] [CrossRef]
- Luo, S.; Song, D.; Shen, K.; Fang, R.; Wang, W. Influence of the Order Exchange of the Node Connection in the Force Analysis of Steel Structures. Front. Mater. 2022, 9, 893291. [Google Scholar] [CrossRef]
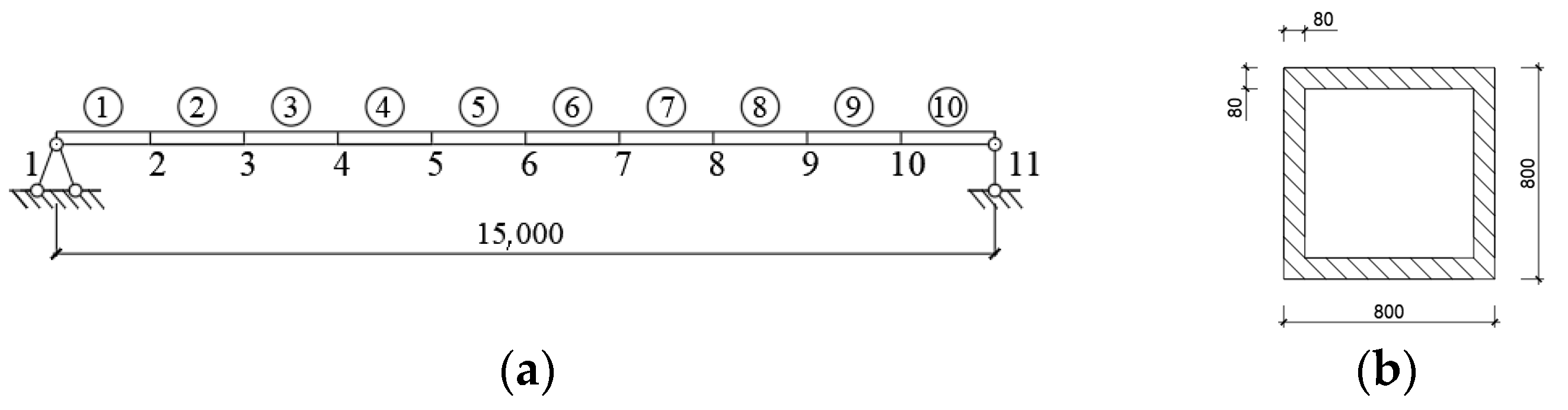







| Material Properties | Elastic Modulus (E) KN/m2 | Sectional Area (A) M2 | Moment of Inertia (I) M4 | Density (ρ) kg/m3 |
|---|---|---|---|---|
| Material property value | 2.1 × 108 | 0.23 | 0.02 | 7.85 × 103 |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Damping ratio | 0.00500 | 0.00800 | 0.01000 | 0.01200 | 0.01400 | 0.01600 | 0.01800 |
| Case | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Damping ratio | 0.02000 | 0.02500 | 0.03000 | 0.03500 | 0.04000 | 0.04500 | 0.05000 |
| Case | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Damping ratio | 0.05500 | 0.06000 | 0.06200 | 0.06400 | 0.06600 | 0.06800 | 0.07000 |
| Case | Set Damping Ratio | First-Order Natural Frequency Obtained by Matrices f’ Hz | First-Order Natural Frequency Obtained by FFT f1′ Hz | Relative Error |
|---|---|---|---|---|
| 1 | 0.00500 | 10.64795 | 10.54688 | 0.95% |
| 2 | 0.00800 | 10.64795 | 10.54688 | 0.95% |
| 3 | 0.01000 | 10.64795 | 10.54688 | 0.95% |
| 4 | 0.01200 | 10.64795 | 10.54688 | 0.95% |
| 5 | 0.01400 | 10.64795 | 10.54688 | 0.95% |
| 6 | 0.01600 | 10.64795 | 10.54688 | 0.95% |
| 7 | 0.01800 | 10.64795 | 10.54688 | 0.95% |
| 8 | 0.02000 | 10.64795 | 10.54688 | 0.95% |
| 9 | 0.02500 | 10.64795 | 10.54688 | 0.95% |
| 10 | 0.03000 | 10.64795 | 10.54688 | 0.95% |
| 11 | 0.03500 | 10.64795 | 10.54688 | 0.95% |
| 12 | 0.04000 | 10.64795 | 10.54688 | 0.95% |
| 13 | 0.04500 | 10.64795 | 10.54688 | 0.95% |
| 14 | 0.05000 | 10.64795 | 10.54688 | 0.95% |
| 15 | 0.05500 | 10.64795 | 10.54688 | 0.95% |
| 16 | 0.06000 | 10.64795 | 10.54688 | 0.95% |
| 17 | 0.06200 | 10.64795 | 10.54688 | 0.95% |
| 18 | 0.06400 | 10.64795 | 10.54688 | 0.95% |
| 19 | 0.06600 | 10.64795 | 10.54688 | 0.95% |
| 20 | 0.06800 | 10.64795 | 10.54688 | 0.95% |
| 21 | 0.07000 | 10.64795 | 10.54688 | 0.95% |
| Case | Set Damping Ratio | Identification Damping Ratio | Relative Error |
|---|---|---|---|
| 1 | 0.00500 | 0.00508 | 1.60% |
| 2 | 0.00800 | 0.00788 | 1.50% |
| 3 | 0.01000 | 0.01006 | 0.60% |
| 4 | 0.01200 | 0.01197 | 0.25% |
| 5 | 0.01400 | 0.01399 | 0.07% |
| 6 | 0.01600 | 0.01599 | 0.06% |
| 7 | 0.01800 | 0.01800 | 0.00% |
| 8 | 0.02000 | 0.02002 | 0.10% |
| 9 | 0.02500 | 0.02510 | 0.40% |
| 10 | 0.03000 | 0.03018 | 0.60% |
| 11 | 0.03500 | 0.03532 | 0.91% |
| 12 | 0.04000 | 0.04027 | 0.67% |
| 13 | 0.04500 | 0.04512 | 0.27% |
| 14 | 0.05000 | 0.04993 | 0.14% |
| 15 | 0.05500 | 0.05456 | 0.80% |
| 16 | 0.06000 | 0.05904 | 1.60% |
| 17 | 0.06200 | 0.06081 | 1.92% |
| 18 | 0.06400 | 0.06277 | 1.92% |
| 19 | 0.06600 | 0.06840 | 3.64% |
| 20 | 0.06800 | 0.07099 | 4.40% |
| 21 | 0.07000 | 0.07385 | 5.50% |
| Case | Set Value | Identification Value at Node 2 | Identification Value at Node 3 | Identification Value at Node 4 | Identification Value at Node 5 | Identification Value at Node 6 |
|---|---|---|---|---|---|---|
| 1 | 0.00500 | 0.00508 | 0.00504 | 0.00500 | 0.00494 | 0.00490 |
| 2 | 0.00800 | 0.00788 | 0.00788 | 0.00787 | 0.00786 | 0.00785 |
| 3 | 0.01000 | 0.01006 | 0.01003 | 0.00997 | 0.00991 | 0.00986 |
| 4 | 0.01200 | 0.01197 | 0.01195 | 0.01193 | 0.01191 | 0.01189 |
| 5 | 0.01400 | 0.01399 | 0.01398 | 0.01397 | 0.01395 | 0.01393 |
| 6 | 0.01600 | 0.01599 | 0.01599 | 0.01598 | 0.01597 | 0.01596 |
| 7 | 0.01800 | 0.01800 | 0.01800 | 0.01800 | 0.01799 | 0.01798 |
| 8 | 0.02000 | 0.02002 | 0.02002 | 0.02002 | 0.02001 | 0.02000 |
| 9 | 0.02500 | 0.02510 | 0.02510 | 0.02510 | 0.02510 | 0.02510 |
| 10 | 0.03000 | 0.03018 | 0.03018 | 0.03018 | 0.03018 | 0.03018 |
| 11 | 0.03500 | 0.03532 | 0.03532 | 0.03532 | 0.03532 | 0.03532 |
| 12 | 0.04000 | 0.04027 | 0.04027 | 0.04027 | 0.04027 | 0.04027 |
| 13 | 0.04500 | 0.04512 | 0.04512 | 0.04512 | 0.04512 | 0.04512 |
| 14 | 0.05000 | 0.04993 | 0.04993 | 0.04993 | 0.04993 | 0.04993 |
| 15 | 0.05500 | 0.05456 | 0.05456 | 0.05456 | 0.05456 | 0.05456 |
| 16 | 0.06000 | 0.05904 | 0.05904 | 0.05904 | 0.05904 | 0.05904 |
| 17 | 0.06200 | 0.06081 | 0.06081 | 0.06081 | 0.06081 | 0.06081 |
| 18 | 0.06400 | 0.06277 | 0.06277 | 0.06277 | 0.06277 | 0.06277 |
| 19 | 0.06600 | 0.06840 | 0.06831 | 0.06819 | 0.06801 | 0.06796 |
| 20 | 0.06800 | 0.07099 | 0.07088 | 0.07072 | 0.07049 | 0.07040 |
| 21 | 0.07000 | 0.07385 | 0.07373 | 0.07350 | 0.07320 | 0.07304 |
| Case | Set Value | Mean Value | Standard Deviation | Root Mean Square Error | Lower Limit of Confidence Interval | Upper Limit of Confidence Interval |
|---|---|---|---|---|---|---|
| 1 | 0.00500 | 0.00499 | 0.00007 | 0.00012 | 0.00491 | 0.00507 |
| 2 | 0.00800 | 0.00787 | 0.00001 | 0.00006 | 0.00785 | 0.00788 |
| 3 | 0.01000 | 0.00997 | 0.00007 | 0.00012 | 0.00987 | 0.01006 |
| 4 | 0.01200 | 0.01193 | 0.00003 | 0.00005 | 0.01189 | 0.01197 |
| 5 | 0.01400 | 0.01396 | 0.00002 | 0.00003 | 0.01394 | 0.01399 |
| 6 | 0.01600 | 0.01598 | 0.00001 | 0.00002 | 0.01596 | 0.01599 |
| 7 | 0.01800 | 0.01799 | 0.00001 | 0.00001 | 0.01798 | 0.01800 |
| 8 | 0.02000 | 0.02001 | 0.00001 | 0.00001 | 0.02000 | 0.02002 |
| 9 | 0.02500 | 0.02510 | 0.00000 | 0.00004 | 0.02510 | 0.02510 |
| 10 | 0.03000 | 0.03018 | 0.00000 | 0.00008 | 0.03018 | 0.03018 |
| 11 | 0.03500 | 0.03532 | 0.00000 | 0.00014 | 0.03532 | 0.03532 |
| 12 | 0.04000 | 0.04027 | 0.00000 | 0.00012 | 0.04027 | 0.04027 |
| 13 | 0.04500 | 0.04512 | 0.00000 | 0.00005 | 0.04512 | 0.04512 |
| 14 | 0.05000 | 0.04993 | 0.00000 | 0.00003 | 0.04993 | 0.04993 |
| 15 | 0.05500 | 0.05456 | 0.00000 | 0.00020 | 0.05456 | 0.05456 |
| 16 | 0.06000 | 0.05904 | 0.00000 | 0.00043 | 0.05904 | 0.05904 |
| 17 | 0.06200 | 0.06081 | 0.00000 | 0.00053 | 0.06081 | 0.06081 |
| 18 | 0.06400 | 0.06277 | 0.00000 | 0.00055 | 0.06277 | 0.06277 |
| 19 | 0.06600 | 0.06817 | 0.00017 | 0.00111 | 0.06796 | 0.06838 |
| 20 | 0.06800 | 0.07070 | 0.00022 | 0.00139 | 0.07042 | 0.07097 |
| 21 | 0.07000 | 0.07346 | 0.00031 | 0.00179 | 0.07308 | 0.07384 |
| Datum Group 1 | Datum Group 2 | Datum Group 3 | Average Value | |
|---|---|---|---|---|
| Identification damping ratio | 0.0382 | 0.0385 | 0.0381 | 0.0383 |
| Relative error | 0.26% | 0.52% | 0.52% | 0.43% |
| Datum Group 1 | Datum Group 2 | Datum Group 3 | Average Value | |
|---|---|---|---|---|
| Identification damping ratio | 0.0341 | 0.0354 | 0.0341 | 0.0345 |
| Relative error | 1.16% | 2.61% | 1.16% |
| Cases | Incentive Type | Damping Ratio Type | Damping Ratio |
|---|---|---|---|
| 1 | Random | Measured damping ratio of node 3 | 0.0383 |
| 2 | Random | Measured damping ratio of node 4 | 0.0345 |
| 3 | Random | Empirical damping ratio | 0.0200 |
| 4 | El Centro seismic wave | Measured damping ratio of node 3 | 0.0383 |
| 5 | El Centro seismic wave | Measured damping ratio of node 4 | 0.0345 |
| 6 | El Centro seismic wave | Empirical damping ratio | 0.0200 |
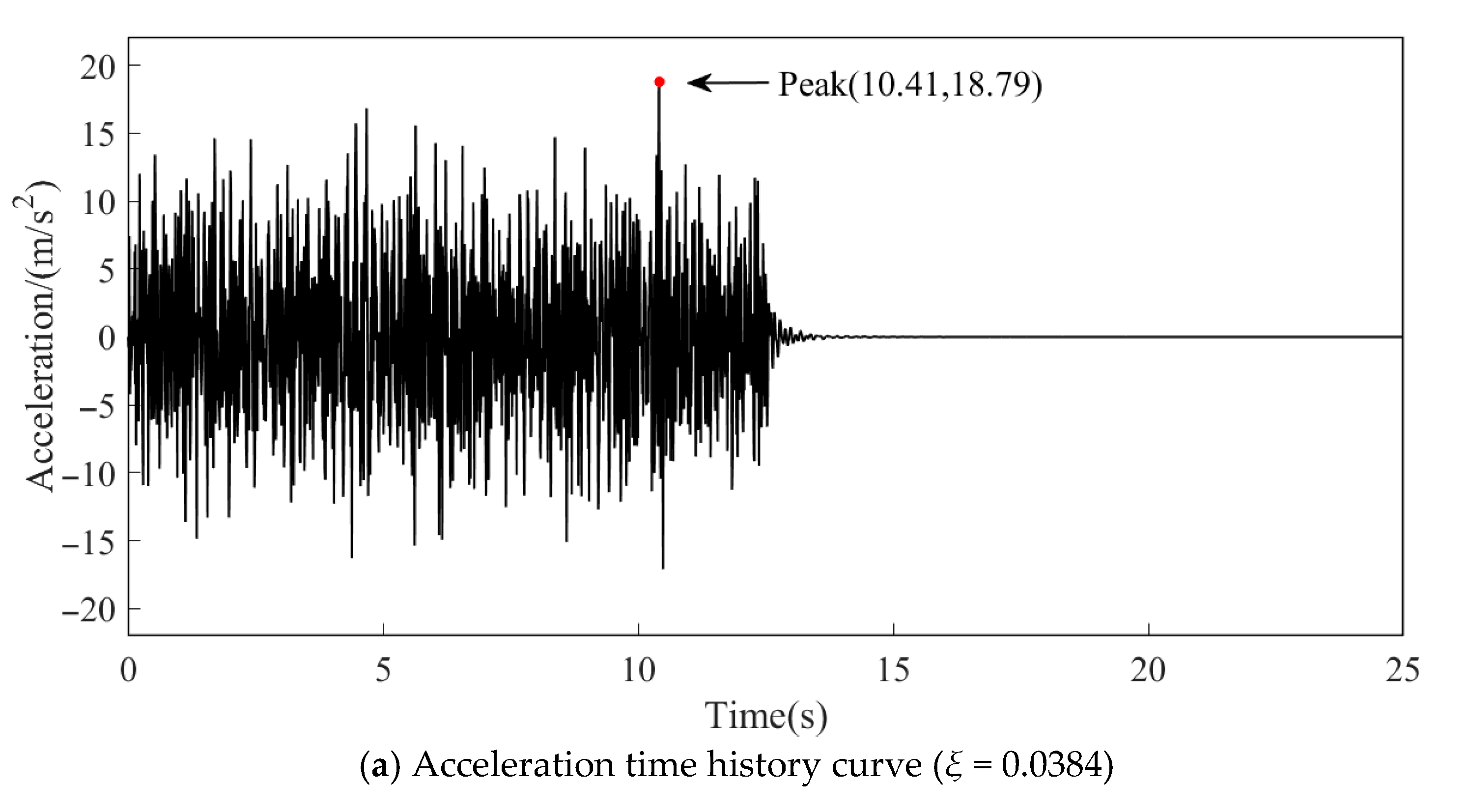
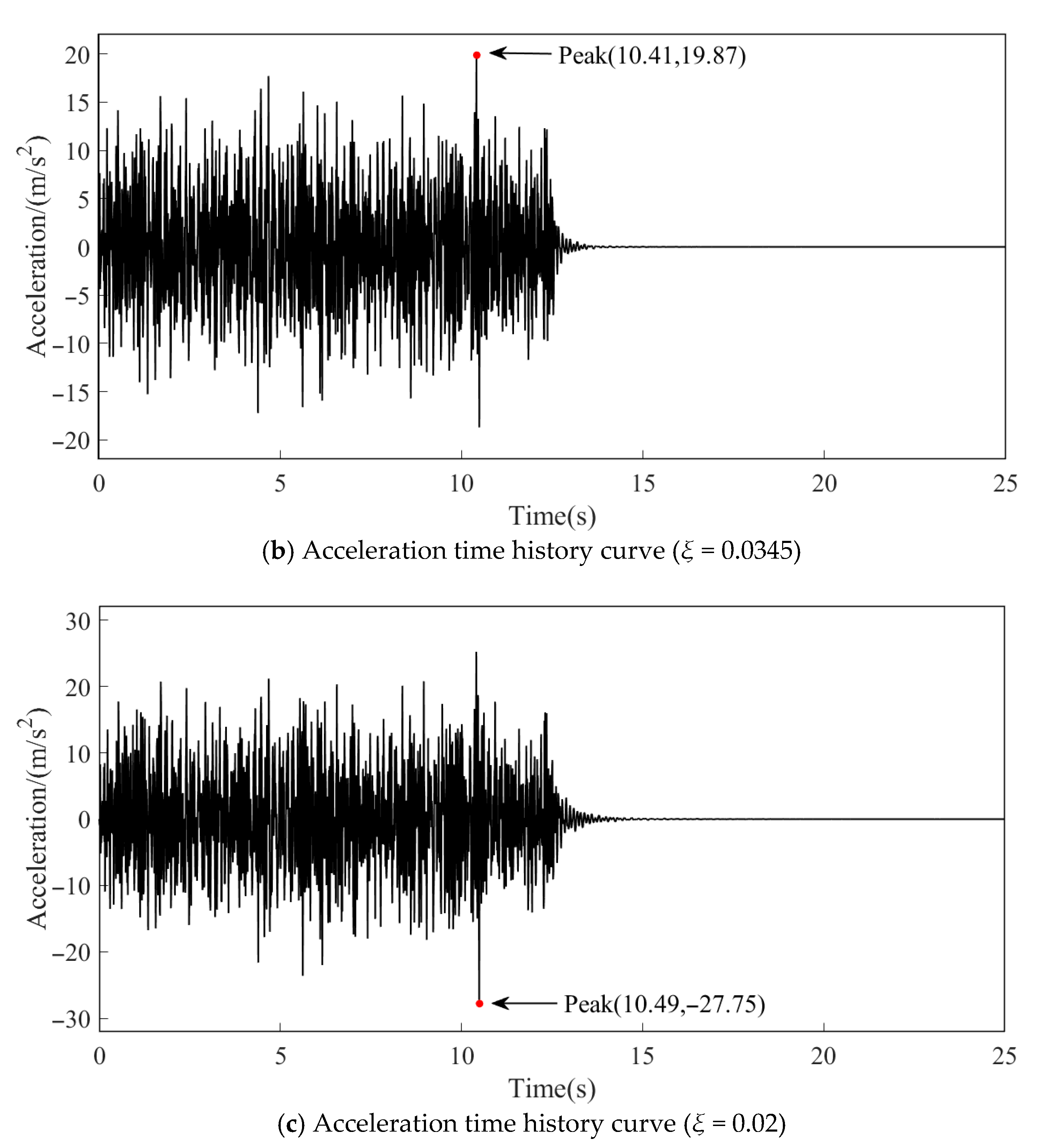
| Case | Damping Ratio | Time (s) | Absolute Value of Peak Acceleration (m/s2) | Relative Error of Peak Acceleration |
|---|---|---|---|---|
| 1 | 0.0383 | 10.41 | 18.7900 | 0 |
| 2 | 0.0345 | 10.41 | 19.8700 | 5.75% |
| 3 | 0.02 | 10.49 | 27.7500 | 47.68% |
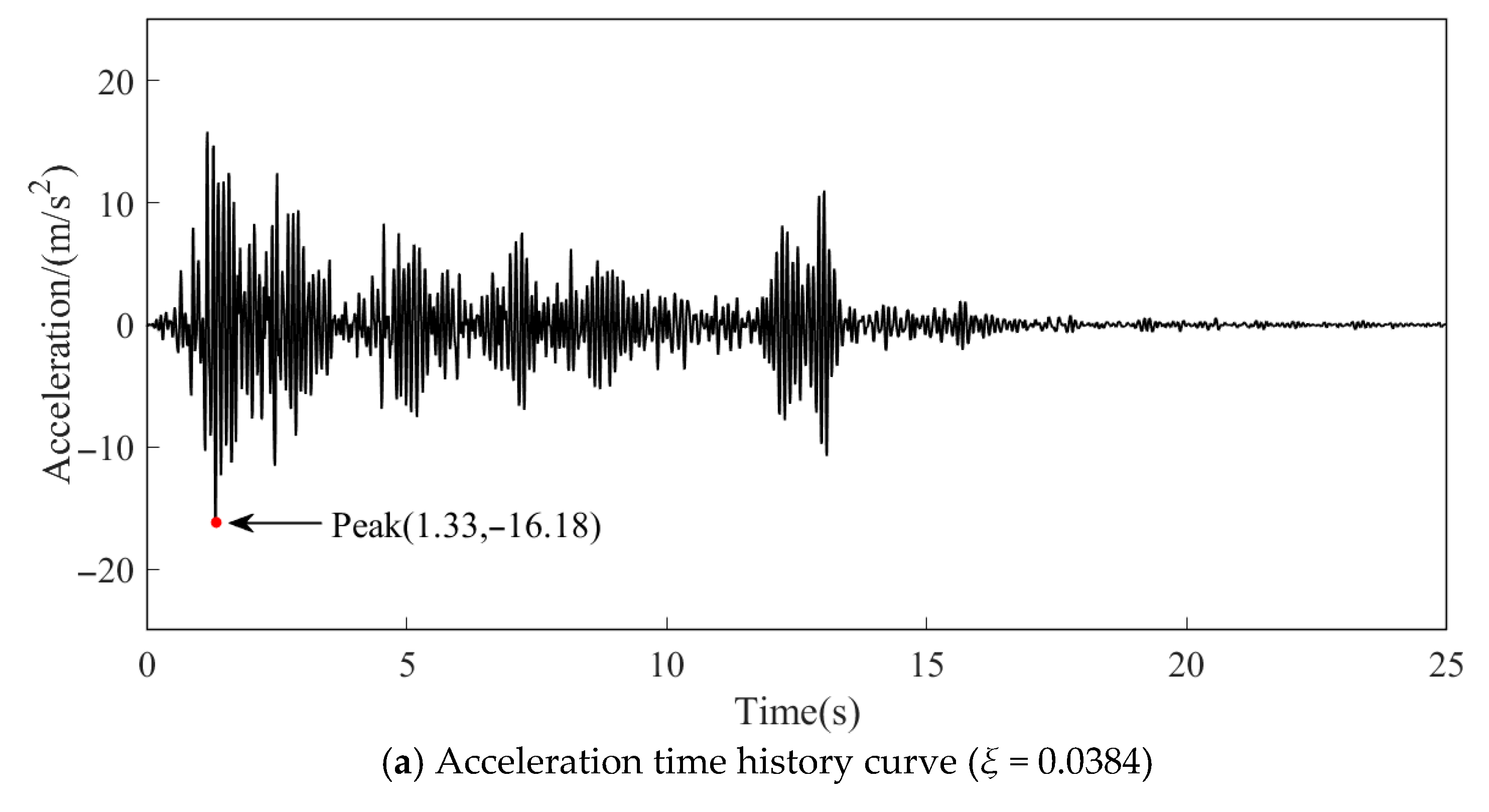
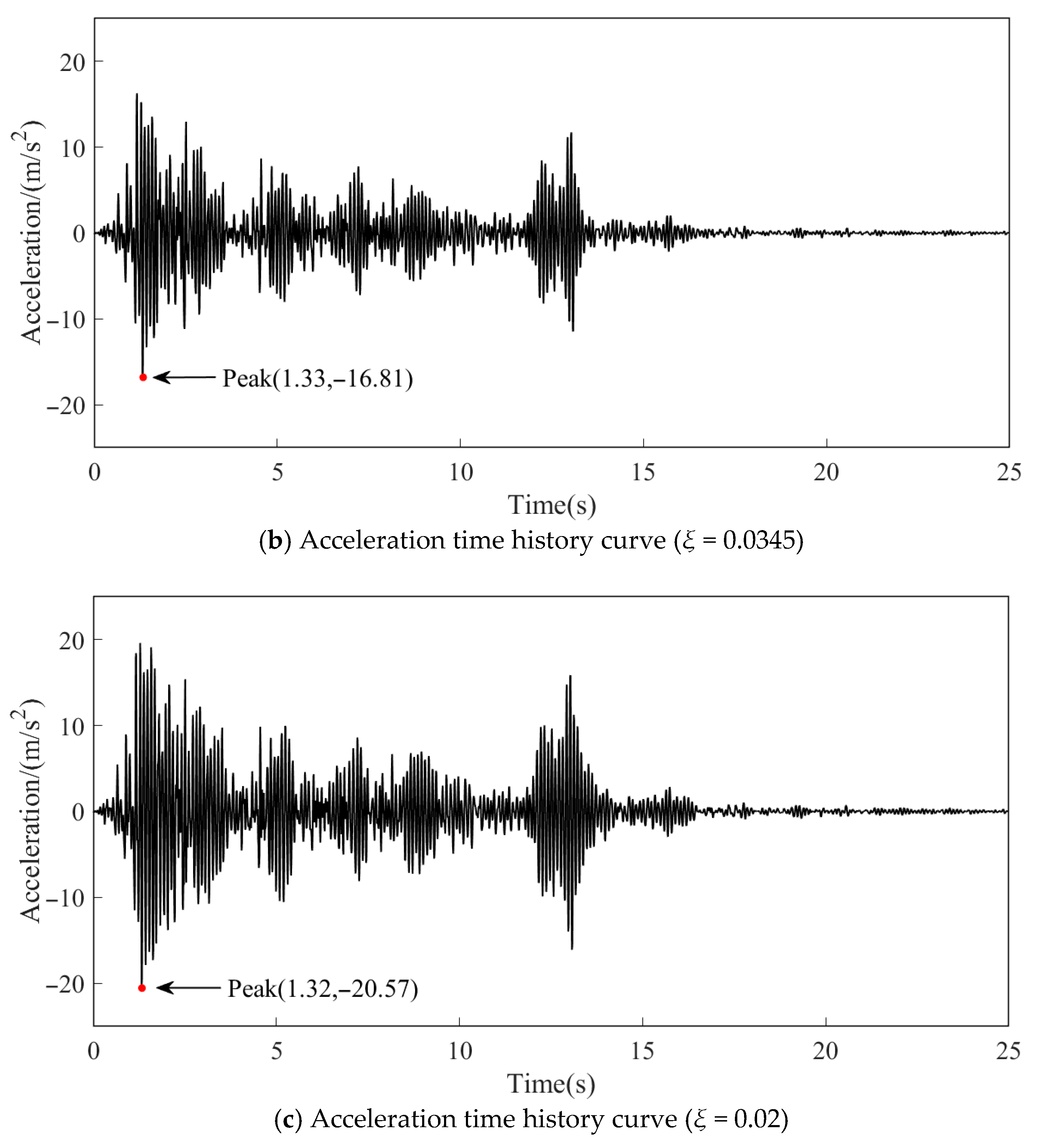
| Case | Damping Ratio | Time (s) | Absolute Value of Peak Acceleration (m/s2) | Relative Error of Peak Acceleration |
|---|---|---|---|---|
| 3 | 0.0383 | 1.33 | 16.18 | 0 |
| 4 | 0.0345 | 1.33 | 16.81 | 3.89% |
| 5 | 0.02 | 1.32 | 20.57 | 27.13% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, S.; Nong, Y.; Hou, G.; Yang, Q. First-Order Structural Modal Damping Ratio Identification by Withdrawing Amplitudes of Free Decaying Responses. Coatings 2025, 15, 962. https://doi.org/10.3390/coatings15080962
Luo S, Nong Y, Hou G, Yang Q. First-Order Structural Modal Damping Ratio Identification by Withdrawing Amplitudes of Free Decaying Responses. Coatings. 2025; 15(8):962. https://doi.org/10.3390/coatings15080962
Chicago/Turabian StyleLuo, Shuai, Youjie Nong, Gang Hou, and Qiuwei Yang. 2025. "First-Order Structural Modal Damping Ratio Identification by Withdrawing Amplitudes of Free Decaying Responses" Coatings 15, no. 8: 962. https://doi.org/10.3390/coatings15080962
APA StyleLuo, S., Nong, Y., Hou, G., & Yang, Q. (2025). First-Order Structural Modal Damping Ratio Identification by Withdrawing Amplitudes of Free Decaying Responses. Coatings, 15(8), 962. https://doi.org/10.3390/coatings15080962







