3D Printed Parts Exhibit Superior Elastic Properties to Milled Ones
Abstract
1. Introduction
2. Materials and Methods
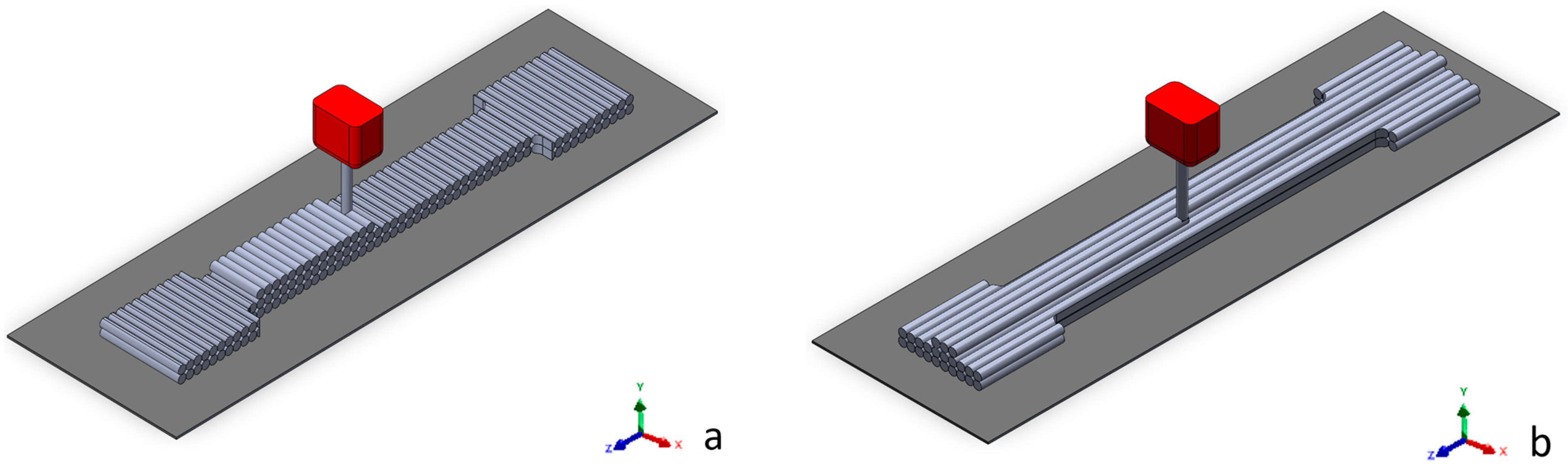
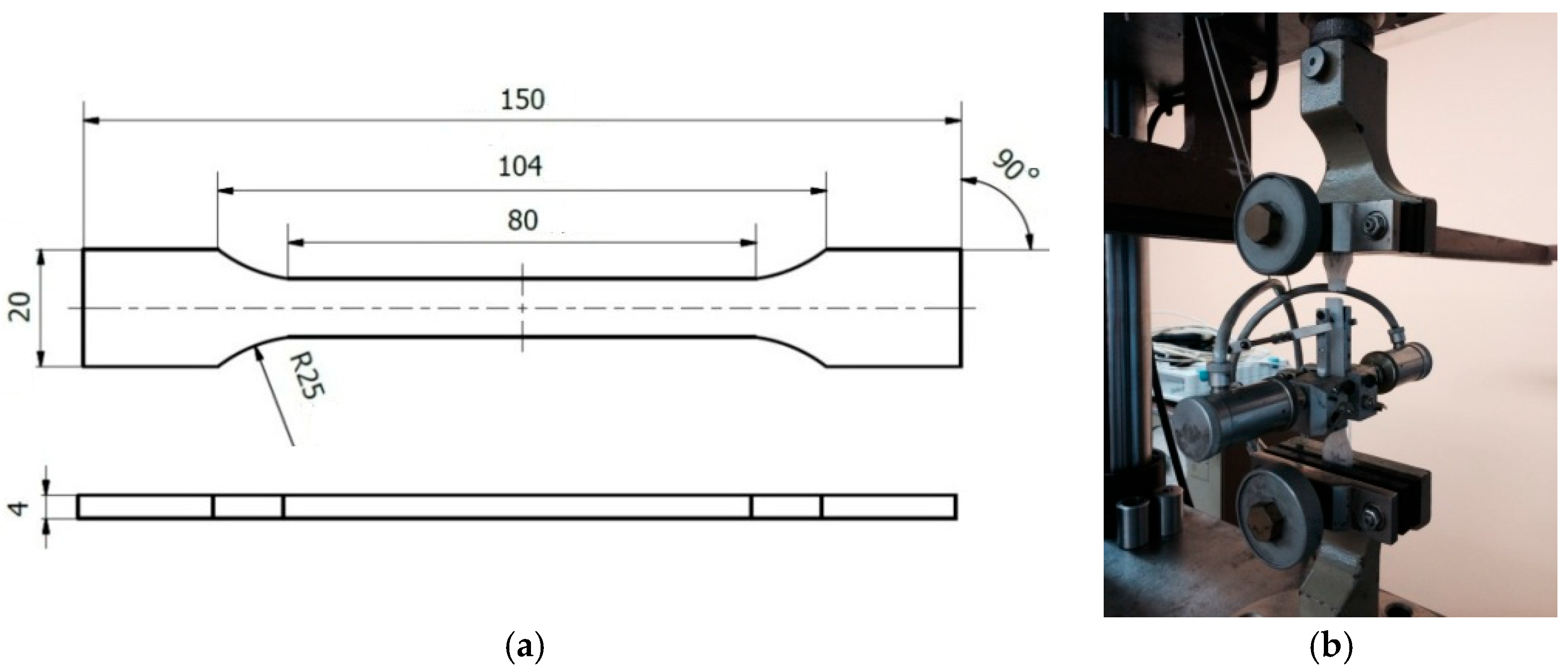
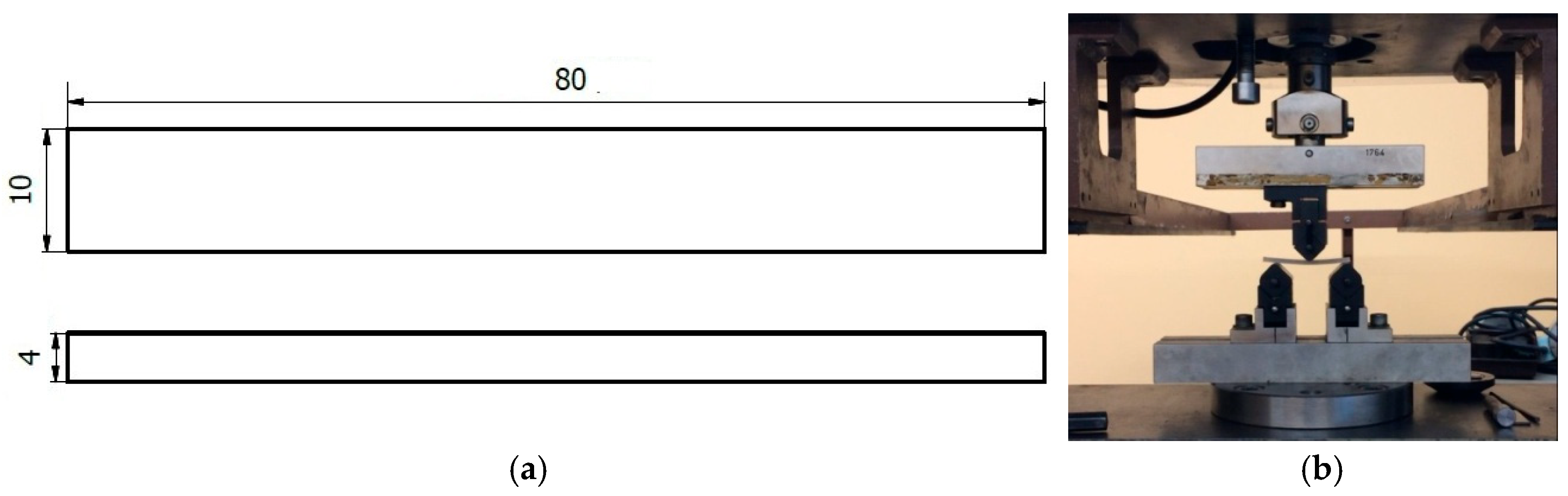
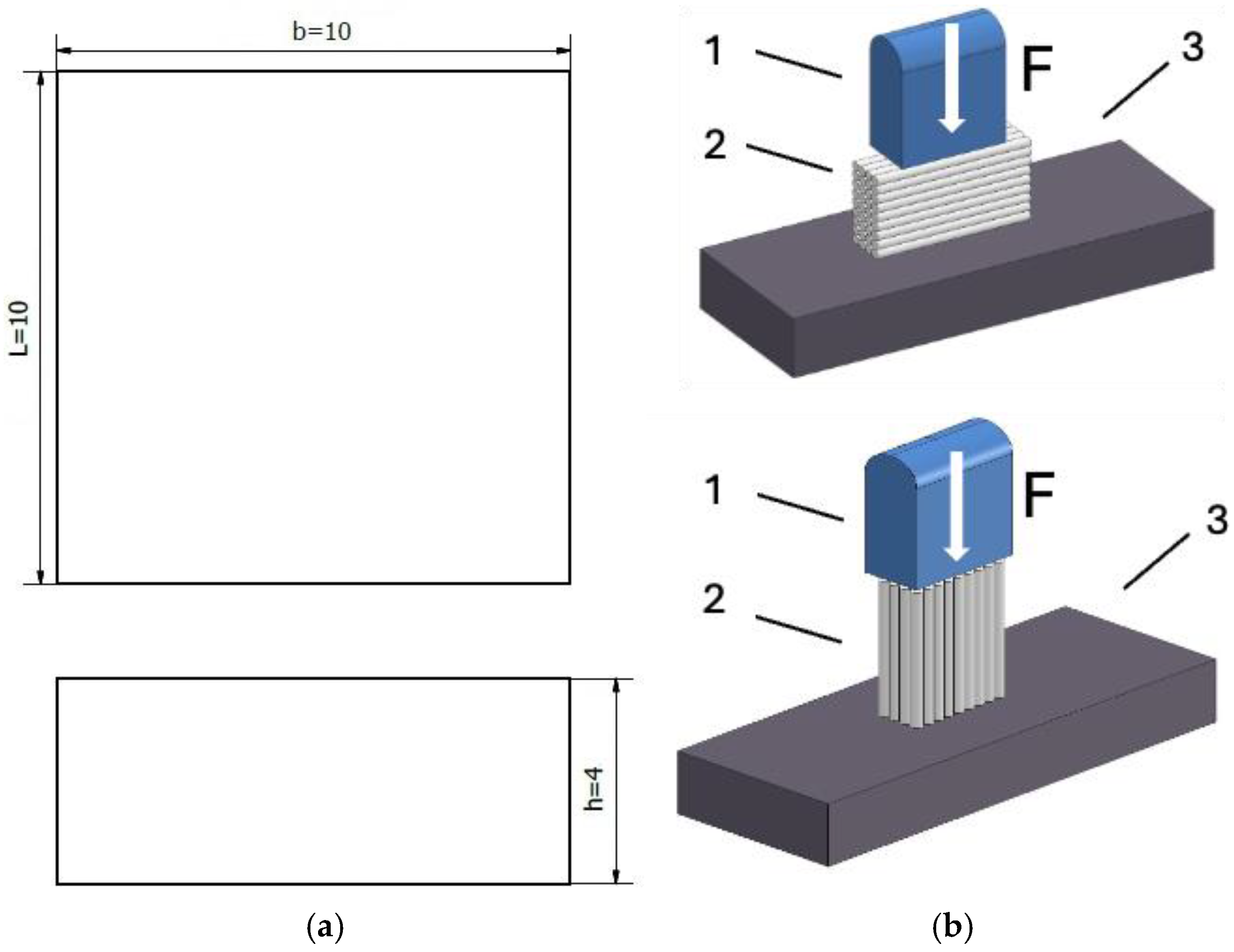
2.1. Sample Preparation
2.2. Testing Procedures
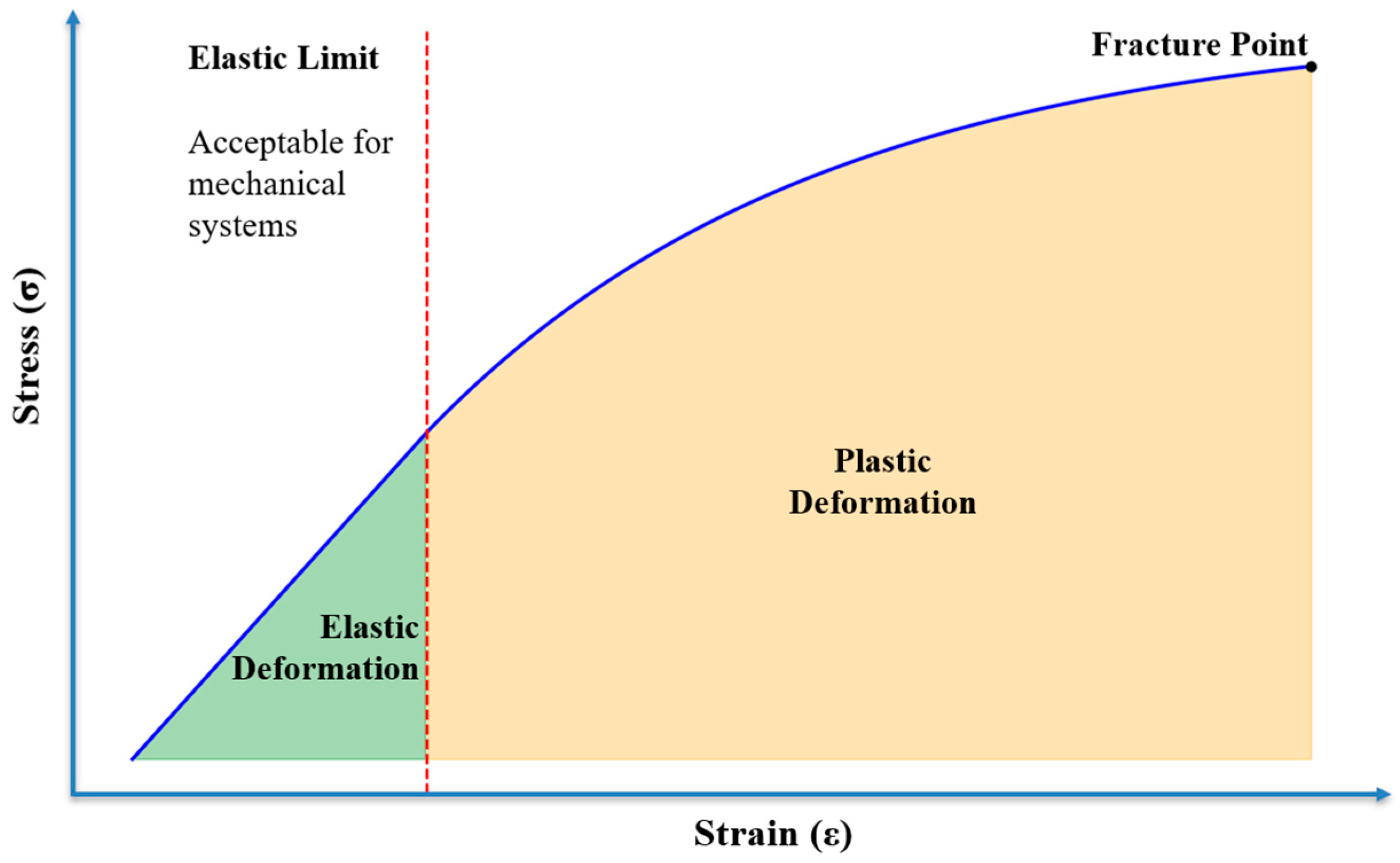
2.3. Evaluation of the Results
3. Results
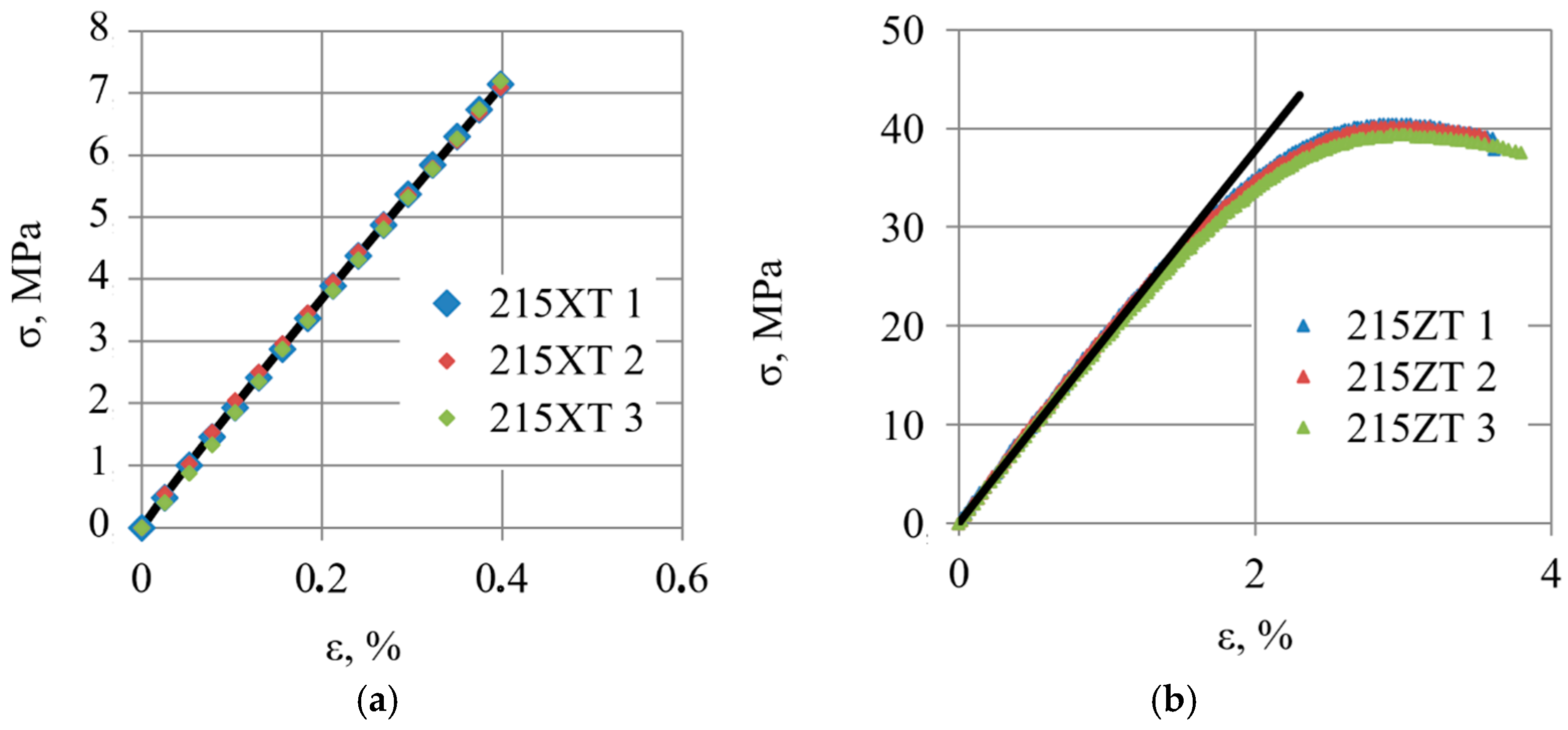
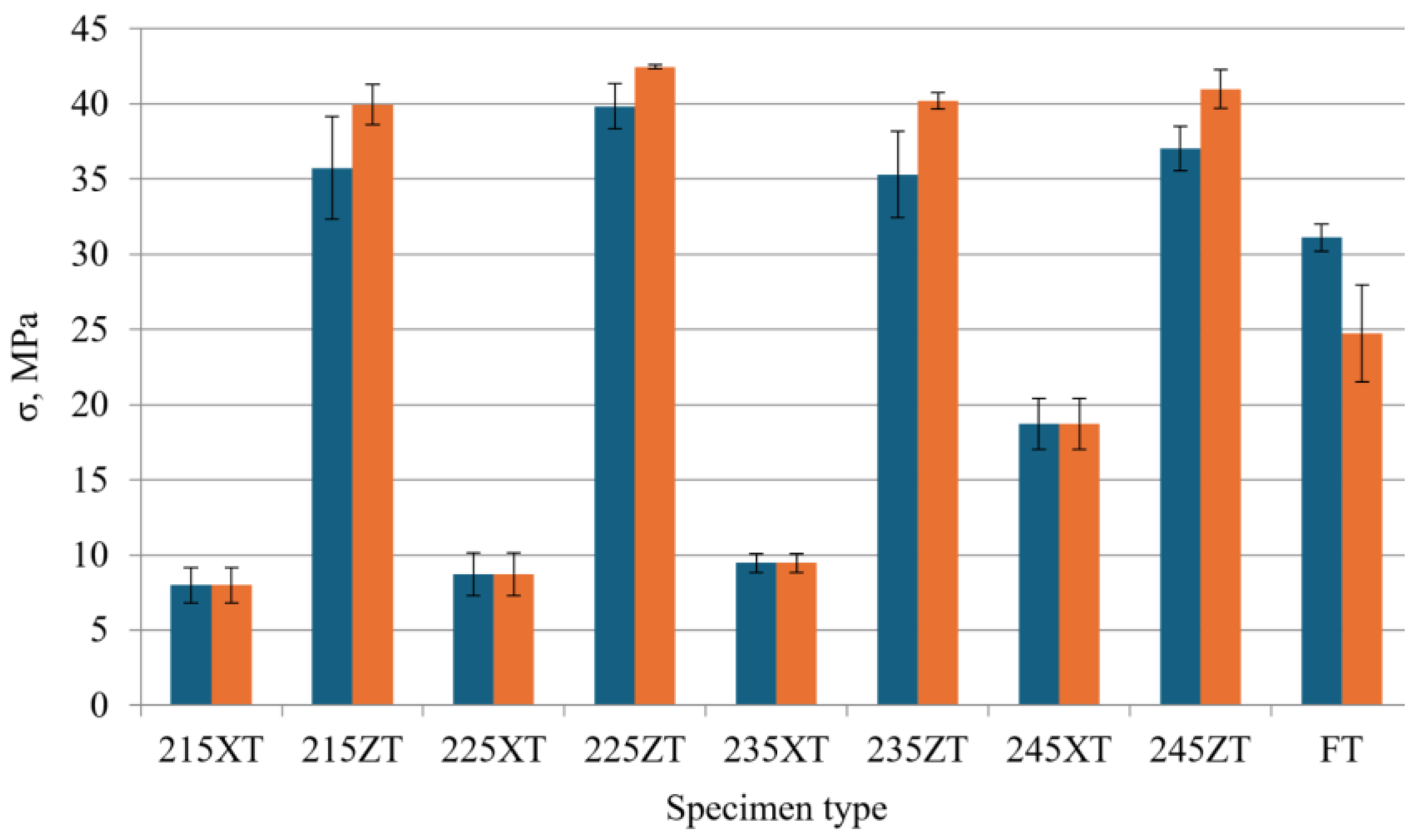
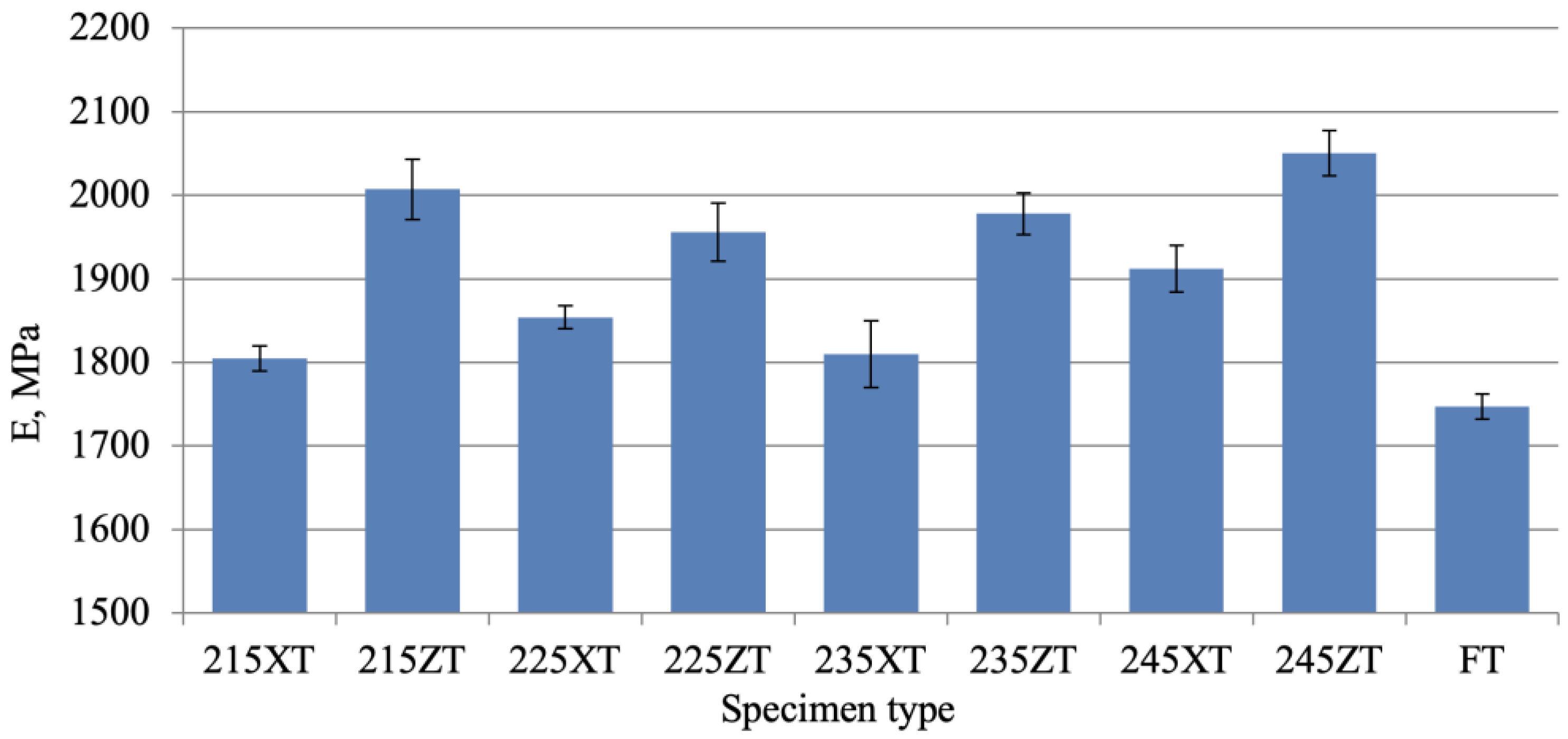
3.1. Tensile Properties
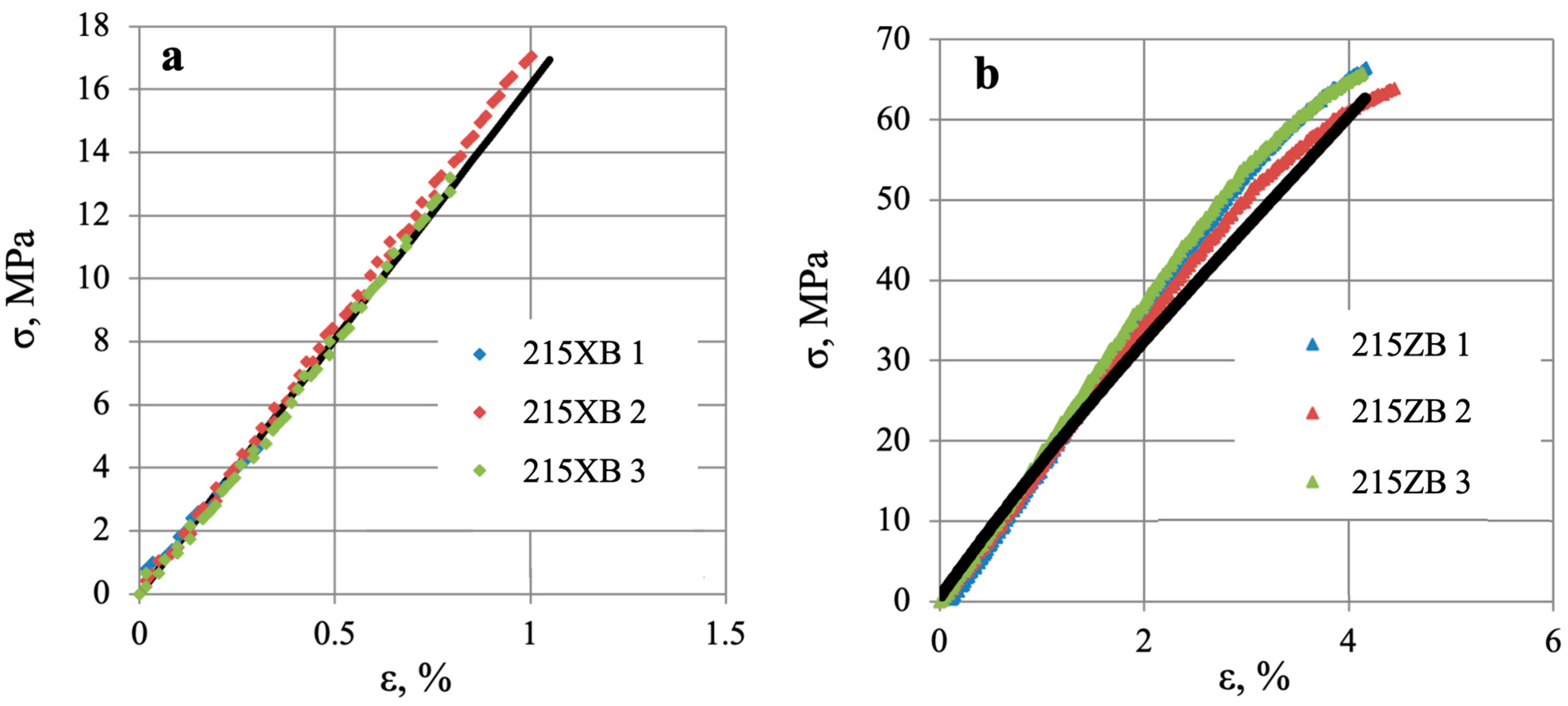
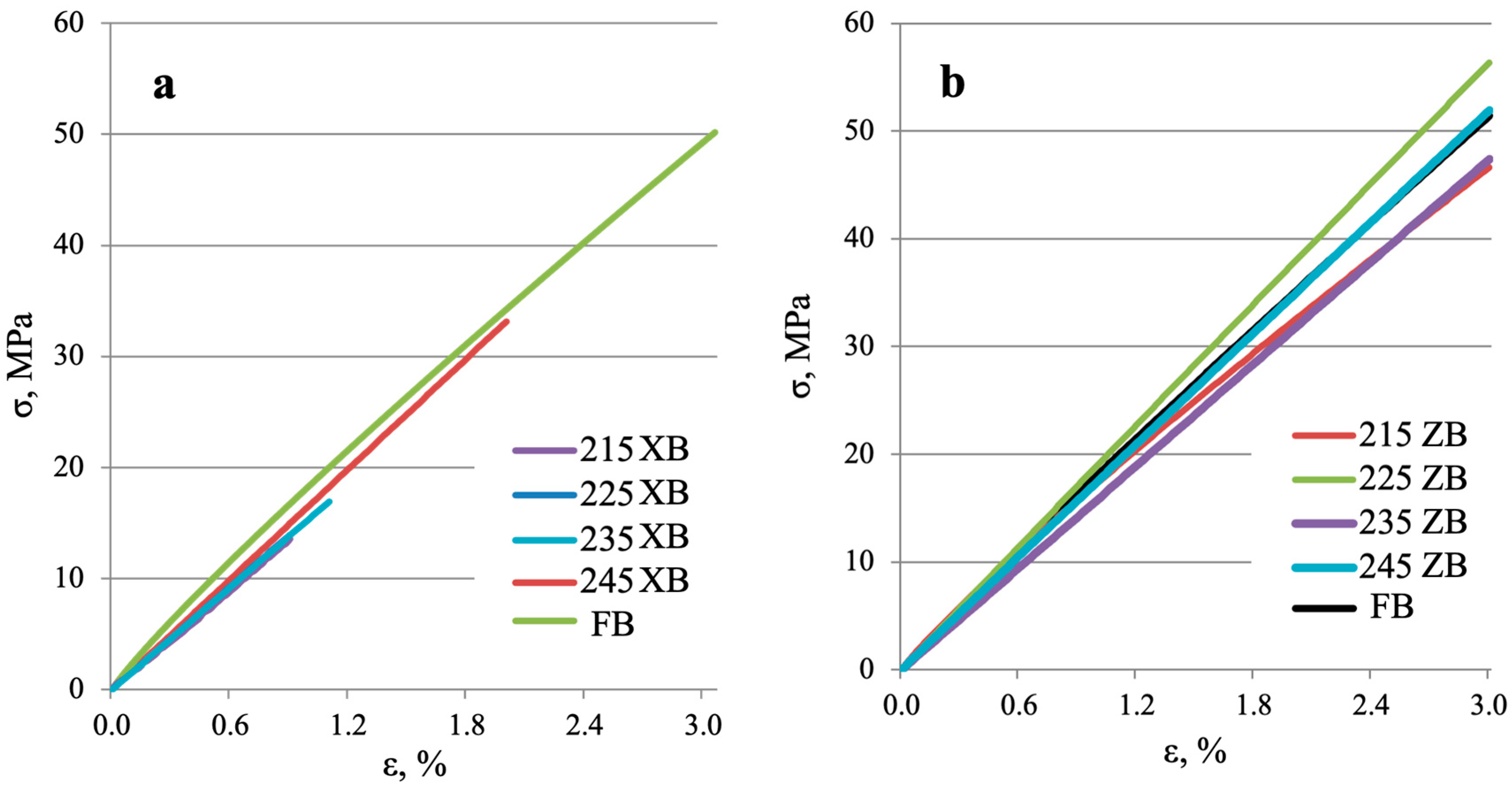
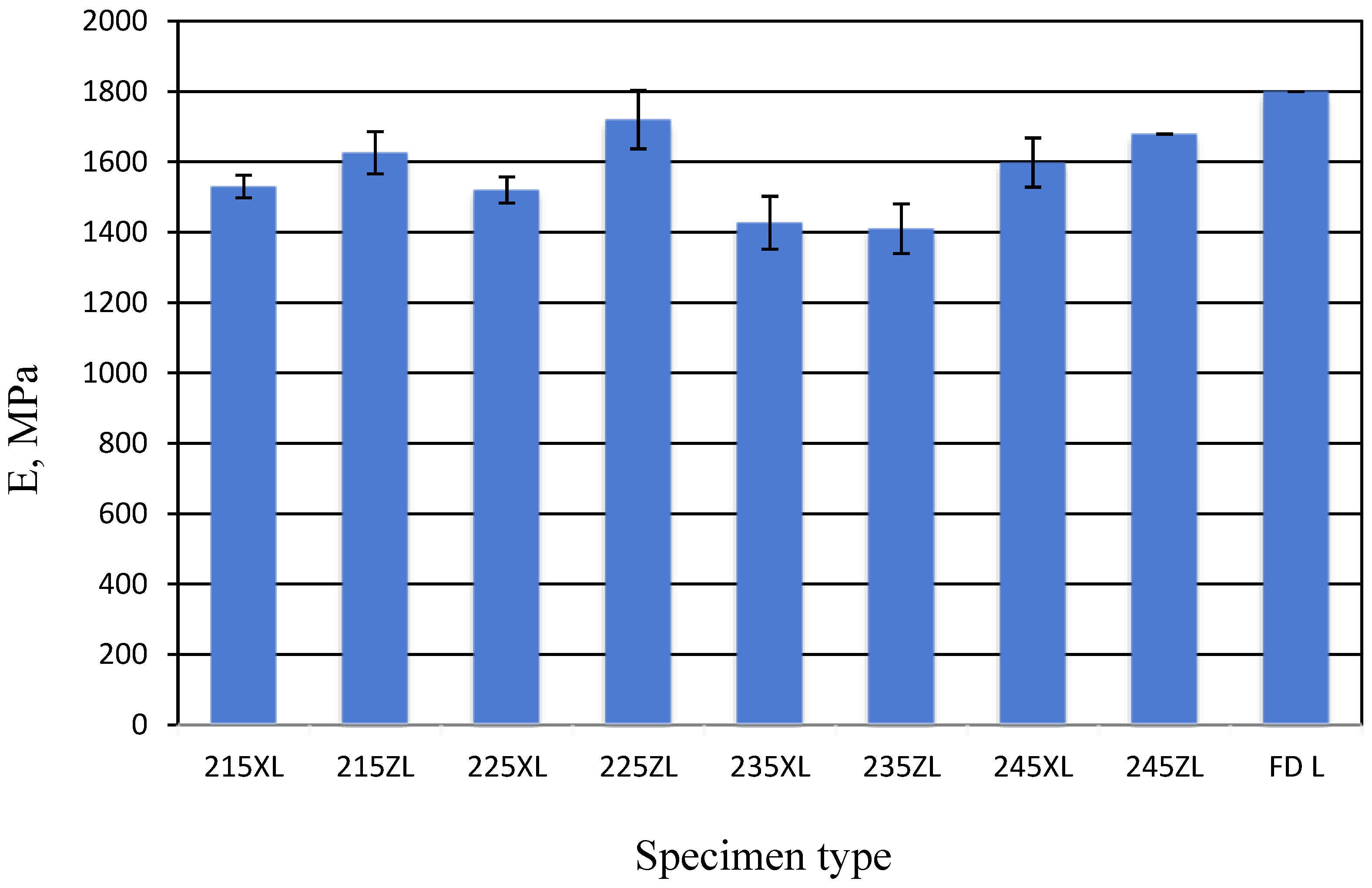
3.2. Bending Properties
3.3. Compression Test
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| σ (Normal Stress), MPa | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Test No. | 215XT | 215ZT | 225XT | 225ZT | 235XT | 235ZT | 245XT | 245ZT | FT |
| 1 | 7.90 | 40.43 | 8.97 | 42.53 | 8.95 | 41.68 | 17.23 | 41.44 | 31.24 |
| 2 | 7.10 | 40.17 | 8.47 | 42.28 | 9.42 | 39.80 | 20.82 | 40.55 | 30.16 |
| 3 | 8.96 | 39.27 | 8.73 | 42.56 | 10.05 | 39.11 | 18.10 | 40.98 | 31.96 |
| σv | 8.00 | 39.96 | 8.72 | 42.46 | 9.47 | 40.20 | 18.72 | 41.00 | 31.12 |
| σs | 0.93 | 0.61 | 0.29 | 0.15 | 0.56 | 1.33 | 1.88 | 0.46 | 0.91 |
| Ev | 1805 | 2007 | 1854 | 1956 | 1810 | 1978 | 1912 | 2050 | 1747 |
| Es | 15.00 | 36.10 | 14.14 | 35.20 | 40.00 | 25.20 | 28.87 | 26.50 | 15.20 |
| σ (Normal Stress at Fracture), MPa | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Test No. | 215XT | 215ZT | 225XT | 225ZT | 235XT | 235ZT | 245XT | 245ZT | FT |
| 1 | 7.9 | 37.88 | 8.97 | 39.79 | 8.95 | 36.08 | 17.23 | 38.49 | 20.99 |
| 2 | 7.1 | 31.79 | 8.47 | 38.39 | 9.42 | 32.14 | 20.82 | 35.51 | 26.40 |
| 3 | 8.96 | 37.55 | 8.73 | 41.42 | 10.05 | 37.72 | 18.1 | 37.13 | 26.77 |
| v | 8 | 35.74 | 8.72 | 39.84 | 9.47 | 35.31 | 18.72 | 37.04 | 24.72 |
| s | 1.18 | 3.4 | 1.42 | 1.51 | 0.62 | 2.86 | 1.69 | 1.49 | 0.9 |
| Normal Stresses (σ—Maximum Normal Stresses), MPa | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Test No. | 215XB | 215ZB | 225XB | 225ZB | 235XB | 235ZB | 245XB | 245ZB | FB |
| 1 | 14.02 | 66.53 | 16.02 | 65.77 | 19.01 | 59.71 | 36.28 | 61.88 | 53 |
| 2 | 17.05 | 63.96 | 14.99 | 66.71 | 20.25 | 59.31 | 33.57 | 62.96 | 50 |
| 3 | 13.19 | 65.90 | 13.20 | 63.51 | 19.67 | 60.43 | 33.16 | 60.38 | - |
| σv | 14.75 | 65.46 | 14.74 | 65.33 | 19.64 | 59.82 | 34.34 | 61.74 | 51 |
| σs | 2 | 1.33 | 1.42 | 1.64 | 0.62 | 0.5 | 1.7 | 1.29 | 1.9 |
| Ev | 1530 | 1626 | 1520 | 1720 | 1427 | 1410 | 1598 | 1679 | 1800 |
| Es | 32 | 60 | 37.2 | 83.2 | 75 | 70.7 | 70 | 121 | 70 |
| Normal Stresses (σ—Maximum Normal Stresses), MPa | |||
|---|---|---|---|
| Test No. | XC | ZC | FC |
| 1 | 54.08 | 39.97 | 45.8 |
| 2 | 50.36 | 44.23 | 47.9 |
| 3 | 52.36 | 43.1 | 44.5 |
| σvg | 52.2 | 43 | 46.1 |
| σs | 0.93 | 0.29 | 0.15 |
| Ea | 1750 | 1080 | 1500 |
References
- Prashar, G.; Vasudev, H.; Bhuddhi, D. Additive Manufacturing: Expanding 3D Printing Horizon in Industry 4.0. Int. J. Interact. Des. Manuf. 2023, 17, 2221–2235. [Google Scholar] [CrossRef]
- Zhou, L.; Miller, J.; Vezza, J.; Mayster, M.; Raffay, M.; Justice, Q.; Al Tamimi, Z.; Hansotte, G.; Sunkara, L.D.; Bernat, J. Additive Manufacturing: A Comprehensive Review. Sensors 2024, 24, 2668. [Google Scholar] [CrossRef]
- Kaur, G.; Singari, R.M.; Kumar, H. A Review of Fused Filament Fabrication (FFF): Process Parameters and Their Impact on the Tribological Behavior of Polymers (ABS). Mater. Today Proc. 2022, 51, 854–860. [Google Scholar] [CrossRef]
- Mazzei Capote, G.A.; Rudolph, N.M.; Osswald, P.V.; Osswald, T.A. Failure Surface Development for ABS Fused Filament Fabrication Parts. Addit. Manuf. 2019, 28, 169–175. [Google Scholar] [CrossRef]
- Abbott, A.C.; Tandon, G.P.; Bradford, R.L.; Koerner, H.; Baur, J.W. Process-Structure-Property Effects on ABS Bond Strength in Fused Filament Fabrication. Addit. Manuf. 2018, 19, 29–38. [Google Scholar] [CrossRef]
- Rouf, S.; Raina, A.; Irfan Ul Haq, M.; Naveed, N.; Jeganmohan, S.; Farzana Kichloo, A. 3D Printed Parts and Mechanical Properties: Influencing Parameters, Sustainability Aspects, Global Market Scenario, Challenges and Applications. Adv. Ind. Eng. Polym. Res. 2022, 5, 143–158. [Google Scholar] [CrossRef]
- Ćwikła, G.; Grabowik, C.; Kalinowski, K.; Paprocka, I.; Ociepka, P. The Influence of Printing Parameters on Selected Mechanical Properties of FDM/FFF 3D-Printed Parts. IOP Conf. Ser. Mater. Sci. Eng. 2017, 227, 012033. [Google Scholar] [CrossRef]
- Mushtaq, R.T.; Iqbal, A.; Wang, Y.; Rehman, M.; Petra, M.I. Investigation and Optimization of Effects of 3D Printer Process Parameters on Performance Parameters. Materials 2023, 16, 3392. [Google Scholar] [CrossRef]
- Barclift, M.W.; Williams, C.B. Examining variability in the mechanical properties of parts manufactured via polyjet direct 3D printing. In Proceedings of the 23rd Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 14–16 August 2023. [Google Scholar]
- Doshi, M.; Mahale, A.; Singh, S.K.; Deshmukh, S. Printing Parameters and Materials Affecting Mechanical Properties of FDM-3D Printed Parts: Perspective and Prospects. Mater. Today Proc. 2022, 50, 2269–2275. [Google Scholar] [CrossRef]
- Asadi-Eydivand, M.; Solati-Hashjin, M.; Farzad, A.; Abu Osman, N.A. Effect of Technical Parameters on Porous Structure and Strength of 3D Printed Calcium Sulfate Prototypes. Robot. Comput. Integr. Manuf. 2016, 37, 57–67. [Google Scholar] [CrossRef]
- Lanzotti, A.; Grasso, M.; Staiano, G.; Martorelli, M. The Impact of Process Parameters on Mechanical Properties of Parts Fabricated in PLA with an Open-Source 3-D Printer. Rapid Prototyp. J. 2015, 21, 604–617. [Google Scholar] [CrossRef]
- Syrlybayev, D.; Zharylkassyn, B.; Seisekulova, A.; Akhmetov, M.; Perveen, A.; Talamona, D. Optimisation of Strength Properties of FDM Printed Parts—A Critical Review. Polymers 2021, 13, 1587. [Google Scholar] [CrossRef]
- Kumar, N.; Jain, P.K.; Tandon, P.; Pandey, P.M. The Effect of Process Parameters on Tensile Behavior of 3D Printed Flexible Parts of Ethylene Vinyl Acetate (EVA). J. Manuf. Process 2018, 35, 317–326. [Google Scholar] [CrossRef]
- Chadha, A.; Ul Haq, M.I.; Raina, A.; Singh, R.R.; Penumarti, N.B.; Bishnoi, M.S. Effect of Fused Deposition Modelling Process Parameters on Mechanical Properties of 3D Printed Parts. World J. Eng. 2019, 16, 550–559. [Google Scholar] [CrossRef]
- Khaliq, J.; Gurrapu, D.R.; Elfakhri, F. Effects of Infill Line Multiplier and Patterns on Mechanical Properties of Lightweight and Resilient Hollow Section Products Manufactured Using Fused Filament Fabrication. Polymers 2023, 15, 2585. [Google Scholar] [CrossRef] [PubMed]
- Rendas, P.; Figueiredo, L.; Cláudio, R.; Vidal, C.; Soares, B. Investigating the Effects of Printing Temperatures and Deposition on the Compressive Properties and Density of 3D Printed Polyetheretherketone. Prog. Addit. Manuf. 2023, 9, 1883–1899. [Google Scholar] [CrossRef]
- Shanmugam, V.; Babu, K.; Kannan, G.; Mensah, R.A.; Samantaray, S.K.; Das, O. The Thermal Properties of FDM Printed Polymeric Materials: A Review. Polym. Degrad. Stab. 2024, 228, 110902. [Google Scholar] [CrossRef]
- Dziewit, P.; Rajkowski, K.; Płatek, P. Effects of Building Orientation and Raster Angle on the Mechanical Properties of Selected Materials Used in FFF Techniques. Materials 2024, 17, 6076. [Google Scholar] [CrossRef]
- Li, Z.; Chang, L. Development of Wear-Resistant Polymeric Materials Using Fused Deposition Modelling (FDM) Technologies: A Review. Lubricants 2025, 13, 98. [Google Scholar] [CrossRef]
- Kuznetsov, V.E.; Solonin, A.N.; Urzhumtsev, O.D.; Schilling, R.; Tavitov, A.G. Strength of PLA Components Fabricated with Fused Deposition Technology Using a Desktop 3D Printer as a Function of Geometrical Parameters of the Process. Polymers 2018, 10, 313. [Google Scholar] [CrossRef]
- Jackson, B.; Fouladi, K.; Eslami, B. Multi-Parameter Optimization of 3D Printing Condition for Enhanced Quality and Strength. Polymers 2022, 14, 1586. [Google Scholar] [CrossRef]
- Mazen, A.; McClanahan, B.; Weaver, J.M. Factors Affecting Ultimate Tensile Strength and Impact Toughness of 3D Printed Parts Using Fractional Factorial Design. Int. J. Adv. Manuf. Technol. 2022, 119, 2639–2651. [Google Scholar] [CrossRef]
- Bakhtiari, H.; Aamir, M.; Tolouei-Rad, M. Effect of 3D Printing Parameters on the Fatigue Properties of Parts Manufactured by Fused Filament Fabrication: A Review. Appl. Sci. 2023, 13, 904. [Google Scholar] [CrossRef]
- ISO 527-2:1993; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. ISO: Geneva, Switzerland, 2003.
- ISO 178:2003; Plastics—Determination of Flexural Properties. ISO: Geneva, Switzerland, 2003.
- ISO 604:2002; Plastics—Determination of Compressive Properties. ISO: Geneva, Switzerland, 2002.



| Manufacturing Method | 3D Printing | Milling | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature, °C | 215 | 225 | 235 | 245 | _ | ||||
| Orientation | X | Z | X | Z | X | Z | X | Z | _ |
| Tensile test | 215XT | 215ZT | 225XT | 225ZT | 235XT | 235ZT | 245XT | 245ZT | FT |
| Bending test | 215XB | 215ZB | 225XB | 225ZB | 235XB | 235ZB | 245XB | 245ZB | FB |
| Compression test | - | - | XC | ZC | - | - | - | - | FC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Striška, L.; Vaičiulis, D.; Tolvaišienė, S.; Udris, D.; Kozulinas, N.; Astrauskas, R.; Ramanavičius, A.; Morkvėnaitė, I. 3D Printed Parts Exhibit Superior Elastic Properties to Milled Ones. Coatings 2025, 15, 963. https://doi.org/10.3390/coatings15080963
Striška L, Vaičiulis D, Tolvaišienė S, Udris D, Kozulinas N, Astrauskas R, Ramanavičius A, Morkvėnaitė I. 3D Printed Parts Exhibit Superior Elastic Properties to Milled Ones. Coatings. 2025; 15(8):963. https://doi.org/10.3390/coatings15080963
Chicago/Turabian StyleStriška, Laisvidas, Dainius Vaičiulis, Sonata Tolvaišienė, Dainius Udris, Nikolajus Kozulinas, Rokas Astrauskas, Arūnas Ramanavičius, and Inga Morkvėnaitė. 2025. "3D Printed Parts Exhibit Superior Elastic Properties to Milled Ones" Coatings 15, no. 8: 963. https://doi.org/10.3390/coatings15080963
APA StyleStriška, L., Vaičiulis, D., Tolvaišienė, S., Udris, D., Kozulinas, N., Astrauskas, R., Ramanavičius, A., & Morkvėnaitė, I. (2025). 3D Printed Parts Exhibit Superior Elastic Properties to Milled Ones. Coatings, 15(8), 963. https://doi.org/10.3390/coatings15080963








