Synergistic Effect of Hetero Interstitial Atoms (C/N/O) on the Thermodynamic Stability in BCC Fe: A DFT Study
Abstract
1. Introduction
2. Calculation Details and Structural Models
2.1. Methods
2.2. Models
3. Results and Discussion
3.1. Stability of Single Interstitial C/N/O Atoms in BCC Fe Supercell
3.1.1. The Analysis of the Formation Energy of Single Interstitial C/N/O Atoms in BCC Fe Supercell
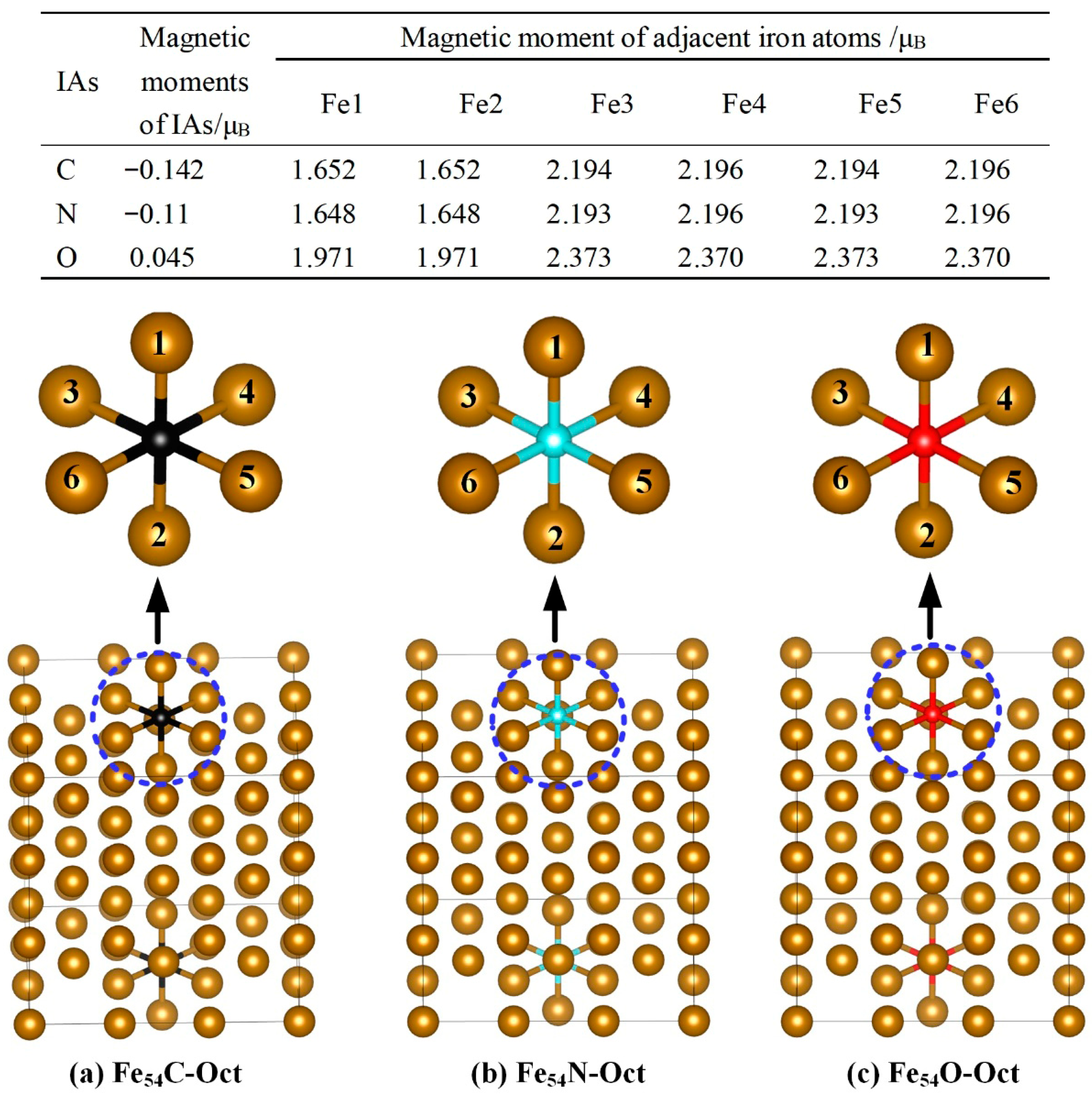
3.1.2. Effect of IAs on Lattice Constants and Magnetic Properties
3.1.3. Verifying Stability of O-Site Interstitial Atom at the Electronic Level
3.2. The Diffusion of a Single IA in Fe54 Supercell
3.3. The Occupying Sites and Stability of Double IAs in BCC Fe Supercell
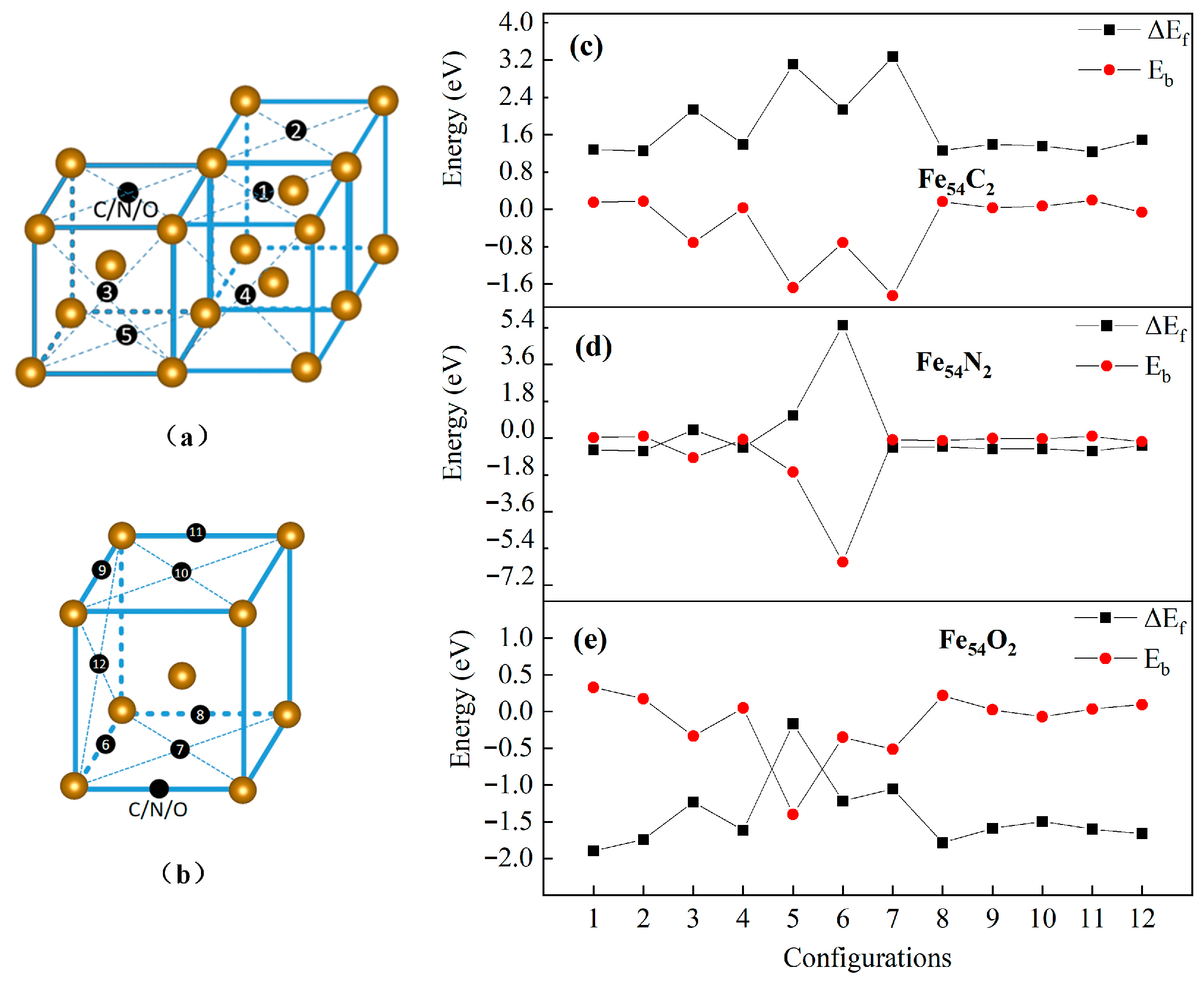
3.3.1. Two Homo IAs in Fe54 Lattice
3.3.2. Two Hetero IAs in Fe54 Lattice
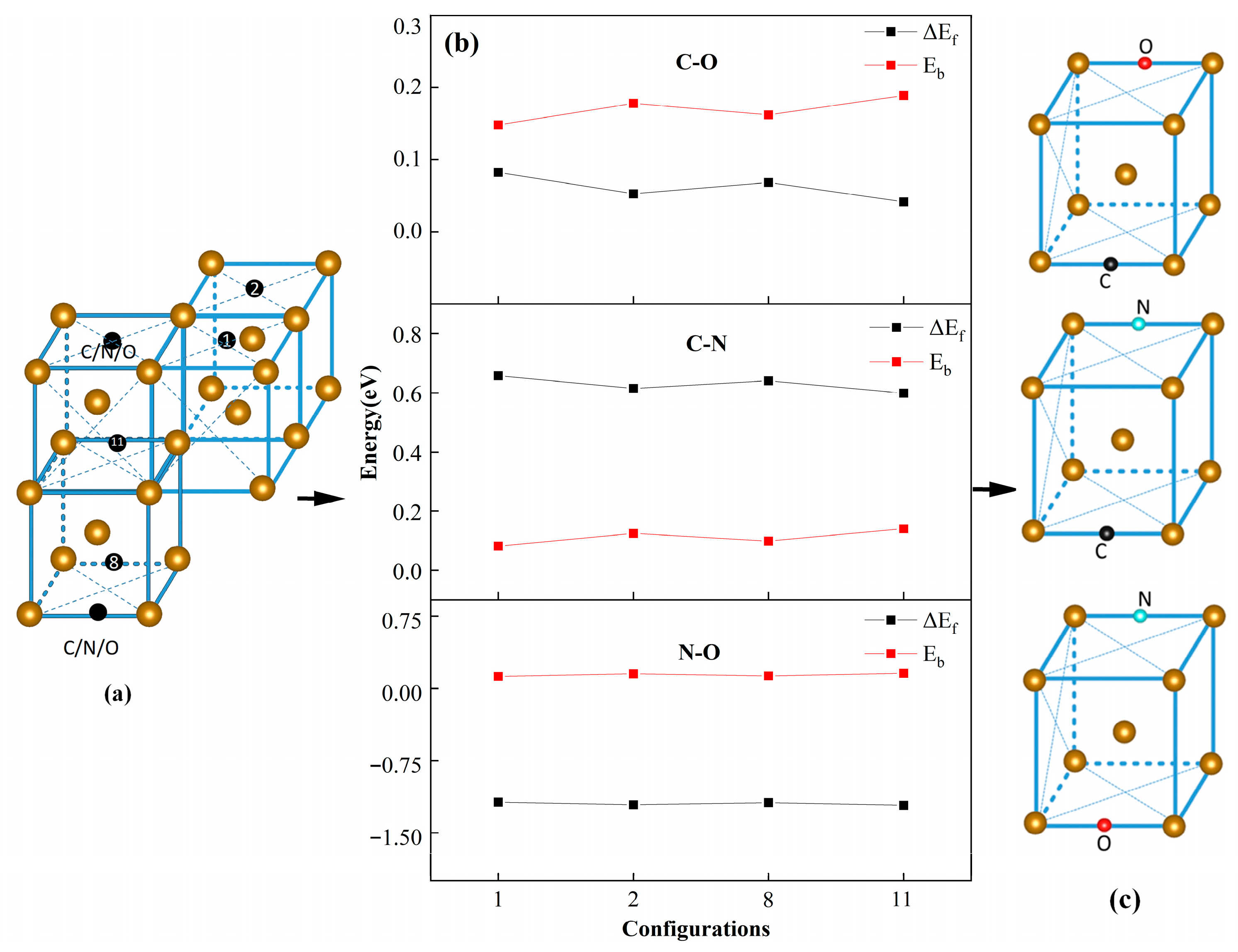
3.4. Synergistic Effects of Hetero IAs by Comparing with the Single and Homo IAs and Studying Oxygen Dissociation Behavior
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UHS-MSS | Ultra-high strength martensitic stainless steels |
| IAs | Interstitial atoms |
| DFT | Density functional theory |
| BCC Fe | Body-centered cubic iron |
| CI-NEB | Climbing-image nudged elastic band |
| VASP | Vienna ab initio Simulation Package |
| PAW | Projector-augmented wave |
| 1NN | The first-nearest-neighbor |
| 2NN | The second-nearest-neighbor |
| DOS | Density of states |
| PDOS | Projected density of states |
| O-sites | Octahedral sites |
| T-sites | Tetrahedral sites |
| BCT | Body-centered tetragonal |
| OCI-site | Octahedral central interstitial site |
| OEI-site | Edge interstitial site |
Appendix A



- Equation A1
| Total Energy (eV) | Formation Energy (eV) | Convergence Uncertainty (eV) | |
|---|---|---|---|
| 1 | −453.36276 | 0.7584 | 0 |
| 2 | −453.36277 | 0.7583 | −1 × 10−4 |
| 3 | −453.36274 | 0.7586 | 0.0002 |
| Alloy | Atom | Bader Charge | Atom Volume (Å3) |
|---|---|---|---|
| Fe54C | C | −1.048 | 7.388 |
| 1NN Fe | 0.056 | 10.677 | |
| 2NN Fe | 0.147 | 11.079 | |
| Fe54N | N | −1.162 | 7.678 |
| 1NN Fe | 0.090 | 10.716 | |
| 2NN Fe | 0.159 | 11.132 | |
| Fe54O | O | −1.020 | 7.965 |
| 1NN Fe | 0.088 | 11.000 | |
| 2NN Fe | 0.169 | 11.291 |
| Configurations | ∆Ef (eV) | Eb (eV) | d (Å) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Fe54C2 | Fe54N2 | Fe54O2 | Fe54C2 | Fe54N2 | Fe54O2 | C-C | N-N | O-O | |
| 1 | 1.276 | −0.577 | −1.895 | 0.146 | 0.029 | 0.329 | 2.915 | 2.913 | 2.767 |
| 2 | 1.250 | −0.638 | −1.742 | 0.172 | 0.090 | 0.176 | 4.002 | 3.890 | 3.883 |
| 3 | 2.140 | 0.414 | −1.231 | −0.718 | −0.962 | −0.335 | 2.382 | 2.484 | 2.358 |
| 4 | 1.393 | −0.481 | −1.616 | 0.029 | −0.067 | 0.050 | 3.483 | 3.499 | 3.522 |
| 5 | 3.106 | 1.120 | −0.166 | −1.684 | −1.668 | −1.400 | 3.469 | 3.423 | 3.434 |
| 6 | 2.140 | 5.530 | −1.218 | −0.718 | −6.078 | −0.348 | 2.382 | 2.407 | 2.354 |
| 7 | 3.276 | −0.457 | −1.052 | −1.854 | −0.091 | −0.514 | 1.522 | 1.952 | 2.370 |
| 8 | 1.258 | −0.425 | −1.786 | 0.164 | −0.123 | 0.220 | 2.864 | 2.466 | 2.779 |
| 9 | 1.391 | −0.538 | −1.588 | 0.031 | −0.010 | 0.022 | 3.484 | 3.417 | 3.535 |
| 10 | 1.355 | −0.523 | −1.496 | 0.067 | −0.025 | −0.070 | 3.346 | 3.454 | 3.387 |
| 11 | 1.233 | −0.640 | −1.602 | 0.173 | 0.092 | 0.036 | 3.998 | 4.470 | 3.896 |
| 12 | 1.489 | −0.366 | −1.661 | −0.067 | −0.182 | 0.095 | 2.698 | 2.620 | 2.551 |
| Configurations | C–O | C–N | N–O | |||
|---|---|---|---|---|---|---|
| ΔEf | Eb | ΔEf | Eb | ΔEf | Eb | |
| 1 | 0.083 | 0.148 | 0.658 | 0.082 | −1.182 | 0.125 |
| 2 | 0.053 | 0.178 | 0.615 | 0.125 | −1.21 | 0.153 |
| 3 | 0.069 | 0.162 | 0.641 | 0.099 | −1.187 | 0.13 |
| 4 | 0.042 | 0.189 | 0.599 | 0.141 | −1.215 | 0.158 |
| Eb (eV) | Em (eV) | Edis (eV) | Tdis (K) | |
|---|---|---|---|---|
| single O | - | 0.897 * | - | 318 |
| CO → C + O | 0.189 | 0.897 * | 1.086 | 384 |
| NO → N + O | 0.158 | 0.897 * | 1.055 | 373 |
References
- Han, T.F.; Ding, Z.M.; Feng, W.X.; Yao, X.Y.; Chen, F.F.; Gao, Y.S. Effects of Process Parameters on Microstructure and Wear Resistance of Laser Cladding A-100 Ultra-High-Strength Steel Coatings. Coatings 2024, 14, 669. [Google Scholar] [CrossRef]
- Yang, Y.X.; Wang, Z.H.; Wang, Q.; Tang, C.Y.; Wan, P.; Cao, D.H.; Dong, C. Microstructure structure and mechanical properties of coherent precipitation strengthened ultrahigh strength maraging stainless steel. Acta Phys. Sin. 2025, 74, 058101. [Google Scholar] [CrossRef]
- Guan, S.Z.; Wang, L.L.; Gao, Q.Y.; Fang, Y.C.; Zhan, X.H. Microstructure Evolution and Mechanical Property Enhancement of 30CrMnSiNi2A Steel Repaired by Laser Cladding with AerMet100 Steel. Met. Mater. Int. 2025, 9, 1–14. [Google Scholar] [CrossRef]
- Li, J.H.; Zhan, D.P.; Jiang, Z.H.; Zhang, H.S.; Yang, Y.K.; Zhang, Y.P. Progress on improving strength-toughness of ultra-high strength martensitic steels for aerospace applications: A review. J. Mater. Res. Technol. 2023, 23, 172–190. [Google Scholar] [CrossRef]
- Wang, Q.P.; Liang, Y.Z.; Chen, X.S.; Yang, Z.W.; Dong, K.W.; Peng, Y.; Zhou, Q.; Wang, K.H.; Kong, J. A novel 2.1 GPa martensitic stainless steel manufactured by laser powder bed fusion and post treatment. J. Mater. Res. Technol. 2025, 36, 1930–1937. [Google Scholar] [CrossRef]
- Gao, S.R.; Liu, H.S.; Fang, X.F.; Lu, W.J.; Li, S.X.; Chen, Y.B.; Lu, S.Y. Underlying Mechanism for “Loss of Passivation” Effect of a High-Carbon Martensitic Stainless Steel Coating via Laser Cladding. J. Electrochem. Soc. 2023, 170, 021513. [Google Scholar] [CrossRef]
- Song, T.; Chen, Z.; Cui, X.; Lu, S.; Chen, H.; Wang, H.; Dong, T.; Qin, B.; Chan, K.C.; Brandt, M.J.N. Strong and ductile titanium–oxygen–iron alloys by additive manufacturing. Nature 2023, 618, 63–68. [Google Scholar] [CrossRef]
- Cui, C.Y.; Xu, H.; Ye, F.Y.; Yang, J.; Cui, X. Microstructure evolution and characteristics of laser cladding with pre-placed powder lightweight refractory NbxMo0.5Ti1.5Ta0.2Cr high-entropy alloy. Intermetallics 2024, 167, 108229. [Google Scholar] [CrossRef]
- Mo, K.K.; Cao, L.C.; Zhao, D.K.; Long, Y.; Zhong, J.L.; Zhong, J.K.; Bi, G.J. Study on the microstructure and wear resistance of laser clad martensitic stainless steel 420 with different content of TiC. Mater. Today Commun. 2025, 46, 112615. [Google Scholar] [CrossRef]
- Patil, M.; Acherjee, B.; Manna, I. Enhancing wear resistance of railway wheel by laser surface cladding of martensitic stainless steel on high carbon rail steel. Mater. Today Commun. 2025, 42, 111353. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Y.H.; Pang, M.; Gao, L.H. Research of the effects of laser power variation on the properties of laser cladding Ni45/Cr3C2/MoS2 self-lubricating wear-resistant coatings on the surface of 300M ultra-high-strength steel. J. Mater. Sci. 2024, 59, 13558–13574. [Google Scholar] [CrossRef]
- Zhan, X.H.; Fang, Y.C.; Gao, Q.Y.; Guan, X.H.; Ci, S.W.; Cai, X.K.; Guan, S.Z. Study on the microstructure evolution performance improvement of Invar alloy repaired by laser cladding Aermet100 ultra-high strength steel. J. Mater. Process. Technol. 2024, 331, 118517. [Google Scholar] [CrossRef]
- Ye, Z.; Lei, Y.; Zhang, J.; Zhang, Y.; Li, X.; Xu, Y.; Wu, X.; Liu, C.S.; Hao, T.; Wang, Z. Effects of oxygen concentration and irradiation defects on the oxidation corrosion of body-centered-cubic iron surfaces: A first-principles study. Chin. Phys. B 2022, 31, 086802. [Google Scholar] [CrossRef]
- Wang, C.Y.; Luo, K.Y.; Wang, J.; Lu, J.Z. Carbide-facilitated nanocrystallization of martensitic laths and carbide deformation in AISI 420 stainless steel during laser shock peening. Int. J. Plast. 2022, 150, 103191. [Google Scholar] [CrossRef]
- Wang, R.; Li, F.; Yu, Z.; Kang, Y.; Li, M.; Hu, Y.; An, H.; Fan, J.; Miao, F.; Zhao, Y.; et al. Influences of partial substitution of C by N on the microstructure and mechanical properties of 9Cr18Mo martensitic stainless steel. Mater. Des. 2023, 236, 112497. [Google Scholar] [CrossRef]
- Coha-Vesga, P.M.; Yuuki-Koga, G.; Mendoza-Oliveros, M.E.; Gil-Coury, F.; Mujica-Roncery, L. Corrosion resistance of nitrogenated high- carbon martensitic stainless steel designed and at low. Rev. UIS Ing. 2023, 22, 181–190. [Google Scholar] [CrossRef]
- Song, Y.; Lu, Y.; Li, Y.; Sun, H.; Li, H.; Xu, H.; Wang, Y. Effect of nitrogen on the thermal deformation behavior of martensitic stainless bearing steel. Mater. Tehnol. 2024, 58, 809–818. [Google Scholar] [CrossRef]
- Lv, N.; Fu, A.; Chen, C.; Bai, H.; Zhao, Z.; Li, X.; Xu, Z.; Meng, G. Influence of oxygen on metastable pitting behavior of super 13Cr stainless steel in CO2-saturated environment. Vacuum 2025, 232, 113845. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, D.; Tang, H.-B.; Zhang, S.-Q.; Ran, X.-Z.; Wang, H.-M. Effect of hot isostatic pressing on fatigue properties of laser melting deposited AerMet100 steel. J. Iron Steel Res. Int. 2013, 20, 79–84. [Google Scholar] [CrossRef]
- Hu, J.P.; Zhu, H.M.; Zhang, J.W.; Ouyang, M.N.; Qiu, C.J.; Duan, J. Effects of TiC addition on microstructure, microhardness and wear resistance of 18Ni300 maraging steel by direct laser deposition. J. Mater. Process. Technol. 2021, 296, 117213. [Google Scholar] [CrossRef]
- Zhu, H.; Ouyang, M.; Hu, J.; Zhang, J.; Qiu, C.J.C.I. Design and development of TiC-reinforced 410 martensitic stainless steel coatings fabricated by laser cladding. Ceram. Int. 2021, 47, 12505–12513. [Google Scholar] [CrossRef]
- Zhu, H.M.; Ben, X.; Li, B.C.; Shen, L.Z.; Pan, C.L.; Qiu, C.J. Influence of Al microalloying on microstructure and mechanical properties of laser directed energy deposited AISI 420 steel. Mater. Today Commun. 2025, 42, 111355. [Google Scholar] [CrossRef]
- Raabe, D.; Tasan, C.C.; Olivetti, E.A. Strategies for improving the sustainability of structural metals. Nature 2019, 575, 64–74. [Google Scholar] [CrossRef]
- He, M.Y.; Shen, Y.F.; Jia, N.; Liaw, P.K. C and N doping in high-entropy alloys: A pathway to achieve desired strength-ductility synergy. Appl. Mater. Today 2021, 25, 101162. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, H.; Zhang, P.; Wang, Z.; Wang, M.; Sha, G.; Lin, H.; Ma, J.; Zhang, Z.; Song, Y.; et al. An exceptionally strong, ductile and impurity-tolerant austenitic stainless steel prepared by laser additive manufacturing. Acta Mater. 2023, 250, 118868. [Google Scholar] [CrossRef]
- Lei, Z.F.; Liu, X.J.; Wu, Y.; Wang, H.; Jiang, S.H.; Wang, S.D.; Hui, X.D.; Wu, Y.D.; Gault, B.; Kontis, P.; et al. Enhanced strength and ductility in a high-entropy alloy via ordered oxygen complexes. Nature 2018, 563, 546–550. [Google Scholar] [CrossRef]
- Jiao, M.Y.; Lei, Z.F.; Wu, Y.; Du, J.L.; Zhou, X.Y.; Li, W.Y.; Yuan, X.Y.; Liu, X.C.; Zhu, X.Y.; Wang, S.D.; et al. Manipulating the ordered oxygen complexes to achieve high strength and ductility in medium-entropy alloys. Nat. Commun. 2023, 14, 806. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Wu, H.H.; Wu, Y.; Liu, X.J.; Peng, X.Y.; Hou, S.; Lu, Z.P. Formation and strengthening mechanism of ordered interstitial complexes in multi-principle element alloys. Acta Mater. 2024, 281, 120364. [Google Scholar] [CrossRef]
- Zhao, D.; Yang, Q.; Wang, D.; Yan, M.; Lu, Z.J.V.; Prototyping, P. Ordered nitrogen complexes overcoming strength-ductility trade-off in an additively manufactured high-entropy alloy. Virtual Phys. Prototyp. 2020, 15, 532–542. [Google Scholar] [CrossRef]
- Dong, X.; Ma, S.; Wu, X.-X.; Na, R.-S. First principles on bcc and fcc phases structure of Fe52T2 (T=Cr,Mn,Co,Ni) alloys. Cailiao Gongcheng 2019, 47, 147–153. [Google Scholar] [CrossRef]
- Leveau, T.; Ventelon, L.; Clouet, E. Interaction of C, N and O interstitial solute atoms with screw dislocations in HfNbTaTiZr. Acta Mater. 2024, 275, 120062. [Google Scholar] [CrossRef]
- Kou, B.; Kou, Z.; Liu, Y.; Han, P. First principles study on interstitial C and substitutional Mn in bcc iron: Structural stability and elastic properties. Mater. Res. Innov. 2014, 18, 775–779. [Google Scholar] [CrossRef]
- You, Y.; Yan, M.F.; Chen, H.T. Interactions of carbon-nitrogen and carbon-nitrogen-vacancy in alpha-Fe from first-principles calculations. Comput. Mater. Sci. 2013, 67, 222–228. [Google Scholar] [CrossRef]
- Barouh, C.; Schuler, T.; Fu, C.-C.; Nastar, M. Interaction between vacancies and interstitial solutes (C, N, and O) in α-Fe: From electronic structure to thermodynamics. Phys. Rev. B 2014, 90, 054112. [Google Scholar] [CrossRef]
- Shang, S.L.; Fang, H.Z.; Wang, J.; Guo, C.P.; Wang, Y.; Jablonski, P.D.; Du, Y.; Liu, Z.K. Vacancy mechanism of oxygen diffusivity in bcc Fe: A first-principles study. Corros. Sci. 2014, 83, 94–102. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, J.; Li, R.; Zhang, P.; Zhao, J.; Dong, C. Solute/impurity diffusivities in bcc Fe: A first-principles study. J. Nucl. Mater. 2014, 455, 354–359. [Google Scholar] [CrossRef]
- Souissi, M.; Chen, Y.; Sluiter, M.H.F.; Numakura, H. Ab initio characterization of B, C, N, and O in bcc iron: Solution and migration energies and elastic strain fields. Comput. Mater. Sci. 2016, 124, 249–258. [Google Scholar] [CrossRef]
- He, T.W.; Jiang, Y.H.; Zhou, R.; Feng, J. Point defect interactions in iron lattice: A first-principles study. RSC Adv. 2016, 6, 45250–45258. [Google Scholar] [CrossRef]
- Lv, Z.; Fan, J.; Guan, K.; Wu, Z.; Zhao, D.; Fu, W. Effects of interstitial atoms (N/O) in bcc Fe from first-principle calculations. Fusion. Eng. Des. 2018, 137, 22–29. [Google Scholar] [CrossRef]
- Razumovskiy, V.I.; Yeddu, H.K.; Spitaler, J. Effect of carbon on elastic properties and microstructure of maraging steel: First-principles and phase-field study. Comput. Mater. Sci. 2019, 162, 1–11. [Google Scholar] [CrossRef]
- You, Y.; Yan, M.F.; Yan, J.H.; Sun, G.; Wang, C. First principles study of interactions of oxygen-carbon-vacancy in bcc Fe. Chin. Phys. B 2019, 28, 106102. [Google Scholar] [CrossRef]
- Ahlawat, S.; Srinivasu, K.; Biswas, A.; Choudhury, N. First-principle investigation of electronic structures and interactions of foreign interstitial atoms (C, N, B, O) and intrinsic point defects in body- and face-centered cubic iron lattice: A comparative analysis. Comput. Mater. Sci. 2019, 170, 109167. [Google Scholar] [CrossRef]
- Kadowaki, M.; Saengdeejing, A.; Muto, I.; Chen, Y.; Masuda, H.; Katayama, H.; Doi, T.; Kawano, K.; Miura, H.; Sugawara, Y.; et al. First-principles analysis of the inhibitive effect of interstitial carbon on an active dissolution of martensitic steel. Corros. Sci. 2020, 163, 108251. [Google Scholar] [CrossRef]
- Ohtsuka, H.; Tsuzaki, K. Recent Studies on the Nature and State of Carbon Atoms in Iron. ISIJ Int. 2021, 61, 2677–2686. [Google Scholar] [CrossRef]
- Luo, W.D.; Hou, T.P.; Liang, X.; Cheng, S.; Zheng, Y.H.; Li, Y.; Ye, X.F.; Wu, K.M. Structure and stability investigation of oxygen interaction with Fe in bcc-Fe. Vacuum 2023, 212, 112005. [Google Scholar] [CrossRef]
- Sagar, S.; Sluiter, M.H.F.; Dey, P. First—Principles study of hydrogen—Carbide interaction in bcc Fe. Int. J. Hydrogen Energy 2024, 50, 211–223. [Google Scholar] [CrossRef]
- Yang, Y.; Ou, X.Q.; Zhang, H.; Song, M. Positioning of interstitial carbon atoms in the deformed Fe-C system. Mater. Today Commun. 2023, 34, 105377. [Google Scholar] [CrossRef]
- Ji, H.; Zhang, P.; Li, G.; Wei, M.; Wang, Y.; Zou, T. The synergistic interaction of interstitial carbon/oxygen, alloying Cr/Ni and vacancy in dilute austenitic iron alloys. Mater. Today Commun. 2024, 41, 110853. [Google Scholar] [CrossRef]
- Liu, C.; Lu, W.; Xia, W.; Du, C.; Rao, Z.; Best, J.P.; Brinckmann, S.; Lu, J.; Gault, B.; Dehm, G.; et al. Massive interstitial solid solution alloys achieve near-theoretical strength. Nat. Commun. 2022, 13, 1102. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, 1133. [Google Scholar] [CrossRef]
- Kresse, G. Ab-intio molecular-dynamics for liquid-metals. J. Non-Cryst. Solids 1995, 193, 222–229. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.C.; Tang, G.; Geng, W.T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Henkelman, G.; Jonsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jonsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Lv, Z.; Zhang, Q.; Li, R.; Hong, Y.; Zhang, X. Combined Effects of Carbon and Nitrogen in Fe20Cr6Mn6CN Alloys from First-Principles Calculation. J. Mater. Eng. Perform. 2021, 30, 8322–8335. [Google Scholar] [CrossRef]
- Lv, Z.; Xiao, S.; Xiao, Z.; Qian, L.; Wang, W.; Zhou, Y.; Fu, W. Structural properties and bonding characteristic of interfaces between VN and VC from density functional calculations. J. Alloys Compd. 2017, 718, 139–149. [Google Scholar] [CrossRef]
- Fang, C.M.; van Huis, M.A.; Zandbergen, H.W. Stability and structures of the ε-phases of iron nitrides and iron carbides from first principles. Scr. Mater. 2011, 64, 296–299. [Google Scholar] [CrossRef]
- Raebiger, H.; Lany, S.; Zunger, A. Charge self-regulation upon changing the oxidation state of transition metals in insulators. Nature 2008, 453, 763–766. [Google Scholar] [CrossRef]
- Wan, L.; Wang, Q.; Ye, X.; Cao, X.; Jin, S.; Gao, T. Insight into structural stability and helium diffusion behavior of Fe-Cr alloys from first-principles. RSC Adv. 2020, 10, 3277–3292. [Google Scholar] [CrossRef]
- Eyméoud, P.; Maugis, P. Magnetic behavior of transition metal solutes in α-iron: A classification. J. Magn. Magn. Mater. 2020, 513, 167223. [Google Scholar] [CrossRef]
- Wang, F.K.; Wang, W.L.; Du, J.; Zhang, L.; Sohn, I.; Zeng, J. Oxidation behavior of Cr-Mn-Si alloyed steel by mold flux melt in high temperatures. J. Mater. Res. Technol. 2024, 29, 3898–3909. [Google Scholar] [CrossRef]
- Fernandez, N.; Ferro, Y.; Kato, D.J.A.M. Hydrogen diffusion and vacancies formation in tungsten: Density Functional Theory calculations and statistical models. Acta Mater. 2015, 94, 307–318. [Google Scholar] [CrossRef]







| Alloys | Formation Energy /eV | Lattice Constant/Å | Volume Variation/Å3 | Average Magnetic Moment/μB | ||
|---|---|---|---|---|---|---|
| ΔEf | a | b | c | ∆V | M | |
| Fe54 | - | 8.493 | 8.493 | 8.493 | 0 | 2.20 |
| Fe54C-Oct | 0.758 | 8.493 | 8.493 | 8.649 | 11.201 | 2.23 |
| Fe54C-Tet | 1.638 | 8.591 | 8.440 | 8.591 | 10.258 | 2.21 |
| Fe54N-Oct | −0.518 | 8.517 | 8.517 | 8.639 | 11.698 | 2.27 |
| Fe54N-Tet | 0.225 | 8.574 | 8.506 | 8.574 | 10.786 | 2.22 |
| Fe54O-Oct | −1.027 | 8.499 | 8.499 | 8.644 | 14.009 | 2.25 |
| Fe54O-Tet | −0.511 | 8.578 | 8.473 | 8.578 | 12.635 | 2.21 |
| Bader Charge | Local Magnetic Moment/μB | |||||
|---|---|---|---|---|---|---|
| Fe54CO | Fe54CN | Fe54NO | Fe54CO | Fe54CN | Fe54NO | |
| C | −1.060 | −1.058 | - | −0.142 | −0.142 | - |
| N | - | −1.149 | −1.157 | - | −0.108 | −0.103 |
| O | −1.083 | - | −1.097 | 0.072 | - | 0.073 |
| Fe1 | 0.123 | 0.091 | 0.092 | 2.042 | 1.639 | 1.704 |
| Fe2 | 0.170 | 0.163 | 0.174 | 2.460 | 2.181 | 2.219 |
| Fe3 | 0.161 | 0.163 | 0.172 | 2.446 | 2.243 | 2.256 |
| Fe4 | 0.285 | 0.351 | 0.378 | 2.332 | 2.230 | 2.272 |
| Fe5 | 0.057 | 0.072 | 0.118 | 1.698 | 1.661 | 2.059 |
| Fe6 | 0.168 | 0.157 | 0.163 | 2.242 | 2.225 | 2.439 |
| Fe7 | 0.161 | 0.165 | 0.146 | 2.194 | 2.210 | 2.494 |
| Alloys | ∆Ef (eV) | Eb (eV) |
|---|---|---|
| Fe54C | 0.758 | - |
| Fe54N | −0.518 | - |
| Fe54O | −1.027 | - |
| Fe54C2 | 1.233 | 0.173 |
| Fe54N2 | −0.640 | 0.092 |
| Fe54O2 | −1.602 | 0.036 |
| Fe54CO | 0.042 | 0.189 |
| Fe54CN | 0.599 | 0.141 |
| Fe54NO | −1.215 | 0.158 |
| Eb (eV) | Em (eV) | Edis (eV) | Tdis (K) | |
|---|---|---|---|---|
| single O | - | 0.557 | - | 202 |
| CO → C + O | 0.189 | 0.557 | 0.746 | 266 |
| NO → N + O | 0.158 | 0.557 | 0.715 | 255 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Mi, T.; Chen, P.; Zhu, H.; Chen, Y.; Zhang, P.; Li, R.; Qiu, C. Synergistic Effect of Hetero Interstitial Atoms (C/N/O) on the Thermodynamic Stability in BCC Fe: A DFT Study. Coatings 2025, 15, 929. https://doi.org/10.3390/coatings15080929
Wang F, Mi T, Chen P, Zhu H, Chen Y, Zhang P, Li R, Qiu C. Synergistic Effect of Hetero Interstitial Atoms (C/N/O) on the Thermodynamic Stability in BCC Fe: A DFT Study. Coatings. 2025; 15(8):929. https://doi.org/10.3390/coatings15080929
Chicago/Turabian StyleWang, Fang, Tengge Mi, Pinghu Chen, Hongmei Zhu, Yong Chen, Pengbo Zhang, Ruiqing Li, and Changjun Qiu. 2025. "Synergistic Effect of Hetero Interstitial Atoms (C/N/O) on the Thermodynamic Stability in BCC Fe: A DFT Study" Coatings 15, no. 8: 929. https://doi.org/10.3390/coatings15080929
APA StyleWang, F., Mi, T., Chen, P., Zhu, H., Chen, Y., Zhang, P., Li, R., & Qiu, C. (2025). Synergistic Effect of Hetero Interstitial Atoms (C/N/O) on the Thermodynamic Stability in BCC Fe: A DFT Study. Coatings, 15(8), 929. https://doi.org/10.3390/coatings15080929









