Dynamic Control of Coating Accumulation Model in Non-Stationary Environment Based on Visual Differential Feedback

Abstract

To address the issue of coating accumulation model failure in unstable environments, this paper proposes a dynamic control method based on visual differential feedback. An image difference model is constructed through online image data modeling and real-time reference image feedback, enabling real-time correction of the coating accumulation model. Firstly, by combining the Arrhenius equation and the Hagen–Poiseuille equation, it is demonstrated that pressure regulation and temperature changes are equivalent under dataset establishment conditions, thereby reducing data collection costs. Secondly, online paint mist image acquisition and processing technology enables real-time modeling, overcoming the limitations of traditional offline methods. This approach reduces modeling time to less than 4 min, enhancing real-time parameter adjustability. Thirdly, an image difference model employing a CNN + MLP structure, combined with feature fusion and optimization strategies, achieved high prediction accuracy: R² > 0.999, RMSE < 0.79 kPa, and σ_e < 0.74 kPa on the test set for paint A; and R² > 0.997, RMSE < 0.67 kPa, and σ_e < 0.66 kPa on the test set for aviation paint B. The results show that the model can achieve good dynamic regulation for both types of typical aviation paint used in the experiment: high-viscosity polyurethane enamel (paint A, viscosity 22 s at 25 °C) and epoxy polyamide primer (paint B, viscosity 18 s at 25 °C). In summary, the image difference model can achieve dynamic regulation of the coating accumulation model in unstable environments, ensuring the stability of the coating accumulation model. This technology can be widely applied in industrial spraying scenarios with high requirements for coating uniformity and stability, especially in occasions with significant fluctuations in environmental parameters or complex process conditions, and has important engineering application value.

1. Introduction

As a critical surface treatment technology, spray coating finds extensive applications across various industrial sectors. The quality of surface coatings depends not only on the intrinsic properties of the paint materials but is also significantly influenced by the spraying process parameters [1]. Variations in these process parameters directly determine key coating characteristics, including deposition uniformity and substrate adhesion strength.

In the field of spray coating process modeling, the 3D coating accumulation model proposed by Yu, et al. [2] has been experimentally validated and successfully applied in practical production. This model accurately characterizes coating deposition behavior under steady-state conditions, establishing a deterministic mapping relationship between process parameters and deposition rates. However, when applied in non-stationary environments (where key parameters such as temperature, humidity, and pressure exhibit significant spatiotemporal fluctuations), the model’s predictive accuracy deteriorates substantially, resulting in so-called “model failure”. This failure mechanism fundamentally stems from dynamic variations in environmental parameters that alter paint characteristics, thereby disrupting the deterministic correlation between process parameters and deposition rates established in the original model. At its core, the predictive validity of conventional coating accumulation models heavily relies on the assumption of environmental stability. This inherent limitation severely constrains their applicability in complex industrial field conditions. Sarikaya [3] investigated the effect of temperature on the properties of Al₂O₃ coatings prepared by the plasma spraying process and established a correlation between temperature and coating properties. Li, et al. [4] investigated the effects of different gas temperatures and pressures on coating roughness and porosity. It can be seen that changes in temperature significantly alter the microstructure and properties of the coating, leading to changes in the coating deposition model. Especially in spraying scenarios where environmental parameters fluctuate significantly or process conditions are complex, dynamic disturbances in the environmental thermal field and airflow field are unavoidable, making it difficult for existing static models to accurately predict coating accumulation behavior. Therefore, it is of great theoretical significance and application value to study the dynamic control methods for coating accumulation models in non-stationary environments.

For the control of coating accumulation models in non-stationary environments, there are two mainstream methods:

(1)

Offline empirical adjustment method for spraying process parameters

This method involves conducting a target plate test before spraying, measuring the coating accumulation model after drying, and trying out the process parameters to cope with the unstable environment [5,6]. Shi et al. [7] established the thickness distribution model of spray gun non-stationary variable flow coating based on the elliptic double β model and the introduction of spray velocity parameters. Nieto Bastida and Lin [8] proposed a coating distribution model based on β-distribution, and determined the lap width of the trajectory to study the coverage and uniformity of the coating by fitting experimental data, which improved the generalization ability of the model. This offline empirical adjustment method of spraying process parameters has a long debugging period, and the spraying process parameters cannot be adapted to the non-stationary environment in real time [9].

(2)

Offline intelligent prediction of spraying process parameters

Utilizing the powerful nonlinear mapping capabilities of artificial neural networks (ANNs), quantitative prediction models of process parameters and coating performance are established, significantly improving accuracy and efficiency [10,11,12]. Core methods include:

• Classic ANN optimization:

Suryawanshi, et al. [13] used a backpropagation neural network to establish a predictive model for the mechanical properties of plasma-deposited WC20Cr3C27Ni coatings. Gerner, et al. [14] used a big data feedforward neural network (a neural network based on different numbers of neurons) to optimize the HVOF spraying process parameters and successfully predict the porosity and hardness of the coating. Ye, et al. [15] used genetic algorithms (GA) to optimize the BP network, improving the mapping accuracy of sandblasting process parameters and coating performance. Han, et al. [16] used the BP network to predict the effects of spraying parameters (distance, power, powder feed rate) on bond strength, hardness, and porosity.

• Hybrid intelligent optimization algorithm:

Ling, et al. [17] combined enhanced extreme learning machines (ELM) with the K-means improved predator algorithm (KHPO) to predict indicators such as film thickness and roughness. Ye, et al. [18] integrated the improved whale algorithm (IWOA) with ANN to analyze the effects of multi-parameter coupling on porosity, hardness, and corrosion resistance. Zhu, et al. [19] used the pollination algorithm (FPA) to optimize the ELM model, correlating the ceramic spraying process with microstructure/mechanical properties. Deng, et al. [20] optimized the backpropagation neural network (BPNN) based on the quantum particle swarm optimization (QPSO) algorithm to predict the microhardness of laser cladding coatings. Mahendru, et al. [21] analyzed the relationship between the process parameters of the suspended plasma spraying process and the coating properties using tree-based machine learning (ML) algorithms (from linear regression and random forests to improved gradient boosting) and deep neural network models. Ye, et al. [22] proposed a hybrid machine learning method that optimizes the support vector machine method using the cuckoo search algorithm (CS-SVM) to predict the microstructural characteristics of thermal barrier coatings based on spray process parameters.

Compared with the offline empirical adjustment method, the offline intelligent prediction method has made significant progress in the field of coating accumulation model control, proposing novel perspectives and methods, but there is still room for improvement. Existing offline intelligent prediction methods for spray coating process parameters primarily obtain coating thickness data through spray coating experiments, then train intelligent networks based on this data to establish prediction models. This approach reduces debugging cycles and optimizes the mapping relationship between multi-parameter spray coating process parameters and coating quality. However, since the model is established using offline data, it shares the same limitations as the offline trial-and-error method for spray coating process parameters, meaning that spray coating process parameters cannot adapt in real-time to unstable environments.

Based on the above analysis, online data modeling emerges as the critical solution for overcoming the real-time adaptability limitations of existing methods in non-stationary environments. This paper proposes a dynamic control method for coating accumulation models in unstable environments, leveraging visual differential feedback. By establishing a predictive model through online image data processing and real-time reference image feedback, this approach enables continuous correction of the coating accumulation model. Consequently, it resolves model failure induced by environmental instability while offering capabilities unattainable with offline modeling methods.

2. Methods

2.1. Data Acquisition of Paint Spray Images Methodology

2.1.1. Principle of Conditional Equivalence for the Establishment of Datasets in Non-Stationary Environments

Assume the ambient temperature is T, the paint viscosity is η, the paint flow rate per unit time is Q, and the film thickness distribution model is F.

The relationship between η and T can be described by the Arrhenius equation. However, since the classic Arrhenius equation is only applicable to Newtonian fluids, and most actual paints are non-Newtonian fluids, rheology must be introduced to correct it [23]. The formula is as follows:

$$\eta (T,\dot{\gamma })=A\cdot e^{{\displaystyle \frac{E_a}{RT}}}\cdot {\dot{\gamma }}^{n-1}$$

(1)

where η (T) is the viscosity at T, A is the pre-factor, E_a is the flow activation energy, R is the gas constant, and T is the absolute temperature. $\dot{\gamma }$ is the shear rate, and n is the rheological index (n < 1 indicates shear thinning).

The relationship between Q and η of the paint can be described by the Hagen–Poiseuille equation [24], and the correction formula for non-Newtonian fluid flow is as follows:

$$Q\left(t\right)={\displaystyle \frac{\pi R^3}{3n+1}}{\left({\displaystyle \frac{R\Delta P\left(t\right)}{2\eta L(T,\dot{\gamma })}}\right)}^{{\displaystyle \frac{1}{n}}}$$

(2)

where R is the radius of the pipe, ΔP is the pressure difference between the two ends of the pipe, and L is the length of the pipe. If n = 1, it degenerates into Newton’s fluid equations.

Additionally, in the spraying process F is affected by the joint influence of atomization pressure, fan control pressure, and flow control pressure, which has a nonlinear coupling. Assuming the atomization pressure is P_w, fan control pressure is P_f, and flow control pressure is P_q, the total pressure difference ΔP can be expressed as a nonlinear combination coupling term of the three pressures:

$$\Delta P=f(P_w,P_f,P_q)$$

(3)

where: $f$ is a nonlinear function.

The effective temperature T_eff(t) of paint is affected by ambient temperature and evaporative cooling effects:

$$T_{\mathrm{eff}}(t)=T_{env}(t)-\alpha \cdot Q(t)\cdot {\displaystyle \frac{dT}{dt}}$$

(4)

α is the heat loss coefficient, and ${\displaystyle \frac{dT}{dt}}$ is the transient heat exchange rate between the paint and the environment.

Therefore, F is a function of Q and thermodynamic state:

$$F(t)={\displaystyle {\int }_0^t\beta \cdot Q(\tau )}\cdot e^{-\lambda (T_{eff}(\tau )-T_0)}d\tau$$

(5)

β is the adsorption coefficient of the substrate; λf is the temperature sensitivity coefficient.

The data sets N_T (temperature control) and N_P (pressure control) are equivalent if the following conditions are met:

$${\displaystyle \frac{\partial F}{\partial T}}{|}_p\cdot \Delta T={\displaystyle \frac{\partial F}{\partial P}}{|}_T\cdot \Delta P$$

(6)

That is, the ratio of temperature and pressure sensitivity to F is constant within the data set. The conditions for equivalence are as follows:

(1)

Rheological steady-state assumption: shear rate $\dot{\gamma }$ remains consistent in N_T and N_P;

(2)

Thermodynamic equilibrium assumption: paint temperature change rate ${\displaystyle \frac{dT}{dt}}<5\%E_a/R$;

(3)

Pressure coupling separability: $\Delta P=g(P_w)\cdot h(P_f)\cdot k(P_q)$.

2.1.2. Data Acquisition Method of Paint Spray Image

Since the process of collecting image data by adjusting the temperature is complicated and costly, the initial image data can be collected by adjusting the atomization pressure, fan control pressure, and flow control pressure according to the equivalence principle of conditions for the establishment of data sets in unstable environments.

The paint mist image acquisition experimental device mainly consists of two parts, as shown in Figure 1. One part is the spraying device, which includes the gas source, filter regulator, proportional solenoid valve, proportional flow control valve, paint container, and spray gun. The gas source is divided into three ways, respectively, for atomization, fan control, and flow control, proportional valve control pressure source, and the size of the pressure is adjusted through the electromagnetic proportional valve. The other part is the image acquisition device, which consists of the upper computer, camera, and light source.

In the image shooting test, there are many factors affecting the shooting effect of paint mist, including camera parameters, light source, and the relative position of the camera and the light source space [25]. Lighting schemes (light source type, position, angle), spatial alignment (relative positions of camera, light source, and spray gun), and basic camera exposure parameters (shutter speed, aperture, ISO) need to be carefully adjusted and fixed during the first experiment. Subsequent experiments under the same spraying conditions do not require repeated adjustments to these basic settings.

During dynamic spraying, paint mist sprayed from the spray gun can interfere with light, causing instability in camera exposure, focus, and white balance. To solve this problem, a camera that supports manual control should be selected to fix the exposure, lock the focus, and preset the white balance to ensure shooting stability. The specific method is as follows:

(1)

Lock exposure parameters: Before starting the spray gun or during paint mist spraying, set and lock parameters such as shutter speed and aperture based on the background and paint mist brightness to prevent the camera from automatically adjusting exposure during the spraying process.

(2)

Fix white balance: In a stable lighting environment (before spraying or during paint mist spraying), set and lock the white balance value to prevent white balance drift caused by changes in paint mist color or ambient light.

(3)

Use industrial cameras with stable algorithms: Select industrial cameras with good interference resistance. Their internal image processing algorithms can better suppress fluctuations in exposure and white balance in dynamic scenes, maintaining image consistency.

The choice and arrangement of the light source directly affect image clarity, grain detail, and background contrast. The type of light source should be chosen to emphasize the contours and movement of the paint particles, such as LED spotlights, halogen lamps, or laser light sources [26]. The position of the light source should be from the back or side of the mist to enhance the light transmission of the particles and to emphasize the levitation effect. The background color should be dark to enhance the brightness contrast of the paint mist and avoid reflective interference.

2.2. Image Data Processing and Labeling Methodology

Based on the above principles and methods of paint spray image data acquisition, the original image data captured are cropped and labeled.

1.

Image cropping method

(1)

Selection criteria for cropping areas

As shown in Figure 2, the distribution of paint spray in the vicinity of the spray gun cap presents obvious spatial characteristics:

Proximal region: the paint mist boundary is clear, the internal particle distribution is more uniform, showing high spatial consistency.

Distal region: the boundary of the paint mist is blurred, the internal particles are not uniformly distributed, showing high randomness and diffusivity.

Based on the above characteristics, in order to ensure the quality of the image data, the region near the gun cap is selected as the focus area for data interception (shown as the red box in Figure 2).

(2)

Cropping operation specifications

Dimension uniformity: Fixed cutting dimensions are a × b pixels to ensure that the data scale of the input model is consistent.

Position reference: With the center of the spray gun cap as the origin, extend a rectangular area of a × b to the right (as shown in the red box in Figure 2) to cover the proximal paint mist core area.

2.

Methods for labeling data

Labeling content: Each frame of the image is annotated with three process parameters corresponding to the atomization pressure, fan control pressure, and flow control pressure, in the format: atomization pressure value P_w_fan control pressure value P_f_flow control pressure value P_q, where the underscore _ is the separator. An example is shown in Figure 3.

Since this paper uses online image data modeling with real-time feedback from the reference image to build the model, when the model changes due to changes in ambient temperature, the model can be corrected by adjusting the pressure value according to the conclusion of Equation (6). Therefore, the dataset includes: the reference image (Image_1), the actual captured image (Image_2), the atomization pressure correction value $P_{w\_c}$, the fan control pressure correction value $P_{f\_c}$, and the flow pressure correction value $P_{q\_c}$; the calculation equation of the three pressure correction values is as follows:

$$\left\{\begin{array}{l}{P}_{w\_c}=P_{w\mathrm{Im}ag{e}_2}-P_{w\mathrm{Im}ag{e}_1}\\ P_{f\_c}=P_{f\mathrm{Im}ag{e}_2}-P_{f\mathrm{Im}ag{e}_1}\\ P_{q\_c}=P_{q\mathrm{Im}ag{e}_2}-P_{q\mathrm{Im}ag{e}_1}\end{array}\right.$$

(7)

The resulting dataset is:

$$N_P=\left\{\begin{array}{l}\left(\mathrm{Im}{{\mathit{age}}_1}^{(1)},\mathrm{Im}{{\mathit{age}}_2}^{(1)},{P_{w\_c}}^{(1)},{P_{f\_c}}^{(1)},{P_{q\_c}}^{(1)}\right),\\ \left(\mathrm{Im}{{\mathit{age}}_1}^{(2)},\mathrm{Im}{{\mathit{age}}_2}^{(2)},{P_{w\_c}}^{(2)},{P_{f\_c}}^{(2)},{P_{q\_c}}^{(2)}\right),\\ \dots \left(\mathrm{Im}{{\mathit{age}}_1}^{(i)},\mathrm{Im}{{\mathit{age}}_2}^{(i)},{P_{w\_c}}^{(i)},{P_{f\_c}}^{(i)},{P_{q\_c}}^{(i)}\right)\end{array}\right\}$$

(8)

where $i$ is the number of samples in the dataset.

2.3. Image Difference Model Construction Methodology

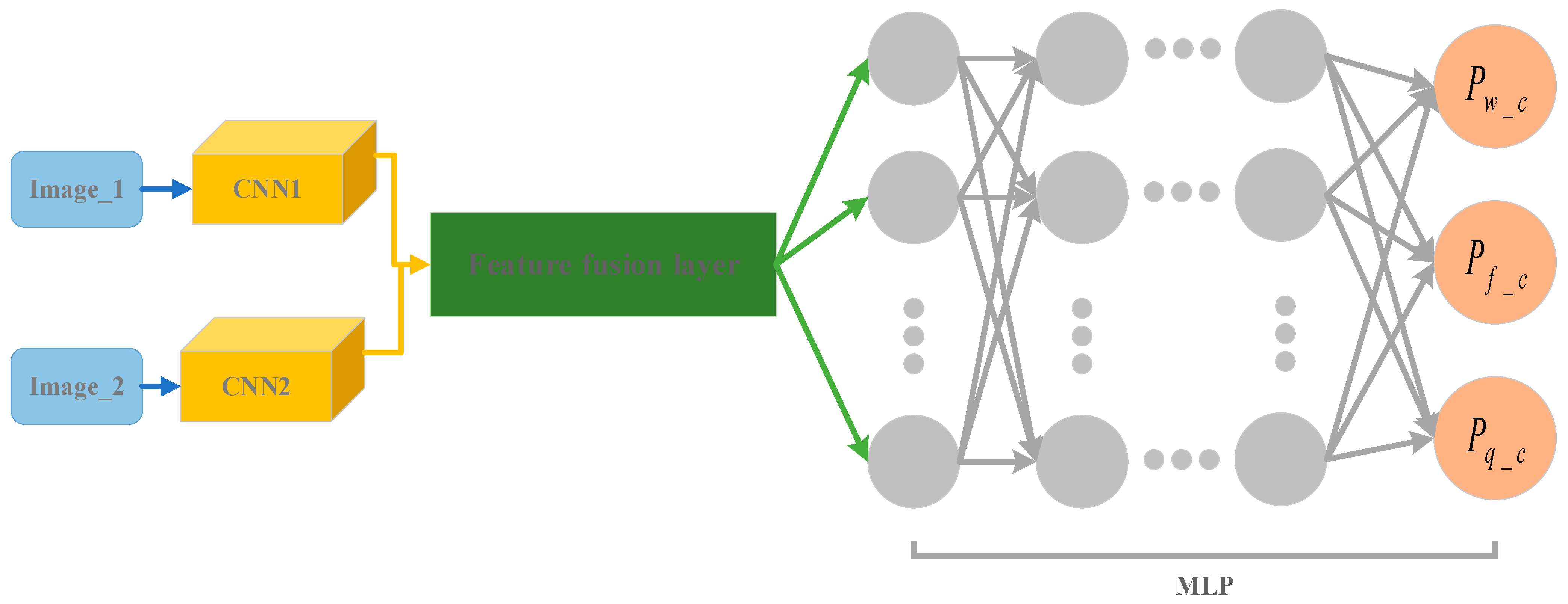
2.3.1. Image Difference Modeling Architecture Design

According to the above dataset N_p contains the features of both image and numerical data. This paper adopts the model architecture of convolutional neural network (CNN) + fully connected layer (MLP) [27]. CNN part extracts the local features of the image through local sensory fields and weight sharing, and ends with the MLP part mapping the high-level features to the numerical output. Mathematically, it can be represented as a composite function:

$$y=f_{MLP}(g_{CNN}(x))$$

(9)

where x is the input image, g_CNN is the CNN feature extractor and f_MLP is the fully connected mapping function.

The structure of the image difference model is shown in Figure 4. The input layer is a dual image input, which consists of Image 1 (Image_1), the reference image, and Image 2 (Image_2), the actual captured image. The reference image provides a stable frame of reference for differential calculations. By comparing the current image to the reference image, it is possible to accurately detect areas of change in the image, quantify the extent of the change, and better analyze the differences in the image under different spray process pressure parameters. The outputs are the atomization pressure correction value $P_{w\_c}$, fan control pressure correction value $P_{f\_c}$, and flow pressure correction value $P_{q\_c}$ (pressure correction value: the numerical value required to adjust the pressure parameter in order to match the real-time image with the reference image). The core structure of the model is a two-branch CNN + feature fusion + MLP, where the two-branch CNN is used to process the input image, the feature fusion layer is responsible for merging the two-branch features and feature differencing, and the MLP part maps the deeply fused high-level features to the output space.

2.3.2. Image Difference Model Optimization

If the prediction accuracy of the above model, as in Figure 4, is insufficient, the model performance can be optimized by adjusting the key parameters and strategies.

• Adjusting the model architecture
  • Increasing the model complexity, both by increasing the number of convolutional layers in the CNN or by using a larger convolutional kernel, in order to improve the feature extraction capability;
  • Adjust the number of channels, which increases the number of filters in each layer of the CNN. You can start with a smaller number, such as 32 or 64, and gradually increase it to enhance feature expression capabilities.
  • Increasing the number of hidden layer neurons in the MLP or adding more hidden layers.
• Optimization of the training process
  • Adjusting the learning rate: In the initial stage, a relatively large learning rate is set to speed up the convergence of the model. If the loss function oscillates or does not converge during the training process, the learning rate may be too large, and then the learning rate is adjusted by exponential decay. By dynamically adjusting the learning rate, the model can converge quickly in the early stage of training, while maintaining a stable convergence state in the later stage, avoiding the overfitting problem caused by too large a learning rate.
  • Adjusting the number of iterations: At the beginning, set a small number of iterations, and gradually increase the number of iterations by i times each time as the experiment proceeds. After each increase in the number of iterations, record the loss function value, accuracy, and other indicators of the model on the training set and validation set. When it is found that the performance of the model on the validation set is no longer improved, or even a downward trend, it indicates that the model may have been overfitted, and at this time, stop increasing the number of iterations, and select the number of iterations when the performance is optimal as the final number of training iterations.
  • Regularization strategy: In order to prevent the model from overfitting, the dropout regularization technique is introduced into the model. Dropout improves the generalization ability of the model by randomly discarding a part of the neurons during the training process to reduce the co-adaptation phenomenon among neurons. At the same time, L2 regularization is applied to the weights of the model to limit the complexity of the model and prevent overfitting by adding the sum of squares of the weights as a penalty term in the loss function.

3. Experimental Method

3.1. Verification Test of the Principle of Equivalence of Conditions for Establishing Data Sets in Unstable Environments

To determine whether spray coating performance under two different temperatures ($T_1$, $T_2$) can achieve equivalent results through adjustments of P_w, P_f and P_q in unstable conditions, the following two experimental setups were implemented. The spray coating effects were evaluated based on the coating thickness distribution.

Group 1: Control spray parameters (spray distance, spray gun movement speed, spray pressure, etc.) are consistent, paint mixture ratios are consistent, only the ambient temperature differs, with the control group temperature being and the experimental group temperature being. Under these conditions, sample parts numbered Sp1 and Sp2 are sprayed.

Group 2: Under conditions T₁ and T₂, the paint viscosities are ${\rho }_1$ and ${\rho }_2$, respectively. Compare the viscosities and adjust P_w, P_f and P_q according to changes in ${\rho }_2$. The adjustment rules are shown in

Table 1. Process parameter adjustment rules.

ρ	Adjustment Items	Adjust Direction	Theoretical Basis
Decrease	Pw	Decrease	Low viscosity → High fluidity → Pressure must be reduced to balance flow
	Pf	Decrease	Increased volume → Increased paint mist cone angle → Pressure must be reduced
	Pq	Increases	Compensate for atomization effects and avoid oversized spray particles.
Increases	Same as above	Reverse adjustment	Maintain symmetry with the above logic.

. The specific adjustment values need to be determined based on experimental experience. Spray the sample part under these conditions. The sample part number is Sp3.

The spray trajectory and coating thickness data collection locations are shown in Figure 5.

According to the above experimental plan, the parameter settings during the experiment are shown in

Table 2. Spray parameter setting.

Group	T/°C	ρ/s	Sp	Pw/kPa	Pf/kPa	Pq/kPa	Other Relevant Parameters
1	18.5	22.16	Sp1	180	120	150	Same
			Sp2	180	120	150
2	24.1	17.62	Sp3	200	110	100

.

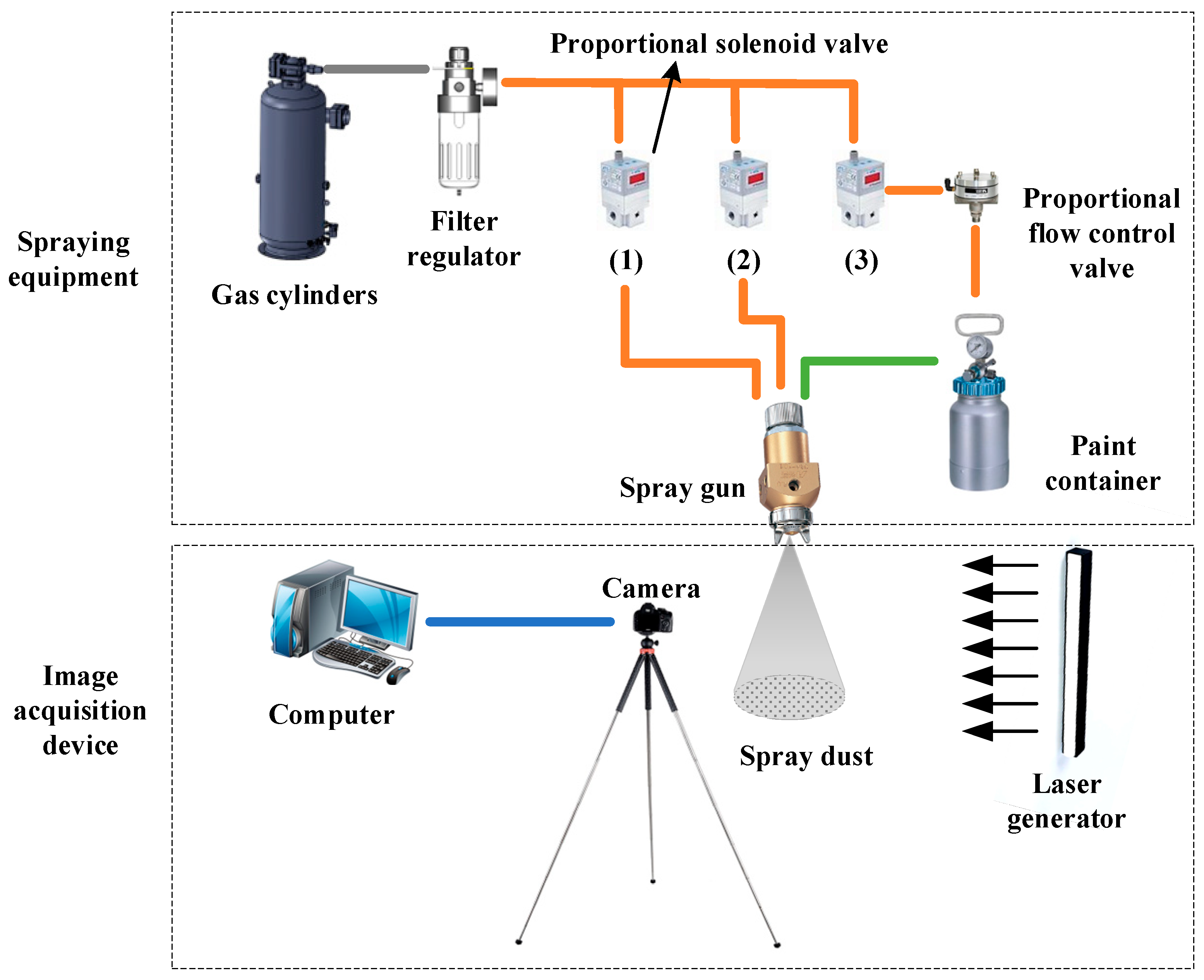
3.2. Paint Mist Capture Device and Test

3.2.1. Experimental Setup

Based on the paint mist image data acquisition method shown in Figure 1, several cameras were evaluated for their performance in accordance with the shooting requirements of this paper, as shown in

Table 3. Industrial camera performance comparison table.

Model	Resolution	Frame Rate (fps)	Shutter Type	Volume (mm3)	Min Exposure (us)	Key Defect
MER2-301-125U3M-L	2048 × 1536	125	Global	29 × 29 × 29	1
Basler ace2 2440	2448 × 2048	75	Global	32 × 32 × 42	1	Insufficient frame rate, unable to meet the dynamic capture requirements of paint mist monitoring
Haikang MV-CE200	2048 × 1536	150	Global	29 × 29 × 42	2	Rolling shutter causes exposure gaps, affecting image quality.
FLIR BFS-U3-16S2M	1440 × 1080	164	Global	26 × 26 × 30	2	Insufficient resolution, unable to meet the requirements for accurately distinguishing paint mist particles.

. The Daheng Image MER2-301-125U3M/C(-L) camera was selected for this study, as its performance meets the requirements, and it features functions such as one-time adjustment of white balance and exposure. During paint mist photography, the one-time adjustment function allows the camera parameters to be fixed, thereby eliminating errors introduced by camera parameters during image analysis. The spray gun used is the Iwata WRA-101-E2P, with a nozzle diameter of 0.8 mm.

The camera is positioned on one side of the spray gun, at the same horizontal height as the spray gun, and perpendicular to the spray gun’s axis. This shooting angle effectively captures the extensive area covered by paint mist, enhancing the sense of space. To minimize turbulence and prevent contamination from paint mist, the camera is positioned 400 mm from the spray gun’s axis, prioritizing alignment with the mist core area while avoiding turbulent zones (paint mist beyond 300 mm from the spray gun), as shown in Figure 6. This ensures that the 300 mm mist cone near the paint outlet is fully within the camera’s depth of field. To eliminate environmental light interference, this experiment was conducted in a darkroom. LED white light was selected as the light source, mounted at two positions on the background panel behind the paint mist, forming approximately a 45° angle with the camera. The side-scattered light intensity of the particles is maximized, and the side lighting causes Fresnel diffraction on the particle edges, enhancing the contrast between the paint mist particles and the background.

The paint used for spraying is aviation paint A and paint B. Paint A is a high-solid polyurethane magnetic paint (suitable for precision parts), and paint B is a low-viscosity epoxy polyamide primer (suitable for quick spraying). The key performance indicators of the paints are shown in

Table 4. The performance indicators of the paints.

Performance	Paint A	Paint B
Viscosity (25 °C, s)	22 ± 1.5	18 ± 1
Solid content (%)	65 ± 2	55 ± 3
Applicable temperature (°C)	15–30	18–30

.

3.2.2. Image Acquisition Testing

According to the principle of equivalence of the data set establishment conditions in a non-stationary environment and the structure of the image differential model as in Figure 4, it can be seen that the operating parameters of the spray gun involved in this paper include the atomization pressure, the fan control pressure, and the flow control pressure. In order to ensure that the experimental design has engineering practice significance, the parameter gradient settings can cover the extreme conditions of the actual spraying scenarios. Based on actual spraying experience, the minimum pressure required to ensure effective atomization of the coating is 100 kPa. The minimum values for effective fan control pressure and flow control pressure are both 50 kPa. The maximum pressure value provided under the current experimental conditions is 300 kPa. Therefore, the atomization pressure range is set to 100–300 kPa, the fan control pressure range is set to 50–300 kPa, and the flow control pressure range is set to 50–300 kPa. Based on the above parameter ranges, an orthogonal experimental design (L15) was employed to arrange the test scheme. This orthogonal array allows for the investigation of optimal combinations of the three factors ($P_w$, $P_f$, $P_q$) within the specified ranges. At the same time, according to the spatial coverage and engineering experience analysis, the number of tests was reduced (from 27 groups in the full factor test to 15 groups). Each factor was tested at five evenly distributed levels across the parameter range, with level settings of 100, 150, 200, 250, and 300 (kPa). The setting of the image acquisition frequency needs to take into consideration the accuracy of the experiment. The frequency of image acquisition needs to be set taking into account the precision of the experiment and the ability of the experimental equipment, and is set to 33 frames per second, with 100 frames for each group of parameters. During shooting, the camera’s exposure time was 10,000.00 (us) and the white balance coefficient was 1.7813. The images were processed by the interception method in Figure 2 and the labeling method in Figure 3, and part of the image data for aviation paint A is shown in Figure 7.

4. Results and Analysis

4.1. Verification Results of the Principle of Equivalence of Conditions for Establishing Data Sets in Unstable Environments

As shown in Figure 8, sprayed samples Sp1, Sp2, and Sp3 were obtained under the spraying conditions listed in Table 2. The coating thickness distribution data were collected according to the method shown in Figure 5. Each set of data corresponds to 30 measurement points distributed at equal intervals on the spray trajectory. The data is shown in

Table A1. Coating thickness measurement data.

Sample	Sp1/μm	Sp2/μm	Sp3/μm
1	1.8	4.1	2.6
2	2.1	4.9	2.4
3	2.4	3.5	2.3
4	2.9	4.7	4.3
5	4.8	5.8	5.1
6	5.1	6.7	6.1
7	6.5	9.7	7.3
8	7.4	11.6	9.2
9	8.2	13.8	11.9
10	11.4	15.4	13.5
11	13.4	15.9	14.6
12	15.4	17.2	15.7
13	17.9	19.1	16.1
14	17.6	20.2	18.3
15	19.5	21.6	18.9
16	19.2	21.5	18.5
17	18.5	20.9	18.0
18	17.5	19.8	16.8
19	16.2	18.2	16.5
20	13.8	16.5	14.4
21	13.9	16.5	13.8
22	10.9	13.6	12.5
23	9.2	12.0	10.8
24	6.2	10.7	9.6
25	7.1	8.9	6.9
26	5.0	7.3	6.7
27	3.5	6.9	6.5
28	3.2	5.4	4.6
29	2.5	4.0	4.0
30	2.0	3.4	4.2

of Appendix A.

Comparing the data from the Sp1 and Sp2 groups, it can be observed that as temperature increases, paint viscosity decreases, leading to changes in coating thickness. The coating thickness increases, and the fan angle expands. The comparison of coating thickness data between the two groups is shown in Figure 9a. Sp3 involves adjusting $P_w$, $P_f$ and $P_q$ under elevated temperature conditions. Comparing the data from Sp1 and Sp3, as shown in Figure 9b, the trends in coating thickness distribution for the two groups are generally consistent. This indicates that by adjusting the pressure, consistent spray coating effects can be achieved at different temperatures.

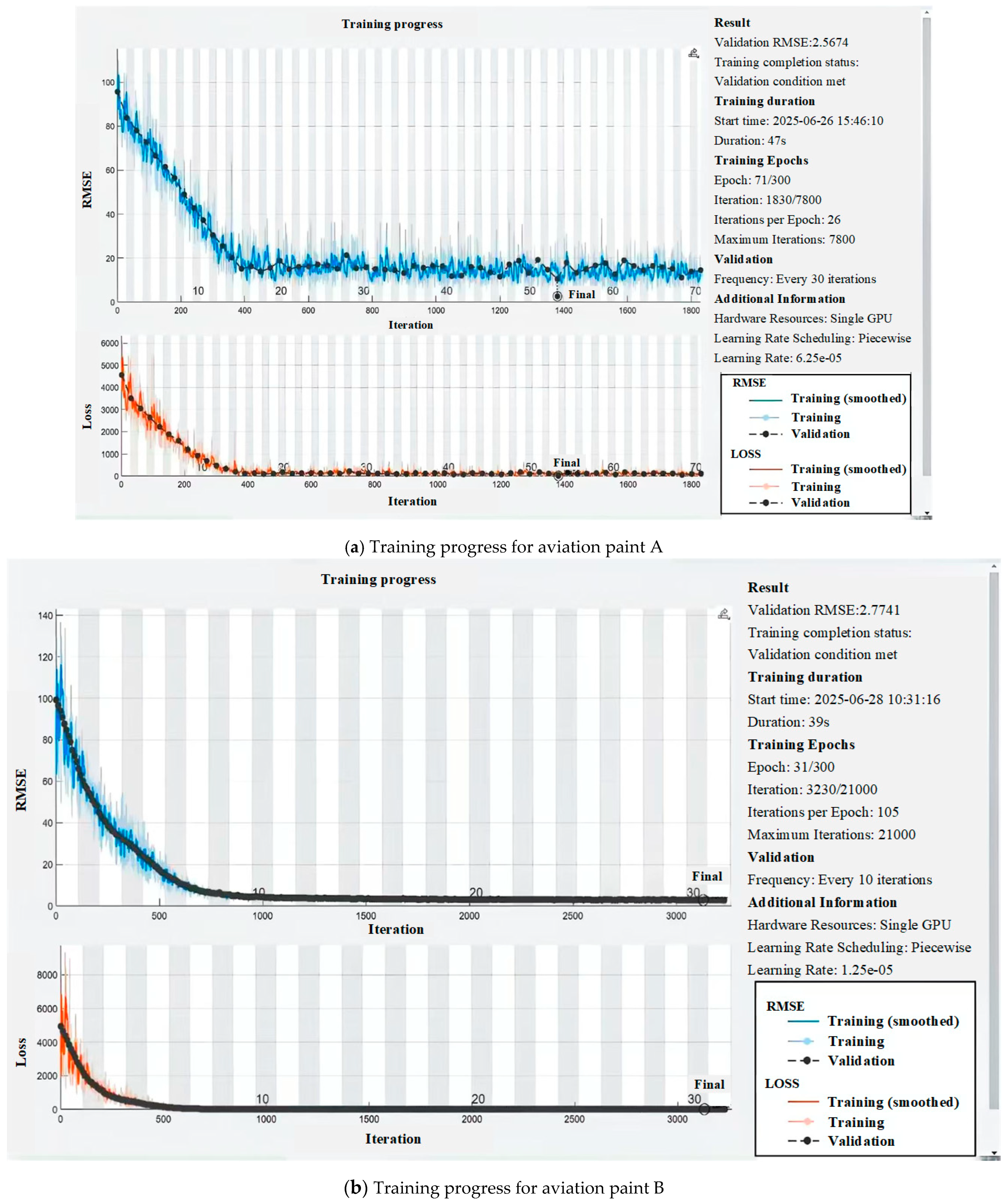
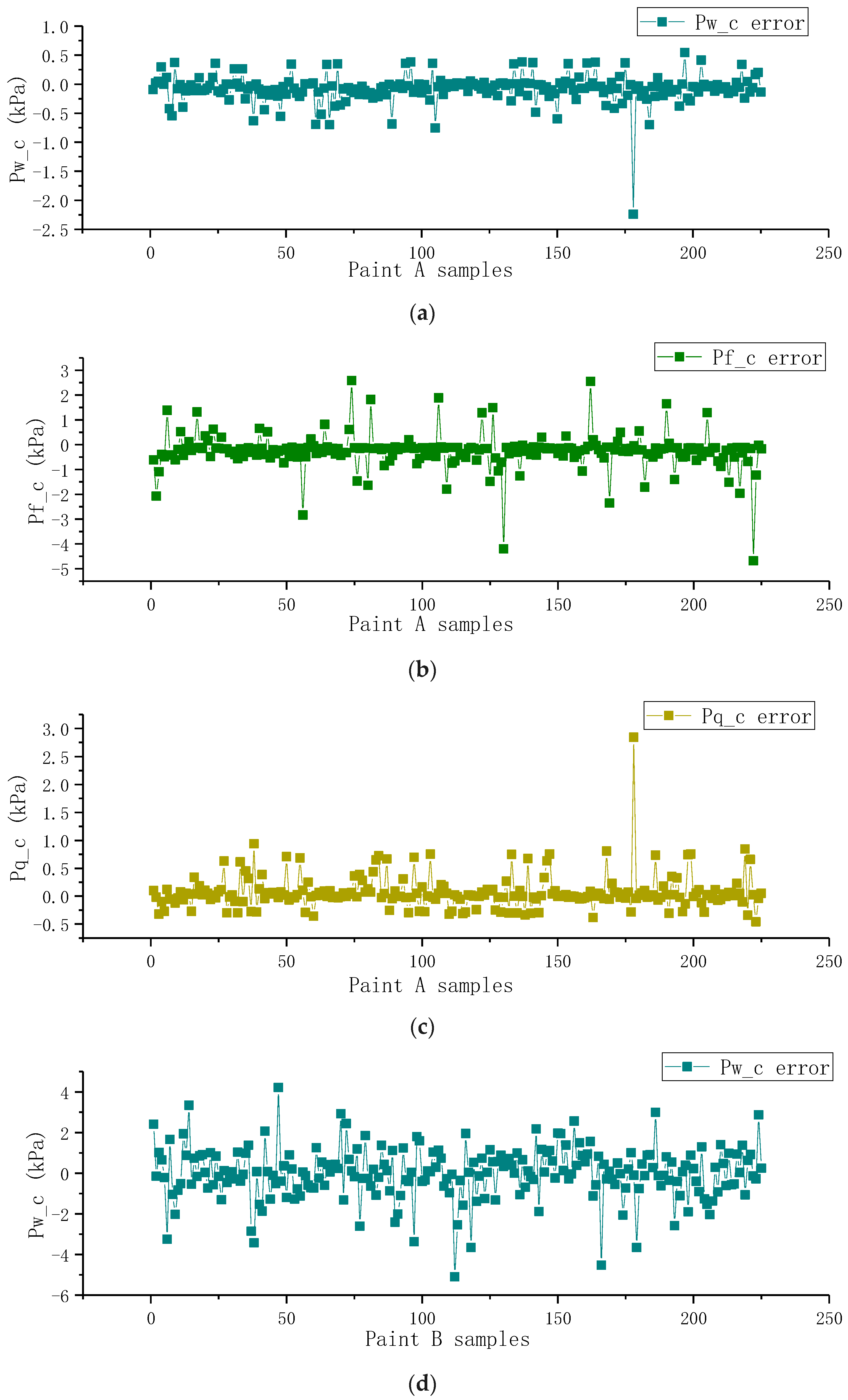
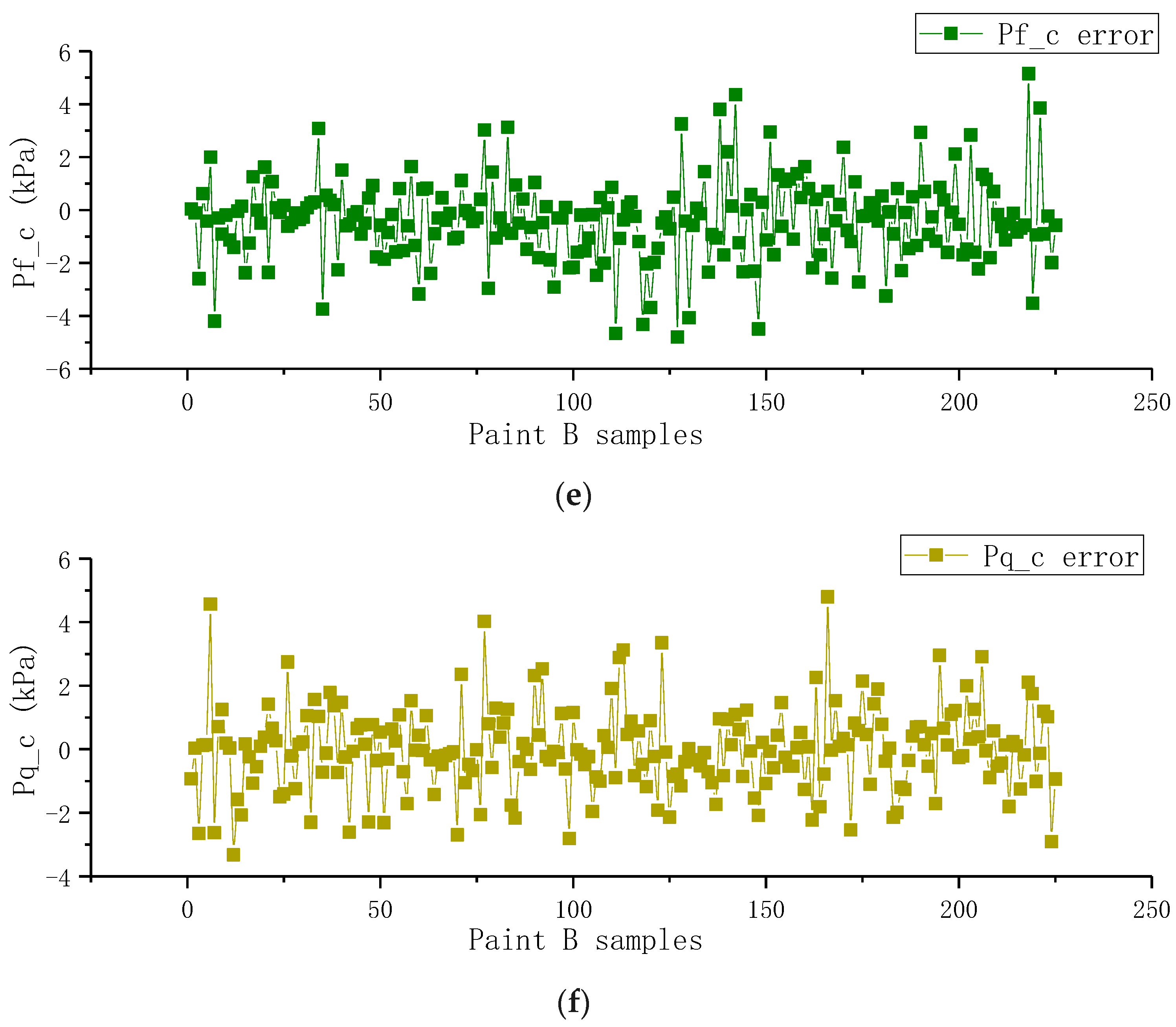
4.2. Image Difference Model Verification Results

According to the image difference model architecture shown in Figure 4, the model inputs used in this paper are Image 1 (Image_1) reference image, as in Figure 10, and Image 2 (Image_2) actual captured image, as in Figure 7; and the dataset formed according to Equations (7) and (8), in which 70% of the data are randomly selected as the training set, 15% as the validation set, and 15% as the test set. Some of the data are shown in

Table 5. Some of the data for aviation paint A.

Image_1	Image_2	${\mathit{P}}_{\mathit{w}\_\mathit{c}}$/kPa	${\mathit{P}}_{\mathit{f}\_\mathit{c}}$/kPa	${\mathit{P}}_{\mathit{q}\_\mathit{c}}$/kPa
		100	0	0
		50	0	0
		0	0	50
		0	0	−150
		0	−50	0

and

Table 6. Some of the data for aviation paint B.

Image_1	Image_2	${\mathit{P}}_{\mathit{w}\_\mathit{c}}$/kPa	${\mathit{P}}_{\mathit{f}\_\mathit{c}}$/kPa	${\mathit{P}}_{\mathit{q}\_\mathit{c}}$/kPa
		150	−100	0
		100	−100	50
		100	−100	0
		−50	0	0
		−50	−100	0

.

The image difference model architecture is shown in Figure 4 in which two CNN branches are used with two convolutional layers, respectively, and each convolutional layer adopts a 3 × 3 convolutional kernel; the feature fusion is chosen to be depth splicing (Depth Concatenation); the MLP part is used with three full-connectivity layers, all of which are 128 neurons; and the activation function adopts the ReLU nonlinear activation. The patience value is set to 10 in the model to balance training efficiency and prevent overfitting. The initial learning rate of the model is 1 × 10⁻³, and it is decayed based on the training cycle according to a decay rate of 0.9, so that the learning rate decreases with the increase of the number of training steps. Through this dynamic adjustment of the learning rate, the model is able to converge quickly in the early stage of training, while maintaining a stable convergence state in the later stage, avoiding the overfitting problem caused by a too large learning rate. To prevent data imbalance, batch normalization is added to the model to mitigate internal covariate bias and improve the learning efficiency of sparse samples. The progress of model training is shown in Figure 11.

Model by defining coefficient on the performance of the validation set (R²) (Equation (10)), root mean square error (RMSE) and standard deviation of residuals (σ_e) to evaluate (Equation (11)). As shown in

Table 7. Performance parameters of the validation set.

Parameters	Aviation Paint A			Aviation Paint B
	${\mathit{P}}_{\mathit{w}\_\mathit{c}}$	${\mathit{P}}_{\mathit{f}\_\mathit{c}}$	${\mathit{P}}_{\mathit{q}\_\mathit{c}}$	${\mathit{P}}_{\mathit{w}\_\mathit{c}}$	${\mathit{P}}_{\mathit{f}\_\mathit{c}}$	${\mathit{P}}_{\mathit{q}\_\mathit{c}}$
R2	0.99995	0.9998	0.9999	0.9989	0.9994	0.9966
RMSE	0.23980	0.86101	0.24336	0.6687	0.7536	0.6226
σe	0.22315	0.8563	0.23264	0.66788	0.7479	0.52176

, in which R² are all greater than 0.99, and the values of the RMSE and σ_e are all smaller, and the model performance is better. Further tests can be carried out.

$$R^2=1-{\displaystyle \frac{{\displaystyle {\sum }_i{({\widehat{y}}_{\iota }-y_i)}^2}}{{\displaystyle {\sum }_i{({\overline{y}}_{\iota }-y_i)}^2}}}$$

(10)

$$RMSE=\sqrt{{\displaystyle \frac{1}{m}}{\displaystyle \sum _{i=1}^n{(y_i-{\widehat{y}}_{\iota })}^2}}$$

(11)

$${\sigma }_e=\sqrt{{\displaystyle \frac{1}{m}}{\displaystyle \sum _{i=1}^m{\left(e_i-\overline{e}\right)}^2}}$$

(12)

where y_i is the true value of the test set samples; ${\widehat{y}}_{\iota }$ is the predicted value of the test set samples; ${\overline{y}}_{\iota }$ is the average of the true values of the test set samples; m is the total number of test set samples, e_i is the sample deviation of the test set, $\overline{e}$ is the average value of the sample deviation of the test set, and m is the total number of samples in the test set.

Based on the above model performance, the model was tested using an independent test set in order to prevent model overfitting. The total model prediction time is 0.38 s. The residuals of the atomization pressure correction value, fan control pressure correction value, and flow control pressure correction value are used as observation objects. The results are shown in Figure 12. The horizontal axis represents the number of samples, which is 225 samples from the test set; the vertical axis represents the residual values of the three pressure correction values (observed−predicted), with units in kPa.

As clearly shown in Figure 12, the residual pressure values for aviation paint A are as follows: $P_{w\_c}$ residual pressure range (−2.5 to 1 kPa), $P_{f\_c}$ residual pressure range (−5 to 3 kPa), and $P_{q\_c}$ residual pressure range (−1 to 3 kPa); the residual pressure values for aviation paint B are as follows: $P_{w\_c}$ residual value range of (−4 to 4 kPa), $P_{f\_c}$ residual value range of (−5 to 5 kPa), and a $P_{q\_c}$ residual value range of (−4 to 5 kPa). The residual values of all three parameters for aviation paint A exhibit significant positive and negative deviations, indicating that the model’s predictions for aviation paint A show notable discrepancies from actual values at certain data points. This phenomenon may be attributed to aviation paint A’s intrinsic material properties or more complex environmental disturbances during testing. In contrast, the residuals for aviation paint B are generally more concentrated, with most data points demonstrating smaller absolute deviations, except for a few outliers. This suggests that the model’s predictive stability for aviation paint B is relatively superior. While aviation paint A exhibits some extreme residuals, the model still maintains an exceptionally high coefficient of determination ($R^2$) overall, implying that these large deviations may stem from isolated special cases rather than systemic flaws in model performance. The minimal fluctuations in aviation paint B’s residuals also align with its high predictive accuracy observed in laboratory tests. In summary, the model demonstrates effective dynamic adjustment capabilities for both aviation paint A and paint B under non-stationary conditions, despite their differing residual characteristics.

The closer the model’s coefficient of determination (R²) is to 1, the stronger the model’s predictive ability [28]; as shown in

Table 8. Performance parameters of the test set.

Parameters	Aviation Paint A			Aviation Paint B
	${\mathit{P}}_{\mathit{w}\_\mathit{c}}$	${\mathit{P}}_{\mathit{f}\_\mathit{c}}$	${\mathit{P}}_{\mathit{q}\_\mathit{c}}$	${\mathit{P}}_{\mathit{w}\_\mathit{c}}$	${\mathit{P}}_{\mathit{f}\_\mathit{c}}$	${\mathit{P}}_{\mathit{q}\_\mathit{c}}$
R2	0.99996	0.99984	0.99992	0.9988	0.9993	0.9979
RMSE	0.26677	0.79033	0.32678	0.6542	0.6696	0.6125
σe	0.2545	0.74442	0.31895	0.6513	0.6361	0.6123

, the model in this paper has R² values very close to 1 in predicting all three pressure corrections for aviation paint A and paint B, indicating that the models have strong predictive capability for these three pressure correction values. Among these, the R² value for $P_{f\_c}$ of aviation paint A is the highest, and the R² value for $P_{w\_c}$ of aviation paint B is the highest, with the surface model demonstrating the best predictive performance for this variable.

Root mean square error (RMSE) is a measure of the difference between predicted values and actual values. The smaller the value, the smaller the prediction error of the model, and the more concentrated and consistent the data [29]. As shown in Table A1, $P_{w\_c}$ has the smallest RMSE (0.26677) in this paper’s model, indicating that the model has the smallest prediction error and highest prediction accuracy for this variable. Although the RMSE of $P_{f\_c}$ is slightly higher (0.79033), its R² value is still very high, indicating that the model still has a very good predictive ability overall.

The standard deviation of residuals (σ_e) is one of the core indicators for evaluating the performance of a regression model, reflecting the consistency and stability of the model’s predictions. The smaller the σ_e value, the lower the dispersion of prediction errors, indicating higher model accuracy. As shown in Table A1, in the model of this paper, the σ_e value of $P_{w\_c}$ in aviation paint A is the smallest, indicating that the model performs optimally in predicting this parameter. Similar to the root mean square error (RMSE), the σ_e value for the three pressure correction values for aviation paint B are close to each other (0.61–0.65), indicating that the model controls the error fluctuations of all outputs relatively evenly, consistent with the conclusions drawn from the RMSE.

Based on the experimental results in Figure 12 and Table 8, we conducted an in-depth analysis of the model performance. Based on the model performance parameters R², RMSE, and σ_e, the results for aviation paint A show that the C value (0.99996) for $P_{w\_c}$ is the highest, indicating that the model has the strongest explanatory power for this variable. Additionally, the RMSE (0.26677) and standard deviation of residuals (σ_e) for $P_{w\_c}$ are the smallest, indicating that the model has the smallest prediction error and highest accuracy for this variable. The results for aviation paint B show that the R² value for $P_{f\_c}$ (0.9993) is the highest, indicating that the model performs best in predicting this variable. The RMSE and σ_e values for the three parameters are relatively consistent, indicating that the model has a balanced explanatory power for the three parameters. In summary, due to the higher viscosity and solid content of paint A (Table 4), its paint mist morphology is more sensitive to environmental fluctuations, resulting in slightly greater residual fluctuations than paint B (Figure 12a–c vs. Figure 12d–f). However, the model still maintains high accuracy ($R^2$ > 0.997) through dynamic learning rates and regularization strategies, confirming its robustness for paints with different rheological properties.

Analyzing from the perspective of modelling efficiency, the time required for each link of the method described in this paper is shown in

Table 9. Time consumption of the modeling session.

Steps	Time Consumption/min
Image Acquisition	1.5
Image capture and labelling	1.4
Image Difference Model Training	1
Model Testing	0.005
Totals	3.905

, and the complete modelling process is <4 min, which has better computational efficiency and supports real-time applications while maintaining higher accuracy.

5. Conclusions

In this paper, a dynamic control method based on visual differential feedback for the coating accumulation model in non-stationary environment is proposed, aiming to solve the problem of coating accumulation model failure in non-stationary environment. A visual differential feedback model that can correct the coating accumulation model in real time is constructed by modeling the online image data with real-time feedback from the reference image. The following are the main conclusions of this paper:

(1)

Using the Arrhenius equation and the Hagen–Poiseuille equation, it was demonstrated that the datasets for pressure regulation and temperature variation are equivalent in terms of the conditions under which they were established. Experimental results indicate that, under conditions where temperature increase (18 °C vs. 24.1 °C) leads to reduced paint viscosity, optimizing spray pressure parameters ($P_w$, $P_f$, $P_q$) can effectively compensate for the effects of temperature changes, ensuring that the coating thickness distribution (Sp3) remains consistent with the low-temperature baseline (Sp1). This finding indicates that dynamic adjustment of pressure parameters can serve as a compensation mechanism for temperature fluctuations, thereby maintaining the stability of the spraying process without relying on strict temperature control. This method significantly reduces the high cost and complexity of environmental temperature control, while minimizing data collection biases caused by temperature fluctuations, providing a theoretical basis and feasible solution for optimizing industrial spraying processes.

(2)

This study employs online image data modeling coupled with real-time feedback to achieve modeling completion within 4 min (Table 9) while maintaining exceptional prediction accuracy ($R^2$ > 0.999, Table 8), enabling real-time stabilization of the coating accumulation model in non-stationary environments.

(3)

The model adopts a dual-branch CNN + MLP architecture, which enhances features through image difference technology to predict pressure correction values. Optimization strategies (such as dynamic learning rate, dropout, and L2 regularization) further improve model performance. Two typical types of aviation paint materials were adopted in the experiment: high-viscosity polyurethane enamel (A, viscosity 22 s) and epoxy polyamide primer (B, viscosity 18 s). The results showed that the model achieved an R² > 0.999 RMSE < 0.79 kPa, and σ_e < 0.74 kPa on the test set for aviation paint A, and an R² > 0.997 RMSE < 0.67 kPa, and σ_e < 0.66 kPa on the test set for aviation paint B. Under the tested conditions, the dual-branch CNN + MLP model demonstrated superior performance and high accuracy in parameter prediction for both paint types through image differentiation and optimization strategies. This verifies its ability to achieve good dynamic adjustment performance for paints with different rheological properties in non-stable environments. However, verification is needed in a broader space.

In summary, this approach reduces data acquisition costs through the pressure–temperature equivalence principle, overcomes the latency of traditional offline methods via real-time online image modeling, and ultimately achieves dynamic stabilization of the coating accumulation model in non-stationary environments through the image difference model.