Multiscale Simulation of Graphene Growth on Cu(111): Insights from DFT, MD, KMC, and Thermodynamic Analyses

Abstract

In chemical vapor deposition (CVD)-mediated graphene growth, copper foil serves as both a catalyst for methane decomposition and as a substrate for graphene nucleation and growth. Due to the low solubility of carbon in copper and the ease of transferring graphene from its surface, copper—particularly the Cu(111) facet—is widely favored for high-quality, monolayer graphene synthesis. In this article, the thermodynamic processes involved in methane dissociation and graphene nucleation on the Cu(111) surface were investigated using density functional theory (DFT). Molecular dynamics simulations were performed for structural optimization and to evaluate the reaction energies. Additionally, the average adsorption energies (ΔEad) of carbon clusters with varying atomic numbers on the Cu(111) surface were calculated. The graphene growth process was further modeled using the kinetic Monte Carlo (KMC) method to simulate carbon atom migration and nucleation dynamics. Thermodynamic analysis based on equilibrium component data was conducted to examine the influence of key operational parameters—temperature, pressure, and the CH₄/H₂ partial pressure ratio—on the graphene deposition rate.

1. Introduction

Graphene, a two-dimensional material composed of a single layer of carbon atoms arranged in a hexagonal lattice, has garnered significant attention due to its exceptional electrical, mechanical, and thermal properties. Among the various methods developed for graphene synthesis, chemical vapor deposition (CVD) has emerged as one of the most promising techniques for producing high-quality, large-area graphene films. Central to the success of CVD-based graphene growth is the choice of substrate, with copper (Cu) being one of the most widely utilized materials. This preference stems from copper’s low carbon solubility, which facilitates the self-limiting growth of monolayer graphene, and its suitability for clean, straightforward transfer processes. Notably, the Cu(111) crystallographic surface offers an atomic lattice that closely matches that of graphene, making it particularly conducive to uniform graphene nucleation and growth. Recent studies have also investigated aromatic hydrocarbons on Cu(111) and showed that their adsorption and stepwise dehydrogenation contribute to graphene formation [1].

Understanding the fundamental thermodynamic and kinetic mechanisms that govern graphene growth on Cu(111) is essential for optimizing the synthesis parameters and improving the material quality. Methane (CH₄) is commonly used as the carbon precursor in CVD processes, and its decomposition into active carbon species on the copper surface is a key step in graphene formation. However, the detailed energetics and atomistic pathways of methane dissociation and subsequent carbon cluster nucleation remain areas of active investigation.

While previous studies have provided valuable insights into the adsorption behavior of hydrocarbon precursors and the catalytic role of Cu(111) surfaces, comprehensive investigations integrating thermodynamic modeling with atomic-level simulations remain limited. The present study distinguishes itself by coupling density functional theory (DFT), molecular dynamics (MD), and kinetic Monte Carlo (KMC) simulations with thermodynamic analysis, thereby offering a multiscale approach to understanding both the equilibrium and kinetic aspects of graphene growth. This integrated framework enables a more detailed and predictive understanding of how process parameters influence deposition mechanisms, which is crucial for advancing controllable CVD synthesis strategies.

In this work, we employed density functional theory (DFT) to analyze the dissociation of methane and the adsorption behavior of carbon clusters on the Cu(111) surface. Molecular dynamics (MD) simulations were used to optimize atomic configurations and compute reaction energies. Furthermore, kinetic Monte Carlo (KMC) simulations provided insight into the time-resolved dynamics of carbon atom diffusion and graphene nucleation. To complement these atomistic models, a thermodynamic analysis based on equilibrium composition data was conducted to explore the impact of temperature, pressure, and the CH₄/H₂ partial pressure ratio on the deposition rate. Together, these methods offer a comprehensive understanding of the CVD graphene growth mechanism on Cu(111), with implications for process optimization and controlled synthesis.

2. Mechanism of Graphene Growth on Cu(111) Surface

2.1. Model Building and Parameterization

In this study, density functional theory (DFT) calculations were performed using the Vienna Ab initio Simulation Package (VASP). The exchange–correlation interactions among electrons were treated within the framework of the Generalized Gradient Approximation (GGA), specifically employing the Perdew–Burke–Ernzerhof (PBE) functional [2]. The valence electrons were described using a plane-wave basis set with a kinetic energy cutoff of 400 eV, while the interactions between valence and core electrons were modeled using the projector augmented wave (PAW) method [3]. The Brillouin zone was sampled using a Monkhorst–Pack k-point grid of 3 × 3 × 1. The energy convergence criterion for self-consistent field (SCF) iterations was set to 1 × 10⁻⁵ eV, and structural optimization was performed until the maximum Hellmann–Feynman force on each atom was below 0.03 eV/Å. These settings ensured a reliable and accurate description of the adsorption and reaction mechanisms on the Cu(111) surface.

Copper (Cu) is a face-centered cubic (FCC) metal, with atoms located at the eight corners and the centers of the six faces of the unit cell. Its low-index crystal surfaces include (111), (100), and (110), among which, the (111) surface exhibits the lowest surface energy and is therefore the most thermodynamically stable [4]. Accordingly, the Cu(111) surface was selected as the theoretical model in this study. The optimized structure of the Cu(111) surface, obtained via density functional theory (DFT) calculations, is presented in Figure 1.

A 4 × 4 supercell of the Cu(111) surface was constructed for the modeling. The slab consisted of seven atomic layers, with atoms sharing the same z-coordinate considered to belong to the same layer. A vacuum layer of 15 Å was added along the z-direction to eliminate spurious interactions between periodic images. To enable structural optimization, the bottom two layers of the slab were fixed to represent the bulk Cu(111) structure, while the remaining five layers—as well as any adsorbed atoms or molecules—were allowed to fully relax. The fixed layers (fourth and fifth from the surface) are not explicitly labeled in the figure.

The Cu(111) surface exhibits an ABC stacking sequence, with four typical adsorption sites: face-centered cubic (Fcc), hexagonal close-packed (Hcp), top, and bridge sites. The Fcc site is positioned among three surface Cu atoms and directly above the third-layer atoms, aligning with the lattice parameters of Cu (lattice constant = 3.61 Å; angle = 90°). The Hcp site lies above a hollow formed by three first-layer Cu atoms and is aligned with atoms in the second layer [5]. The top site corresponds to the location directly above a surface Cu atom, while the bridge site is located between two adjacent surface Cu atoms. Since the dissociation products of CH₄—carbon and hydrogen atoms—are most stable when adsorbed at the Fcc site, only Fcc-site adsorption was considered in the calculations of CH₄ dissociation.

2.2. Dehydrogenation of Methane on the Cu(111) Surface

Upon dehydrogenation of CH₄ on the Cu substrate surface, the initial state involves the adsorption of CH₄ molecules. Following a stepwise dehydrogenation mechanism, the process ultimately leads to the adsorption of carbon (C) atoms and four hydrogen (H) atoms. Three intermediates are formed during the dehydrogenation process on the methane Cu(111) surface: methyl (CH₃), methylene (CH₂), and hypomethyl (CH). These intermediates correspond to the four-step dehydrogenation reaction, as outlined in Equations (1)–(4).

CH₄ → CH₃ + H

(1)

CH₃ → CH₂ + H

(2)

CH₂ → CH + H

(3)

CH → C + H

(4)

To determine the energy required for each step of the reaction, the structures of the reactants and products for each reaction step are first optimized. The geometries presented in Figure 2 represent the final state of each basic dehydrogenation step on the Cu(111) surface, where Cu atoms are depicted as orange spheres, C atoms as gray spheres, and H atoms as white spheres.

The energy profile for the dehydrogenation of methane on the Cu(111) surface, leading to the generation of adsorbed carbon atoms, is shown in Figure 3. The dehydrogenation process of methane occurs through four basic steps, with the corresponding reaction energies (ΔE) provided in Equations (5)–(8).

CH₄ → CH₃ + H          ΔE = 0.94 eV

(5)

CH₃ → CH₂ + H          ΔE = 0.62 eV

(6)

CH₂ → CH + H           ΔE = 0.30 eV

(7)

CH → C + H              ΔE = 1.23 eV

(8)

From Equations (5)–(8), it is evident that all four dehydrogenation steps are endothermic. As illustrated in Figure 3, the energy distribution during methane dehydrogenation shows that the final step, where CH dehydrogenates to form carbon atoms, requires as much as 1.23 eV. Moreover, the energy of the final product, C + 4H, is 3.09 eV higher than that of the adsorbed CH₄. This suggests that the dehydrogenation of methane to form carbon atoms demands a significant amount of energy [6,7]. Consequently, it has been proposed that CH_n (n = 1, 2, 3, 4) groups may play a role in the formation of graphene, and that lowering the dehydrogenation barrier could accelerate graphene growth [7].

2.3. Nucleation of Carbon Atoms on the Cu(111) Surface

The average adsorption energy of carbon atoms on the Cu(111) surface is defined as

ΔE_ad = [E_C/Cu − E_Cu + E_C]/N_C

(9)

where E_C/Cu is the total energy of the system after adsorption of carbon clusters on the surface of Cu(111), E_Cu is the energy of the pure Cu(111) surface, E_C is the energy of individual carbon atoms in the vacuum, and N_C is the number of carbon atoms in the clusters.

The average binding energy calculated for the nucleation process of carbon on the Cu(111) surface is shown in Figure 4. A negative binding energy indicates that the adsorption of the atoms is exothermic, and the system tends toward a more stable state. The average C adsorption energies for C₁, C₃, C₅, C₆, C₁₀, and C₁₃ on the Cu(111) surface were calculated to be −5.11 eV, −6.52 eV, −6.40 eV, −6.54 eV, −6.74 eV, and −6.86 eV, respectively [8,9,10,11]. To further validate our results, we compared the binding energy of the C₆ cluster (−6.54 eV) with the values reported in previous studies. For example, Zhang et al. reported a binding energy of approximately −6.5 eV for similar carbon clusters on Cu(111), which is in excellent agreement with our result. This comparison supports the reliability of our computational approach and enhances the significance of the calculated adsorption energies [12]. The results of the DFT calculations show that as the number of carbon atoms increases, the average binding energy of carbon atoms becomes stronger for the formation of the C₃ straight chain compared to the formation of C₄ and C₅ rings. Additionally, the binding energy is further enhanced for the formation of C₆, C₁₀, and C₁₃ clusters. The higher the number of carbon atoms, the stronger the binding of carbon to the Cu surface, as well as the interactions between carbon atoms. The average binding energy of carbon atoms in the C₃ chain is also stronger than that in the C₄ and C₅ rings. Therefore, when the concentration of carbon atoms on the Cu(111) surface is low, the formation of straight chains is more stable. However, as the concentration of adsorbed carbon increases, the formation of carbon rings becomes more favorable, and a higher concentration of adsorbed carbon atoms favors the formation of graphene.

The structures optimized by the adsorption of atoms with different carbon numbers on the Cu(111) surface are shown in Figure 5, where orange represents Cu and gray represents C. Carbon forms both linear and cyclic chain configurations on the Cu(111) surface. Due to the stronger C-C interactions relative to C-Cu interactions, the C₁₀ two-carbon hexacyclic structure has the potential to be converted into a carbon chain under specific conditions, even in studies involving C_x (x = 1–13). However, when the three-carbon hexacyclic structure of C₁₃ is formed, it is not easily broken to form a carbon chain, and the structure remains relatively stable. At this stage, three bonds must be broken to dissociate C₁₃ and form a carbon chain [13]. The energy difference between the linear chain and the cyclic chain typically decreases with an increase in the number of carbon atoms, facilitating the conversion of the carbon linear chain into graphene. Moreover, the larger the number of carbon atoms in the chain, the higher the energy barrier to the formation of carbon chains, making the formation of long chains more difficult [14,15,16]. It was deduced that the polymerization of polymer rings, along with the polymerization of these rings with carbon polymers, is the key factor in the growth of graphene. Therefore, when these polymers form the carbon ring structure on the Cu(111) surface, a higher concentration of such structures leads to greater stability [17].

3. Graphene Growth Mechanism Based on Kinetic Monte Carlo Method

Due to the copper substrate surface, the gas flow is divided into two mechanisms: a mass transfer mechanism and surface reaction mechanism [18]. The kinetic Monte Carlo model (KMC) method was further utilized to simulate the growth of graphene using the CVD method to calculate the mass transport coefficient, $h_g$, of the reactant gas in the mass transport process using methane as the carbon source.

$$h_g={\displaystyle \frac{D_g}{\delta }}$$

(10)

where $D_g$ is the gas diffusion coefficient and satisfies

$$D_g=D_0{({\displaystyle \frac{T}{T_0}})}^n({\displaystyle \frac{P_0}{P}})$$

(11)

where $T_0$ = 273 K, $P_0$ is the standard atmospheric pressure, $D_0$ is the diffusion coefficient constant. Here, $D_0$ = 4.86 × 10⁻⁵ and $n$= 1.81; substituting these into the $h_g$ expression, we obtain Equation (12):

$$h_g={\displaystyle \frac{D_0}{\delta }}{\left({\displaystyle \frac{T}{T_0}}\right)}^{1.81}\left({\displaystyle \frac{p_0}{p}}\right)$$

(12)

where the average boundary layer thickness is set as $\delta$= 0.02 m. The mass transport coefficient $h_g$ of the reacting gases at different growth temperatures and pressures was numerically simulated for a horizontal reactor (as shown in Figure 6, with a chamber length of 140 cm, a base surface of 6 cm, and a diameter of 8 cm), which is commonly used in laboratories today [19]. Each gas component at the inlet was set to CH₄:H₂ = 15:7 (sccm), and the growth temperature was 1310 K. The results of calculating the changes in methane concentration at both atmospheric pressure (101,325 pa) and low pressure (660 pa) with the time step set to 1 s are shown in Figure 7 and Figure 8.

To improve the accuracy and robustness of the results, a sensitivity analysis was carried out to investigate the influence of the boundary layer thickness ($\delta$) on the mass transfer behavior. The simulations were repeated with $\delta$ values of 0.005 m, 0.01 m, 0.02 m, and 0.03 m to evaluate their impact on the calculated mass transfer coefficient h_g and the spatial distribution of the methane concentration. The results revealed that $\delta$ significantly affects the mass transport dynamics, particularly under low-pressure conditions, where slight variations in $\delta$ led to noticeable differences in gas concentration gradients. This finding underscores the importance of considering the dependence on $\delta$ in mass transfer modeling, as fixed $\delta$ values may underestimate the boundary layer’s influence on the reaction kinetics. Incorporating this analysis enhances the reliability and physical relevance of the simulation outcomes.

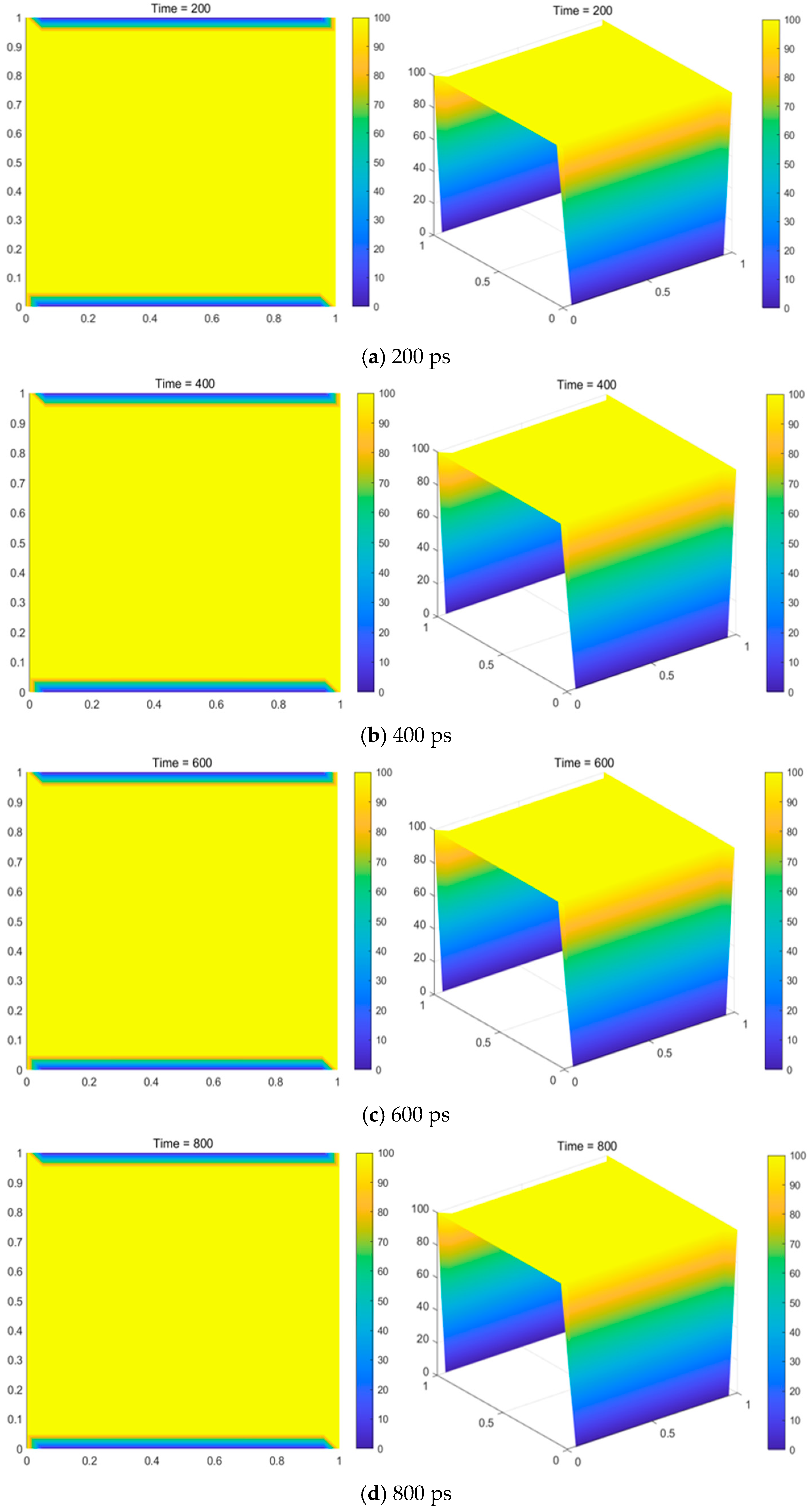
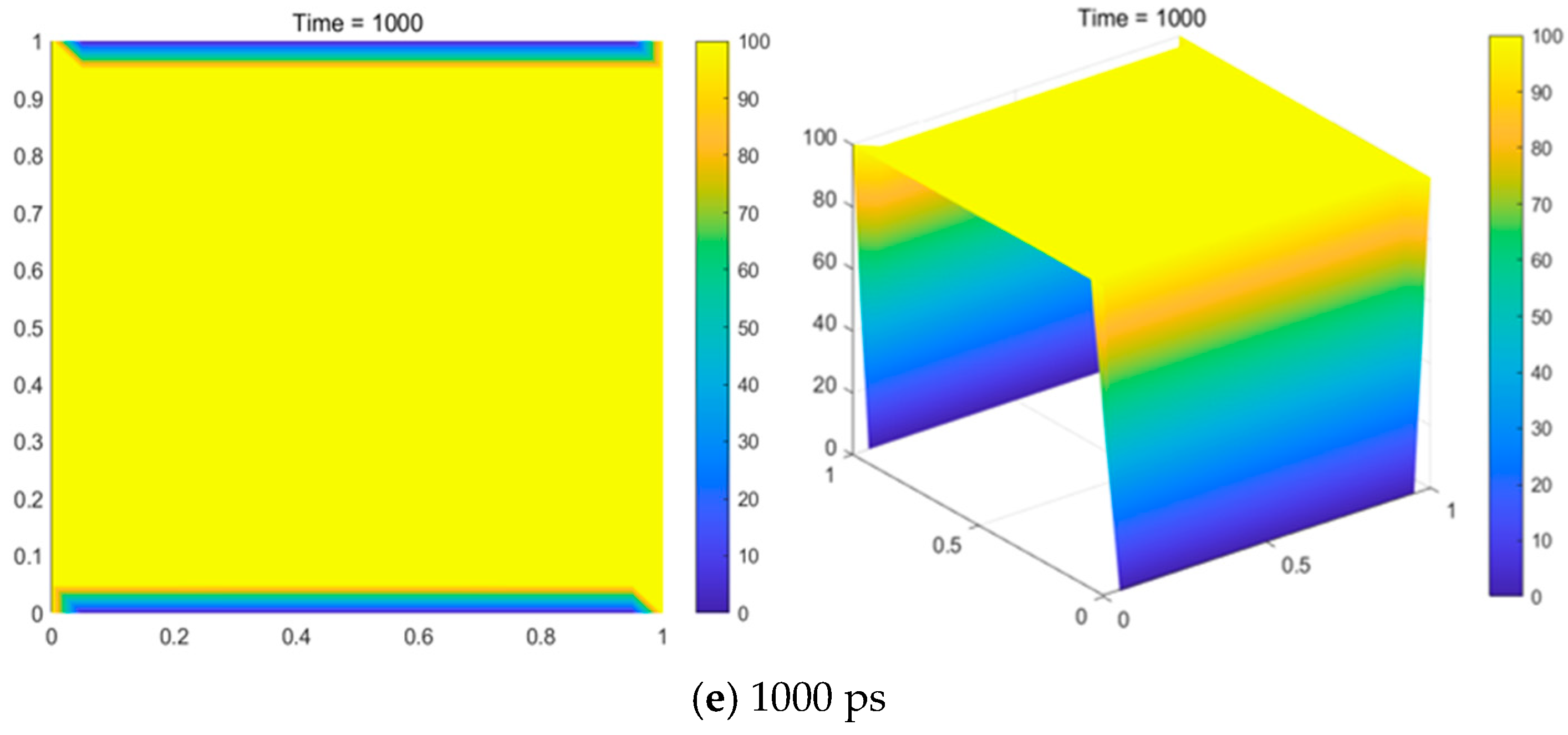
From Figure 7, it can be observed that under atmospheric pressure conditions, as the time step increases, the voids between the graphene sheets were gradually filled by carbon atoms. However, the rate of graphene film formation was slow. This was due to the relatively high pressure, which caused the transport coefficient h_g of methane to decrease with increasing pressure. Consequently, this process is limited by mass transport control. The variation in CH₄ concentration with the time step at a pressure of 660 Pa is shown in Figure 8.

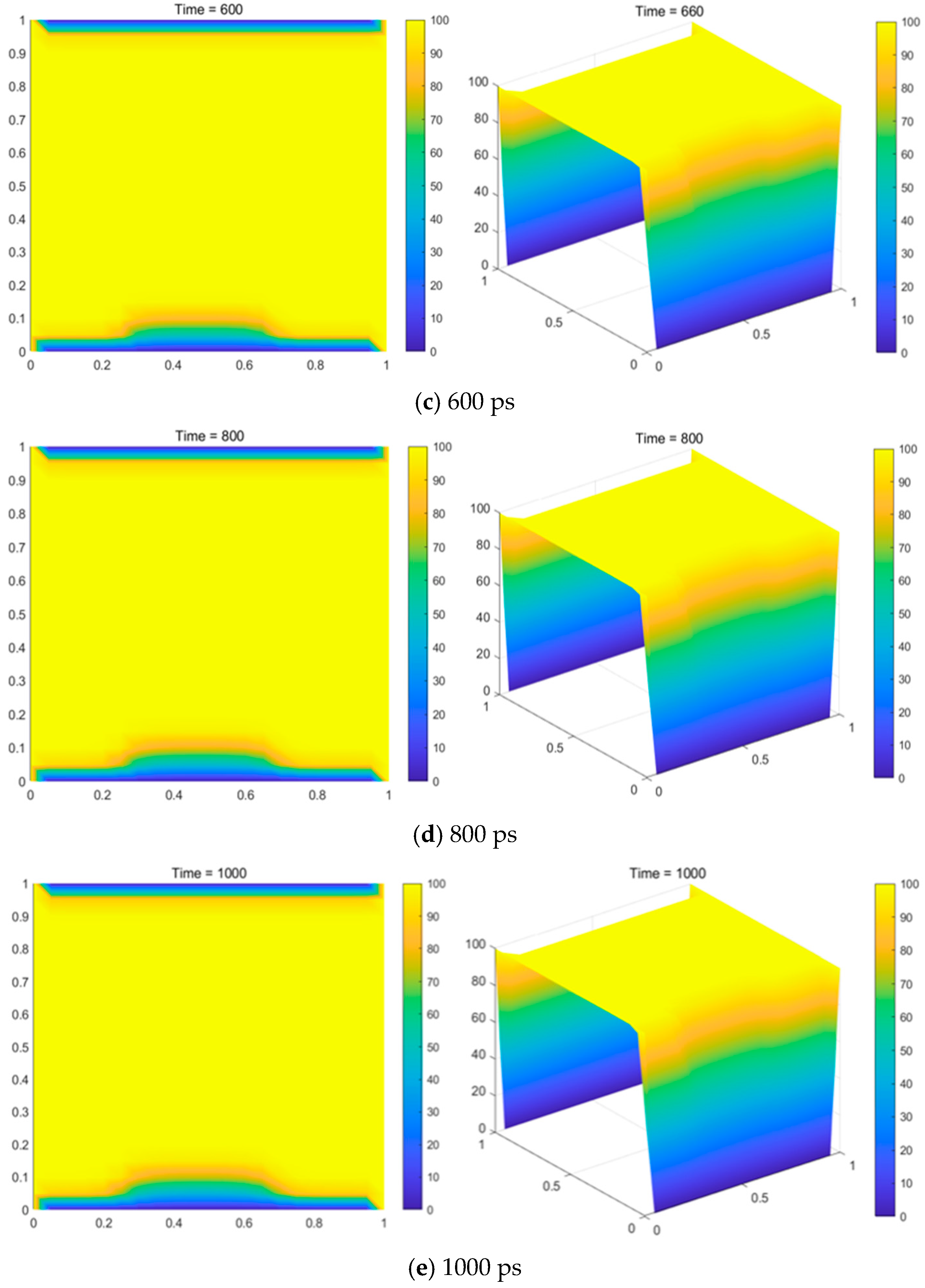
The change in CH₄ concentration with the time step under low-pressure conditions is shown in Figure 8. It can be seen that under low-pressure conditions, the CH₄ concentration on the surface of the copper foil increased with time. As the CH₄ partial pressure rose, the nucleation rate of graphene accelerated, and a larger graphene coverage area formed on the copper foil surface within a certain time period. This led to a rapid decrease in the catalytic activity of the substrate [20]. Due to the low gas flow rate in the confined space, the thickness of the boundary layer on the copper substrate surface increased. Over time, this boundary layer will cover the entire copper surface. As the boundary layer thickness (δ) increased, h_g approached k_s, at which point, the growth of graphene was limited by both the surface chemical reaction and mass transport mechanisms. With increasing CH₄ concentration over time, the diffusive flow inside the confined reactor gradually dominated and became uniformly distributed, with the process eventually being controlled by surface chemistry.

It can be observed from Figure 7 and Figure 8 that both high temperature and high pressure, or high temperature and low pressure, promoted the CH₄ pyrolysis reaction and accelerated the overall reaction rate. Additionally, higher temperatures and lower pressures enhanced the mass transport ability of the CH₄ gas. However, for the typical straight tube model, under low-pressure conditions, a higher CH₄ concentration led to a higher deposition rate on the graphene surface over the same period of time, making it easier to prepare large-area graphene compared to atmospheric pressure conditions. However, as the CH₄ concentration increased, the graphene nucleation density also rose, which is unfavorable for the production of high-quality graphene. To achieve a lower nucleation density and improve the quality of the graphene, it is necessary to reduce the partial pressure of methane.

4. Dynamics Monte Carlo Simulation Results and Discussion

4.1. Microscopic Processes of Graphene Growth at Different Times

In Figure 9, the brown atoms represent Cu atoms, the black atoms represent carbon atoms, and the partial pressure ratio of methane to hydrogen was 1:5 at a temperature of T = 1310 K and a pressure of P = 101,325 Pa. The simulation of the graphene growth process showed that in the early stages, carbon clusters primarily aggregated to form graphene islands (Figure 9a). As the growth time increased, these graphene islands gradually adsorbed more carbon atoms from the surroundings, forming a lamellar structure with varied shapes (Figure 9b). With continued growth, the voids between the graphene flakes gradually filled with carbon atoms, eventually leading to the formation of a more complete graphene film (Figure 9c,d).

4.2. Effect of Temperature on the Growth Rate of Graphene

To investigate the effect of temperature on graphene growth, simulations were carried out at temperatures of T = 1230 K, 1250 K, 1270 K, 1290 K, 1310 K, and 1330 K. The pressure was set to 101,325 Pa, and the partial pressure ratio of methane to hydrogen was 1:5. It was found that the dehydrogenation reaction of methane on the Cu(111) surface, the migration of carbon atoms, and polymerization were all influenced by the growth temperature, which in turn affected graphene growth. At high temperatures, the catalytic cracking ability of copper on methane was enhanced, leading to more methane dehydrogenation and the formation of carbon atoms. This provides more carbon for graphene growth. This process is controlled by surface chemical reactions, and as the diffusion of carbon atoms accelerates, the growth of graphene on the copper surface becomes faster, leading to an increased coverage of graphene on the copper foil.

Figure 10 shows the variation in surface coverage with graphene at different temperatures at P = 101,325 Pa. It can be seen in the figure that an increase in temperature can increase the growth rate of graphene.

4.3. Effect of CH₄/H₂ Ratio on Graphene Growth Rate

The effect of different partial pressure ratios of CH₄ and H₂ (1:20, 1:10, 1:7.5, 1:5, and 1:3) on the morphology of graphene was simulated at a set pressure of 101,325 Pa and a temperature of 1310 K. The surface morphology of the graphene obtained using the various CH₄:H₂ ratios is shown in Figure 11.

It was found that as the methane to hydrogen partial pressure ratio increased, the graphene morphology transitioned from a more regular hexagonal shape (Figure 11a) to an irregular lamellar structure (Figure 11b,c), and eventually to a blade-like shape with a larger area (Figure 11d,e). At low CH₄:H₂ partial pressure ratios, the etching effect of hydrogen on the graphene was stronger than the diffusive deposition rate of carbon atoms, resulting in the formation of a regular hexagonal graphene structure. At higher CH₄:H₂ partial pressure ratios, the surface diffusion deposition of carbon atoms became dominant, leading to faster graphene growth. This enhanced the diffusion of carbon atoms, causing the graphene to form a larger, irregular blade-like shape.

In summary, the growth rate of graphene accelerates with increasing temperature, and the nucleation density on the graphene surface is reduced. At a temperature of T = 1310 K, a large area of graphene can be obtained, which enhances the graphene surface deposition rate. The diffusion of carbon atoms is promoted under a high CH₄:H₂ ratio, leading to graphene exhibiting a large, leaf-like, and irregular shape. In contrast, at a low CH₄:H₂ ratio, graphene tends to form a smaller area with a more regular hexagonal shape. Therefore, a low CH₄:H₂ ratio facilitates the formation of uniform single-layer graphene in the typical model.

5. Thermodynamic Analysis of Carbon Deposition

5.1. Equilibrium Gas-Phase Components

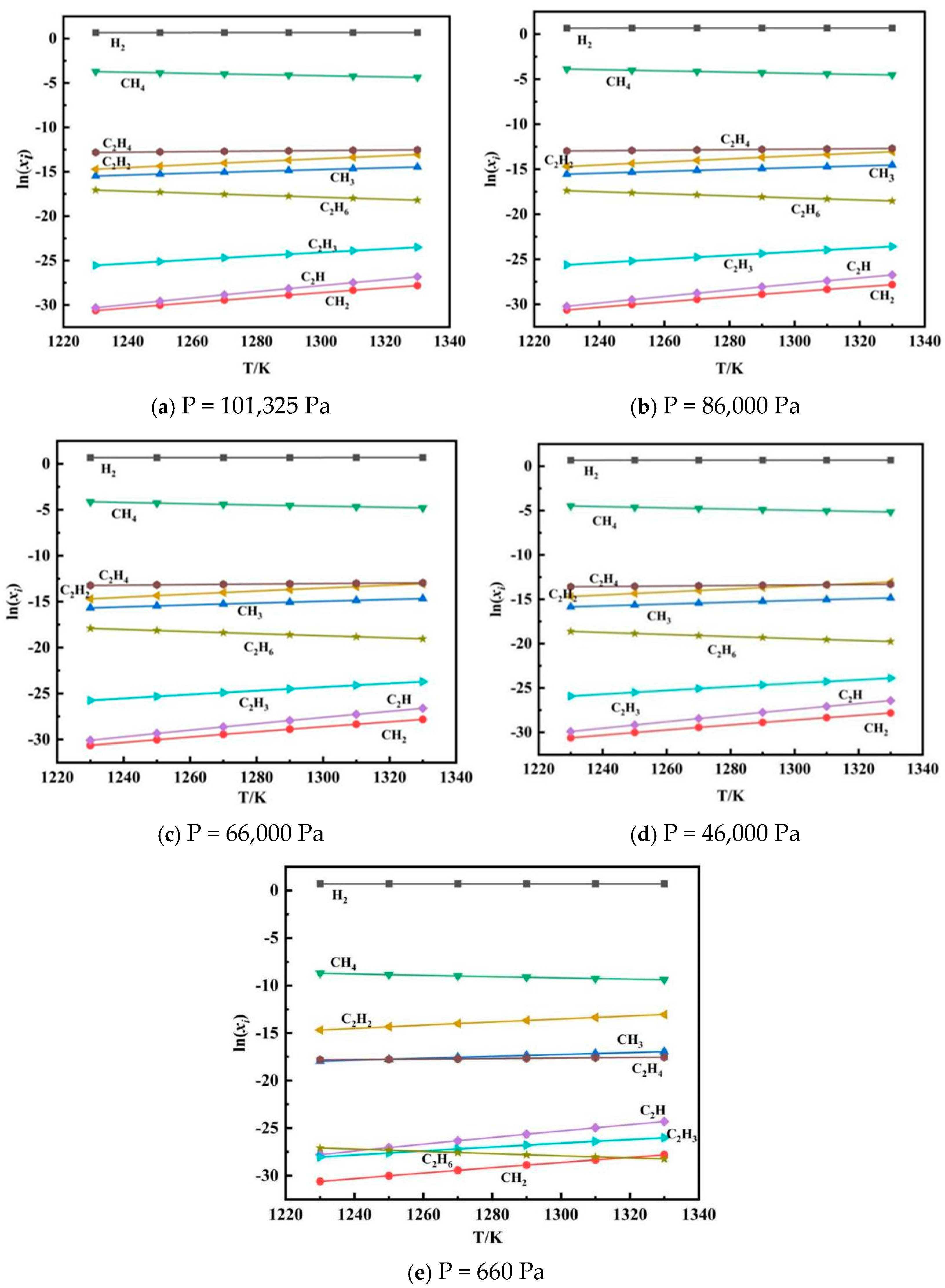
Since the equilibrium gas-phase components can be used to illustrate the concentrations of each gas-phase species when the reaction reaches equilibrium, the changes in each gas-phase component with temperature were investigated. The simulations were carried out with 1 mol of methane at the inlet and pressures of 101,325 Pa, 86,000 Pa, 66,000 Pa, 46,000 Pa, and 660 Pa. Given that the contents of H, C, CH, C₂, C₃, C₄, and C₅ are much lower than those of H₂, CH₄, C₂H₄, C₂H₂, CH₃, C₂H₆, C₂H₃, C₂H, and CH₂, the equilibrium mole fractions (x_i) of the first nine gas-phase components were primarily analyzed. Here, x_i represents the mole fraction of the ith component when the reaction reaches equilibrium. The results are shown in Figure 12.

As shown in Figure 12, the content of H₂ remained relatively stable with increasing temperature. CH₄ and C₂H₆ showed a gradual decline rather than a sharp decrease. The content of C₂H₄ exhibited a nearly constant trend, with only slight fluctuations. In contrast, the contents of C₂H₂, CH₃, C₂H, C₂H₃, and CH₂ exhibited a more noticeable increase with temperature. At low temperatures, the main components were CH₄ and C₂H₆, but as the temperature increased, the main components shifted to C₂H₂ and CH₃. Additionally, C₂H₂ decomposed into C and H₂ again in the hydrogen-rich atmosphere at the outlet of the reactor at lower temperatures.

For pressures of 101,325 Pa, 86,000 Pa, 66,000 Pa, 46,000 Pa, and 660 Pa, the trends in the equilibrium gas-phase components were generally similar. However, a key difference was observed: as the pressure decreased, the intersection of the curves shifted to the left, indicating that the content of C₂H₄ changed more noticeably at lower pressures. This suggests that a low pressure is favorable for the carbon deposition process. This study shows that high temperature, excess hydrogen, and a relatively low pressure are favorable conditions for increasing the carbon yield.

5.2. Effect of Temperature and Pressure on Carbon Deposition Rate

The variation in the carbon deposition rate with temperature was calculated with 1 mol of methane at the inlet and pressures of 101,325 Pa, 86,000 Pa, 66,000 Pa, 46,000 Pa, and 660 Pa. The results are shown in Figure 13.

As shown in Figure 13, the carbon yield increased significantly with rising temperature. However, when the temperature exceeded 1310 K, the curve began to stabilize. This indicates that beyond a certain temperature, further increases in temperature do not enhance the carbon deposition rate, but rather reduce it. Therefore, in actual production processes, controlling the temperature is crucial for optimizing the carbon deposition rate. Additionally, higher temperatures lead to higher energy consumption in the production process, which directly increases production costs. As a result, in the practical production of graphene, it is recommended to maintain the reactor’s internal temperature around 1310 K.

Figure 13 also shows that at the same temperature, as the pressure decreased, the carbon yield increased significantly. However, when the pressure reached a certain level, increasing the temperature no longer led to a significant change in the carbon yield. At this point, although increasing the temperature raises energy consumption, the curves exhibited a peak. As the pressure increased, the peak shifted to the right, meaning that with higher pressure, the temperature at which the carbon yield peaks also increases, but the peak value itself noticeably decreases. Therefore, without considering the special structure of the equipment in CVD graphene production, lowering the pressure favors carbon deposition. However, this comes with higher equipment requirements and increased energy consumption.

The study shows that in actual production, the main reasons for a decrease in the carbon deposition rate are as follows: (1) The instability of the control over the operating temperature, pressure, and feed ratio, especially the temperature, which has a significant impact on carbon yield. At high temperatures, side reactions are more likely to occur, resulting in a lower carbon yield. (2) The heat transfer phenomenon in the reactor causes a temperature gradient on the surface of the metal substrate, leading to a non-uniform carbon yield. (3) Due to mass transfer effects, the molar concentration of reactive gases on the surface of the carbon in the reactor is uneven, which affects the carbon yield. (4) Carbon deposition on the walls of the CVD reactor occurs, and this carbon, being of lower purity, cannot be fully recovered [21]. Among these factors, unstable production conditions are the primary reason for the low carbon yield. Therefore, improving the operating conditions, optimizing the reactor structure, and enhancing equipment control can further improve the carbon yield.

5.3. Effect of CH₄/H₂ Ratio on Carbon Deposition Rate

It has been reported that H₂ can catalyze both methane cracking and the etching of graphene, while methane serves as a source of carbon atoms. A high methane concentration will increase the graphene growth rate and make the graphene morphology tend to be irregular, whereas a higher hydrogen concentration will lead to the etching of graphene [22,23]. Therefore, the change in the morphology of the graphene surface is, to some extent, a result of the interplay between the pyrolysis of the carbon source gas and the etching effect of the hydrogen gas.

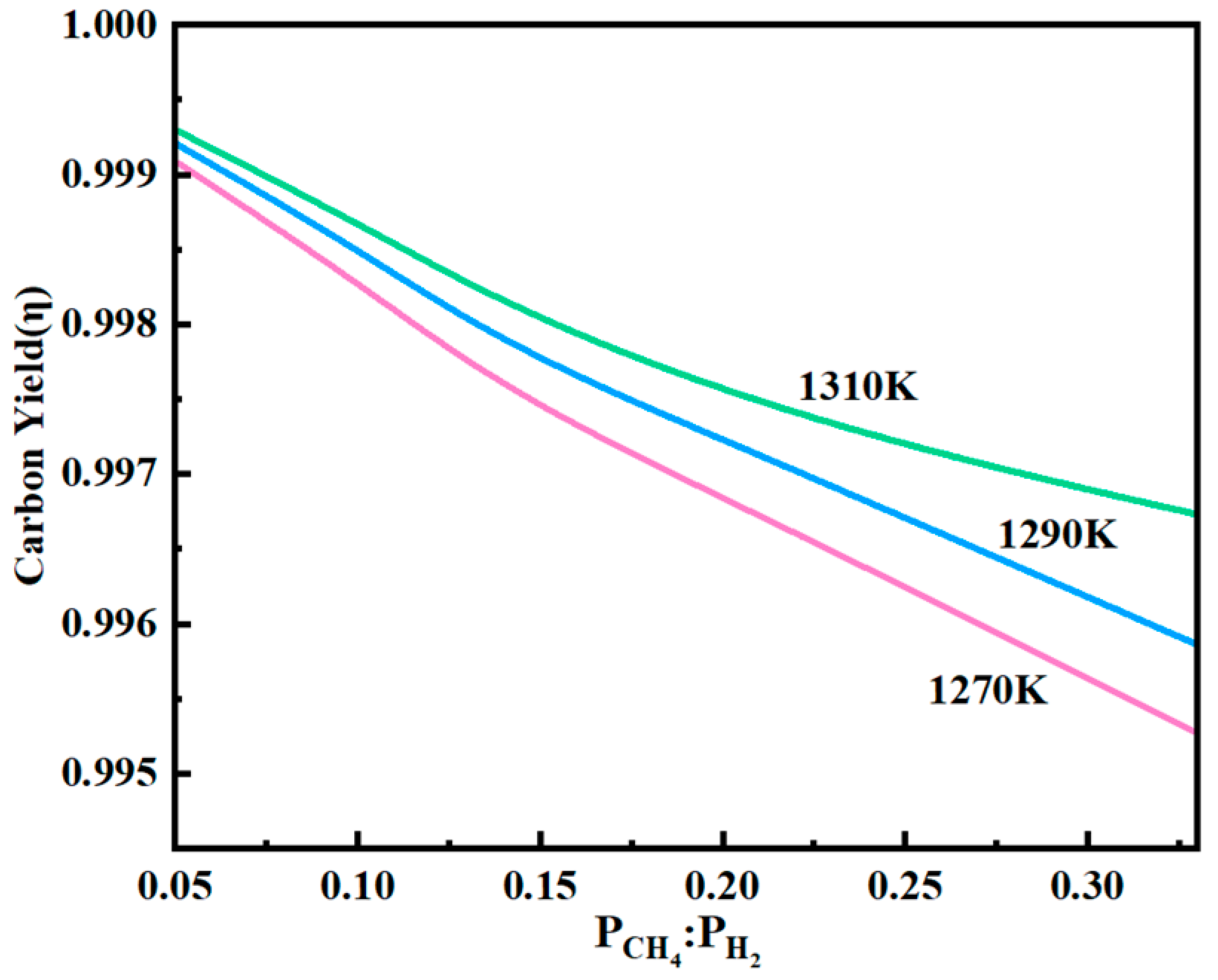
To investigate the effect of the partial pressure ratio of CH₄ and H₂ on the deposition rate of graphene, the growth of graphene was examined by setting the partial pressure ratio of CH₄ and H₂ to 1:20, 1:10, 1:7.5, 1:5, and 1:3, under pressures of 101,325 Pa and temperatures of 1270 K, 1290 K, and 1310 K. The changes in carbon deposition with the varying partial pressure ratios of CH₄:H₂ are shown in Figure 14.

As shown in Figure 14, the carbon deposition rate decreased significantly with increasing CH₄:H₂ partial pressure ratio. Therefore, maintaining an excess of hydrogen is essential during graphene growth when using the CVD method. When the temperature was raised to 1310 K, the carbon yield curve flattened with increasing CH₄:H₂ ratio, indicating that the partial pressure ratio has minimal influence on the carbon yield at this stage. This occurs because at a total pressure of 101,325 Pa (or slightly above), an excessively high H₂ molar fraction at the inlet results in a relatively low CH₄ concentration, thereby limiting the availability of carbon for deposition. Consequently, the carbon production rate becomes CH₄-limited. Additionally, an excessive H₂ concentration leads to a high H₂ content in the exhaust gas, which presents two practical issues: (1) an increased volume of tail gas requiring more complex separation and processing, and (2) elevated energy consumption for H₂ recovery and recycling. These factors collectively contribute to a significant rise in production costs. Thus, although excess hydrogen is necessary to suppress unwanted reactions and promote high-quality graphene formation, a very low CH₄:H₂ ratio can adversely affect process efficiency. At low CH₄:H₂ ratios, the etching effect of hydrogen outweighed the deposition of carbon atoms, underscoring the need to carefully balance the gas ratio. To optimize the carbon yield and graphene quality while minimizing operational costs, the CH₄:H₂ partial pressure ratio must be appropriately selected. This requires further investigation through a detailed kinetic model of the gas-phase transport and surface reaction mechanisms.

The thermodynamic analysis indicated that the optimal operating temperature for graphene preparation via the CVD method is 1310 K under atmospheric pressure conditions (101,325 Pa). When the CH₄/H₂ ratio was fixed, the carbon deposition rate increased with temperature, highlighting the critical role of temperature control in ensuring a high carbon yield. Thus, maintaining a stable temperature is essential in practical production to avoid yield fluctuations.

At a constant temperature, increasing the CH₄/H₂ partial pressure ratio led to a decline in carbon yield. Specifically, a higher hydrogen partial pressure suppressed the dehydrogenation of methane, thereby reducing the availability of active carbon species and limiting graphene growth. While a moderate excess of hydrogen is necessary to control graphene morphology and suppress unwanted reactions, an excessive hydrogen content decreases both the carbon deposition rate and overall carbon productivity. Consequently, low-pressure CVD processes are often employed to enhance carbon deposition efficiency and graphene quality. However, implementing low-pressure techniques imposes more stringent demands on the reactor design, equipment sealing, and process control. These requirements typically lead to increased energy consumption and higher production costs. As a result, developing atmospheric-pressure CVD processes for high-quality graphene growth has become a key focus for industrial-scale production, aiming to balance performance, cost-efficiency, and equipment feasibility.

6. Conclusions

In this study, the growth kinetics of graphene on Cu(111) surfaces was investigated through first-principles calculations and transition state search methods to determine the energy barriers associated with methane dehydrogenation. The influence of the key operating parameters—temperature, pressure, and the CH₄/H₂ partial pressure ratio—on graphene deposition via chemical vapor deposition (CVD) was explored based on thermodynamic equilibrium analyses. The main conclusions are as follows:

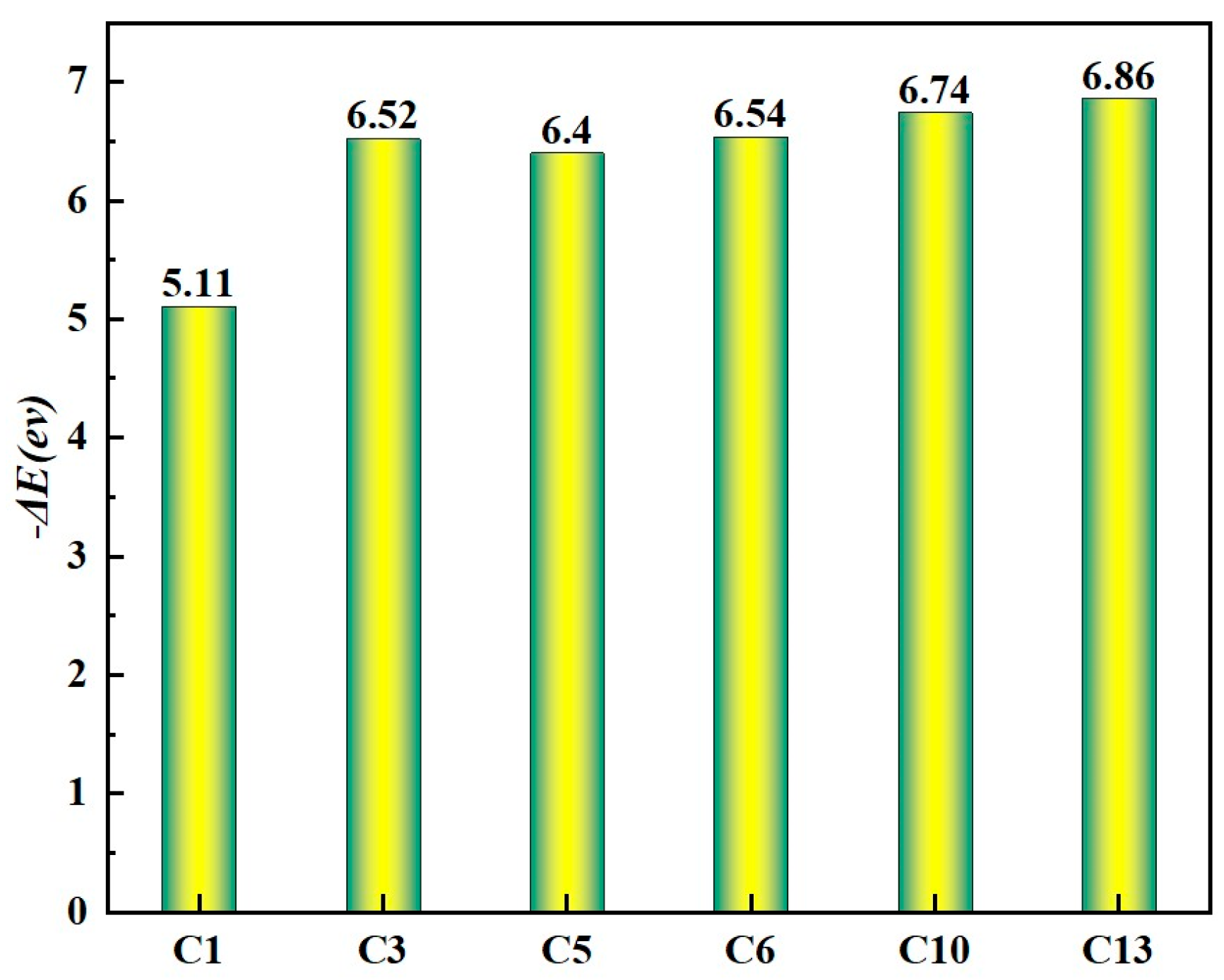
(1)

The final product energy of C + 4H is 3.09 eV higher than that of adsorbed CH₄, indicating that methane dehydrogenation to carbon atoms is energetically demanding. In particular, the dehydrogenation step from CH to C requires an energy input of 1.23 eV. This suggests that intermediate CH_n (n = 1–4) species are more directly involved in graphene formation, and that reducing the dehydrogenation barriers is key to accelerating the graphene growth rate.

(2)

An increase in temperature enhances the graphene growth rate, reduces the surface nucleation density, and promotes surface carbon deposition. At high CH₄:H₂ ratios, the enhanced diffusion of carbon atoms results in the formation of large, irregular, leaf-like graphene domains. In contrast, low CH₄:H₂ ratios favor the formation of smaller, uniform hexagonal domains, making them more suitable for single-layer graphene growth under typical CVD conditions.

(3)

The thermodynamic analysis of equilibrium gas-phase compositions revealed that high temperatures, an excess of hydrogen, and a relatively low pressure promote carbon deposition. The carbon yield increases with temperature, but when the temperature exceeds 1310 K, the yield curve flattens or even decreases. Therefore, maintaining a reactor temperature near 1310 K is optimal for balancing the carbon yield and energy efficiency.

(4)

At a constant temperature, decreasing the system pressure significantly increases the carbon yield. However, once the pressure falls below a certain threshold, further increases in temperature do not substantially improve the deposition rate. Additionally, the temperature corresponding to peak carbon yield shifts with increasing pressure, while the peak value itself decreases. Thus, although low-pressure conditions are beneficial for carbon deposition, they also demand more advanced equipment and have a higher energy consumption.

(5)

As the partial pressure ratio of CH₄ to H₂ increases, the carbon deposition rate decreases. While a moderate excess of hydrogen supports graphene growth by preventing unwanted side reactions, excessively high hydrogen concentrations reduce CH₄ availability and limit carbon production. Moreover, excess hydrogen complicates tail gas separation and increases the energy demand for gas recycling. Therefore, in practical production settings, the CH₄/H₂ ratio must be carefully optimized. Although low-pressure techniques are preferred for high-quality graphene growth, achieving efficient atmospheric-pressure CVD remains a critical goal for scalable, cost-effective industrial production.

This work provides valuable insights by combining first-principles calculations with multiscale kinetic and thermodynamic analyses, which enrich the current understanding of graphene growth mechanisms on Cu(111). The comprehensive approach employed here not only clarifies the rate-limiting steps and the effect of process parameters but also offers practical guidance for optimizing CVD conditions in industrial applications. Moreover, the study opens up new perspectives for future research, including the exploration of catalyst surface modifications and alternative precursor gases to further enhance graphene quality and growth efficiency.

Although direct experimental data comparisons are limited, the available experimental findings qualitatively support our theoretical predictions regarding growth trends and parameter effects. Future work will include more systematic validation against experimental results to further strengthen the model’s applicability and reliability.