Characterization of Boride Layers on S235 Steel and Calculation of Activation Energy Using Taylor Expansion Model
Abstract
1. Introduction
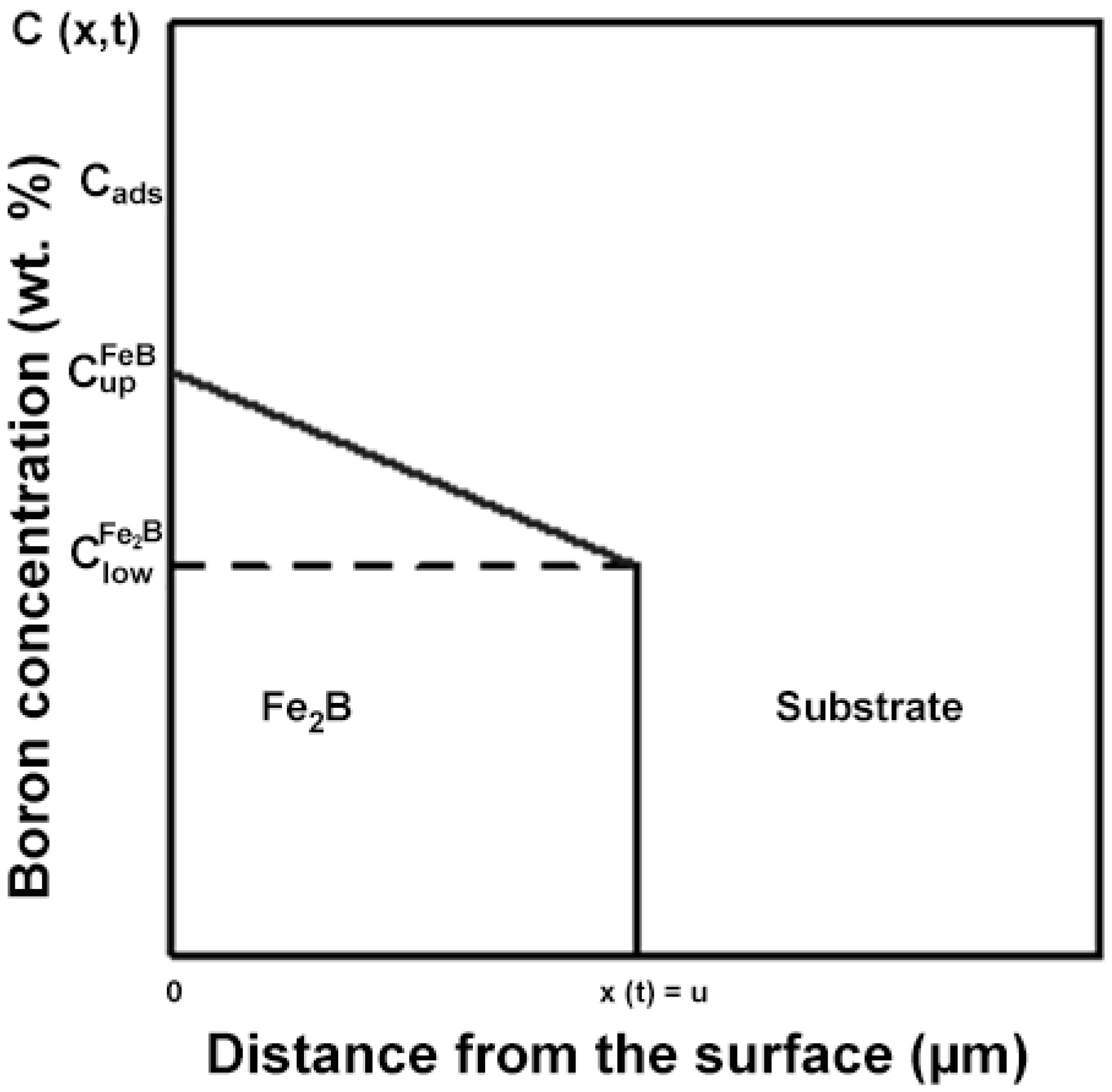
2. The Taylor Expansion Model
3. Material and Experimental Techniques
4. Results and Discussions
4.1. SEM Observations of Boronized Layers
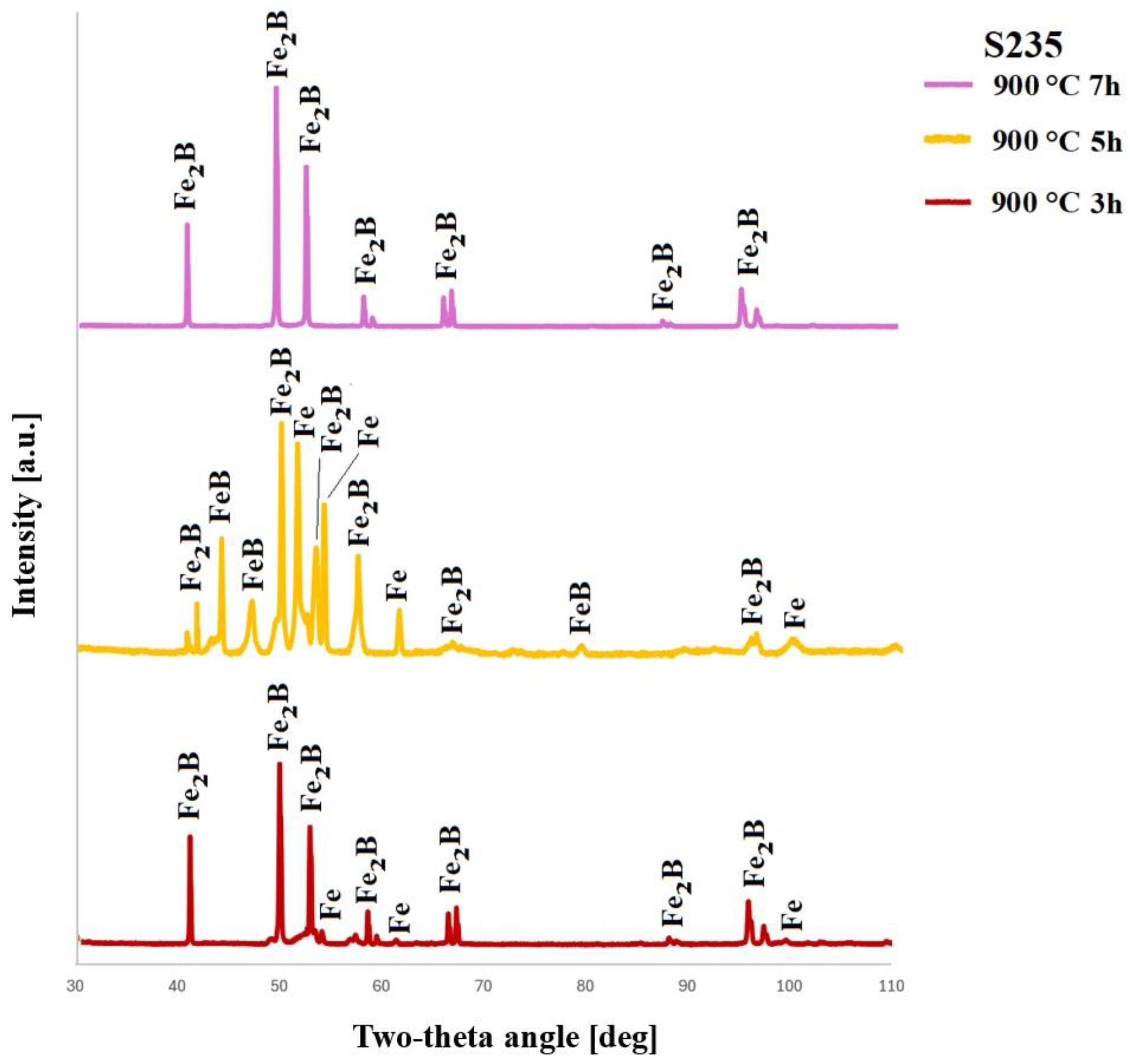
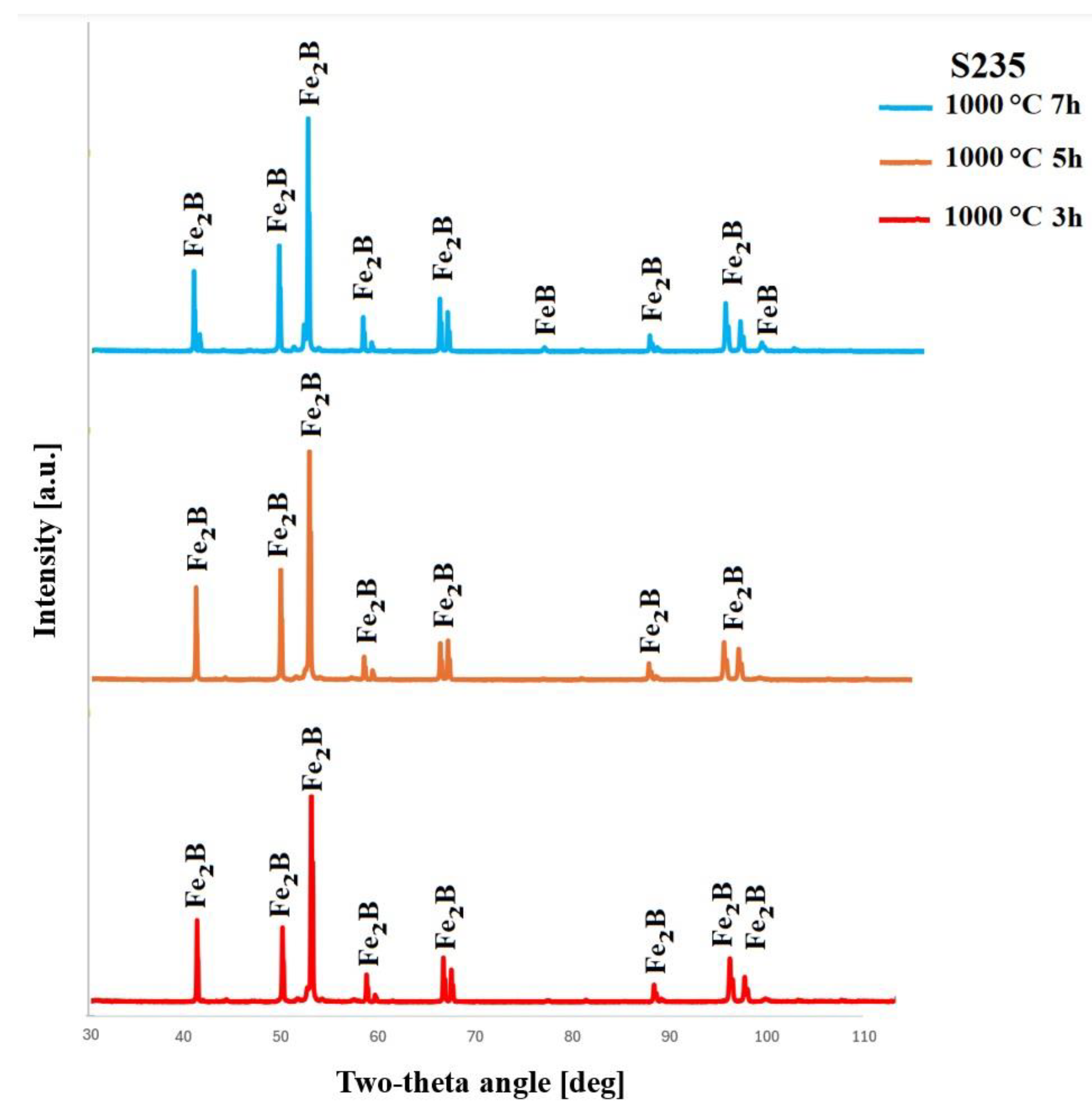
4.2. XRD Results
4.3. Calculation Results from the Taylor Expansion Model
5. Conclusions
- (1)
- The boride layers exhibited a jagged morphology, characterized by varying lengths of boride needles, resulting in compact and dense coatings.
- (2)
- XRD analysis confirmed the occurrence of an Fe2B layer under most boriding conditions. However, very low diffraction peaks corresponding to the FeB phase were observed in two specific cases.
- (3)
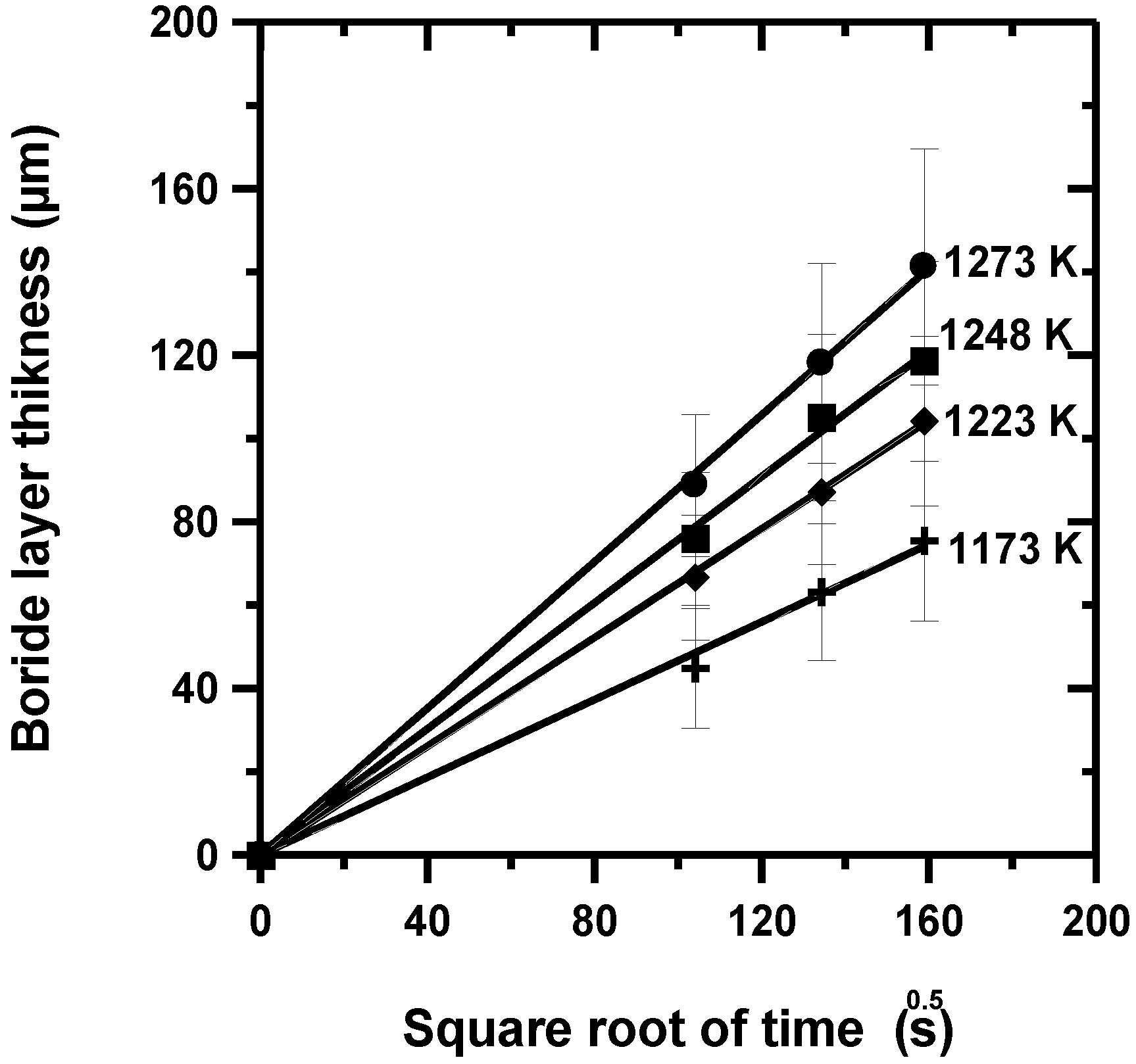
- The time change in the layer thickness revealed a parabolic growth law with a thickness ranging from 45 ± 7 to 141.40 ± 14 µm.
- (4)
- The B activation energy in Fe2B was estimated to be 157.70 kJ mol−1 using the Taylor expansion model, which is consistent with values reported in the literature.
- (5)
- For future studies, the Taylor expansion model may be adopted with other alloys involving the diffusion of elements such as boron, carbon, and nitrogen to simulate their diffusion kinetics.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kulka, M. Current Trends in Boriding Techniques; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Chaparro-Pérez, K.D.; Olivares-Luna, M.; Rosales-Lopez, J.L.; Castillo-Vela, L.E.; Espino-Cortes, F.P.; Hernández-Simón, L.M.; Campos-Silva, I. Insights on the pulsed-DC powder-pack boriding process: Kinetic, statistic, and electric field dynamics in low and medium temperatures. Surf. Coat. Technol. 2024, 494, 131390. [Google Scholar] [CrossRef]
- Kartal Sireli, G.; Yuce, H.; Arslan, M.; Karimzadehkhoei, M.; Timur, S. Improving the Surface Performance of Discarded AISI T1 Steel by Cathodic Reduction and Thermal Diffusion-Based Boriding. J. Mater. Eng. Perform. 2023, 32, 9504–9514. [Google Scholar] [CrossRef]
- Tavakoli, H.; Mousavi Khoie, S.M.; Rasooli, F.; Marashi, S.P.H.; Momeni, F. Electrochemical and physical characteristics of the steel treated by plasma-electrolysis boronizing. Surf. Coat. Technol. 2015, 276, 529–533. [Google Scholar] [CrossRef]
- Anthymidis, K.G.; Stergioudis, E.; Tsipas, D.N. Boriding in a fluidized bed reactor. Mater. Lett. 2001, 51, 156–160. [Google Scholar] [CrossRef]
- Gunes, I.; Ulker, S.; Taktak, S. Kinetics of plasma paste boronized AISI 8620 steel in borax paste mixtures. Prot. Met. Phys. Chem. Surf. 2013, 49, 567–573. [Google Scholar] [CrossRef]
- Genç, A.; Urtekin, L.; Danışmaz, M. Characterization and Optimization of Boride Coatings on AISI 1137 Steel: Enhancing Surface Properties and Wear Resistance. Coatings 2025, 15, 10. [Google Scholar] [CrossRef]
- Ortiz-Domínguez, M.; Gómez-Vargas, O.A.; Bárcenas-Castañeda, M.; Castellanos-Escamilla, V.A. Comparison and Analysis of Diffusion Models: Growth Kinetics of Diiron Boride Layers on ASTM A283 Steel. Materials 2022, 15, 8420. [Google Scholar] [CrossRef]
- Sari, E.S.; Zeren, M.; Koç, F.G. The effect of different powder mixtures used in the boriding process on the surface properties of AISI 304 stainless steel material. Mater. Res. Express 2024, 11, 066511. [Google Scholar] [CrossRef]
- Morales-Robles, Á.J.; Ortiz-Domínguez, M.; Gómez-Vargas, O.A.; Moreno-González, M.d.l.L. Boronize Coatings Studied with a New Mass Transfer Model. Materials 2024, 17, 5309. [Google Scholar] [CrossRef]
- Brakman, C.M.; Gommers, A.W.J.; Mittemeijer, E.J. Boriding of Fe and Fe–C, Fe–Cr, and Fe–Ni alloys; Boride-layer growth kinetics. J. Mater. Res. 1989, 4, 1354–1370. [Google Scholar] [CrossRef]
- Yu, L.G.; Chen, X.J.; Khor, A.K.; Sundararajan, G. FeB/Fe2B phase transformation during SPS pack-boriding: Boride layer growth kinetics. Acta Mater. 2005, 53, 2361–2368. [Google Scholar] [CrossRef]
- Mebarek, B.; Maatoug, A.; Mostefaoui, S.A.M.; Benali, H.; El Guerri, Y. Adomian decomposition method for modelling the growth of FeB/Fe2B layer in boronizing process. Zast. Mater. 2025, 66, 148–157. [Google Scholar]
- Ramdan, R.D.; Takaki, T.; Yashiro, K.; Tomita, Y. The Effects of Structure Orientation on the Growth of Fe2B Boride by Multi-Phase-Field Simulation. Mater. Trans. 2010, 51, 62–67. [Google Scholar] [CrossRef]
- Campos, I.; Islas, M.; Ramírez, G.; Villa-Velázquez, C.; Mota, C. Growth kinetics of borided layers: Artificial neural network and least square approaches. Appl. Surf. Sci. 2007, 253, 6226–6231. [Google Scholar] [CrossRef]
- Campos-Silva, I.; Cedeño-Velázquez, J.; Contla-Pacheco, A.D.; Arzate-Vázquez, I.; Castillo-Vela, L.E.; Olivares-Luna, M.; Rosales-Lopez, J.L.; Espino-Cortes, F.P. Microstructural and kinetics analysis of FeB–Fe2B layer grown by pulsed-DC powder-pack boriding on AISI 316 L. J. Vac. Sci. Technol. A 2024, 42, 053101. [Google Scholar] [CrossRef]
- Okamoto, H. B-Fe (boron-iron). J. Phase Equilibria Diffus. 2004, 25, 297–298. [Google Scholar] [CrossRef]
- Velázquez-Altamirano, J.C.; Torres-Avila, I.P.; Teran-Méndez, G.; Capula-Colindres, S.I.; Cabrera-Sierra, R.; Carrera-Espinoza, R.; Hernández-Sánchez, E.A. Stochastic Model and Investigation into the Probability Distribution of the Thickness of Boride Layers Formed on Low-Carbon Steel. Coatings 2019, 9, 756. [Google Scholar] [CrossRef]
- Kunst, H.; Schaaber, O. Beobachtungen beim Oberflaechenborieren von Stahl. HTM Haerterei Tech. Mittelungen 1967, 22, 1–25. [Google Scholar]
- Vidal-Torres, J.; Ocampo-Ramírez, A.; Rodríguez-Castro, G.A.; Fernández-Valdés, D.; Meneses-Amador, A.; Campos-Silva, I. Experimental and numerical evaluation of multi-pass scratch on borided ARMCO iron. Surf. Coat. Technol. 2024, 477, 130320. [Google Scholar] [CrossRef]
- Demirci, S.; Tünçay, M.M. Growth kinetics of the borided 316L stainless steel obtained by selective laser. J. Cent. South Univ. 2025, 32, 332–349. [Google Scholar] [CrossRef]
- Malakhov, D.V.; DeBoer, A.A. Thermodynamic Aspects of Powder-Pack Boronizing. J. Phase Equilibria Diffus. 2024, 45, 367–383. [Google Scholar] [CrossRef]
- Keddam, M.; Kulka, M.; Makuch, N.; Pertek, A.; Małdziński, L. A kinetic model for estimating the boron activation energies in the FeB and Fe2B layers during the gas-boriding of Armco iron: Effect of boride incubation times. Appl. Surf. Sci. 2014, 298, 155–163. [Google Scholar] [CrossRef]
- Campos-Silva, I.; Ortiz-Domínguez, M.; Cimenoglu, H.; Escobar-Galindo, R.; Keddam, M.; Elías-Espinosa, M.; López-Perrusquia, N. Diffusion model for growth of Fe2B layer in pure iron. Surf. Eng. 2011, 27, 189–195. [Google Scholar] [CrossRef]
- Elias-Espinosa, M.; Ortiz-Domínguez, M.; Keddam, M.; Flores-Rentería, M.A.; Damián-Mejía, O.; Zuno-Silva, J.; Hernández-Ávila, J.; Cardoso-Legorreta, E.; Arenas-Flores, A. Growth Kinetics of the Fe2B Layers and Adhesion on Armco Iron Substrate. J. Mater. Eng. Perform. 2014, 23, 2943–2952. [Google Scholar] [CrossRef]
- Ruiz-Trabolsi, P.A.; Cesar Velázquez, J.; Orozco-Álvarez, C.; Carrera Espinoza, R.; Yescas-Hernández, J.A.; González-Arévalo, N.E.; Hernández-Sánchez, E. Kinetics of the Boride Layers Obtained on AISI 1018 Steel by Considering the Amount of Matter Involved. Coatings 2021, 11, 259. [Google Scholar] [CrossRef]
- Kartal, G.; Eryilmaz, O.L.; Krumdick, G.; Erdemir, A.; Timur, S. Kinetics of electrochemical boriding of low carbon steel. Appl. Surf. Sci. 2011, 257, 6928–6934. [Google Scholar] [CrossRef]
- Dybkov, V.I. Diffusional Growth Kinetics of Boride Layers at the 13% Cr Steel Interface with Amorphous Boron. Defect Diffus. Forum 2007, 263, 183–188. [Google Scholar] [CrossRef]

| Element (wt.%) | C | Si | Mn | S |
|---|---|---|---|---|
| S 235 steel | 0.22 | 0.05 | 1.60 | 0.05 |
| T (K) | (µm s −0.5) |
|---|---|
| 1173 | 0.4661 |
| 1223 | 0.6522 |
| 1248 | 0.7571 |
| 1273 | 0.8804 |
| T (K) | |
|---|---|
| 1173 | 5.75 |
| 1223 | 11.26 |
| 1248 | 15.17 |
| 1273 | 20.52 |
| Material | Boriding Method | Temperature Interval (K) | Activation Energy (kJmol−1) | Computation Method | Ref. |
|---|---|---|---|---|---|
| Armco Fe | Gas | 1073–1273 | 78.03 (FeB) 120.65 (Fe2B) | Kinetic model | [23] |
| Armco Fe | Paste | 1123–1323 | 157 (Fe2B) | Diffusion model | [24] |
| Armco Fe | Powder | 1123–1323 | 157.6 (Fe2B) | Diffusion model | [25] |
| AISI 1018 | PDCPB | 973–1123 | 133.8–152.3 (FeB) 129.5–145.9 (Fe2B) | Dybkov model | [2] |
| AISI 1018 | Powder | 1173–1273 | 91.20–155.22 (FeB + Fe2B) | Empirical parabolic law | [26] |
| SLM AISI 316 L | Powder | 1123–1223 | 256.61 (FeB) 161.61 (Fe2B) | Diffusion model | [21] |
| AISI 1018 | Electrochemical | 1123–1223 | 172.75 ± 8.6 (FeB + Fe2B) | Empirical parabolic law | [27] |
| S235 | Powder | 1173–1273 | 157.70 (Fe2B) | Taylor expansion model | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keddam, M.; Orihel, P.; Jurci, P.; Kusy, M. Characterization of Boride Layers on S235 Steel and Calculation of Activation Energy Using Taylor Expansion Model. Coatings 2025, 15, 579. https://doi.org/10.3390/coatings15050579
Keddam M, Orihel P, Jurci P, Kusy M. Characterization of Boride Layers on S235 Steel and Calculation of Activation Energy Using Taylor Expansion Model. Coatings. 2025; 15(5):579. https://doi.org/10.3390/coatings15050579
Chicago/Turabian StyleKeddam, Mourad, Peter Orihel, Peter Jurci, and Martin Kusy. 2025. "Characterization of Boride Layers on S235 Steel and Calculation of Activation Energy Using Taylor Expansion Model" Coatings 15, no. 5: 579. https://doi.org/10.3390/coatings15050579
APA StyleKeddam, M., Orihel, P., Jurci, P., & Kusy, M. (2025). Characterization of Boride Layers on S235 Steel and Calculation of Activation Energy Using Taylor Expansion Model. Coatings, 15(5), 579. https://doi.org/10.3390/coatings15050579







