Ab Initio MD Study of the Mechanism of Carbonization of Si(001) Surfaces with Methane at High Temperatures
Abstract
1. Introduction
2. Methods
3. Results and Discussion
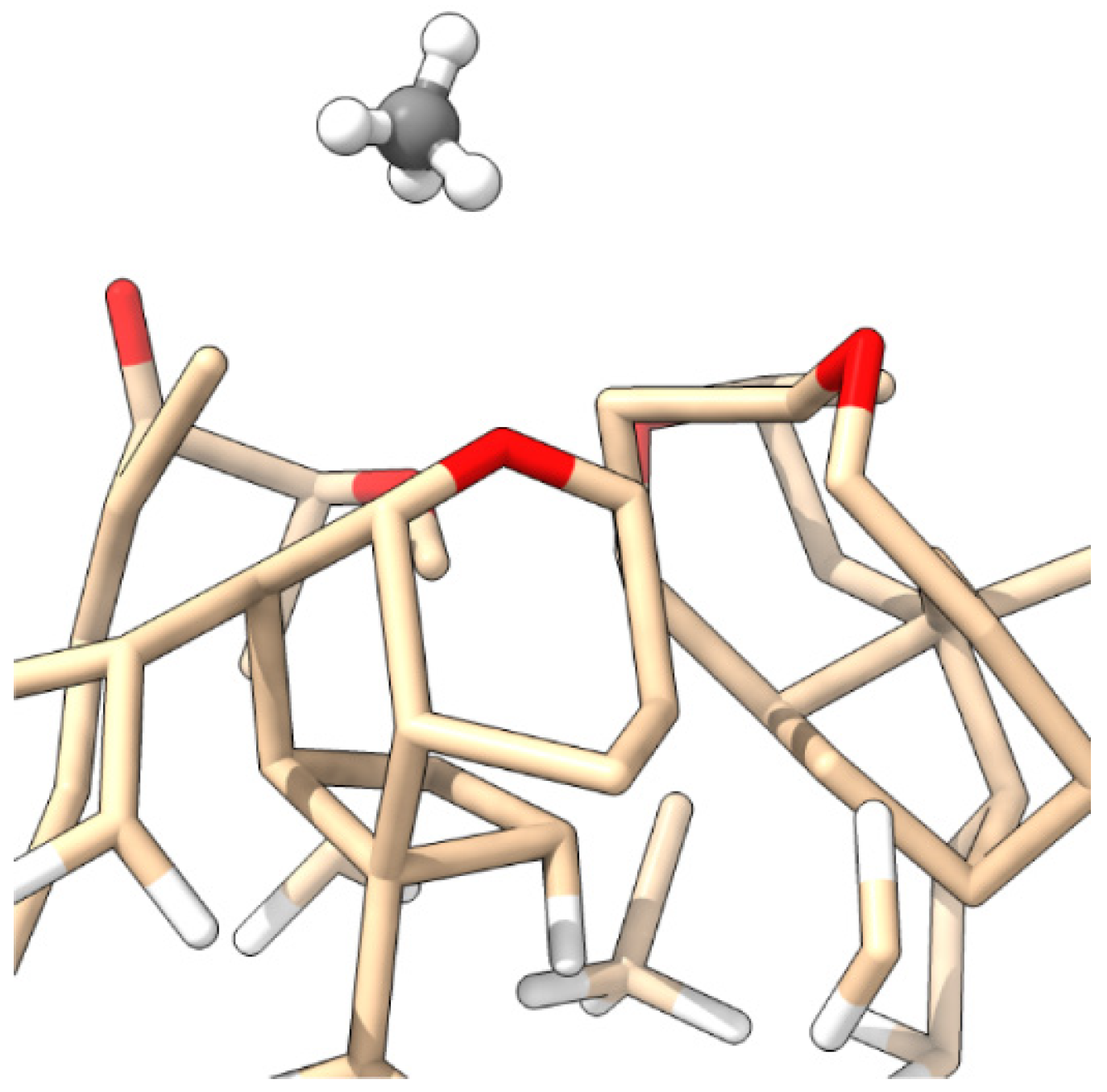
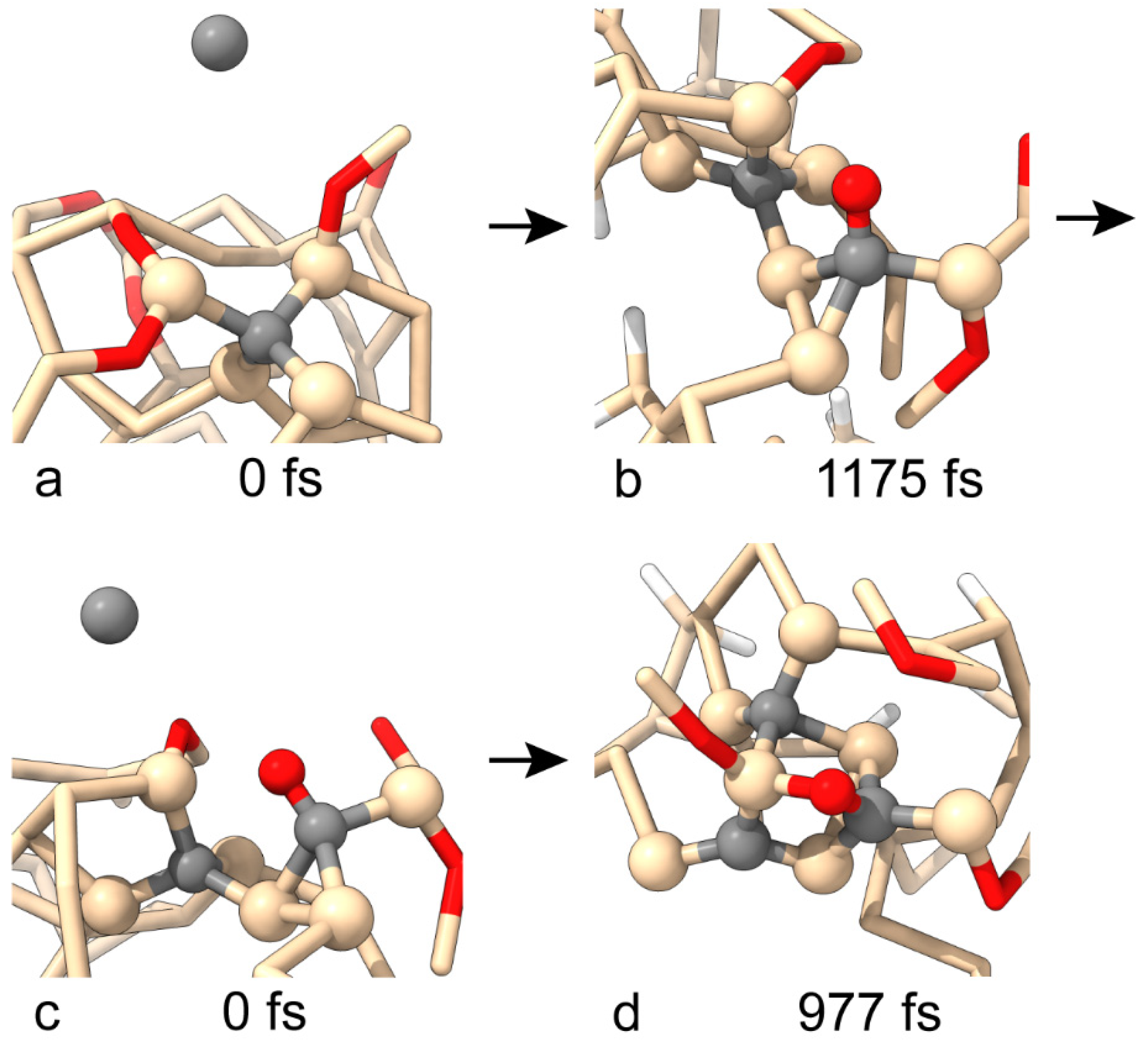
3.1. Building a SiC Crystallite Seed Through the Si(001) Surface with Native Oxide
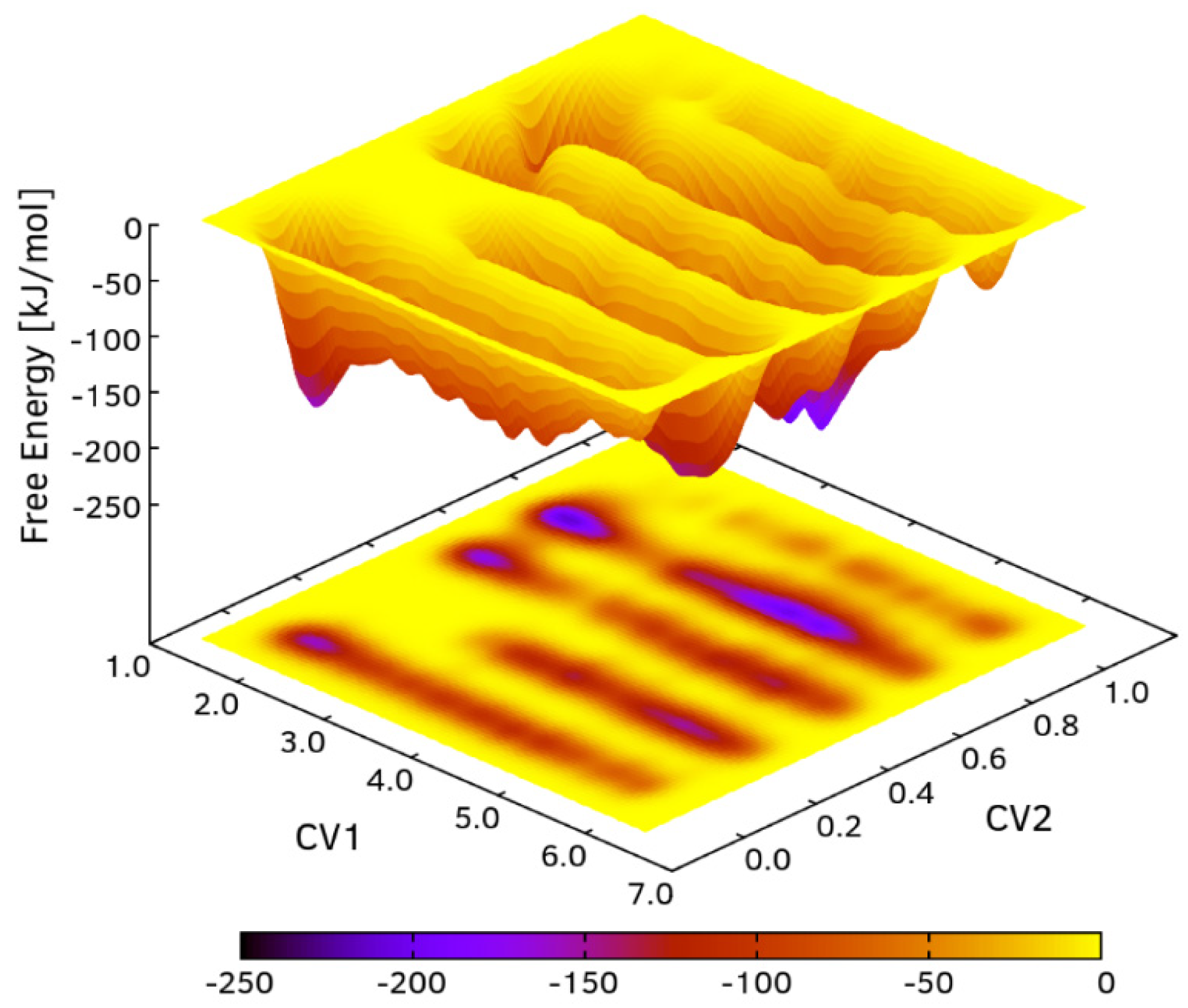
3.2. Free Energy Surface
3.3. Overall Remarks and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wesch, W. Silicon carbide: Synthesis and processing. Nucl. Instrum. Methods Phys. Res. B 1996, 116, 305–321. [Google Scholar]
- He, K.; Shen, R.; Hao, L.; Li, Y.; Peng, Z.; Jiang, J.; Li, X. Advances in Nanostructured Silicon Carbide Photocatalysts. Acta Phys. Chim. Sin. 2022, 38, 2201021. [Google Scholar]
- Xu, M.; Girish, Y.R.; Rakesh, K.P.; Wu, P.; Manukumar, H.M.; Byrappa, S.M.; Byrappa, K. Recent advances and challenges in silicon carbide (SiC) ceramic nanoarchitectures and their applications. Mater. Today Commun. 2021, 28, 102533. [Google Scholar] [CrossRef]
- Abderrak, H.; Hmida, E.S.B.H. Silicon Carbide: Synthesis and Properties. Properties and Applications of Silicon Carbide; IntechOpen: Rijeka, Croatia, 2011. [Google Scholar]
- Faust, J.W., Jr. Silicon Carbide—1973; Marshall, R.C., Faust, J.W., Jr., Ryan, C.E., Eds.; University of South Carolina Press: Columbia, SC, USA, 1974; p. 668. [Google Scholar]
- Stinton, D.P.; Lackey, W.J. Effect of deposition conditions on the properties of pyrolytic SiC coatings for HTGR fuel particles. Ceram. Bull. 1978, 57, 568. [Google Scholar]
- Lipon, H.G. Silicon Carbide—A High Temperature Semiconductor; O’Connor, J.R., Smiltens, J., Eds.; Pergamon Press: Oxford, UK, 1960; p. 371. [Google Scholar]
- Berger, C.; Song, Z.; Li, T.; Li, X.; Ogbazghi, A.Y.; Feng, R.; Dai, Z.; Marchenko, A.N.; Conrad, E.H.; First, P.N. Ultrathin epitaxial graphite: 2D electron gas properties and a route toward graphene-based nanoelectronics. J. Phys. Chem. 2004, 108, 19912–19916. [Google Scholar]
- Geim, A.K.; MacDonald, A.H. Graphene: Exploring carbon flatland. Phys. Today 2007, 60, 35–41. [Google Scholar]
- Xu, X.; Hu, X.; Chen, X. SiC Single Crystal Growth and Substrate Processing. In Light-Emitting Diodes; Solid State Lighting Technology and Application Series; Li, J., Zhang, G.Q., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 4. [Google Scholar]
- Nishino, S.; Powell, J.A.; Will, H.A. Production of large-area single-crystal wafers of cubic SiC for semiconductor devices. Appl. Phys. Lett. 1983, 42, 460. [Google Scholar]
- Severino, A.; D’Arrigo, G.; Bongiorno, C.; Scalese, S.; La Via, F.; Foti, G. Thin crystalline 3C-SiC layer growth through carbonization of differently oriented Si substrates. J. Appl. Phys. 2007, 102, 023518. [Google Scholar]
- Severino, A.; Bongiorno, C.; Piluso, N.; Italia, M.; Camarda, M.; Mauceri, M.; Condorelli, G.; Di Stefano, M.A.; Cafra, B.; La Magna, A.; et al. High-quality 6 inch (111) 3C-SiC films grown on off-axis (111) Si substrates. Thin Solid Film. 2010, 518, 165–169. [Google Scholar]
- Kalered, E. Quantum Chemical Studies of the Chloride-Based CVD Process for Silicon Carbide. Master’s Thesis, Linköpings Universitet, Linköping, Sweden, 2012. [Google Scholar]
- Sukkaew, P.; Danielsson, Ö.; Kordina, O.; Janzén, E.; Ojamäe, L. Ab Initio Study of Growth Mechanism of 4H–SiC: Adsorption and Surface Reaction of C2H2, C2H4, CH4, and CH3. J. Phys. Chem. C 2017, 121, 1249–1256. [Google Scholar]
- Chen, X.; Zhao, H.; Ai, W. Study on the competitive growth mechanism of SiC polytypes using Kinetic Monte Carlo method. J. Cryst. Growth 2021, 559, 126042. [Google Scholar]
- Polley, C.M.; Fedderwitz, H.; Balasubramanian, T.; Zakharov, A.A.; Yakimova, R.; Backe, O.; Ekman, J.; Dash, S.P.; Kubatkin, S. Bottom-Up Growth of Monolayer Honeycomb SiC. Phys. Rev. Lett. 2023, 130, 076203. [Google Scholar] [PubMed]
- Huang, L.; Ren, K.; Zhang, G.; Wan, J.; Zhang, H.; Zhang, G.; Qin, H. Tunable Thermal Conductivity of Two-Dimensional SiC Nanosheets by Grain Boundaries: Implications for the Thermo-Mechanical Sensor. ACS Appl. Nano Mater. 2024, 7, 15078–15085. [Google Scholar] [CrossRef]
- Milenov, T.I.; Trifonov, D.V.; Kalchevski, D.A.; Kolev, S.K.; Avramova, I.; Russev, S.; Genkov, K.; Avdeev, G.; Dimov, D.; Karaivanova, D.M.; et al. Study of the Chemical Vapor Deposition of Nano-sized Carbon Phases on {001} Silicon. Materials 2023, 16, 7190. [Google Scholar] [CrossRef]
- Kalchevski, D.A.; Trifonov, D.V.; Kolev, S.K.; Aleksandrov, H.A.; Milenov, T.I. Ab initio study of the mechanism of carbonization of {111} Si-substrate at high temperature. Mater. Chem. Phys. 2024, 317, 129180. [Google Scholar]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Kuehne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schuett, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package-Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar]
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar]
- Lippert, G.; Hutter, J.; Parrinello, M. The Gaussian and augmented-plane-wave density functional method for ab initio molecular dynamics simulations. Theor. Chem. Acc. 1999, 103, 124–140. [Google Scholar]
- Lippert, G.; Hutter, J.; Parrinello, M. A hybrid Gaussian and plane wave density functional scheme. Mol. Phys. 1997, 92, 477–487. [Google Scholar]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar]
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar]
- Gruden, M.; Andjeklovic, L.; Jissy, A.K.; Stepanovic, S.; Zlatar, M.; Cui, Q.; Elstner, M. Benchmarking Density Functional Tight Binding Models for Barrier Heights and Reaction Energetics of Organic Molecules. J. Comput. Chem. 2017, 38, 2171–2185. [Google Scholar]
- Kuhne, T.D.; Krack, M.; Mohamed, F.R.; Parrinello, M. Efficient and Accurate Car-Parrinello-like Approach to Born-Oppenheimer Molecular Dynamics. Phys. Rev. Lett. 2007, 98, 066401. [Google Scholar]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar]
- Laio, A.; Gervasio, F.L. Metadynamics: A method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar]
- Braun, E.; Moosavi, S.M.; Smit, B. Anomalous effects of velocity rescaling algorithms: The flying ice cube effect revisited. J. Chem. Theory Comput. 2018, 14, 5262–5272. [Google Scholar]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar]
- CP2K. Simple Metadynamics Simulation Using the Coordination Numbers as Variables. Available online: https://www.cp2k.org/exercises:2015_cecam_tutorial:mtd1 (accessed on 15 February 2024).
- Asvany, O. Understanding the Infrared Spectrum of Bare CH5+. Science 2005, 309, 1219–1222. [Google Scholar] [PubMed]
- Akiba, K.; Moriyama, Y.; Mizozoe, M.; Inohara, H.; Nishii, T.; Yamamoto, Y.; Minoura, M.; Hashizume, D.; Iwasaki, F.; Takagi, N.; et al. Synthesis and Characterization of Stable Hypervalent Carbon Compounds (10-C-5) Bearing a 2,6-Bis(p-substituted phenyloxymethyl)benzene Ligand. J. Am. Chem. Soc. 2005, 127, 5893–5901. [Google Scholar] [CrossRef] [PubMed]
- Grimes, R.N. Carboranes; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Kumar, P.V.; Gupta, G.S. Study of formation of silicon carbide in the Acheson process. Steel Res. Int. 2002, 73, 31–38. [Google Scholar] [CrossRef]
- Sato, N.; Funato, Y.; Shima, K.; Sugiura, H.; Fukushima, Y.; Momose, T.; Koshi, M.; Shimogaki, Y. Elementary gas-phase reactions of radical species during chemical vapor deposition of silicon carbide using CH3SiCl3. Int. J. Chem. Kinet. 2020, 53, 638–645. [Google Scholar] [CrossRef]
- Gao, F.; Lin, R.Y. Theoretical Modeling of Chemical Vapor Deposition of Silicon Carbide In A Hot Wall Reactor. Mat. Res. Soc. Symp. Proc. 1994, 335, 177–182. [Google Scholar] [CrossRef]
- Walch, S.P.; Dateo, C.E. Thermal Decomposition Pathways and Rates for Silane, Chlorosilane, Dichlorosilane, and Trichlorosilane. J. Phys. Chem. A 2001, 105, 2015–2022. [Google Scholar]
- Tanaka, S.; Komiyam, H. Growth Mechanism of Silicon Carbide Films by Chemical Vapor Deposition below 1273. J. Am. Cerom. Soc. 1990, 73, 3046–3052. [Google Scholar] [CrossRef]
- Stenberg, P.; Sukkaew, P.; Farkas, I.; Kordina, O.; Janzén, E.; Ojamäe, L.; Danielsson, Ö.; Pedersen, H. Silicon Chemistry in Fluorinated Chemical Vapor Deposition of Silicon Carbide. J. Phys. Chem. C 2017, 121, 2711–2720. [Google Scholar]

| Reagent | Product | Activation FE [kJ/mol] |
|---|---|---|
| Sislab + CH4 | -Si-CH3 + -Si-H | 45 |
| -Si-CH3 | -Si-CH2-Si- + -Si-H | 166 |
| -Si-CH2-Si- | -Si-C(H)(Si-)-Si- + -Si-H | 164 |
| -Si-C(H)(Si-)-Si- | Si4C + -Si-H | 144 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalchevski, D.A.; Trifonov, D.V.; Kolev, S.K.; Aleksandrov, H.A.; Dimov, D.A.; Popov, V.N.; Milenov, T.I. Ab Initio MD Study of the Mechanism of Carbonization of Si(001) Surfaces with Methane at High Temperatures. Coatings 2025, 15, 427. https://doi.org/10.3390/coatings15040427
Kalchevski DA, Trifonov DV, Kolev SK, Aleksandrov HA, Dimov DA, Popov VN, Milenov TI. Ab Initio MD Study of the Mechanism of Carbonization of Si(001) Surfaces with Methane at High Temperatures. Coatings. 2025; 15(4):427. https://doi.org/10.3390/coatings15040427
Chicago/Turabian StyleKalchevski, Dobromir A., Dimitar V. Trifonov, Stefan K. Kolev, Hristiyan A. Aleksandrov, Dimitar A. Dimov, Valentin N. Popov, and Teodor I. Milenov. 2025. "Ab Initio MD Study of the Mechanism of Carbonization of Si(001) Surfaces with Methane at High Temperatures" Coatings 15, no. 4: 427. https://doi.org/10.3390/coatings15040427
APA StyleKalchevski, D. A., Trifonov, D. V., Kolev, S. K., Aleksandrov, H. A., Dimov, D. A., Popov, V. N., & Milenov, T. I. (2025). Ab Initio MD Study of the Mechanism of Carbonization of Si(001) Surfaces with Methane at High Temperatures. Coatings, 15(4), 427. https://doi.org/10.3390/coatings15040427










