1. Introduction
Ruts and cracks are the two primary issues affecting roads. Ruts are related to the asphalt mixture’s ability to resist permanent deformation, while cracks are associated with the mixture’s resistance to fracture. The asphalt content directly influences these two properties: a higher asphalt content enhances the mixture’s crack resistance, whereas a lower content improves its resistance to deformation. The high or low asphalt content in asphalt mixtures creates a conflict between deformation resistance and cracking resistance. There should be a balance point where these properties are equated. Unfortunately, current design methods for determining optimal asphalt content do not achieve this balance well. This is mainly due to two reasons: firstly, these methods are based on air voids ratio or asphalt film thickness, which do not inherently balance stability and cracking resistance; secondly, the criteria for determining optimal asphalt content lack uniformity, leading to inconsistent results. Asphalt pavement structures are layered, with different mechanical properties in each layer, resulting in varying deformation and cracking characteristics. For instance, in a three-layer asphalt pavement, the middle layer is most prone to rutting, while the lower layer is crucial for preventing reflective and fatigue cracks. Additionally, the thickness of each layer affects the pavement’s overall cracking and deformation resistance. Current asphalt mixture design methods do not adequately consider these structural factors, leading to a disconnect between pavement structure design and mixture material design. This results in an underutilization of each layer’s potential for deformation and cracking resistance. Therefore, for a hot mix asphalt (HMA) overlay to perform effectively, it must achieve a balance between adequate resistance to both ruts and cracks. Additionally, each asphalt layer possesses unique properties. The deformation and crack resistance characteristics vary from layer to layer, necessitating different asphalt content requirements for each layer. The optimum asphalt content can be estimated using theoretical formulas, but due to the variability in actual material properties, these formulas only provide a rough estimate. The final optimum asphalt content must be determined experimentally. Methods for determining the optimum asphalt content include the Marshall method, Superpave method, Hveem method, French LCPC method, and the TxDOT method used in Texas, USA. All these methods are based on the high-temperature performance of asphalt mixtures and do not adequately consider cracking characteristics. Additionally, different methods can yield significantly different optimum asphalt contents for the same materials. Regardless of the method used, the goal is the same: to design asphalt mixtures with good deformation resistance, cracking resistance, water stability, aging resistance, and ease of construction.
In the past, HMA designs, such as the Marshall method, focused solely on rutting resistance. Superpave mixtures were often too dry, frequently associated with cracking issues, such as reflective and top-down cracking. In 2006, Zhou [
1] first proposed a balanced design that considered both rutting and cracking resistance. Subsequently, Scullion and Hu [
2] used this method to design extremely thin asphalt mixtures and applied the results to road profiles based on their research findings. At the same time, Walubita and Hu [
3,
4] compared the balanced design method (BDM) of TxDOT through laboratory evaluation. The results showed that the balanced design was more effective. Reflective cracking is one of the major forms of deterioration in pavement and is very common when HMA overlays are constructed over a base with discontinuities in its surface. Idris et al. [
5] conducted an in-depth review of the available literature and evaluated 17 reflective cracking testing devices, among which the best three were chosen based on their availability, ease of use, variability, repeatability of the test results, and field validation.
Fatigue cracking, a major distress in asphalt pavements, is worsened by traffic and climate conditions, such as moisture effects on constituents and interfacial properties. Silva et al. [
6] conducted more tests to assess moisture-induced damage effects on asphaltic materials, focusing on the failure of asphalt binders, the aggregate–binder interface, and mixture. He et al. [
7] prepared nine types of recycled asphalt mixtures with different percentages of reclaimed asphalt pavement and rejuvenators. They conducted Hamburg rutting tests, semi-circular bending tests, and freeze–thaw splitting tests to study the rutting resistance, cracking resistance, and water stability of the asphalt mixtures. The test results indicated that the recycled asphalt mixtures prepared with the optimal asphalt content determined by the Superpave method did not meet the specification requirements for cracking resistance. Applying the BDM to the design of hot recycled asphalt mixtures can yield high-performance recycled asphalt mixtures that meet all specification requirements. However, like other mixture design methods, the BDM does not take into account the layer properties. In order to investigate the feasibility of recycling the recycled plastic-modified asphaltic mixtures, Lim et al. [
8] conducted a series of laboratory tests, such as Marshall stability, indirect tensile strength, Cantabro abrasion loss, and resilient modulus tests to evaluate the performance of recycled asphalt concrete containing 20% aged content.
Currently, the material design of asphalt mixtures is primarily based on test methods that focus on high-temperature performance, without adequately considering the cracking characteristics of the mixtures. Moreover, asphalt mixtures designed using these methods have no direct relationship with the behavior of pavement structures. However, in reality, different structural layers have varying requirements for rutting and cracking resistance. Therefore, it is necessary to integrate and correlate pavement structure design with asphalt mixture material design to effectively delay the occurrence of ruts and cracks. Consequently, obtaining experimental methods, indicators, and standards for evaluating the deformation and fracture characteristics of asphalt mixtures is essential. The rutting test is currently the recognized method for assessing the high-temperature (permanent deformation) stability of asphalt mixtures, with the Hamburg wheel tracking test being the most representative. The rutting test provides an experimental method for evaluating the material’s resistance to deformation and can serve as a basis for establishing corresponding indicators and standards.
Rutting prediction and modeling have been extensively researched for many years, leading to the development of various models aimed at forecasting rutting or permanent deformation. Generally, these models can be classified into two categories: (1) layer strain rutting models and (2) shear strain rutting models. The VESYS rutting model, which is utilized in this paper, falls under the category of layer strain rutting models. A key feature of the VESYS layer rutting model is its focus on characterizing the properties of individual layers rather than relying on global parameters. For each layer, the VESYS model requires specific permanent deformation parameters, denoted as αi and μi. However, one of its drawbacks is the need to acquire these layer properties and conduct repeated load tests for each layer. Despite this challenge, recognizing the complexity of HMA mixtures, it is essential to accurately characterize the permanent deformation properties of each HMA layer to make more precise predictions. Therefore, the VESYS layer rutting model was ultimately chosen for modeling rutting in HMA overlays.
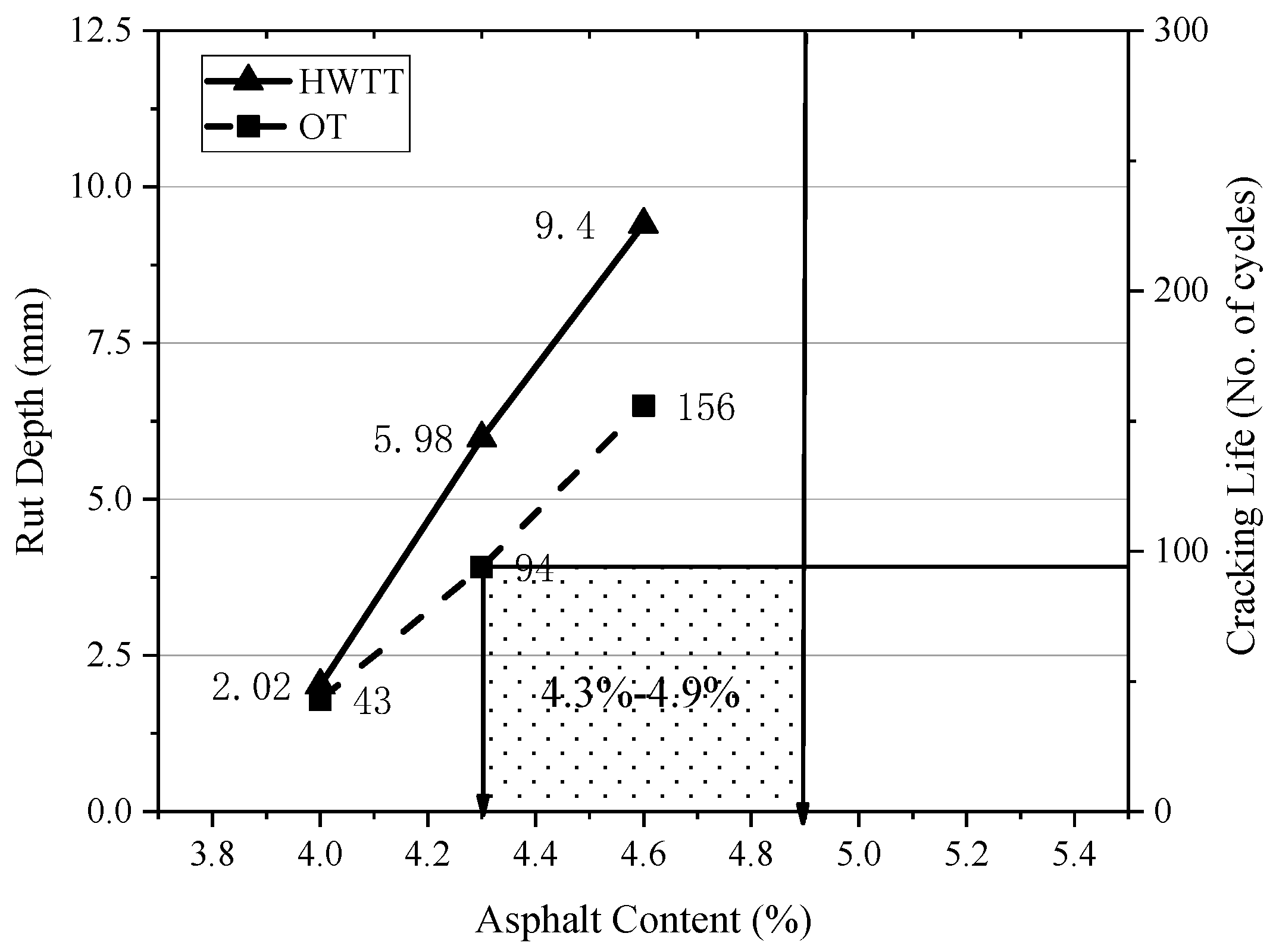
This paper takes the commonly used AC-20 asphalt mixture for the intermediate layer of asphalt pavements as the subject of analysis. It evaluates its high-temperature rutting resistance and low-temperature cracking resistance through the Hamburg wheel tracking test (HWTT) and the overlay tests (OTs), respectively. Initially, the effective range of asphalt content is determined. On the other hand, the VESYS rutting prediction model is utilized. Permanent deformation parameters of the asphalt mixture are obtained through testing, and the predicted rutting amount is calculated using the deflection values at the top and bottom of the asphalt layer. Subsequently, the rutting contribution rate calculated from the finite element model and the allowable rutting depth value for the intermediate layer are used to further determine the optimal range of asphalt content for the intermediate layer asphalt mixture. We take the intermediate layer of asphalt pavement on high-grade highways as an example to demonstrate the feasibility of this design method. By comparing the rutting depth obtained from the VESYS rutting prediction model under each asphalt content with the allowable rutting depth, the research results show that the asphalt content designed by the BDM based on the rutting resistance performance of the intermediate layer for this pavement structure and this kind of material is 4.3%–4.6%. In actual engineering, it is recommended to take 4.4% as the optimal asphalt content for AC20.
2. Asphalt Mixture BDM
2.1. Basic Conception of BDM
The so-called BDM refers to the approach that combines the structural characteristics of asphalt pavement and, based on the properties of each asphalt layer, designs the optimal asphalt content for HMA mixtures. This ensures that the designed asphalt mixture can balance the rutting resistance and crack resistance of the asphalt layer at that particular position, thereby achieving the best possible performance.
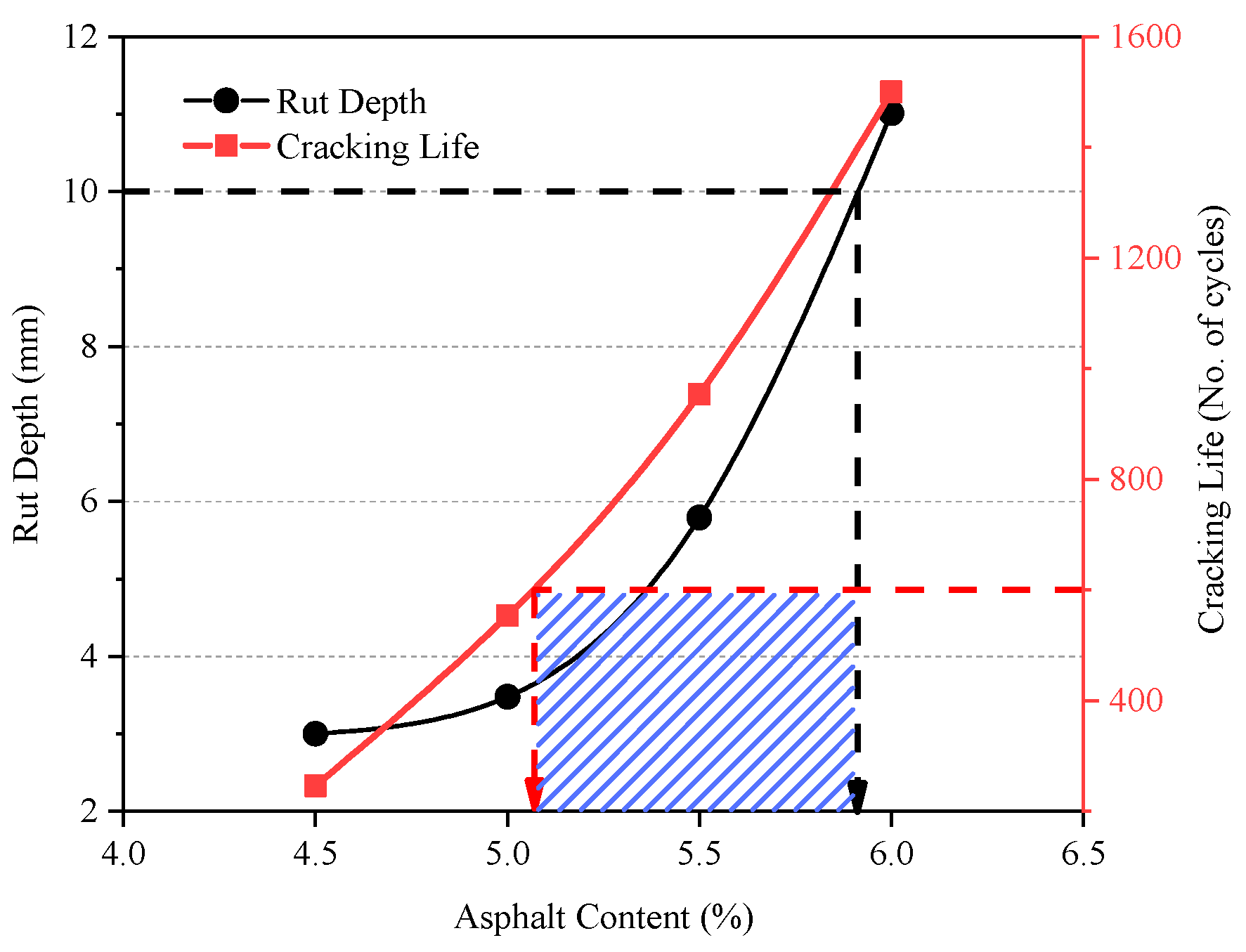
Selecting an appropriate trial asphalt content is crucial for successfully determining the balanced asphalt content, ensuring that the designed mixture meets both rutting and cracking standards. Balanced design is a method for HMA mixture design that can balance the requirements for rutting and cracking resistance. The HWTT and OT apparatus are used to evaluate the rutting and cracking resistance of HMA mixtures, respectively. The upper limit of the asphalt content range is determined by the immersed HWTT. The lower limit of the asphalt content range is determined by the OT.
The immersed HWTT is widely accepted for evaluating the high-temperature stability of asphalt mixtures. In this study, the test was stopped after 20,000 wheel passes, with data collected from 11 points as the roller moved from the end to the front. The rut depth was indicated by negative values from the initial height, with the average of points 5, 6, and 7 used as the final rut depth. The test temperature was 50 °C, and the maximum rut depth after 20,000 wheel passes should be less than 12.5 mm.
As for the evaluation of cracking resistance, there are various existing methods both domestically and internationally, each with its own strengths and limitations. These include the indirect tensile test, small beam fatigue test, temperature stress test for confined specimens, and semi-circular bend test. Research indicates that in the early stage of reflective crack propagation in asphalt mixtures, opening mode cracks (caused by temperature and load) dominate. As the crack extent increases and reaches a certain stage, shear-mode expansion due to load becomes the main factor. Therefore, controlling early stage opening mode reflective cracks can effectively delay the progression of cracks to the top of the asphalt layer. Based on this principle, the OT was developed by the Texas Transportation Institute in the US. It can evaluate the cracking resistance of asphalt mixtures by simulating the development and characteristics of reflective cracks. The test temperature was 25 °C, and the OT cycle count should be no less than 300.
Once the types and gradations of the raw materials and the pavement structure have been established, it is essential to select three or four different asphalt contents for testing, while adhering to the fundamental requirements of VMA/VFA. In reality, the requirement for rutting resistance sets an upper limit for the trial asphalt content; exceeding this limit will result in an HMA mixture that fails to meet the necessary rutting resistance standards. Conversely, the requirement for cracking resistance establishes a lower limit for the trial asphalt content; falling below this threshold will compromise the mixture’s cracking resistance and overall durability. A typical graphical representation is provided below, with the shaded area in
Figure 1 indicating the effective range of asphalt content.
If there is no overlap in the figure, it is necessary to adjust the raw materials of the asphalt mixture, redesign the gradation, or change the type of mixture, etc.
Although the asphalt content range determined by the balanced design can balance crack resistance and rutting resistance, it still does not take into account the properties of different layers. For instance, the lower limit of the trial asphalt content determined by the OT can meet the cracking resistance requirement. However, due to the higher contribution of permanent deformation from the intermediate layer, the upper limit of the trial asphalt content determined by the HWTT may not necessarily meet the rutting resistance requirement. Therefore, based on the results of the balanced design, further optimization of this method is necessary.
2.2. Specific Steps of BDM
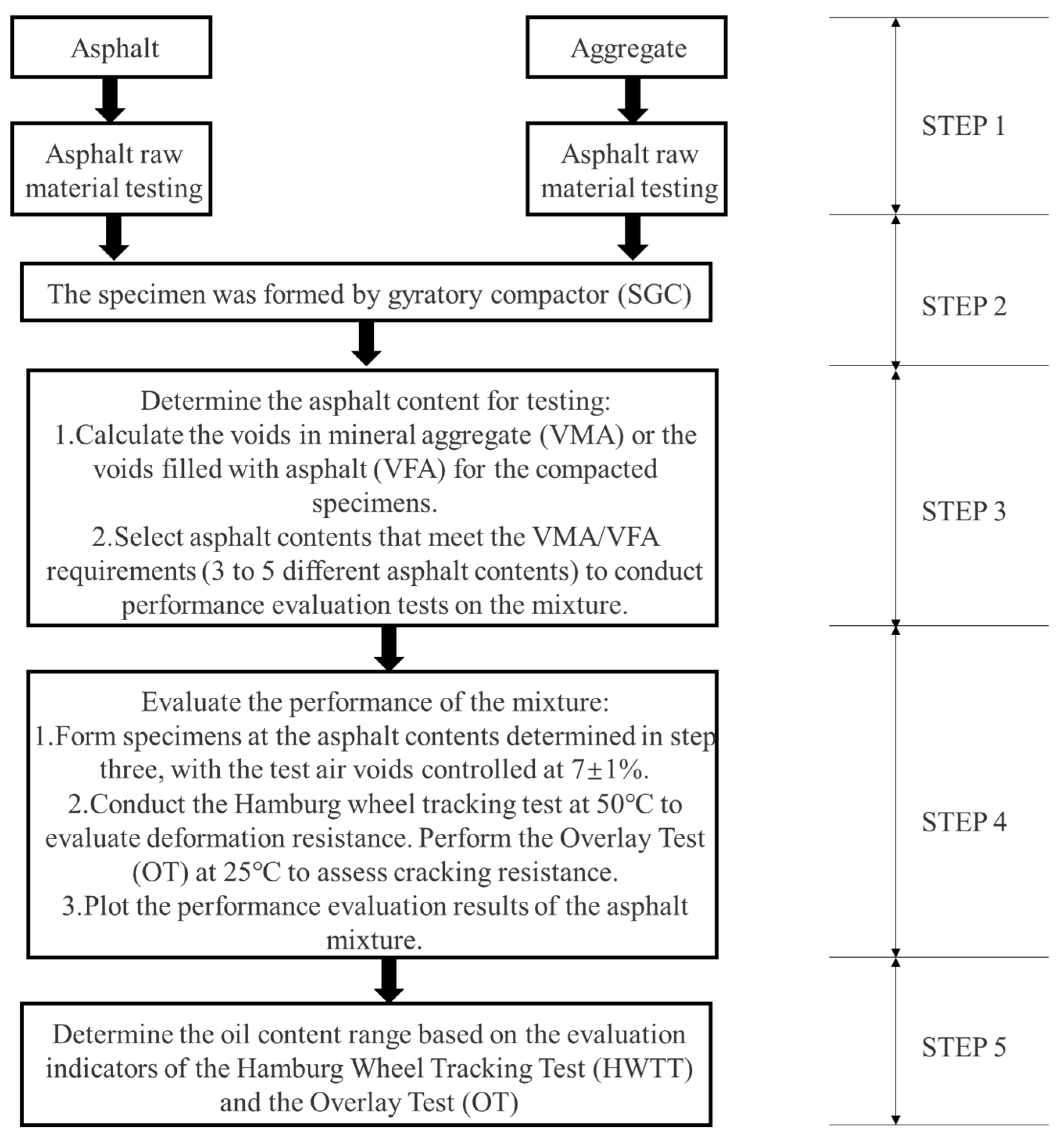
(1) Preliminary determination of the effective asphalt content range
In Step 4, specimens are compacted with an air void content of 7 ± 1% as required by the test procedure. A 7% air void content is used for specimen compaction because it represents the threshold for water permeability in pavements and is closer to the actual construction requirement of achieving a compaction level greater than 93%.
During the preliminary selection of the optimal asphalt content, the following four scenarios may occur:
- (1)
The asphalt mixture fails to meet both rutting and cracking resistance requirements;
- (2)
The asphalt mixture meets only the cracking resistance requirement;
- (3)
The asphalt mixture meets only the rutting resistance requirement;
- (4)
The asphalt mixture satisfies both cracking and rutting resistance requirements at an appropriate oil content.
If Scenario 1 occurs, among the 3 to 4 asphalt contents chosen within the range that meets basic requirements, like asphalt film thickness or VMA/VFA, none fall within the asphalt content range set by the immersed HWTT (upper limit) and OT (lower limit). The asphalt mixture design needs to be redesigned, including attempting different gradation types, material varieties, or different asphalt grades.
When Scenario 2 arises, among the 3 to 4 asphalt contents selected within the basic requirements range for asphalt film thickness or VMA/VFA, only those at the lower limit set by the OT are acceptable. And they exceed the upper limit set by the immersed HWTT. In this case, the asphalt content is too high, and the mixture needs redesign as in Scenario 1.
The occurrence of Scenario 3 suggests that this type of asphalt mixture has good rutting resistance, but it does not meet the cracking resistance requirement within the tested oil content range. In this case, one should return to Step 3 in
Figure 2 and further increase several sets of asphalt contents for HWTT and OT.
For Scenario 4, it indicates that the preliminary selection of asphalt content is complete, and the next step can proceed to more accurately determine the oil content.
The BDM can be briefly described as follows: when the materials, pavement structure layer thickness, and mix gradation are determined, select 3–4 asphalt contents within the range that meets basic requirements like asphalt film thickness or VMA/VFA. Use the immersed HWTT to set the upper limit and the OT to set the lower limit of the asphalt content range. The range between these limits is the “effective range” of asphalt content determined by the BDM, ensuring both rutting resistance and cracking resistance.
(2) Oil content optimization considering horizon characteristics
The functional or characteristic role of each asphalt layer in an asphalt pavement is an important consideration in this method. Although the BDM introduced in the previous section takes into account both the rutting and cracking resistance of asphalt mixtures in a balanced manner, it does not consider the functional role of the asphalt layer within the pavement structure. Therefore, it is essential to further optimize the asphalt content based on the existing BDM, taking into account the characteristics of each layer’s position.
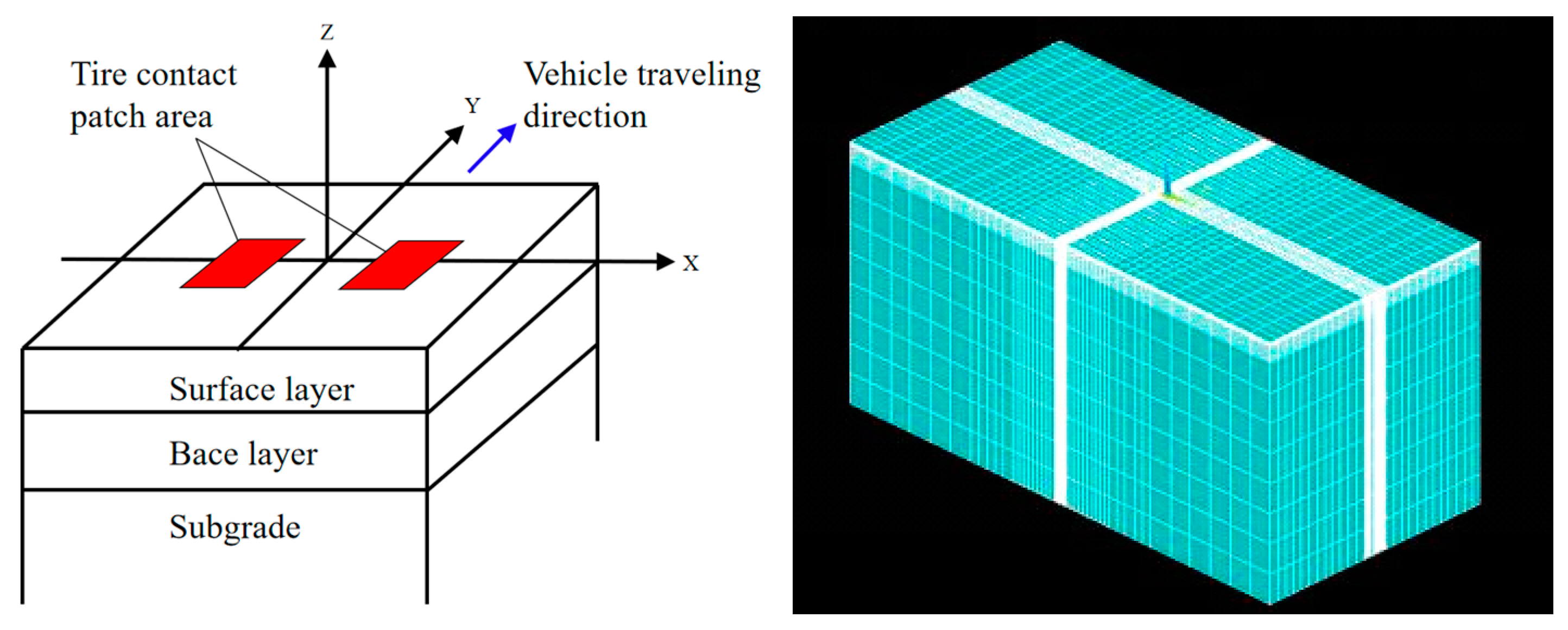
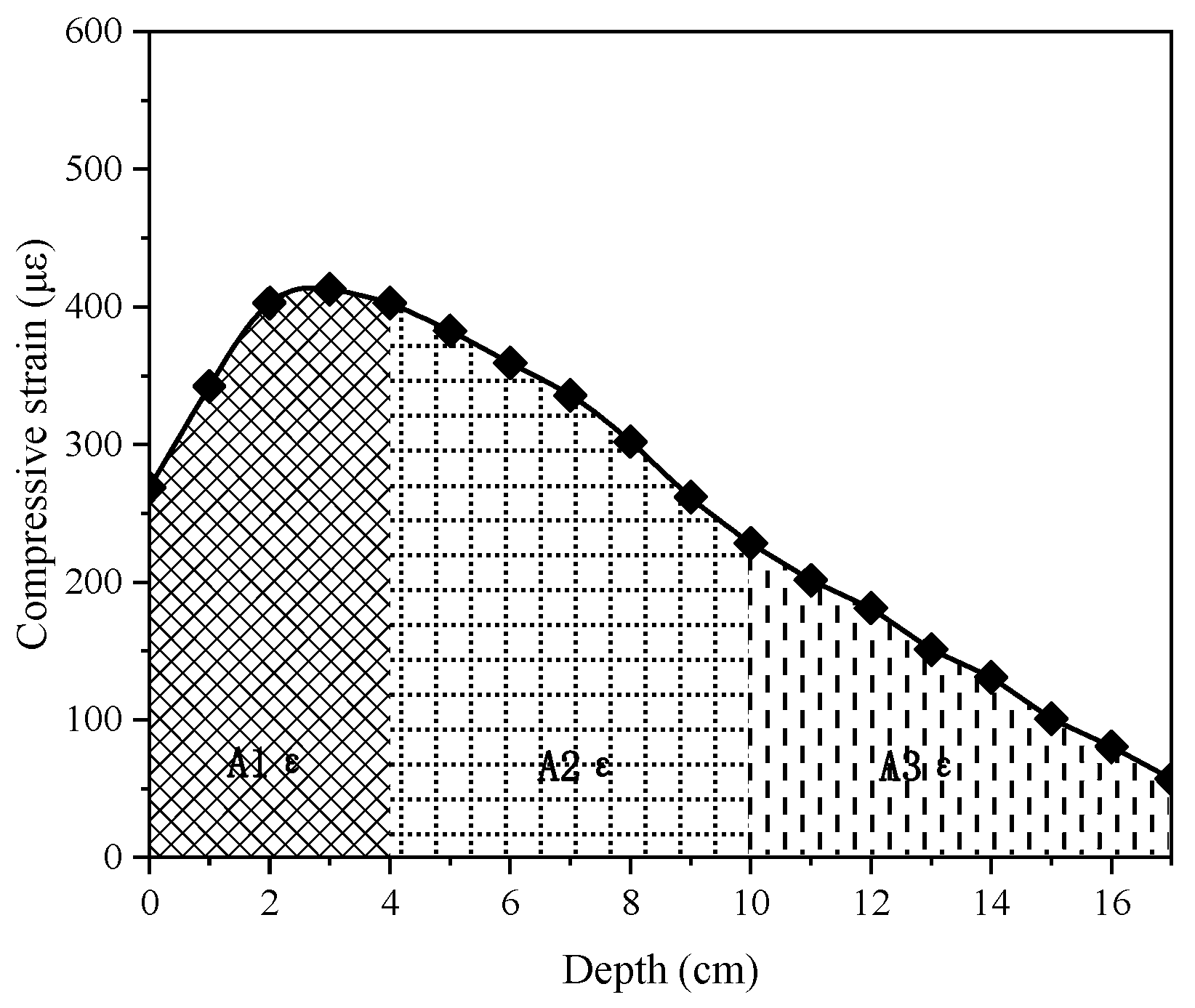
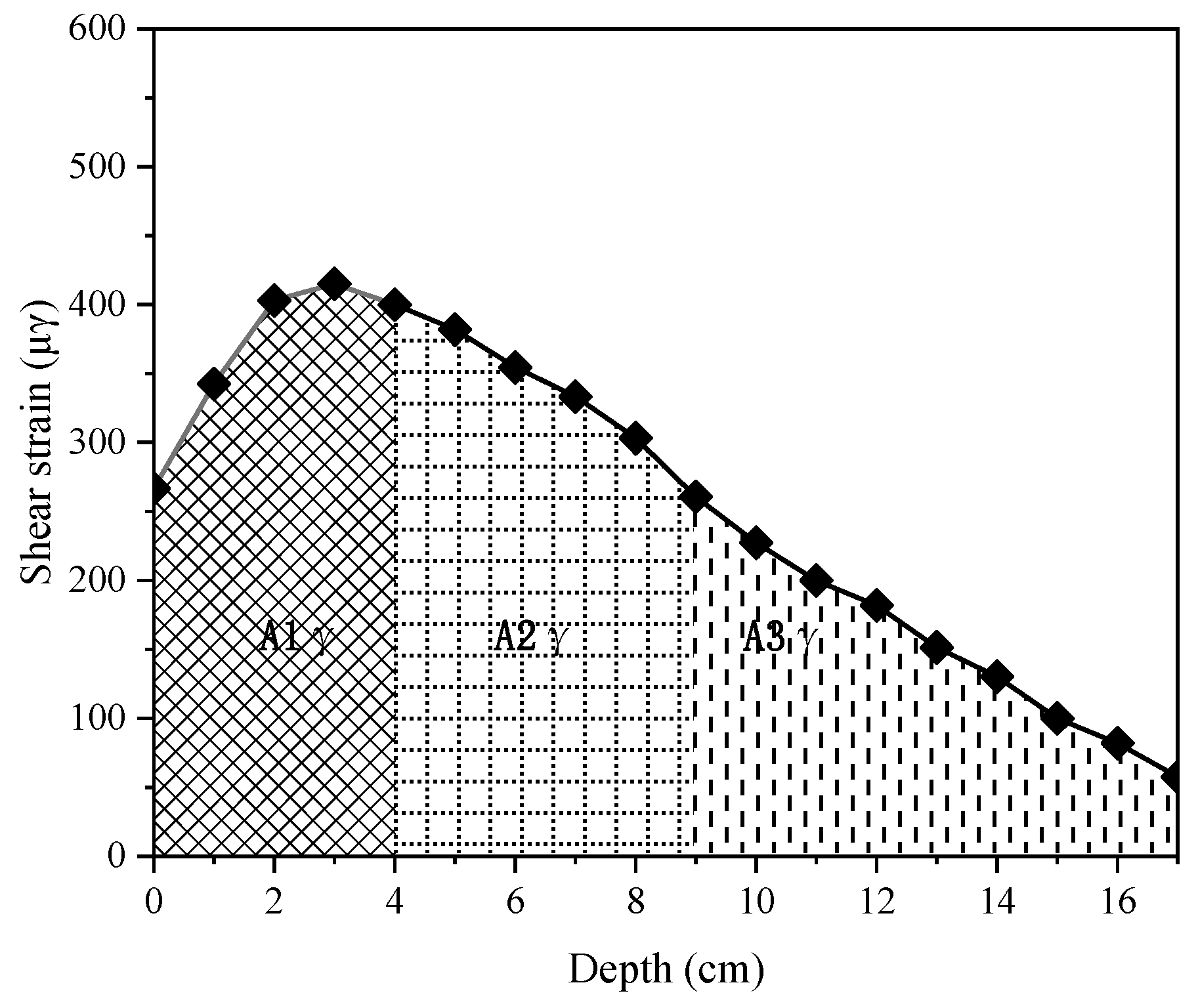
Regarding the rutting resistance of the intermediate layer, to optimize the upper limit of the asphalt content, it is first necessary to clarify two values: the estimated rutting depth and the allowable rutting depth. By comparing these two values, the optimal range of asphalt content for the intermediate layer’s rutting performance can be determined. The estimated rutting depth is calculated using the VESYS rutting prediction model, while the allowable rutting value is obtained after calculating the rutting contribution rate using the ANSYS1.0 finite element software.
The specific optimization steps for asphalt content based on layer characteristics, using the intermediate layer of a highway asphalt pavement as an example, are described as follows:
Step 1: Within the effective range of asphalt content initially determined by the BDM, select 3 to 4 different asphalt contents again. Conduct repeated loading creep tests and dynamic modulus tests for each. Additionally, perform dynamic modulus tests for the upper and lower layers to facilitate subsequent finite element calculations.
Step 2: Establish an ANSYS finite element model. Using a UTM testing machine, conduct dynamic modulus tests to measure the dynamic modulus values of each layer’s asphalt mixture. Convert these values into viscoelastic parameters through calculations and input them into the finite element model. Calculate the deflection values at the top and bottom of the intermediate layer and estimate the rutting contribution rate of the intermediate layer.
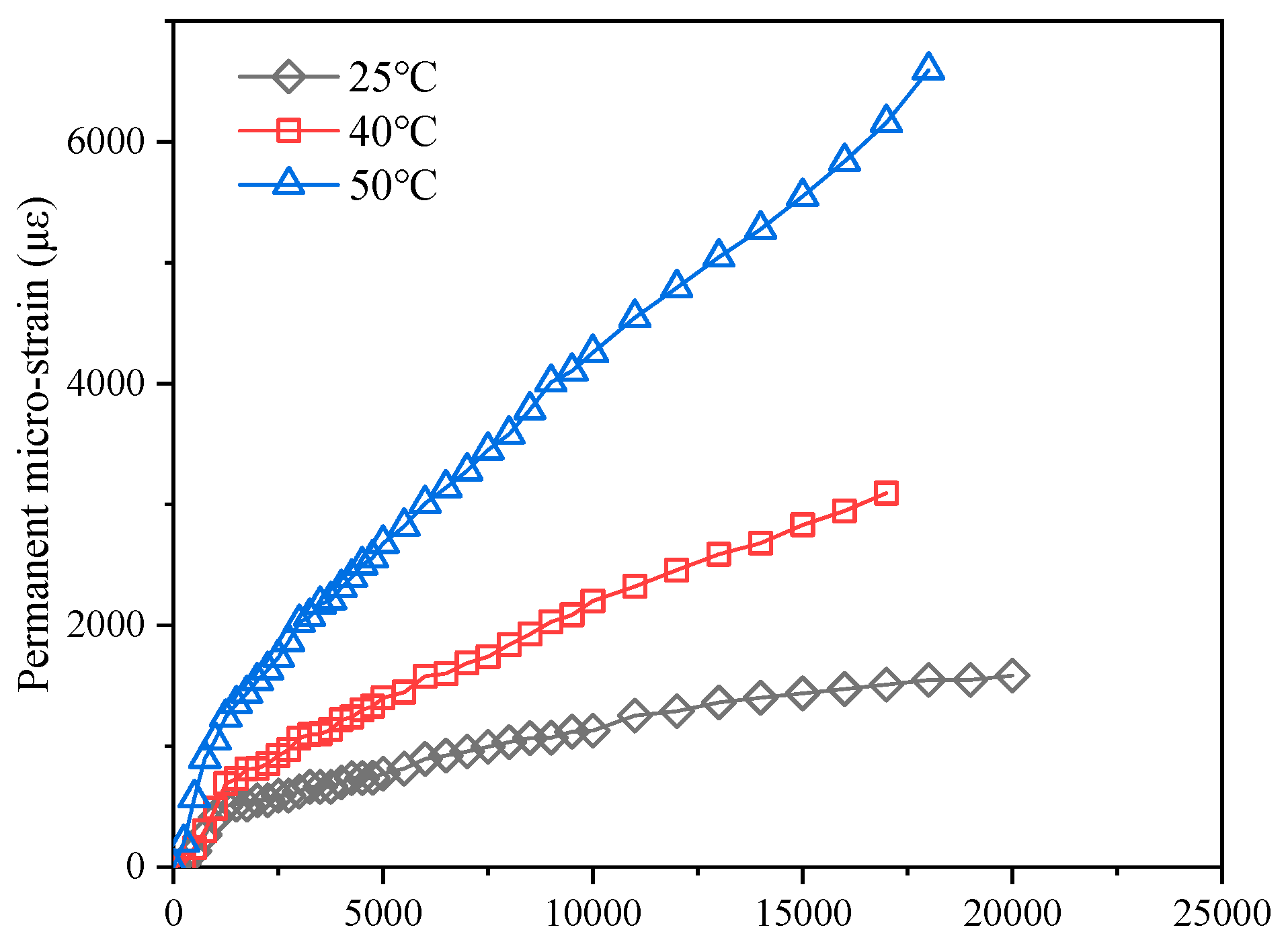
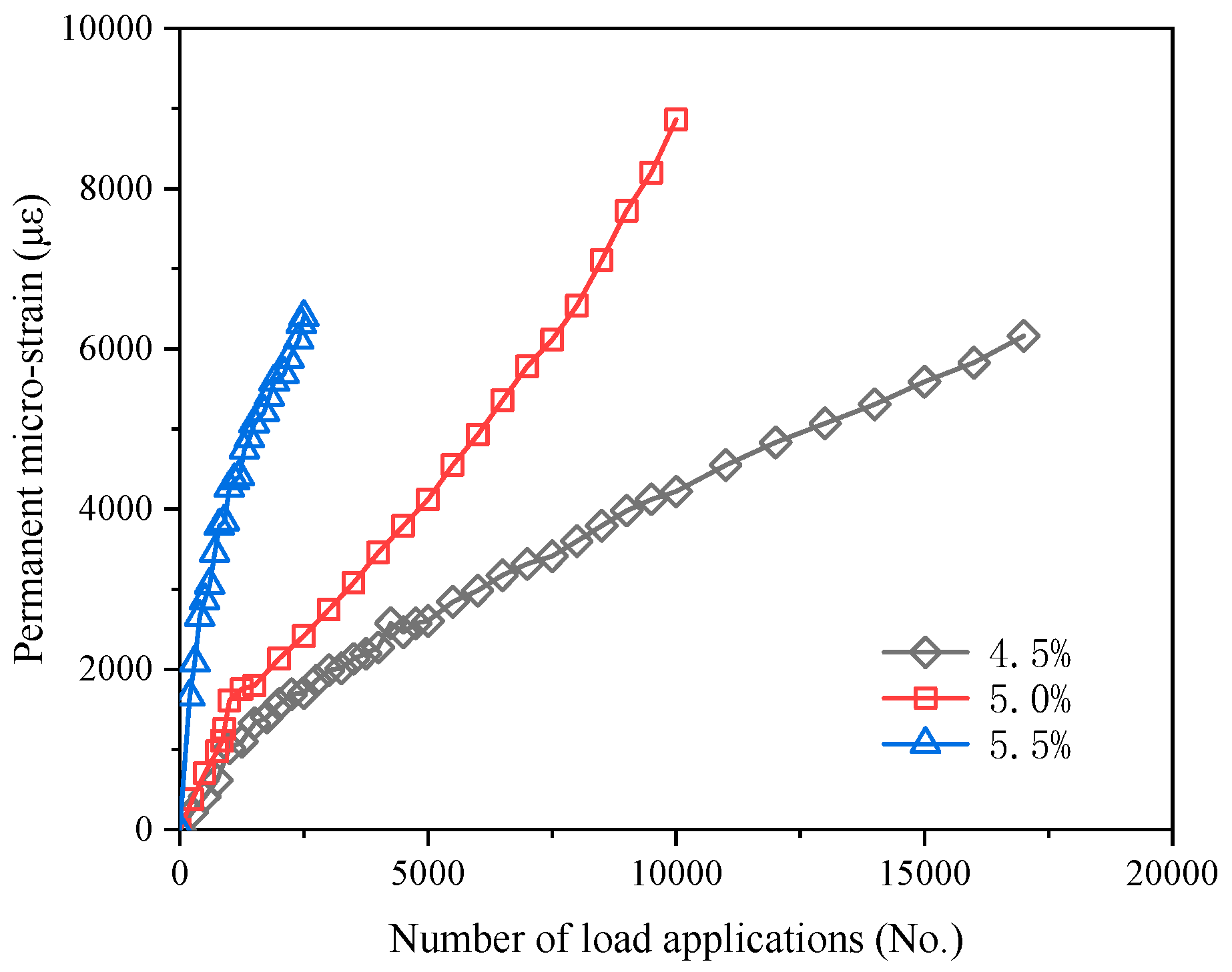
Step 3: Process the results of the repeated loading creep tests to obtain the permanent deformation parameters μ and α required for the VESYS rutting prediction model.
Step 4: Substitute the deflection values at the top and bottom of the intermediate layer, along with the μ and α values for each asphalt content, into the VESYS rutting prediction model. Calculate the estimated rutting amount for the intermediate layer and make necessary adjustments.
Step 5: Use the finite element calculation results to estimate the rutting contribution rate of the intermediate layer. In conjunction with the requirements for asphalt pavement rutting depth specified in the “Technical Specifications for Maintenance of Highway Asphalt Pavements [
9]”, determine the allowable rutting value for the intermediate layer.
Step 6: Compare the estimated rutting value obtained in Step 4 with the allowable rutting value obtained in Step 5. If the estimated rutting value is less than the allowable rutting value, the asphalt content is acceptable. This comparison helps to determine the optimal range of asphalt content for the intermediate layer’s rutting resistance performance.
5. Discussion
The comparison between Marshall, Superpave, and current AASHTO design procedures and the BDM in this manuscript is as follows:
5.1. Comparison of Several Procedures with BDM
Marshall design procedure focuses on the analysis of asphalt mixture density and air void characteristics. It ensures proper volumetric proportions and determines the optimum binder-to-aggregate ratio by taking the midpoint of a suitable range. However, the link between volumetric parameters and pavement performance is weak. The Superpave design procedure can determine the best asphalt usage based on volumetric characteristics, emphasizing gradation design and asphalt material selection. Specimens are made using a gyratory compactor to simulate actual construction compaction. It sets control standards based on traffic but is complex and can result in insufficient field compaction. AASHTO design procedures are based on empirical formulas and statistics for pavement structure design. They rely on field tests and historical data, adjusting parameters for different traffic and climate conditions and focus on pavement structure. Different design procedures can lead to significantly different optimal asphalt contents for the same materials. Almost none of these procedures consider pavement structure, layer position, or thickness. This disconnects pavement structure and material design, underutilizing material properties. Performance tests mainly focus on high-temperature stability, with less attention to low-temperature crack resistance. Compared with the above procedures, the BDM proposed in this manuscript emphasizes meeting field performance requirements. It considers the characteristics of asphalt layers to balance crack and deformation resistance when determining the optimal asphalt content. Results can be further optimized based on specific road structures and performance needs.
5.2. Challenges in Implementing Asphalt Content in Full Scale Pavement Applications
In full scale pavement applications, the implementation of the author’s suggested asphalt content mainly faces the following challenges. Both the rutting resistance standard and the referenced OT test—based cracking resistance standard need correction using pavement survey data. For the cracking resistance standard, it can be determined by comprehensively analyzing pavement survey data (like cumulative load/thermal stress—induced crack—free axle passes), relevant material-based cracking test results, and theoretically calculated fatigue lives of pavement layers under temperature-load coupling. Then, further correction is done using tracking pavement survey data, with structural layer thickness and position also considered. The rutting resistance standard is established based on existing pavement survey data, including rutting data under different load applications, relevant material-based rutting test results, and a rutting prediction model. Similarly, this standard is refined with tracking pavement survey data. This study offers a specific approach and steps for the middle surface layer’s characteristics. Future research can optimize the effective asphalt content by integrating the characteristics of the upper and lower surface layers.
5.3. Alignment of Research Content with Existing Pavement Design Standards
The premise of the initial selection of the asphalt stone ratio is that the VMA of the asphalt mixture must meet the requirements of the pavement specifications, and the mixture forming test controls the range of void ratio, which matches the existing pavement design standards. The contribution rate of each asphalt layer to rutting on asphalt pavement is different, and the contribution rate is affected by changes in modulus and thickness. By predicting the depth of rutting and calculating the contribution rate of the middle layer rutting, the oil stone ratio can be further optimized based on the initial selection of the oil stone ratio in the early stage. The oil stone ratio initially selected in the early stage is a range of values that can meet the requirements of both crack resistance and high temperature stability. Within this range, further consideration needs to be given to whether the optimal oil content should be taken as the median value, a smaller value, or a larger value (existing standards often take the median value in a general way). In fact, due to differences in pavement structure thickness and materials, each layer has different emphasis on the high temperature stability and low temperature stability of the mixture. By calculating and predicting the amount of ruts, the requirements for high temperature stability and low temperature crack resistance of this layer can be clarified, and the range can be further narrowed within the initial selection of oil stone ratio to determine the optimal oil stone ratio. In fact, the standards all propose a unified rutting allowance value for the overall road surface to control high temperature stability because the contribution rate of rutting in each layer of the road surface is different. Therefore, accurately obtaining the rutting allowance value for each layer as an indicator is more accurate. The high temperature stability requirements of each layer narrow down the range of the oil stone ratio.
5.4. Analysis of Asphalt Durability
This study did not explore the impact of oxidation on asphalt performance, only conducting the asphalt raw material’s rotational thin-film heating test. It was found that the air voids ratio greatly affects asphalt durability. When initially selecting the asphalt content, the mineral gap rate (VMA) was considered. Three to five binder-to-aggregate ratios were preliminarily chosen within the VMA specification range. During mix performance testing, the air voids ratio of the asphalt mixture was controlled at 7 ± 1%. The early volume index control ensures the durability of the asphalt mixture. However, the relationship between durability and oxidation requires further study.
The optimum asphalt content is recommended to be 4.3%–4.6%. but there are no field test sections to support the effectiveness of these numbers, Therefore, the study will be further developed in subsequent research to verify the long-term performance.