1. Introduction
In the context of the accelerated advancement in the domain of aerospace science and technology, there has been an emergence of increasingly stringent requirements for the suppression of stray light in critical-space low-light detection systems, such as satellite laser communication and gravitational wave detection. The surface scattering characteristics of the optical components directly determine the distribution of stray light within the system. Non-target stray light outside the field of view, caused by light scattering from the surface of the metal structural components, severely restricts the signal-to-noise ratio of the system, which greatly affects the stability of the system.
Brass has excellent mechanical properties, physical properties, and high electrical and thermal conductivity and corrosion resistance; it is widely used in electronics, telecommunications equipment, household appliances, connectors, and accessories. Red copper exhibits high electrical conductivity and good wear resistance, making it a suitable material for use in conductive springs, wires, and cables. These characteristics position the copper alloy for a broad range of applications in the aviation sector, where stringent material performance requirements are in place. The bidirectional reflectance distribution function (BRDF) is an effective means to characterize the scattering properties of target surfaces. In this study, a microelement model is employed to derive expressions for the contributions of both specular and diffuse reflection components. Experimental measurements and analyses were conducted in conjunction with the model, enabling the distillation of the governing laws underlying multifactorial influences. These aspects constitute the innovative contributions of this research.
In the field of optical characterization and materials science, the scattering properties of metal surfaces are one of the current research hotspots. The bidirectional reflection distribution function (BRDF), as a physical parameter describing light scattering properties, can be used to characterize the anisotropic scattering properties in the hemispherical space on a material surface. The study of the BRDF properties of material surfaces not only helps to understand the optical properties of material surfaces but also provides theoretical support and data support for material surface processing and practical engineering applications.
As early as 1978, Ishibashi et al. [
1] conducted durability, heat, and weathering tests on selectively absorbing surfaces of stainless steel, measured specular reflection, diffuse reflection, and angular dependence and determined the absorbance of stainless steel to be 0.91–0.93 using an integrating sphere, exploring the possibility of obtaining a lower radiative property of stainless-steel surfaces in the infrared region without significantly reducing the high absorbance. Weaver et al. [
2] explored the optical properties of metallic materials, which provided a reference for the experimental study of the light reflection behavior of metal surfaces. Nayar et al. [
3] investigated the reflectance models based on physical and geometrical optics, and through the reflectance curves predicted by the two models, they proposed a reflectance framework consisting of three parts, the diffuse reflection flap, specular reflection flap, and specular cusp, and analyzed the effect of surface roughness on it. Ward [
4] proposed a mathematical model based on the anisotropic reflectance of metal surfaces, which can effectively restore and reproduce surface spatial reflectance data.
Earlier this century, Li and Torrance [
5] investigated the angular distribution of light scattered on several rough metal surfaces and used the BRDF model based on the Kirchhoff approximation to establish the relationship between the surface-height statistics and the angular distribution of the scattered light. The fitting yielded roughness statistics that matched very well with the measurements of the high-frequency small-scale roughness components. Ngan et al. [
6] built a new setup for the efficient acquisition of anisotropic BRDFs, which is capable of acquiring anisotropic materials at a high resolution so that the sampling microfacet distributions computed from the measurements can be fitted with improved fit and intrinsically reproduce the measurements. Xie et al. [
7] combined the effects on the surface profile from the surface wettability theory and wet conditions, conducted an experimental comparison, and measured the BRDF value of the surface of three exterior decorative materials for buildings, namely granite, coated glass, and an Ethylene Propylene Diene Monomer (EPDM), under the conditions of two dry and wet wavelength bands (visible band 0.6328 μm and near-infrared band 1.34 μm) and different angles of incidence. The data showed that if a stable water film with a translucent smooth interface function is formed above the surface of the material, its BRDF value will show obvious specular reflection components in different degrees. eZhang et al. [
8] measured the BRDF at a wavelength of 660 nm for a copper foam sheet with a pore size of 90 ppi and a porosity of 98.6% at different incidence angles of 0°, 15°, 30°, 45°, 60°, and 75°, respectively, and the results showed that the reflected energy at the backward direction is greater than the forward in the conditions of oblique incidence; with the increase in the incident angle, the asymmetry parameter decreases, the high reflected energy area becomes larger, and the integrated hemispherical reflectance increases. Vitali et al. [
9] presented Vis-NIR spectral BRDF measurements of laser-polished metallic, opaque, flat samples commonly employed in laser metal machining and concluded that in addition to the roughness, the optical properties seem to depend on the atmospheric composition of the polishing process. Renhorn et al. [
10] built a physics-based model for a rough-surface BRDF that accurately describes two orders of magnitude of BRDF scattering data for easy numerical computation, taking into account angles of incidence and scattering, the effective index, surface autocovariance, and correlation length. Durikovic et al. [
11] conducted BRDF spectral measurements, rendered synthetic images of metallic paints, measured the spectral reflectance of multiple paint samples, and used the measured data to fit the analytical BRDF model to obtain the directional optical effect of incident radiation parameter. Cui et al. [
12] explored the relationship between the incident angle, surface temperature, and scattering characteristics of metal surfaces and showed that the temperature field has a more pronounced effect on the scattering characteristics.
In recent years, researchers and scholars have begun to focus on the application and optimization of BRDF in specific scenarios, such as the study of BRDF optimization modeling for painted metal materials [
13]. Ma et al. [
14] conducted spectrally polarized BRDF measurements of brass in the visible light band, built an exponential model of the BRDF, and discussed the influences of wavelength, angle, polarization of incident, and reflected light on the BRDF, showing that the effect of wavelength on the BRDF depends on the color of the sample and that the polarization of incident light has little influence on the variation tendency of the BRDF versus the incident zenith angle and wavelength. Zou et al. [
15] reviewed the development of devices to measure the BRDF, collected research results in this field, summarized outstanding problems related to BRDF measurement, and proposed directions of future research in the area. Chen et al. [
16] measured the BRDF in the near-infrared band of brass rough surfaces under variable temperature conditions and built a six-parameter model of the BRDF, which showed that the temperature, heating time, and surface roughness have significant effects on the BRDF and that the overall error is not higher than 3.29%. Research on the BRDF of rough metal surfaces and deterministic structures [
17,
18] has been investigated by several early scholars. Miao Yupei et al. [
19] established a hybrid polarization model for metal surfaces that integrates both specular reflection and inter-reflection based on the physical mechanism of Fresnel reflection between light and metal surfaces. By employing microfacet theory, they analyzed the specular reflection BRDF while approximating the inter-reflection BRDF using the phase Mueller matrix, ultimately deriving the hybrid reflection loss for multi-view 3D reconstruction. Xie Yinmo et al. [
20] conducted a comparative analysis of the BRDF for anisotropic machined surfaces produced through three different processing methods (face milling, planing, and surface grinding) under varying incident angles, while also measuring and analyzing the directional reflection characteristics of fabrics with distinct texture structures.
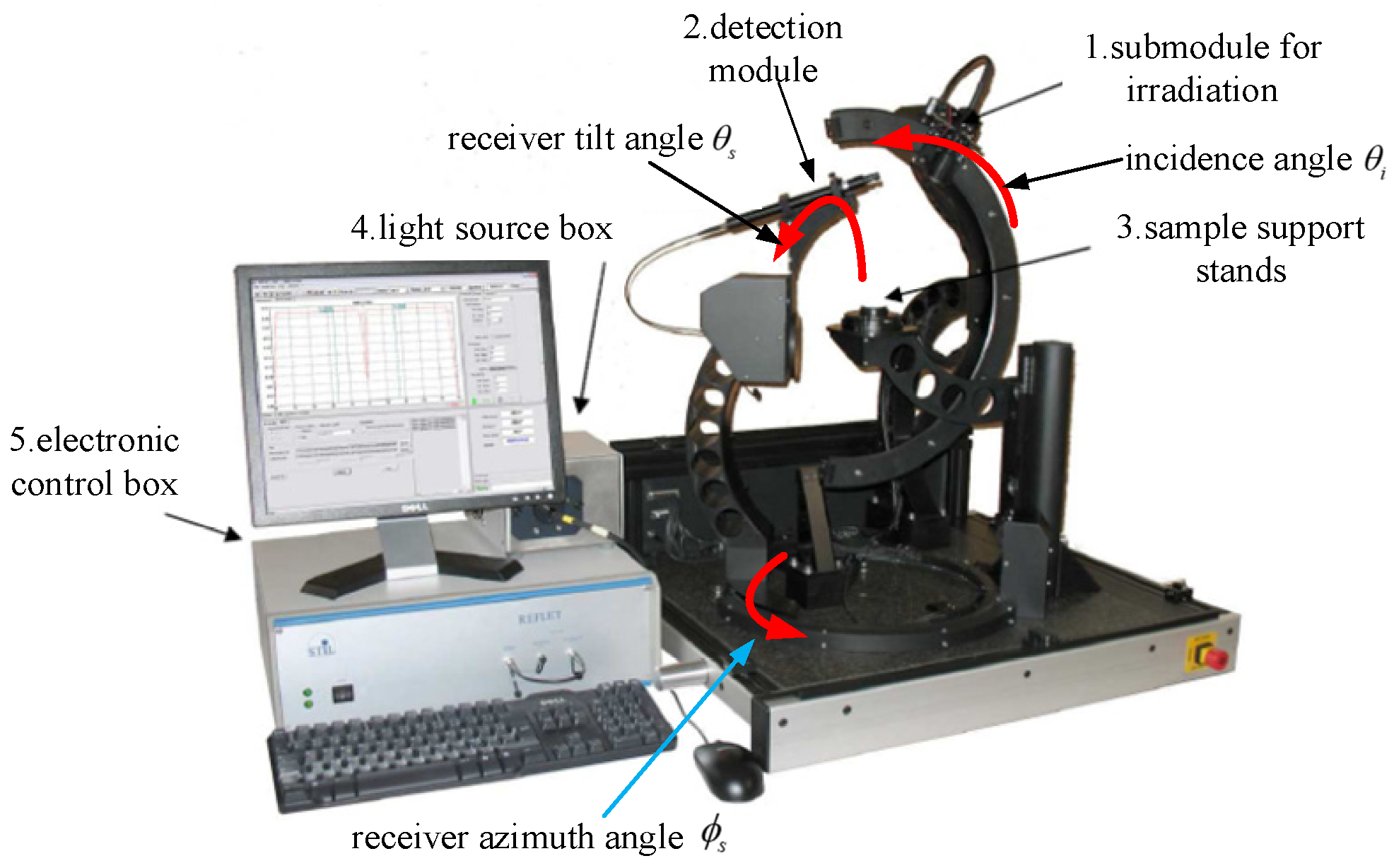
This paper builds a BRDF measurement system. The overall system consists of four subsystems: light source, scanning, detection, and software control. It realizes operation control and scanning trajectory parameter setting, sets different experimental variables, collects BRDF values on the surface of metal structural components, analyzes the BRDF peak and the scattering distribution law under various influencing factors, and studies the surface scattering characteristics of the components. Thereby, precise measurement of the scattering signal at the target position is achieved, which is one of the innovations of this work. In addition, the establishment of the BRDF model can fully reflect the reflection information on the surface of the metal structural components. How to establish the model based on the distribution characteristics of its microstructure and how to solve the model parameters are also the innovations of this topic.
This paper establishes a high-light BRDF model based on the microfacet element theory and analyzes and compares the scattering characteristics of the surfaces of typical metal materials, such as brass, aerospace aluminum, oxygen-free copper, and red copper, using a compact mechanized optical system. This study explores the influence of the optical properties of the material surfaces on the light scattering characteristics. Furthermore, this paper combines data related to the roughness of the material surfaces with the aforementioned data and compares the scattering characteristics of the four typical metal materials under white-light irradiation.
2. Bidirectional Reflection Distribution Function and Microfacet Theory
The bidirectional reflection distribution function is a mathematical model that describes the reflection properties of an object’s surface to light and is an effective tool for understanding and modeling the interaction of light with material surfaces [
21,
22,
23,
24,
25,
26,
27]. The Microfacet Element Theory is a physical model that explains the BRDF based on the light scattering properties of the surface microstructure, which assumes that the surface consists of a number of tiny mirrors (microfacet elements), each of which reflects light independently.
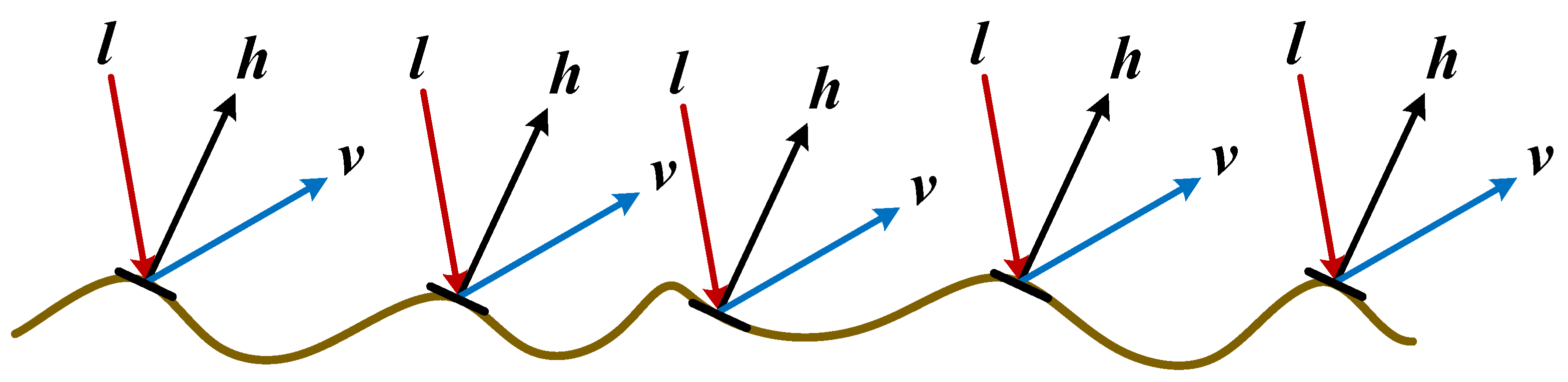
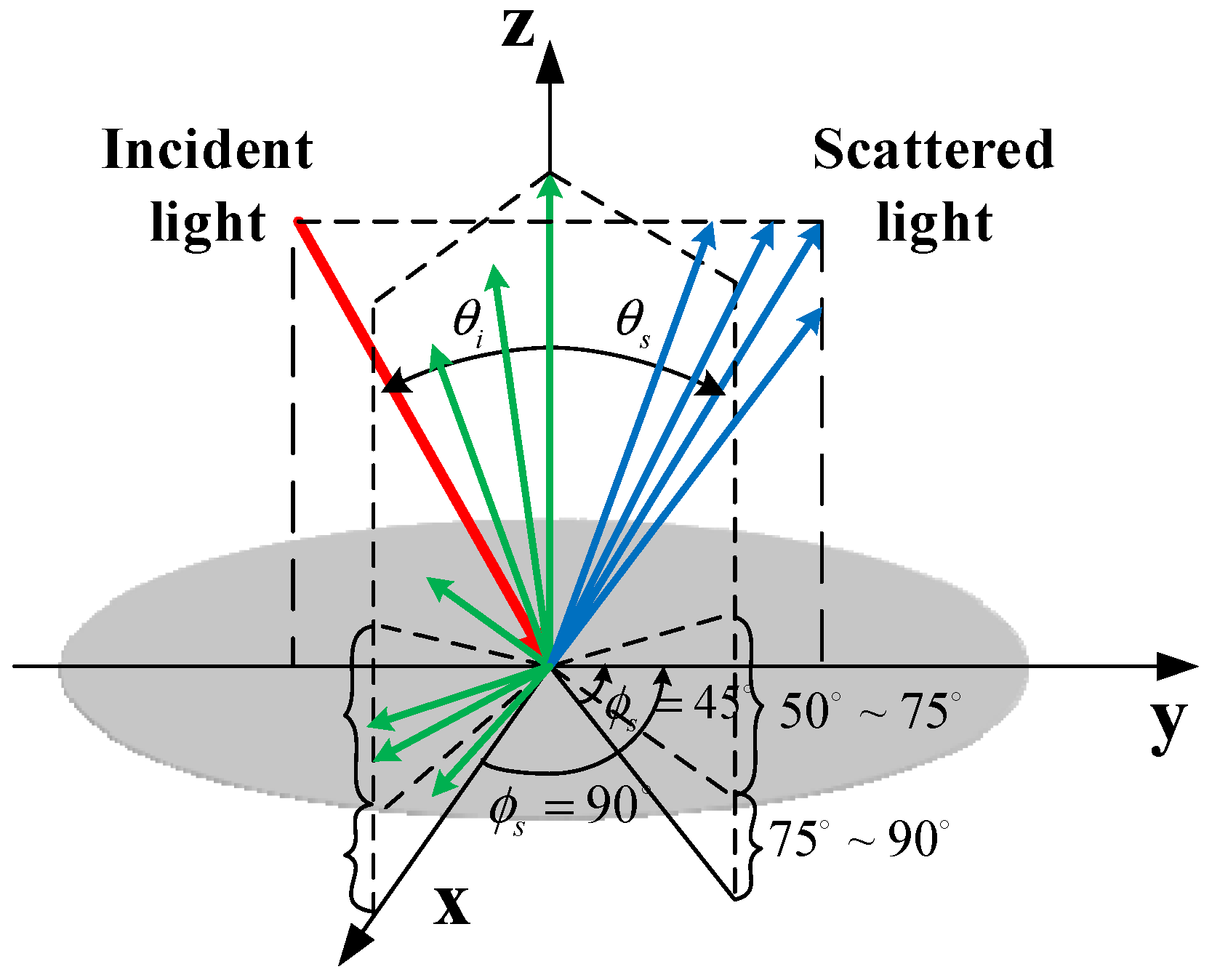
When the light strikes the surface along the
direction and is observed in the
direction, since the microfacet element will only reflect the incident light to the direction symmetric about the normal, only the microfacet element with the normal vector
will reflect the incident light in the
direction to the
direction, as shown in
Figure 1 [
28,
29,
30,
31,
32]:
The normal distribution function (NDF) is used to describe the probability of the normal distribution of all the microfacial elements that make up the surface: input a vector to the NDF, and the NDF will return the ratio of the number of microfacial elements whose normal vector is to the total number of microfacial elements.
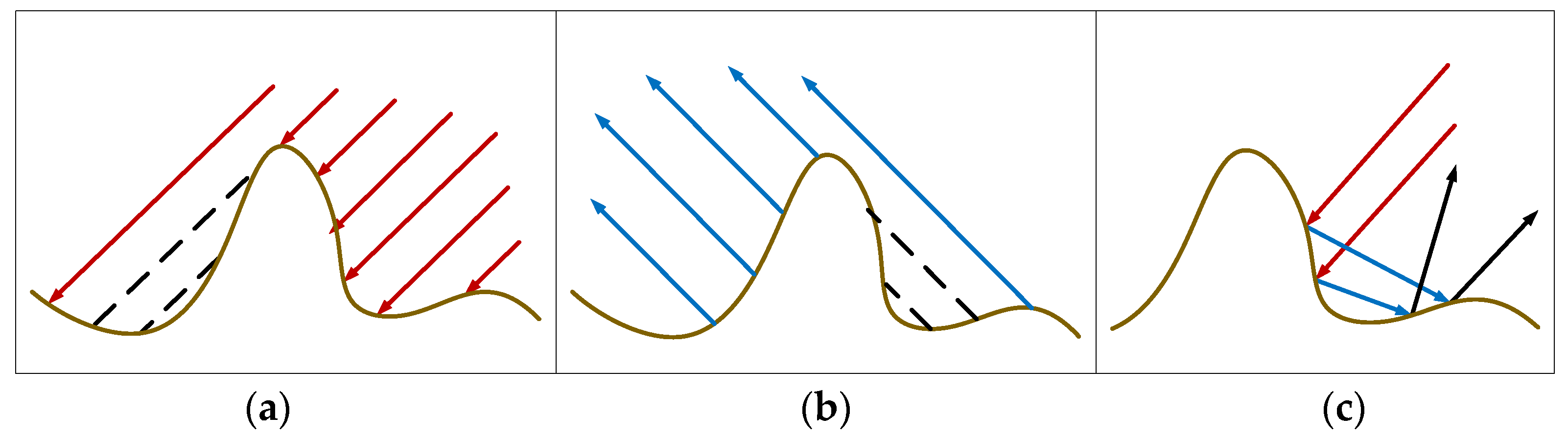
When the object surface reflection occurs, due to the existence of rough surface undulations, not all microfacets can complete the reflection. As shown in
Figure 2a, part of the incident light was blocked and failed to reach the surface element; this phenomenon is called the shadowing effect. As shown in
Figure 2b, part of the reflected light that was blocked failed to reach the observation point; this phenomenon is called the masking effect. There are also multiple reflections of light between microfacets, as shown in
Figure 2c, which may be the source of part of the diffuse light.
In order to mitigate the effects of masking and shading effects of light rays between surface microfacets, a geometric attenuation factor (GAF) is introduced. In this paper, we use the geometric attenuation factor
correction model of the random surface microfacets theory [
33] to calculate the value of the proportion of light that can be reflected from the
direction to the
direction without being shaded.
The light in the two different media on the critical surface will not be all reflected but will be part of the refraction; this is the proportion of the reflection in line with the Fresnel Equations .
Using the Torrance–Sparrow model [
34,
35], based on the microfacet element theory, which describes the reflection properties of light on rough surfaces, the behavior of light on the surface of real objects can be predicted and simulated more accurately than other models. In this paper, this model is used to model the bidirectional reflection distribution function of high light by combining the three functions mentioned above:
wherein
is the macroscopic surface normal,
is the microfacet normal,
is the angle between the incident light and the macroscopic surface normal,
is the angle between the reflected light and the macroscopic surface normal, and
represents the scattering intensity. This represents a well-established modeling framework, as evidenced by previous studies that have employed this approach with the microfacet tangent plane approximation theory. Through this methodology, scholars have derived analytical expressions quantifying the contributions of both specular and diffuse reflection components from sea surfaces, ultimately establishing a numerical model for oil film reflectance characterization on rough marine surfaces [
36].
4. Results and Analyses
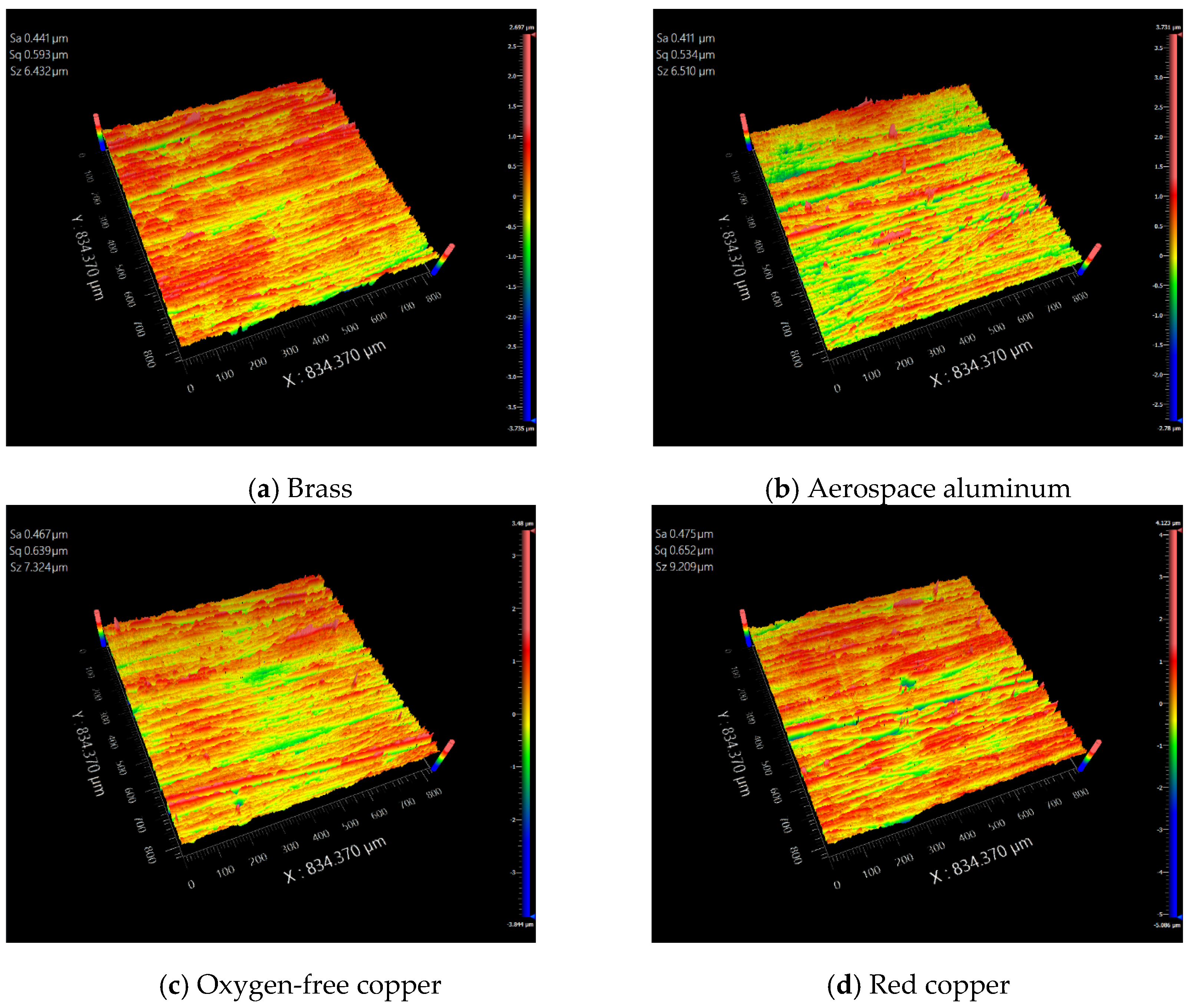
Before studying the white-light BRDF and scattering intensity of the four metal samples selected in this paper, the surface roughness of the four metal samples needed to be examined in order to determine the subsequent experiments to be conducted under the condition that the surface roughness is roughly the same, and the results shown in
Figure 4 were obtained after measuring the samples using the white-light interferometer.
The surface roughness data of the samples selected in this paper are displayed in
Figure 4. In this figure, ‘Sa’ is the arithmetic mean height, indicating the arithmetic mean height of the surface, i.e., the average of the absolute values of the heights of all the points on the surface; ‘Sq’ is the root-mean-square height, indicating the root-mean-square height of the surface, i.e., the square root of the average of the squares of the heights of all the points on the surface; and ‘Sz’ is the maximum height, indicating the maximum difference in the heights of the surface, i.e., the vertical distance between the highest point on the surface and the vertical distance between the highest and lowest points on the surface. In general, ‘Sa’ is used to reflect the average roughness of the surface; the larger the value, the rougher the surface. The average surface roughness of the brass samples is 0.441 μm, the average surface roughness of the aerospace aluminum samples is 0.411 μm, the average surface roughness of the oxygen-free copper samples is 0.467 μm, the average surface roughness of the violet copper samples is 0.475 μm, and the surface roughness data of the four samples tested have an error in the range of 0.050 μm.
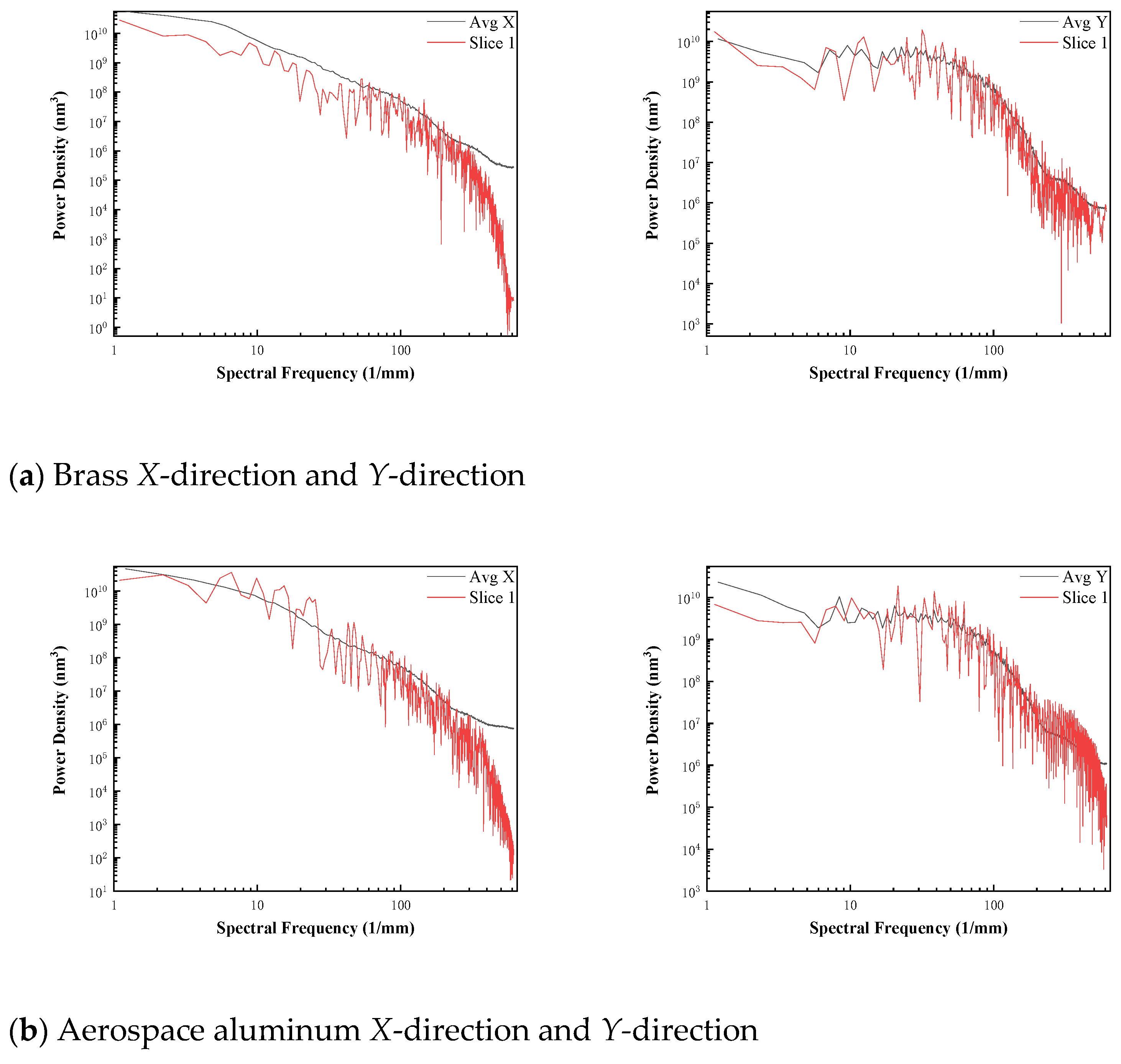
The power spectral density data for the four materials selected for this paper are shown in
Figure 5, which demonstrates the power spectral density in the
X-directions and
Y-directions of the test surfaces of the four materials.
White light scattering occurs when it strikes the surface of a material, and the scattering intensity is affected by the angle of incidence, scattering angle, and azimuth angle. The change in the angle of incidence affects the path length and depth of the interaction between the beam and the material, thus affecting the scattering intensity.
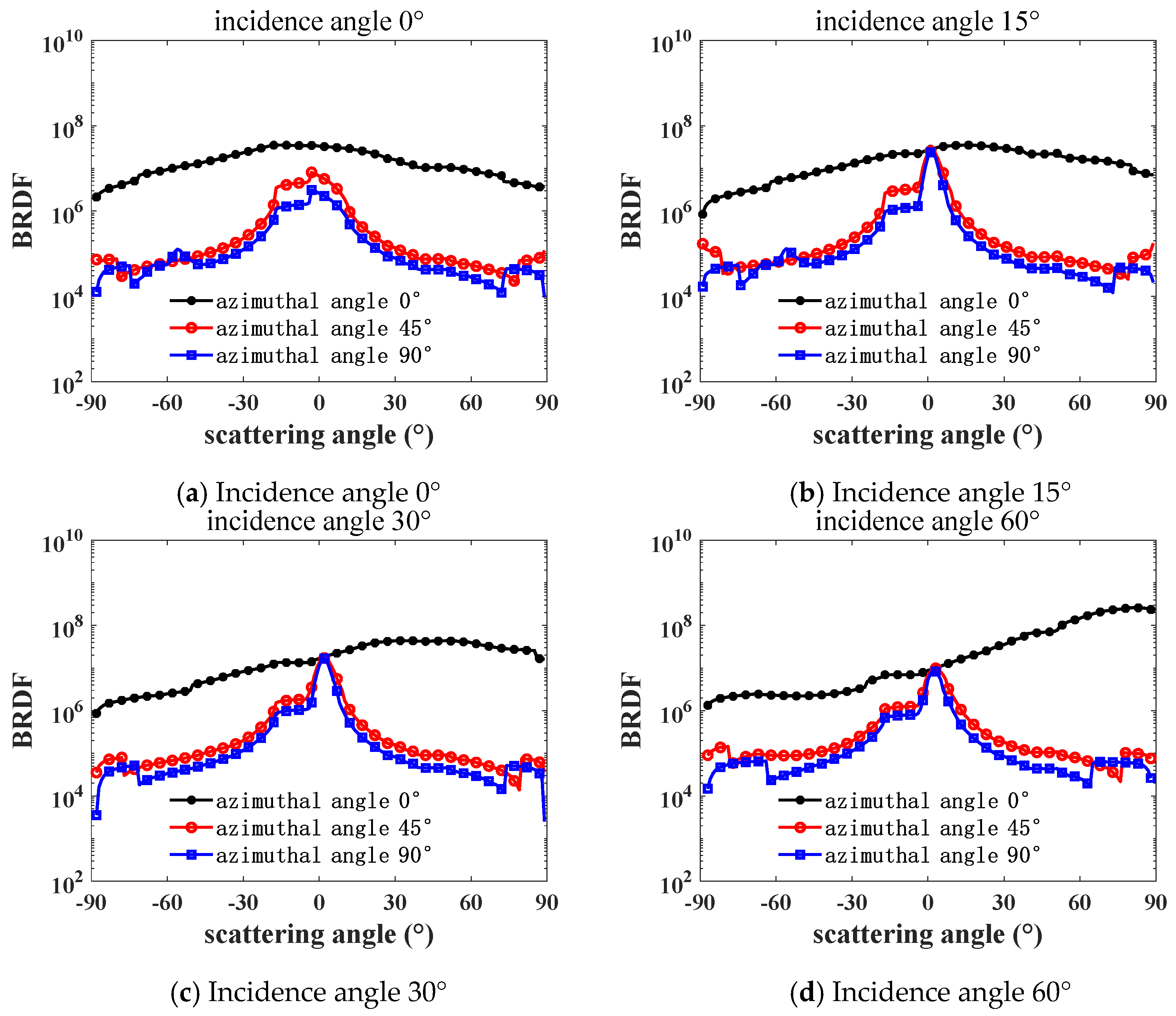
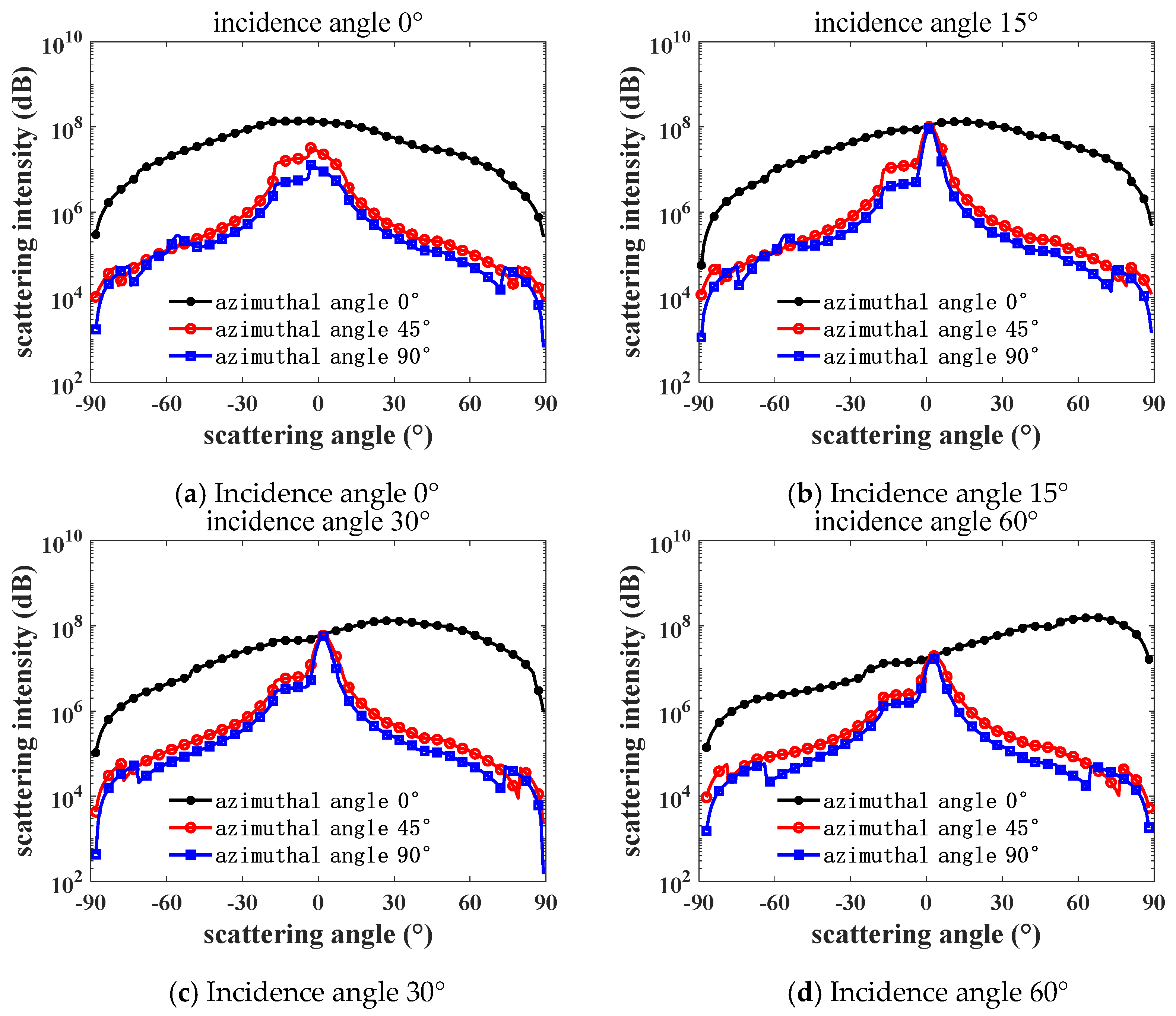
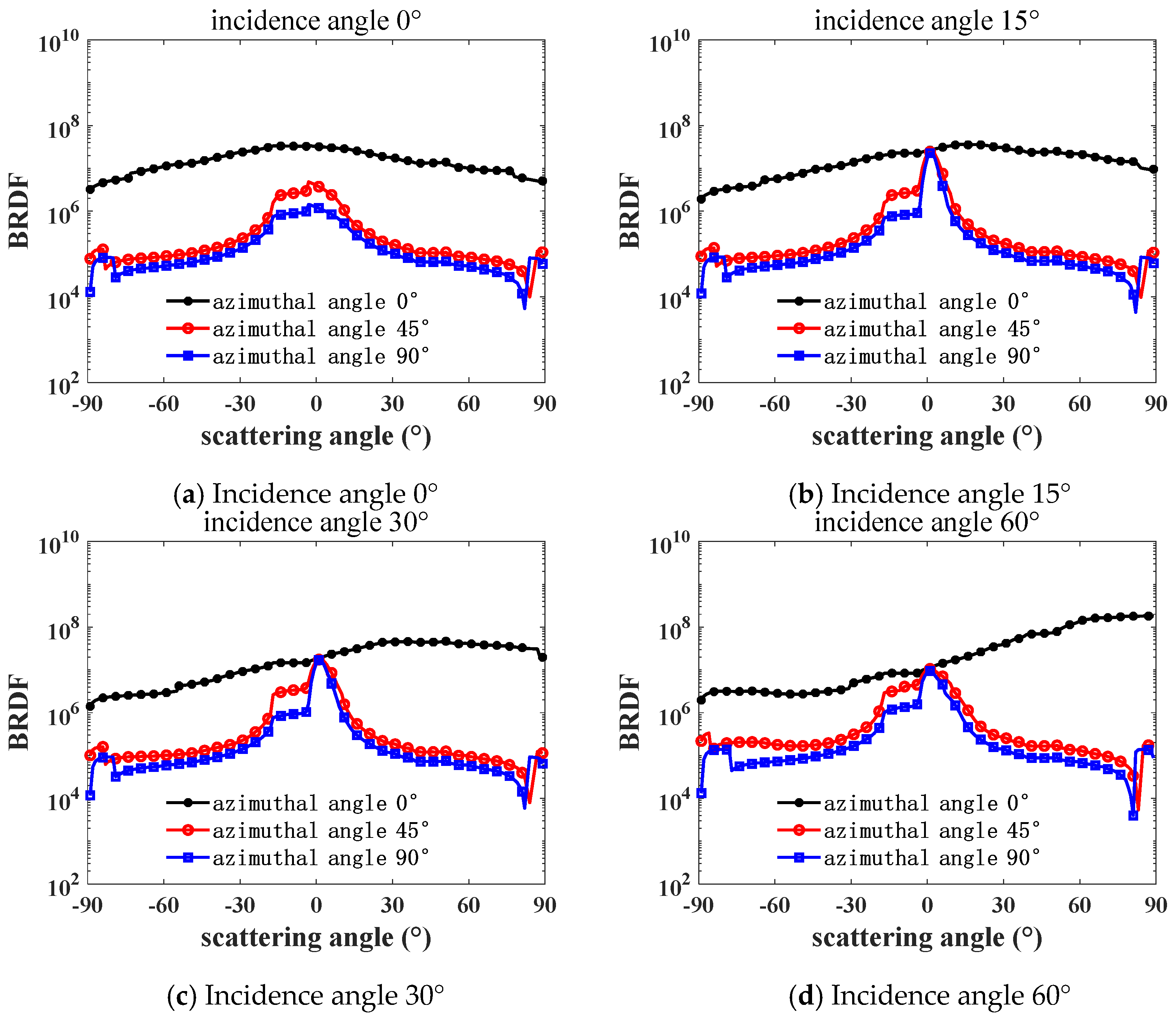
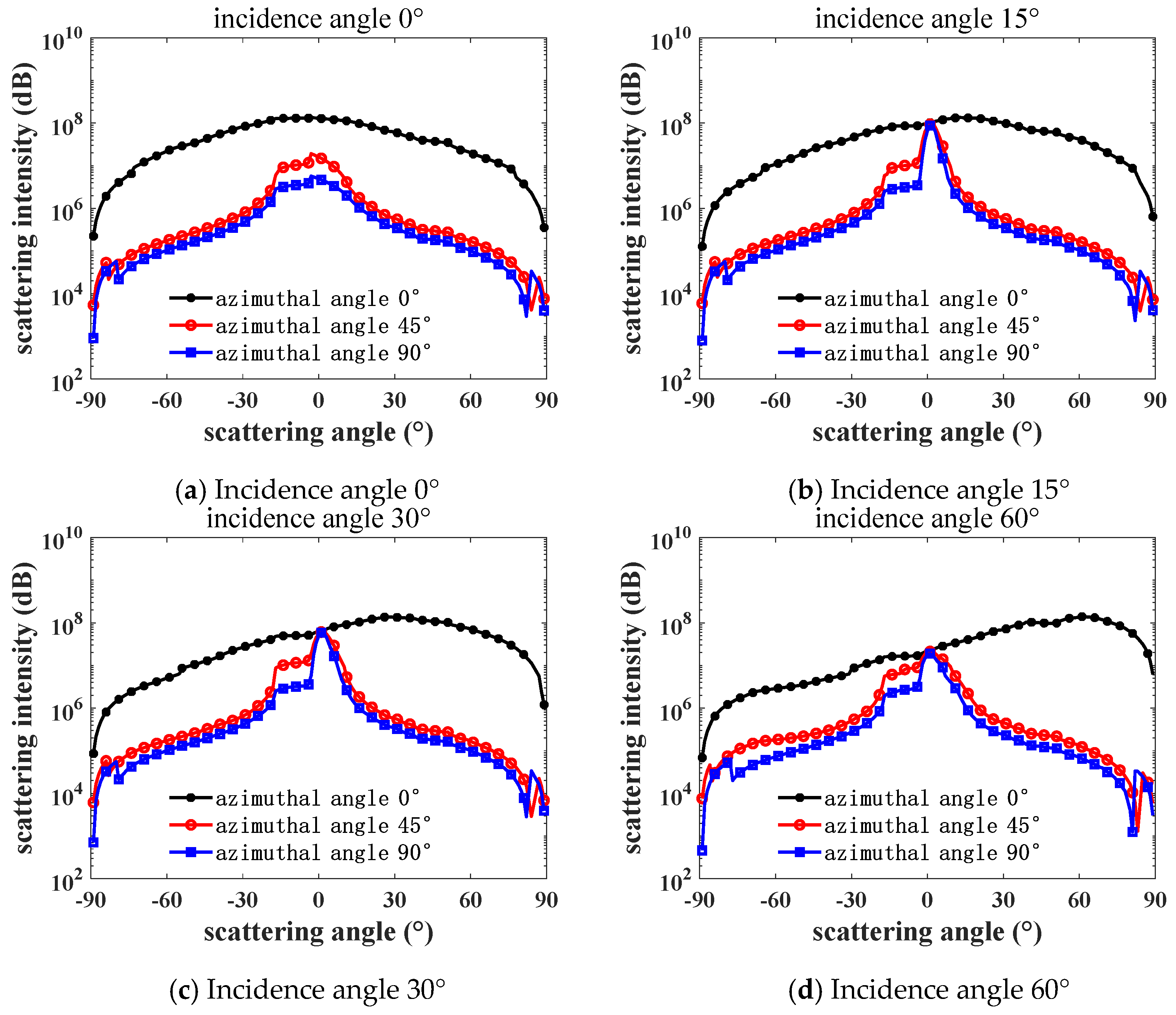
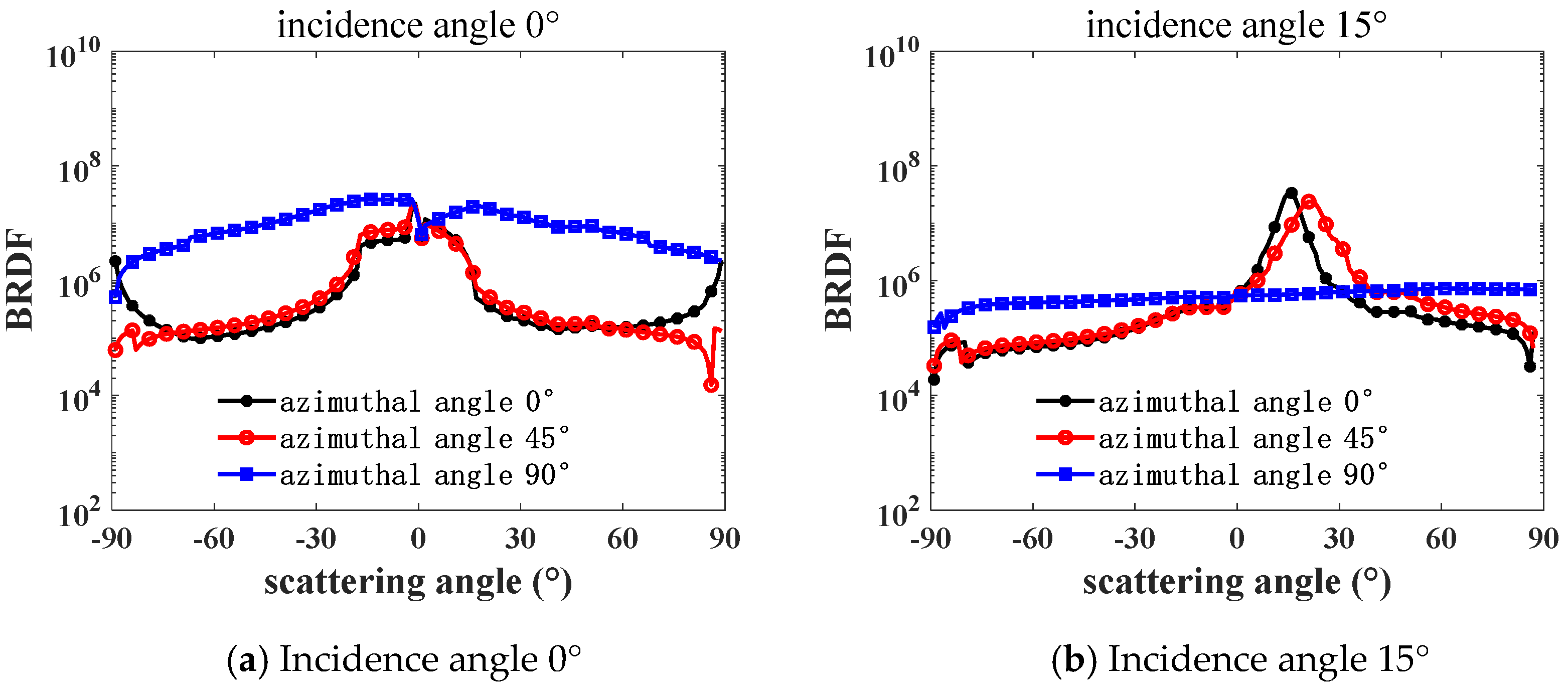
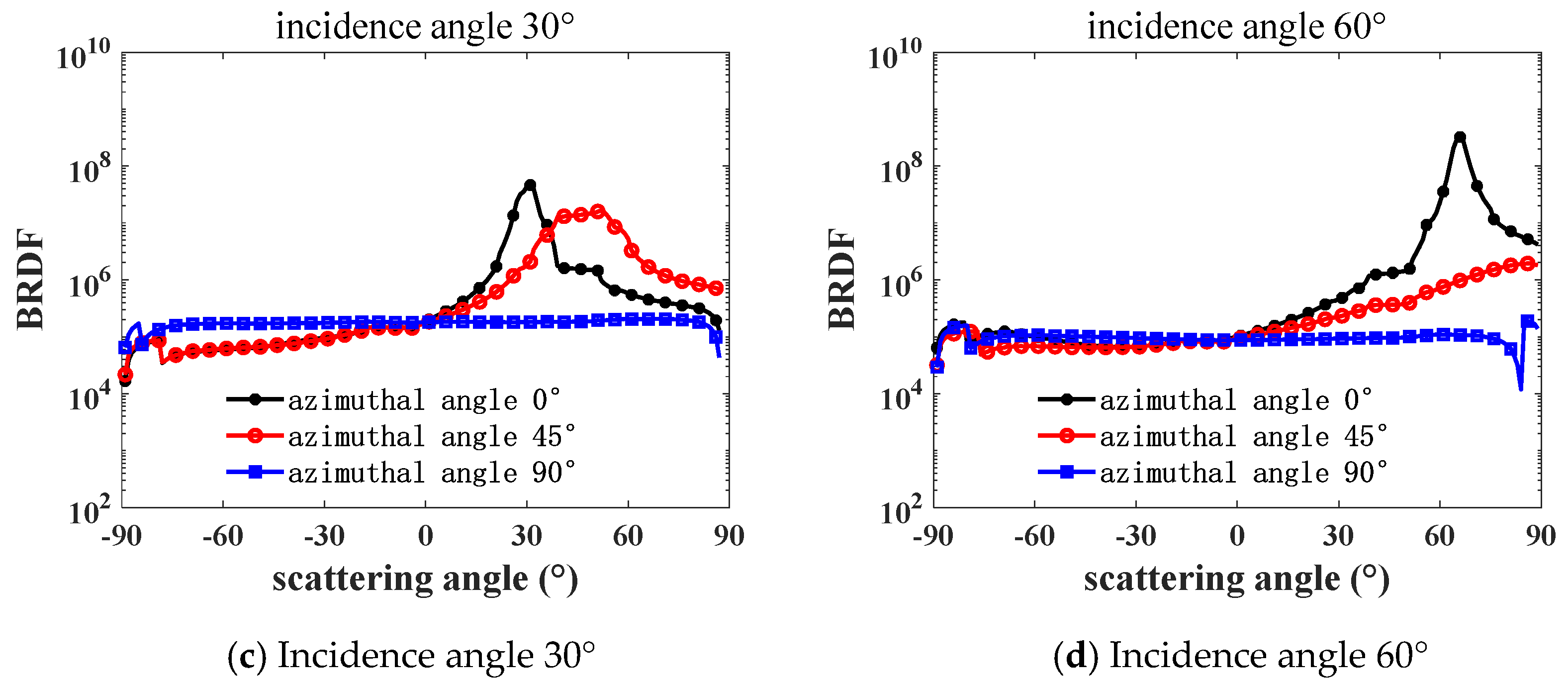
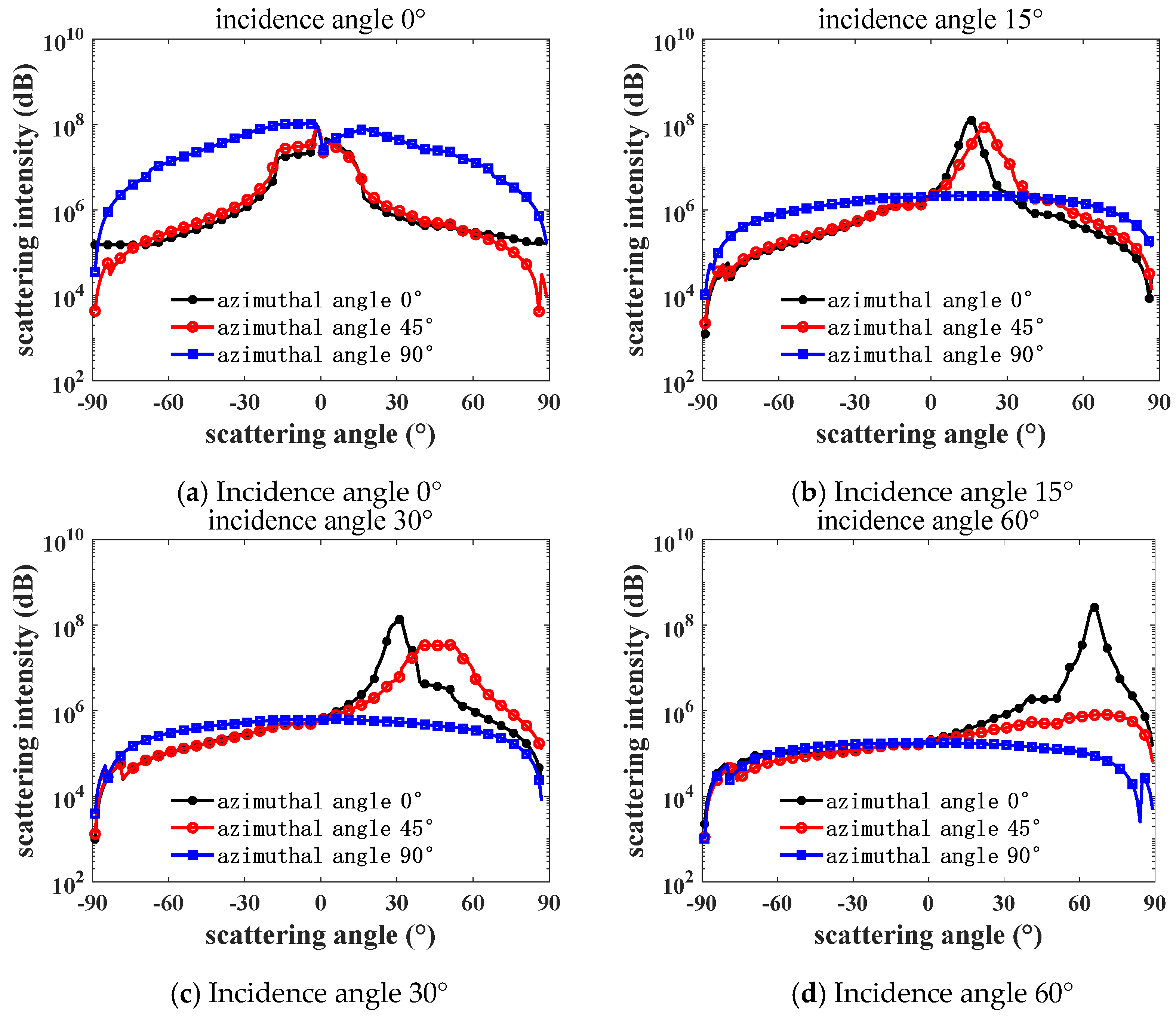
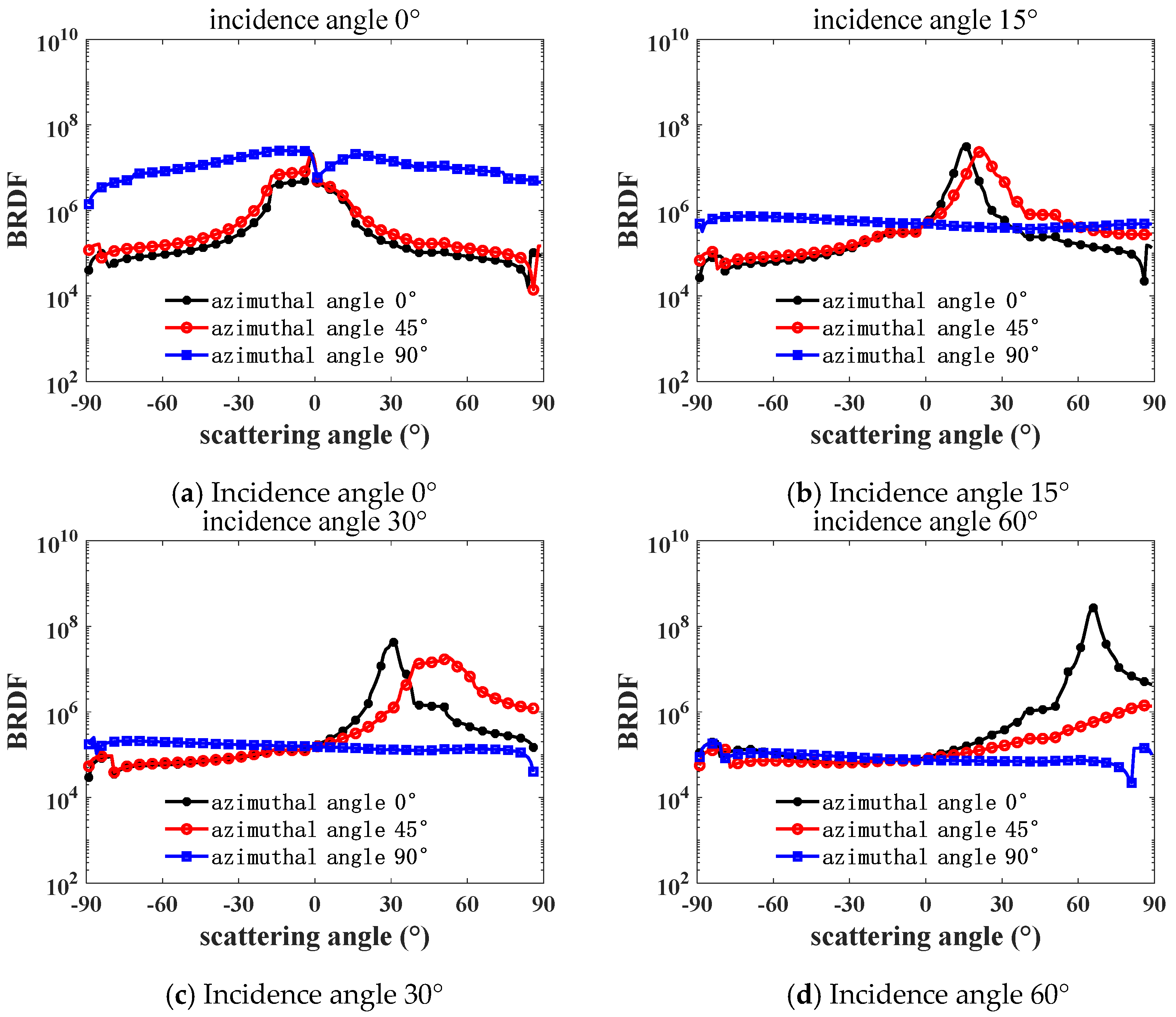
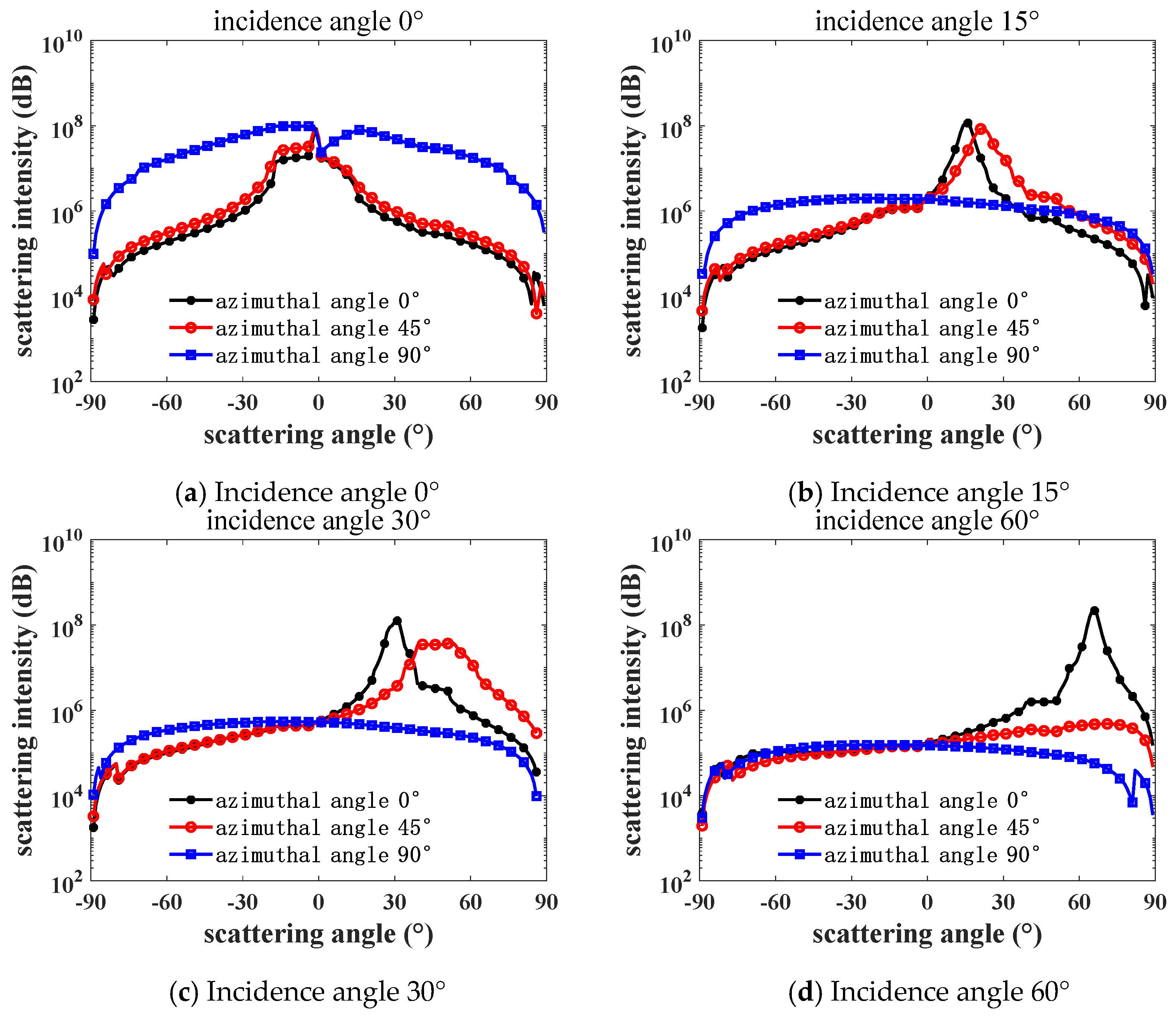
Figure 6 and
Figure 7 show the variation curves of the white-light BRDF and scattering intensity with the scattering angle for brass at different incidence and azimuth angles. The BRDF shows how bright the surface is viewed along the scattering direction, and the scattering intensity means the total power of the scattered light along the scattering direction. It can be seen that surface is brightest around the mirroring direction, and it is brighter while the incidence angle is larger. However, the peak value of the scattering intensity has a minimum value at an incidence angle between 30° and 60°.
Comparing and analyzing
Figure 6 and
Figure 7, in the direction of the incidence angle
= 0 and scattering angle
= 0, the differences in the BRDF and scattering intensity at different azimuth angles in the direction of incidence angle and scattering angle are obvious, and it can be obtained that the selected brass surface is anisotropic. When the azimuth angle
= 0°, the BRDF and scattering intensities show a tendency of the forward scattering gradually exceeding the backward scattering with the increase in the incidence angle, especially in the direction of the specular reflection of forward scattering, i.e., when
≈
, the BRDF and scattering intensities reach the peak. This phenomenon indicates that the brass surface has significant specular reflection properties and good flatness.
In
Figure 6, the forward scattering BRDF values are positively correlated with the incidence angle in the range of the scattering angle
> 75°, and the closer the scattering angle is to 90°, the more obvious it is that the BRDF value is greater than the scattering intensity value. In
Figure 6, the BRDF and scattering intensity are compared at a large scattering angle
= ±83° when the azimuth angle
= 90° and the incident angle
≠ 0°. Both the forward and backward scattering intensities decrease with increasing incidence angle, which is due to the fact that at larger incidence angles, the light rays may undergo more internal reflections and absorptions from the surface, and some of the light rays are either completely absorbed or lose most of their energy after multiple reflections, resulting in a decrease in the scattering intensity.
Therefore, when the scattered light is perpendicular to the brass surface and the azimuth angle is 0°, the forward scattering has the strongest scattering intensity in the specular reflection direction.
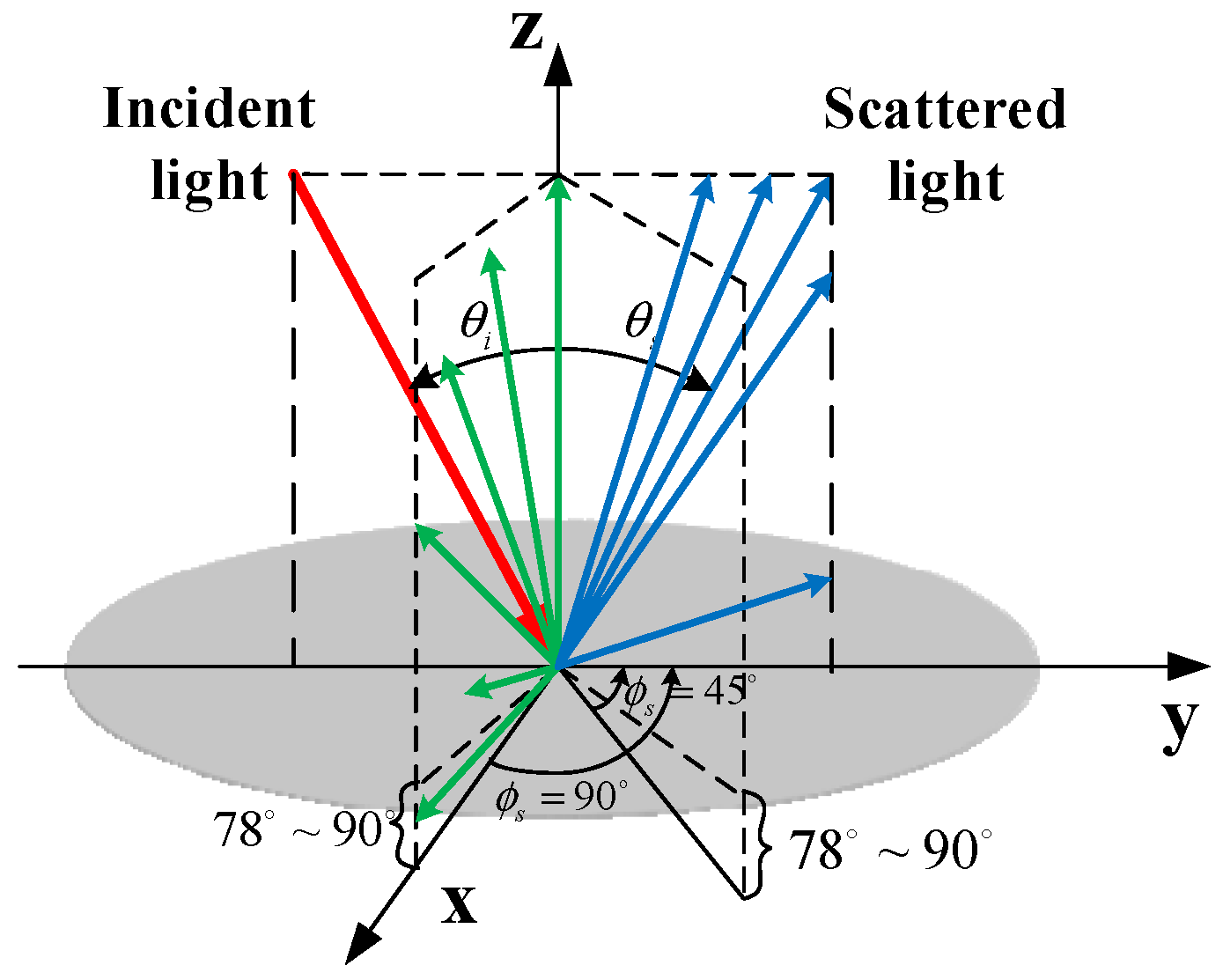
Figure 8 shows a schematic diagram of white light scattering on the brass surface, and combined with the scattering intensity curve analyzed in
Figure 7, when the azimuth angle
≠ 0°, the scattering angle has strong scattering at around 0°. By analyzing the BRDF and surface roughness, the brass surface roughness is low, exhibiting specular high-light and directional range reflections.
Figure 9 and
Figure 10 show the variation curves of the white-light BRDF and scattering intensity with the scattering angle for aerospace aluminum at different incidence and azimuth angles.
Comparing and analyzing
Figure 9 and
Figure 10, when the azimuthal angle is
≠ 0°, the BRDF and scattering intensity are the largest in the specular reflection direction of forward scattering (i.e., at
≈
). When the azimuth angle
≠ 0°, the scattering angle is within 78–90°, and the BRDF and scattering intensity increase and then decrease with the increasing angle, with fluctuations in a small range. Compared with the brass surface, the BRDF and scattering intensity of the aerospace aluminum surface are much larger than those of the brass surface in the range of large scattering angles, i.e., it has better specular high-light performance than brass in the range of large scattering angles, and its directional strong scattering has a smaller range, as shown in
Figure 11. Analyzing the surface roughness of aerospace aluminum, although it has a high surface roughness, its excellent high-light properties at large scattering angles make it widely used in aerospace devices such as aircraft, rockets, and satellites, where its high reflectivity and optical properties improve the performance of the device in extreme environments.
Figure 12 and
Figure 13 show the variation curves of the white-light BRDF and scattering intensity with the scattering angle for oxygen-free copper at different incidence and azimuth angles.
Comparing and analyzing
Figure 12 and
Figure 13, when the incident angle
= 0°, the scattering intensity observed at azimuth angles of 0° and 45° decreases with the increase in the scattering angle, with the peak at
= 0°, i.e., the strongest scattering of oxygen-free copper in the direction perpendicular to the surface of the material, while the scattering intensity observed at an azimuth angle of 90° is larger than that at other azimuths and is the smallest at a scattering angle of 0° (i.e., perpendicular to the surface of the material), which may be due to the uneven material surface at the measurement point. As with brass and aerospace aluminum surfaces, the BRDF values and scattering intensities at different azimuths are not the same, so it can be seen that the measured oxygen-free copper surface is also anisotropic.
When ≠ 0° and = 0°, the oxygen-free copper surface exhibits stronger forward scattering than backward scattering, and the BRDF and scattering intensity reaches the peak in the forward scattering direction ≈ , which exhibits a very obvious high scattering intensity specular reflection. In contrast, the BRDF and scattering intensity of the brass and aerospace aluminum surfaces gradually increase with the increase in the scattering angle in the forward scattering direction, peak in the specular reflection direction, and then decrease with the further increase in the scattering angle; whereas, except for the high scattering intensity of the oxygen-free copper surfaces in the forward scattering ≈ , the scattering intensities of the oxygen-free copper surfaces in other scattering angles are obviously lower than those of the brass and aerospace aluminum surfaces, which suggests that the oxygen-free copper surface has a lower surface scattering intensity. In addition, the highest forward scattering intensity is observed at an azimuth angle of 0°, and the BRDF and scattering intensity in the specular reflection direction increase significantly with the increase in the incidence angle, i.e., the larger the incidence angle is, the oxygen-free copper surfaces have significantly more high-light characteristics in the specular reflection direction.
When ≠ 0° and = 45°, forward scattering is larger than backward scattering. The peaks of the BRDF and scattering intensities occur in directions larger than the specular reflection angle.
When
≠ 0° and
= 90°, the variation in the BRDF and scattering intensity with the scattering angle is flatter than that on other azimuthal angles, i.e., the scattering light distribution of the material is more homogeneous when viewed at a 90° azimuthal angle. When the incident angle
≥ 30°, the scattering intensity at a 90° azimuth angle is smaller in forward scattering than at other azimuth angles. When 0° <
< 45°, the BRDF and the scattering intensity change more gently at smaller scattering angles and decrease with the increase in the scattering angle at larger scattering angles. When 45° <
< 90°, the scattering angle is in the range of 84–90°, the scattering intensity increases, and the BRDF becomes significantly larger, i.e., when observed at an azimuthal angle of 90°, the surface of oxygen-free copper appears to be highlighted in this range. Unlike brass and aerospace aluminum surfaces, the angle of incidence has a greater effect on the scattering characteristics of oxygen-free copper materials.
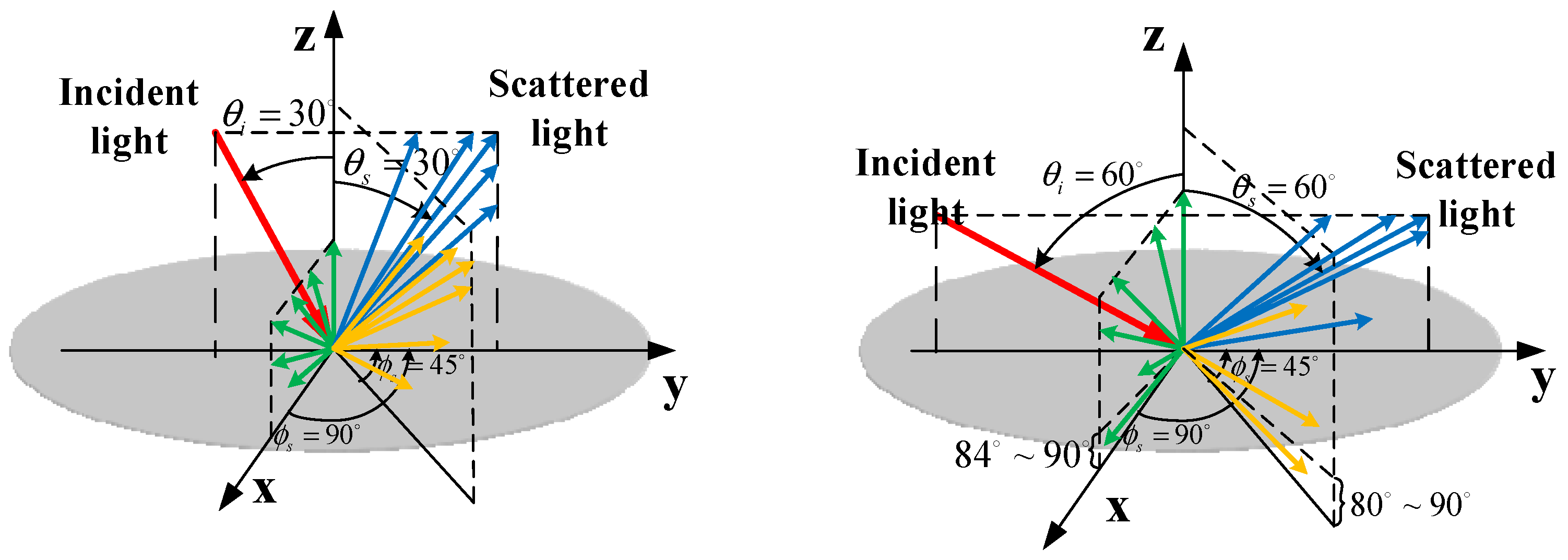
Figure 14 illustrates the surface scattering of the oxygen-free copper surface at
= 30° and
= 60°.
Figure 15 and
Figure 16 show the variation curves of the white-light BRDF and scattering intensity with the scattering angle for red copper at different incidence and azimuth angles.
Comparing and analyzing
Figure 15 and
Figure 16, the BRDF and scattering intensity of the red copper surface with the incidence angle, scattering angle, azimuthal change rule, and the oxygen-free copper surface are very similar; only the value of the BRDF and scattering intensity is slightly lower than that of the oxygen-free copper surface, which indicates that it has a lower surface scattering intensity, which can be obviously reflected from the values of the two surfaces’ roughness, i.e., the roughness of the red copper surface is higher than the roughness of the oxygen-free copper surface, which makes it more suitable for some applications with high requirements on optical surfaces. This is also evident from the roughness of both surfaces, which indicates that the red copper surface has a higher average roughness than the oxygen-free copper surface. This makes the red copper surface more suitable for applications that have higher requirements for optical surfaces.
A comparison of the surface roughness of the four typical metal materials and the variation curves of the white-light BRDF and the scattering intensity with the scattering angle at different incidence and azimuth angles reveals that, for materials with similar surface roughness values, the oxygen-free copper and red copper surfaces exhibit lower surface scattering intensities and clearer specular reflectance characteristics compared to brass and aerospace aluminum surfaces, which display a pronounced range of high scattering intensities and specular reflections. The specific properties are influenced by the material preparation and treatment process. Furthermore, the incidence angle exerts a more pronounced influence on the scattering characteristics of the oxygen-free copper and red copper surfaces, particularly when the incidence angle exceeds 45°. In such instances, the BRDF and scattering intensity exhibit a pronounced increase at larger scattering angles.
Through the experimental results of this paper, it can be concluded that according to the aforementioned laws, in roughly the same roughness conditions, the four materials according to their own characteristics of the reflection of white light have different performances.
The brass surface can effectively inhibit specular highlights and directional range reflections; the aerospace aluminum surface in the large scattering angle has excellent high-light reflection characteristics; and the red copper surface roughness is slightly higher than the surface roughness of the oxygen-free copper, so the red copper is more suitable for applications in environments with higher requirements for optical surfaces. Under the premise that the surface roughness is roughly the same, the brass and aerospace aluminum surfaces show obvious high scattering intensities and specular reflection ranges, while the oxygen-free copper and red copper surfaces have lower surface scattering intensities and clearer specular reflection characteristics.
Based on the above data, the following analysis is presented.
The brass surface has obvious specular reflection characteristics, manifested in the direction perpendicular to the reflective surface and an azimuth angle of 0° when forward scattering in the direction of the specular reflection has the strongest scattering. At the same time, at a scattering angle of 50–75°, it also has strong scattering, which is appropriate for applications that require specular highlights and directional range reflections.
Aerospace aluminum surfaces also have the strongest scattering in the forward scattering specular reflection direction perpendicular to the direction of the reflecting surface at an azimuth angle of 0° and have better specular high-light performance over a wide range of scattering angles. Aerospace aluminum is suitable for applications that require strong scattering over a wide range of scattering angles.
The oxygen-free copper and red copper surfaces have lower surface scattering strengths and clearer specular reflection properties than the first two materials. The incident angle has a larger effect on its scattering properties, which are significantly enhanced at large scattering angles. They are suitable for applications that require more detailed optical surfaces.
As a result, for different types of optical scenarios, these metallic surfaces exhibit their own unique scattering properties at different incidence, azimuthal, and scattering angles. Depending on their properties, suitable metallic surfaces can be selected to meet specific application requirements, such as specular reflection, directional range reflection, or applications requiring less surface scattering intensity. In addition, material preparation and treatment processes also have an impact on these scattering properties, so these factors need to be taken into account to select the most suitable metallic materials for practical applications.