Modulating Mechanisms of Surfactants on Fluid/Fluid/Rock Interfacial Properties for Enhanced Oil Recovery: A Multi-Scale Evaluation from SARA-Based Experiments to Atomistic Simulations

Abstract

Low-Salinity Water Flooding (LSWF) has gained attention for its cost-effectiveness and environmental advantages, yet its underlying mechanisms remain not fully understood. Oil recovery in LSWF is primarily governed by interfacial dynamics and formation wettability. This research investigates the effects of seawater dilution in carbonate reservoirs through laboratory analyses and displacement experiments. Results show that oil recovery efficiency is largely driven by rock–fluid interactions rather than fluid–fluid interactions, with optimal brine concentrations enhancing wettability alteration, boundary flexibility, and mineral leaching. These findings highlight the importance of considering both fluid–rock interactions and mineral reactivity, rather than attributing recovery to a single mechanism. Molecular dynamics simulations further supported the experimental observations. Overall, the study emphasizes that early and well-designed low-salinity injection strategies can maximize LSWF performance. The results elucidate the key interaction mechanisms between surfactants and the various components of heavy oil through atomic-scale precision modeling and dynamic process tracking. These simulations clarify, at the microscopic level, the differences in displacement dynamics and efficiency of organic solvent systems toward different hydrocarbon components.

1. Introduction

Oil field pump technology, as an artificial lift technology, is widely employed in the petroleum industry today [1,2]. Low-Salinity Water Flooding (LSWF) has emerged as a promising enhanced oil recovery (EOR) technique, garnering significant attention for its cost-effectiveness, environmental benefits, and potential to significantly improve hydrocarbon displacement efficiency compared to conventional water flooding. The process involves injecting brine with a carefully optimized salinity and ionic composition into reservoirs, which triggers a complex set of interactions that can mobilize residual oil [3,4].

Despite its demonstrated potential, the widespread application of LSWF, particularly in carbonate reservoirs, is hindered by an incomplete understanding of its fundamental mechanisms. Mechanisms proposed for LSWF in carbonate formations can be categorized into two main groups [5,6,7,8,9,10,11,12]: (I) rock/liquid interactions, encompassing phenomena such as double-layer expansion, pH alterations, PDI interactions, and mineral dissolution [13,14,15,16,17,18]; and (II) fluid/fluid interactions, focusing on dispersion, saline oil interfacial dynamics, permeability, and viscoelasticity [19,20,21,22,23,24,25,26]. While extensive research has been conducted on both rock/liquid and interfacial fluid interactions within the context of LSWF, rock/liquid interactions have been identified as more crucial.

In addition, the surfactant role during the EOR process was limited.

The primary objective of this study is to elucidate the unresolved fundamental mechanisms underlying LSWF, with a specific focus on carbonate reservoirs. Through integrated experimental and molecular dynamics simulation approaches, this research aims to clarify the dominant role of rock–fluid interactions over fluid–fluid interactions in governing wettability alteration and oil recovery efficiency. The study further seeks to identify optimal brine compositions and injection strategies to maximize the effectiveness of LSWF.

2. Materials and Methods

2.1. Materials

Characterizing reservoir rock samples, petroleum, and formation water compositions is fundamental for Low-Salinity Water Flooding (LSWF) applications. The efficiency of LSWF when applied to carbonate strata is determined by factors like subsurface temperature, crude oil attributes, geochemical properties, and the ionic composition of both injected and connate brines. Alterations to any of these variables can produce divergent LSWF responses, ultimately dictating oil recovery outcomes [27,28,29,30].

2.1.1. Crude Oil

The dead crude oil examined in this research was obtained from Dagang Oilfield, (Tianjin, China); having been extracted it was no longer under reservoir pressures. To prepare the oil for analysis, it was first centrifuged and filtered to remove all particulate matter, water, and dispersed particles. Additionally, to ensure the stability of the Low-Salinity Water Flooding (LSWF) process and to prevent reservoir damage due to colloidal instability, the Colloidal Instability Index (CII) for asphaltene precipitation was taken into account. With a Colloidal Instability Index under 0.9, the experimental hydrocarbon fluid poses no risk of asphaltene precipitation during testing. Table S1 shows the physical parameters of crude oil.

2.1.2. Core Sample

The core samples used in this study are 10 cm in length and 3.22 cm in diameter. These samples underwent analysis using powder X-ray Diffraction (p-XRD) (Almelo, The Netherlands) and X-ray Fluorescence (XRF) (Bruker, Karlsruhe, Germany) [31] to determine their mineral composition [32]. Table S2 shows the composition of rock by XRF. The component of the core sample is shown in Table S2.

2.1.3. Brine

Each brine solution was prepared with purified water [33] through the dissolution of analytical-grade salts, specifically NaCl, MgCl₂·6H₂O, CaCl₂·2H₂O, NaHCO₃, MgSO₄, KCl, and Na₂SO₄. The formation brine composition mimicked that of a particular hydrocarbon-bearing formation in India. Seawater (SW) was used as the base brine, and diluted seawater solutions were prepared at various dilution factors (2, 5, and 10 times dilution, denoted as 2 dSW, 5 dSW, and 10 dSW, respectively).

2.2. Methods

2.2.1. Interfacial Tension (IFT)

Interfacial tension (IFT) observations were conducted using a Krüss drop shape analyzer, employing the pendant drop technique. Crude oil droplets were suspended on a J-needle suspended within the brine phase, with the detachment process recorded on video. The final image prior to droplet detachment was utilized for IFT determination. To ensure measurement accuracy, the instrument underwent prior calibration, and every interfacial tension measurement reflects the mean of three replicate determinations. The tests were conducted at 90 °C under ambient pressure.

2.2.2. Rheological Properties at the Petroleum–Brine Boundary

Measuring surface interactions allows evaluation of the viscoelastic behavior of the oil–water boundary. Increased interfacial viscoelasticity facilitates the formation of cohesive oil clusters while minimizing droplet breakup [6]. Rheological measurements were conducted using an Anton Paar MCR 102 viscometer fitted with a biconical interfacial fixture (68.28 mm diameter, 5° cone angle) [7]. During testing, controlled shear deformation was applied at the constant-area interface. The methodology involved adding 110 mL of brine to the cup, with the rheometer’s normal force transducer automatically detecting the interface. Crude oil (110 mL) was then carefully layered onto the bob, flowing outward to minimize interfacial disturbance. A segmented stainless-steel cap prevented solvent evaporation, while a Peltier plate maintained the temperature. Strain amplitude sweeps established the linear viscoelastic region (LVR) [8]. Subsequent 12 h dynamic tests at 0.3 Hz frequency (data collected at 15 min intervals) tracked molecular transport from solution to interface, with equilibrium values reported. All comparative assessments of low-salinity (LSW) versus high-salinity water (HSW) were performed within the LVR. Measurements at 30 °C and 70 °C evaluated temperature effects, though instrumentation limitations precluded testing at 90 °C.

2.2.3. Zeta Potential Measurements

Zeta potential determinations employed electrophoretic methodology utilizing an Anton Paar Lite-sizer 500 [9]. For rock/brine interface analysis, suspensions were formulated with a 0.01% weight concentration, sonicated for 3 min, and allowed to stabilize for 12 h prior to supernatant measurement after decantation. Oil/brine interface measurements required sonicating 500 microliters of crude petroleum with 100 milliliters of saline solution before equilibration and analysis. All measurements constituted triplicate trials of 100 runs each, with averaged values reported [10]. Experiments were conducted at both 30 °C and 70 °C, though equipment constraints prevented measurements at 90 °C. Complementary pH measurements were performed at the interfaces between rock/brine and oil/brine at 30 °C to contextualize interfacial reactions [11]. High-temperature zeta potential samples excluded pH analysis due to irreversible alterations upon cooling to 30 °C, which would complicate the interpretation of results.

2.2.4. Contact Angle (CA) Measurement

Carbonate rock samples were polished and cleaned via Soxhlet extraction to ensure a uniform surface [12]. Initial wettability (θi) was established by saturating the samples with formation water at 90 °C for one week. The samples were then aged in crude oil at 90 °C for four weeks to achieve an oil-wet state (θ₀ ≈ 149°). To assess wettability alteration, aged samples were immersed in various brines at 90 °C for seven days, after which the final contact angle (θf) was measured using a drop shape analyzer at 90 °C after a 60 min stabilization period. Measurements were performed in duplicates to ensure reproducibility [13]. The Wettability Alteration Index (WAI) was calculated as WAI = (θ₀ − θf)/(θ₀ − θi) to quantify the shift towards water-wetness.

2.2.5. Coreflooding

Coreflooding experiments were conducted under reservoir conditions (90 °C, 1000 psi confining pressure) using a Teledyne Isco pump, with produced fluids gathered in a collection vessel [14]. The core preparation procedure included drying at 120 °C, vacuum saturation with formation water to determine porosity, and establishment of irreducible water saturation (Swir) by oil flooding. Cores were then aged in crude oil for four weeks at 90 °C to restore reservoir wettability. Secondary waterflooding was initiated by injecting brine at 0.3 mL/min. To mitigate capillary end effects, the flow rate was increased stepwise after water breakthrough.

2.2.6. Simulation Parameters and Calculation Processes

The simulations were conducted using Materials Studio software 2022, with model construction and initialization performed by the Amorphous Cell module and molecular dynamics executed via the Discover module. The COMPASS II force field was employed, where the system’s total energy consists of bonded interactions (including bond stretching, angle bending, dihedral torsion, out-of-plane vibrations, and cross-coupling terms dependent on intramolecular atomic geometries) and non-bonded interactions (van der Waals forces modeled via Lennard–Jones potential and electrostatic energies governed by Coulomb’s law). This framework effectively simulates the diffusion behavior of four heavy oil fractions (saturates, aromatics, resins, asphaltenes) in a surfactant-based organic solvent system (Figure 1).

3. Results and Discussion

3.1. IFT

The interfacial tension (IFT) of brine/oil systems exhibits inherent complexity, as models developed for surfactant-enhanced systems fail to fully explain oil/brine behavior due to fundamental mechanistic differences. In surfactant-mediated systems, tension-reducing agents originate from the aqueous phase, whereas in native petroleum/brine environments, amphiphilic constituents (mainly asphaltenes) originate in the crude—an inherently complex blend [17]. Asphaltenes function as natural surfactants because their molecular structure contains both hydrophilic and hydrophobic moieties [18]; hydrophilic groups orient toward aqueous phases while hydrophobic segments align with organic phases, facilitating spontaneous adsorption at oil/brine interfaces and consequent IFT reduction. Figure 2 demonstrates monotonic IFT–salinity dependence: tension decreases from seawater (SW) to 5× diluted SW (5 dSW). This characteristic trend—documented in prior studies—stems from IFT’s multivariate dependence on salt concentration, acidity index, petroleum constituents, thermal conditions, and compressive force. The observed behavior is explicable through interactions between dissolved salt concentrations and indigenous surfactant (asphaltene) concentrations within crude oil.

In zone A, transitioning from low- to high-salinity water increases the activity coefficient of salt ions, prompting their migration to the lactic acid phase. This shift, especially when ions are present in the saltwater (due to the stronger electrostatic influence on polar materials compared to monovalent cations), amplifies the solubility in both the aqueous and oil phases. Consequently, the salt concentration at the negative surface increases, leading to a reduction in the interfacial tension (IFT) value. Upon reaching higher salinity levels in zone B, incorporating positive ions into the solution aids in dissolving asphaltene components in water, promoting aggregation. This process causes asphaltene molecules to revert to the main oleic acid phase, markedly reducing their accumulation at the liquid–liquid boundary and leading to salt deposition. As a consequence, the surface concentration of asphaltenes decreases and the IFT value increases. The balance between these two opposing phenomena, detailed in zones A and B, defines the optimal salinity level. In the context of synthetic seawater (SW) dilution, the ideal salt concentration is found to be twice that of standard seawater (5 dSW).

3.2. Interfacial Rheology

The nature of the interfacial modulus strongly affects the formation progression of the heavy oil recovery process, where the creation of large oil exchanges yields higher profits compared to smaller, ruptured oil exchanges. The construction of petroleum dams depends heavily on the elastic measurement at the interface, where elevated interfacial elasticity enhances the likelihood of fracture propagation and, consequently, oilfield formation [19]. As interfacial elasticity rises, so does the critical number of capillaries destroyed by the liquid. Under Low-Salinity Water Flooding (LSWF) conditions, decreasing ionic strength leads to increased interfacial elasticity, although this trend is not consistently significant and exhibits non-monotonic behavior. Figure 3 illustrates that the tendency of the interfacial modulus is not uniform. The highest dilution, represented by 5 dSW, corresponds with the IFT results, indicating that the diluted properties of the saltwater interface act as a driving force at the oil/saltwater interface, promoting the accumulation and interaction with salt ions. Over time, these interactions significantly increase the interfacial elastic modulus. Under elevated salinity conditions, the oil–brine phase boundary is primarily governed by asphaltene constituents and ionic species, forming a compact and complex nanostructure [20], and this interaction results in an elastic surface. Conversely, at low salinity, this boundary is primarily occupied by asphalt molecules, and steric hindrance caused by the asphaltene molecules themselves leads to an increase in asphaltene concentration at the boundary, preventing the formation of a network between asphaltene molecules and salt ions and resulting in the unstable and slow formation of a unique network structure, ultimately yielding an interface lacking deformation and flexibility.

These findings reveal that both interfacial tension (IFT) and interfacial elasticity reach their optimal conditions at a dilution of twice the standard seawater (5 dSW), where 5 dSW exhibits the lowest IFT and highest elastic modulus. These characteristics are crucial for forming large oil accumulations by preventing premature coalescence. The low IFT facilitates the formation of small, highly flexible interfaces capable of regaining their shape, contributing significantly to the dynamics of oil recovery [24].

3.3. Zeta Potential

Interfacial dynamics between mineral/brine and hydrocarbon/saline interfaces play a crucial role in determining the wettability of petroleum/brine/mineral systems, where the surface integrity of both oil and solid substrates is strongly governed by these phenomena. Consequently, a thicker water film forms, enhancing water wetting properties. Conversely, when the interaction dynamics are reversed, a suction force is created at the interface, breaking the water film barrier and allowing the moisture from hydrocarbons to migrate onto mineral substrate. Figure 4 illustrates the impact of varying salt concentrations on the zeta potential (G) at these interfaces. As demonstrated in Figure 4, the zeta potential for both solid/brine and oil/brine interfaces becomes more negative with decreasing saltwater salinity and the oil/brine interface attains a lower zeta potential. A decrease in pH generally leads to a reduction in zeta potential, affected by diverse molecular transformations, notably hydrogen ion exchange reactions, and the effect of solution pH on the surface charge in saline water.

At the interface between oil and saltwater, the potential, denoted as g, exhibits a negative polarity across the entire range of salinity, becoming increasingly reduced upon dilution. The key interfacial charge at the oil–aqueous solution interface depends on various determinants, including the amounts of single-charged and double-charged ions, crude oil makeup, acid–base balance, and asphaltene content [34]. The acidic constituents of crude oil undergo protonation reactions with divalent ions, resulting in the formation of stable complexes. The interplay between formation mechanisms, interfacial stability, and charge strength at the oil–saltwater interface is predominantly governed by high-salinity conditions, where competition between acidic and basic components, along with ionic complexes in crude oil, shapes the charge distribution. Conversely, under conditions of low salinity, decreased concentrations of acidic component ions lead to enhanced dissociation, resulting in elevated pH values and subsequent negativity in the g potential. As illustrated in Figure 4, the dissociation of acidic components can be considered a primary reaction dictating the limiting charge at the oil–saltwater interface.

3.4. Contact Angle

The contact angle serves as a fundamental method for assessing changes in rock surface wettability, directly gauging the affinity of the injected liquid. Figure 5 illustrates the maximum WAI corresponding to a salt content of 10 times diluted seawater (10 dSW). It suggests that as the solution’s pH value increases, the maximum moisture change is observed during the 10 dSW dilution stage, indicative of the humidity change mechanism in carbonate rock [35]. The rise in the solution’s pH value is associated with the well-known mechanism of calcium dissolution [36]. During the dilution process with synthetic seawater (SW), the ion concentration gradually decreases, and the fundamental equilibrium of high-salt-concentration fresh water (FW) is restored upon injection into the formation. This equilibrium restoration prompts the dissolution of rock ions into the injected brine, leading to a decrease in rock humidity, along with the release of adsorbed components. This typically elevates the OH concentration in the diluted solution, consequently raising the solution’s pH value. In particularly, at the 10 dSW salinity level, the calcium/pH resolution is not primarily influenced by low resolutions. This outcome can be correlated with the findings in Section 3.4. The elevated Ca²⁺ concentration resulting from calcite dissolution enhances the repulsion between rock and salt water [37], destabilizing the interface and promoting water film formation. The overall film stability depends on the interplay between these phenomena. Notably, the Z potential increases rapidly at 10 dSW, with the latter effect outweighing the former [38]. The elevated negative charge at the boundary between rock and saline water is counterbalanced by the oil and saline boundary, ensuring water film stability and maximal humidity variation at the optimal salinity [39]. Beyond the optimal salt degree, the accumulation of anionic potential at the mineral–electrolyte interface is counterbalanced by elevated calcium ion concentrations, resulting from carbonate dissolution, preserving stable conditions under low-salinity environments [40]. This charge transfer predominantly influences film stability at low salinity, impacting the humidity of the diluted saline solution, as depicted in the WAI measurements in Figure 6. The reduction in this charge primarily arises from slight alterations in carbonate surface humidity, which is particularly noticeable at salt levels lower than the optimal salinity.

Through the assessment of the rock–liquid interface, it was found that the optimal salinity for both experiments was 10 times diluted seawater (10 dSW), which contrasts with the optimal salinity identified in the fluid–liquid interface study (5 dSW). The discrepancy in optimal salinity levels suggests distinct behaviors in the liquid–liquid and rock–liquid interfaces, influenced by interaction types and core properties. Consequently, a comprehensive understanding of the total core system was established to quantify the potential for petroleum production across various optimal salt concentrations.

3.5. Coreflooding

Considering the obtained data, one may deduce that liquid–liquid versus solid–liquid systems demonstrate varying preferred brine strengths. The primary goal involves maximizing oil extraction from the reservoir. To achieve this, we conducted a series of secondary and continuous rock extraction experiments under various optimal conditions. Figure 7 depicts the characteristics, design, and optimal conditions of the rock cores, along with the results obtained. The flow area index was calculated to facilitate comparison of all outcomes. It was assumed that all rock cores shared the same rock type, implying that their Formation Factor (FZI) values were nearly identical.

The results of the aforementioned source region movement indicate that achieving the second horizontal movement is possible at a maximum recovery rate of 10 dSW rather than 2 dSW. This suggests that the rock salt encounters a low-salinity flood, the effects of which penetrate deeper than the salt interface. Furthermore, it was observed that the oil recovery increases as pore volume increases. At a pore volume of 2, the oil recovery stabilizes at 60%. This is corroborated by Figure 7. Compared to SW and 2 dSW, the prolonged low-salinity exposure of 10 dSW signifies the maximum duration necessary to breach the secondary recovery threshold. The prolonged exposure to low salinity provides ample time to activate mechanisms that enhance crude oil interaction. Increasing the permeation time by 10 DV facilitates piston movement, forming a homogeneous ground layer and thereby elevating the recovery rate. The extraction of diluted brine correlates closely with the crude oil permeation time [41]. Notably, in the third stage of petroleum production, injecting saltwater at different dilutions does not increase petroleum production maximally. This implies that the low-salinity mechanism does not apply uniformly during the initial and secondary phases of oil recovery. In the secondary mining stage, continuous oil reservoirs exist within the oil reservoir layer, allowing low-salinity injection water to interact fully with pores and large pore oil in the rock [42]. However, after secondary clamping, capillary forces increase and crude oil becomes discontinuous within the rock matrix, predominantly existing in pores. This residual oil cannot be fully recovered due to the increased capillary deficiency caused by the high-level injection of weak saltwater and other substances in the third stage [43], primarily caused by increased surface tension where low-salinity water meets crude oil [44]. Hence, utilizing low-salinity water during secondary flooding is advisable [45,46,47].

The notable increase in crude oil production is attributed to the complex interactions between calcium dissolution and the increased elastic viscosity of rocks and saline boundaries. Oil resulting from calcite dissolution exhibits clear viscoelasticity, facilitating easy passage through porous spaces with reduced cracking, thus favoring the formation of larger ribs that are easier to replace and recover. While previous research on LSWF in China has elucidated the dissolution mechanism in laboratory settings, its practical application has faced scrutiny. While short solidification times may overlook calcite dissolution effects, longer solidification times could enhance calcite dissolution. In conclusion, enhanced oil recovery potential can be achieved by absorbing oil at catalyst temperatures. These findings indicate that 10 dSW results in approximately 14% increased recovery compared to single SW injections, representing a positive deviation from conventional dosing.

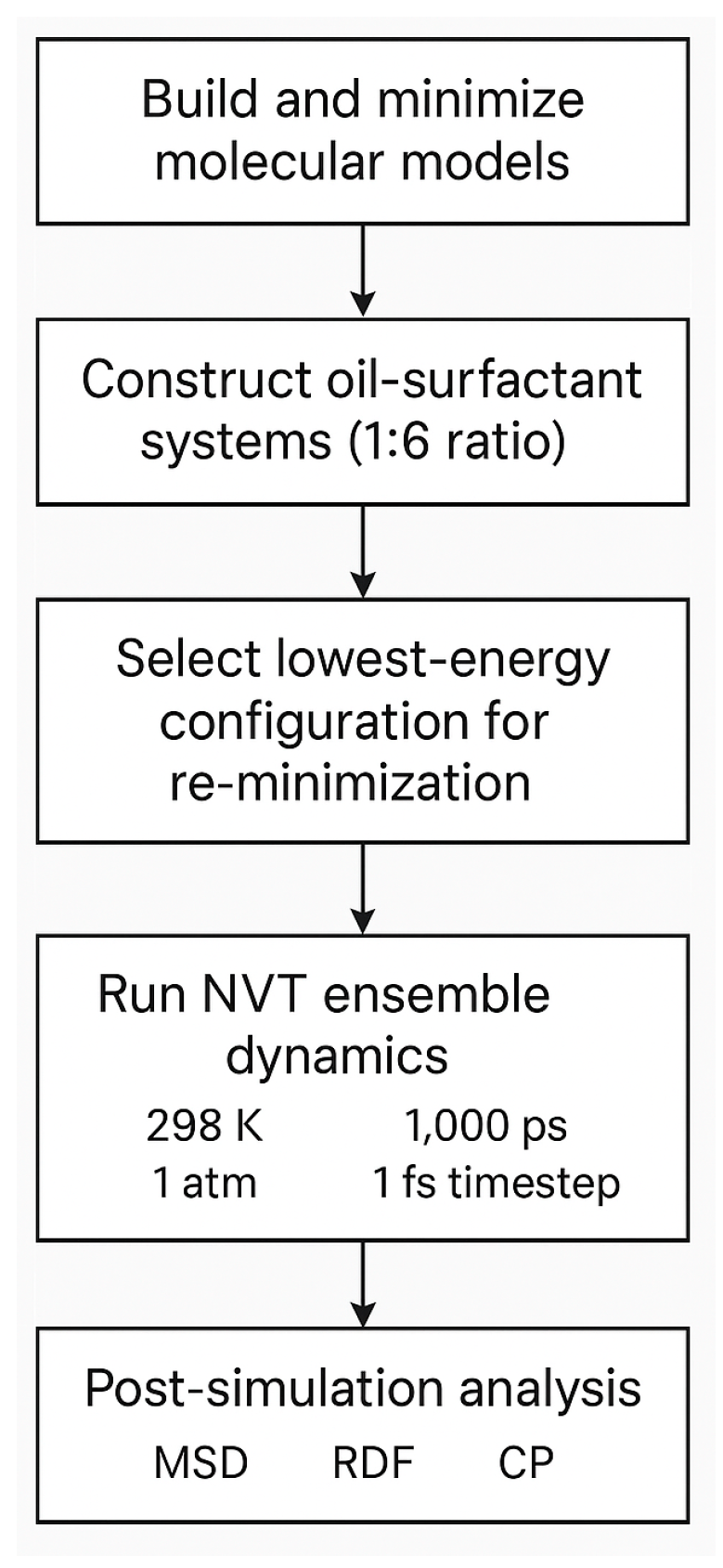
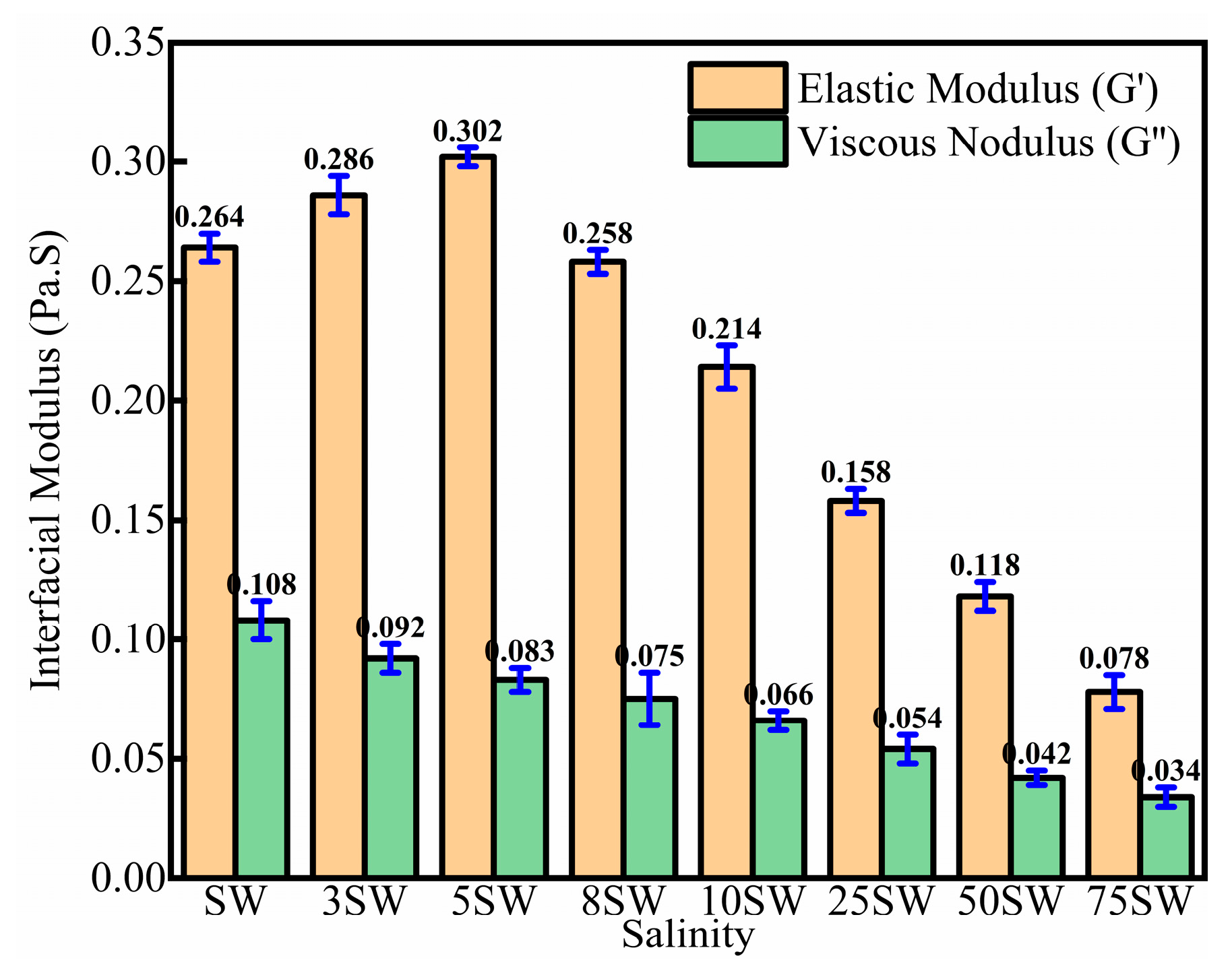
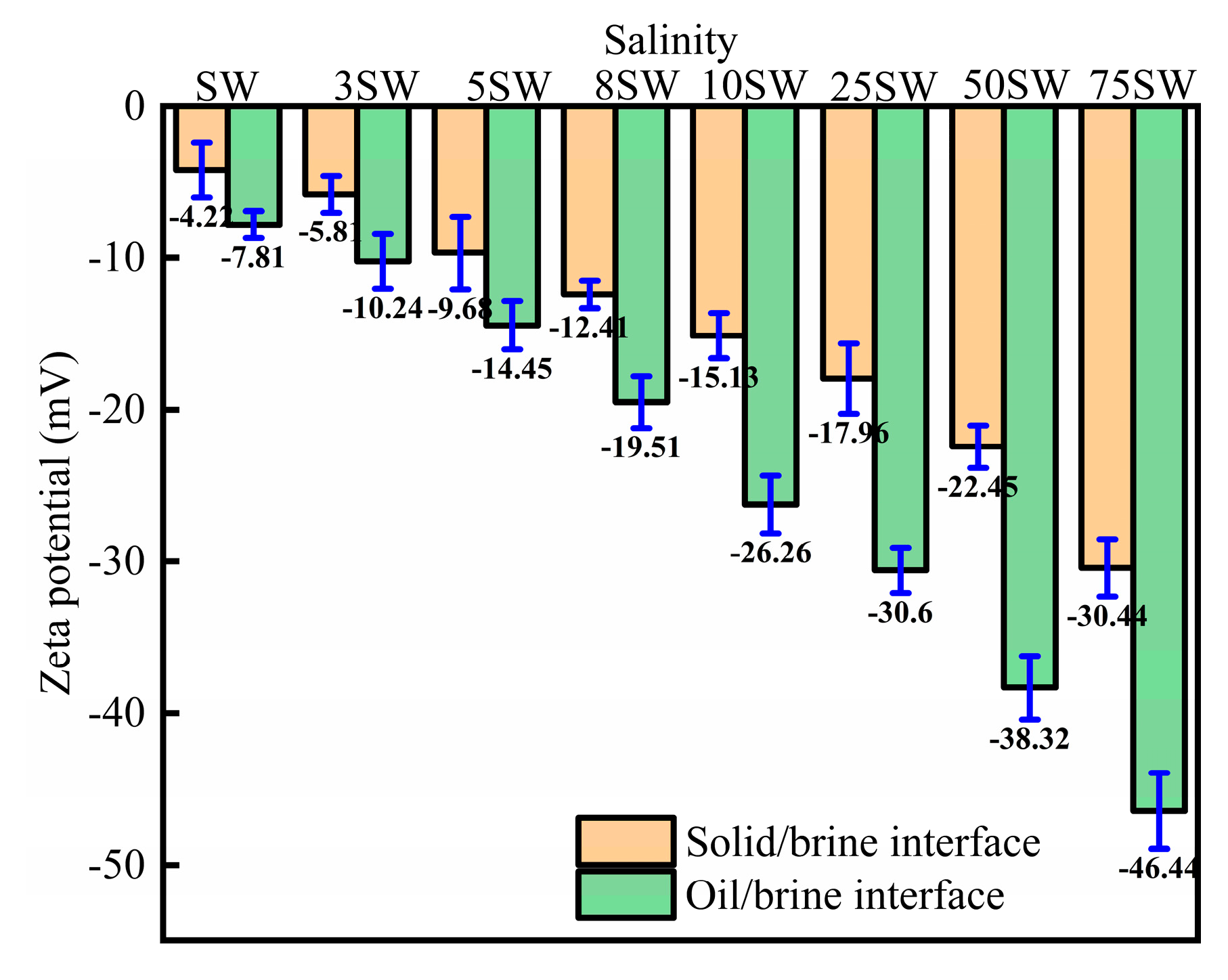
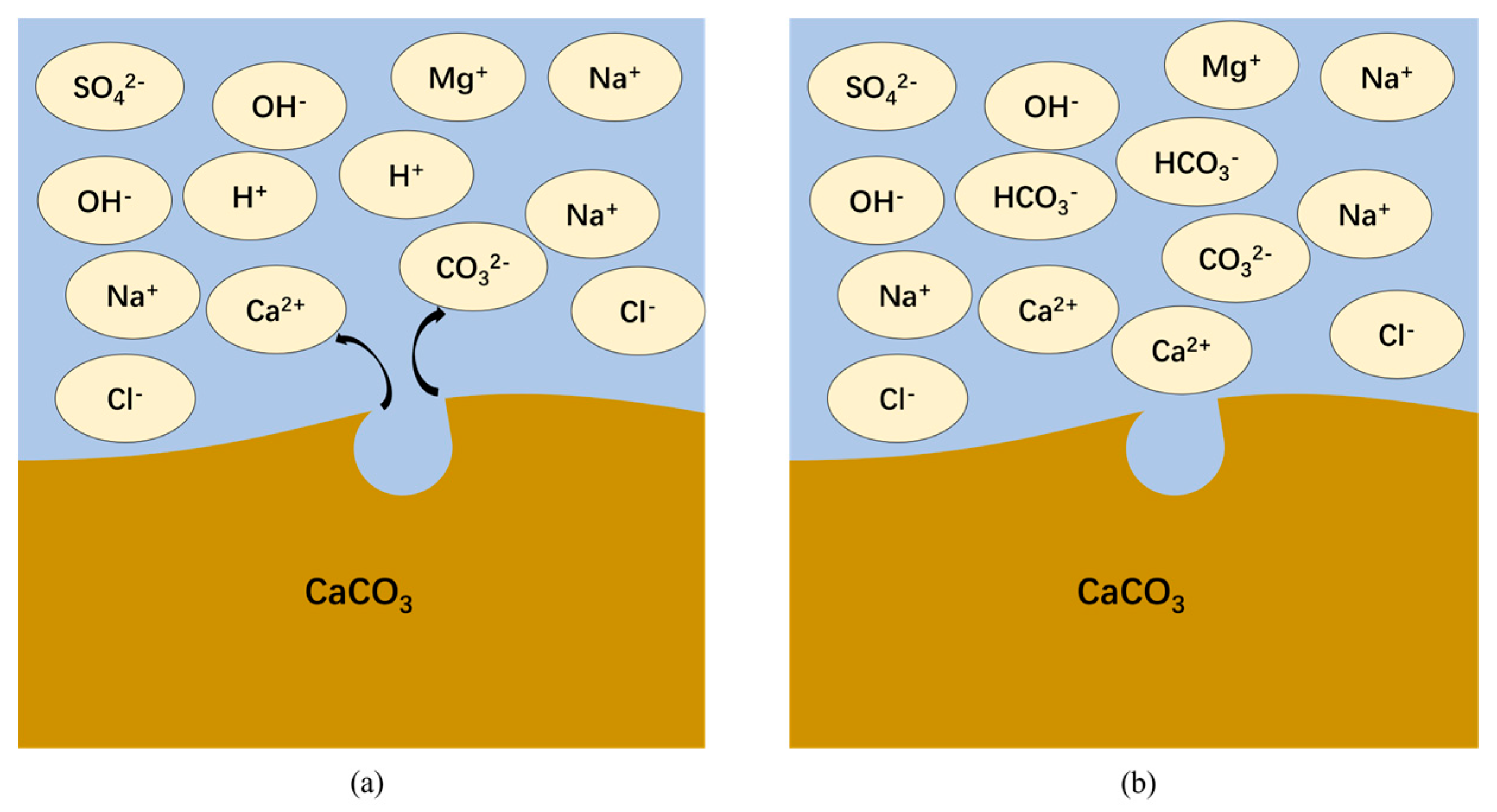
3.6. Simulation Results (Rock/Liquid)

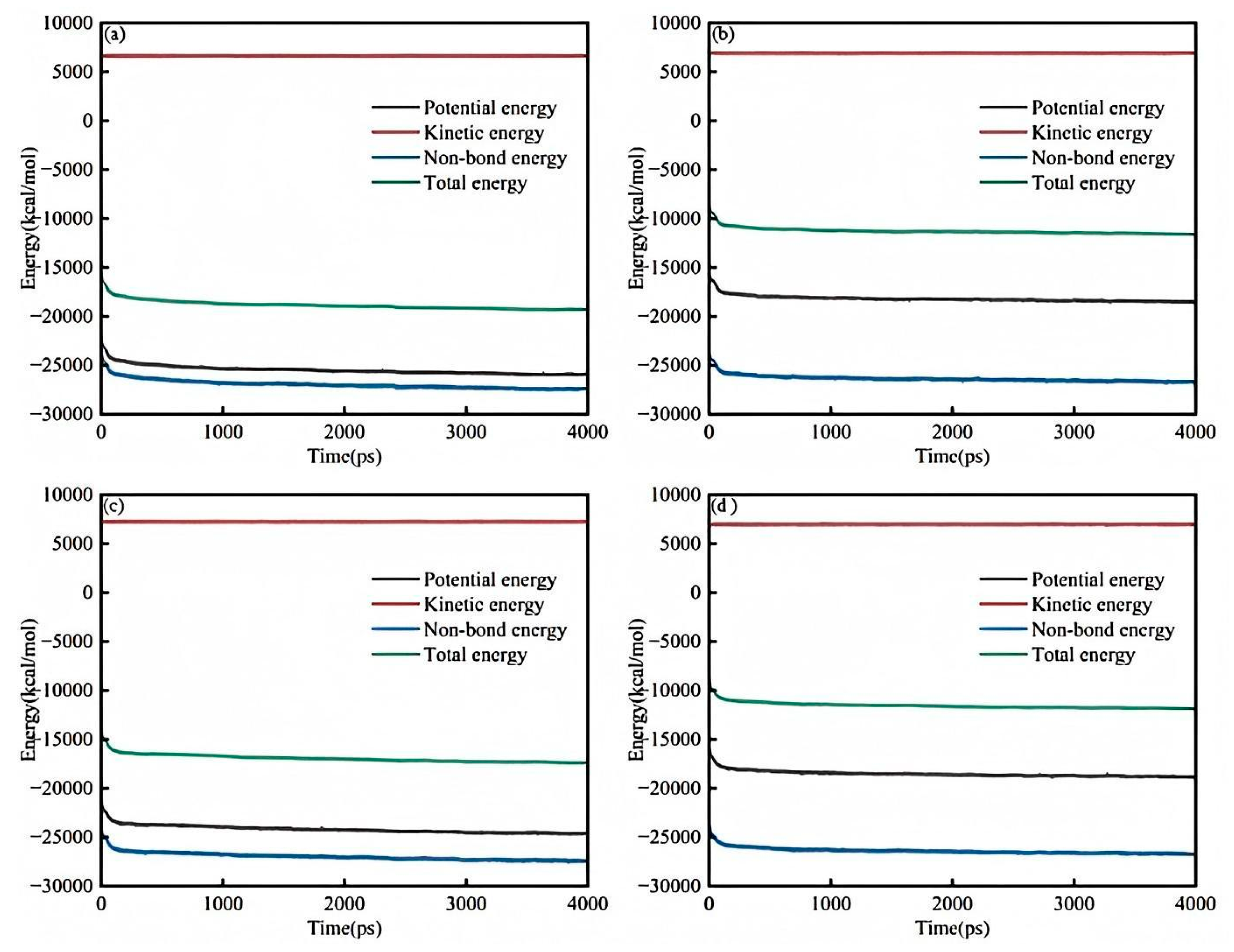
Figure 8a shows the energy balance diagram of the saturated component and the sodium laureth sulfate system. As can be seen from the figure, the energy fluctuates in the first 100 ps, and the energy is stable after 100 ps. When the simulation time is the same, the kinetic energy is the largest, followed by the total energy, the potential energy, and the smallest non-bond energy. When the simulation time is 4000 ps, the dynamic energy is stable at about 7000 kcal/mol, the total energy is stable at about −19,000 kcal/mol, the potential energy is stable at about −26,000 kcal/mol, and the non-energetic energy is stable at about −27,000 kcal/mol. The energy balance diagram shows that 4000 ps is sufficient to stabilize the simulation. Figure 8b shows the energy balance diagram of the aromatic fraction and the sodium laureth sulfate system. As can be seen from the figure, the energy fluctuates in the first 100 ps, and the energy is stable after 100 ps. When the simulation time is the same, the kinetic energy is the largest, followed by the total energy, the potential energy, and the smallest non-bond energy. When the simulation time is 4000 ps, the dynamic energy is stable at about 7000 kcal/mol, the total energy is stable at about −12,000 kcal/mol, the potential energy is stable at −18,000 kcal/mol, and the non-energetic energy is stable at about −27,000 kcal/mol. The energy balance diagram shows that 4000 ps is sufficient to stabilize the simulation. Figure 8c is a diagram of the energy balance between the colloid and sodium laureth sulfate system. As can be seen from the figure, the energy fluctuates in the first 100 ps, and the energy is stable after 100 ps. When the simulation time is the same, the kinetic energy is the largest, followed by the total energy, the potential energy, and the smallest non-bond energy. When the simulation time is 4000 ps, the dynamic energy is stable at about 7000 kcal/mol, the total energy is stable at −18,000 kcal/mol, the potential energy is stable at −25,000 kcal/mol, and the non-energetic energy is stable at about −28,000 kcal/mol. The energy balance diagram shows that 4000 ps is sufficient to stabilize the simulation. Figure 8d is a diagram of the energy balance of asphaltene and the sodium laureth sulfate system. As can be seen from the figure, the energy fluctuates in the first 100 ps, and the energy is stable after 100 ps. When the simulation time is the same, the kinetic energy is the largest, followed by the total energy, the potential energy, and the smallest non-bond energy. When the simulation time is 4000 ps, the dynamic energy is stable at about 7000 kcal/mol, the total energy is stable at −12,000 kcal/mol, the potential energy is stable at −19,000 kcal/mol, and the non-energetic energy is stable at about −27,000 kcal/mol. The energy balance diagram shows that 4000 ps is sufficient to stabilize the simulation.

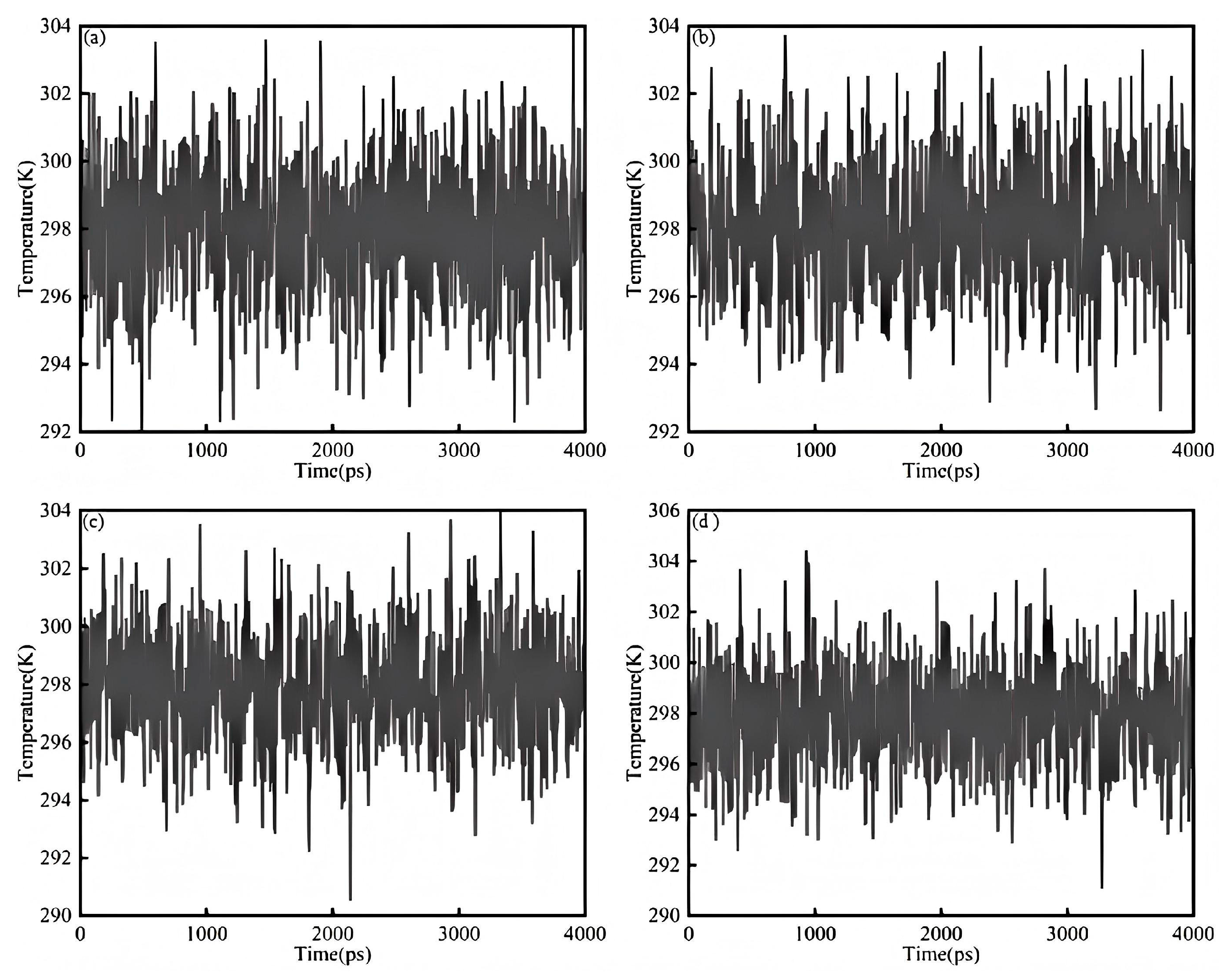
Figure 9a shows the temperature equilibrium diagram of the saturated component and the sodium laureth sulfate system. It can be seen from the figure that the temperature fluctuation range is from 292 K to 304 K and the overall temperature is around 298 K, indicating that the simulation has reached the temperature equilibrium state and the data is valid. The temperature range is within 0 to 4000 ps without major changes. Figure 9b shows the temperature balance of aromatic components and the sodium laureth sulfate system. It can be seen from the figure that the temperature fluctuation range is from 292 K to 304 K and the overall temperature is around 298 K, indicating that the simulation has reached the temperature equilibrium state and the data is valid. The temperature range is within 0 to 4000 ps without major changes. Figure 9c shows the temperature balance diagram of the colloid and sodium laureth sulfate system. It can be seen from the figure that the temperature fluctuation range is from 290 K to 304 K and the overall temperature is around 298 K, indicating that the simulation has reached the temperature equilibrium state and the data is valid. The temperature range is within 0 to 4000 ps without major changes. Figure 9d shows the temperature equilibrium diagram of asphaltene and the sodium laureth sulfate system. It can be seen from the figure that the temperature fluctuation range is from 291 K to 305 K and the overall temperature fluctuation is around 298 K, indicating that the simulation has reached the temperature equilibrium state and the data is valid. The temperature range is within 0 to 4000 ps without major changes.

Figure 10a shows the MSD diffusion diagram of the saturated component and the sodium laureth sulfate system. It can be seen from the figure that the diffusion coefficient of the saturation component is greater than that of sodium laureth sulfate at 1800 ps to 3700 ps, and the diffusion coefficient of sodium laureth sulfate is greater than that of sodium laureth sulfate at the rest of the time. The diffusion of the saturation fraction increases with the increase in simulation time, the MSD value gradually increases, and when the simulation time is close to 2000 ps, the MSD coefficient rises faster. The MSD value of sodium laureth sulfate gradually rises with simulation time; when the simulation time is close to 3100 ps, the MSD coefficient rises more rapidly. This is because the simulation is unstable over short time frames, meaning the interaction between the saturation fraction and sodium laureth sulfate does not reach a stable value, and instead gradually increases. Figure 10b is an MSD diffusion diagram of aromatic components and the sodium laureth sulfate system. It can be seen from the figure that the diffusion coefficient of sodium laureth sulfate is greater than that of the aromatic fraction. The diffusion of aromatic content is such that the MSD value gradually increases with the increase in simulation time, and the MSD coefficient increases rapidly when the simulation time is close to 3400 ps. The MSD value of sodium laureth sulfate increased gently with the simulation time; when the simulation time was close to 3500 ps, the MSD coefficient rises rapidly. This is because the simulation is unstable over short time frames, meaning the interaction between the aromatic content and sodium laureth sulfate does not reach a stable value, and instead gradually increases. Figure 10c is an MSD diffusion diagram of the colloid and sodium laureth sulfate system. It can be seen from the figure that the diffusion coefficient of sodium laureth sulfate is greater than that of glia. The MSD value continued to increase with the increase in simulation time, and the MSD coefficient increased rapidly when the simulation time was close to 3300 ps. The MSD value of sodium laureth sulfate rises gently with the simulation time; when the simulation time is close to 3600 ps, the MSD coefficient rises rapidly. At the same time, the interaction between the glia and sodium laureth sulfate did not reach a stable value, meaning it gradually increased. Figure 10d is an MSD diffusion diagram of asphaltene and the sodium laureth sulfate system. It can be seen from the figure that the diffusion coefficient of sodium laureth sulfate is greater than that of asphaltene. The diffusion of asphaltene causes a gradual increase in MSD value as the simulation time increases, and the MSD coefficient increases rapidly when the simulation time is close to 3100 ps. The MSD value of sodium laureth sulfate increased steadily with the simulation time and increased rapidly when the simulation time was close to 3300 ps. This is because the simulation is unstable over short time frames, meaning the interaction between asphaltene and sodium laureth sulfate does not reach a stable value, and instead gradually increases.

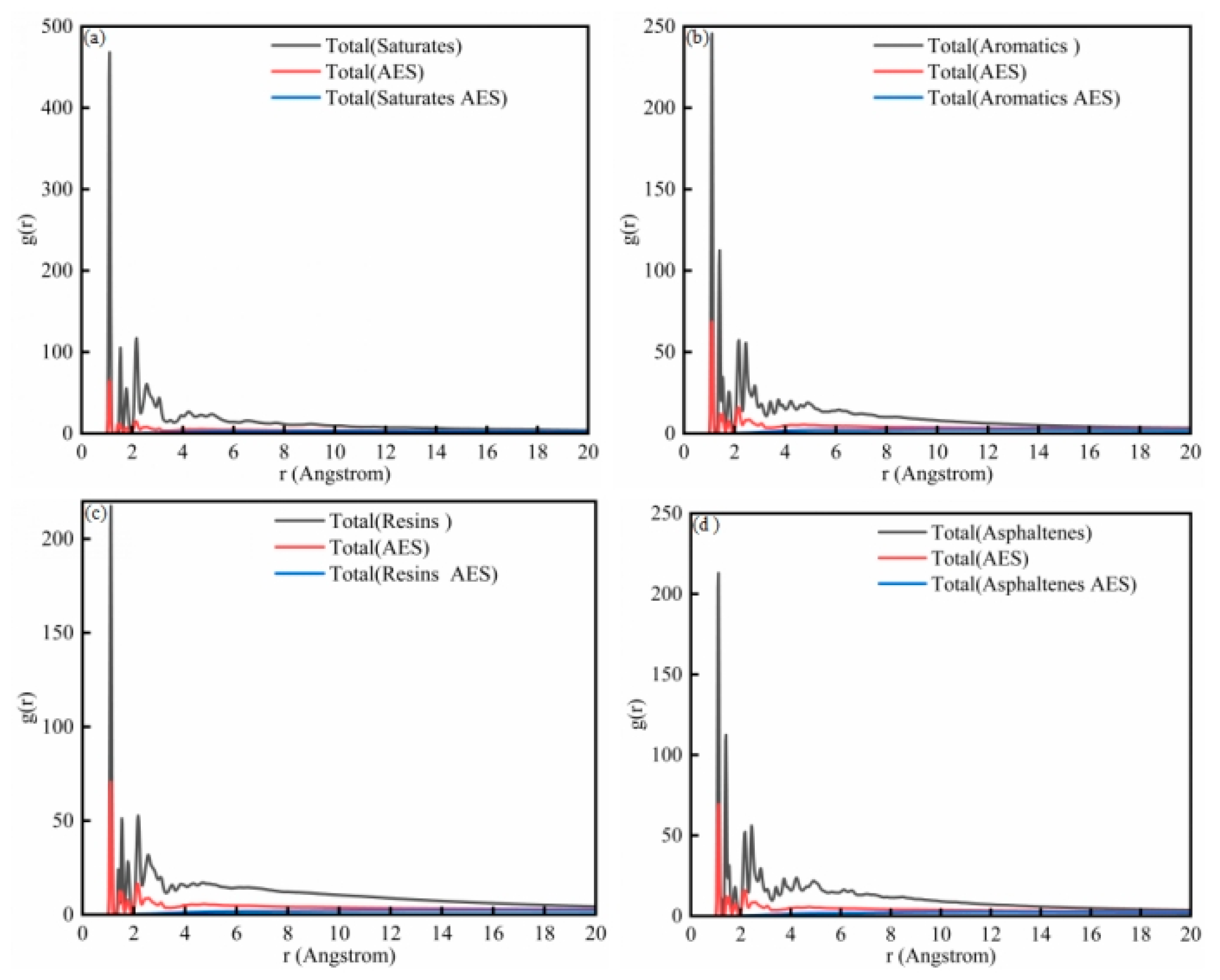
Figure 11a shows the RDF plot of the saturated component and the sodium laureth sulfate system. For the saturation fraction, there are three main peaks, with peak positions of 1.1 A, 1.5 A, and 2.2 A, respectively. For sodium laureth sulfate, a major peak position occurs at 1.1 A. The results of the radial distribution function show that the relative positions of the interactions between the saturated atoms are higher than those between sodium laureth sulfate. The total blue curve, the saturation fraction and sodium laureth sulfate plot, show that there is no obvious peak between the saturated molecule and the sodium laureth sulfate molecule as a whole, and the peak position reaches equilibrium after 7 A. Figure 11b is the RDF diagram of the aromatic component and sodium laureth sulfate system. For aromatic components, there are four main peaks, with peak positions of 1.1 A, 1.4 A, 2.2 A, and 2.5 A, respectively. For sodium laureth sulfate, a major peak position occurs at 1.1 A. The results of the radial distribution function show that the relative position of the interaction between the aromatic atoms is higher than that between sodium laureth sulfate. The total blue curve, the plot of the aromatic fraction and sodium laureth sulfate, shows that there is no obvious peak between the aromatic molecule and the sodium laureth sulfate molecule as a whole, and the peak position reaches equilibrium after 7 A. Figure 11c is an RDF diagram of the colloid and sodium laureth sulfate system. For glia, there are three main peaks, with peak positions of 1.1 A, 1.5 A, and 2.2 A, respectively. For sodium laureth sulfate, a major peak position occurs at 1.1 A. The results of the radial distribution function show that the relative position of the interaction between the colloidal atoms is higher than that between sodium laureth sulfate. The total blue curve, the graph of the colloid and sodium laureth sulfate, shows that there is no obvious peak between the colloid and sodium laureth sulfate molecules as a whole, and the peak position reaches equilibrium after 6 A. Figure 11d is the RDF diagram of asphaltene and the sodium laureth sulfate system. For asphaltene, there are four main peaks, with peak positions of 1.1 A, 1.4 A, 2.2 A, and 2.4 A, respectively. For sodium laureth sulfate, a major peak position occurs at 1.1 A. The results of the radial distribution function show that the relative positions of the interactions between asphaltene atoms are higher than those between sodium laureth sulfate. The overall blue curve, the graph of asphaltene and sodium laureth sulfate, shows that there is no obvious peak between the asphaltene molecule and the sodium laureth sulfate molecule as a whole, and the peak position reaches equilibrium after 7 A.

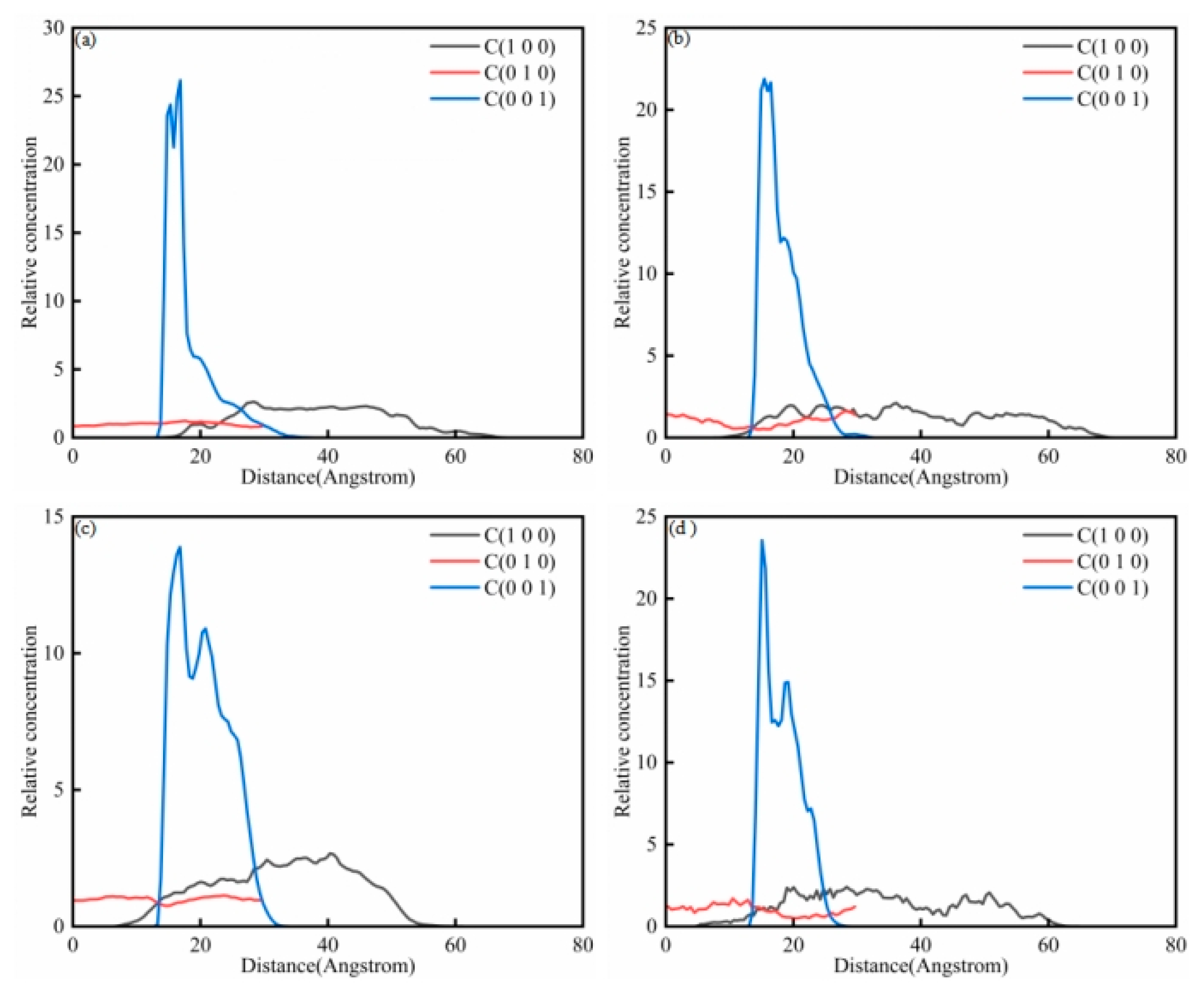
Figure 12a shows the analysis of saturated concentration in the saturated component–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration for different crystal planes. In the C001 crystal plane, the overall trend is for an initial rise first and then a fall; the maximum value occurs at 17. There was an overall upward trend from 13 to 17, followed by a downward trend between 17 and 38. In the C100 crystal plane, there is an upward trend from 12 to 29, a gentle trend from 29 to 36, and a downward trend between 36 and 68. In the C010 crystal plane, 0 to 30 shows a flat trend. From 14 to 23, the concentration of crystal plane C010 is greater than that of crystal plane C100 and less than that of crystal plane C001. Figure 12b shows the analysis of aromatic concentration in the aromatic component–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C001 crystal plane, there is an initial rise and then a fall, with a maximum value at 15. There is an upward trend from 13 to 15, and then a downward trend from 15 to 33. In the C100 crystal plane, there is an upward trend from 7 to 20 and a general trend of fluctuating decline from 20 to 70. In the C010 crystal plane, 0 to 30 showed a trend of first decreasing and then rising. From 14 to 26, the concentration of crystal plane C100 is greater than that of crystal plane C010 and less than that of C001. Figure 12c shows the analysis of colloidal concentration in the colloid–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C001 crystal plane, the overall trend is an initial rise and then a fall, with a maximum value at 16. The results showed an upward trend from 13 to 16, followed by an overall downward trend from 16 to 34. In the C100 crystal plane, there is an upward trend from 6 to 41 and a downward trend from 41 to 61. In the C010 crystal plane, 0 to 12 showed a gentle trend, 12 to 24 showed a downward trend and then rose, and 24 to 30 showed a downward trend. From 13 to 28, the concentration of crystal plane C100 is greater than that of crystal plane C010 and less than that of crystal plane C001. Figure 12d shows the analysis of asphaltene concentration in the asphaltene–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C001 crystal plane, the overall trend is an initial rise and then a fall, with a maximum value at 15. There was an upward trend from 13 to 15, followed by an overall downward trend from 15 to 29. In the C100 crystal plane, it shows an upward trend from 0 to 20, a downward trend from 20 to 44, and an overall upward trend and then a downward trend from 44 to 65. In the C010 crystal plane, 0 to 13 showed a gentle trend and 13 to 30 showed a trend of first decreasing and then rising. From 15 to 25, the concentration of crystal plane C100 is greater than that of crystal plane C010 and less than that crystal plane C001.

Figure 13a shows the concentration analysis diagram for sodium laureth sulfate in the saturated fraction–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C100 crystal plane, the overall trend shows an initial decline, flowed by a rise, and then a second decline before rising again. From 0 to 15, there is a downward trend; 15 to 45 shows an overall upward trend; and 45 to 73 shows a downward trend and then an upward trend. In the C010 crystal plane, 0 to 11 showed an upward trend and 11 to 30 showed a downward trend. In the C001 crystal plane, 13 to 21 showed an upward trend, 21 to 42 showed a downward trend and then rose, and 42 to 66 showed a downward trend. From 16 to 30, the concentration of crystal plane C010 is greater than that of C100 and less than that of C001. Figure 13b shows the concentration analysis of sodium laureth sulfate in the aromatic component–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C100 crystal plane, the overall trend is to increase first, then decrease, and finally rise. From 0 to 23, there is an overall upward trend; 23 to 50 shows a downward trend; and 50 to 73 shows an upward trend. In the C010 crystal plane, 0 to 30 showed a trend of rising first and then decreasing. In the C001 crystal plane, 13 to 24 showed an upward trend, 24 to 43 showed a downward trend and then rose, and 43 to 71 showed a downward trend. From 16 to 30, the concentration of crystal plane C100 is greater than that of C010 and less than that of C001. Figure 13c shows the concentration analysis of sodium laureth sulfate in the colloid–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C100 crystal plane, there is an overall trend of an initial decline, followed by a rise, and finally another decline. From 0 to 40, there is an overall downward trend; 40 to 55 shows an upward trend; and 55 to 73 shows a downward trend. In the C010 crystal plane, 0 to 30 showed a trend of rising first and then decreasing. In the C001 crystal plane, 13 to 30 showed an upward trend and 30 to 69 showed an overall downward trend. From 15 to 30, the concentration of C010 in the crystal plane is greater than that of C100 and less than that of C001. Figure 13d shows the concentration analysis diagram for sodium laureth sulfate in the asphaltene–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C100 crystal plane, there is an overall decrease and then an increase. From 0 to 45, there is an overall downward trend, and from 45 to 73, it rises first and then decreases. In the C010 crystal plane, 0 to 15 showed a trend of first rising and then falling and 15 to 30 showed a gentle trend. In the C001 crystal plane, 13 to 25 showed an upward trend, 25 to 43 showed a downward trend and then rose, and 43 to 65 showed a downward trend. From 16 to 26, the concentration of crystal plane C100 is greater than that of C010 and less than that of C001.

Figure 14a shows the diffusion conformation diagram of saturated fractions in sodium laureth sulfate. The diffusion effect of saturated molecules gradually increases as the simulation progresses. When the simulation begins, the saturated molecules clump together, but as the simulation progresses, the saturated molecules diffuse in the solvent. When 3200 ps is reached, the saturation partial diffusion is stable. When 4000 ps is reached, there is little difference in saturated molecular diffusion. Figure 14b shows the diffusion conformation of aromatic molecules in sodium laureth sulfate. The diffusion effect of aromatic molecules gradually increases with the simulation time. When the simulation begins, the aromatic molecules clump together, but as the simulation progresses, the aromatic molecules diffuse in the solvent. When 2400 ps is reached, the aromatic diffusion is stable. When 4000 ps is reached, there is little difference in aromatic molecular diffusion. Figure 14c shows the conformation diagram of the diffusion of glia in sodium laureth sulfate. The diffusion effect gradually increases with the simulation time. When the simulation begins, the glial molecules clump together, but as the simulation progresses, the glial molecules diffuse in the solvent. When 2400 ps is reached, the colloidal diffusion is stable. When 4000 ps it reaches, there is little difference in the diffusion of glial molecules. Figure 14d shows the diffusion conformation diagram of asphaltene in sodium laureth sulfate. The asphaltene diffusion effect gradually increases with the simulation time. When the simulation begins, the asphaltene molecules clump together, but as the simulation progresses, the asphaltene molecules diffuse in the solvent. When 2400 ps is reached, asphaltene diffusion is stable. When 4000 ps is reached, there is little difference in the diffusion of asphaltene molecules.

Figure S1 shows the energy balance diagram of the SARA component and the sodium laureth sulfate system. It can be seen from the figure that the energy fluctuates in the first 50 ps and the energy is stable after 50 ps. When the simulation time is the same, the kinetic energy is the largest, followed by the total energy, the non-bond energy, and the potential energy. The results indicate that the simulation energy system reached equilibrium when the simulation system reached 2500 ps.

Figure S2 shows the temperature equilibrium diagram of the saturated component and the sodium laureth sulfate system. It can be seen from the figure that the temperature fluctuation range is from 291 K to 307 K and the overall temperature is around 298 K, indicating that the simulation has reached the temperature equilibrium state and the data is valid. The results indicated that the simulation system reached equilibrium when the simulation time reached 2500 ps.

Figure S3a shows the MSD diffusion diagram of the saturated component and the sodium laureth sulfate system. It can be seen from the figure that the diffusion coefficient of the saturated part is greater than that of sodium laureth sulfate. The diffusion of the saturation fraction increases with simulation time. The MSD value gradually increases when the simulation time is close to 2300 ps. The MSD coefficient fluctuated up and down. The MSD value of sodium laureth sulfate increases gently with the simulation time. This is because the simulation is unstable over short time frames, meaning the interaction between saturated content and sodium laureth sulfate does not reach a stable value, and instead gradually increases. Figure S3b is an MSD diffusion diagram of aromatic components and the sodium laureth sulfate system. It can be seen from the figure that the diffusion coefficient of sodium laureth sulfate is greater than that of the aromatic. The diffusion of aromatic content shows that the MSD value gradually increases with the increase in simulation time, and the MSD coefficient increases rapidly when the simulation time is close to 2300 ps. The MSD value of sodium laureth sulfate increased steadily with the simulation time, increasing rapidly when the simulation time was close to 2400 ps. This is because the simulation is unstable in short time frames, meaning the interaction between aromatic content and sodium laureth sulfate does not reach a stable value, and instead gradually increases. Figure S3c is an MSD diffusion diagram of the colloidal and sodium laureth sulfate system. It can be seen from the figure that the diffusion coefficient of sodium laureth sulfate is greater than that of glia. When the simulation time is close to 1500 ps, the MSD coefficient first rises rapidly, then slowly, and finally rises rapidly again. The MSD value of sodium laureth sulfate rising gently with increasing simulation time, and the MSD coefficient rises rapidly when the simulation time is close to 2300 ps. At the same time, the interaction between glia and sodium laureth sulfate did not reach a stable value, so it gradually increased. Figure S3d is an MSD diffusion diagram of asphaltene and sodium laureth sulfate system. It can be seen from the figure that the diffusion coefficient of sodium laureth sulfate is greater than that of asphaltene. The diffusion of asphaltene shows that the MSD value increases gradually with the increase in simulation time, and the MSD coefficient increases rapidly when the simulation time is close to 2200 ps. The MSD value of sodium laureth sulfate rose steadily with the simulation time, increasing rapidly when the simulation time approached 2200 ps. This is because the simulation is unstable in short time frames, meaning the interaction between asphaltene and sodium laureth sulfate does not reach a stable value, and instead gradually increases.

Figure S4a shows the RDF plot of the saturated component and the sodium laureth sulfate system. For the saturation fraction, there are three main peaks, with peak positions of 1.1 A, 1.5 A, and 2.2 A, respectively. For sodium laureth sulfate, a major peak position occurs at 1.1 A. The results of the radial distribution function show that the relative positions of the interactions between the saturated atoms are higher than those between sodium laureth sulfate. The total blue curve, the diagram of saturated component and sodium laureate lysozyme sulfate, shows that there is no obvious peak between the saturated molecule and the sodium laureate lysozyme sulfate molecule, and the peak position reaches equilibrium after 6 A. Figure S4b is the RDF diagram of the aromatic component and sodium laureth sulfate system. For aromatic components, there are four main peaks, with peak positions of 1.1 A, 1.4 A, 2.2 A, and 2.5 A, respectively. For sodium laureth sulfate, a major peak position occurs at 1.1 A. The results of the radial distribution function show that the relative position of the interaction between the aromatic atoms is higher than that between sodium laureth sulfate. The total blue curve, the plot of the aromatic fraction and sodium laureth sulfate, shows that there is no obvious peak between the aromatic molecule and the sodium laureth sulfate molecule as a whole, and the peak position reaches equilibrium after 6 A. Figure S4c is an RDF diagram of the colloid and sodium laureth sulfate system. For glia, there are three main peaks, with peak positions of 1.1 A, 1.5 A, and 2.2 A, respectively. For sodium laureth sulfate, a major peak position occurs at 1.1 A. The results of the radial distribution function show that the relative position of the interaction between the colloidal atoms is higher than that between sodium laureth sulfate. The total blue curve, the graph of the colloid and sodium laureth sulfate, shows that there is no obvious peak between the colloid and sodium laureth sulfate molecules as a whole, and the peak position reaches equilibrium after 6 A. Figure S4d is the RDF diagram of asphaltene and sodium laureth sulfate system. For asphaltene, there are four main peaks, with peak positions of 1.1 A, 1.4 A, 2.2 A, and 2.4 A, respectively. For sodium laureth sulfate, a major peak position occurs at 1.1 A. The results of the radial distribution function show that the relative positions of the interactions between asphaltene atoms are higher than those between sodium laureth sulfate. The overall blue curve, the plot of asphaltene and sodium laureth sulfate, shows that there is no obvious peak between the asphaltene molecule and the sodium laureth sulfate molecule as a whole, and the peak position reaches equilibrium after 6 A.

Figure S5a shows the analysis of saturated concentration in the saturated component–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C001 crystal plane, the concentration initially decreases and then rises before finally falling and rising again. The maximum value occurs at 35. It shows a downward trend from 0 to 10, followed by an upward trend from 10 to 19, a downward trend from 19 to 23, and finally an upward trend from 23 to 35. In the C100 crystal plane, the trend rises and then decreases from 0 to 5, rises and then decreases from 5 to 18, rises from 18 to 24, and decreases from 24 to 35. In the C010 crystal plane, 0 to 5 shows an upward trend, 5 to 16 shows a downward trend, 16 to 25 shows a trend of first rising and then falling, and 25 to 35 shows a trend of first rising and then falling. From 6 to 11, the concentration of crystal plane C100 is greater than that of crystal plane C001 and less than that of crystal plane C010. From 21 to 29, the concentration of crystal plane C001 is greater than that of crystal plane C010 and less than that of C100. Figure S5b shows the analysis of aromatic concentration in the aromatic component–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C001 crystal plane, the concentration first decreases and then rises, before finally falling and rising again. The maximum value occurs at 1. This crystal plane shows a downward trend from 0 to 8, rises and then falls from 8 to 22, rises from 22 to 30, and finally falls before rising again from 30 to 36. In the C100 crystal plane, it first rises and then decreases from 0 to 10, rises and then decreases from 10 to 15, rises from 15 to 26, and decreases and then rises from 26 to 36. In the C010 crystal plane, 0 to 6 shows an upward trend, 6 to 14 shows a downward trend, 14 to 16 shows a rapid upward trend, and 16 to 36 shows a general downward trend. From 15 to 19, the concentration of crystal plane C001 was greater than that of crystal plane C100 and less than that of C010. From 19 to 24, the concentration of crystal plane C100 was greater than that of crystal plane C001 and less than that crystal plane C010. Figure S5c shows the analysis of colloidal concentration in the colloid–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C001 crystal plane, the overall trend is an initial fall, then a rise, then a fall, and finally a rises and then another fall, with a maximum value at 9. It shows a downward trend from 0 to 4, followed by a rapid upward trend from 4 to 9, a flat trend from 9 to 15, a downward trend from 15 to 24, and finally a trend of rising and then falling from 24 to 36. In the C100 crystal plane, there is a trend of first decreasing and then rising rapidly from 0 to 8, a general downward trend from 8 to 25, and a trend of first rising and then decreasing from 25 to 36. In the C010 crystal plane, 0 to 5 shows a downward trend, 5 to 9 shows a gentle trend, 9 to 15 shows a trend of first rising and then falling, 15 to 25 shows a trend of first rising and then falling, 25 to 33 shows a trend of first rising and then falling, and finally 33 to 36 shows an upward trend. From 4 to 9, the concentration of crystal plane C001 is greater than that of crystal plane C010 and less than that of crystal plane C100. From 21 to 27, the concentration of crystal plane C100 was greater than that of crystal plane C001 and less than that of crystal plane C010. Figure S5d shows the analysis of asphaltene concentration in the asphaltene–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C001 crystal plane, the curve first decreases, then rises, then falls, and finally rises, with a maximum value at 34. It shows a downward trend from 0 to 13, followed by an upward trend and then a downward trend from 13 to 23, an overall upward trend from 23 to 32, and finally a flat trend from 32 to 37. In the C100 crystal plane, there is a downward trend from 0 to 6, an upward trend from 6 to 14, a downward trend and then an upward trend from 14 to 23, and a downward trend and then an upward trend from 23 to 37. In the C010 crystal plane, 0 to 13 shows a trend of rising first and then decreasing, 13 to 33 shows an overall upward trend, and 33 to 37 shows a downward trend. From 10 to 27, the concentration of crystal plane C010 was greater than that of crystal plane C001 and less than that of crystal plane C100.

Figure S6a shows the concentration analysis diagram of sodium laureth sulfate in the saturated component–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C100 crystal plane, the overall trend exhibits an initial rise, then a decrease, then a rise, and finally a decrease. From 0 to 6, there is an upward trend; 6 to 11 shows a downward trend and then an upward trend; 11 to 15 shows a downward trend; 15 to 26 shows a downward trend; and 26 to 35 shows a trend of first rising and then decreasing. In the C010 crystal plane, 0 to 5 shows a downward trend, 5 to 15 shows an upward trend, 15 to 23 shows a downward trend and then an upward trend, 23 to 28 shows a downward trend and then an upward trend, and 28 to 35 shows a downward trend and then an upward trend. In the C001 crystal plane, 0 to 14 shows an upward trend, 14 to 19 shows a rapid downward trend, 19 to 29 shows an overall upward trend, and 29 to 35 shows a downward trend. From 7 to 12, the concentration of crystal plane C100 is greater than that of C010 and less than that of C001. At 20 to 24, the concentration of C001 in the crystal plane is greater than that of C100 and less than that of C010. Figure S6b shows the concentration analysis of sodium laureth sulfate in the aromatic component–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C100 crystal plane, the overall trend is to first increase, then decrease, and finally rise and then decrease. From 0 to 16, there is an upward trend; 16 to 27 shows a downward trend; and 27 to 33 shows a trend of rising first and then decreasing. In the C010 crystal plane, 0 to 7 shows a downward trend, 7 to 14 shows an upward trend, 14 to 20 shows a downward trend, 20 to 29 shows an upward trend, and 29 to 33 shows a downward trend and then an upward trend. In the C001 crystal plane, 0 to 24 shows an overall upward trend and 24 to 33 shows a downward trend and then an upward trend. From 14 to 19, the concentration of crystal plane C001 is greater than that of C010 and less than that of C100. From 23 to 25, the crystal plane C100 concentration is greater than that of C010 and less than that of C001. Figure S6c shows the concentration analysis of sodium laureth sulfate in the colloid–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C100 crystal plane, the overall trend is for an initial decline, then a rise, and finally a decline. From 0 to 7, there is a downward trend; 7 to 25 shows an overall upward trend; and 25 to 37 shows a downward trend and then an upward trend. In the C010 crystal plane, 0 to 8 shows an upward trend, 8 to 18 shows a downward trend, 18 to 25 shows an upward trend, 25 to 32 shows a downward trend and then an upward trend, and 32 to 37 shows a downward trend and then an upward trend. In the C001 crystal plane, 0 to 5 shows an upward trend, 5 to 10 shows a rapid downward trend, 10 to 16 shows a flat trend, 16 to 25 shows a rapid upward trend, 25 to 35 shows a downward trend, and 35 to 37 shows an upward trend. From 6 to 9, the concentration of the crystal plane C001 is greater than that of C100 and less than that of C010. From 22 to 31, the crystal plane C100 concentration is greater than that of C010 and less than that of C001. Figure S6d shows the concentration analysis diagram of sodium laureth sulfate in the asphaltene–sodium laureth sulfate system. It can be seen from the figure that there are differences in concentration on different crystal planes. In the C100 crystal plane, the overall trend is an initial decrease and then a rise. From 0 to 14, there is a downward trend; 14 to 35 is an upward trend; and 35 to 37 is a downward trend. In the C010 crystal plane, 0 to 4 shows a downward trend, 4 to 16 shows an upward trend, 16 to 34 shows a downward trend, and 34 to 37 shows an upward trend. In the C001 crystal plane, 0 to 7 shows a trend of rising first and then falling, 7 to 19 shows an upward trend and then a fall, 19 to 23 shows an upward trend, and 23 to 37 shows an overall downward trend. From 9 to 21, the concentration of the crystal plane C001 is greater than that of C100 and less than that of C010.

Figure S7a shows the diffusion conformation diagram of the saturated fractions in sodium laureth sulfate. The diffusion effect of saturated molecules gradually increases as the simulation progresses. When the simulation begins, the saturated molecules clump together, but as the simulation progresses, the saturated molecules diffuse in the solvent. When 1000 ps is reached, the saturation diffusion is stable. When 2500 ps is reached, there is little difference in saturated molecular diffusion. Figure S7b shows the diffusion conformation of aromatic molecules in sodium laureth sulfate. The diffusion effect of aromatic molecules gradually increases with the simulation time. When the simulation begins, the aromatic molecules clump together, but as the simulation progresses, the aromatic molecules diffuse in the solvent. When 1000 ps is reached, the aromatic diffusion is stable. When 2500 ps is reached, there is little difference in aromatic molecular diffusion. Figure S7c shows the conformation diagram of the diffusion of glia in sodium laureth sulfate. The diffusion effect gradually increases with the simulation time. When the simulation begins, the glial molecules clump together, but as the simulation progresses, the glial molecules diffuse in the solvent. When 1000 ps is reached, colloidal diffusion is stable. When 2500 ps is reached, there is little difference in the diffusion of colloidal molecules. Figure S7d shows the diffusion conformation diagram of asphaltene in sodium laureth sulfate. The asphaltene diffusion effect gradually increases with the simulation time. When the simulation begins, the asphaltene molecules clump together, but as the simulation progresses, the asphaltene molecules diffuse in the solvent. When 1000 ps is reached, asphaltene diffusion is stable. When 2500 ps is reached, there is little difference in asphaltene molecular diffusion.

4. Conclusions

This study demonstrates that the optimal salinity for enhancing oil recovery via LSWF differs fundamentally between fluid–fluid and rock–fluid interactions. While fluid–fluid performance (IFT reduction, interfacial elasticity) peaks at 2 dSW, rock–fluid interactions (wettability alteration via calcite dissolution) are maximized at 10 dSW. Coreflooding confirms that rock–fluid optimization is paramount when designing, as this yields a 14% increase in oil recovery compared to 7% from fluid–fluid optimization. The key novelty of this work lies in its integrated multi-scale approach, which quantifies the distinct optimal salinities for these competing mechanisms and conclusively identifies rock–fluid interactions as the dominant driver for recovery in carbonates, advancing beyond studies that focus on a single mechanism. For field application, we recommend injecting brine optimized for rock–fluid interactions (e.g., 10 dSW) during secondary flooding to maximize contact and wettability alteration. A practical strategy could involve injecting at the rock–fluid optimum from the outset, as it effectively harnesses the most influential mechanism. Subsequent work should focus on formulating tailored brines that synergistically enhance both interaction types. In addition, the molecular dynamics simulation results indicated the corresponding role of surfactants on SARA liberation from mineral surfaces.