Abstract
The effects of high-temperature modified phosphogypsum (HPG), incorporated at contents of 40%, 50%, and 60%, on the compressive strength and elastic modulus of mortar and concrete were investigated. Additionally, the influence of graded granulated blast furnace slag powder (GGBS), quicklime, and silica fume on the mechanical properties of HPG-based mortar (HPGM) and HPG-based concrete (HPGC) was discussed. Moreover, the microstructure of HPGM was analyzed using scanning electron microscopy (SEM). A two-dimensional mesoscale model of HPGC was developed to predict how variations in HPG content, coarse aggregate characteristics, and interfacial transition zone (ITZ) characteristics influence the compressive strength and elastic modulus of HPGC. The experimental results showed that high volumes of HPG weakened the mechanical properties of HPGM and HPGC, while appropriate amounts of mineral admixtures offset the negative effects caused by calcium hydroxide (Ca(OH)2) crystals and impurities within the system. The simulation results indicated that the maximum deviation between the mesoscale model prediction and experimental data was only 8.38%, which verified the accuracy of the mesoscale model prediction. The compressive strength of HPGC initially decreased and subsequently increased with the rise in the modulus and content of coarse aggregate, whereas it declined with higher HPG dosage and increased ITZ thickness. In contrast, the elastic modulus of HPGC showed a gradual increase with rising coarse aggregate content and improved ITZ mechanical properties, while it decreased as HPG content and ITZ thickness increased.
1. Introduction
In the face of global carbon reduction targets, the traditional cement industry urgently needs to transform to reduce its environmental impact and dependence on non-renewable resources. Phosphogypsum, a by-product of phosphate fertilizer production, is characterized by high production volumes and low utilization rates. It primarily consists of calcium sulfate dihydrate (CaSO4·2H2O) and has potential as a novel cementitious material. Research on the application of phosphogypsum in building materials can not only promote the green transformation of the cement industry, but also facilitate the resourceful utilization of industrial waste, which is of great significance to the construction of an environmentally friendly building materials industry [1,2].
In recent years, researchers have intensified their efforts to improve the utilization rate of phosphogypsum by advancing studies on its fundamental properties, modification techniques, and reaction mechanisms. As a result, phosphogypsum has been widely applied in building materials, including cementitious materials, mortar, concrete, and filling materials [3,4,5,6,7,8,9,10]. Regarding the research on the basic properties of phosphogypsum, Zhang et al. [11] and Gao et al. [12] conducted experiments to investigate the mixing ratios, compressive properties, elastic modulus, and water resistance of phosphogypsum, confirming its potential as a non-load-bearing material in engineering applications. Based on the above research, Ma et al. [13] successfully employed phosphogypsum as a filler material for partition walls. In addition, phosphogypsum can serve as a partial replacement for cement in concrete, enabling the adjustment of concrete strength through the optimization of its proportion. Bagade et al. [14] studied the impact of phosphogypsum substitution rates on concrete compressive strength using 5%, 10%, and 15% phosphogypsum replacements. The results showed that the compressive strength of concrete increased with 5% and 10% phosphogypsum replacements but significantly decreased at a 15% phosphogypsum substitution rate. Similarly, Wang et al. [15] tested concrete samples with 20%, 25%, and 30% phosphogypsum replacements. Their results indicated a decrease in compressive strength with increasing phosphogypsum content, suggesting that the phosphogypsum dosage should not exceed 25%.
The above research findings reveal that an appropriate amount of phosphogypsum enhances concrete strength, while an excessive amount weakens it. This is mainly attributed to the lower strength of phosphogypsum compared to cement, which reduces the matrix strength when used in large quantities. To enhance the utilization of phosphogypsum, modified technology has emerged. Huang et al. [16] proposed a novel cementitious material composed primarily of phosphogypsum, supplemented with grade granulated blast furnace slag powder (GGBS), steel slag, cement, and other admixtures. Through carefully designing and optimizing the mix ratio, they successfully developed a water-hardened material with a 28-day compressive strength exceeding 40 MPa. Tian et al. [17] utilized phosphogypsum, combined with cement, GGBS, and other admixtures, to create foam concrete. The experimental results indicated that the strength of the phosphogypsum foam concrete reached its peak when the phosphogypsum content ranged from 45% to 55%, and the ratio of cement to mineral powder was 1:1. Additionally, the research results of Li et al. [18] and An et al. [19] confirmed the strengthening effect of mechanically and thermally modified phosphogypsum on phosphogypsum-based cementitious materials. To elucidate the enhancement mechanism, Liu et al. [20] investigated the phase composition and microstructure of thermally modified phosphogypsum-based cement pastes using XRD and SEM. The results showed that the modified samples exhibited increased hydration products and denser microstructures. Jiang et al. [21] suggested that quicklime could neutralize phosphorus and fluorine impurities in phosphogypsum, increasing the number of contact points of CaSO4·2H2O, thus enhancing the properties of phosphogypsum-based building materials.
On the mesoscale, concrete is recognized as a composite material consisting of coarse aggregate, mortar, and the interfacial transition zone (ITZ). Consequently, employing mesoscale models to reveal the intricate connections between the mesoscale component characteristics and macroscale mechanical properties of concrete represents an efficient and viable approach [22,23]. Wu et al. [24] and Zheng et al. [25] established a two-dimensional (2D) concrete mesoscopic model, revealing the influence of factors, such as coarse aggregate content, the elastic modulus of coarse aggregate, and mortar material, on the elastic modulus of concrete. Zhou et al. [23] and Qu et al. [26], respectively, constructed concrete mesoscopic models of different dimensions to predict the influence of coarse aggregate shape, particle size, and porosity on the compressive strength of concrete. The above research results confirm that the mesoscale model can effectively reflect the effect of mesoscopic components on the compressive strength and elastic modulus of concrete.
In summary, the existing research on phosphogypsum-based materials has predominantly focused on low content levels, with limited studies on high-volume phosphogypsum materials, and performance enhancement technologies remain immature. Additionally, there is a relative lack of combined experimental and simulation studies for phosphogypsum-based concrete at the microscale, mesoscale, and macroscale. Therefore, this study proposed to prepare HPG-based mortar (HPGM) and HPG-based concrete (HPGC) specimens with HPG replacement contents of 40%, 50%, and 60%. The impact of HPG content on the compressive strength and elastic modulus of HPGM and HPGC were investigated. Additionally, the improvements in the macro-mechanical properties of HPGM and HPGC, achieved by incorporating GGBS, quicklime, and silica fume, were systematically analyzed. A microstructural analysis of HPGM was also conducted using SEM. To predict the macroscopic mechanical properties of HPGC under varying conditions, a 2D mesoscale model of HPGC was developed. Based on this, the influence of HPG content, coarse aggregate characteristics (shape, content, elastic modulus) and ITZ characteristics (thickness and mechanical properties) on the compressive strength and elastic modulus of HPGC was quantified. This provides important theoretical support and practical guidance for the engineering application of phosphogypsum at large dosages.
2. Materials and Method
2.1. Raw Materials
Phosphogypsum (PG), primarily consisting of CaSO4·2H2O, inherently lacks cementitious properties. However, some research has shown that high-temperature modification can induce partial dehydration, converting phosphogypsum into α- or β-hemihydrate gypsum (CaSO4·0.5H2O) or even anhydrous gypsum (CaSO4) [18,19,20]. Specifically, high-temperature modification at 160 °C for 2 h effectively promotes the transformation of CaSO4·2H2O into CaSO4·0.5H2O, while requiring a relatively short processing time. The resulting phosphogypsum-based materials exhibit excellent mechanical properties. Accordingly, this study employs high-temperature modification at 160 °C for 2 h to process PG with a particle size of 0.15 mm, aiming to produce excellent performance high-temperature modified phosphogypsum (HPG).
The P·O 42.5 Portland cement was provided by Hailuo Cement Co., Ltd., Guiyang, China, and its specific surface area was 330 m2/kg. The S95 grade granulated blast furnace slag powder (GGBS) was bought from Gongyi Longze Water Purification Materials Co., Ltd., Zhengzhou, China, and has a specific surface area of 450 m2/kg. The ultrafine quicklime with 98.3% effective CaO content, produced by Yibin Sichuan Ash Biotechnology Co., Ltd., Yibin, China, was selected for the test. The silica fume with SiO2 content of 96% or more was selected for the test, which was bought from Henan Province Gongyi Qingyang Water Treatment Materials Co., Ltd., Zhengzhou, China. The chemical compositions of the materials, including cement, PG, HPG, GGBS, quicklime, and silica fume, were shown in Table 1. The experimental photography and microstructures of PG and HPG are shown in Figure 1. Manufactured sand from Guizhou Province, with a fineness modulus of 2.8, was used as fine aggregate. Continuous grading basalt gravels from Guizhou Province with a grain size of 5–25 mm were collected. The retarders belonging to the protein class of retarders were gained from Shanghai Chenqi Chemical Technology Co., Ltd., Shanghai, China. The polycarboxylate superplasticizer with a water reduction rate of 25–27% was obtained from Guizhou Zhucheng Hengchuang Construction Engineering Co., Ltd., Guiyang, China.

Table 1.
Main chemical compositions of raw materials (wt%).

Figure 1.
Powdered forms and microscopic morphology of PG and HPG. (a) PG powder. (b) Microscopic PG. (c) HPG powder. (d) Microscopic HPG.
2.2. Preparation of Specimens
Referring to the Chinese standard GB/T 50081-2019 [27] and JCJ/T 70-2009 [28], the HPGM and HPGC specimens were prepared and tested during the experiment. The size of HPGM specimens for the compression and modulus of elasticity test was 70.7 mm × 70.7 mm × 70.7 mm, 70.7 mm × 70.7 mm × 220 mm, respectively. The size of HPGC specimens for the compression test was 100 mm × 100 mm × 100 mm, and the size for modulus of elasticity was 150 mm × 150 mm × 300 mm. In addition, there were three specimens for each group of performance tests. All the HPGM and HPGC specimens used in this experiment were prepared according to the mixing proportion shown in Table 2 and Table 3. Firstly, the specimens were de-molded 24 h after casting. Then, they were cured at the required age in a standard curing room, maintained at a temperature of (20 ± 2) °C and a relative humidity no less than 95%.

Table 2.
Mixture proportion of HPGM.

Table 3.
Mixture proportion of HPGC.
2.3. Experimental Process
In this research, the PG with a particle size of 0.15 mm was dried in an electric blast drying oven for 2 h at 160 °C. The testing machine model is 101-4B. The microstructural morphology of PG, HPG, and HPGM was observed using SEM, ZEISS GeminiSEM 300, Jena, Germany. Concerning the Chinese standard JGJ/T 70-2009 [29], the uniaxial compression and modulus of elasticity tests of the HPGM specimens were carried out. Meanwhile, the uniaxial compression, splitting tensile, and modulus of elasticity tests of the HPGC specimens were conducted with reference to the Chinese standard GB/T 50081-2019 [28]. The rock and concrete test system (RMT), with the RMT-301 model, was used to evaluate the mechanical properties of HPGM and HPGC.
3. Experimental Results
3.1. Effect of HPG Content on Mechanical Properties of HPGM
To investigate the effect of a high volume of HPG incorporation on the mechanical properties of HPGM, a series of specimens were prepared with HPG substituting cement at ratios of 40%, 50%, and 60%. And the mortar without HPG was the reference group mortar. The outcomes of the 28-day compressive strength and elastic modulus of HPGM are depicted in Figure 2.
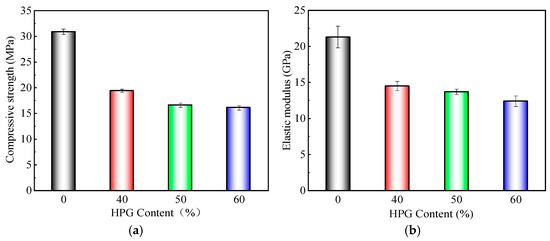
Figure 2.
Effect of HPG content on mechanical properties of HPGM. (a) Compressive strength. (b) Elastic modulus.
As observed from Figure 2, the incorporation of a high volume of HPG significantly affected both the compressive strength and elastic modulus of HPGM. Compared to the reference mortar, which exhibited a compressive strength of 30.9 MPa and an elastic modulus of 31.3 GPa, the HPGM with 40%, 50%, and 60% HPG content showed compressive strengths of 19.4, 16.6, and 16.1 MPa, respectively, with the maximum reduction reaching 47.89%. Similarly, the elastic modulus of HPGM decreased to 14.5, 14.3, and 12.1 GPa, respectively, with a maximum decrease of 43.19%. The experimental findings demonstrate that substituting cement with a high volume of HPG significantly degrades the mechanical properties of the mortar. Notably, both compressive strength and elastic modulus exhibit a gradual decline as the HPG content increases. This is mainly due to the high volume of HPG and its rapid coagulation when in contact with water, which leads to a poor mixing uniformity of the HPGM and increases internal structural defects. These defects weaken the overall integrity of the material, thereby reducing both its compressive strength and elastic modulus. Additionally, the primary hydration product of HPG, CaSO4·2H2O, exhibits inferior strength and wear resistance compared to the hydration products of cement. This disparity further exacerbates the decline in mechanical properties. As HPG content increases, the reduction in compressive strength and elastic modulus becomes more pronounced. Moreover, when excessive HPG is incorporated, the reaction between CaSO4·2H2O and the aluminum phase in the system occurs more readily, generating a significant number of ettringite with expansion. This exacerbates internal stresses and defects, further degrading the mechanical properties of HPGM.
3.2. Effect of Mineral Admixtures on the Mechanical Properties of HPGM
3.2.1. Effect of GGBS on the Compressive Strength of HPGM
Some studies have shown that common mineral admixtures, such as GGBS, silica fume, and quicklime, exhibit excellent pozzolanic or micro-aggregate effects, which can significantly enhance the mechanical properties of HPGM when incorporated in appropriate amounts [29,30]. In this section, HPG was used to replace cement at replacement rates of 40%, 50%, and 60%. Additionally, varying amounts of GGBS (10%, 15%, 20%, 25%) were used to replace part of the remaining cement used to prepare HPGM, with the mortar without GGBS serving as the reference group mortar. The influence of GGBS content on the 28-day compressive strength of HPGM was investigated, and the results are presented in Figure 3.
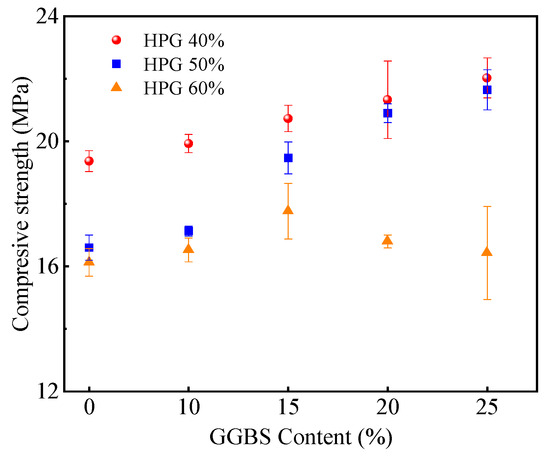
Figure 3.
Effect of GGBS on the compressive strength of HPGM.
Figure 3 demonstrated that GGBS, within a range of 10% to 25%, had a notable impact on the 28-day compressive strength of HPGM. For HPGM with 60% HPG, the compressive strength initially increased and reached a maximum value of 17.8 MPa at 15% GGBS, representing a 10.2% improvement over the reference mortar (16.1 MPa). However, further increases in GGBS content led to a subsequent decrease in compressive strength. For HPGM containing 40% or 50% HPG, the compressive strength gradually increased with the increase in GGBS content. However, when the GGBS content was increased from 20% to 25%, the compressive strength of HPGM increased only slightly. These findings suggested that moderate amounts of GGBS could effectively improve the compressive strength of HPGM, while excessive amounts of GGBS had diminishing returns or even negative effects. The observed phenomenon is primarily attributed to the hydration of GGBS, which consumes Ca(OH)2 crystals within the system, thereby mitigating their adverse effects in the ITZ. Additionally, under the double activation of Ca(OH)2 and sulfate ions, the hydration of GGBS generates a flocculent calcium silicate hydrate (C-S-H) gel, calcium aluminate hydrated (C-A-H) gel, and acicular ettringite. These products interlock and densify the HPGM, thereby further enhancing their compressive strength. However, excessive GGBS substitution reduces cement content, limiting the formation of C-S-H and C-A-H gels from cement hydration and subsequently, weakening the HPGM. Considering the effect of GGBS on the compressive strength of HPGM with 40%, 50% and 60% HPG content, the optimal GGBS substitution rate is 20%.
3.2.2. Effect of Quicklime and Silica Fume on the Mechanical Properties of HPGM
To further enhance the mechanical properties of HPGM, this study prepared control groups of HPGM by using 40%, 50%, and 60% HPG to substitute cement. Meanwhile, based on the previous experimental results and relevant literature, a fixed replacement rate of 20% GGBS was used, with an additional 7% quicklime and 5% silica fume incorporated to prepare HPGM [10]. Using this approach, the effects of these mineral admixtures on the 28-day compressive strength and elastic modulus of HPGM were investigated. The results are shown in Figure 4.
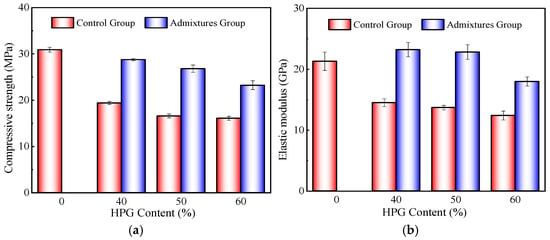
Figure 4.
Effect of mineral admixtures on mechanical properties of HPGM. (a) Compressive strength. (b) Elastic modulus.
As seen from Figure 4, the combined addition of GGBS, quicklime, and silica fume significantly enhances the 28-day compressive strength and elastic modulus of HPGM. Taking HPGM with 50% HPG as an example, the compressive strength and elastic modulus of the HPGM with mineral admixtures were 26.8 MPa and 22.8 GPa, respectively. This represented a remarkable increase of 61.4% and 66.4% compared to the control group HPGM, which had a compressive strength of 16.6 MPa and an elastic modulus of 13.7 GPa. In addition, the compressive strength of HPGM with multiphase admixtures was further improved, compared with HPGM with only 20% GGBS. These findings suggested that the mechanical properties of HPGM can be further bolstered by the proper addition of quicklime and silica fume. The main reason is that quicklime and silica fume possess fine particles, which effectively improve the particle gradation of the HPGM cementitious system and fill the internal pores. Furthermore, the superposition effect is easily produced between multiphase admixtures. The addition of an appropriate amount of quicklime not only eliminates the retardation and deterioration effects produced by the impurities contained in HPG, but also generates a large amount of Ca(OH)2, which activates the activity of GGBS and silica fume materials. During this process, the hydration of GGBS and silica fume consumes Ca(OH)2, mitigating its adverse effects in the ITZ. Moreover, the hydration products, such as C-S-H and C-A-H gels, refine the pore size of the HPGM, improving the bonding between the components, and enhancing the densification of the HPGM. In summary, the appropriate combination of GGBS, quicklime, and silica fume effectively offsets the negative impact of HPG as a cement replacement, significantly enhancing the mechanical properties of HPGM.
3.3. Effect of HPG Content on Mechanical Properties of HPGC
For a systematic investigation of the influence of a high volume of HPG on the mechanical properties of HPGC, this study prepared HPGC specimens containing 40%, 50%, and 60% HPG, respectively. Additionally, there was a reference group concrete without HPG. Subsequently, the 28-day compressive strength and elastic modulus of HPGC were measured. The test results are presented in Figure 5.
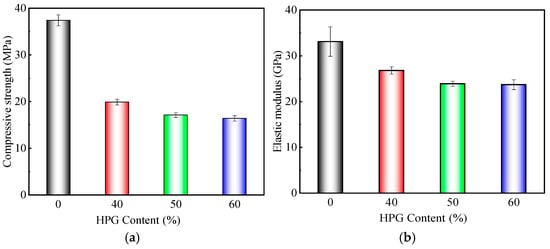
Figure 5.
Effect of HPG content on mechanical properties of HPGC. (a) Compressive strength. (b) Elastic modulus.
Figure 5 illustrated that the compressive strength and elastic modulus of HPGC were significantly reduced after the incorporation of a high volume of HPG. Moreover, as the HPG content increased, the compressive strength and elastic modulus of HPGC decreased gradually. When the HPG content was 40%, the HPGC specimens exhibited a compressive strength of 19.9 MPa and an elastic modulus of 23.7 GPa, representing decreases of 46.8% and 19.0%, respectively, compared to the reference group. As the HPG content increased to 60%, the reductions in compressive strength and elastic modulus of the HPGC escalated to 56.1% and 28.4%, respectively. The reason for the observed phenomenon is that when HPGC is prepared by replacing cement with HPG in high volumes, the amount of C-S-H gel formed by cement hydration in the system is significantly reduced. Correspondingly, the content of CaSO4·2H2O, which exhibits low strength and stability, increases due to the hydration of HPG. This leads to the formation of massive ettringite when CaSO4·2H2O reacts with the aluminum phase in the system. With the substantial accumulation of ettringite, microscopic cracks are easily induced inside the HPGC, resulting in a significant decrease in the compressive strength and elastic modulus. In addition, HPG contains abundant soluble phosphorus, fluorides, and other impurities, which hinder the hydration reaction of the system. Consequently, the internal structure of HPGC becomes more porous, and its compactness is reduced.
3.4. Effect of Mineral Admixtures on Mechanical Properties of HPGC
To eliminate the adverse effects of HPG incorporation on the mechanical properties of HPGC, this study investigated the improvement of compressive strength and elastic modulus of HPGC through the incorporation of mineral admixtures. The results are shown in Figure 6. The control groups were the HPGC specimens with HPG institution contents of 0, 40%, 50%, and 60%. The admixture groups were based on the control groups, with the further addition of 20% GGBS, 7% quicklime, and 5% silica fume.
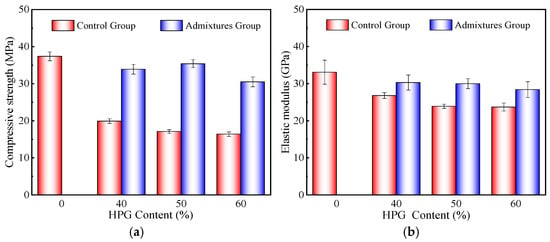
Figure 6.
Effect of mineral admixtures on mechanical properties of HPGC. (a) Compressive strength. (b) Elastic modulus.
Figure 6 indicated that the compressive strength and elastic modulus of HPGC could be effectively improved by adding appropriate amounts of mineral admixtures. Compared with that of 40%, 50% and 60% HPGC (without mineral admixtures), the compressive strength and elastic modulus of HPGC with mineral admixtures increased by 77.9%, 98.2% and 86.0%, respectively, while the elastic modulus increased by 13.1%, 25.5% and 19.8%, respectively. The results showed that the mechanical properties of HPGC can be effectively optimized through the proper proportioning of mineral admixtures, achieving a strength grade of C30. The main reason is the occurrence of a gradient hydration phenomenon when multiple mineral admixtures are mixed. The addition of an appropriate amount of quicklime not only weakens the negative impact of impurities in HPG, but also strengthens the alkalinity of the system. With the hydration reaction, on the one hand, the hydration of GGBS and silica fume consumes the enriched Ca(OH)2 crystals in the system, improving the microstructural morphology of ITZ. On the other hand, the hydration of GGBS and silica fume generates abundant C-S-H and C-A-H gels under the activation of Ca(OH)2. Through that, the internal microstructural pores of HPGC are effectively filled, and the bonding between the components is enhanced. Thus, the compactness of HPGC is improved. In summary, the multiphase admixtures tend to produce advantageous superposition effects among them, which effectively improve the mechanical properties of HPGC.
3.5. Microstructure
To reveal the improvement mechanism of HPGM performance by the above admixtures, the microstructure and product morphology of three groups of HPGM specimens at 28 days were analyzed using SEM in this study. The three groups of HPGM specimens consisted of 50% HPG, 50% HPG-20% GGBS, and 50% HPG-20% GGBS-7% quicklime-5% silica fume, respectively. Among them, the last group of HPGM samples were added externally with quicklime and silica fume. The results are shown in Figure 7.

Figure 7.
Microstructure of HPGM. (a) 50% HPG. (b) 50% HPG-20% GGBS. (c) 50% HPG-20% GGBS-7% quicklime-5% silica fume.
As seen from Figure 7a, the hydration products of HPGM with a 50% HPG substitution content were predominantly lumpy CaSO4·2H2O and flocculent C-S-H gel. However, these hydration products exhibited inadequate interconnectivity among each other, characterized by high porosity and obvious microcracks, resulting in the inferior macroscopic mechanical properties of HPGM. In contrast, when 20% GGBS was doped (e.g., Figure 7b), the internal microstructure of HPGM became significantly denser. The content of pores and microcracks was reduced, and the sizes of microcracks significantly decreased, compared with the HPGM without GGBS substitution. This is because the incorporation of a moderate amount of GGBS reduces the generation of Ca(OH)2 crystals in the system, thereby mitigating the adverse effects stemming from the excessive accumulation of Ca(OH)2 at the ITZ. Furthermore, the synergistic effect of Ca(OH)2 and sulfate ions in the system activates the latent reactivity of the GGBS, fostering the formation of C-S-H and C-A-H gels, as well as ettringite. Based on the above study, when 7% quicklime and 5% silica fume were externally added (e.g., Figure 7c), the hydration products within the HPGM exhibited a tight interlocking arrangement. Moreover, the pores were partially filled with ettringite, and no obvious microcracks were observed. The primary reason is the gradient hydration process between multiphase admixtures, which leads to a superposition effect. This effect not only mitigates the negative impact of impurities in HPG on the hardened matrix, but also enhances the alkaline environment within the system. Subsequently, the alkaline conditions stimulate the Pozzolanic effect of GGBS and silica fume, generating a greater quantity of C-S-H and C-A-H gels, as well as ettringite. This optimization effectively refines the ITZ, fills internal pores, and enhances the interfacial bonding between components, ultimately promoting the mechanical properties of the HPGM.
4. Numerical Simulation
4.1. Mesoscale Model
On the mesoscale, concrete is regarded as a multiphase inhomogeneous composite material. The material properties of the internal components of concrete, e.g., coarse aggregate, mortar matrix, and ITZ, have a significant influence on its macroscopic mechanical properties [31,32,33]. Through constructing concrete mesoscale models, the shape, position, and grading distribution of coarse aggregates in concrete can be accurately portrayed. Moreover, these models can also describe the damage of ITZ and the expansion of cracks, thereby realizing the cross-scale prediction of the mechanical properties of concrete [34,35]. Among them, 2D circular and polygonal aggregate models are the mainstream forms of existing research [32,36]. Therefore, this study employed Python language for the secondary development of the finite element software ABAQUS 2022, constructing the 2D circular and polygonal HPGC model.
4.1.1. Coarse Aggregate Grading and Particle Size Distribution
The gradation and particle size of coarse aggregates are important factors affecting the compactness of concrete. Reasonable coarse aggregate gradation design not only helps to reduce the amounts of cementitious materials, but also effectively fills the internal voids, thereby improving the overall compactness of concrete. Therefore, based on the Fuller grading theory and Walraven formula, this section initially determined the content and particle size range of the coarse aggregates [37,38]. Meanwhile, considering that the range of the coarse aggregate particle sizes used in the actual tests is 5–25 mm, this study divided the range into three intervals, 5–10 mm, 10–15 mm, and 15–25 mm, and assigned each particle size interval in the ratio of approximately 3:3:4.
The specific expression for the Fuller grading theory is given below:
where and are the sieve diameter and maximum coarse aggregate size, respectively; and is the percentage of coarse aggregate mass.
The specific expression of the Walraven formula is as follows:
where refers to the particle size in the concrete section; is the probability that the particle size in the concrete section is smaller than the sieve aperture ; and refers to aggregate percentage, where = 0.75 is generally taken.
4.1.2. Coarse Aggregate Generation and Placement
During the actual mixing, pouring, and molding of concrete, the position of coarse aggregates in concrete presents randomness. In addition, there is no cross-over between coarse aggregate particles. Therefore, the generation, placement, and interference test of coarse aggregates were an important part of the establishment of the mesoscale model. The specific steps for the model generation are as follows:
(1) The volume fraction of coarse aggregates cannot exceed the volume of the mesoscale model, and the location of coarse aggregates cannot exceed the boundary constraints of the mesoscale model. (2) To improve the generation efficiency of the model, priority is given to the generation and placement of coarse aggregates with a larger particle size. (3) The newly generated coarse aggregates must not overlap or intersect with those that are already placed. (4) A sufficient distance must be maintained between coarse aggregates to ensure that a certain thickness of the ITZ surrounds each aggregate. This distance prevents interference between the ITZs.
Based on the above coarse aggregate gradation theory, combined with the steps for coarse aggregate generation and placement, this paper constructed circular aggregate and polygonal aggregate mesoscale models, respectively. Figure 8 gives the schematic diagram of the single coarse aggregate generation and the schematic diagram of the coarse aggregate model under three working conditions.
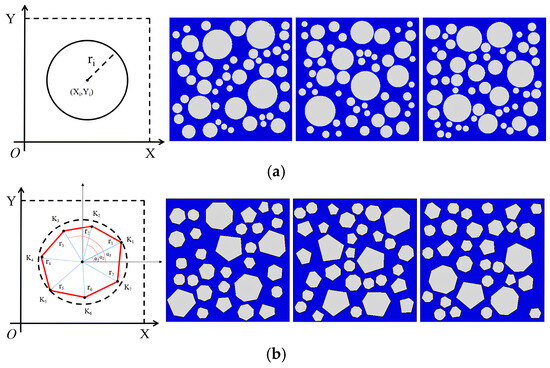
Figure 8.
Diagram of circular and polygonal aggregate model generation. (a) Model with circular aggregate shape. (b) Model with polygonal aggregate shape.
4.2. Constitutive Model
4.2.1. Concrete Plastic Damage Model
Concrete, as a typical brittle material, produces different degrees of damage and stiffness degradation when subjected to external loads. To accurately portray the cumulative effect of damage, stiffness degradation, and plastic deformation of concrete under external loading, the Concrete Damage Plastic (CDP) model has been employed. This model incorporates damage variables, enabling a sophisticated simulation of the nonlinear response of concrete-like brittle materials to applied forces. Recognized for its efficacy in modeling the fracture and damage mechanisms in concrete structures, the CDP model has been widely used for mechanical analyses and safety assessments of concrete structures [39,40].
The CDP model attributes the fracture damage of concrete materials to compression damage or tensile cracking and characterizes the stiffness degradation of the material by introducing the damage variables and . Meanwhile, the model controls the damage evolution process of concrete materials through tensile and compressive equivalent plastic strain parameters (, ), as shown in Figure 9. This not only accurately portrays the degradation characteristics of material stiffness, but also effectively controls the whole process of concrete damage evolution. Considering this, this paper adopted the concrete constitutive relationship provided by the Chinese standard GB 50010-2010 [41] to determine the parameters in the CDP model. The equations are as follows:
where and denote the concrete compressive and tensile stresses, respectively. is the tensile damage factor. refers to the compressive damage factor. refers to the initial modulus of elasticity. and denote the compressive and tensile equivalent plastic strain, respectively. is the inelastic strain. refers to the cracking strain.
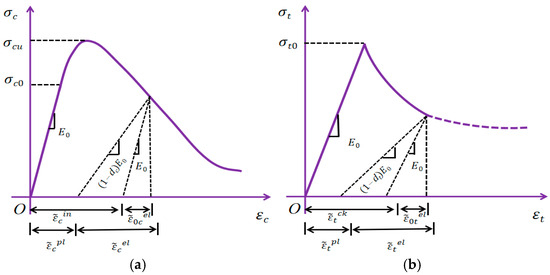
Figure 9.
Diagram of concrete damage plastic constitutive model. (a) Compressive damage plastic constitutive. (b) Tensile damage plastic constitutive.
4.2.2. Parameters of Each Component Material
In the mesoscopic simulation of concrete, coarse aggregates were considered linearly elastic materials due to their strength characteristics, and the numerical simulation results agree with the experimental data [42]. For the complex mechanical behavior of mortar and ITZ, the CDP model was adopted. This kind of treatment was consistent with the research ideas of Jin [43] and Xiao [44]. The mechanical parameters for the mortar were set as follows: the compressive strength and elastic modulus were directly taken from the experimental data shown in Figure 2. The tensile strength was determined as one-tenth of the compressive strength [45,46]. The Poisson ratio was established based on the data provided in the literature [47]. Regarding the mechanical properties of the ITZ, some studies [48,49] suggested that the ratio of ITZ to mortar mechanical properties typically ranges from 0.75 to 0.90. To quantify this characteristic, a value of 0.8 was adopted in this study. The specific material parameters for HPGC are detailed in Table 4.

Table 4.
Mechanical property parameters of materials.
4.3. Validation of the Mesoscale Model
Based on the mechanical property test parameters of HPGM and HPGC, a 2D mesoscale concrete model was constructed in this study, aiming to reveal the mechanical response of HPGC under uniaxial compression conditions using numerical simulation. Considering the randomness of coarse aggregate distribution in actual concrete, the mesoscale model simulated three circular aggregate specimens with a size of 100 mm × 100 mm and a coarse aggregate content of approximately 40%. The ITZ thickness of the mesoscale model was determined to be 0.2 mm, according to Kim et al. [48]. To balance the computational efficiency and simulation accuracy, the model mesh size was set to 1 mm and divided using a quadrilateral-dominated mesh in ABAQUS software.
4.3.1. Verification of Damage Modes of HPGC
Some experimental studies have shown that the compressive damage patterns of concrete specimens in high- and low-friction environments exhibit two typical patterns: “X” and “V”. This phenomenon was also confirmed by numerical simulation results [50,51]. Given the results presented above, this study simulated the failure of HPGC under the conditions of high friction and low friction, respectively, using fixed hinges to support the whole bottom or support only the midpoint of the bottom. The schematic diagrams are shown in Figure 10. Additionally, the detailed material parameters of coarse aggregates, 60% HPGM, and the corresponding ITZ in Table 4 were embedded in the model. As seen in Figure 11, HPGC specimens in the field test exhibited a bi-directional “X” damage pattern, which is consistent with the damage characteristics observed in the mesoscale model under high friction constraints. Therefore, the fixed hinge supporting all the bottoms was chosen for the subsequent studies.
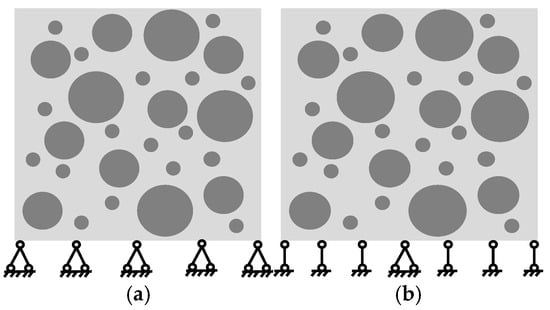
Figure 10.
Bottom boundary conditions. (a) High friction. (b) Low friction.
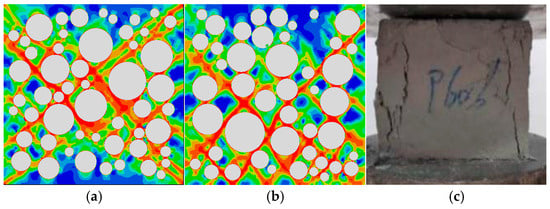
Figure 11.
Comparison of failure modes of different bottom boundary conditions. (a) High friction. (b) Low friction. (c) Experimental shooting.
4.3.2. Verification of Mechanical Properties of HPGC
To further verify the effectiveness of the HPGC mesoscale model, the detailed material parameters of coarse aggregates, different components of HPGM, and the corresponding ITZ in Table 4 were embedded in the model. Subsequently, a compression test simulation study was carried out for HPGC. The comparison of deviation between the simulation results and the experimental results is summarized in Table 5. Through an in-depth analysis of Table 5, the uniaxial compressive strength and elastic modulus predicted by the HPGC model agreed well with the experimental results. Taking the HPG content as a variable, the maximum deviation of the simulated compressive strength from the measured value was only 5.74% when the HPG dosage was 40%, while the maximum difference in the elastic modulus was 8.38% when the HPG dosage was 60%. It is noteworthy that the maximum deviation between model predictions and experimental data never exceeded the 10% threshold, regardless of the variation in HPG content. This verified the high accuracy and reliability of the model in predicting the compressive strength and elastic modulus of HPGC.

Table 5.
Deviations in mechanical properties of HPG concrete for each group.
4.4. Analysis of Simulation Results
4.4.1. Effect of HPG Content on Compressive Mechanical Properties of HPGC
To investigate the effect of HPG content on the compressive mechanical properties of HPGC, this study employed a circular aggregate model to predict the compressive strength and elastic modulus of HPGC containing 40%, 50%, and 60% HPG content. Additionally, to minimize the effect of random aggregate distribution on the model outcomes, three working conditions were set for each group of HPGC to conduct the simulations. The results are shown in Figure 12 and Figure 13.
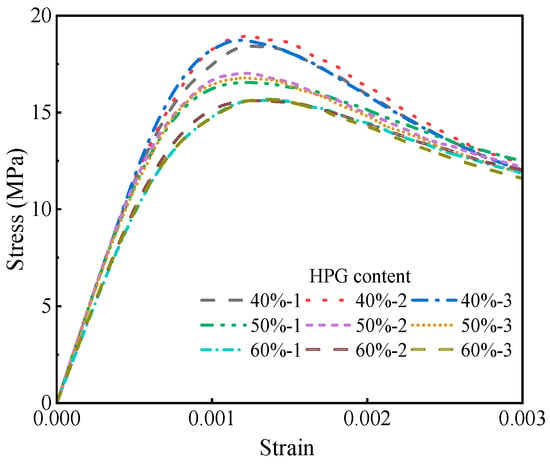
Figure 12.
Simulation results of stress-strain curves for HPGC with varying HPG content.
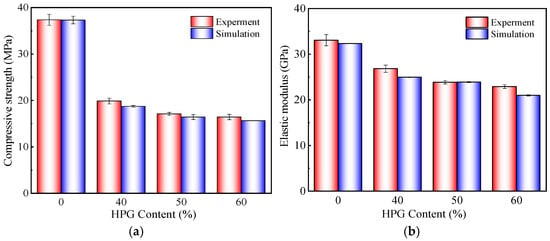
Figure 13.
Comparison between experimental and simulation results of HPGC. (a) Compressive strength. (b) Elastic modulus.
Figure 12 revealed that the HPG content exerted a significant influence on the mechanical properties of HPGC, manifesting in alterations to the stress-strain curve morphology, compressive strength, and elastic modulus. When the HPG content increased, the peak stress and elastic modulus of HPGC showed a decreasing trend, while the peak strain shifted to the right. Under a fixed HPG dosage, the stress-strain curves of each group of HPGC specimens under the three working conditions showed the same overall direction, but the curves fluctuated slightly near the peak stress and in the softening stage. Specifically, these curves can be categorized into three stages: (a) The initial loading stage, where the load is small and there is no significant change in the specimens. During this stage, all specimens exhibit approximately linear behavior. (b) With the increase in load, damage and cracking begin to occur at the ITZ. Subsequently, the cracks gradually propagate into the mortar, resulting in a nonlinear behavior characterized by a reduction in stiffness in the ascending portion of the curve. (c) After the peak load, the cracks rapidly propagate and penetrate through the specimens, causing a decrease in stress until failure occurs. As seen in Figure 13, the increase in HPG substitution rate significantly reduced the compressive strength and elastic modulus of HPGC. The simulated trends were consistent with the experimental observations. Compared to the experimental reference concrete (37.37 MPa compressive strength, 33.07 GPa elastic modulus), HPGC simulations with 40%, 50%, and 60% HPG content exhibited decreases in compressive strength of 49.9%, 56.1%, and 58.1%, respectively, and in elastic moduli of 24.6%, 27.8%, and 36.6%, respectively. These findings indicated that with the HPG content above 40%, both the compressive strength and elastic modulus of HPGC decreased significantly. However, within the 40–60% HPG substitution range, the relative differences between the compressive strength and elastic modulus of HPGC remained narrow, with just 16.4% and 15.9%, respectively. This phenomenon is attributed to the fact that under compressive loading, the coarse aggregate remains largely intact, with the strength of HPGC primarily depending on the mechanical properties of the mortar matrix and ITZ. When the HPG substitution rate ranges from 40% to 60%, the mechanical properties of both the mortar matrix and the ITZ are significantly weakened, resulting in a marked decrease in the mechanical performance of HPGC. However, within this range, the differences in the mechanical properties of the mortar matrix and ITZ become insignificant, leading to minor variations in the results of the mechanical properties predicted by the HPGC mesoscale model.
4.4.2. Effect of Coarse Aggregate Shape on Compressive Mechanical Properties of HPGC
Due to the difference in the shape of coarse aggregates, concrete can be categorized into two main types: pebble-type concrete and gravel-type concrete. Accordingly, in this study, two types of HPGC mesoscale models with circular and polygonal aggregate shapes were constructed, with the other conditions remaining unchanged, aiming to investigate the effect of coarse aggregate shape on the mechanical properties and damage modes of HPGC. The results are, respectively, shown in Figure 14 and Figure 15.
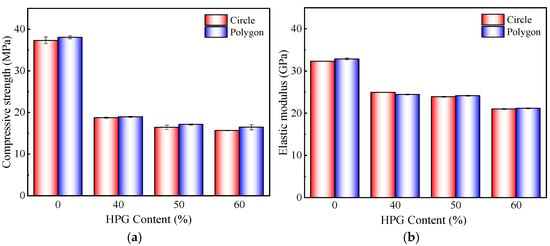
Figure 14.
Comparison of simulation results of mechanical properties of HPGC with different aggregate shapes. (a) Compressive strength. (b) Elastic modulus.

Figure 15.
Comparison of failure mode of HPGC with different aggregate shapes. (a) The failure mode of HPGC with circular aggregate shape. (b) The failure mode of HPGC with polygonal aggregate shape.
As shown in Figure 14, the compressive strength and elastic modulus predictions of the polygonal aggregate model were slightly higher than those of the circular aggregate model. However, the discrepancies between the predictions of the two models were minimal, with none exceeding 1%. The differences in compressive strength were 1.0%, 0.9%, and 0.5%, respectively, and the differences in elastic moduli were 0.8%, 0.8%, and 0.5%, respectively. This comparison indicated that the shape of coarse aggregates had a negligible effect on the compressive strength and elastic modulus of HPGC. Although polygonal aggregates, being more angular than circular ones, enhance interlocking with the mortar matrix and strengthen HPGC integrity, they also lead to a significant increase in the ITZ content. Since the ITZ is the vulnerable section with inferior mechanical properties in HPGC, excessive ITZ negatively impacts its overall performance. In summary, the polygonal aggregate model shows a slight but insignificant advantage over the circular aggregate model. Figure 15 revealed the damage pattern of HPGC when subjected to external loading. In the initial loading stage, the damage first occurred at the ITZ. Then, as the internal stress of HPGC continuously increased, the damaged cracks at the ITZ gradually connected. Subsequently, the connected damage cracks extended to the adjacent mortar matrix region, leading to the redistribution of internal stresses in the HPGC. When the compressive stress in the HPGC reached its peak, the internal cracks in the mortar rapidly expanded and connected. Ultimately, this led to the formation of a penetrating main crack, which triggered the fracture damage of the HPGC. Comparing the damage modes of the circular and polygonal aggregate models, the damage process and final morphology of the two models were similar. In brief, the two models exhibited their characteristics in performance prediction for HPGC, and the numerical differences were minimal. To simplify the simulation process, the coarse aggregates in the subsequent models were uniformly adopted as circles.
4.4.3. Effect of Coarse Aggregate Content on Compressive Mechanical Properties of HPGC
Aggregates typically serve as the skeleton of concrete, and their content significantly influences the mechanical properties of the composite material. Therefore, the present study, varying the volume fractions of coarse aggregate at 20%, 25%, 30%, 35%, 40%, and 45%, established mesoscale models to assess the influence of aggregate content on the stress-strain behavior, compressive strength, and elastic modulus of HPGC. The simulation results are depicted in Figure 16 and Figure 17.
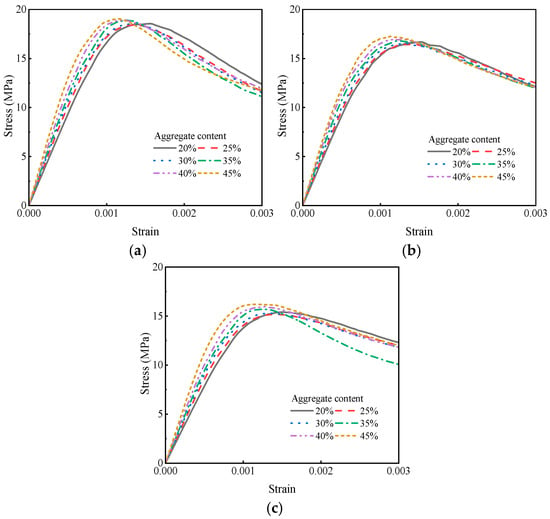
Figure 16.
Simulation results of the stress-strain curve of HPGC with different coarse aggregate content. (a) HPGC with 40% HPG. (b) HPGC with 50% HPG. (c) HPGC with 60% HPG.
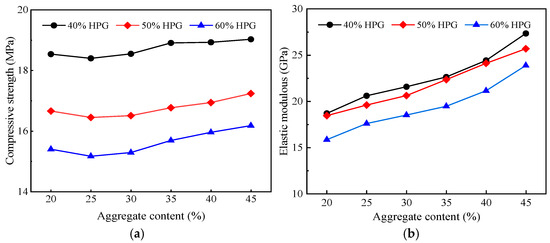
Figure 17.
Simulation results of mechanical properties of HPGC with different aggregate content. (a) Compressive strength. (b) Elastic modulus.
As seen in Figure 16, the stress-strain curves for HPGC with 40%, 50%, and 60% HPG content exhibited similar overall trends upon comparison. However, slight fluctuations in the curves were noted near the peak stress and during the softening stage for each group of HPGC. Taking the HPGC with 40% HPG as an example, the peak strain of HPGC gradually shifted to the left with the increase in coarse aggregate content. The softening part of the HPGC stress-strain curve gradually became steeper, indicating that HPGC exhibited greater brittleness as the aggregate content increased. Specifically, as the coarse aggregate content increased, the compressive strength of HPGC with 40%, 50%, and 60% HPG content showed a tendency to first decrease and then increase, while the elastic moduli gradually increased with the increase in coarse aggregate content, which was depicted in Figure 17. Fixing the coarse aggregate content at 25%, the compressive strengths of the three groups of HPGC all decreased to their lowest levels, which were 0.8%, 1.3%, and 1.5% lower than those at a coarse aggregate content of 20%, respectively. However, when the coarse aggregate content was increased to 45%, the compressive strength of the three groups of HPGC improved by 3.4%, 4.8%, and 6.7%, respectively, compared to the coarse aggregate content of 25%. The main reason is that, in the mortar matrix, coarse aggregates can be regarded as impurities. As the coarse aggregate content increases from 20% to 25%, the impurity content in the mortar matrix also rises, leading to an increase in internal defects, such as ITZ, pore, and crack content. This, in turn, reduces the overall mechanical properties of the HPGC. However, coarse aggregates generally exhibit better strength than the mortar matrix and can enhance the interlocking between coarse aggregates and the mortar matrix. With the further increase in coarse aggregate content, its improvement effect on the compressive strength of HPGC offsets its negative impact. In contrast, the elastic moduli of the three groups of HPGC show a positive correlation with the increases in coarse aggregate content. When the coarse aggregate content increases from 20% to 45%, the elastic modulus enhancement is 46.3%, 39.3%, and 50.7% for HPGC containing 40%, 50%, and 60% HPG, respectively. Thus, it is evident that the effect of coarse aggregate content on the elastic modulus of HPGC is more significant than its effect on compressive strength.
4.4.4. Effect of Coarse Aggregate Elastic Modulus on Compressive Mechanical Properties of HPGC
Due to the variation in geographic locations, environments, and economic conditions, there are significant differences in the properties of coarse aggregates selected from various regions. Therefore, this study fixed both HPG and coarse aggregate content at 40%, varying the elastic modulus of coarse aggregates at 53 GPa, 63 GPa, 73 GPa, 83 GPa, and 93 GPa, aiming to investigate the impact of the elastic modulus of aggregates on the mechanical properties of HPGC. The resulting simulations are presented in Figure 18.
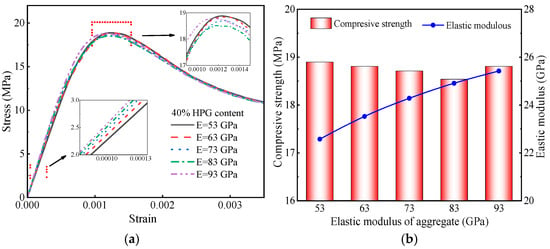
Figure 18.
Simulation results of mechanical properties of HPGC with different elastic moduli of coarse aggregate. (a) Stress-strain curve. (b) Compressive strength and elastic modulus.
As shown in Figure 18, changes in the elastic modulus of the coarse aggregate had minimal impact on the overall trend of the HPGC stress-strain curve. However, this significantly influenced the compressive strength and elastic modulus of HPGC, which was particularly evident in the linear stage and near the peak stress, where noticeable fluctuations occurred. Specifically, as the elastic modulus of the coarse aggregate increased, the compressive strength of HPGC displayed an initial decrease, followed by an increase. When the elastic modulus of the coarse aggregate was set at 83 GPa, the HPGC exhibited its lowest compressive strength, at 18.54 MPa, which was 1.9% lower than the compressive strength of HPGC with a coarse aggregate elastic modulus of 53 GPa. The elastic modulus of HPGC gradually increased as the elastic modulus of the coarse aggregate rose. Notably, as the elastic modulus of the coarse aggregate elevated to 93 GPa, the elastic modulus of HPGC increased to 25.42 GPa, marking a 12.6% improvement compared to HPGC with a 53 GPa coarse aggregate elastic modulus. The above results revealed that the fluctuations in the elastic modulus of coarse aggregates, ranging from 53 to 93 GPa, obviously affected the compressive strength and elastic modulus of HPGC. However, the magnitude of the impact appeared to be slight, especially in the compressive strength. Additionally, the high elastic modulus of coarse aggregates did not necessarily improve the performance of HPGM. Similarly, other studies in the literature [52] also observed that concrete achieves greater strength when the elastic modulus of the aggregate closely matches that of the mortar. Conversely, the greater the difference between them, the lower the strength of the concrete. Therefore, in the subsequent preparation and applications of HPGC, it is advisable to choose coarse aggregates with an elastic modulus similar to the mortar, based on specific requirements, to achieve a higher compressive strength.
4.4.5. Effect of ITZ Thickness on Compressive Mechanical Properties of HPGC
At the mesoscale, ITZ is one of the critical components of concrete. Some studies indicated that the actual thickness of the ITZ in concrete is approximately 10–50 μm. However, when the ITZ thickness is set too small in the mesoscale model, mesh deformations may occur, making model convergence difficult. If the ITZ thickness is set between 100 and 800 μm, and appropriate mechanical parameters are selected, the numerical simulation results align well with experimental data [48,49]. Therefore, to investigate the effect of ITZ thickness on the mechanical properties of HPGC, the ITZ thicknesses were set to 0, 0.02, 0.06, 0.2, 0.6, and 1 mm in this study. The contents of coarse aggregates and HPG in the mesoscale model were fixed at 40%, and the elastic modulus of the coarse aggregates was set at 73 GPa. Based on these parameters, mechanical simulations were performed to analyze the concrete behavior at different ITZ thicknesses. The results are depicted in Figure 19.
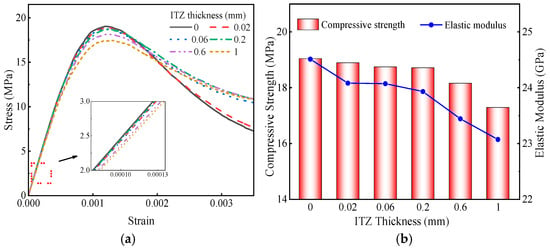
Figure 19.
Simulation results of mechanical properties of HPGC with different ITZ thicknesses. (a) Stress-strain curve. (b) Compressive strength and elastic modulus.
As shown in Figure 19, the overall trend of HPGC stress-strain curves of different ITZ thicknesses appeared to be similar. Notably, for HPGC without ITZ or with an ITZ thickness in the range of 0 to 0.01 mm, the slope of the descending portion of the stress-strain curve exhibited a greater magnitude. As the ITZ thickness further increased, the slope tended to flatten. For the compressive strength and elastic modulus of HPGC, they showed a gradual decrease with the increase in ITZ thickness. When the ITZ thickness increased to 0.2 mm, the compressive strength and elastic modulus of the HPGC decreased to 18.89 MPa and 24.08 GPa, respectively. Compared to HPGC without an ITZ or with an ITZ thickness smaller than 10−2 mm, the differences were within 2% and could be negligible. As the ITZ thickness further increased to 1 mm, the HPGC exhibited its lowest compressive strength and elastic modulus at 17.29 MPa and 23.07 GPa, respectively. Compared to HPGC without an ITZ, the maximum reduction in compressive strength and elastic modulus was 9.2% and 5.9%, respectively. This phenomenon is attributed to the complex structure and inferior mechanical properties of the ITZ, which make it more susceptible to damage under external loads. Specifically, an increase in ITZ thickness results in a relative decrease in the effective mortar matrix content within the model. Consequently, compression damage and crack propagation occur more easily under compressive loads, reducing the mechanical performance of HPGM. In conclusion, the ITZ thickness significantly influences the mechanical properties and stress-strain behavior of concrete. Moreover, the simulation results indicate that an ITZ thickness of 0.2 mm is considered reasonable in this simulation and should not be ignored or taken to be too large or too small.
4.4.6. Effect of ITZ Mechanical Parameters (ITZMP) on Compressive Mechanical Properties of HPGC
Research has shown that coarse aggregates are considered linearly elastic materials, which have little effect on the mechanical properties of concrete [42]. However, the ITZ in concrete is a fragile component that directly and significantly affects the overall mechanical performance of the material [38,40]. Hence, in the mesoscale model, the ITZMP were set at ratios of 0.45, 0.6, 0.75, 0.8, 0.85, and 0.9 relative to the mechanical parameters of the mortar. The ITZ thickness was maintained at 0.2 mm in the mesoscale model, with 40% content of both coarse aggregates and HPG, and the elastic modulus of the coarse aggregate was fixed at 73 GPa. This approach was used to quantify the influence of ITZMP on the stress-strain curve, compressive strength, and elastic modulus of HPGC. The results are depicted in Figure 20 and Figure 21.
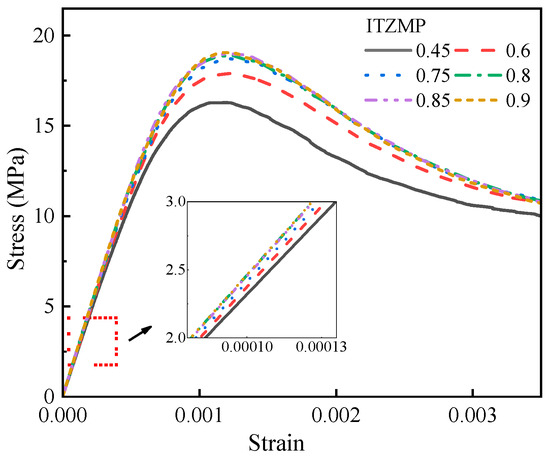
Figure 20.
Simulation results of stress-strain curves of HPGC with different ITZMP.
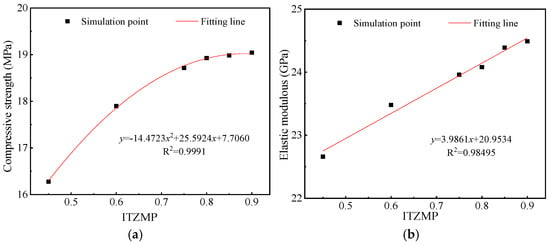
Figure 21.
Simulation results of mechanical properties of HPGC with different ITZMP. (a) Compressive strength. (b) Elastic modulus.
As illustrated in Figure 20, with the increase in the ITZMP, both the compressive strength and elastic modulus of HPGC exhibited a gradual increasing tendency. Notably, as the ITZMP increased from 0.45 to 0.75, the softening stage of the stress-strain curve experienced a more pronounced change, characterized by a significant reduction in residual stress. As the ITZMP continued to increase, the overall change pattern of the stress-strain curve tended to moderate, with the variation being relatively limited. Specifically, from Figure 21, when the ITZMP increased from 0.6 to 0.75, the HPGC compressive strength rose by 4.6%. However, as the ITZMP increases from 0.75 to 0.9, the enhancement in HPGC compressive strength was only 1.7%. The findings indicate that although a moderate increase in the ITZMP positively influences the compressive strength of HPGC, this effect diminishes once the ITZMP exceeds a certain threshold. Data analysis reveals a significant quadratic relationship between the compressive strength of HPGC and ITZMP, with a correlation coefficient of 0.9991. In contrast, the correlation between the elastic modulus and ITZMP follows a linear trend, with a correlation coefficient of 0.9850. This is attributed to the fact that the ITZ, being the weakest section of HPGC, significantly affects its performance. An increase in ITZMP improves the mechanical properties of the ITZ, thereby enhancing the overall mechanical properties of HPGC.
5. Conclusions
In this study, a comprehensive investigation into the mechanical properties of HPGM and HPGC was conducted. Initially, experiments were conducted to explore the impact of HPG content and the addition of mineral admixtures on the mechanical properties of these materials. Following these experiments, a mesoscale model for HPGC was constructed to predict the effects of HPG content, coarse aggregate, and ITZ on the compressive strength and elastic modulus of HPGC. The main conclusions are as follows:
- (1)
- The replacement cement with a high volume of HPG resulted in a significant decrease in the mechanical properties of HPGM and HPGC. Moreover, as the HPG content increased, the compressive strength and elastic modulus of HPGM and HPGC gradually decreased. Notably, the influence of HPG content on the compressive strength of HPGM and HPGC was higher than that on the elastic modulus.
- (2)
- The incorporation of GGBS could significantly improve the mechanical properties of HPGM and HPGC, with 20% GGBS content being the optimal ratio for HPGM with a high volume of HPG. Additionally, adding an appropriate amount of quicklime and silica fume further enhanced the compressive strength and elastic moduli of HPGM and HPGC. The results demonstrate that the appropriate incorporation of mineral admixtures can significantly enhance the mechanical properties of HPGM and HPGC at 40%, 50%, and 60% dosages. This improvement brings their strength levels in line with, or even exceeding, the requirements for the corresponding grades of mortar and concrete. This approach not only offers innovative strategies for the development and application of green building materials in practical engineering, but also provides an effective solution for mitigating the environmental impact of phosphogypsum.
- (3)
- A 2D mesoscale model for HPGC was established, and the compressive strength and elastic moduli of HPGC with 40%, 50%, and 60% HPG content were predicted. Upon analysis, the simulation results agreed well with the experimental results. Furthermore, the maximum deviations of compressive strength and elastic modulus were 5.74% and 8.38%, respectively. Both of them were less than 10%, which verified the accuracy of the mesoscale model. Mesoscopic numerical simulation not only facilitates an in-depth analysis of the mechanical properties and failure modes of concrete in practical engineering applications, but also accurately predicts the effects of each component on the mechanical properties of concrete. Furthermore, it provides essential theoretical support for engineering design, reduces the trial-and-deviation process, and significantly improves engineering efficiency.
- (4)
- The shape of the coarse aggregate had a minimal effect on the compressive strength and elastic modulus of HPGC, as predicted by the mesoscale model. As the elastic modulus and content of coarse aggregate increased, the compressive strength of HPGC initially decreased and then increased, while the elastic modulus of HPGC gradually increased. When the ITZ thickness increased, both the compressive strength and elastic modulus of HPGC decreased gradually. Conversely, as the ITZMP increased, the compressive strength and elastic modulus of HPGC gradually enhanced, although the rate of change diminished once a certain threshold was surpassed.
Author Contributions
Methodology, Y.C. and S.W.; Validation, F.Z., W.L. and G.S.; Formal analysis, Q.L., J.H. and Z.Y.; Investigation, L.W.; Resources, L.L.; Writing—original draft, X.C.; Writing—review & editing, P.L.; Funding acquisition, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Natural Science Foundation of China (grant numbers 52178182, 52108262 and U1934217), the Science and Technology Research and Development Program Project of China Railway Group Limited (Major special project, No.: 2020-Special-02, 2021-Special-08, 2022-Special-09; Major projects, No.: 2023-Major projects-07, 2023-Major projects-08, 2021-Special-02; Key project, No.: 2022-Key-46), and the Science and Technology Research and Development Subject of China Construction Second Engineering Bureau Ltd. (No.: 2024ZC120012 and 2023ZX12001). The authors have also received research grants from the Natural Science Foundation for Distinguished Young Scholars of Hunan Province (2022JJ10075), and the Hunan Science and Technology Plan Project (2023SK2014).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding authors.
Conflicts of Interest
Authors Qizhi Li and Guangqiang Shao were employed by the China Construction Second Engineering Bureau Ltd. Authors Peng Liu and Zhiwu Yu were employed by the China Railway Group Ltd. Authors Feng Zhang and Wei Li were employed by the China Railway 20th Bureau Group Sixth Engineering Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zhang, J.; Xie, W.; Dong, X.; Yang, H. Research progress on comprehensive utilization of phosphogypsum for materials: A review. Mater. Rep. 2023, 37, 22010110. [Google Scholar]
- Wei, Z.Q.; Deng, Z.B. Research hotpots and trends of comprehensive utilization of phosphogypsum: Bibliometric analysis. J. Environ. Radioact. 2022, 242, 106778. [Google Scholar] [CrossRef]
- Qin, X.; Cao, Y.; Guan, H.; Hu, Q.; Liu, Z.; Xu, J.; Hu, B.; Zhang, Z.; Luo, R. Resource utilization and development of phosphogypsum-based materials in civil engineering. J. Clean. Prod. 2023, 387, 135858. [Google Scholar] [CrossRef]
- Calderón-Morales, B.R.; García-Martínez, A.; Pineda, P.; García-Tenório, R. Valorization of phosphogypsum in cement-based materials: Limits and potential in eco-efficient construction. J. Build. Eng. 2021, 44, 102506. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Xie, F.; Guo, J.Y. Study on performance optimization and mechanism of phosphogypsumbased composite cementitious materials. Inorg. Chem. Ind. 2022, 54, 136–145. [Google Scholar]
- Shen, Y.; Qian, J.; Huang, Y.; Yang, D. Synthesis of belite sulfoaluminate-ternesite cements with phosphogypsum. Cem. Concr. Compos. 2015, 63, 67–75. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Y.S.; Yan, Y. Utilization of original phosphogypsum as raw material for the preparation of self-leveling mortar. J. Clean. Prod. 2016, 127, 204–213. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, J.; Chen, F.; Shui, Z. The chloride permeability of persulphated phosphogypsum-slag cement concrete. J. Wuhan Univ. Technol.-Mater. 2016, 31, 1031–1037. [Google Scholar] [CrossRef]
- Jiang, G.; Wu, A.; Wang, Y.; Lan, W. Low cost and high efficiency utilization of hemihydrate phosphogypsum: Used as binder to prepare filling material. Constr. Build. Mater. 2018, 167, 263–270. [Google Scholar] [CrossRef]
- Wu, H.K.; Cheng, X.; Wang, L.L. Research on the performances of high-temperature modified phosphogypsum-mineral powder-cement mortar. Non-Met. Mines 2022, 45, 30–33. [Google Scholar]
- Zhang, H.G.; Wu, Q.; Jia, X.F.; Chen, H.N.; Xie, G.Y. Experimental investigation on compressive strength of cast-in-situ phosphogypsum. J. Hunan Univ. 2016, 43, 127–134. [Google Scholar]
- Gao, F.; Zhao, Z.M.; Quan, S.C.; Yao, Y.; Yang, L. Experimental study on elastic modulus and poisson ration of the building phosphogypsum. Low Temp. Archit. Technol. 2017, 39, 1–4. [Google Scholar]
- Ma, K.J.; Gao, F.G.; Zhang, H.G.; Luo, Y.Q.; Duan, Y.Z.; Jiang, Y.W. Energy-saving and structure integration of new reinforced concrete structure system. J. Guizhou Univ. Technol. 2008, 37, 34–43. [Google Scholar]
- Bagade, M.A.; Satone, S.R. An experimental investigation of partial replacement of cement by various percentage of phosphogypsum in cement concrete. Int. J. Eng. Res. Appl. 2012, 2, 785–787. [Google Scholar]
- Wang, Y.Y.; Wang, J.R.; Liu, J.X.; Ren, J. Research on preparation of binding material and concrete with phosphogypsum. Multipurp. Util. Miner. Resour. 2014, 5, 70–73. [Google Scholar]
- Huang, Y.; Lin, Z.S. Investigation on phosphogypsum-steel slag-granulated blast-furnace slag-limestone cement. Constr. Build. Mater. 2010, 24, 1296–1301. [Google Scholar] [CrossRef]
- Tian, T.; Yan, Y.; Hu, Z.; Xu, Y.; Chen, Y.; Shi, J. Utilization of original phosphogypsum for the preparation of foam concrete. Constr. Build. Mater. 2016, 115, 143–152. [Google Scholar] [CrossRef]
- Li, B.; Li, L.; Chen, X.; Ma, Y.; Zhou, M. Modification of phosphogypsum using circulating fluidized bed fly ash and carbide slag for use as cement retarder. Constr. Build. Mater. 2022, 338, 127630. [Google Scholar] [CrossRef]
- An, H.; Fu, R.; Lu, Y.; Kong, D.; Luo, S.; Wang, L.; Lv, F. Effect of heat treatment time on splitting tensile properties of phosphogypsum-based composite cementitious material. Bull. Chin. Ceram. Soc. 2022, 41, 545–552. [Google Scholar]
- Liu, S.; Ouyang, J.; Ren, J. Mechanism of calcination modification of phosphogypsum and its effect on the hydration properties of phosphogypsum-based supersulfated cement. Constr. Build. Mater. 2020, 243, 118226. [Google Scholar] [CrossRef]
- Jiang, G.Z.; Wu, A.X.; Wang, Y.M.; Li, J.Q. Effect of lime on properties of filling cementitious material prepared by hemihydrate phosphogypsum. J. Chin. Ceram. Soc. 2020, 48, 86–93. [Google Scholar]
- Zhou, C.S.; Li, K.F.; Ma, F. Numerical and statistical analysis of elastic modulus of concrete as a three-phase heterogeneous composite. Comput. Struct. 2014, 139, 33–42. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Jin, H.; Wang, B.L. Modeling and mechanical influence of meso-scale concrete considering actual aggregate shapes. Constr. Build. Mater. 2019, 228, 116785. [Google Scholar] [CrossRef]
- Wu, B.J.; Li, Z.X.; Tang, K.K. Numerical modeling on micro-to-macro evolution of crack network for concrete materials. Theor. Appl. Fract. Mech. 2020, 107, 102525. [Google Scholar] [CrossRef]
- Zheng, J.; Zhou, X.; Wu, Z.; Jin, X. Numerical method for predicting young’s modulus of concrete with aggregate shape effect. J. Mater. Civ. Eng. 2011, 23, 1609–1615. [Google Scholar] [CrossRef]
- Qu, H.C.; Chen, G.R. Numerical simulation of different-shaped random aggregates’ influence on concrete’s compression strength. Adv. Mater. Res. 2008, 33–37, 623–630. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- JGJ/T 70-2009; Standard for Test Method of Basic Properties of Construction Mortar. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2009.
- Cheng, X.; Chen, S.H.; Hu, Q.; Liu, C.; Wang, L.L.; Kong, D.W. Study on the strength performance of modified phosphogypsum-based cement mortar. Non-Met. Mines 2022, 45, 37–40+45. [Google Scholar]
- Buhari, B.M.; Raju, R. Flexural behavior of ternary blended concrete containing silica fume and phosphogypsum. Int. J. Sci. Technol. Eng. 2016, 3, 9–14. [Google Scholar]
- Li, K.-Q.; Li, D.-Q.; Li, P.-T.; Liu, Y. Meso-mechanical investigations on the overall elastic properties of multi-phase construction materials using finite element method. Constr. Build. Mater. 2019, 228, 116727. [Google Scholar] [CrossRef]
- Zhou, X.Q.; Hao, H. Mesoscale modelling of concrete tensile failure mechanism at high strain rates. Comput. Struct. 2008, 86, 2013–2026. [Google Scholar] [CrossRef]
- Liu, Z.; Peng, H.; Cai, S.C. Mesoscale analysis of stress distribution along ITZs in recycled concrete with variously shaped aggregates under uniaxial compression. J. Mater. Civ. Eng. 2015, 27, 04015024. [Google Scholar] [CrossRef]
- Jin, L.; Wan, S.; Li, D.; Miao, L.; Du, X. Influence of concrete strength and aggregate size on the size effect of shear capacity of RC beam-column joints under monotonic loading. Mesoscale Numer. Tests 2022, 37, 671–685. [Google Scholar] [CrossRef]
- Cheng, X.; Cao, J.X.; Wang, L.L.; Zhao, Y.S.; Kong, D.W. Research progress in mechanical properties of concrete based on the mesoscopic model. China Concr. Cem. Prod. 2022, 1, 27–32+37. [Google Scholar] [CrossRef]
- Zheng, Z.; Zeng, C.; Tian, C.; Wei, X. Mesoscale numerical investigation on the size effect of concrete uniaxial compressive strength under different contact friction. Constr. Build. Mater. 2022, 346, 128416. [Google Scholar] [CrossRef]
- Wittmann, F.H.; Roelfstra, P.E.; Sadouki, H. Simulation and analysis of composite structures. Mater. Sci. Eng. 1985, 68, 239–248. [Google Scholar] [CrossRef]
- Walraven, J.C.; Reinhardt, H.W. Theory and experiments on the mechanical behavior of cracks in plain and reinforced concrete subjected to shear loading. Heron 1981, 26, 26–35. [Google Scholar]
- Jin, L.; Yu, W.; Du, X.; Yang, W. Meso-scale simulations of size effect on concrete dynamic splitting tensile strength: Influence of aggregate content and maximum aggregate size. Eng. Fract. Mech. 2020, 230, 106979. [Google Scholar] [CrossRef]
- Zheng, Y.X.; Zhang, Y.; Zhuo, J.B. Mesoscale synergistic effect mechanism of aggregate grading and specimen size on compressive strength of concrete with large aggregate size. Constr. Build. Mater. 2023, 367, 130346. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
- Xu, L.; Jin, Y.; Jing, S.; Liu, J.; Huang, Y.; Zhou, C. Comparisons of tensile fracturing behaviors of hydraulic fully graded and wet-screened concretes: A mesoscale study. Adv. Mater. Sci. Eng. 2018, 2018, 6965723. [Google Scholar] [CrossRef]
- Jin, L.; Yu, W.X.; Du, X.L. Size effect on static splitting tensile strength of concrete: Experimental and numerical studies. J. Mater. Civ. Eng. 2020, 32, 04020308. [Google Scholar] [CrossRef]
- Xiao, J.; Li, W.; Corr, D.J.; Shah, S.P. Effects of interfacial transition zones on the stress-strain behavior of modeled recycled aggregate concrete. Cem. Concr. Res. 2013, 52, 82–99. [Google Scholar] [CrossRef]
- Peng, Y.L.; Chu, H.; Pu, J.W. Numerical simulation of recycled concrete using convex aggregate model and base force element method. Adv. Mater. Sci. Eng. 2016, 2016, 5075109. [Google Scholar] [CrossRef]
- Jayasuriya, A.; Adams, M.P.; Bandelt, M.J. Understanding variability in recycled aggregate concrete mechanical properties through numerical simulation and statistical evaluation. Constr. Build. Mater. 2018, 178, 301–312. [Google Scholar] [CrossRef]
- Ma, H.F.; Chen, H.X.; Li, B.K. Meso-structure numerical simulation of concrete specimens. J. Hydraul. Eng. 2004, 35, 27–35. [Google Scholar]
- Kim, S.M.; Al-Rub, R.K.A. Meso-scale computational modeling of the plastic-damage response of cementitious composites. Cem. Concr. Res. 2011, 41, 339–358. [Google Scholar] [CrossRef]
- Pedersen, R.R.; Simone, A.; Sluys, L.J. Mesoscopic modeling and simulation of the dynamic tensile behavior of concrete. Cem. Concr. Res. 2013, 50, 74–87. [Google Scholar] [CrossRef]
- Chen, H.B.; Xu, B.; Wang, J. Parametric analysis on compressive strain rate effect of concrete using mesoscale modeling approach. Constr. Build. Mater. 2020, 246, 118375. [Google Scholar] [CrossRef]
- Xiao, J.; Li, W.; Liu, Q. Meso-level numerical simulation on mechanical properties of modeled recycled concrete under uniaxial compression. J. Tongji Univ. 2011, 39, 791–797. [Google Scholar]
- Kuang, G.P. Study on Strain Rate Effect of Concrete Based on Three-Dimensional Mesomodel; Harbin Institute of Technology: Harbin, China, 2017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).