Principles of Machine Learning and Its Application to Thermal Barrier Coatings
Abstract
1. Introduction
2. Current Status of Machine Learning and Its Application in Materials Design and Development
2.1. Big Data in Materials Science
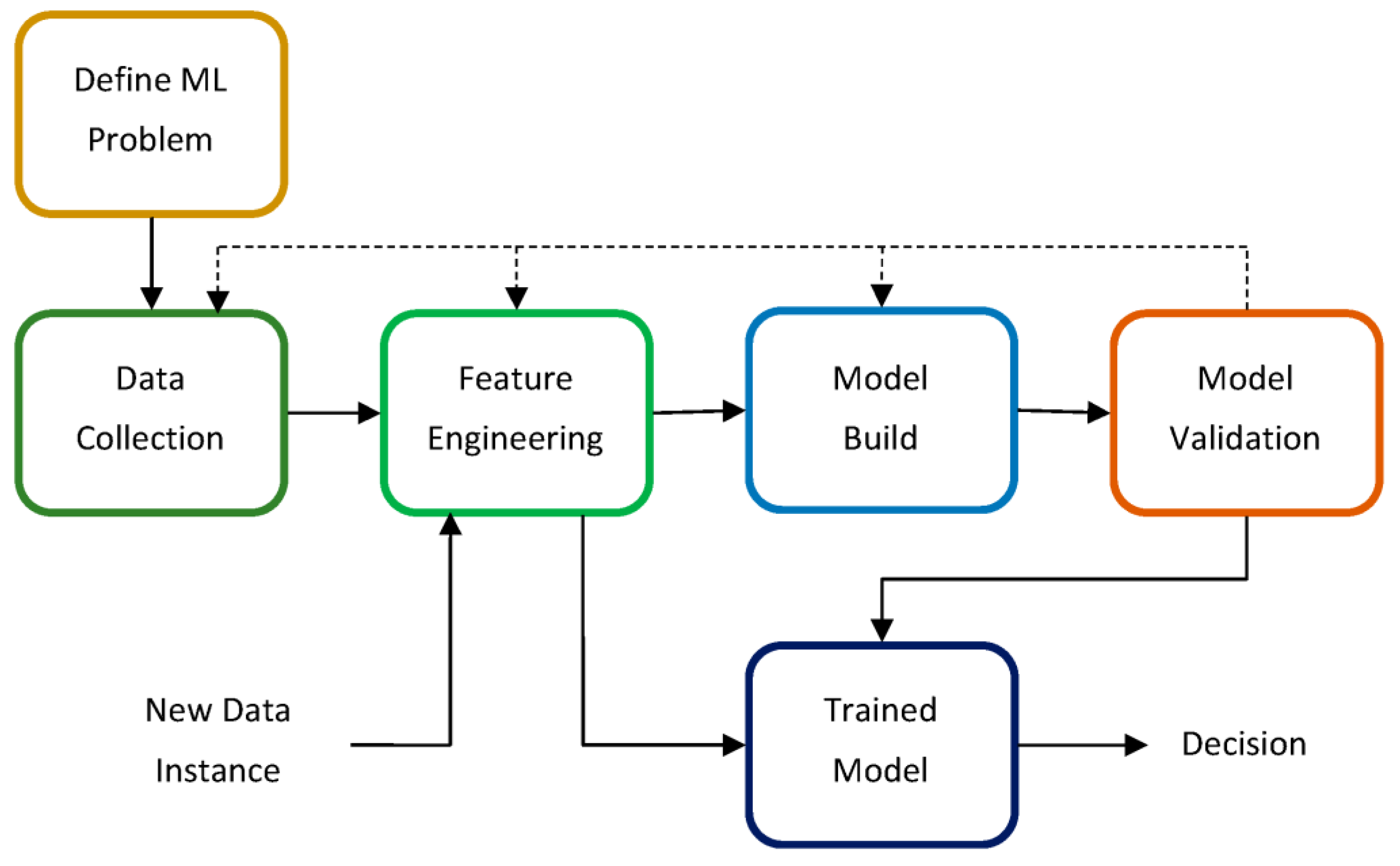
2.2. Machine Learning Framework for Materials Design and Development
2.2.1. Classes of ML Problems
2.2.2. Feature Engineering and Dimension Reduction
2.2.3. ML Algorithms
k-Nearest Neighbor (kNN) Method
Decision Tree
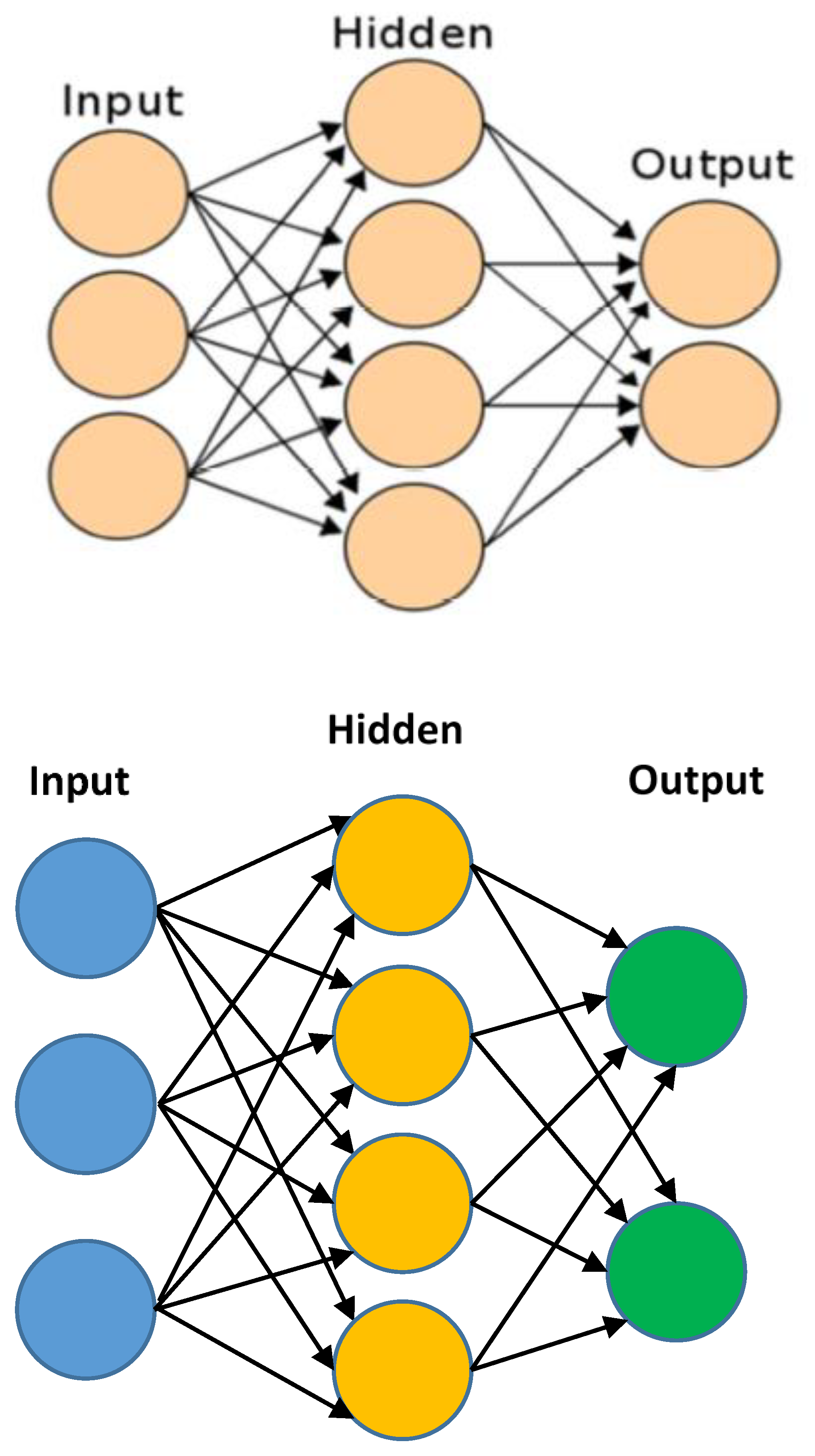
Neural Networks
Support Vector Machines and Support Vector Regression
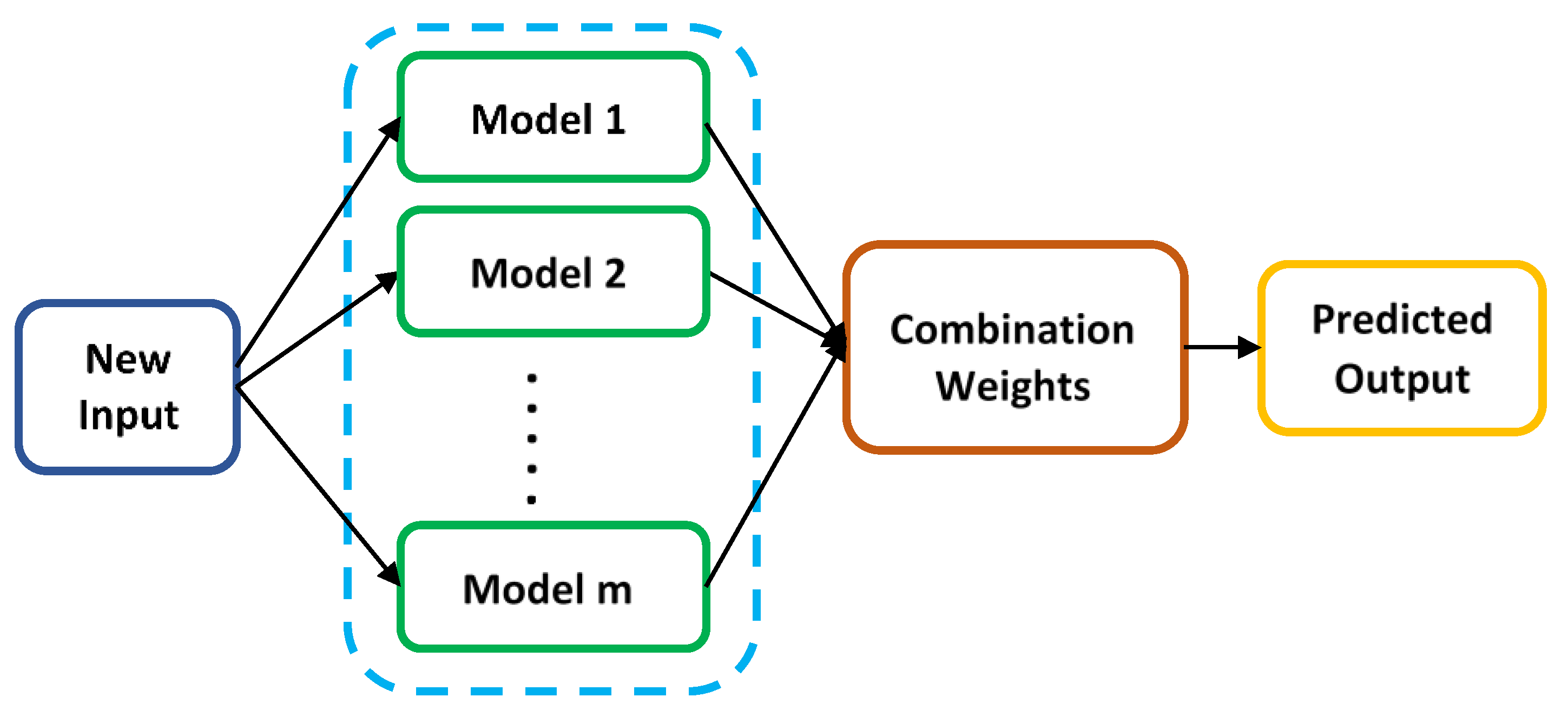
2.2.4. Ensemble Learning Algorithms
Gradient Boosting Tree Algorithm
Random Forest Algorithm
2.2.5. Deep Learning Algorithms
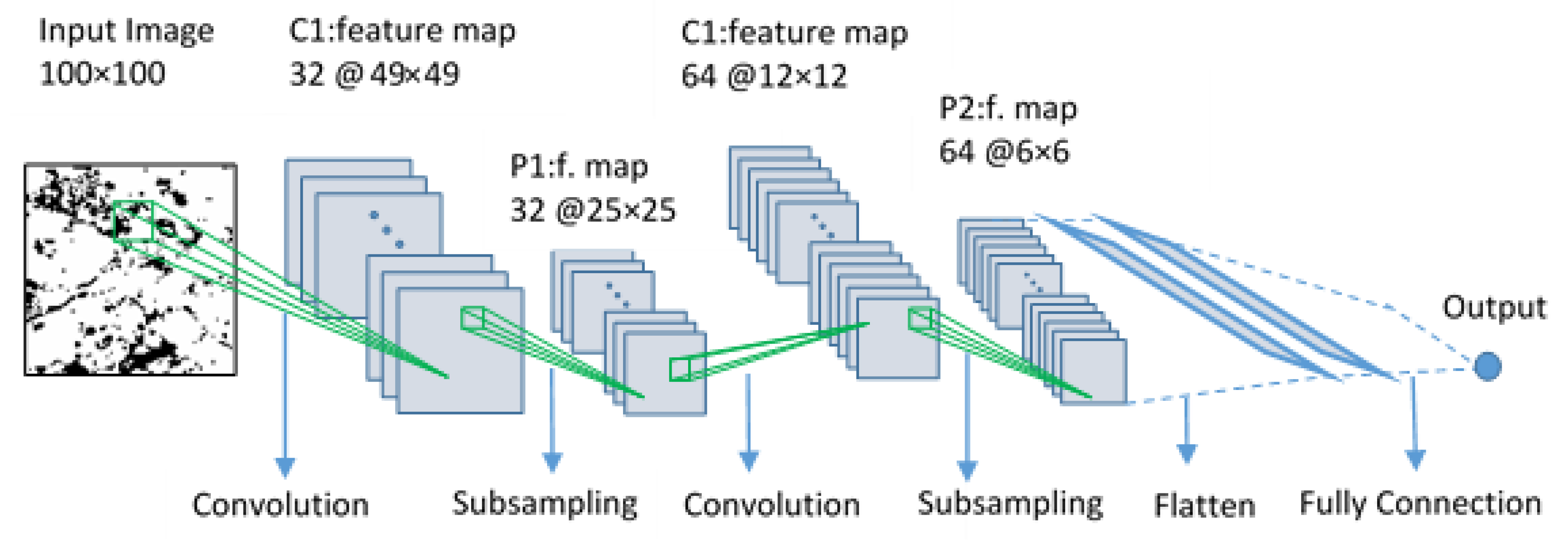
Convolutional Neural Network (CNN)
Recurrent Neural Network (RNN)
2.2.6. Model Validation Methods
2.3. ML Applications in Materials Science
2.3.1. Material Property Prediction
Shallow Learning Applications
Ensemble Learning Applications
DL Applications
2.3.2. New Materials Discovery
Shallow Learning Applications
Ensemble Learning Applications
2.3.3. ML Approach for Thermal Conductivity Evaluation
3. Prediction of Thermal Conductivity of TBC Using ML
- (1)
- Polynomial Regression;
- (2)
- Neural Network;
- (3)
- Gradient Boosting Regressor.
3.1. Data Collection
3.1.1. Basic Information Gathering
3.1.2. Data Extracting
- Step 1: Importing plot;
- Step 2: Calibrating x- and y-axis;
- Step 3: Digitizing dataset points;
- Step 4: Exporting dataset.
3.1.3. Dataset Used in the Present Study
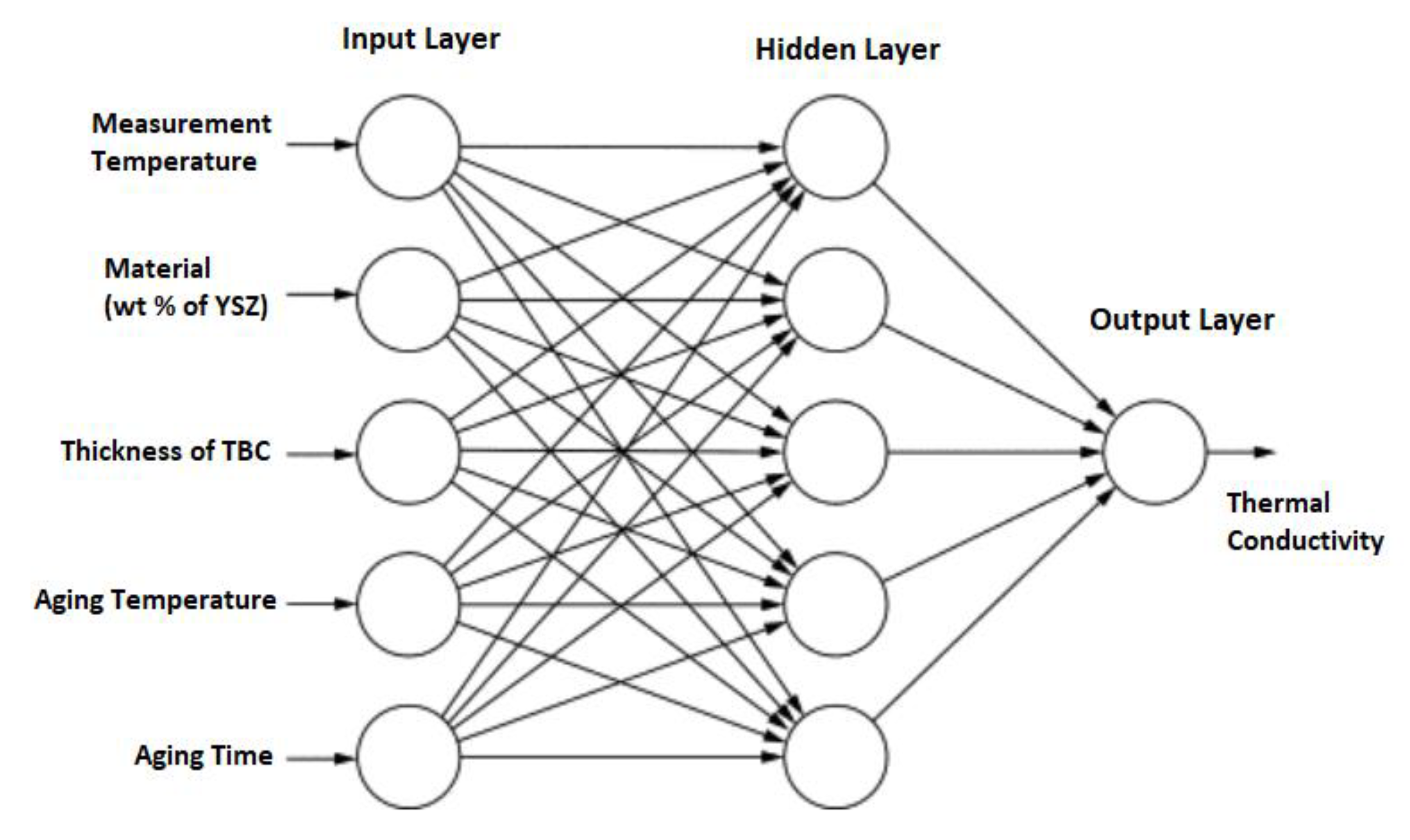
- Input variables for the prediction of thermal conductivity:
- Temperature;
- wt.% of Y2O3;
- Thickness of TBC;
- Aging Temperature;
- Aging Time;
- Output: Conductivity.
3.2. Exploratory Data Analysis
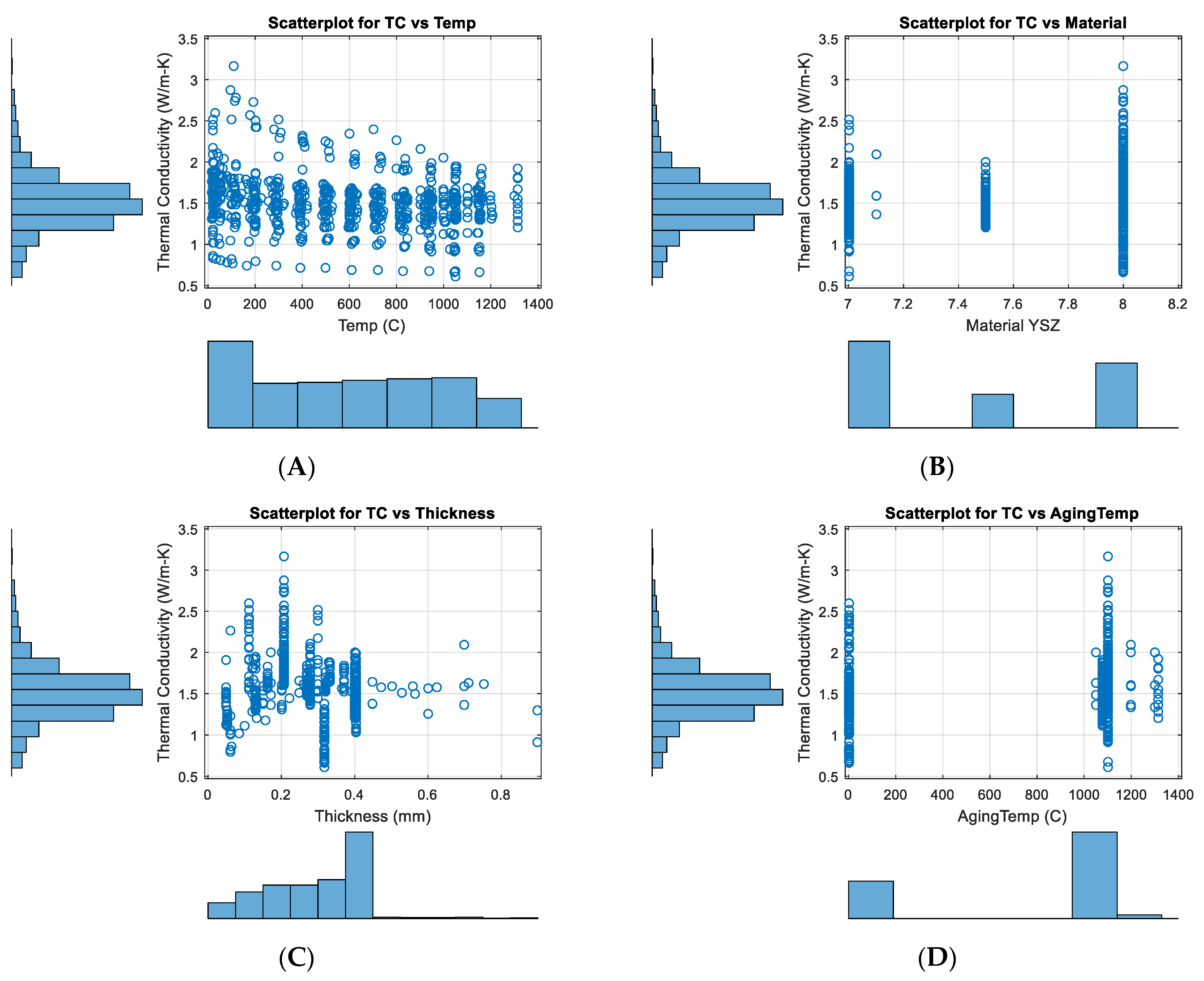
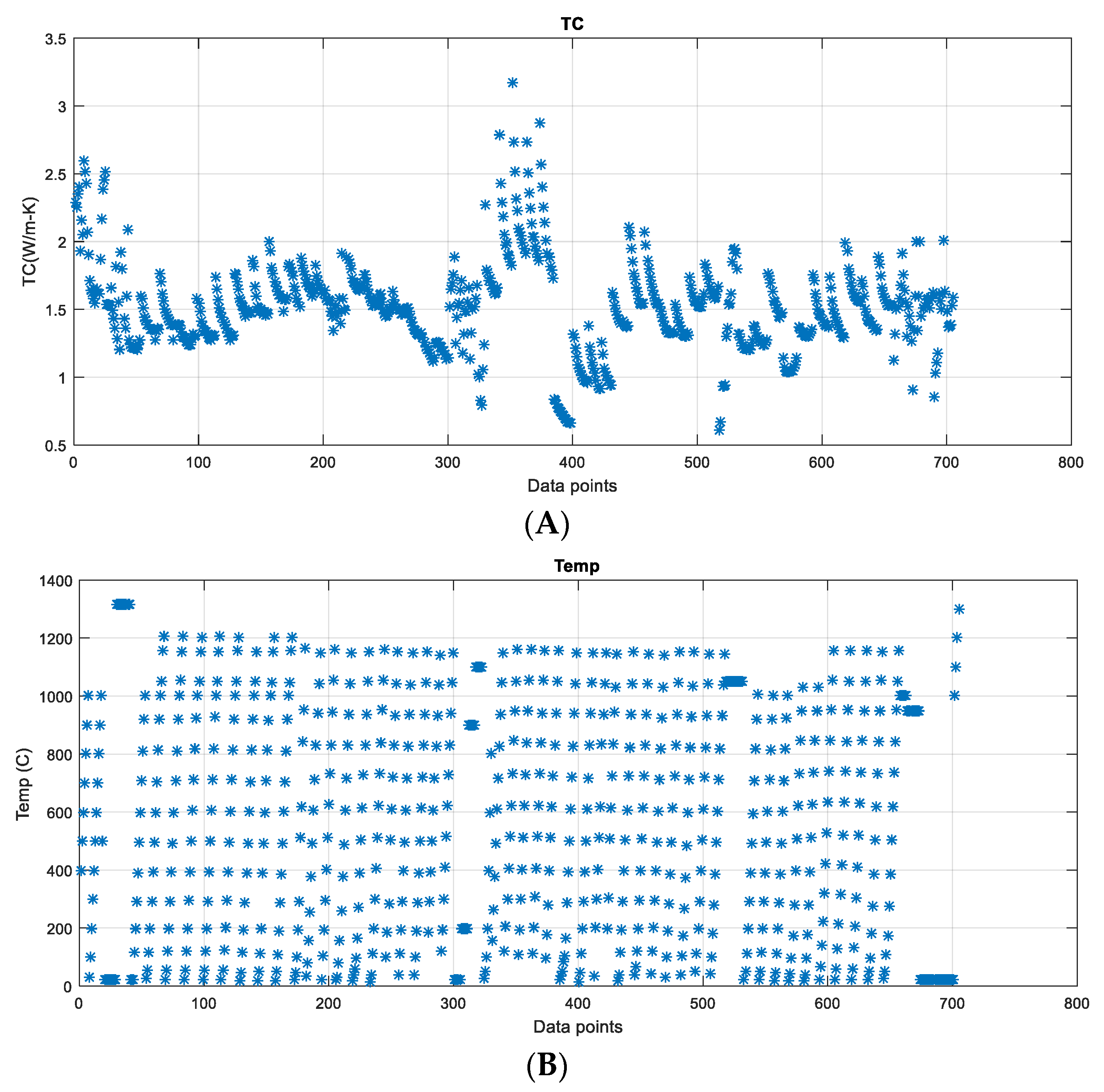
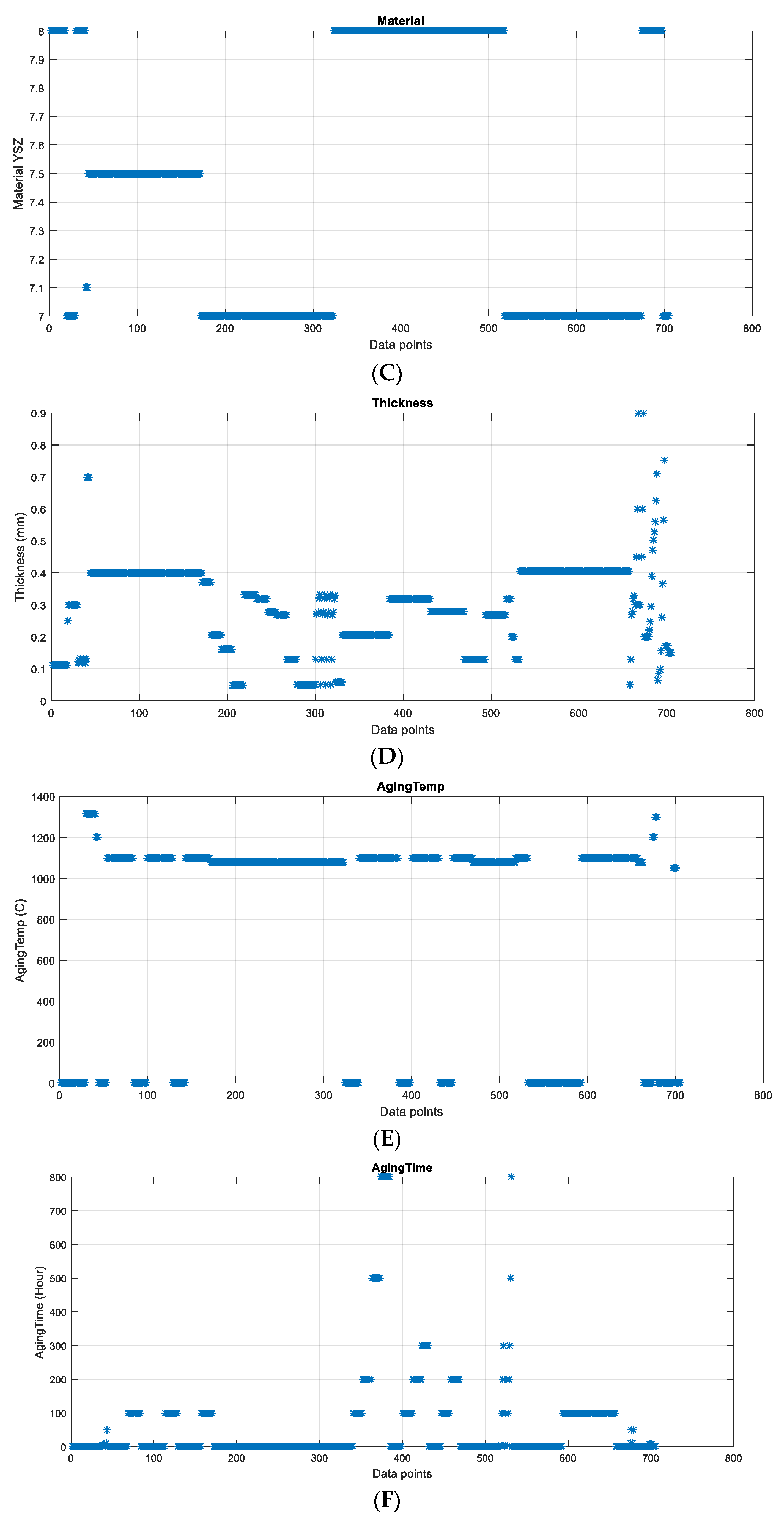
3.2.1. Exploratory Graphs
3.2.2. Correlation Analysis and Principal Components Analysis (PCA)
| explained = |
| 29.495 |
| 21.514 |
| 15.645 |
| 13.993 |
| 10.258 |
| 9.0946 |
| sum(explained) = 100 |
| sum(explained(1:4)) = 80.64 |
| sum (explained (1:5)) = 90.905 |
3.3. Prediction of Thermal Conductivity Using Polynomial Regression
3.3.1. Polynomial Regression Model
3.3.2. Multistage Predictive Modeling Framework
Forward Selection Orthogonal Least Squares Algorithm
Multistage Predictive Modeling Procedure
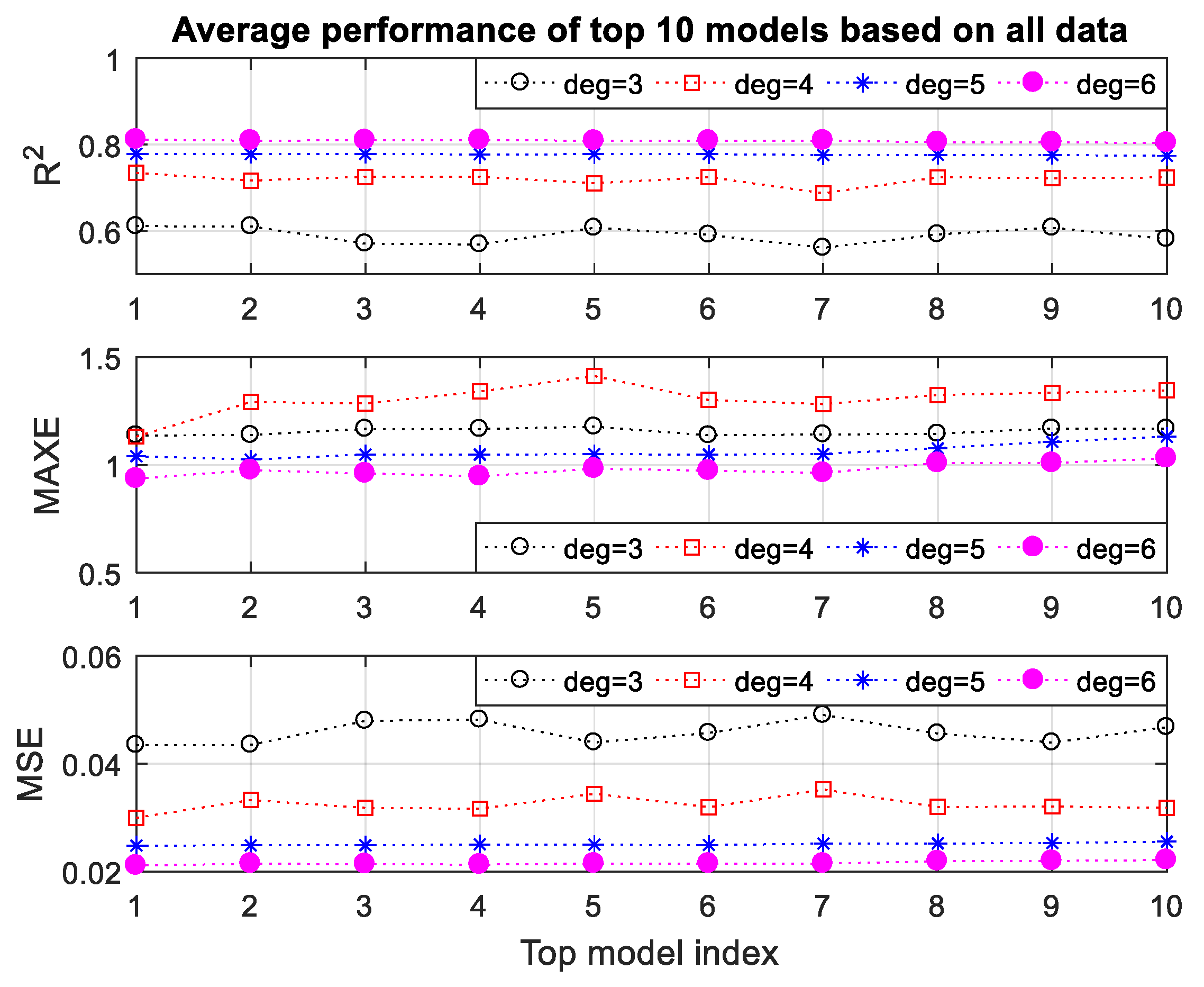
Model Performance Evaluation
- Coefficient of Determination (R2)
- 2.
- Mean Squared Error (MSE)
- 3.
- Maximum Absolute Error (MAXE)
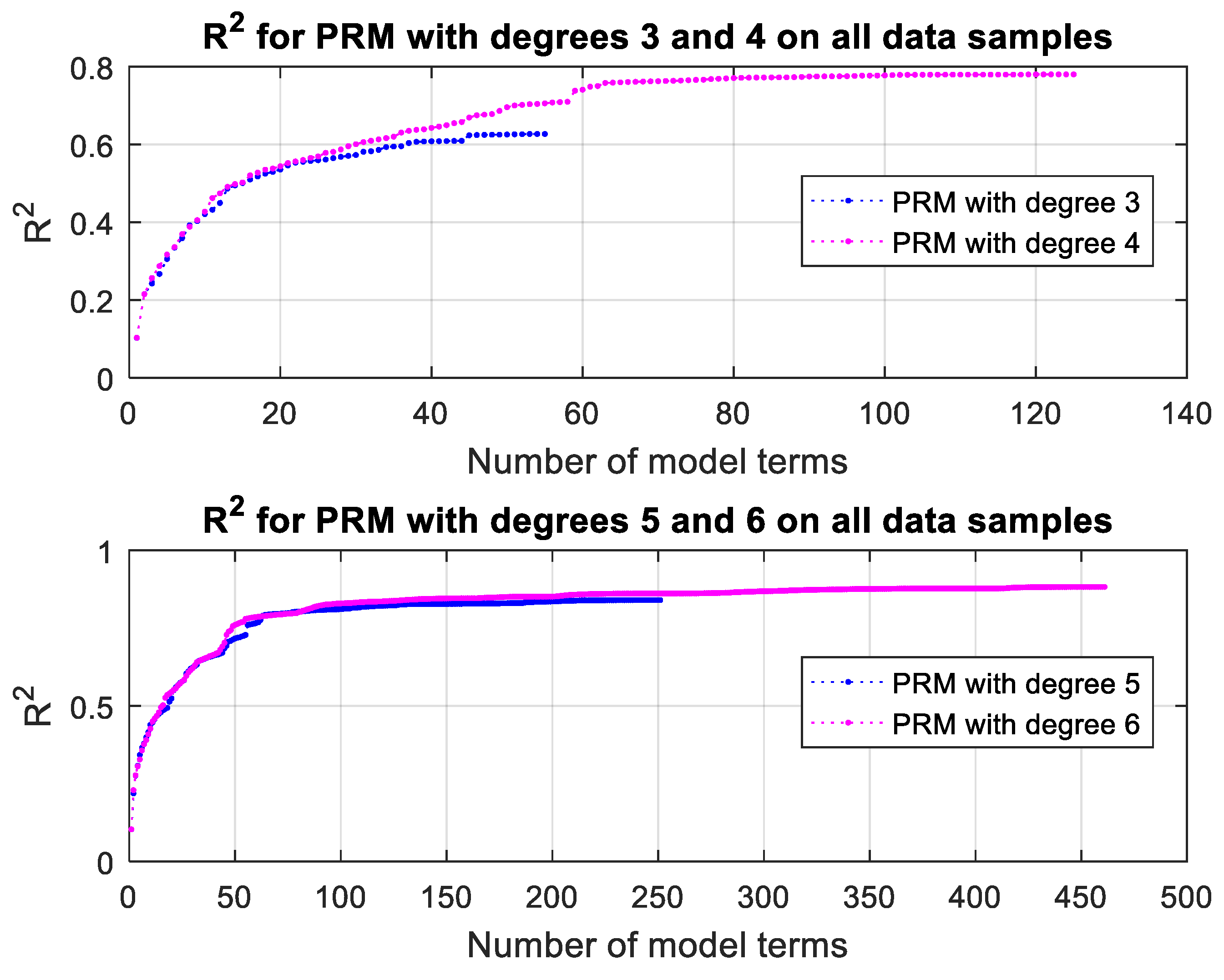
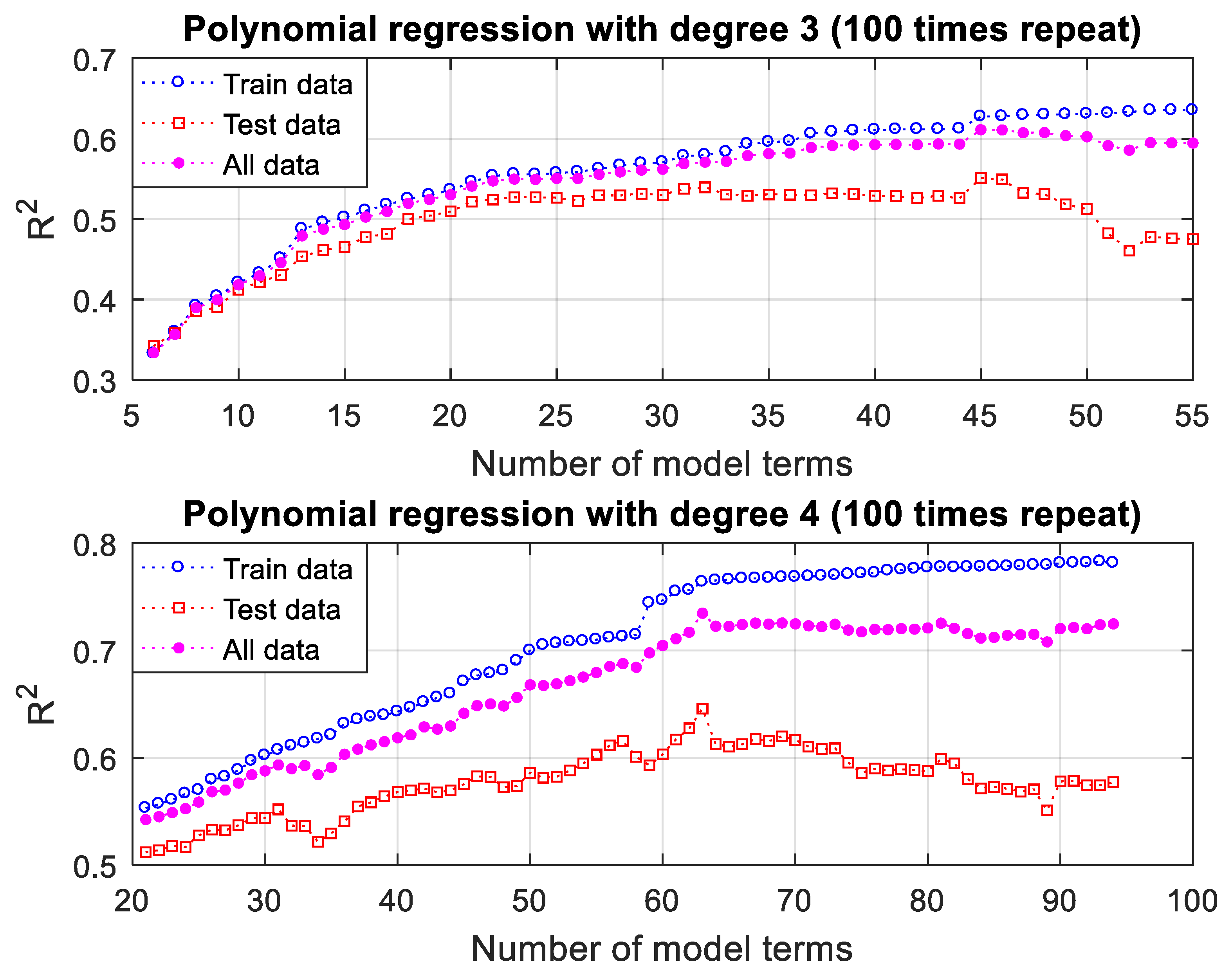
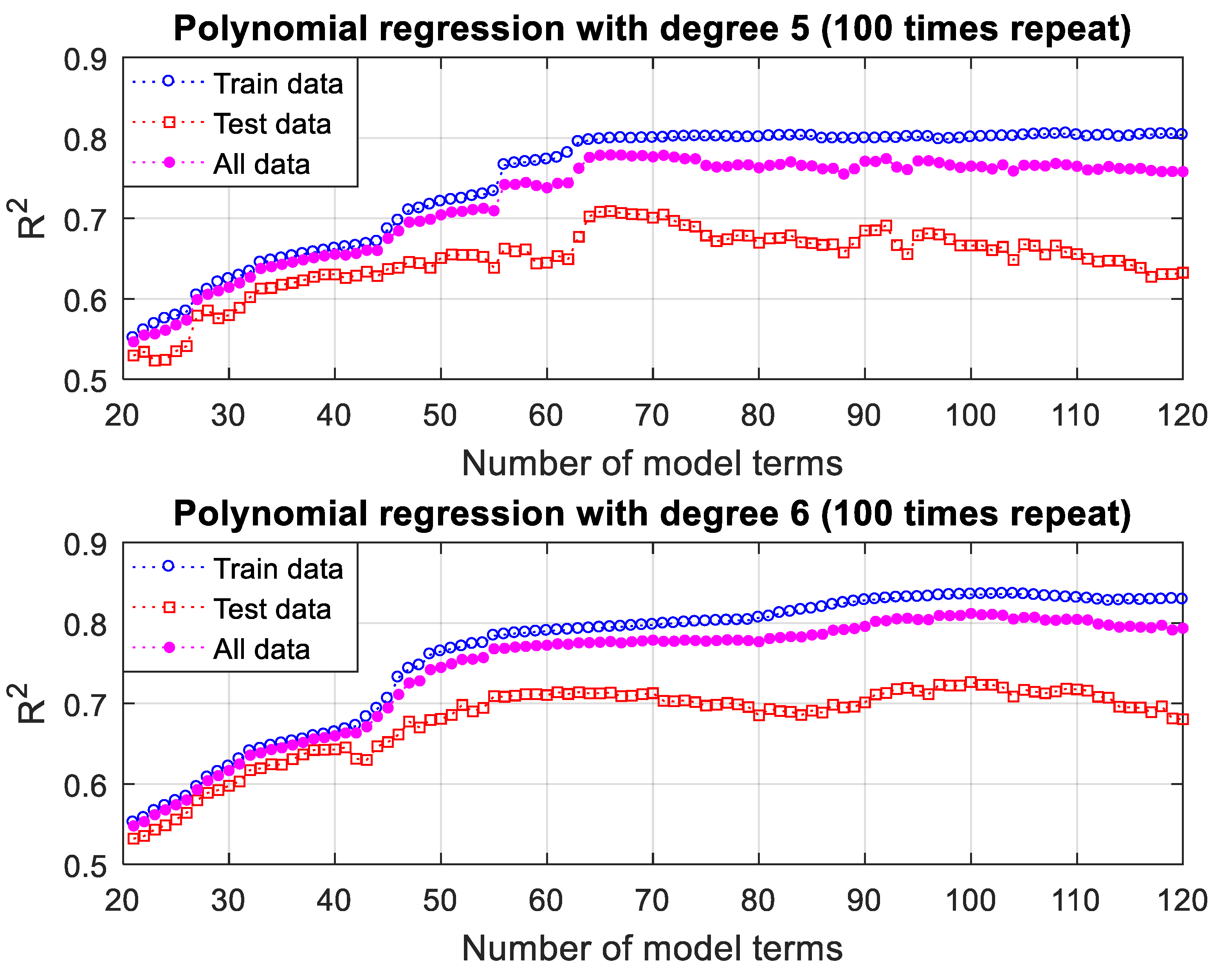
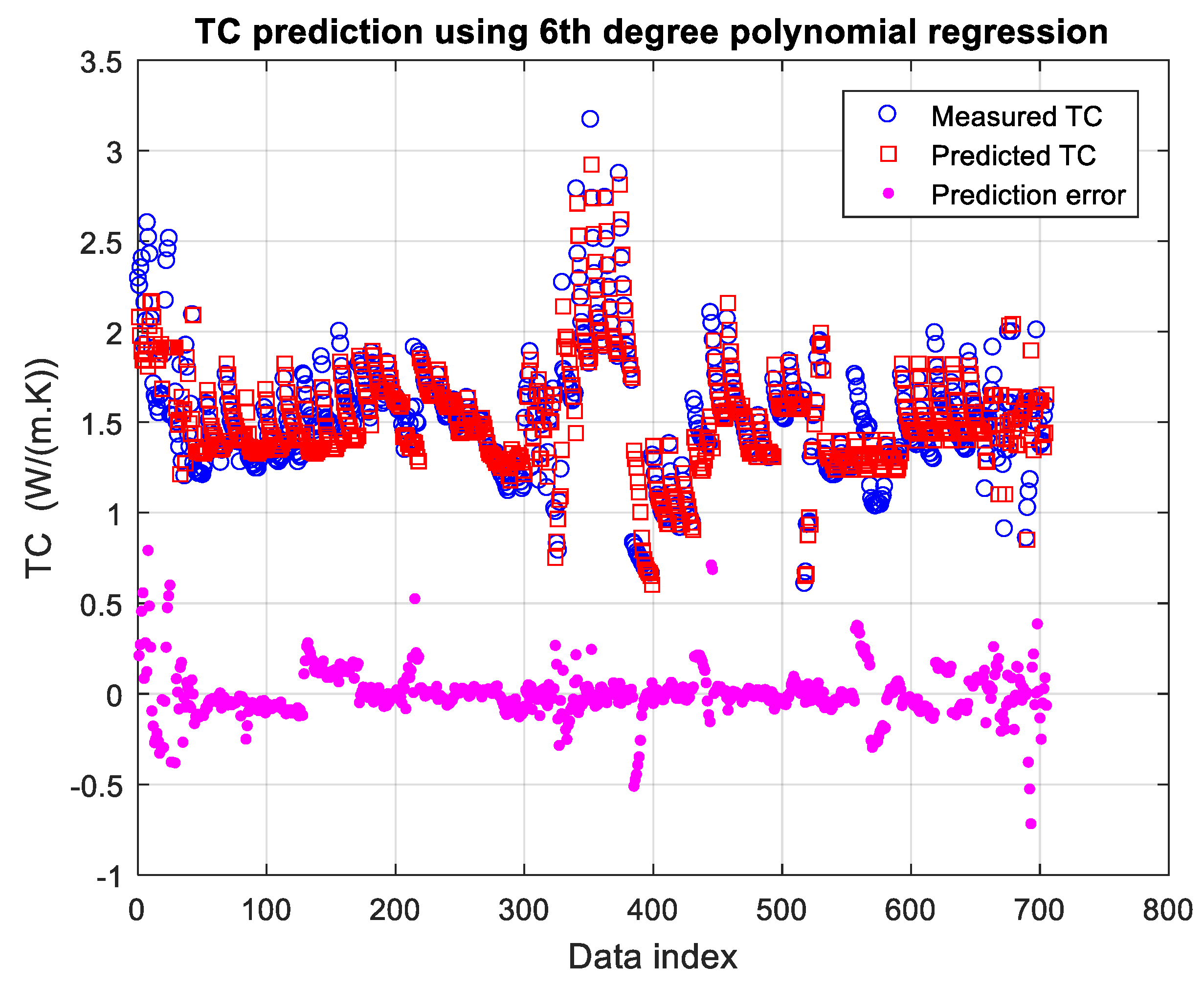
3.3.3. Polynomial Regression Modeling Results and Discussion
3.4. Prediction of Thermal Conductivity using Neural Networks
3.4.1. Neural Network Description
Basics of Neural Networks
3.4.2. Training Algorithms
Bayesian Regularization
- The maximum number of epochs (repetitions) is reached;
- The maximum amount of time is exceeded;
- Performance is minimized to the goal;
- The performance gradient falls below the minimum threshold;
- µ exceeds µmax.
Levenberg–Marquardt Algorithm
- The maximum number of epochs (repetitions) is reached;
- The maximum amount of time allocated for training is exceeded;
- The performance of the network is minimized to a predefined goal;
- The performance gradient falls below a minimum threshold (min grad);
- The value of µ exceeds a specified maximum (µ max);
- The validation performance (if used) has increased more than a certain number of times (max fail) since the last time it decreased.
3.4.3. Neural Network Training Topology and Details
Dataset Splitting
Training Parameters Setting
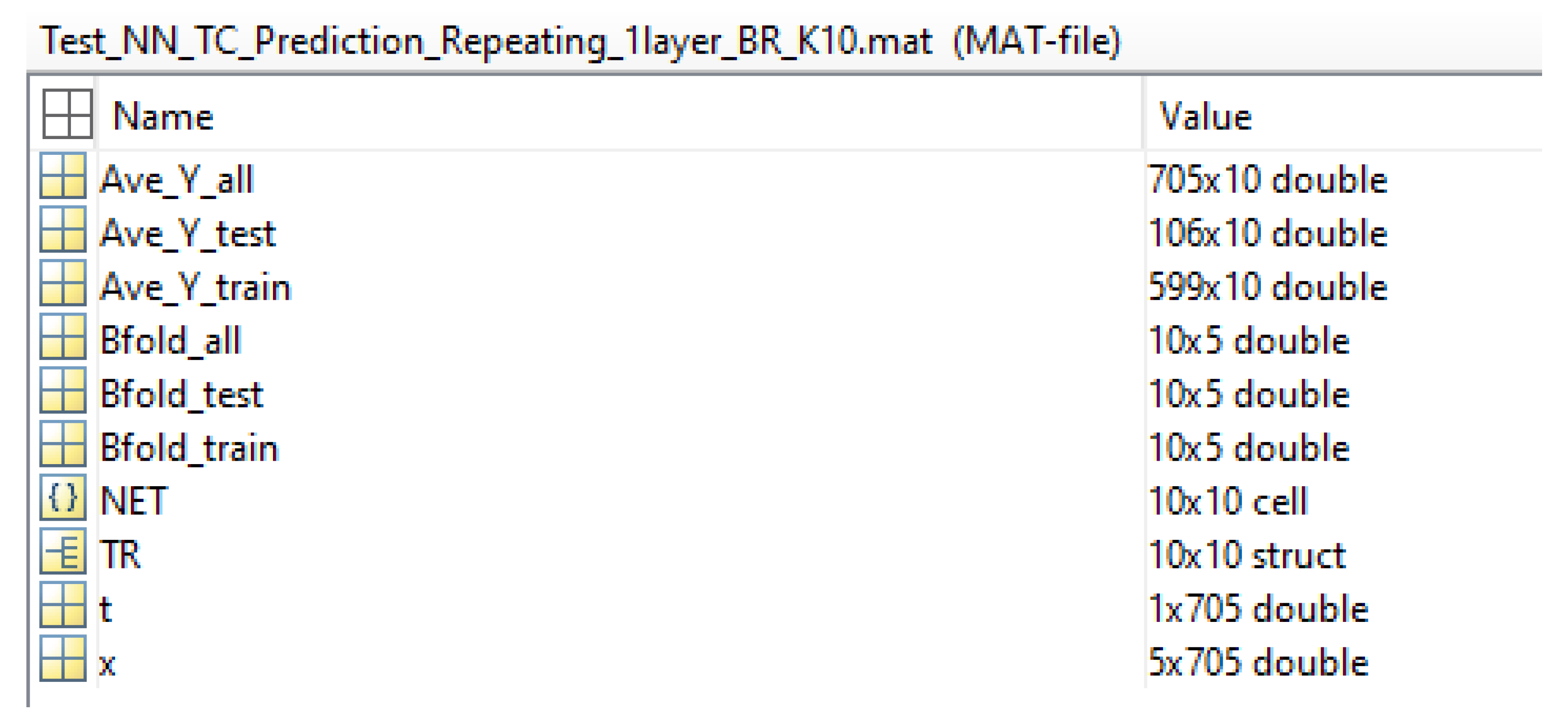
Exporting Training Results
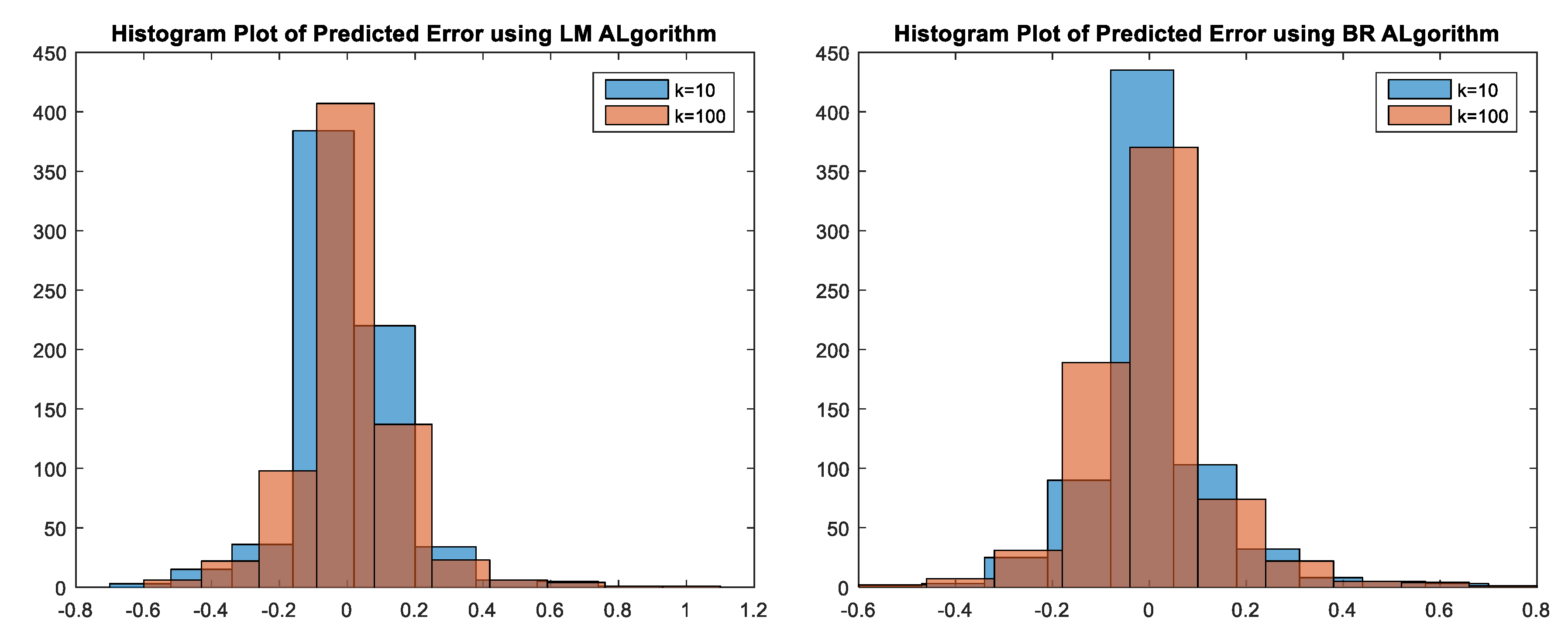
3.4.4. Neural Network (NN) Training Results and Discussion
Results Using Single-Layer NN
Results Using Two-Layer NN
3.5. Prediction of Thermal Conductivity Using Gradient Boosting Regression
3.5.1. Basics of Gradient Boosting Regression (GBR)
- A loss function to be optimized.
- 2.
- A weak-learner or base-learner model to make prediction.
- 3.
- An addictive model to add base-learners to minimize the loss function.
3.5.2. Gradient Boosting Regression (GBR) Topology and Details
- data= pd.read_excel(“xy_data_NRC.xlsx”, header = 0)
- X0 = data.iloc[range(705),1:6]
- y = data.iloc[range(705),0]
- sc = StandardScaler()
- Xn = sc.fit_transform(X0)
- from sklearn.preprocessing import PolynomialFeatures
- poly_features = PolynomialFeatures(degree = 2, include_bias = False)
- X = poly_features.fit_transform(Xn)
- X, y = shuffle(X, y, random_state = 13)
- X = X.astype(np.float32)
- params= {‘n_estimators’: 500, ‘max_depth’: 4, ‘min_samples_split’: 2, ‘learning_rate’: 0.01, ‘loss’: ‘ls’}
- clf = gbr(**params)
- clf = clf.fit(X_train,y_train)
- scoring = [‘r2’]
3.5.3. Prediction Results Using GBR
3.6. Summary of Prediction of TC Using ML
4. Conclusions
- This state-of-the-art review covers areas of AI as applied to materials design, characterization, and development, including big data, available algorithms for both ML and DL, NN, and SVM approaches, and various algorithms.
- This paper has also undertaken the prediction of thermal conductivity (TC) in 6–8 wt% YSZ TBCs using ML models. Recent studies have found the improved capability of ML in predicting TC of TBCs. Various ML models and algorithms have been researched, namely support vector regression (SVR), Gaussian process regression (GPR) and convolution neural network (CNN) regression algorithms.
- A large volume of experimental thermal conductivity (TC) data for YSZ (Yttria-Stabilized Zirconia) thermal barrier coatings (TBCs) has been compiled from the existing literature. This dataset serves as the basis for training, testing and validating ML models. The TC data is strongly influenced by five key factors, which have been identified and considered in this analysis. After collecting the TC data, several preprocessing steps such as sorting, filtering, extracting and exploratory analysis were conducted on the dataset. Three different approaches, namely polynomial regression, NN and GBR, were employed for predicting the thermal conductivity. The training, testing and prediction results obtained from these approaches were carefully analyzed, presented and discussed. Based on the results, it was observed that the NN model using the Bayesian regularization (BR) technique and the GBR approach exhibited better prediction capabilities compared to polynomial regression.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Name and Category | Website and References | Description |
|---|---|---|
| AFLOWLIB Computational | aflowlib.org [118] | Online computational platform for determining thermodynamic stability, electronic band structures, vibrational dispersions and thermomechanical properties of various inorganic compounds. |
| Computational Materials Repository Computational | cmr.fysik.dtu.dk [114] | Material database system supporting a variety of tools for collecting, storing, grouping, searching, retrieving and analyzing electronic structure calculations generated by many modern electronic-structure simulators. |
| Crystallography open database Crystallography | crystallography.net [119] | Online database that provides information on a variety of known atomic coordinates of crystal structures of organic, inorganic, metal-organic compounds and minerals collected from several research publications. |
| MARVEL NCCR Computational | nccr-marvel.ch [120] | Material informatics platform focusing on the design and discovery of new materials via data driven, high performance quantum mechanical simulations. Research tools, computational data and simulation software accessible through the materials cloud platform. |
| Materials Project Computational | materialsproject.org [121] | Online platform that provides access to density functional theory (DFT) calculations on a large number of metallic compounds, energy materials and also mechanical properties of many materials. |
| MatNavi(NIMS) General Materials data | mits.nims.go.jp/ index_en.html [122] | Integrated material database system comprising structures and properties for various materials including polymers and inorganic substances. |
| Organic materials database Computational | omdb.mathub.io [123] | Electronic structure database of three-dimensional organic crystals that also provides tools for search queries. |
| Open quantum materials database Computational | oqmd.org [124] | A high throughput database comprising the thermodynamic and structural properties of the known crystalline solids which are calculated using the density functional theory computation technique. |
| Open materials database Computational | openmaterialsdb.se [125] | A high throughput computational database which is based on structures from the Crystallography open database and provides information on the properties of various materials. |
| SUNCAT/CatApp Catalysts | suncat.stanford.edu/catapp [126] | Materials informatics center focusing on catalyst and materials design for next-generation energy solutions. Computational results for thousands of surface reactions and online tools accessible at catalysis-hub.org. |
| Chemspider Chemical data | chemspider.com [127] | Chemical structure database containing information on physio-chemical properties, interactive spectra, links to chemical vendor’s catalogs, literature references and patents collected from a wide range of data sources. |
| Citrination General Materials Data | citrination.com [128] | Materials informatics platform containing information on the computed and experimental properties of various materials and chemicals. |
| NIST Materials Data Repository (DSpace) General Materials Data | materialsdata.nist.gov/dspace/xmlui [129] | File repository that accepts materials data in any format related to specific research publications. The repository is implemented using a technology called Dspace. |
| NanoHUB Nanomaterials | nanohub.org [130] | Premier online resource that offers course materials, lectures, seminars, tutorials, professional networking and interactive simulation tools for nanotechnology. |
| Nanomaterials Registry Nanomaterials | nanomaterialregistry.org [131] | A central web-based repository that provides links to associated journals and publications, interactive simulation tools, computational results and information such as physio-chemical characteristics, and biological and environmental study data for different nanomaterials. |
| NIST Interatomic Potentials Repository Computational | ctcms.nist.gov/potentials [132] | A reliable source for interatomic potentials and related files for various metals. Evaluation tools to help researchers judge the quality and applicability of their interatomic models are also available. |
| PubChem Chemical data | pubchem.ncbi.nlm.nih.gov [133] | A database that contains information on chemical substances and their biological activities. |
| TEDesignLab Thermoelectrics | tedesignlab.org [134] | A virtual platform that contains raw experimental and computational thermoelectric data and a suite of interactive web-based tools that help in the design of new thermoelectric material. |
| UCSB-MRL thermoelectric database Thermoelectrics | mrl.ucsb.edu:8080/datamine/thermoelectric.jsp [135] | A large repository created by extracting thermoelectric materials data from several publications. |
| Name and Category | Website and References | Description |
|---|---|---|
| Inorganic Crystal Structure Database Crystallography | cds.dl.ac.uk/cds/datasets/ crys/icsd/llicsd.html [136] | Repository providing information of various inorganic crystal structures. |
| Cambridge Crystallographic Data Centre Crystallography | ccdc.cam.ac.uk/pages/Home.aspx [137] | Non-profit organization that compiles and maintains the Cambridge Structural Database, which contains information of various organic and metal organic small molecule crystal structures. |
| NIST Standard Reference Data General Materials Data | nist.gov/srd/dblistpcdatabases.cfm [138] | Generic material property data that provides measurable quantitative information related to physical, chemical or biological properties of known substances. |
| CALPHAD databases (e.g., Thermocalc SGTE) Thermodynamics | thermocalc.com/products-services/ databases/thermodynamic [139] | Journal publishing the experimental and theoretical information on phase equilibria and thermochemical properties of various materials. |
| ASM Alloy Center Database Alloys | mio.asminternational.org/ac [140] | Database for researching accurate materials data of compositions, properties, performance details and processing guidelines from authoritative sources for specific metals and alloys. |
| ASM Phase Diagrams Thermodynamics | asminternational.org/AsmEnterprise/APD [141] | Online repository that provides information related to binary and ternary alloy phase diagrams and associated crystal data for many alloy systems. |
| MatDat General Materials Data | matdat.com [142] | Online database that provides information on published design-relevant material data to the industrial, academic and research community. |
| Pauling File General Materials Data | paulingfile.com [143] | Online database that includes information on the crystal structures, physical properties and phase diagrams for various non-organic solid-state materials. |
| Springer Materials General Materials Data | materials.springer.com [144] | Materials research platform that provides curated data for identifying material properties and a set of advanced functionalities for data analysis and visualization of materials properties. |
| Total Materia General Materials Data | totalmateria.com [145] | Online materials database that includes search and cross-reference tools, chemical composition, properties and specifications for various metals, polymers, ceramics and composites. |
| Year | Author | Material | Research Topic | |
|---|---|---|---|---|
| 1 | 1998 | Taylor [146] | Al2O3 and ZrO2 and of four and eight alternating layers of Al2O3–ZrO2 | TC vs. temp and different thickness |
| 2 | 1998 | Raghavan [147] | 5.8 wt.% yttria YSZ | TC vs. temp and densities (% of theoretical) and grain diameters (in nm) |
| 3 | 1999 | An [86] | Al2O3 and 8YSZ | TC vs. temp |
| 4 | 2000 | Zhu [148] | EB-PVD. ZrO2-8 wt.%Y2O3 (8YSZ) | TC vs. time for different thickness |
| 5 | 2002 | Nicholls [87] | EB-PVD TBCs 7YSZ | TC vs. Yttia (wt%), TC vs. T and grain size; thermal conductivities of dopant modified EB-PVD TBCs at 4 mol% addition and 250 mm thickness; data measured at room temperature |
| 6 | 2002 | Zhu [149] | YSZ-Nd-Yb and YSZ-Gd-Yb; 8YSZ | TC vs. temp and time; TC vs. total dopant concentration |
| 7 | 2004 | Cernuschi [150] | 8Y2O3ZrO2, 22 wt.%MgO–ZrO2, and 25 wt.%CeO2–2.5Y2O3–ZrO2 | TC vs. temp for different cycles |
| 8 | 2004 | Jang [88] | EB-PVD ZrO2-4 mol% Y2O3 | TC vs. substrate thickness (areal thermal diffusion time) |
| 9 | 2004 | Singh [89] | EB-PVD 8YSZ, ZrO2–8% Y2O3 HfO2-40% wtZrO2-27 wt%Y2O3 | TC vs. time and number of layers |
| 10 | 2004 | Matsumoto [90] | ZrO2–Y2O3–La2O3 | TC vs. La2O3 content % |
| 11 | 2005 | Wolfe [151] | ZrO2– 8 wt.% Y2O3 | TC vs. time and number of layers |
| 12 | 2006 | Renteria [76] | three morphologically different EB-PVD PYSZ TBC | TC vs. temp and time |
| 13 | 2006 | Rätzer-Scheibe [91] | EB-PVD PYSZ | TC vs. temp and thickness |
| 14 | 2006 | Ma [152] | SPPS-7YSZ and SPPS LK-Zr | TC vs. temp and time |
| 15 | 2007 | Almeida [92] | EB-PVD 2O3–ZrO2 | TC vs. temp |
| 16 | 2007 | Rätzer-Scheibe [84] | EB-PVD ZrO2–7wt.%Y2O3 | TC vs. temp and heat treatment time and thickness |
| 17 | 2007 | Schulz [93] | EB-PVD (Three types) FeCrAlY; PYSZ | TC vs. temp; aging time |
| 18 | 2008 | Jang [94] | EB-PVD ZrO2–4 mol% Y2O3 | TC vs. number of layers, porosity |
| 19 | 2009 | Matsumoto [95] | EB-PVD YSZ, La2O3 and HfO2 | TC vs. annealing time |
| 20 | 2010 | Yu [153] | plasma sprayed Sm2Zr2O7 | TC vs. temp and different heat-treating temperature |
| 21 | 2011 | Jang [96] | EB-PVD ZrO2–4 mol% Y2O3 | TC vs. coating thickness |
| 22 | 2011 | Liu [97] | EB-PVD 7wt% Y2O3 (7YSZ) | TC vs. substrate rotation speed |
| 23 | 2012 | Limarga [154] | EB-PVD 3wt% Y2O3 (3YSZ) | TC vs. temp and different heat-treating temperature and time |
| 24 | 2012 | Łatka [155] | ZrO2+8 wt.%Y2O3 (8YSZ) | TC vs. temp |
| 25 | 2012 | Zhang [156] | (La0.95Mg0.05)2Ce2O6.95 (La0.95Mg0.05)2Ce2O6.95 La2Ce2O7 | TC vs. temp |
| 26 | 2013 | Jang [157] | ZrO2–4 mol.%Y2O3 (TZ4Y) | TC vs. temp and different sintered temp and different GD2O3 percentile |
| 27 | 2013 | Bobzin [98] | EB–PVD 7YSZ, La2Zr2O7, 7YSZ + Gd2Zr2O7 DCL, Gd2Zr2O7, 7YSZ + Gd2Zr2O7 | TC vs. temp |
| 28 | 2013 | Sun [158] | Yb2O3–Y2O3–ZrO2 | TC vs. temp |
| 29 | 2013 | Zhao [159] | EB-PVD ZrO2 Y2O3 (8YSZ), 4TiYSZ, to 16TiYSZ | TC vs. temp |
| 30 | 2014 | Jordan [160] | SPPS YSZ TBCs with IPBs | TC for different trials |
| 31 | 2014 | Lu [161] | LSMZATO, La1−xSrxMg1−xZnxAl11 xTixO19 | TC vs. temp |
| 32 | 2014 | Wang [162] | YSZ/NiCoCrAlY | TC vs. temp (numerical) |
| 33 | 2015 | Rai [163] | YSZ and GZO | TC for different layer and thickness |
| 34 | 2016 | Guo [164] | 1RE1Yb–YSZ 1La1Yb–YSZ | TC vs. temp |
| 35 | 2016 | Arai [165] | YSZ (0, 5, 10, 15 wt%) | TC vs. porosity, width of pore, at 570 K |
| 36 | 2016 | Guo [166] | La2Zr2O7 | TC vs. temp |
| 37 | 2016 | Wang [167] | 8YSZ | Numerical work (mathematic model) TC vs. porosity and pores size |
| 38 | 2016 | Zhang [168] | La2(Ce0.3Zr0.7)2O7-3 wt.%Y2O3 | TC vs. temp (deposited at 5, 15 and 25 RPM) |
| 39 | 2017 | Meng [169] | (a) La2Zr2O7; (b) Nd2Zr2O7; (c) Sm2Zr2O7; (d) Gd2Zr2O7. | TC vs. temp, concentration increase in oxygen vacancies |
References
- Reyes, K.G.; Maruyama, B.; Editors, G. The machine learning revolution in materials? MRS Bull. 2019, 44, 530–537. [Google Scholar] [CrossRef]
- Himanen, L.; Geurts, A.; Foster, A.S.; Rinke, P. Data-Driven Materials Science: Status, Challenges, and Perspectives. Adv. Sci. 2019, 6, 1900808. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Chu, X.; Sun, X.Y.; Xu, K.; Deng, H.X.; Chen, J.; Wei, Z.; Lei, M. Machine learning in materials science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, T.; Ju, W.; Shi, S. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Agrawal, A.; Choudhary, A. Perspective: Materials informatics and big data: Realization of the “fourth paradigm” of science in materials science. APL Mater. 2016, 4, 053208. [Google Scholar] [CrossRef]
- Zhou, T.; Song, Z.; Sundmacher, K. Big Data Creates New Opportunities for Materials Research: A Review on Methods and Applications of Machine Learning for Materials Design. Engineering 2019, 5, 1017–1026. [Google Scholar] [CrossRef]
- Pokluda, J.; Kianicová, M. Damage and Performance Assessment of Protective Coatings on Turbine Blades. In Gas Turbines, 1st ed.; SCIYO, 2010; pp. 283–306. Available online: https://www.intechopen.com/chapters/12092 (accessed on 10 March 2023).
- Vaßen, R.; Jarligo, M.O.; Steinke, T.; Mack, D.E.; Stöver, D. Overview on advanced thermal barrier coatings. Surf. Coat. Technol. 2010, 205, 938–942. [Google Scholar] [CrossRef]
- Warren, J.A. The Materials Genome Initiative and artificial intelligence. MRS Bull. 2018, 43, 452–457. [Google Scholar] [CrossRef]
- Hautier, G.; Jain, A.; Ong, S.P. From the computer to the laboratory: Materials From the computer to the laboratory: Materials discovery and design using first-principles calculations. J. Mater. Sci. 2012, 47, 7317–7340. [Google Scholar] [CrossRef]
- Jose, R.; Ramakrishna, S. Materials 4.0: Materials big data enabled materials discovery. Appl. Mater. Today 2018, 10, 127–132. [Google Scholar] [CrossRef]
- National Science and Technology Council. Materials Genome Initiative for Global Competitiveness; Aeromat 23 Conference and Exposition American Society for Metals; American Society for Metals: Charlotte, NC, USA, 2012. [Google Scholar]
- Mueller, T.; Kusne, G.K.; Ramprasad, R. Machine learning in materials science: Recent progress and emerging applications. In Reviews in Computational Chemistry; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Anderson, T.; Arguelles, C.; Arlen, T.C.; et al. Determining neutrino oscillation parameters from atmospheric muon neutrino disappearance with three years of IceCube DeepCore data. Phys. Rev. D-Part. Fields Gravit. Cosmol. 2015, 91, 072004. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Medford, A.J.; McDowell, D.L. Vision for Data and Informatics in the Future Materials Innovation Ecosystem. JOM 2016, 68, 2126–2137. [Google Scholar] [CrossRef]
- Hill, J.; Mulholland, G.; Persson, K.; Seshadri, R.; Wolverton, C.; Meredig, B. Materials science with large-scale data and informatics: Unlocking new opportunities. MRS Bull. 2016, 41, 399–409. [Google Scholar] [CrossRef]
- Ravichandran, T.; Liu, Y.; Kumar, A.; Srivastava, A.; Hanachi, H.; Heppler, G. Data-Driven Performance Prediction Using Gas Turbine Sensory Signals. In Proceedings of the 2020 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), London, ON, Canada, 30 August–2 September 2020. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Nigsch, F.; Bender, A.; van Buuren, B.; Tissen, J.; Nigsch, E.; Mitchell, J.B.O. Melting point prediction employing k-nearest neighbor algorithms and genetic parameter optimization. J. Chem. Inf. Model. 2006, 46, 2412–2422. [Google Scholar] [CrossRef] [PubMed]
- Maisarah, A.R.I.; Fauziah, M.; Sazali, Y. Comparison of classifying the material mechanical properties by using k-Nearest Neighbor and Neural Network Backpropagation. Int. J. Res. Rev. Artif. Intell. 2011, 1, 7–11. [Google Scholar]
- Addin, O.; Sapuan, S.M.; Othman, M. A Naïve-bayes classifier and f-folds feature extraction method for materials damage detection. Int. J. Mech. Mater. Eng. 2007, 2, 55–62. [Google Scholar]
- Doreswamy, S. An Expert Decision Support System for Engineering Materials Selections and Their Performance Classifications on Design Parameters. Int. J. Comput. Appl. 2006, 1, 17–34. [Google Scholar]
- Langseth, H.; Nielsen, T.D. Classification using Hierarchical Naïve Bayes models. Mach. Learn. 2006, 63, 135–159. [Google Scholar] [CrossRef]
- Doreswamy; Hemanth, K.S.; Vastrad, C.M.; Nagaraju, S. Data Mining Technique for Knowledge Discovery from Engineering Materials Data Sets. In Advances in Computer Science and Information Technology; Springer: Berlin/Heidelberg, Germany, 2011; pp. 512–522. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Quinlan, J.R. Improved use of continuous attributes in C4.5. J. Artif. Intell. Res. 1996, 4, 77–90. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth International Group: Belmont, CA, USA, 1984. [Google Scholar]
- Balachandran, P.V.; Broderick, S.R.; Rajan, K. Identifying the “inorganic gene” for high-temperature piezoelectric perovskites through statistical learning. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 2271–2290. [Google Scholar] [CrossRef] [PubMed]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Schölkopf, B.; Smola, A.J.; Bach, F. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Fang, S.F.; Wang, M.P.; Qi, W.H.; Zheng, F. Hybrid genetic algorithms and support vector regression in forecasting atmospheric corrosion of metallic materials. Comput. Mater. Sci. 2008, 44, 647–655. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictions. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Breiman, L. Heuristics of instability and stabilization in model selection. Ann. Stat. 1996, 24, 2350–2383. [Google Scholar] [CrossRef]
- Isayev, O.; Oses, C.; Toher, C.; Gossett, E.; Curtarolo, S.; Tropsha, A. Universal fragment descriptors for predicting properties of inorganic crystals. Nat. Commun. 2017, 8, 15679. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Oliynyk, A.O.; Antono, E.; Sparks, T.D.; Ghadbeigi, L.; Gaultois, M.W. High-Throughput Compounds Synthesis of full-Heusler componds. Chem. Mater 2016, 28, 7324–7331. [Google Scholar] [CrossRef]
- Legrain, F.; Carrete, J.; van Roekeghem, A.; Madsen, G.K.H.; Mingo, N. Materials Screening for the Discovery of New Half-Heuslers: Machine Learning versus ab Initio Methods. J. Phys. Chem. B 2018, 122, 625–632. [Google Scholar] [CrossRef]
- Carrete, J.; Li, W.; Mingo, N.; Wang, S.; Curtarolo, S. Finding unprecedentedly low-thermal-conductivity half-heusler semiconductors via high-throughput materials modeling. Phys. Rev. X 2014, 4, 011019. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning: Machine Learning Book. 2016. Available online: http://www.deeplearningbook.org/ (accessed on 10 March 2020).
- Deng, L.; Yu, D. Deep Learning: Methods and Applications. Found. Trends Signal Process. 2014, 7, 197–387. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Catalini, C.; Goldfarb, A. Crowdfunding: Geography, Social Networks, and the Timing of Investment Decisions. J. Econ. Manag. Strateg. 2015, 24, 253–274. [Google Scholar] [CrossRef]
- Prabhu, D.R.; Winfree, W.P. Neural Network Based Processing of Thermal NDE Data for Corrosion Detection. In Review of Progress in Quantitative Nondestructive Evaluation: Volumes 12A and 12B; Thompson, D.O., Chimenti, D.E., Eds.; Springer: Boston, MA, USA, 1993; pp. 775–782. [Google Scholar]
- Postolache, O.; Ramos, H.G.; Ribeiro, A.L. Detection and characterization of defects using GMR probes and artificial neural networks. Comput. Stand. Interfaces 2011, 33, 191–200. [Google Scholar] [CrossRef]
- Sadowski, L. Non-destructive investigation of corrosion current density in steel reinforced concrete by artificial neural networks. Arch. Civ. Mech. Eng. 2013, 13, 104–111. [Google Scholar] [CrossRef]
- Butcher, J.B.; Day, C.R.; Austin, J.C.; Haycock, P.W.; Verstraeten, D.; Schrauwen, B. Defect Detection in Reinforced Concrete Using Random Neural Architectures. Comput. Civ. Infrastruct. Eng. 2014, 29, 191–207. [Google Scholar] [CrossRef]
- Guo, Z.; Malinov, S.; Sha, W. Modelling beta transus temperature of titanium alloys using artificial neural network. Comput. Mater. Sci. 2005, 32, 1–12. [Google Scholar] [CrossRef]
- Altun, F.; Kişi, Ö.; Aydin, K. Predicting the compressive strength of steel fiber added lightweight concrete using neural network. Comput. Mater. Sci. 2008, 42, 259–265. [Google Scholar] [CrossRef]
- Gajewski, J.; Sadowski, T. Sensitivity analysis of crack propagation in pavement bituminous layered structures using a hybrid system integrating Artificial Neural Networks and Finite Element Method. Comput. Mater. Sci. 2014, 82, 114–117. [Google Scholar] [CrossRef]
- Xu, L.; Wencong, L.; Chunrong, P.; Qiang, S.; Jin, G. Two semi-empirical approaches for the prediction of oxide ionic conductivities in ABO3 perovskites. Comput. Mater. Sci. 2009, 46, 860–868. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Hassan, M.Y.; Abdullah, M.P.; Rahman, H.A.; Hussin, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Javed, S.; Khan, A.; Majid, A.; Mirza, A.; Bashir, J. Lattice constant prediction of orthorhombic ABO3 perovskites using support vector machines. Comput. Mater. Sci. 2007, 39, 627–634. [Google Scholar] [CrossRef]
- Majid, A.; Khan, A.; Javed, G.; Mirza, A.M. Lattice constant prediction of cubic and monoclinic perovskites using neural networks and support vector regression. Comput. Mater. Sci. 2010, 50, 363–372. [Google Scholar] [CrossRef]
- Majid, A.; Khan, A.; Choi, T.-S. Predicting lattice constant of complex cubic perovskites using computational intelligence. Comput. Mater. Sci. 2011, 50, 1879–1888. [Google Scholar] [CrossRef]
- Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. NPJ Comput. Mater. 2016, 2, 16028. [Google Scholar] [CrossRef]
- Atha, D.J.; Jahanshahi, M.R. Evaluation of deep learning approaches based on convolutional neural networks for corrosion detection. Struct. Health Monit. 2018, 17, 1110–1128. [Google Scholar] [CrossRef]
- Gibert, X.; Patel, V.M.; Chellappa, R. Deep Multitask Learning for Railway Track Inspection. IEEE Trans. Intell. Transp. Syst. 2017, 18, 153–164. [Google Scholar] [CrossRef]
- Hou, W.; Wei, Y.; Guo, J.; Jin, Y.; Zhu, C. Automatic Detection of Welding Defects using Deep Neural Network. J. Phys. Conf. Ser. 2018, 933, 012006. [Google Scholar] [CrossRef]
- Lin, Y.; Nie, Z.; Ma, H. Structural Damage Detection with Automatic Feature-Extraction through Deep Learning. Comput. Civ. Infrastruct. Eng. 2017, 32, 1025–1046. [Google Scholar] [CrossRef]
- Zhao, M.; Pan, W.; Wan, C.; Qu, Z.; Li, Z.; Yang, J. Defect engineering in development of low thermal conductivity materials: A review. J. Eur. Ceram. Soc. 2017, 37, 1–13. [Google Scholar] [CrossRef]
- Petricca, L.; Moss, T.; Figueroa, G.; Broen, S. Corrosion detection using AI a comparison of standard computed vision techniques and deep learning model. Comput. Sci. Inf. Technol. 2016, 91, 91–99. [Google Scholar]
- Zhang, A.; Wang, K.C.P.; Li, B.; Yang, E.; Dai, X.; Peng, Y.; Fei, Y.; Liu, Y.; Li, J.Q.; Chen, C. Automated Pixel-Level Pavement Crack Detection on 3D Asphalt Surfaces Using a Deep-Learning Network. Comput. Civ. Infrastruct. Eng. 2017, 32, 805–819. [Google Scholar] [CrossRef]
- Jha, D.; Ward, L.; Paul, A.; Liao, W.K.; Choudhary, A.; Wolverton, C.; Agrawal, A. ElemNet: Deep Learning the Chemistry of Materials from Only Elemental Composition. Sci. Rep. 2018, 8, 17593. [Google Scholar] [CrossRef] [PubMed]
- Goh, G.B.; Siegel, C.; Vishnu, A.; Hodas, N.O.; Baker, N. Chemception: A Deep Neural Network with Minimal Chemistry Knowledge Matches the Performance of Expert-developed QSAR/QSPR Models. 2017. Available online: http://arxiv.org/abs/1706.06689 (accessed on 10 March 2023).
- Carrera, G.; Branco, L.; Aires-de-Sousa, J.; Afonso, C. Exploration of quantitative structure–property relationships (QSPR) for the design of new guanidinium ionic liquids. Tetrahedron 2008, 64, 2216–2224. [Google Scholar] [CrossRef]
- Qian, X.; Peng, S.; Li, X.; Wei, Y.; Yang, R. Thermal conductivity modeling using machine learning potentials: Application to crystalline and amorphous silicon. Mater. Today Phys. 2019, 10, 100140. [Google Scholar] [CrossRef]
- Kautz, E.J.; Hagen, A.R.; Johns, J.M.; Burkes, D.E. A Machine Learning Approach to Thermal Conductivity Modeling: A Case Study on Irradiated Uranium-Molybdenum Nuclear Fuels. Comput. Mater. Sci. 2019, 161, 107–118. [Google Scholar] [CrossRef]
- Wei, H.; Zhao, S.; Rong, Q.; Bao, H. Predicting the effective thermal conductivities of composite materials and porous media by machine learning methods. Int. J. Heat Mass Transf. 2018, 127, 908–916. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, Q. Gaussian approximation potential for studying the thermal conductivity of silicene. J. Appl. Phys. 2019, 126, 105103. [Google Scholar] [CrossRef]
- Gu, S.; Lu, T.J.; Hass, D.D.; Wadley, H.N.G. Thermal conductivity of zirconia coatings with zig-zag pore microstructures. Acta Mater. 2001, 49, 2539–2547. [Google Scholar] [CrossRef]
- Wang, Z.; Kulkarni, A.; Deshpande, S.; Nakamura, T.; Herman, H. Effects of pores and interfaces on effective properties of plasma sprayed zirconia coatings. Acta Mater. 2003, 51, 5319–5334. [Google Scholar] [CrossRef]
- Jadhav, A.D.; Padture, N.P.; Jordan, E.H.; Gell, M.; Miranzo, P.; Fuller, E.R. Low-thermal-conductivity plasma-sprayed thermal barrier coatings with engineered microstructures. Acta Mater. 2006, 54, 3343–3349. [Google Scholar] [CrossRef]
- Renteria, A.F.; Saruhan, B.; Schulz, U.; Raetzer-Scheibe, H.J.; Haug, J.; Wiedenmann, A. Effect of morphology on thermal conductivity of EB-PVD PYSZ TBCs. Surf. Coat. Technol. 2006, 201, 2611–2620. [Google Scholar] [CrossRef]
- Wei, S.; Fu-chi, W.; Qun-Bo, F.; Zhuang, M. Effects of defects on the effective thermal conductivity of thermal barrier coatings. Appl. Math. Model. 2012, 36, 1995–2002. [Google Scholar] [CrossRef]
- Schulz, U.; Schmücker, M. Microstructure of ZrO2 thermal barrier coatings applied by EB-PVD. Mater. Sci. Eng. A 2000, 276, 1–8. [Google Scholar] [CrossRef]
- Peters, M.; Leyens, C.; Schulz, U.; Kaysser, W.A. EB-PVD Thermal Barrier Coatings for Aeroengines and Gas Turbines. Adv. Eng. Mater. 2001, 3, 193–204. [Google Scholar] [CrossRef]
- Unal, O.; Mitchell, T.E.; Heuer, A.H. Microstructures of Y2O3-Stabilized ZrO2 Electron Beam-Physical Vapor Deposition Coatings on Ni-Base Superalloys. J. Am. Ceram. Soc. 1994, 77, 984–992. [Google Scholar] [CrossRef]
- Schulz, U.; Fritscher, K.; Rätzer-Scheibe, H.-J.; Kaysser, W.A.; Peters, M. Thermocyclic Behaviour of Microstructurally Modified EB-PVD Thermal Barrier Coatings. Mater. Sci. Forum 1997, 251–254, 957–964. [Google Scholar] [CrossRef]
- Schulz, U. Phase Transformation in EB-PVD Yttria Partially Stabilized Zirconia Thermal Barrier Coatings during Annealing. J. Am. Ceram. Soc. 2000, 83, 904–910. [Google Scholar] [CrossRef]
- Lugscheider, E.; Barimani, C.; Döpper, G. Ceramic thermal barrier coatings deposited with the electron beam-physical vapour deposition technique. Surf. Coat. Technol. 1998, 98, 1221–1227. [Google Scholar] [CrossRef]
- Rätzer-Scheibe, H.J.; Schulz, U. The effects of heat treatment and gas atmosphere on the thermal conductivity of APS and EB-PVD PYSZ thermal barrier coatings. Surf. Coat. Technol. 2007, 201, 7880–7888. [Google Scholar] [CrossRef]
- Amato, F.; López, A.; Peña-Méndez, E.M.; Vaňhara, P.; Hampl, A.; Havel, J. Artificial neural networks in medical diagnosis. J. Appl. Biomed. 2013, 11, 47–58. [Google Scholar] [CrossRef]
- An, K.; Ravichandran, K.S.; Dutton, R.E.; Semiatin, S.L. Microstructure, Texture, and Thermal Conductivity of Single-Layer and Multilayer Thermal Barrier Coatings of Y2O3-Stabilized ZrO2 and Al2O3 Made by Physical Vapor Deposition. J. Am. Ceram. Soc. 1999, 82, 399–406. [Google Scholar] [CrossRef]
- Nicholls, J.R.; Lawson, K.J.; Johnstone, A.; Rickerby, D.S. Methods to reduce the thermal conductivity of EB-PVD TBCs. Surf. Coat. Technol. 2002, 151–152, 383–391. [Google Scholar] [CrossRef]
- Jang, B.K.; Yoshiya, M.; Yamaguchi, N.; Matsubara, H. Evaluation of thermal conductivity of zirconia coating layers deposited by EB-PVD. J. Mater. Sci. 2004, 39, 1823–1825. [Google Scholar] [CrossRef]
- Singh, J.; Wolfe, D.E.; Miller, R.A.; Eldridge, J.I.; Zhu, D.M. Tailored microstructure of zirconia and hafnia-based thermal barrier coatings with low thermal conductivity and high hemispherical reflectance by EB-PVD. J. Mater. Sci. 2004, 39, 1975–1985. [Google Scholar] [CrossRef]
- Matsumoto, M.; Yamaguchi, N.; Matsubara, H. Low thermal conductivity and high temperature stability of ZrO2-Y2O3-La2O3 coatings produced by electron beam PVD. Scr. Mater. 2004, 50, 867–871. [Google Scholar] [CrossRef]
- Rätzer-Scheibe, H.J.; Schulz, U.; Krell, T. The effect of coating thickness on the thermal conductivity of EB-PVD PYSZ thermal barrier coatings. Surf. Coat. Technol. 2006, 200, 5636–5644. [Google Scholar] [CrossRef]
- Almeida, D.S.; Silva, C.R.M.; Nono, M.C.A.; Cairo, C.A.A. Thermal conductivity investigation of zirconia co-doped with yttria and niobia EB-PVD TBCs. Mater. Sci. Eng. A 2007, 443, 60–65. [Google Scholar] [CrossRef]
- Schulz, U.; Rätzer-Scheibe, H.J.; Saruhan, B.; Renteria, A.F. Thermal conductivity issues of EB-PVD thermal barrier coatings. Materwiss. Werksttech. 2007, 38, 659–666. [Google Scholar] [CrossRef]
- Jang, B.K. Thermal conductivity of nanoporous ZrO2-4 mol% Y2O3 multilayer coatings fabricated by EB-PVD. Surf. Coat. Technol. 2008, 202, 1568–1573. [Google Scholar] [CrossRef]
- Matsumoto, M.; Kato, T.; Yamaguchi, N.; Yokoe, D.; Matsubara, H. Thermal conductivity and thermal cycle life of La2O3 and HfO2 doped ZrO2-Y2O3 coatings produced by EB-PVD. Surf. Coat. Technol. 2009, 203, 2835–2840. [Google Scholar] [CrossRef]
- Jang, B.K.; Sakka, Y.; Yamaguchi, N.; Matsubara, H.; Kim, H.T. Thermal conductivity of EB-PVD ZrO2-4 mol% Y2O3 films using the laser flash method. J. Alloys Compd. 2011, 509, 1045–1049. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, H.; Lei, X.; Zheng, Y. Dependence of microstructure and thermal conductivity of EB-PVD thermal barrier coatings on the substrate rotation speed. Phys. Procedia 2011, 18, 206–210. [Google Scholar] [CrossRef]
- Bobzin, K.; Bagcivan, N.; Brögelmann, T.; Yildirim, B. Influence of temperature on phase stability and thermal conductivity of single- and double-ceramic-layer EB-PVD TBC top coats consisting of 7YSZ, Gd2Zr2O7 and La2Zr2O7. Surf. Coat. Technol. 2013, 237, 56–64. [Google Scholar] [CrossRef]
- Behrens, J.T. Principles and Procedures of Exploratory Data Analysis. Psychol. Methods 1997, 2, 131–160. [Google Scholar] [CrossRef]
- Blum, A.L.; Langley, P. Selection of relevant features and examples in machine learning. Artif. Intell. 1997, 97, 245–271. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S.A.; Luo, W. Orthogonal least squares methods and their application to non-linear system identification. Int. J. Control 1989, 50, 1873–1896. [Google Scholar] [CrossRef]
- Chen, S.; Cowan, C.F.N.; Grant, P.M. Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans. Neural Netw. 1991, 2, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Miller, A. Subset Selection in Regression, 2nd ed.; Chapman & Hall: Boca Raton, FL, USA, 2002. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Foresee, F.D.; Hagan, M.T. Gauss-Newton approximation to Bayesian learning. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 9–12 June 1997; Volume 3, pp. 1930–1935. [Google Scholar]
- Kayri, M. Predictive abilities of Bayesian regularization and levenberg-marquardt algorithms in artificial neural networks: A comparative empirical study on social data. Math. Comput. Appl. 2016, 21, 20. [Google Scholar] [CrossRef]
- Sorich, M.J.; Miners, J.O.; McKinnon, R.A.; Winkler, D.A.; Burden, F.R.; Smith, P.A. Comparison of Linear and Nonlinear Classification Algorithms for the Prediction of Drug and Chemical Metabolism by Human UDP-Glucuronosyltransferase Isoforms. J. Chem. Inf. Comput. Sci. 2003, 43, 2019–2024. [Google Scholar] [CrossRef]
- Xu, M.; Zeng, G.; Xu, X.; Huang, G.; Jiang, R.; Sun, W. Application of Bayesian Regularized BP Neural Network Model for Trend Analysis, Acidity and Chemical Composition of Precipitation in North Carolina. Water Air Soil Pollut. 2006, 172, 167–184. [Google Scholar] [CrossRef]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural Networks and the Bias/Variance Dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training Feedforward Networks with the Marquardt Algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Landis, D. The Computational Materials Repository. Comput. Sci. Eng. 2012, 14, 51–57. [Google Scholar] [CrossRef]
- Demuth, H.; Meale, M. Neural Network Toolbox User’s Guide; The matchWorks Inc., 2004; Available online: http://cda.psych.uiuc.edu/matlab_pdf/nnet.pdf (accessed on 10 March 2023).
- Keprate, A.; Ratnayake, R.M.C. Using gradient boosting regressor to predict stress intensity factor of a crack propagating in small bore piping. In Proceedings of the 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 10–13 December 2017; pp. 1331–1336. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Curtarolo, S.; Setyawan, W.; Hart, G.L.W.; Jahnatek, M.; Chepulskii, R.V.; Taylor, R.H.; Wang, S.; Xue, J.; Yang, K.; Levy, O.; et al. AFLOW: An automatic framework for high-throughput materials discovery. Comput. Mater. Sci. 2012, 58, 218–226. [Google Scholar] [CrossRef]
- Gražulis, S.; Daškevič, A.; Merkys, A.; Chateigner, D.; Lutterotti, L.; Quirós, M.; Serebryanaya, N.R.; Moeck, P.; Downs, R.T.; Le Bail, A. Crystallography Open Database (COD): An open-access collection of crystal structures and platform for world-wide collaboration. Nucleic Acids Res. 2012, 40, 420–427. [Google Scholar] [CrossRef] [PubMed]
- Materials Cloud. Available online: https://www.materialscloud.org (accessed on 10 March 2020).
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 11002. [Google Scholar] [CrossRef]
- Ogata, T. New stage of MatNavi, materials database at NIMS Toshio Ogata and Masayoshi Yamazaki Materials Information Station (MIS) National Institute for Materials Science (NIMS) Tsukuba, Japan. In Materials Database at NIMS, in Harnessing the Materials Genome; 2012; Volume 21, Available online: https://dc.engconfintl.org/cgi/viewcontent.cgi?article=1007&context=materials_genome (accessed on 10 March 2023).
- Borysov, S.S.; Geilhufe, R.M.; Balatsky, A.V. Organic materials database: An open-access online database for data mining. PLoS ONE 2017, 12, e0171501. [Google Scholar] [CrossRef]
- Kirklin, S.; Saal, J.E.; Meredig, B.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C. The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies. NPJ Comput. Mater. 2015, 1, 15010. [Google Scholar] [CrossRef]
- Armiento, R. The High-Throughput Toolkit (httk). Available online: http://httk.openmaterialsdb.se/ (accessed on 10 March 2020).
- Mamun, O.; Winther, K.T.; Boes, J.R.; Bligaard, T. High-throughput calculations of catalytic properties of bimetallic alloy surfaces. Sci. Data 2019, 6, 76. [Google Scholar] [CrossRef]
- Pence, H.; Williams, A. ChemSpider: An Online Chemical Information Resource. Chem. Educ. Today 2010, 87, 1123–1124. [Google Scholar] [CrossRef]
- Hill, J.; Mannodi-Kanakkithodi, A.; Ramprasad, R.; Meredig, B. Materials Data Infrastructure and Materials Informatics; Chapter 9, Computational Materials System Design; Springer International Publishing AG: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Materials Data Repository, nist.gov. Available online: https://materialsdata.nist.gov/ (accessed on 10 March 2023).
- Klimeck, G.; Ahmed, S.S.; Kharche, N.; Korkusinski, M.; Usman, M.; Prada, M.; Boykin, T.B. Atomistic simulation of realistically sized nanodevices using NEMO 3-D-Part II: Applications. IEEE Trans. Electron Devices 2007, 54, 2090–2099. [Google Scholar] [CrossRef]
- Ostraat, M.L.; Mills, K.C.; Guzan, K.A.; Murry, D. The Nanomaterial Registry: Facilitating the sharing and analysis of data in the diverse nanomaterial community. Int. J. Nanomed. 2013, 8, 7–13. [Google Scholar] [CrossRef]
- Hale, L.; Trautt, Z.; Becker, C. Interatomic Potentials Repository Project. 2018. Available online: http://www.ctcms.nist.gov/potentials/ (accessed on 10 March 2020).
- Kim, S.; Thiessen, P.A.; Bolton, E.E.; Chen, J.; Fu, G.; Gindulyte, A.; Han, L.; He, J.; He, S.; Shoemaker, B.A.; et al. PubChem substance and compound databases. Nucleic Acids Res. 2016, 44, D1202–D1213. [Google Scholar] [CrossRef]
- Gorai, P.; Gao, D.; Ortiz, B.; Miller, S.; Barnett, S.A.; Mason, T.; Lv, Q.; Stevanović, V.; Toberer, E.S. TE Design Lab: A virtual laboratory for thermoelectric material design. Comput. Mater. Sci. 2016, 112, 368–376. [Google Scholar] [CrossRef]
- Gaultois, M.W.; Sparks, T.D.; Borg, C.K.H.; Seshadri, R.; Bonificio, W.D.; Clarke, D.R. Data-driven review of thermoelectric materials: Performance and resource onsiderations. Chem. Mater. 2013, 25, 2911–2920. [Google Scholar] [CrossRef]
- Belsky, A.; Hellenbrandt, M.; Karen, V.L.; Luksch, P. New developments in the Inorganic Crystal Structure Database (ICSD): Accessibility in support of materials research and design. Acta Crystallogr. Sect. B 2002, 58, 364–369. [Google Scholar] [CrossRef]
- Allen, F.H.; Bellard, S.; Brice, M.D.; Cartwright, B.A.; Doubleday, A.; Higgs, H.; Hummelink, T.; Hummelink-Peters, B.G.; Kennard, O.; Motherwell, W.D.S.; et al. The Cambridge Crystallographic Data Centre: Computer-based search, retrieval, analysis and display of information. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1979, 35, 2331–2339. [Google Scholar] [CrossRef]
- NIST Standard Reference Data: SRD Definition per Public Laws, nist.gov. Available online: https://www.nist.gov/srd (accessed on 10 March 2023).
- Klaver, T.P.C.; Simonovic, D.; Sluiter, M.H.F. Brute Force Composition Scanning with a CALPHAD Database to Find Low Temperature Body Centered Cubic High Entropy Alloys. Entropy 2018, 20, 911. [Google Scholar] [CrossRef]
- ASM Alloy Center Database. Available online: https://www.asminternational.org/materials-resources/online-databases/-/journal_content/56/10192/15468704/DATABASE/ (accessed on 10 March 2023).
- Cr (Chromium) Binary Alloy Phase Diagrams. In Alloy Phase Diagrams; ASM International: Almere, The Netherlands, 2016.
- MATDAT. Available online: https://www.matdat.com/ (accessed on 10 March 2020).
- Blokhin, E.; Villars, P. The PAULING FILE Project and Materials Platform for Data Science: From Big Data Toward Materials Genome. In Handbook of Materials Modeling: Methods: Theory and Modeling; Andreoni, W., Yip, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–26. [Google Scholar]
- Kalinichenko, L. New Data Access Challenges for Data Intensive Research in Russia. In Proceedings of the International Conference DAMDID/RCDL, Obninsk, Russia, 13–16 October 2015. [Google Scholar]
- Explosive Welding of Non-Ferrous Alloys: Part One. Available online: totalmateria.com (accessed on 10 March 2020).
- Taylor, R.E. Thermal conductivity determinations of thermal barrier coatings. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 1998, 245, 160–167. [Google Scholar] [CrossRef]
- Raghavan, S.; Wang, H.; Dinwiddie, R.B.; Porter, W.D.; Mayo, M.J. The effect of grain size, porosity and yttria content on the thermal conductivity of nanocrystalline zirconia. Scr. Mater. 1998, 39, 1119–1125. [Google Scholar] [CrossRef]
- Zhu, D.; Miller, R.A.; Nagaraj, B.A.; Bruce, R.W. Thermal conductivity of EB-PVD thermal barrier coatings evaluated by a steady-state laser heat flux technique. Surf. Coat. Technol. 2001, 138, 1–8. [Google Scholar] [CrossRef]
- Zhu, D.; Miller, R.A. Thermal Conductivity and Sintering Behavior of Advanced Thermal Barrdxr Coatings. In Proceedings of the 26th Annual International Conference on Advanced Ceramics and Composites sponsored by the American Ceramics Society Cocoa, Cocoa Beach, FL, USA, 13–18 January 2002. [Google Scholar]
- Cernuschi, F.; Ahmaniemi, S.; Vuoristo, P.; Mäntylä, T. Modelling of thermal conductivity of porous materials: Application to thick thermal barrier coatings. J. Eur. Ceram. Soc. 2004, 24, 2657–2667. [Google Scholar] [CrossRef]
- Wolfe, D.E.; Singh, J.; Miller, R.A.; Eldridge, J.I.; Zhu, D.M. Tailored microstructure of EB-PVD 8YSZ thermal barrier coatings with low thermal conductivity and high thermal reflectivity for turbine applications. Surf. Coat. Technol. 2005, 190, 132–149. [Google Scholar] [CrossRef]
- Ma, X.; Wu, F.; Roth, J.; Gell, M.; Jordan, E.H. Low thermal conductivity thermal barrier coating deposited by the solution plasma spray process. Surf. Coat. Technol. 2006, 201, 4447–4452. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, H.; Tao, S.; Zhou, X.; Ding, C. Thermal conductivity of plasma sprayed Sm2Zr2O7 coatings. J. Eur. Ceram. Soc. 2010, 30, 799–804. [Google Scholar] [CrossRef]
- Limarga, A.M.; Shian, S.; Baram, M.; Clarke, D.R. Effect of high-temperature aging on the thermal conductivity of nanocrystalline tetragonal yttria-stabilized zirconia. Acta Mater. 2012, 60, 5417–5424. [Google Scholar] [CrossRef]
- Łatka, L.; Cattini, A.; Pawłowski, L.; Valette, S.; Pateyron, B.; Lecompte, J.P.; Kumar, R.; Denoirjean, A. Thermal diffusivity and conductivity of yttria stabilized zirconia coatings obtained by suspension plasma spraying. Surf. Coat. Technol. 2012, 208, 87–91. [Google Scholar] [CrossRef]
- Zhang, H.S.; Wei, Y.; Li, G.; Chen, X.G.; Wang, X.L. Investigation about thermal conductivities of La2Ce2O7 doped with calcium or magnesium for thermal barrier coatings. J. Alloys Compd. 2012, 537, 141–146. [Google Scholar] [CrossRef]
- Jang, B.K.; Kim, S.; Oh, Y.S.; Kim, H.T.; Sakka, Y.; Murakami, H. Effect of Gd2O3 on the thermal conductivity of ZrO2-4 mol.% Y2O3 ceramics fabricated by spark plasma sintering. Scr. Mater. 2013, 69, 165–170. [Google Scholar] [CrossRef]
- Sun, L.; Guo, H.; Peng, H.; Gong, S.; Xu, H. Phase stability and thermal conductivity of ytterbia and yttria co-doped zirconia. Prog. Nat. Sci. Mater. Int. 2013, 23, 440–445. [Google Scholar] [CrossRef]
- Zhao, M.; Pan, W. Effect of lattice defects on thermal conductivity of Ti-doped, Y2O3-stabilized ZrO2. Acta Mater. 2013, 61, 5496–5503. [Google Scholar] [CrossRef]
- Jordan, E.H.; Jiang, C.; Roth, J.; Gell, M. Low thermal conductivity yttria-stabilized zirconia thermal barrier coatings using the solution precursor plasma spray process. J. Therm. Spray Technol. 2014, 23, 849–859. [Google Scholar] [CrossRef]
- Lu, H.; Wang, C.A.; Zhang, C. Low thermal conductivity Sr2+, Zn2+ and Ti4+ ions co-doped LaMgAl11O19 for potential thermal barrier coating applications. Ceram. Int. 2014, 40, 16273–16279. [Google Scholar] [CrossRef]
- Wang, L.; Zhong, X.H.; Zhao, Y.X.; Yang, J.S.; Tao, S.Y.; Zhang, W.; Wang, Y.; Sun, X.G. Effect of interface on the thermal conductivity of thermal barrier coatings: A numerical simulation study. Int. J. Heat Mass Transf. 2014, 79, 954–967. [Google Scholar] [CrossRef]
- Rai, A.K.; Schmitt, M.P.; Bhattacharya, R.S.; Zhu, D.; Wolfe, D.E. Thermal conductivity and stability of multilayered thermal barrier coatings under high temperature annealing conditions. J. Eur. Ceram. Soc. 2015, 35, 1605–1612. [Google Scholar] [CrossRef]
- Guo, L.; Li, M.; Ye, F. Phase stability and thermal conductivity of RE2O3 (RE = La, Nd, Gd, Yb) and Yb2O3 co-doped Y2O3 stabilized ZrO2 ceramics. Ceram. Int. 2016, 42, 7360–7365. [Google Scholar] [CrossRef]
- Arai, M.; Ochiai, H.; Suidzu, T. A novel low-thermal-conductivity plasma-sprayed thermal barrier coating controlled by large pores. Surf. Coat. Technol. 2016, 285, 120–127. [Google Scholar] [CrossRef]
- Guo, X.; Hu, B.; Wei, C.; Sun, J.; Jung, Y.G.; Li, L.; Knapp, J.; Zhang, J. Image-based multi-scale simulation and experimental validation of thermal conductivity of lanthanum zirconate. Int. J. Heat Mass Transf. 2016, 100, 34–38. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Ling, X.; Weng, Y. Effects of pore microstructure on the effective thermal conductivity of thermal barrier coatings. Appl. Therm. Eng. 2016, 102, 234–242. [Google Scholar] [CrossRef]
- Xiaofeng, Z.; Xiwen, S.; Xiangzhong, C.; Min, X.; Shengli, A. Morphology and thermal conductivity of La2(Ce0.3Zr0.7)2O7-3 wt.%Y2O3 coatings. Surf. Coat. Technol. 2016, 291, 216–221. [Google Scholar] [CrossRef]
- Meng, M.; Chua, Y.J.; Wouterson, E.; Ong, C.P.K. Ultrasonic signal classification and imaging system for composite materials via deep convolutional neural networks. Neurocomputing 2017, 257, 128–135. [Google Scholar] [CrossRef]





| Paper No. | Year | Author | wt.% of Y2O3 | Sample No. |
|---|---|---|---|---|
| [86] | 1999 | An | 8 | 18 |
| [87] | 2002 | Nichols | 7 | 1 |
| [88] | 2004 | Jang | 7 | 10 |
| [89] | 2004 | Singh | 8 | 11 |
| [90] | 2004 | Matsumoto | 7.1 | 3 |
| [76] | 2006 | Renteria | 7.5 | 128 |
| [91] | 2006 | Scheibe | 7 | 152 |
| [92] | 2007 | Almeida | 8 | 7 |
| [84] | 2007 | Scheibe | 7 | 187 |
| [93] | 2007 | Schulz | 7 | 146 |
| [94] | 2008 | Jang | 7 | 10 |
| [95] | 2009 | Matsumoto | 7 | 6 |
| [96] | 2011 | Jang | 8 | 18 |
| [97] | 2011 | Liu | 7 | 4 |
| [98] | 2013 | Bobzin | 7 | 4 |
| Number of Total Samples | 705 |
| Variables | Unit | Description | Functions |
|---|---|---|---|
| TC | W/(m∙K) | Thermal conductivity of TBC layer | Output |
| Temp | °C | Temperature during measurement | Inputs |
| Material | NA | wt.% of Y2O3 | |
| Thickness | mm | Thickness of the top layer of the TBC | |
| AgingTemp | ℃ | Temperature of heat treatment | |
| AgingTime | Hour | Time of heat treatment |
| TC | Temp | Material | Thickness | AgingTemp | AgingTime | |
|---|---|---|---|---|---|---|
| TC | 1 | −0.21871 | 0.071464 | −0.14227 | 0.175485 | 0.317287 |
| Temp | −0.21871 | 1 | 0.2324 | −0.09883 | 0.147777 | 0.076015 |
| Material | 0.071464 | 0.2324 | 1 | −0.18194 | 0.137038 | 0.234873 |
| Thickness | −0.14227 | −0.09883 | −0.18194 | 1 | −0.19923 | −0.05417 |
| AgingTemp | 0.175485 | 0.147777 | 0.137038 | −0.19923 | 1 | 0.290966 |
| AgingTime | 0.317287 | 0.076015 | 0.234873 | −0.05417 | 0.290966 | 1 |
| Polynomial Degree | Number of Terms | R2 (on All Data) |
|---|---|---|
| 1 | 5 | 0.19114 |
| 2 | 20 | 0.40414 |
| 3 | 55 | 0.62683 |
| 4 | 125 | 0.78005 |
| 5 | 251 | 0.84011 |
| 6 | 461 | 0.88241 |
| Selection Step | ERR | Input/Model Term Index | Sum of ERR |
|---|---|---|---|
| 1 | 0.10067 | 5 | 0.10067 |
| 2 | 0.059308 | 1 | 0.15998 |
| 3 | 0.022232 | 3 | 0.18221 |
| 4 | 0.0089309 | 4 | 0.19114 |
| 5 | 1.22 × 10−6 | 2 | 0.19114 |
| Selection Step | ERR | Input/Model Term Index | Sum of ERR |
|---|---|---|---|
| 1 | 0.1019 | 17 | 0.1019 |
| 2 | 0.086333 | 7 | 0.18823 |
| 3 | 0.029454 | 16 | 0.21768 |
| 4 | 0.027596 | 18 | 0.24528 |
| 5 | 0.056016 | 13 | 0.3013 |
| 6 | 0.023156 | 20 | 0.32445 |
| 7 | 0.013976 | 12 | 0.33843 |
| 8 | 0.015815 | 8 | 0.35424 |
| 9 | 0.010708 | 6 | 0.36495 |
| 10 | 0.013737 | 3 | 0.37869 |
| 11 | 0.0049433 | 2 | 0.38363 |
| 12 | 0.0061258 | 1 | 0.38976 |
| 13 | 0.0026508 | 11 | 0.39241 |
| 14 | 0.0029095 | 10 | 0.39532 |
| 15 | 0.0033999 | 5 | 0.39872 |
| 16 | 0.0010177 | 14 | 0.39974 |
| 17 | 0.00084935 | 9 | 0.40058 |
| 18 | 0.00050989 | 19 | 0.40109 |
| 19 | 0.0028143 | 15 | 0.40391 |
| 20 | 0.00023171 | 4 | 0.40414 |
| Train Data (100 Times) | Test Data (100 Times) | All Data (100 Times) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| # of Terms | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 45 | 0.62749 | 1.1053 | 0.041667 | 0.55114 | 0.94892 | 0.050533 | 0.61107 | 1.1367 | 0.04344 |
| 46 | 0.62768 | 1.1072 | 0.041603 | 0.54925 | 0.9571 | 0.050934 | 0.61082 | 1.1384 | 0.043469 |
| 32 | 0.57957 | 1.1156 | 0.04701 | 0.53946 | 0.96682 | 0.051537 | 0.57073 | 1.167 | 0.047916 |
| 31 | 0.57842 | 1.0936 | 0.047111 | 0.53765 | 0.97857 | 0.052283 | 0.56895 | 1.1664 | 0.048145 |
| 47 | 0.62909 | 1.1043 | 0.041448 | 0.53262 | 1.03 | 0.053746 | 0.60734 | 1.1774 | 0.043908 |
| 38 | 0.6083 | 1.0821 | 0.043814 | 0.53212 | 0.93576 | 0.053089 | 0.59125 | 1.1371 | 0.045669 |
| 29 | 0.56916 | 1.1071 | 0.04812 | 0.5316 | 0.94384 | 0.05256 | 0.56089 | 1.1414 | 0.049008 |
| 39 | 0.60982 | 1.0894 | 0.043646 | 0.53089 | 0.93726 | 0.053284 | 0.59215 | 1.1444 | 0.045573 |
| 48 | 0.62975 | 1.0957 | 0.041373 | 0.53083 | 1.0299 | 0.053977 | 0.60747 | 1.1686 | 0.043894 |
| 35 | 0.59576 | 1.1181 | 0.045229 | 0.53067 | 0.95151 | 0.052893 | 0.58136 | 1.1678 | 0.046762 |
| Train Data (100 Times) | Test Data (100 Times) | All Data (100 Times) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| # of Terms | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 63 | 0.76379 | 0.87438 | 0.026429 | 0.64568 | 1.0605 | 0.044038 | 0.73468 | 1.1313 | 0.02995 |
| 62 | 0.75617 | 0.88107 | 0.027252 | 0.62731 | 1.2072 | 0.057195 | 0.71697 | 1.292 | 0.033241 |
| 69 | 0.76814 | 0.88605 | 0.025935 | 0.61991 | 1.2078 | 0.055133 | 0.72555 | 1.2849 | 0.031774 |
| 67 | 0.76705 | 0.88869 | 0.02606 | 0.61712 | 1.2599 | 0.053943 | 0.72542 | 1.3401 | 0.031637 |
| 61 | 0.75483 | 0.88853 | 0.027398 | 0.61692 | 1.3323 | 0.062347 | 0.71083 | 1.4122 | 0.034388 |
| 70 | 0.76839 | 0.88623 | 0.025899 | 0.6164 | 1.2297 | 0.055927 | 0.72479 | 1.3009 | 0.031905 |
| 57 | 0.71268 | 1.1149 | 0.032142 | 0.61543 | 1.0718 | 0.047358 | 0.68768 | 1.282 | 0.035185 |
| 68 | 0.76739 | 0.88766 | 0.026022 | 0.61537 | 1.2589 | 0.055661 | 0.72449 | 1.3246 | 0.03195 |
| 64 | 0.7652 | 0.87173 | 0.026248 | 0.6124 | 1.2677 | 0.055151 | 0.72249 | 1.3347 | 0.032029 |
| 66 | 0.76697 | 0.89022 | 0.026063 | 0.61239 | 1.2683 | 0.054678 | 0.72414 | 1.3462 | 0.031786 |
| Train Data (100 Times) | Test Data (100 Times) | All Data (100 Times) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| # of Terms | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 66 | 0.79891 | 0.85624 | 0.022456 | 0.70892 | 0.93127 | 0.034216 | 0.77879 | 1.04 | 0.024808 |
| 65 | 0.79815 | 0.85049 | 0.022541 | 0.70813 | 0.92153 | 0.033986 | 0.77841 | 1.0249 | 0.02483 |
| 67 | 0.79966 | 0.85581 | 0.022374 | 0.70673 | 0.94112 | 0.034698 | 0.77866 | 1.0485 | 0.024839 |
| 68 | 0.79883 | 0.85777 | 0.022474 | 0.70504 | 0.94058 | 0.035055 | 0.77754 | 1.0478 | 0.02499 |
| 69 | 0.79939 | 0.85926 | 0.022415 | 0.70469 | 0.94026 | 0.035019 | 0.77802 | 1.0502 | 0.024936 |
| 71 | 0.79997 | 0.86136 | 0.022347 | 0.70454 | 0.93829 | 0.035062 | 0.77839 | 1.048 | 0.02489 |
| 64 | 0.79699 | 0.84963 | 0.022671 | 0.7025 | 0.95808 | 0.035076 | 0.77577 | 1.0511 | 0.025152 |
| 70 | 0.79967 | 0.86065 | 0.022387 | 0.70069 | 0.97523 | 0.036334 | 0.77647 | 1.077 | 0.025177 |
| 72 | 0.80123 | 0.86336 | 0.022217 | 0.697 | 1.0077 | 0.037491 | 0.77616 | 1.1076 | 0.025271 |
| 73 | 0.80134 | 0.86947 | 0.022191 | 0.69149 | 1.0307 | 0.038879 | 0.77416 | 1.1308 | 0.025528 |
| Train Data (100 Times) | Test Data (100 Times) | All Data (100 Times) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| # of Terms | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 100 | 0.83527 | 0.77303 | 0.018422 | 0.72653 | 0.85674 | 0.031695 | 0.81188 | 0.93618 | 0.021077 |
| 97 | 0.8342 | 0.7724 | 0.018524 | 0.72343 | 0.90631 | 0.033052 | 0.80933 | 0.9756 | 0.02143 |
| 101 | 0.83554 | 0.77389 | 0.018379 | 0.72315 | 0.8829 | 0.033182 | 0.81028 | 0.96055 | 0.021339 |
| 102 | 0.83581 | 0.77315 | 0.018361 | 0.72308 | 0.8703 | 0.032871 | 0.81081 | 0.94719 | 0.021263 |
| 98 | 0.83462 | 0.77269 | 0.018476 | 0.72221 | 0.90712 | 0.033362 | 0.80922 | 0.98244 | 0.021454 |
| 99 | 0.83496 | 0.77386 | 0.018445 | 0.72208 | 0.89571 | 0.033394 | 0.80944 | 0.9735 | 0.021435 |
| 103 | 0.83607 | 0.77357 | 0.018332 | 0.71998 | 0.89182 | 0.033889 | 0.80967 | 0.96321 | 0.021443 |
| 94 | 0.83183 | 0.77169 | 0.018791 | 0.71942 | 0.94028 | 0.034201 | 0.80591 | 1.0085 | 0.021873 |
| 93 | 0.83143 | 0.77165 | 0.018835 | 0.71791 | 0.94227 | 0.034348 | 0.80528 | 1.0088 | 0.021938 |
| 95 | 0.8321 | 0.77179 | 0.018755 | 0.71573 | 0.96354 | 0.035515 | 0.80437 | 1.0307 | 0.022107 |
| LM Algorithm | BR Algorithm | |||
|---|---|---|---|---|
| Percentage | Number of Data Points | Percentage | Number of Data Points | |
| Training | 70 | 493 | 85 | 599 |
| Validation | 15 | 106 | 0 | 0 |
| Testing | 15 | 106 | 15 | 106 |
| Cases | Single-Layer | Two-Layer | |
|---|---|---|---|
| nn | nn1 | nn2 | |
| 1 | 10 | 4 | 2 |
| 2 | 20 | 6 | 2 |
| 3 | 30 | 6 | 4 |
| 4 | 40 | 8 | 2 |
| 5 | 50 | 8 | 4 |
| 6 | 60 | 8 | 6 |
| 7 | 70 | 10 | 2 |
| 8 | 80 | 10 | 4 |
| 9 | 90 | 10 | 6 |
| 10 | 100 | 10 | 8 |
| Training Parameters | Default Value | Definition |
|---|---|---|
| net.trainParam.epochs | 1000 | Maximum number of epochs to train |
| net.trainParam.goal | 0 | Performance goal |
| net.trainParam.mu | 0.005 | Marquardt adjustment parameter |
| net.trainParam.mu_dec | 0.1 | Decrease factor for mu |
| net.trainParam.mu_inc | 10 | Increase factor for mu |
| net.trainParam.mu_max | 1 × 1010 | Maximum value for mu |
| net.trainParam.max_fail | inf | Maximum validation failures |
| net.trainParam.min_grad | 1 × 10−7 | Minimum performance gradient |
| net.trainParam.show | 25 | Epochs between displays (NaN for no displays) |
| net.trainParam.showCommandLine | false | Generate command-line output |
| net.trainParam.showWindow | true | Show training GUI |
| net.trainParam.time | inf | Maximum time to train in seconds |
| LM | 10 Train | 10 Test | 10 All | ||||||
|---|---|---|---|---|---|---|---|---|---|
| nn | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 10 | 0.6826 | 0.9918 | 0.0360 | 0.5748 | 0.8232 | 0.0457 | 0.6617 | 1.0755 | 0.0381 |
| 20 | 0.7694 | 0.8975 | 0.0257 | 0.6509 | 0.9232 | 0.0406 | 0.7329 | 1.0689 | 0.0299 |
| 30 | 0.7753 | 0.9422 | 0.0250 | 0.6270 | 0.9293 | 0.0466 | 0.7238 | 1.2181 | 0.0311 |
| 40 | 0.7609 | 0.9386 | 0.0268 | 0.6162 | 0.8681 | 0.0401 | 0.7235 | 1.0816 | 0.0309 |
| 50 | 0.7444 | 0.9675 | 0.0283 | 0.6117 | 0.9441 | 0.0451 | 0.6965 | 1.1875 | 0.0344 |
| 60 | 0.7436 | 1.0142 | 0.0295 | 0.5512 | 1.3672 | 0.0865 | 0.6568 | 1.7214 | 0.0417 |
| 70 | 0.7974 | 0.8665 | 0.0225 | 0.6489 | 0.8708 | 0.0397 | 0.7470 | 1.1126 | 0.0284 |
| LM | 10 Train | 10 Test | 100 All | ||||||
| nn | R2 | MAE | MSE | R2 | MAE | MSE | R2 | MAE | MSE |
| 90 | 0.7954 | 0.9860 | 0.0226 | 0.5319 | 1.4754 | 0.0739 | 0.7004 | 1.7896 | 0.0349 |
| 100 | 0.8078 | 0.8757 | 0.0212 | 0.6312 | 0.9481 | 0.0472 | 0.7315 | 1.4427 | 0.0317 |
| LM | 100 Train | 100 Test | 100 All | ||||||
|---|---|---|---|---|---|---|---|---|---|
| nn | R2 | MAE | MSE | R2 | MAE | MSE | R2 | MAE | MSE |
| 10 | 0.6774 | 0.9883 | 0.0363 | 0.5459 | 0.9828 | 0.0529 | 0.6449 | 1.1464 | 0.0398 |
| 20 | 0.7117 | 0.9841 | 0.0331 | 0.5754 | 0.9967 | 0.0520 | 0.6741 | 1.1705 | 0.0378 |
| 30 | 0.7544 | 0.9340 | 0.0275 | 0.6123 | 0.9289 | 0.0456 | 0.7122 | 1.1762 | 0.0324 |
| 40 | 0.7609 | 0.9429 | 0.0270 | 0.5726 | 1.1360 | 0.0556 | 0.7024 | 1.3485 | 0.0339 |
| 50 | 0.7643 | 0.9531 | 0.0267 | 0.5885 | 1.0932 | 0.0528 | 0.7097 | 1.3440 | 0.0334 |
| 60 | 0.7777 | 0.9321 | 0.0250 | 0.5993 | 1.1853 | 0.0675 | 0.7146 | 1.4348 | 0.0343 |
| 70 | 0.7766 | 0.9609 | 0.0254 | 0.5732 | 1.0903 | 0.0543 | 0.7140 | 1.3496 | 0.0330 |
| 90 | 0.7874 | 0.9396 | 0.0240 | 0.5705 | 1.2272 | 0.0670 | 0.7081 | 1.5107 | 0.0348 |
| 100 | 0.7991 | 0.9282 | 0.0226 | 0.5795 | 1.1686 | 0.0610 | 0.7242 | 1.4433 | 0.0321 |
| BR | 10 Train | 10 Test | 10 All | ||||||
|---|---|---|---|---|---|---|---|---|---|
| nn | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 10 | 0.7643 | 0.8418 | 0.0262 | 0.6202 | 1.1756 | 0.0541 | 0.7321 | 1.2170 | 0.0304 |
| 20 | 0.8469 | 0.6833 | 0.0170 | 0.6443 | 1.0706 | 0.0528 | 0.8034 | 1.1250 | 0.0224 |
| 30 | 0.8540 | 0.7328 | 0.0163 | 0.7228 | 0.7228 | 0.7179 | 0.0313 | 0.8339 | 0.0185 |
| 40 | 0.8255 | 0.7904 | 0.0195 | 0.6588 | 0.9704 | 0.0479 | 0.7895 | 1.0908 | 0.0238 |
| 50 | 0.8563 | 0.6921 | 0.0159 | 0.6861 | 0.9551 | 0.0398 | 0.8261 | 1.0484 | 0.0195 |
| 60 | 0.8606 | 0.6599 | 0.0156 | 0.5310 | 1.8826 | 0.1611 | 0.7548 | 1.8988 | 0.0375 |
| 70 | 0.8275 | 0.7896 | 0.0192 | 0.6733 | 0.8740 | 0.0369 | 0.8040 | 1.0180 | 0.0219 |
| 80 | 0.8540 | 0.7017 | 0.0161 | 0.6608 | 1.0552 | 0.0464 | 0.8167 | 1.1335 | 0.0207 |
| 90 | 0.8492 | 0.7088 | 0.0167 | 0.6983 | 1.0233 | 0.0388 | 0.8212 | 1.0845 | 0.0200 |
| 100 | 0.8595 | 0.6963 | 0.0160 | 0.6992 | 0.6992 | 0.9259 | 0.0328 | 0.8346 | 0.9658 |
| BR | 100 Train | 100 Test | 100 All | ||||||
|---|---|---|---|---|---|---|---|---|---|
| nn | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 10 | 0.7856 | 0.8410 | 0.0239 | 0.6554 | 0.9931 | 0.0466 | 0.7595 | 1.1017 | 0.0273 |
| 20 | 0.8441 | 0.7420 | 0.0173 | 0.6868 | 0.9604 | 0.0388 | 0.8169 | 1.0409 | 0.0205 |
| 30 | 0.8522 | 0.7239 | 0.0164 | 0.6775 | 0.9916 | 0.0437 | 0.8185 | 1.0678 | 0.0205 |
| 40 | 0.8466 | 0.7338 | 0.0171 | 0.6510 | 1.1477 | 0.0649 | 0.8047 | 1.2102 | 0.0243 |
| 50 | 0.8468 | 0.7405 | 0.0170 | 0.6632 | 1.1140 | 0.0493 | 0.8098 | 1.1783 | 0.0219 |
| 60 | 0.8502 | 0.7383 | 0.0167 | 0.6631 | 1.1337 | 0.0581 | 0.8088 | 1.2029 | 0.0229 |
| 70 | 0.8518 | 0.7123 | 0.0164 | 0.6303 | 1.3802 | 0.0822 | 0.7916 | 1.4364 | 0.0263 |
| 80 | 0.8494 | 0.7213 | 0.0167 | 0.6614 | 1.1500 | 0.0585 | 0.8098 | 1.2133 | 0.0230 |
| 90 | 0.8487 | 0.7289 | 0.0168 | 0.6539 | 1.1900 | 0.0723 | 0.8033 | 1.2615 | 0.0252 |
| 100 | 0.8503 | 0.7133 | 0.0167 | 0.6499 | 1.1991 | 0.0611 | 0.8051 | 1.2549 | 0.0233 |
| 10 Train | 10 Test | 10 All | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| nn1 | nn2 | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 4 | 2 | 0.4996 | 1.0426 | 0.0556 | 0.4062 | 1.1792 | 0.0786 | 0.4764 | 1.3394 | 0.0592 |
| 6 | 2 | 0.6660 | 0.9897 | 0.0382 | 0.4469 | 1.1897 | 0.0651 | 0.6178 | 1.3659 | 0.0435 |
| 6 | 4 | 0.6835 | 0.9355 | 0.0343 | 0.5479 | 1.0531 | 0.0588 | 0.6451 | 1.1437 | 0.0398 |
| 8 | 2 | 0.6717 | 0.9355 | 0.0358 | 0.5069 | 1.0985 | 0.0573 | 0.6390 | 1.1896 | 0.0404 |
| 8 | 4 | 0.7320 | 0.9554 | 0.0297 | 0.5834 | 1.1156 | 0.0562 | 0.6833 | 1.3080 | 0.0358 |
| 8 | 6 | 0.7363 | 0.9673 | 0.0297 | 0.6414 | 0.8477 | 0.0414 | 0.7067 | 1.0266 | 0.0329 |
| 10 | 2 | 0.7021 | 0.9618 | 0.0326 | 0.5784 | 0.8267 | 0.0501 | 0.6703 | 1.0191 | 0.0368 |
| 10 | 4 | 0.6482 | 0.9385 | 0.0387 | 0.5421 | 0.9438 | 0.0554 | 0.6119 | 1.0221 | 0.0437 |
| 10 | 6 | 0.7229 | 0.9049 | 0.0315 | 0.6180 | 0.8010 | 0.0443 | 0.6954 | 1.0116 | 0.0342 |
| 10 | 8 | 0.7624 | 0.8974 | 0.0263 | 0.6766 | 0.7962 | 0.0380 | 0.7388 | 0.9780 | 0.0292 |
| 100 Ttrain | 100 Test | 100 All | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| nn1 | nn2 | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 4 | 2 | 0.5141 | 1.0472 | 0.0548 | 0.4633 | 0.9372 | 0.0627 | 0.4972 | 1.1178 | 0.0565 |
| 6 | 2 | 0.6012 | 1.0126 | 0.0449 | 0.4914 | 1.1610 | 0.0867 | 0.5656 | 1.3142 | 0.0519 |
| 6 | 4 | 0.6426 | 0.9800 | 0.0403 | 0.5168 | 1.0306 | 0.0588 | 0.6082 | 1.1624 | 0.0441 |
| 8 | 2 | 0.6395 | 0.9831 | 0.0404 | 0.5418 | 0.9678 | 0.0534 | 0.6138 | 1.1124 | 0.0433 |
| 8 | 4 | 0.7052 | 0.9656 | 0.0330 | 0.5564 | 1.0385 | 0.0540 | 0.6677 | 1.1793 | 0.0374 |
| 8 | 6 | 0.7162 | 0.9272 | 0.0318 | 0.5812 | 1.0167 | 0.0585 | 0.6754 | 1.1749 | 0.0373 |
| 10 | 2 | 0.6827 | 0.9705 | 0.0354 | 0.5729 | 0.9255 | 0.0512 | 0.6518 | 1.0926 | 0.0391 |
| 10 | 4 | 0.7275 | 0.9397 | 0.0304 | 0.5694 | 1.0280 | 0.0511 | 0.6870 | 1.1677 | 0.0352 |
| 10 | 6 | 0.7158 | 0.9591 | 0.0318 | 0.5830 | 0.9806 | 0.0497 | 0.6797 | 1.1410 | 0.0359 |
| 10 | 8 | 0.7512 | 0.9049 | 0.0279 | 0.6127 | 0.9300 | 0.0459 | 0.7160 | 1.0583 | 0.0319 |
| 10 Train | 10 Test | 10 All | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| nn1 | nn2 | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 4 | 2 | 0.7152 | 0.9551 | 0.0321 | 0.6615 | 0.7508 | 0.0357 | 0.7071 | 0.9696 | 0.0327 |
| 6 | 2 | 0.7608 | 0.9108 | 0.0266 | 0.6623 | 0.8873 | 0.0383 | 0.7459 | 0.9839 | 0.0284 |
| 6 | 4 | 0.8327 | 0.7700 | 0.0185 | 0.6875 | 1.0085 | 0.0441 | 0.8019 | 1.0303 | 0.0224 |
| 8 | 2 | 0.8046 | 0.8324 | 0.0219 | 0.7244 | 0.7237 | 0.0297 | 0.7932 | 0.8941 | 0.0231 |
| 8 | 4 | 0.8583 | 0.6963 | 0.0157 | 0.6798 | 1.1972 | 0.0492 | 0.8196 | 1.2427 | 0.0207 |
| 8 | 6 | 0.8773 | 0.6274 | 0.0138 | 0.6989 | 1.1218 | 0.0372 | 0.8462 | 1.1616 | 0.0173 |
| 10 | 2 | 0.8607 | 0.6391 | 0.0155 | 0.6848 | 1.0583 | 0.0431 | 0.8259 | 1.1097 | 0.0197 |
| 10 | 4 | 0.8693 | 0.6572 | 0.0145 | 0.6324 | 1.8664 | 0.1027 | 0.7950 | 1.8878 | 0.0278 |
| 10 | 6 | 0.8842 | 0.5968 | 0.0130 | 0.6953 | 1.1535 | 0.0426 | 0.8463 | 1.1784 | 0.0174 |
| 10 | 8 | 0.8890 | 0.5804 | 0.0123 | 0.6124 | 1.8345 | 0.1261 | 0.7963 | 1.8483 | 0.0294 |
| 100 Train | 100 Test | 100All | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| nn1 | nn2 | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 4 | 2 | 0.6881 | 0.9444 | 0.0348 | 0.5918 | 0.9074 | 0.0457 | 0.6735 | 1.0273 | 0.0364 |
| 6 | 2 | 0.7620 | 0.9166 | 0.0265 | 0.6240 | 1.0206 | 0.0540 | 0.7343 | 1.1326 | 0.0306 |
| 6 | 4 | 0.8237 | 0.8006 | 0.0196 | 0.6766 | 1.0300 | 0.0433 | 0.7950 | 1.1024 | 0.0232 |
| 8 | 2 | 0.8111 | 0.8039 | 0.0209 | 0.6781 | 1.0534 | 0.0500 | 0.7819 | 1.1362 | 0.0253 |
| 8 | 4 | 0.8607 | 0.6759 | 0.0155 | 0.6799 | 1.0881 | 0.0464 | 0.8240 | 1.1322 | 0.0202 |
| 100 Train | 100 Test | 100All | ||||||||
| nn1 | nn2 | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| 10 | 2 | 0.8429 | 0.7348 | 0.0175 | 0.6450 | 1.2597 | 0.0636 | 0.7967 | 1.3176 | 0.0244 |
| 10 | 4 | 0.8740 | 0.6275 | 0.0140 | 0.6788 | 1.1092 | 0.0458 | 0.8352 | 1.1381 | 0.0188 |
| 10 | 6 | 0.8846 | 0.6083 | 0.0128 | 0.6900 | 1.1417 | 0.0468 | 0.8443 | 1.1681 | 0.0179 |
| 10 | 8 | 0.8886 | 0.6002 | 0.0124 | 0.6392 | 1.5001 | 0.0608 | 0.8321 | 1.5185 | 0.0196 |
| Train | Test | All | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Hyper Parameters | R2 | MAXE | MSE | R2 | MAXE | MSE | R2 | MAXE | MSE |
| deg 1 (10 times) | 0.9364 | 0.5969 | 0.0071 | 0.7637 | 0.7723 | 0.0261 | 0.9024 | 0.7723 | 0.0109 |
| deg 1 (100 times) | 0.9360 | 0.6022 | 0.0071 | 0.7531 | 0.8268 | 0.0268 | 0.9007 | 0.8493 | 0.0111 |
| deg 2 (10 times) | 0.9450 | 0.5881 | 0.0061 | 0.7290 | 0.8203 | 0.0299 | 0.9024 | 0.8203 | 0.0109 |
| deg 2 (100 times) | 0.9441 | 0.5953 | 0.0062 | 0.7326 | 0.8265 | 0.0289 | 0.9033 | 0.8379 | 0.0108 |
| Approach | Settings | R2 | MAXE | MSE |
|---|---|---|---|---|
| Polynomial Input Selection | OLS Algorithm Repeating 100 Times for 6th degree PRM | 0.8121 | 0.9321 | 0.0211 |
| Neural Network | Double Layer 10 + 6 nodes | 0.8443 | 1.1681 | 0.0179 |
| Gradient Boosting Regression | 1 Degree Inputs | 0.9024 | 0.7723 | 0.0109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, K.; Kumar, A.; Patnaik, P. Principles of Machine Learning and Its Application to Thermal Barrier Coatings. Coatings 2023, 13, 1140. https://doi.org/10.3390/coatings13071140
Liu Y, Chen K, Kumar A, Patnaik P. Principles of Machine Learning and Its Application to Thermal Barrier Coatings. Coatings. 2023; 13(7):1140. https://doi.org/10.3390/coatings13071140
Chicago/Turabian StyleLiu, Yuan, Kuiying Chen, Amarnath Kumar, and Prakash Patnaik. 2023. "Principles of Machine Learning and Its Application to Thermal Barrier Coatings" Coatings 13, no. 7: 1140. https://doi.org/10.3390/coatings13071140
APA StyleLiu, Y., Chen, K., Kumar, A., & Patnaik, P. (2023). Principles of Machine Learning and Its Application to Thermal Barrier Coatings. Coatings, 13(7), 1140. https://doi.org/10.3390/coatings13071140






