Influences of Magnetization Direction on the Flux Leakage Field of Weld Defects
Abstract
1. Introduction
- (1)
- (2)
- (3)
- Due to its mechanical structure, the detection device has a simple implementation and installation process [14].
2. Magnetic Field Distribution Characteristics in Different Magnetization Directions
- = the magnetic flux within the ferromagnetic material;
- = the magnetic flux that leaks into the air during the magnetization process.

- = the magnetic field leaked into the air during the magnetization process;
- = the flux leakage field caused by material bumps;
- = the flux leakage field caused by material defects.
- = the angle between the magnetization direction and the welding direction;
- = the flux leakage field produced by the parallel component,, of the magnetic field;
- = the flux leakage field produced by the perpendicular component, , of the magnetic field.
3. Simulation Analysis of Weld Flux Leakage Field Distribution
3.1. Construction of Finite Element Models
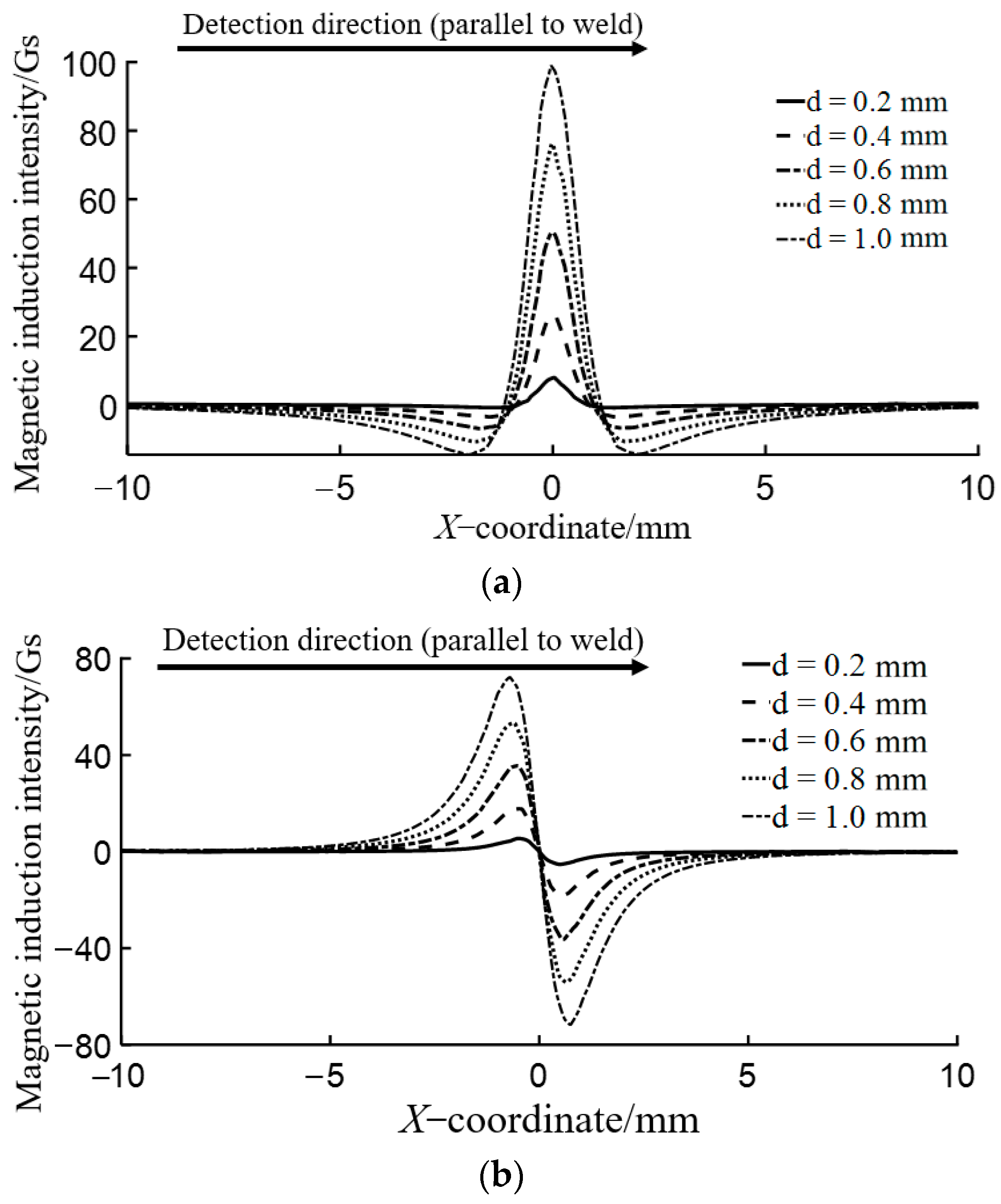
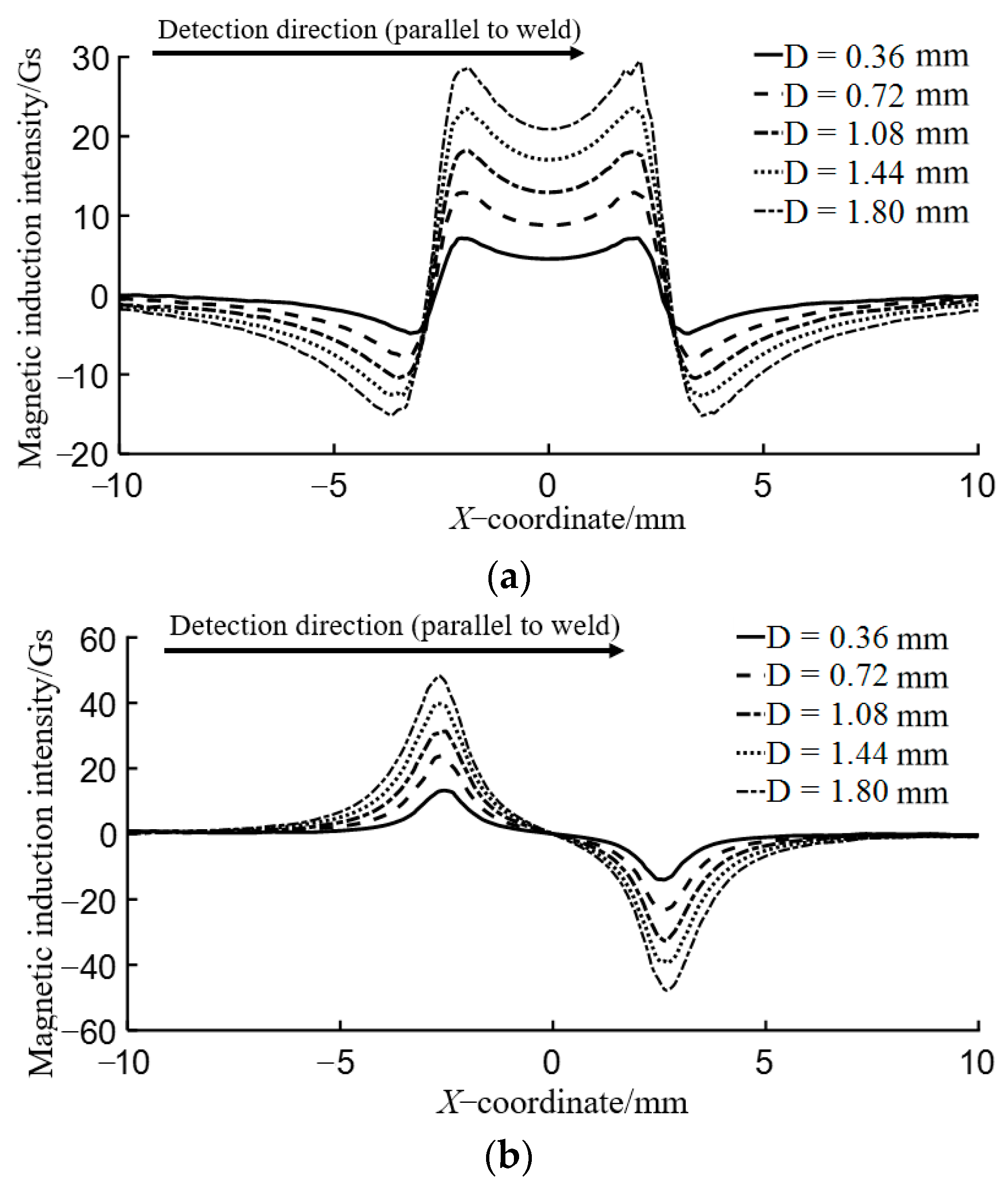
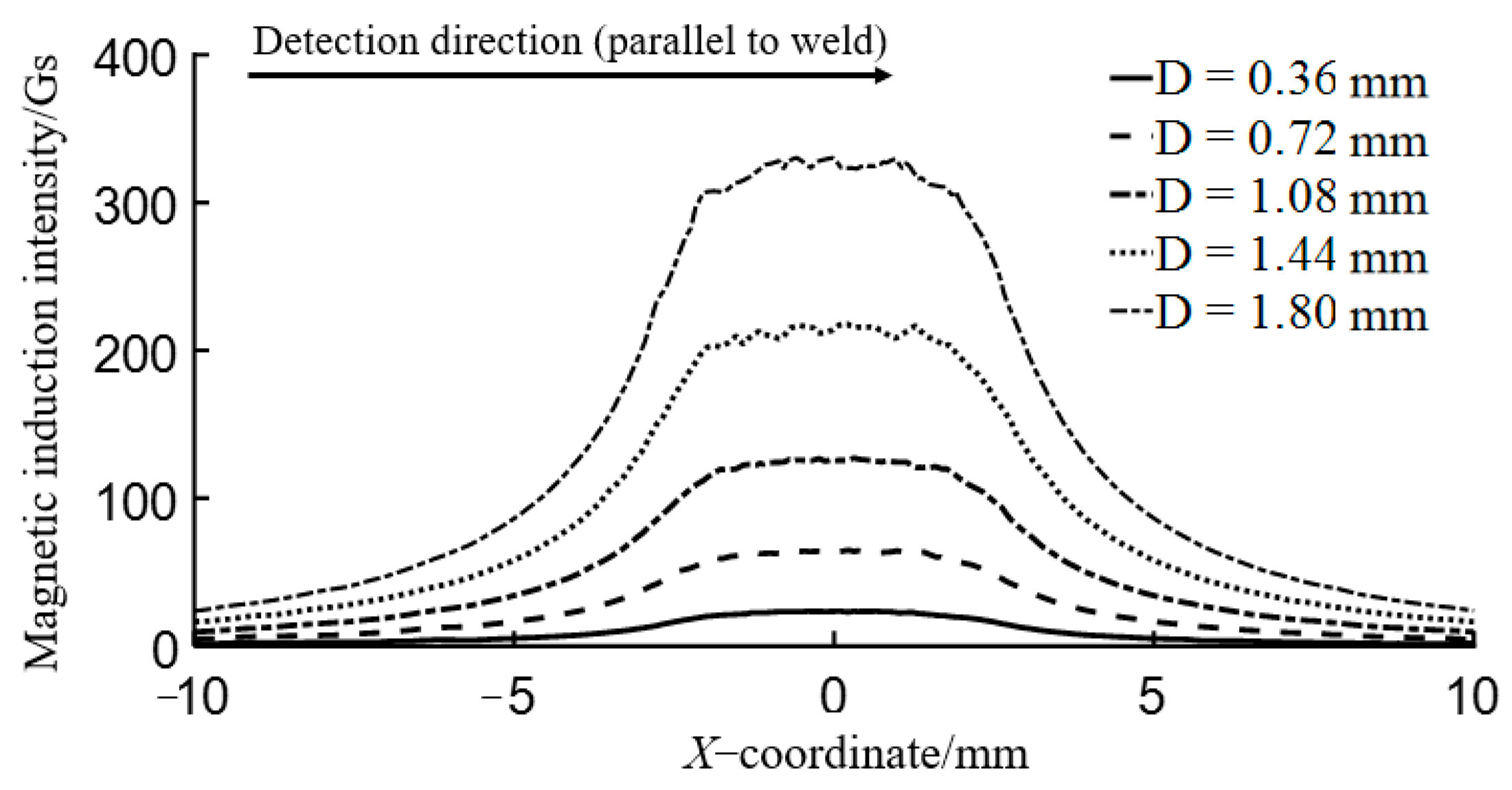
3.2. Analysis of Simulation Results
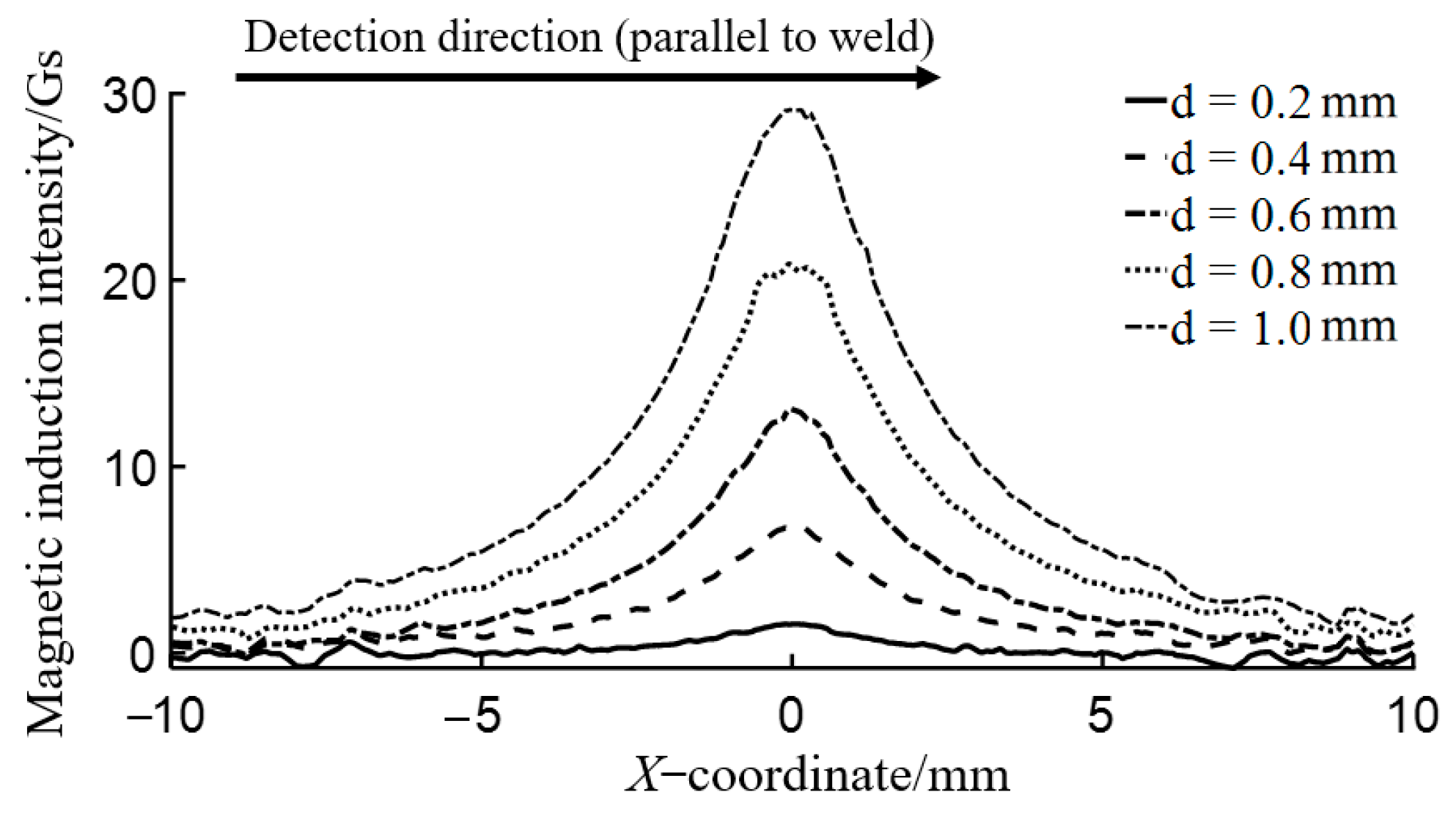
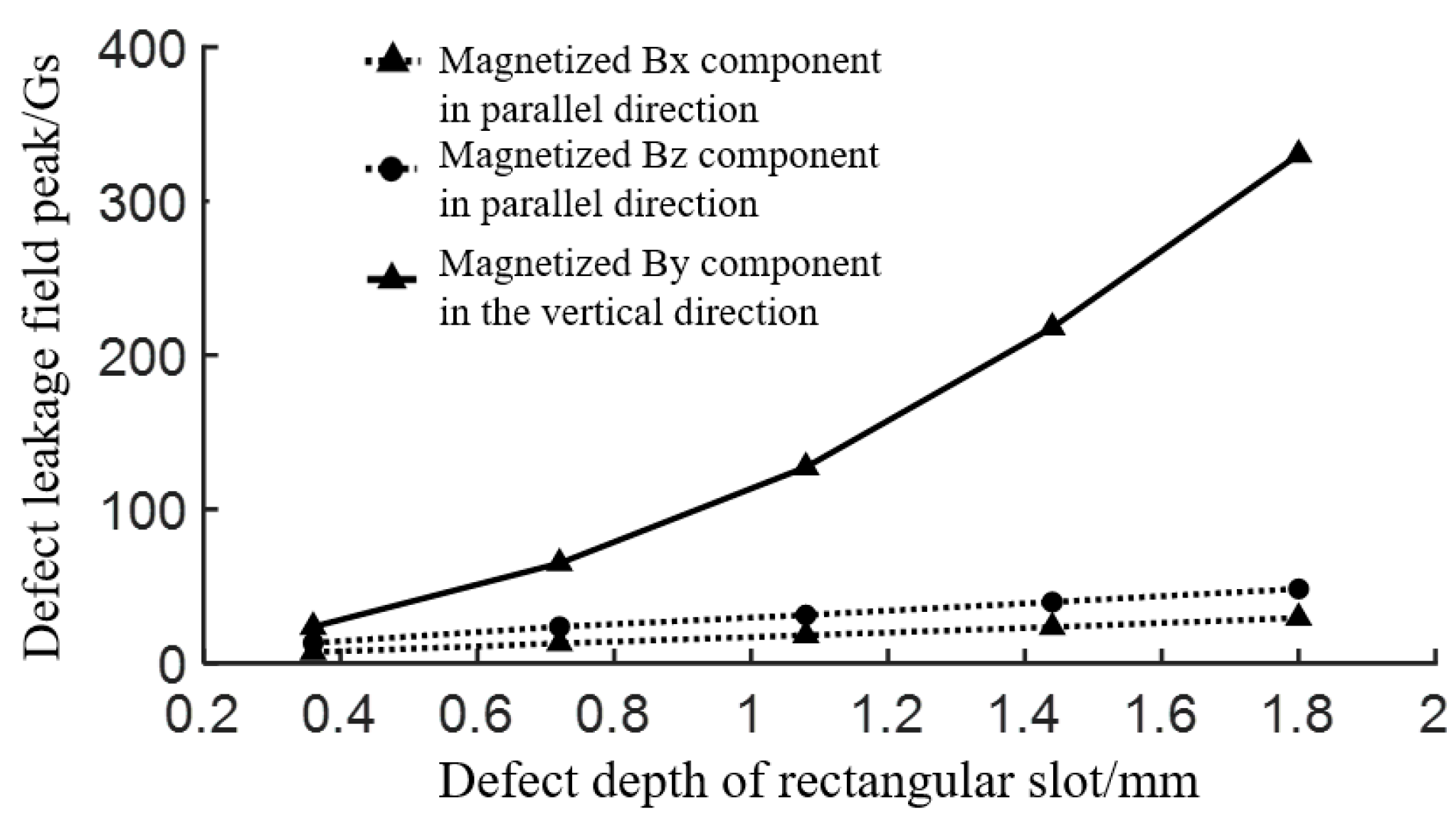
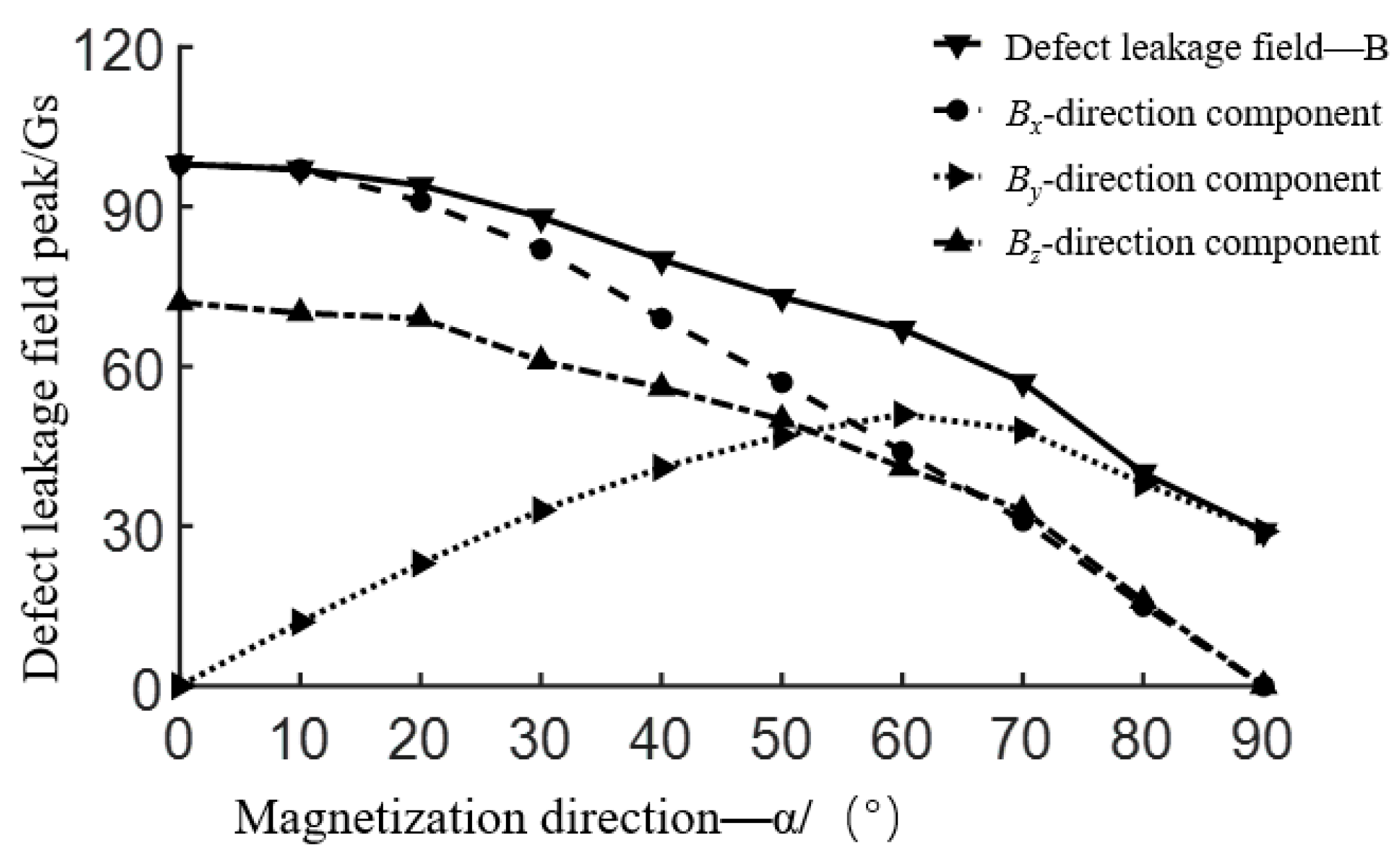
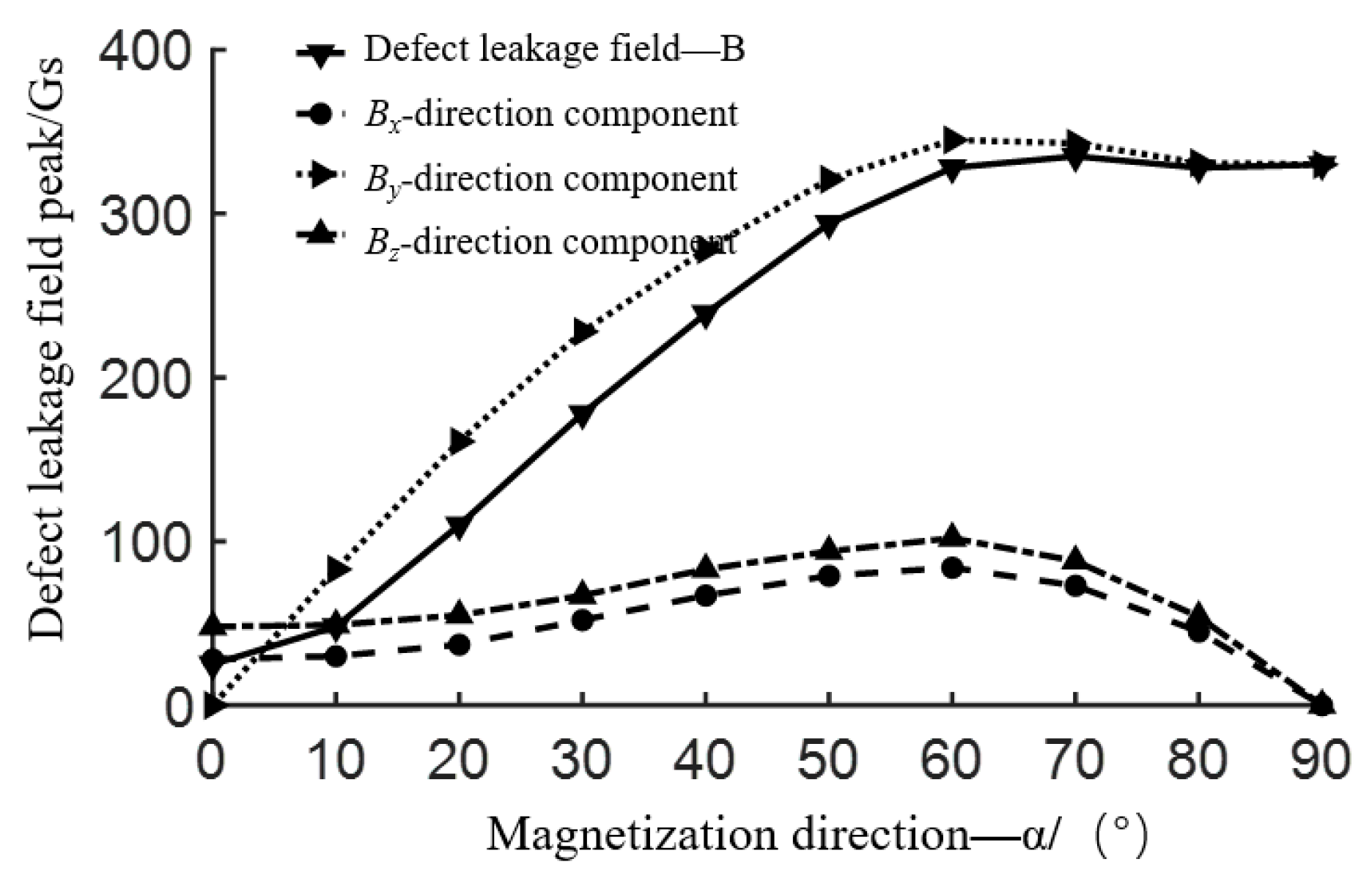
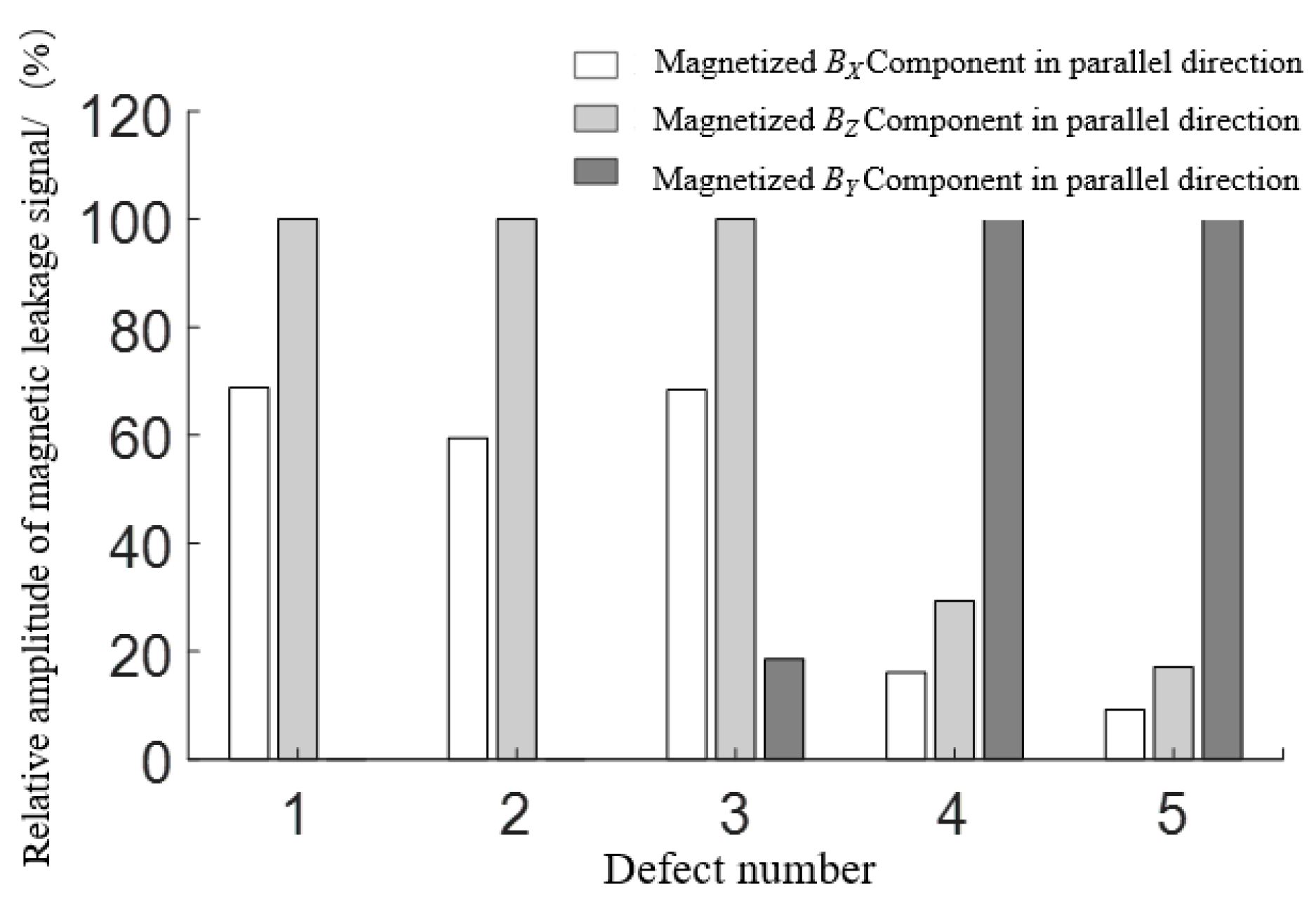
3.3. Analysis of Influence of Magnetization Direction on Flux Leakage Field
4. Experimental Verification
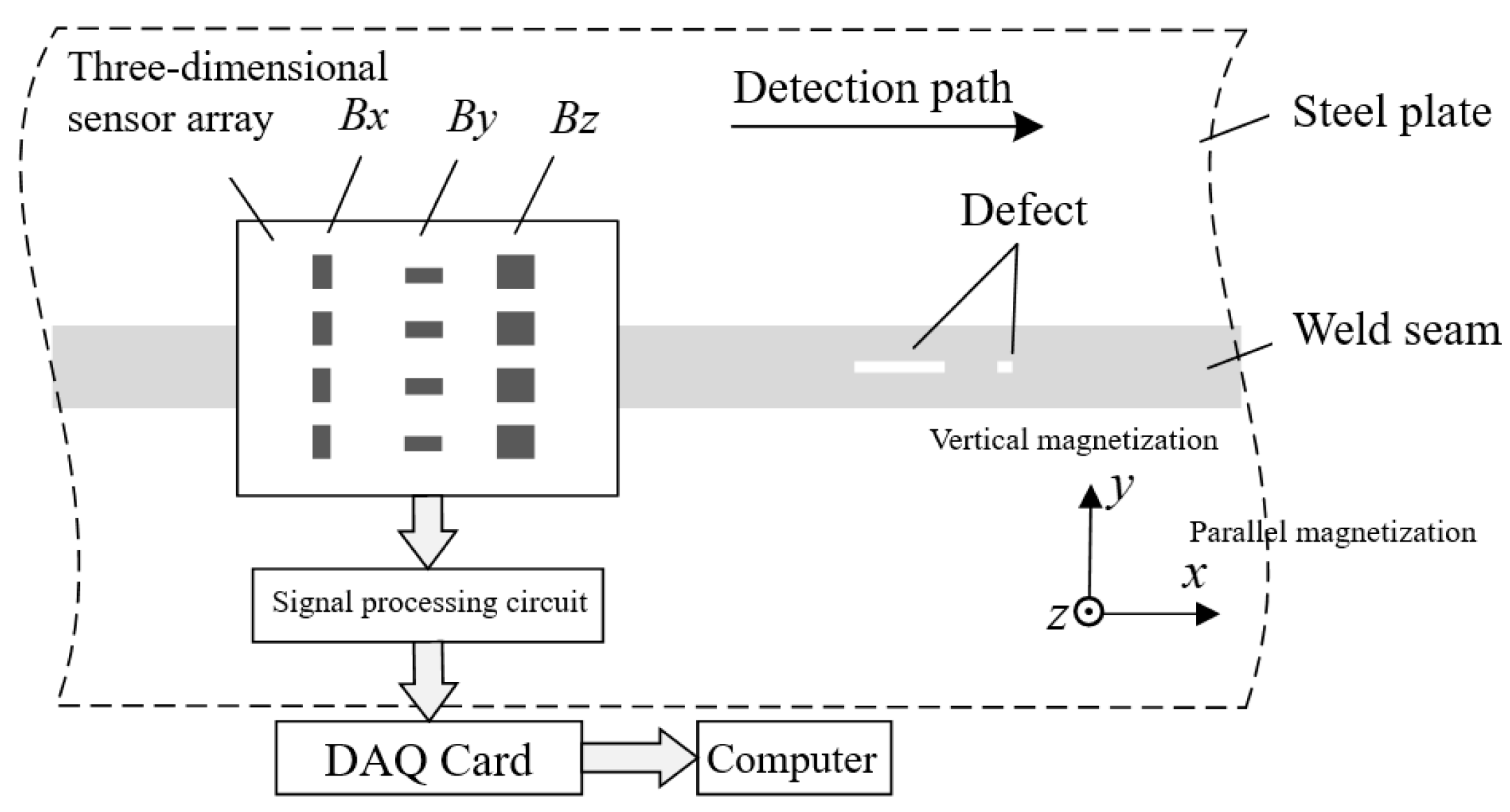
4.1. MFL Detection System for Welds
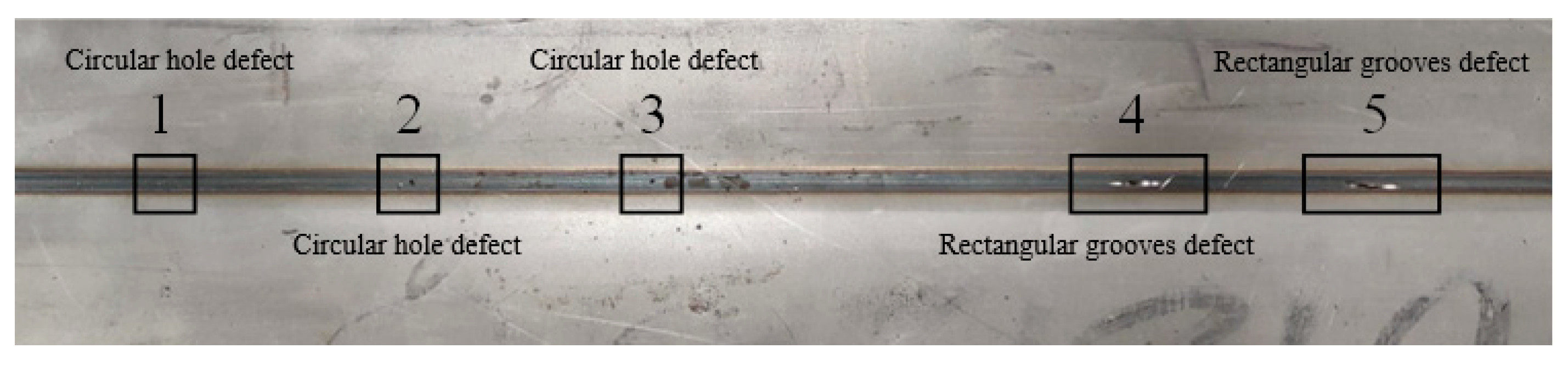
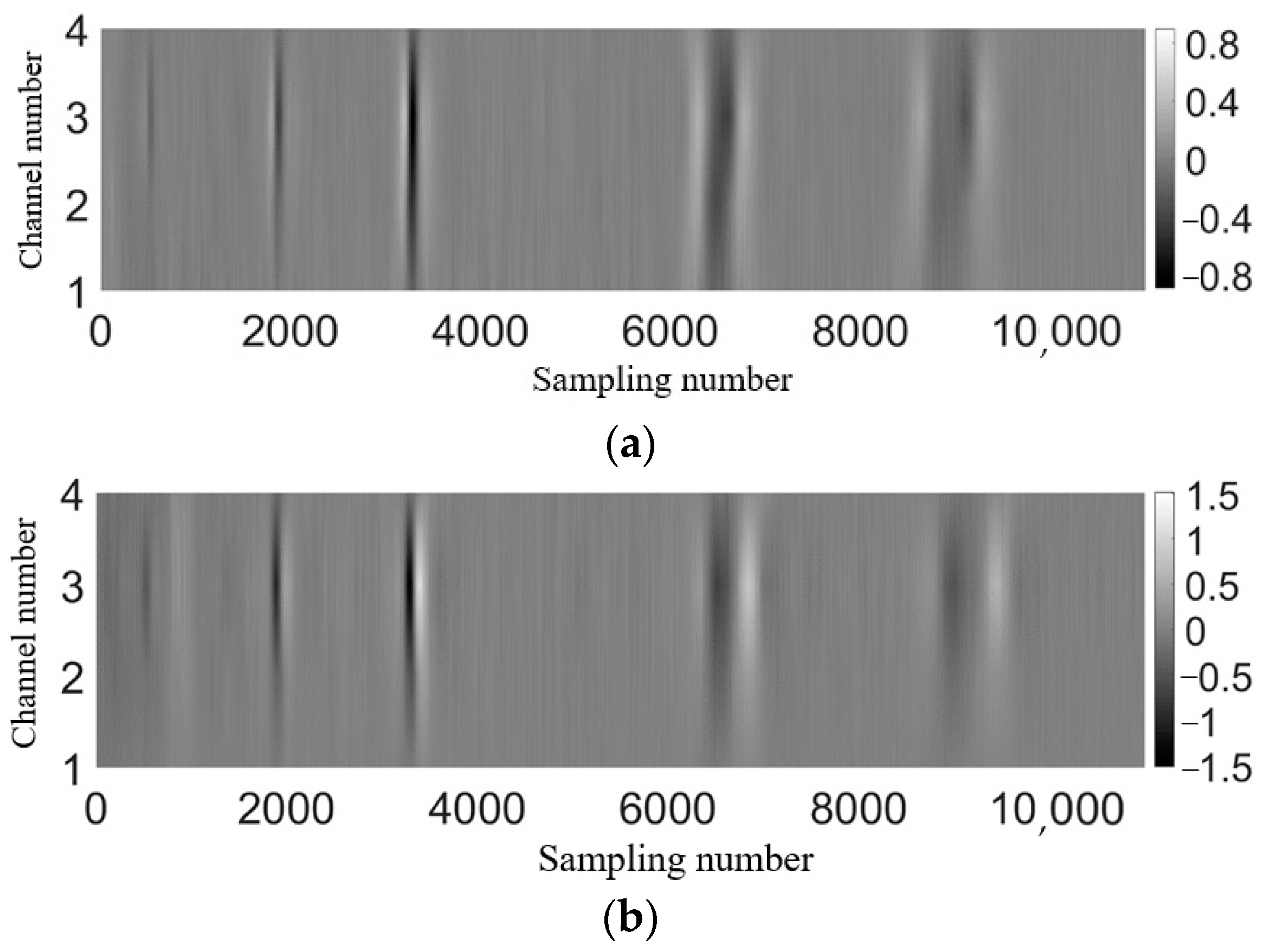
4.2. Analysis of Test Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.S. Research on image detection and recognition for defects on the surface of the steel plate based on magnetic flux leakage signals. In Proceedings of the 29th Chinese Control and Decision Conference, Chongqing, China, 28–30 May 2017; pp. 6139–6144. [Google Scholar]
- Yang, Z.; Anthonie, B.; Chen, R. Numerical and experimental study of wheel-rails impact vibration and noise generated at an insulated rails joint. Int. J. Impact Eng. 2018, 113, 29–39. [Google Scholar] [CrossRef]
- Zhang, Q.; Zou, D.Q.; Yang, Q.Q. Research and analysis of damaged morphology and structure on the head of switch rail. Metall. Anal. 2019, 39, 23–28. [Google Scholar]
- Dudkin, E.P.; Andreeva, L.A.; Sultanov, N.N. Methods of noise and vibration protection on urban rails transport. Procedia Eng. 2017, 189, 829–835. [Google Scholar] [CrossRef]
- Wang, S.F.; Liu, L.Y.; Liu, H.T.; Chen, S. Crack initiation and spalling analysis of inner rail on heavy haul railway curve based on damage accumulation and weight parameter. China Railw. Sci. 2017, 27, 31–35. [Google Scholar]
- Mao, B.Y.; Lu, Y.; Wu, P.L. Signal processing and defect analysis of pipeline inspection applying MFL methods. Intell. Serv. Robot. 2014, 7, 203–209. [Google Scholar] [CrossRef]
- Kalil, K.E.; Sen, D.; Nagarajaiah, S. Vibration-based structural health monitoring under changing environmental conditions using Kalman filtering. Mech. Syst. Signal Process. 2019, 117, 1–15. [Google Scholar]
- Fotiadou, E.; Laar, J.V.; Oei, S.G.; Vullings, R. Enhancement of low-quality fetal electrocardiogram based on time-sequenced adaptive filtering. Med. Biol. Eng. Comput. 2018, 56, 2313–2323. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; He, L.Y.; Zhang, H.; Cao, Y.; Fernandes, H. The axial crack testing model for long distance oil-gas pipeline based on MFL internal inspection method. Measurement 2017, 103, 275–282. [Google Scholar] [CrossRef]
- Lepage, B.; Brillon, C. Dynamic ECA lift-off compensation. AIP Conf. Proc. 2015, 1650, 424–433. [Google Scholar]
- Ye, Y.; Ping, W.; Wu, N.; Ge, F.; Zhou, F. Optimisation for accuracy improving of MSB signal detection. Electron. Lett. 2017, 53, 1578–1580. [Google Scholar] [CrossRef]
- Shi, P.; Ke, J.; Zhang, P.; Xie, S.; Chen, Z.; Zheng, X. Quantitative inversion of stress and crack in ferromagnetic materials based on metal magnetic memory method. IEEE Trans. Magn. 2018, 54, 6202011. [Google Scholar] [CrossRef]
- Kim, D.; Udpa, L.; Udpa, S.S. Lift-off invariance transformations for eddy current nondestructive evaluation signals. AIP Conf. Proc. 2002, 615, 615–622. [Google Scholar]
- Gui, Y.T.; Sophian, A.; Taylor, D.; Rudlin, J. Multiple sensors on pulsed eddy-current detection for 3-D subsurface crack assessment. IEEE Sens. J. 2005, 5, 90–96. [Google Scholar]
- Dutta, S.M.; Ghorbel, F.H.; Stanley, R.K. Simulation and analysis of 3-D magnetic flux leakage. IEEE Trans. Magn. 2009, 45, 1966–1972. [Google Scholar] [CrossRef]
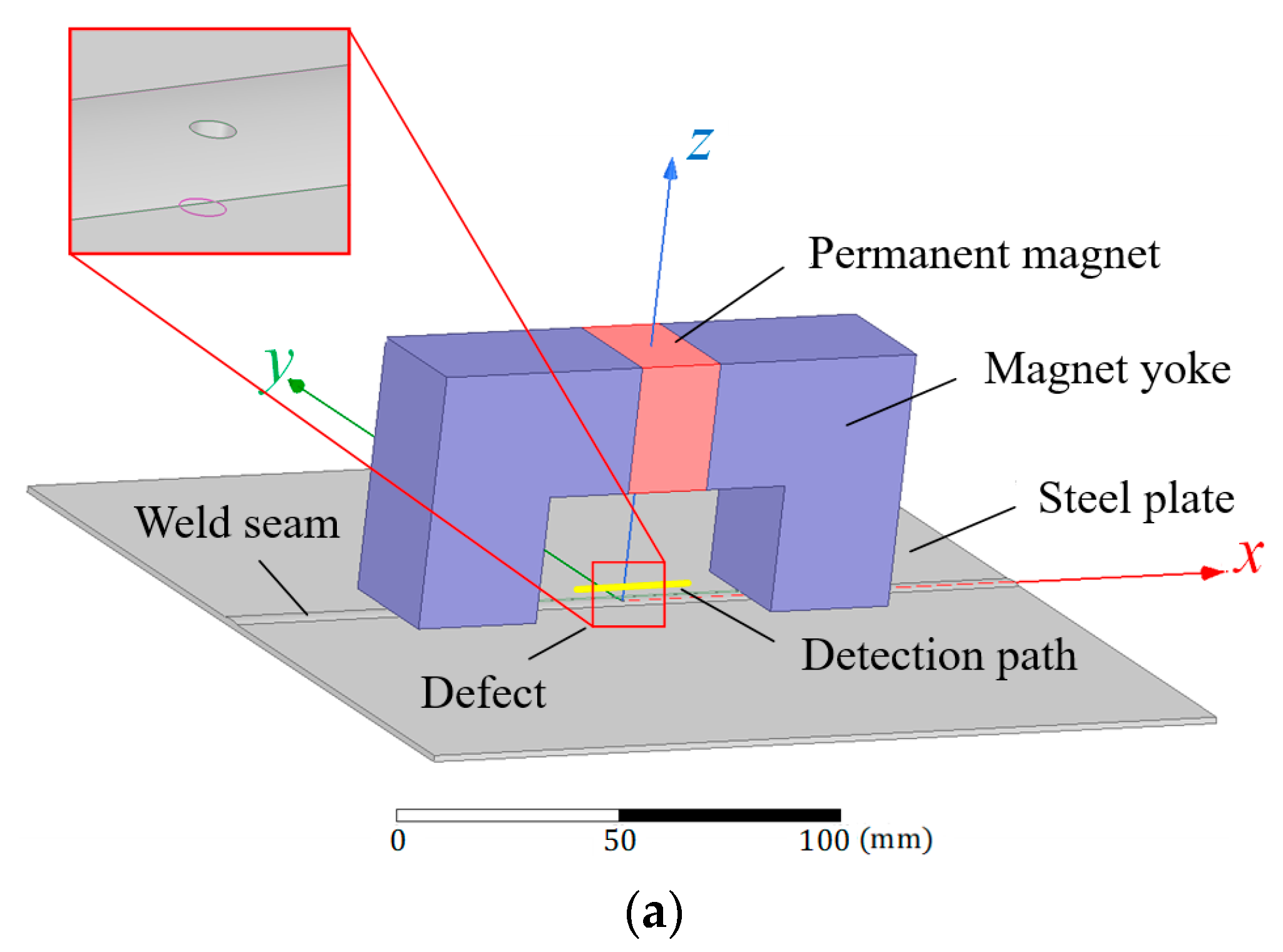
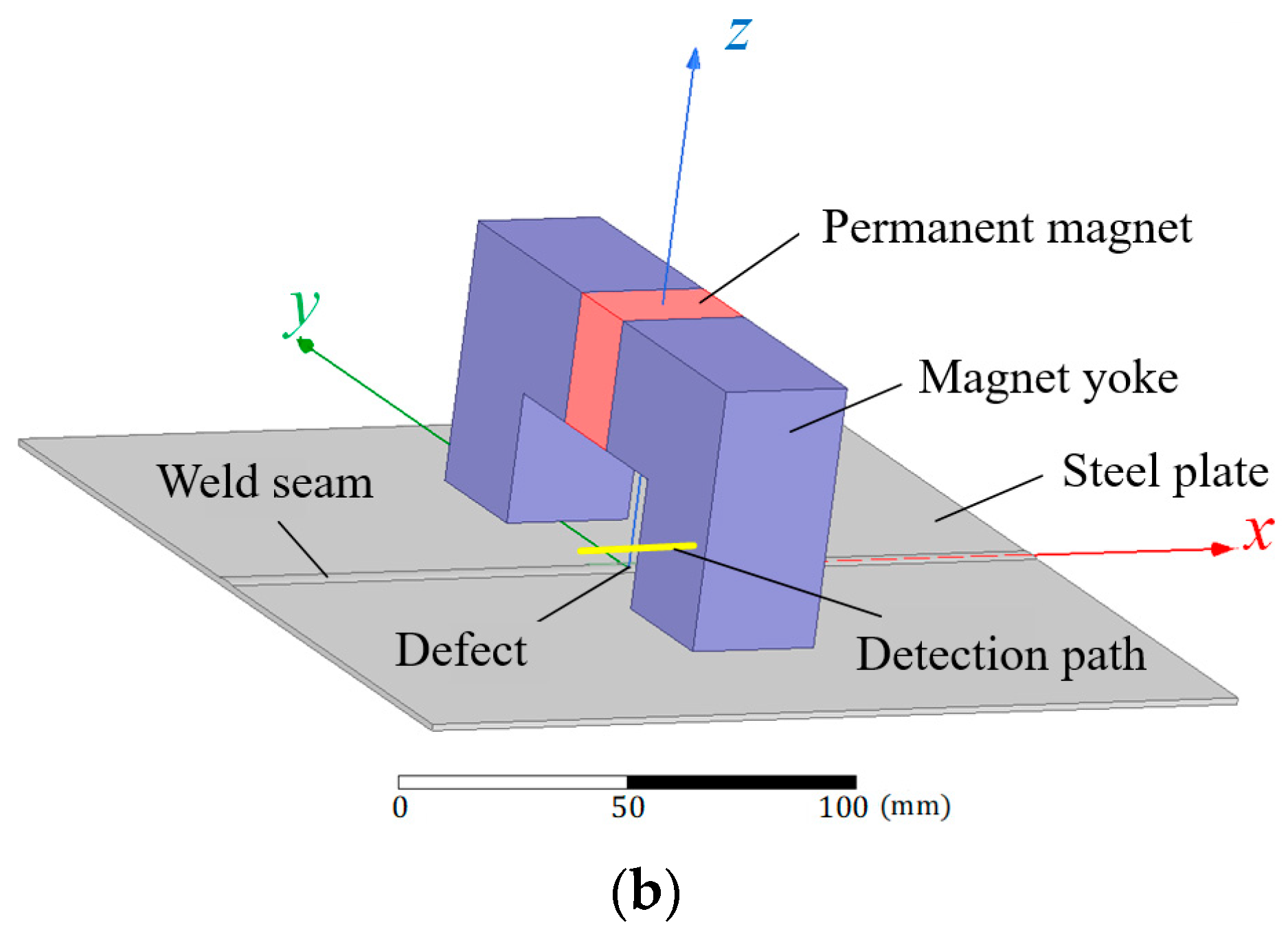



| Simulation Components | Materials | Dimension Parameters/mm |
|---|---|---|
| Magnetic yoke | ferrite | 160 × 80 × 80 (with a pole spacing of 60) |
| Permanent magnet | NdFe30 | 30 × 40 × 40 |
| Sheet steel | Q235 | 200 × 200 × 1.5 |
| Weld | Q235 | 200 × 6 × 0.3 (circular arc) |
| Circular hole defect | vacuum | The depth is 1.8 mm, and the different diameters are 0.2, 0.4, 0.6, 0.8, and 1.0 mm |
| Rectangular grooves defect | vacuum | The length is 5 mm, the width is 0.5 mm, and the depth is 0.36, 0.72, 1.08, 1.44, and 1.80 mm |
| Types | No. | Defect Size Parameters | ||
|---|---|---|---|---|
| Circular hole | Diameter | Depth | ||
| 1 | 0.3 mm | 100%t (1.0 mm) | ||
| 2 | 0.5 mm | 100%t (1.0 mm) | ||
| 3 | 1.0 mm | 100%t (1.0 mm) | ||
| Crack | Length | Width | Depth | |
| 4 | 4.0 mm | 1.0 mm | 100%t (1.0 mm) | |
| 5 | 5.0 mm | 1.0 mm | 100%t (1.0 mm) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; Ji, K.; Wang, P. Influences of Magnetization Direction on the Flux Leakage Field of Weld Defects. Coatings 2023, 13, 1005. https://doi.org/10.3390/coatings13061005
Ye Y, Ji K, Wang P. Influences of Magnetization Direction on the Flux Leakage Field of Weld Defects. Coatings. 2023; 13(6):1005. https://doi.org/10.3390/coatings13061005
Chicago/Turabian StyleYe, Yunfei, Kailun Ji, and Ping Wang. 2023. "Influences of Magnetization Direction on the Flux Leakage Field of Weld Defects" Coatings 13, no. 6: 1005. https://doi.org/10.3390/coatings13061005
APA StyleYe, Y., Ji, K., & Wang, P. (2023). Influences of Magnetization Direction on the Flux Leakage Field of Weld Defects. Coatings, 13(6), 1005. https://doi.org/10.3390/coatings13061005






