Effects of Substrates on Thin-Film Growth of Nickel Zinc Ferrite by Spin-Spray Deposition
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hao, A.; Ismail, M.; He, S.; Qin, N.; Huang, W.; Wu, J.; Bao, D. Improved Unipolar Resistive Switching Characteristics of Au-Doped Nickel Ferrite Magnetic Thin Films for Nonvolatile Memory Applications. J. Alloy Compd. 2018, 732, 573–584. [Google Scholar] [CrossRef]
- Abdellatif, M.H.; Azab, A.A.; Moustafa, A.M. Dielectric Spectroscopy of Localized Electrical Charges in Ferrite Thin Film. J. Electron. Mater. 2018, 47, 378–384. [Google Scholar] [CrossRef]
- Harris, V.G. Modern Microwave Ferrites. IEEE Trans. Magn. 2012, 48, 1075–1104. [Google Scholar] [CrossRef]
- Sahu, B.N.; Venkataramani, N.; Prasad, S.; Krishnan, R. Effect of Thickness on Magnetic and Microwave Properties of RF-Sputtered Zn-Ferrite Thin Films. AIP Adv. 2017, 7, 056102. [Google Scholar] [CrossRef]
- Chen, Z.; Harris, V.G. Ferrite Film Growth on Semiconductor Substrates towards Microwave and Millimeter Wave Integrated Circuits. J. Appl. Phys. 2012, 112, 081101. [Google Scholar] [CrossRef]
- Sai, R.; Vinoy, K.J.; Bhat, N.; Shivashankar, S.A. CMOS-Compatible and Scalable Deposition of Nanocrystalline Zinc Ferrite Thin Film to Improve Inductance Density of Integrated RF Inductor. IEEE Trans. Magn. 2013, 49, 4323–4326. [Google Scholar] [CrossRef]
- Wang, G.; Liu, H.; Wu, H.; Li, X.; Qiu, H.; Yang, Y.; Qu, B.; Ren, T.-L.; Han, X.; Zhang, R.; et al. Epitaxial Yttrium Iron Garnet Film for Fabrication of High Frequency On-Chip Inductors. Appl. Phys. Lett. 2016, 109, 162405. [Google Scholar] [CrossRef]
- Nur-E-Alam, M.; Vasiliev, M.; Belotelov, V.; Alameh, K. Properties of Ferrite Garnet (Bi, Lu, Y)3(Fe, Ga)5O12 Thin Film Materials Prepared by RF Magnetron Sputtering. Nanomaterials 2018, 8, 355. [Google Scholar] [CrossRef]
- Zhong, X.; Phuoc, N.N.; Soh, W.T.; Ong, C.K.; Li, L. Dynamic Magnetization of NiZn Ferrite Doped FeSiAl Thin Films Fabricated by Oblique Sputtering. J. Magn. Magn. Mater. 2017, 432, 373–381. [Google Scholar] [CrossRef]
- Emori, S.; Gray, B.A.; Jeon, H.-M.; Peoples, J.; Schmitt, M.; Mahalingam, K.; Hill, M.; McConney, M.E.; Gray, M.T.; Alaan, U.S.; et al. Coexistence of Low Damping and Strong Magnetoelastic Coupling in Epitaxial Spinel Ferrite Thin Films. Adv. Mater. 2017, 29, 1701130. [Google Scholar] [CrossRef]
- Sánchez-Arenillas, M.; Oujja, M.; Moutinho, F.; de la Figuera, J.; Cañamares, M.V.; Quesada, A.; Castillejo, M.; Marco, J.F. Bulk and Surface Characterisation of Micrometer-Thick Cobalt Ferrite Films Grown by IR PLD. Appl. Surf. Sci. 2019, 470, 917–922. [Google Scholar] [CrossRef]
- Abe, M.; Tamaura, Y. Ferrite Plating in Aqueous Solution: New Technique for Preparing Magnetic Thin Film. J. Appl. Phys. 1984, 55, 2614–2616. [Google Scholar] [CrossRef]
- Abe, M.; Tada, M.; Matsushita, N.; Shimada, Y. Phenomenological Theory of Permeability in Films Having No In-Plane Magnetic Anisotropy: Application to Spin-Sprayed Ferrite Films. J. Appl. Phys. 2006, 99, 08M907. [Google Scholar] [CrossRef]
- Liu, H.; Yu, Z.; Fu, B.; Ran, M.; Wu, C.; Jiang, X.; Guo, R.; Lan, Z.; Sun, K. Anisotropic Growth and Magnetic Properties of Nickel–Zinc Ferrite Thin Film by Spin Spray Deposition. Ceram. Int. 2020, 47, 1318–1324. [Google Scholar] [CrossRef]
- Ran, M.; Yu, Z.; Sun, K.; Wu, C.; Qing, H.; Liu, H.; Lan, Z.; Jiang, X. Effects of Aqueous Ethanol Solutions on the Structural and Magnetic Properties of NiZn Ferrite Thin Films Prepared by Spin-Spray Deposition. Ceram. Int. 2021, 47, 15520–15526. [Google Scholar] [CrossRef]
- Ko, S.W.; Li, J.; Podraza, N.J.; Dickey, E.C.; Trolier-McKinstry, S. Spin Spray-Deposited Nickel Manganite Thermistor Films For Microbolometer Applications. J. Am. Ceram. Soc. 2011, 94, 516–523. [Google Scholar] [CrossRef]
- Zhou, Z.; Obi, O.; Nan, T.X.; Beguhn, S.; Lou, J.; Yang, X.; Gao, Y.; Li, M.; Rand, S.; Lin, H.; et al. Low-Temperature Spin Spray Deposited Ferrite/Piezoelectric Thin Film Magnetoelectric Heterostructures with Strong Magnetoelectric Coupling. J. Mater. Sci. Mater. Electron. 2014, 25, 1188–1192. [Google Scholar] [CrossRef]
- Obi, O.; Liu, M.; Lou, J.; Stoute, S.; Xing, X.; Sun, N.X.; Warzywoda, J.; Sacco, A.; Oates, D.E.; Dionne, G.F. Spin-Spray Deposited NiZn-Ferrite Films Exhibiting μr′ > 50 at GHz Range. J. Appl. Phys. 2011, 109, 07E527. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Z.; Behugn, S.; Liu, M.; Lin, H.; Yang, X.; Gao, Y.; Nan, T.; Xing, X.; Hu, Z.; et al. Growth Behavior and RF/Microwave Properties of Low Temperature Spin-Sprayed NiZn Ferrite. J. Mater. Sci. Mater. Electron. 2015, 26, 1890–1894. [Google Scholar] [CrossRef]
- Li, M.; Zhou, Z.; Liu, M.; Lou, J.; Oates, D.E.; Dionne, G.F.; Wang, M.L.; Sun, N.X. Novel NiZnAl-Ferrites and Strong Magnetoelectric Coupling in NiZnAl-Ferrite/PZT Multiferroic Heterostructures. J. Phys. D Appl. Phys. 2013, 46, 275001. [Google Scholar] [CrossRef]
- Mirzaee, S.; Farjami shayesteh, S.; Mahdavifar, S.; Hekmatara, S.H. Synthesis, Characterization and Monte Carlo Simulation of CoFe2O4/Polyvinylpyrrolidone Nanocomposites: The Coercivity Investigation. J. Magn. Magn. Mater. 2015, 393, 1–7. [Google Scholar] [CrossRef]
- Salcedo Rodríguez, K.L.; Bridoux, G.; Heluani, S.P.; Pasquevich, G.A.; Esquinazi, P.D.; Rodríguez Torres, C.E. Influence of Substrate Effects in Magnetic and Transport Properties of Magnesium Ferrite Thin Films. J. Magn. Magn. Mater. 2019, 469, 643–649. [Google Scholar] [CrossRef]
- An, X.; Ingole, P.G.; Choi, W.-K.; Lee, H.-K.; Hong, S.U.; Jeon, J.-D. Development of Thin Film Nanocomposite Membranes Incorporated with Sulfated β-Cyclodextrin for Water Vapor/N2 Mixture Gas Separation. J. Ind. Eng. Chem. 2018, 59, 259–265. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Kumari, S.; Pradhan, D.K.; Kumar, A.; Katiyar, R.S.; Cohen, R.E. Effect of Substrate Temperature on Structural and Magnetic Properties of C-Axis Oriented Spinel Ferrite Ni0.65Zn0.35Fe2O4 (NZFO) Thin Films. J. Alloy. Compd. 2018, 766, 1074–1079. [Google Scholar] [CrossRef]
- Wu, Y.; Tang, Z.; Xu, Y.; Zhang, B.; He, X. A New Shorted Microstrip Method to Determine the Complex Permeability of Thin Films. IEEE Trans. Magn. 2010, 46, 886–888. [Google Scholar] [CrossRef]
- Li, Y.F.; Li, E.; Zhang, Y.P.; Zhao, C.; Yang, T. Ultra-Wideband Variable Temperature Measurement System for Complex Permeability of Magnetic Thin Film Fe 66 Co 17 B 16 Si 1. IEEE Trans. Magn. 2018, 54, 1–7. [Google Scholar] [CrossRef]
- Nawle, A.C.; Humbe, A.V.; Babrekar, M.K.; Deshmukh, S.S.; Jadhav, K.M. Deposition, Characterization, Magnetic and Optical Properties of Zn Doped CuFe2O4 Thin Films. J. Alloy Compd. 2017, 695, 1573–1582. [Google Scholar] [CrossRef]
- Brabers, V.A.M. Chapter 3 Progress in Spinel Ferrite Research. In Handbook of Magnetic Materials; Elsevier: Amsterdam, The Netherlands, 1995; Volume 8, pp. 189–324. [Google Scholar]
- Taniguchi, A.; Taniguchi, T.; Wagata, H.; Katsumata, K.; Okada, K.; Matsushita, N. Liquid-Phase Atomic Layer Deposition of Crystalline Hematite without Post-Growth Annealing. CrystEngComm 2019, 21, 4184–4191. [Google Scholar] [CrossRef]
- Khan, M.A.; Comyn, T.P.; Bell, A.J. Growth and Characterization of Tetragonal Bismuth Ferrite–Lead Titanate Thin Films. Acta Mater. 2008, 56, 2110–2118. [Google Scholar] [CrossRef]
- Yang, S.; Chen, F.; Gao, X.; Shen, Q.; Zhang, L. Enhanced Power Factor of Textured Al-Doped-ZnO Ceramics by Field-Assisted Deforming. J. Am. Ceram. Soc. 2017, 100, 1300–1305. [Google Scholar] [CrossRef]
- Wu, C.; Wang, W.; Li, Q.; Wei, M.; Luo, Q.; Fan, Y.; Jiang, X.; Lan, Z.; Jiao, Z.; Tian, Y.; et al. Barium hexaferrites with narrow ferrimagnetic resonance linewidth tailored by site-controlled Cu doping. J. Am. Ceram. Soc. 2022, 105, 7492–7501. Available online: https://ceramics.onlinelibrary.wiley.com/doi/abs/10.1111/jace.18702 (accessed on 3 March 2023). [CrossRef]
- Kitayama, M.; Hirao, K.; Toriyama, M.; Kanzaki, S. Thermal Conductivity of SS-Si3N4: I, Effects of Various Microstructural Factors. J. Am. Ceram. Soc. 1999, 82, 3105–3112. [Google Scholar] [CrossRef]
- Alben, R.; Becker, J.J.; Chi, M.C. Random Anisotropy in Amorphous Ferromagnets. J. Appl. Phys. 1978, 49, 1653–1658. [Google Scholar] [CrossRef]
- Herzer, G. Anisotropies in Soft Magnetic Nanocrystalline Alloys. J. Magn. Magn. Mater. 2005, 294, 99–106. [Google Scholar] [CrossRef]
- Mesbahinia, A.; Almasi-Kashi, M.; Ghasemi, A.; Ramezani, A. First Order Reversal Curve Analysis of Cobalt-Nickel Ferrite. J. Magn. Magn. Mater. 2019, 473, 161–168. [Google Scholar] [CrossRef]
- Zheng, H.; Luo, J.; Wu, Q.; Zheng, P.; Zheng, L.; Han, M.; Zhang, Y. Hexagonal Barium Ferrite Films on a Pt(1 1 1)/Si(0 0 1) Substrate and Their Local Magnetic Properties. J. Magn. Magn. Mater. 2019, 479, 99–104. [Google Scholar] [CrossRef]
- Zhang, Y.; Dai, B.; Li, J.; Zhu, H.; Zhu, X.; Li, X.; Ren, J.; Ren, Y. Break the Acher’s Limit: Improve Both Resonance Frequency and Initial Permeability in Patterned FeNi Strip Film. J. Alloy. Compd. 2017, 725, 598–605. [Google Scholar] [CrossRef]
- Jin, H.; Miyazaki, T. Soft Magnetism. In The Physics of Ferromagnetism; Miyazaki, T., Jin, H., Eds.; Springer Series in Materials Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 305–338. ISBN 978-3-642-25583-0. [Google Scholar]

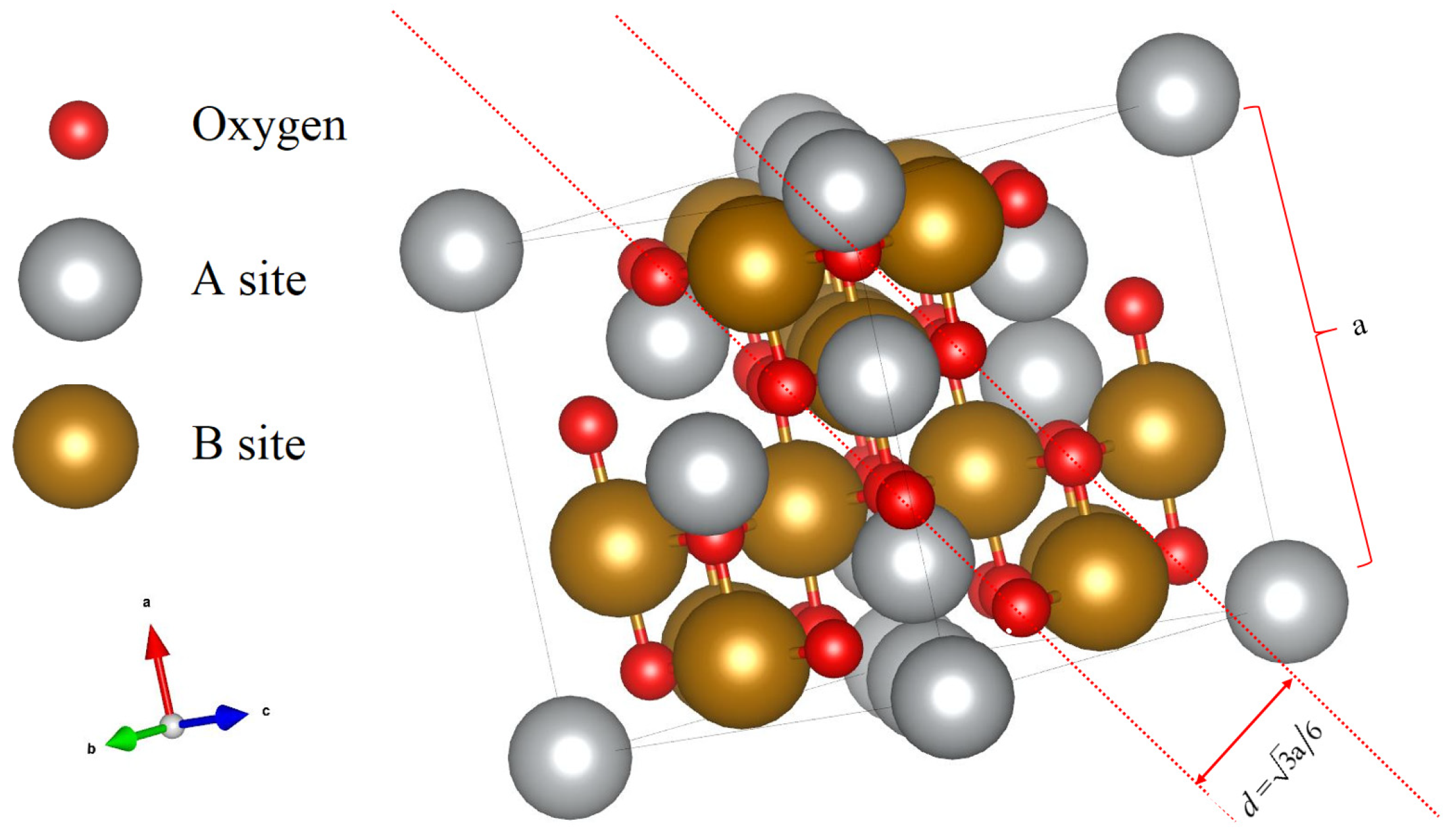


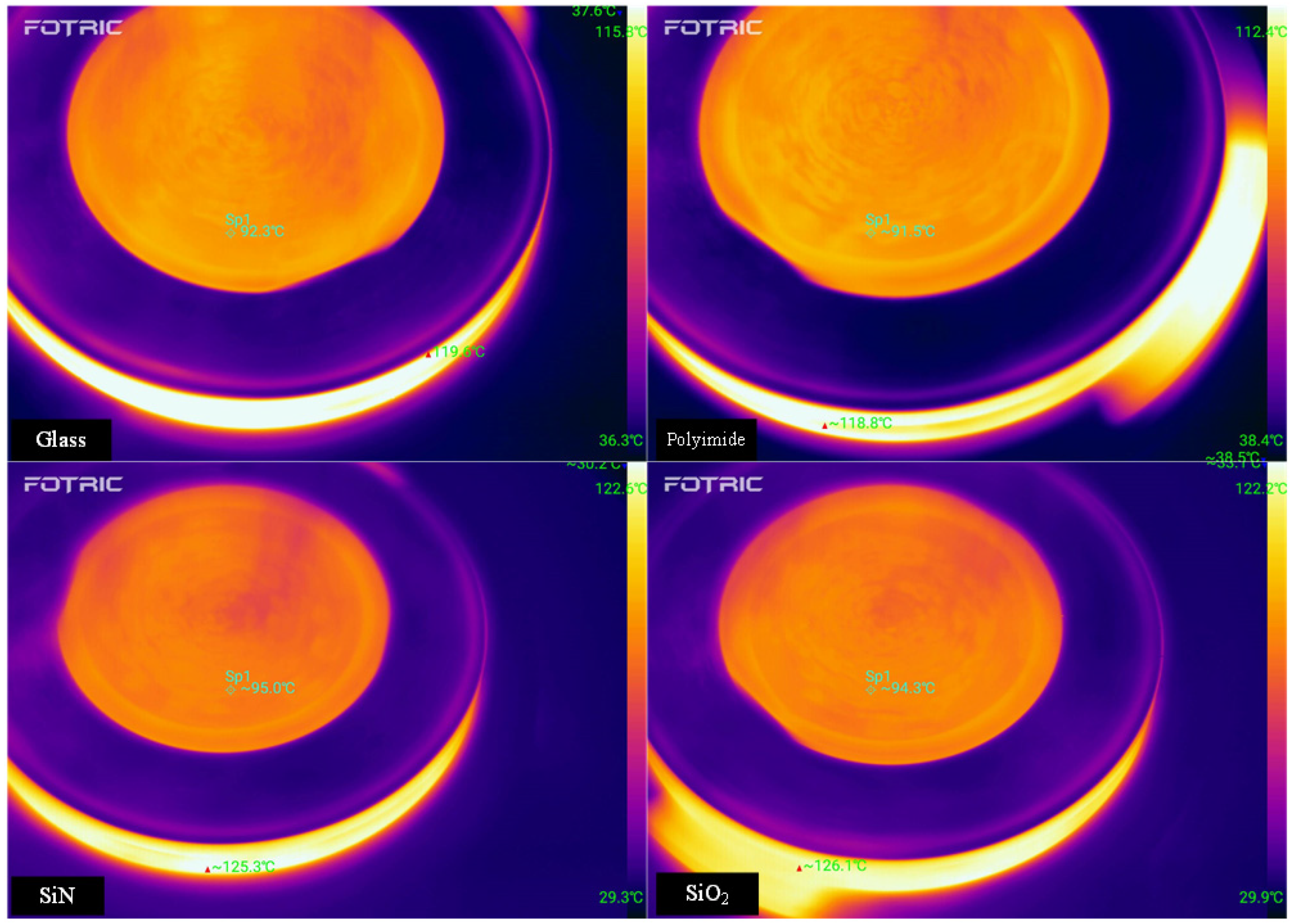

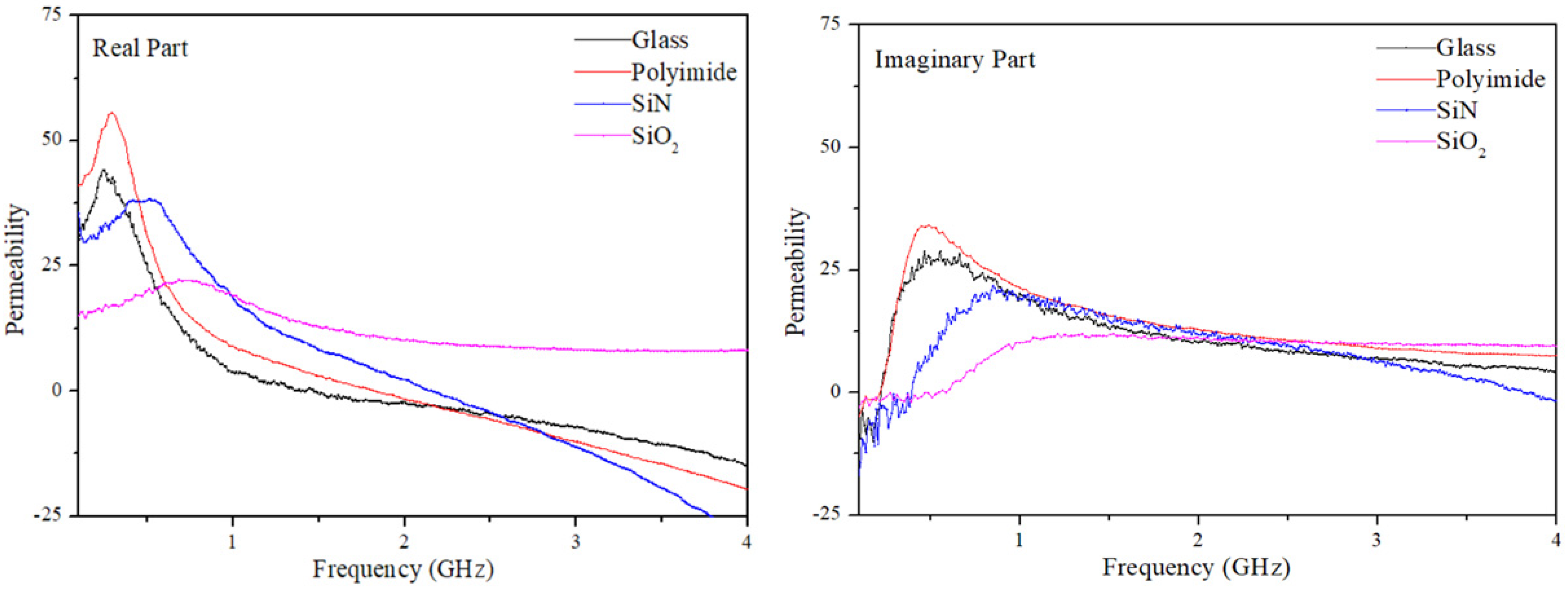
| Substrate Type | a (Å) | Grain Diameter (nm) | Growth Rate (nm/min) | Contact Angle (°) | Thermal Conductivity (W·m−1·K−1) | Temperature (°C) |
|---|---|---|---|---|---|---|
| Glass | 8.4100 | 148.3 ± 22.3 | 52 | 52.51 | 0.8 | 92.3 |
| Polyimide | 8.4089 | 64.1 ± 7 | 42 | 75.42 | 0.2 | 91.5 |
| SiN | 8.4103 | >200 | 93 | 52.68 | 124.6 | 95.0 |
| SiO2 | 8.4104 | >200 | 72 | 56.04 | 1.2 | 94.3 |
| Substrate Type | Ms (KA/m) | Hc (Oe) | fr (MHz) | μ′max |
|---|---|---|---|---|
| Glass | 441 | 23 | 465 | 44 |
| Polyimide | 445 | 46 | 485 | 55 |
| SiN | 402 | 40 | 853 | 38 |
| SiO2 | 315 | 31 | 1215 | 22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yu, Z.; Song, X.; Ran, M.; Jiang, X.; Lan, Z.; Sun, K. Effects of Substrates on Thin-Film Growth of Nickel Zinc Ferrite by Spin-Spray Deposition. Coatings 2023, 13, 690. https://doi.org/10.3390/coatings13040690
Liu H, Yu Z, Song X, Ran M, Jiang X, Lan Z, Sun K. Effects of Substrates on Thin-Film Growth of Nickel Zinc Ferrite by Spin-Spray Deposition. Coatings. 2023; 13(4):690. https://doi.org/10.3390/coatings13040690
Chicago/Turabian StyleLiu, Hai, Zhong Yu, Xinglian Song, Maojun Ran, Xiaona Jiang, Zhongwen Lan, and Ke Sun. 2023. "Effects of Substrates on Thin-Film Growth of Nickel Zinc Ferrite by Spin-Spray Deposition" Coatings 13, no. 4: 690. https://doi.org/10.3390/coatings13040690
APA StyleLiu, H., Yu, Z., Song, X., Ran, M., Jiang, X., Lan, Z., & Sun, K. (2023). Effects of Substrates on Thin-Film Growth of Nickel Zinc Ferrite by Spin-Spray Deposition. Coatings, 13(4), 690. https://doi.org/10.3390/coatings13040690







