Inkjet Printing of High Aspect Ratio Silver Lines via Laser-Induced Selective Surface Wetting Technique
Abstract
1. Introduction
2. Materials and Methods
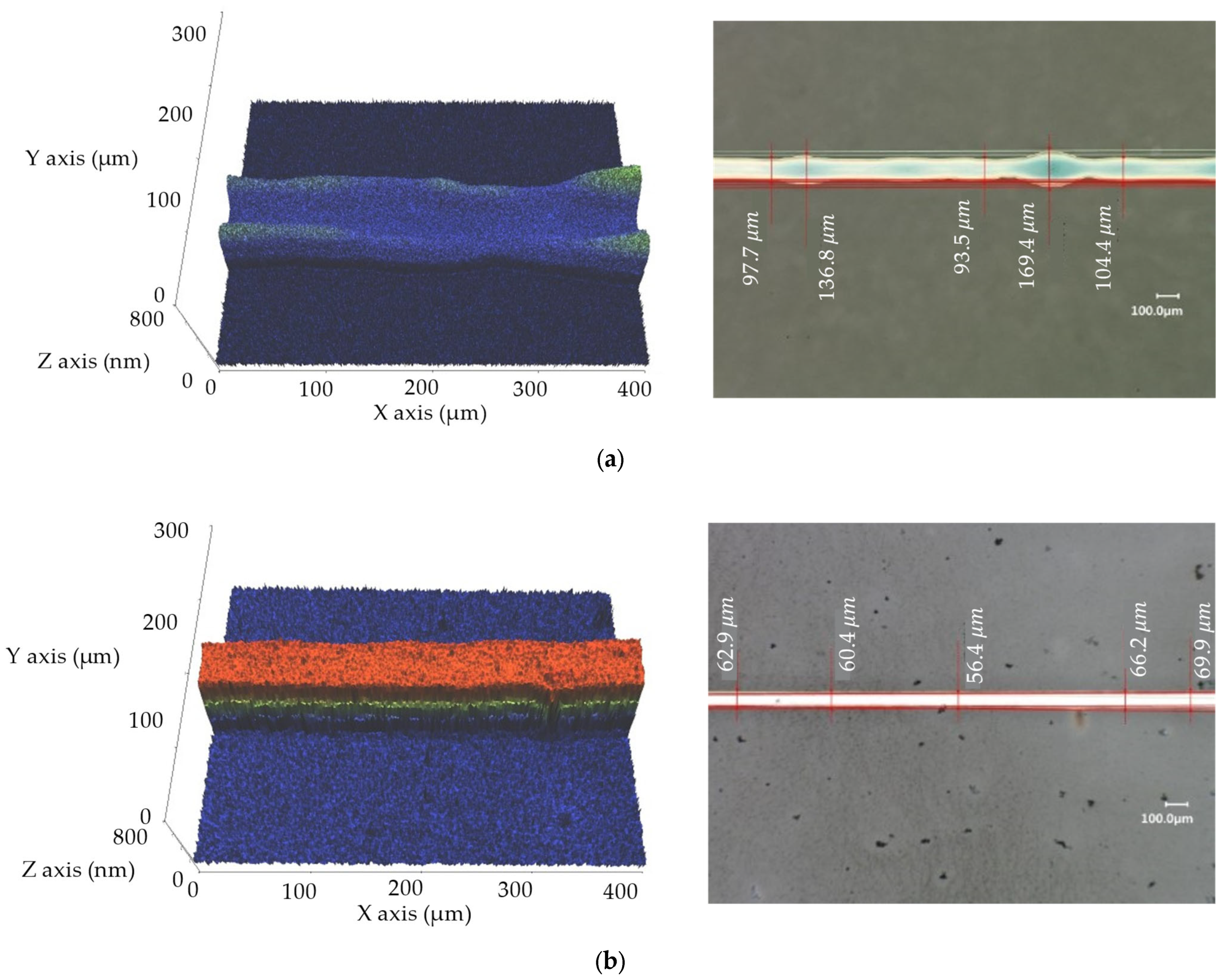
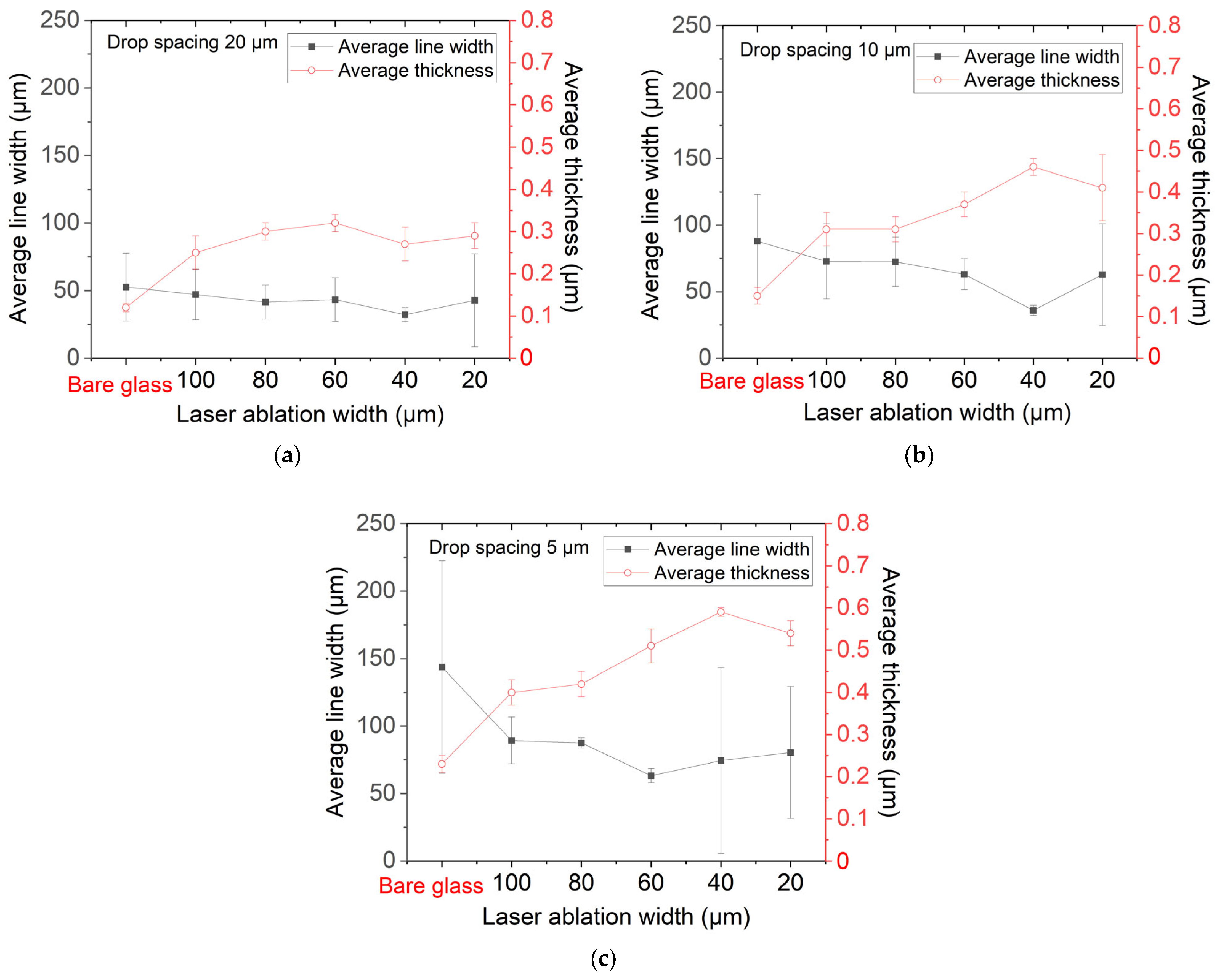
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mantysalo, M.; Mansikkamaki, P. An inkjet-deposited antenna for 2.4 GHz applications. Int. J. Electron. Commun. 2009, 63, 31–35. [Google Scholar] [CrossRef]
- Shahpari, M.; Thiel, D.V. The Impact of Reduced Conductivity on the Performance of Wire Antennas. IEEE Trans. Antennas Propag. 2015, 63, 11. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, R.; Li, Y.; Feng, H.; Li, Z.; He, L. Recent development of implantable and flexible nerve electrodes. Smart Mater. Med. 2020, 1, 131–147. [Google Scholar] [CrossRef]
- Kumar, K.S.; Ren, H.; Chen, P.Y. A Review of Printable Flexible and Stretchable Tactile Sensors. AAAS Res. 2019, 2019, 32. [Google Scholar]
- Fukuda, K.; Someya, T. Recent Progress in the Development of Printed Thin-Film Transistors and Circuits with High-Resolution Printing Technology. Adv. Mater. 2017, 29, 1602736. [Google Scholar] [CrossRef] [PubMed]
- Bu, F.; Guan, C.; Huang, W.; Zhou, W.; Xu, Y.; Du, Y. Recent developments of advanced micro-supercapacitors: Design, fabrication and applications. Npj Flex. Electron. 2020, 4, 31. [Google Scholar] [CrossRef]
- Choi, K.H.; Yoo, J.T.; Lee, C.K.; Lee, S.Y. All-inkjet-printed, solid-state flexible supercapacitors on paper. Energy Environ. Sci. 2016, 9, 2812–2821. [Google Scholar] [CrossRef]
- Lei, Z.; Xiaoding, C.; Tao, K.; Yunlong, Z.; Liangyu, L. Geometrical Morphology of Inkjet-Printed Finger Electrodes on Untreated Multi-Crystalline Silicon Solar Cells. IEEE J. Photovolt. 2019, 9, 571–577. [Google Scholar] [CrossRef]
- Efimov, A.; Arsenov, P.; Kornyushin, D.; Lizunova, A.; Volkov, I. Aerosol Jet Printing of Silver Lines with A High Aspect Ratio on A Heated Silicon Substrate. Materials 2020, 13, 730. [Google Scholar] [CrossRef]
- Li, D.; Lai, W.Y.; Zhang, Y.Z.; Huang, W. Printable Transparent Conductive Films for Flexible Electronics. Adv. Mater. 2018, 30, 1704738. [Google Scholar] [CrossRef]
- Huang, Q.; Zhu, Y. Printing Conductive Nanomaterials for Flexible and Stretchable Electronics: A Review of Materials, Processes, and Applications. Adv. Mater. Technol. 2019, 4, 1800546. [Google Scholar] [CrossRef]
- Fuller, S.B.; Wilhelm, E.J.; Jacobson, J.M. Ink-jet printed nanoparticle microelectromechanical systems. J. Microelectromech. Syst. 2002, 11, 54–60. [Google Scholar] [CrossRef]
- Ko, S.H.; Pa1, H.; Grigoropoulos, C.P.; Luscombe, C.K.; Fréchet JM, J.; Poulikakos, D. All-inkjet-printed flexible electronics fabrication on a polymer substrate by low-temperature high-resolution selective laser sintering of metal nanoparticles. Nanotechnology 2007, 18, 34. [Google Scholar] [CrossRef]
- Van Osch, T.; Perelaer, J.; de Laat, A.; Schubert, U. Inkjet printing of narrow conductive tracks on untreated polymeric substrates. Adv. Mater. 2008, 20, 343–345. [Google Scholar] [CrossRef]
- Stringer, J.; Derby, B. Limits to feature size and resolution in ink jet printing. J. Eur. Ceram. Soc. 2009, 29, 13–18. [Google Scholar] [CrossRef]
- Moon, Y.J.; Kang, H.S.; Lee, S.H.; Kang, K.T.; Cho, Y.J.; Hwang, J.Y.; Moon, S.J. Effect of contact angle and drop spacing on the bulging frequency of inkjet-printed silver lines on FC-coated glass. J. Mech. Sci. Technol. 2014, 28, 1441–1448. [Google Scholar] [CrossRef]
- Kamyshny, A.; Magdassi, S. Conductive Nanomaterials for Printed Electronics. Small 2014, 10, 3515–3535. [Google Scholar] [CrossRef]
- Moon, Y.J.; Kang, H.S.; Kang, K.T.; Moon, S.J.; Hwang, J.Y. Effect of Thickness on Surface Morphology of Silver Nanoparticle Layer During Furnace Sintering. J. Electron. Mater. 2015, 44, 1192–1199. [Google Scholar] [CrossRef]
- Lee, I.S.; Ryu, K.T.; Park, K.H.; Moon, S.J.; Moon, Y.J.; Hwang, J.Y. Temperature effect on physical properties and surface morphology of printed silver ink during continuous laser scanning sintering. Int. J. Heat Mass Transf. 2017, 108, 1960–1968. [Google Scholar] [CrossRef]
- Derby, B. Inkjet Printing of Functional and Structural Materials: Fluid Property Requirements, Feature Stability, and Resolution. Annu. Rev. Mater. Res. 2010, 40, 395–414. [Google Scholar] [CrossRef]
- Yang, C.; Hong, K.; Jang, J.; Chung, D.S.; An, T.K.; Choi, W.-S.; Park, C.E. Solution-processed flexible ZnO transparent thin-film transistors with a polymer gate dielectric fabricated by microwave heating. Nanotechnology 2009, 20, 465201. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Kwack, Y.; Kim, S.H.; Kyu, T. Ambipolar thin-film transistors and an inverter based on pentacene/self-assembled monolayer modified ZnO hybrid structures for balanced hole and electron mobilities. Org. Electron. 2011, 12, 411–418. [Google Scholar] [CrossRef]
- Kinloch, A.J. Adhesion and Adhesives: Science and Technology, Chapman and Hall. Br. Polym. J. 1987, 20, 18–32. [Google Scholar]






| Contact Angle (Degree) | Surface Energy (mJ m −2) | ||||||
|---|---|---|---|---|---|---|---|
| Deionized Water | Diiodomethane | TGME | |||||
| Pristine ZnO-PFOTES | 111.3 | 53.3 | 40.4 | 0.513 | 35.8 | 36.3 | 0.0141 |
| Laser-treated ZnO-PFOTES | 49.0 | 46.3 | 5.6 | 25.9 | 25.6 | 51.5 | 0.503 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sim, I.; Park, S.; Shin, K.-Y.; Yang, C.; Kang, H.; Hwang, J.Y.; Moon, S.-J. Inkjet Printing of High Aspect Ratio Silver Lines via Laser-Induced Selective Surface Wetting Technique. Coatings 2023, 13, 683. https://doi.org/10.3390/coatings13040683
Sim I, Park S, Shin K-Y, Yang C, Kang H, Hwang JY, Moon S-J. Inkjet Printing of High Aspect Ratio Silver Lines via Laser-Induced Selective Surface Wetting Technique. Coatings. 2023; 13(4):683. https://doi.org/10.3390/coatings13040683
Chicago/Turabian StyleSim, Iseok, Seongju Park, Kwon-Yong Shin, Chanwoo Yang, Heuiseok Kang, Jun Young Hwang, and Seung-Jae Moon. 2023. "Inkjet Printing of High Aspect Ratio Silver Lines via Laser-Induced Selective Surface Wetting Technique" Coatings 13, no. 4: 683. https://doi.org/10.3390/coatings13040683
APA StyleSim, I., Park, S., Shin, K.-Y., Yang, C., Kang, H., Hwang, J. Y., & Moon, S.-J. (2023). Inkjet Printing of High Aspect Ratio Silver Lines via Laser-Induced Selective Surface Wetting Technique. Coatings, 13(4), 683. https://doi.org/10.3390/coatings13040683






