Effect of Grain Sizes on the Friction and Wear Behavior of Dual-Phase Microstructures with Similar Macrohardness and Composition
Abstract
1. Introduction
2. Experimental Section
2.1. Material and Heat Treatment
2.2. Microstructure Characterization
2.3. Microhardness of Ferrite and Martensite
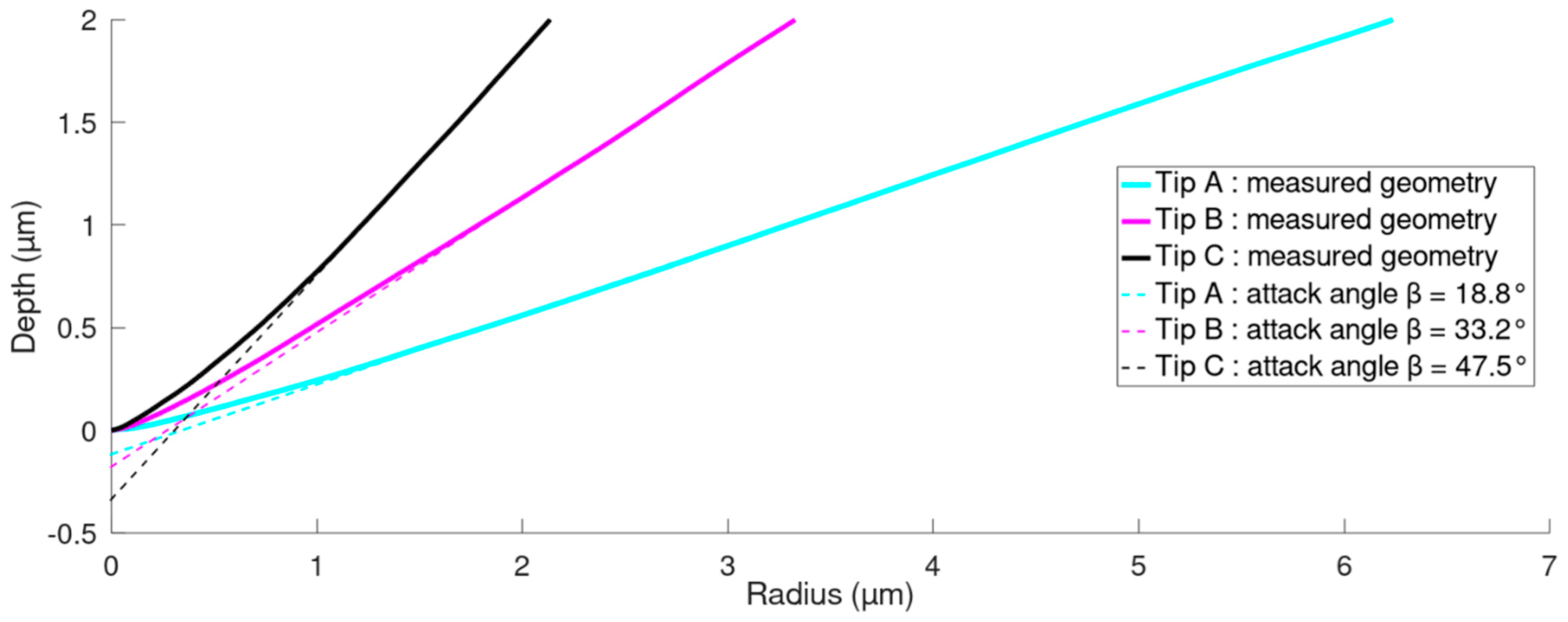
2.4. Scratch Tests
3. Experimental Results
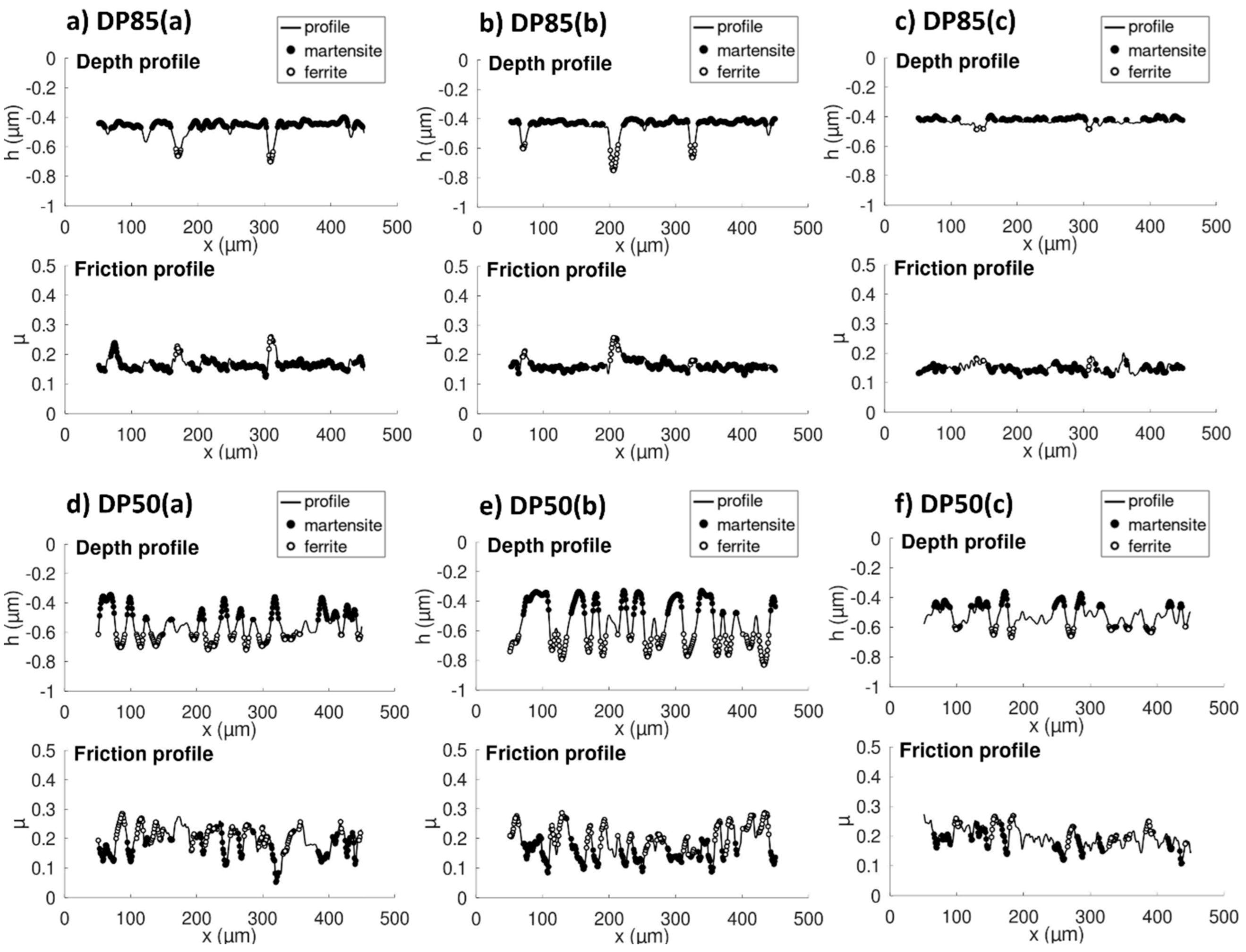
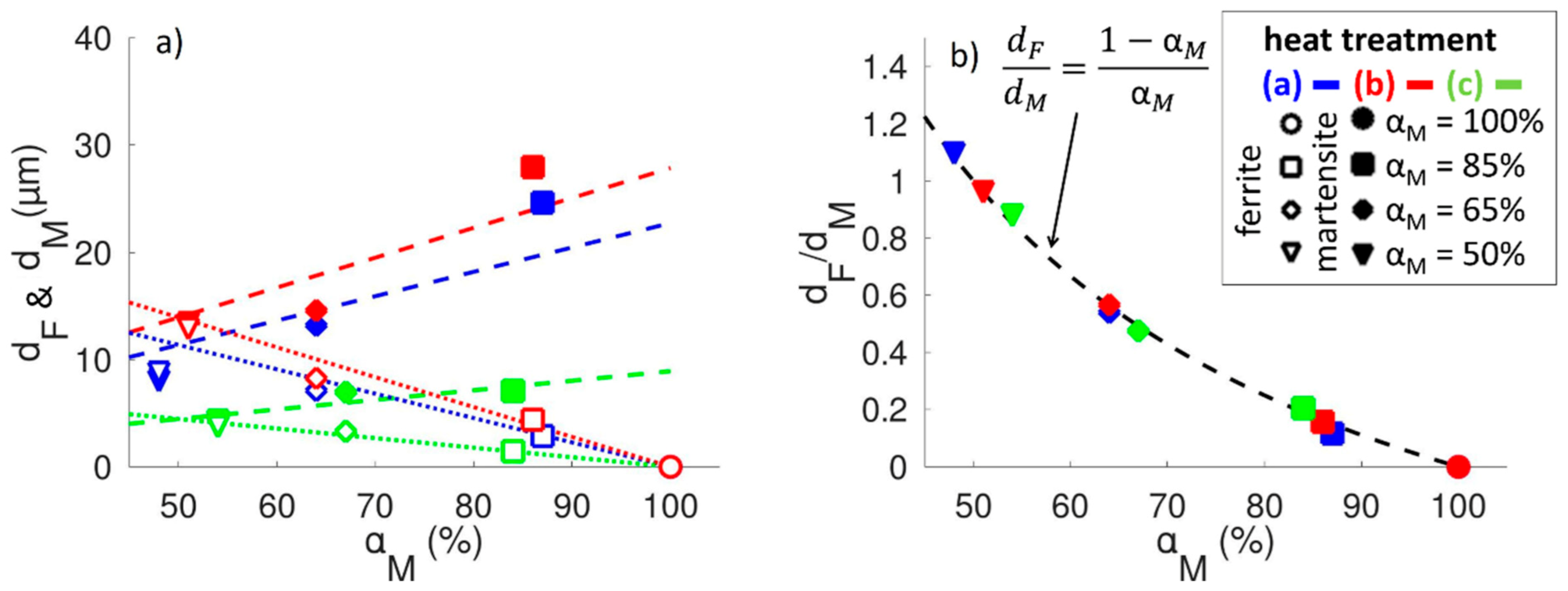
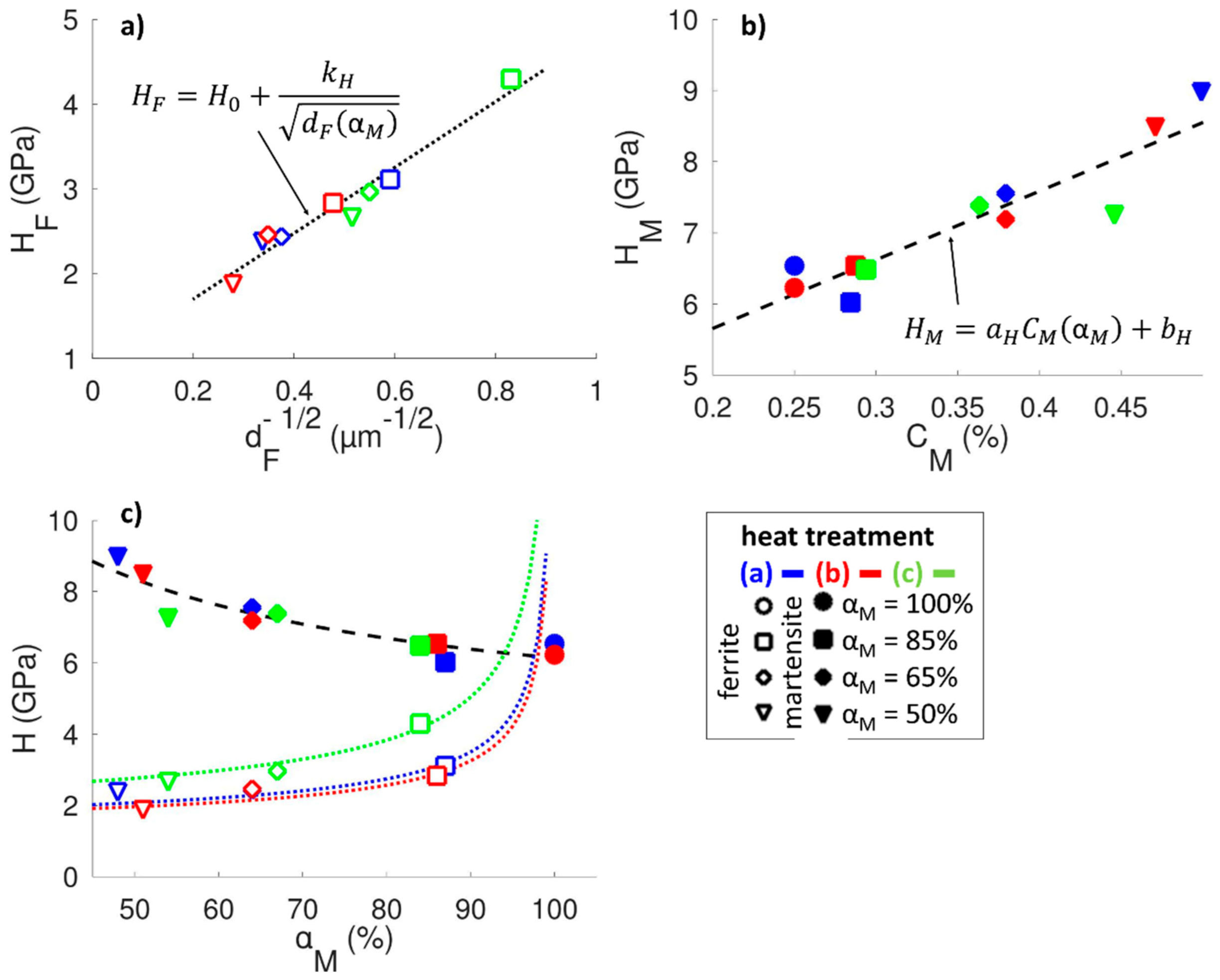
3.1. Microstructure and Hardness Characterization
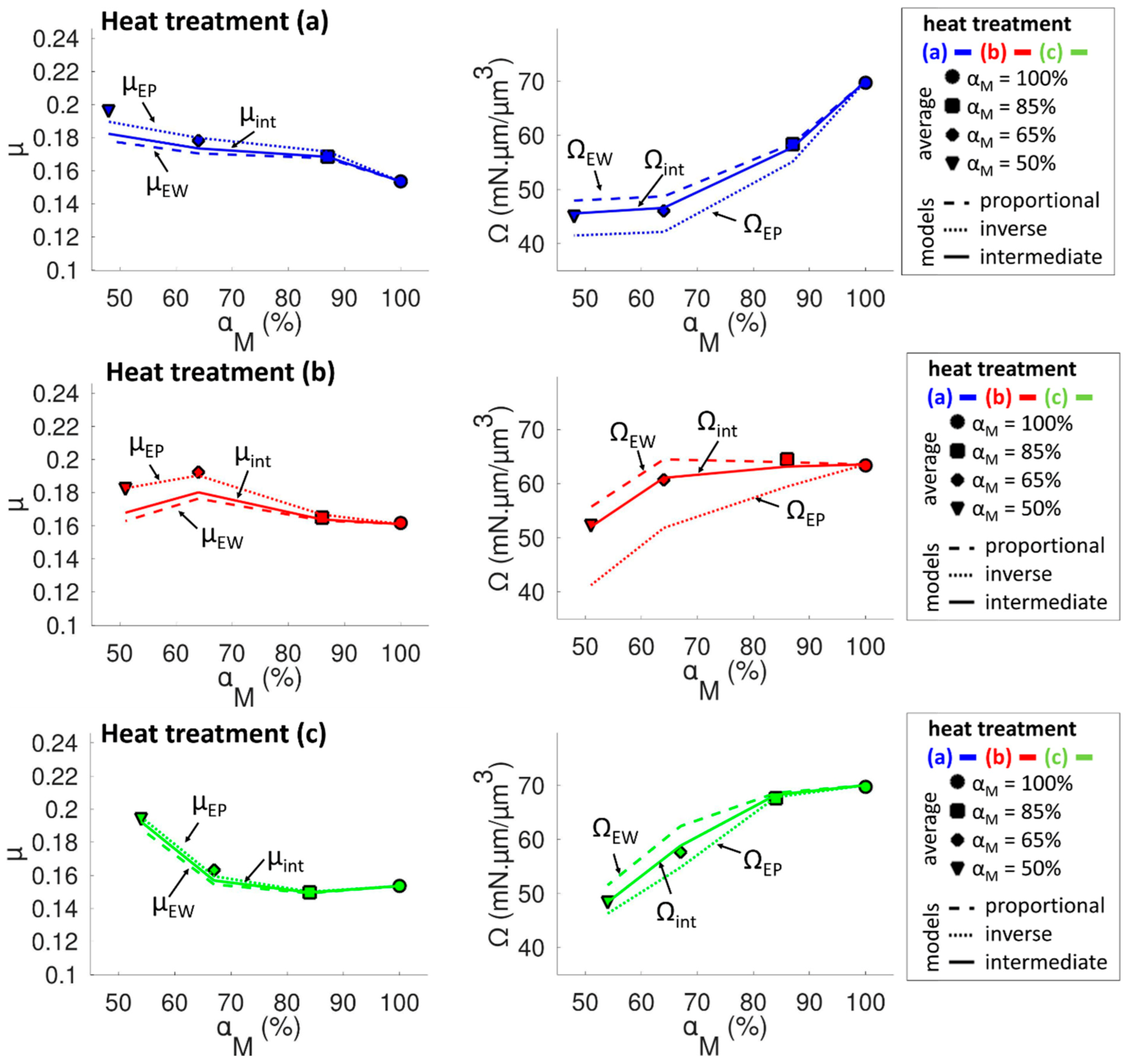
3.2. Friction Coefficient and Specific Wear Resistance
4. Model for Friction and Wear Resistance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saghafian, H.; Kheirandish, S. Correlating microstructural features with wear resistance of dual phase steel. Mater. Lett. 2007, 61, 3059–3063. [Google Scholar] [CrossRef]
- Modi, O.P.; Pandit, P.; Mondal, D.P.; Prasad, B.K.; Yegneswaran, A.H.; Chrysanthou, A. High-stress abrasive wear response of 0.2% carbon dual phase steel: Effects of microstructural features and experimental conditions. Mater. Sci. Eng. A 2007, 458, 303–311. [Google Scholar] [CrossRef]
- Abouei, V.; Saghafian, H.; Kheirandish, S. Dry Sliding Oxidative Wear in Plain Carbon Dual Phase Steel. J. Iron Steel Res. Int. 2007, 14, 43–48. [Google Scholar] [CrossRef]
- Tyagi, R.; Nath, S.K.; Ray, S. Effect of martensite content on friction and oxidative wear behavior of 0.42 Pct carbon dual-phase steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2002, 33, 3479–3488. [Google Scholar] [CrossRef]
- Trevisiol, C.; Jourani, A.; Bouvier, S. Effect of Martensite Morphology on Tribological Behaviour of a Low-Alloy Steel. Metallogr. Microstruct. Anal. 2019, 8, 123–134. [Google Scholar] [CrossRef]
- Trevisiol, C.; Jourani, A.; Bouvier, S. Experimental study and modelling of the effect of microstructure on friction and wear mechanisms of low alloy steel. Mater. Res. Express 2017, 4, 125802. [Google Scholar] [CrossRef]
- Trevisiol, C.; Jourani, A.; Bouvier, S. Effect of microstructures with the same chemical composition and similar hardness levels on tribological behavior of a low alloy steel. Tribol. Int. 2018, 127, 389–403. [Google Scholar] [CrossRef]
- Mazaheri, Y.; Kermanpur, A.; Najafizadeh, A. Nanoindentation study of ferrite-martensite dual phase steels developed by a new thermomechanical processing. Mater. Sci. Eng. A 2015, 639, 8–14. [Google Scholar] [CrossRef]
- Delincé, M.; Jacques, P.J.; Pardoen, T. Separation of size-dependent strengthening contributions in fine-grained Dual Phase steels by nanoindentation. Acta Mater. 2006, 54, 3395–3404. [Google Scholar] [CrossRef]
- Kadkhodapour, J.; Schmauder, S.; Raabe, D.; Ziaei-Rad, S.; Weber, U.; Calcagnotto, M. Experimental and numerical study on geometrically necessary dislocations and non-homogeneous mechanical properties of the ferrite phase in dual phase steels. Acta Mater. 2011, 59, 4387–4394. [Google Scholar] [CrossRef]
- Farivar, H.; Richter, S.; Hans, M.; Schwedt, A.; Prahl, U.; Bleck, W. Experimental quantification of carbon gradients in martensite and its multi-scale effects in a DP steel. Mater. Sci. Eng. A 2018, 718, 250–259. [Google Scholar] [CrossRef]
- Penfornis, C.; Jourani, A.; Mazeran, P.E. Experimental and modelling study of the effect of martensite volume fraction on friction and wear of dual-phase steel at microscopic scale. Wear 2021, 484, 203878. [Google Scholar] [CrossRef]
- Axén, N.; Jacobson, S. A model for the abrasive wear resistance of multiphase materials. Wear 1994, 174, 187–199. [Google Scholar] [CrossRef]
- Axén, N.; Hutchings, I.M.; Jacobson, S. A model for the friction of multiphase materials in abrasion. Tribol. Int. 1996, 29, 467–475. [Google Scholar] [CrossRef]
- Axén, N.; Lundberg, B. Abrasive wear in intermediate mode of multiphase materials. Tribol. Int. 1995, 28, 523–529. [Google Scholar] [CrossRef]
- Loubet, J.L.; Bauer, M.; Tonck, A.; Bec, S.; Gauthier-Manuel, B. Nanoindentation with a surface force apparatus. In Mechanical Properties and Deformation Behavior of Materials Having Ultra-Fine Microstructures; Springer: Berlin/Heidelberg, Germany, 1993; ISBN 9789401047753. [Google Scholar]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Krauss, G. Martensite in steel: Strength and structure. Mater. Sci. Eng. A 1999, 273, 40–57. [Google Scholar] [CrossRef]
- Peng-Heng, C.; Preban, A.G. The effect of ferrite grain size and martensite volume fraction on the tensile properties of dual phase steel. Acta Metall. 1985, 33, 897–903. [Google Scholar] [CrossRef]
- Tabor, D. The Hardness of Metals; Oxford University Press: Oxford, UK, 1951. [Google Scholar] [CrossRef]
- Ashrafi, H.; Shamanian, M.; Emadi, R.; Saeidi, N. Correlation of Tensile Properties and Strain Hardening Behavior with Martensite Volume Fraction in Dual-Phase Steels. Trans. Indian Inst. Met. 2017, 70, 1575–1584. [Google Scholar] [CrossRef]
- Mazaheri, Y.; Kermanpur, A.; Najafizadeh, A. Strengthening Mechanisms of Ultrafine Grained Dual Phase Steels Developed by New Thermomechanical Processing. ISIJ Int. 2015, 55, 218–226. [Google Scholar] [CrossRef]
- Fereiduni, E.; Banadkouki, S.G. Reliability/unreliability of mixture rule in a low alloy ferrite-martensite dual phase steel. J. Alloys Compd. 2013, 577, 351–359. [Google Scholar] [CrossRef]
- Zhang, F.; Ruimi, A.; Wo, P.C.; Field, D.P. Morphology and distribution of martensite in dual phase (DP980) steel and its relation to the multiscale mechanical behavior. Mater. Sci. Eng. A 2016, 659, 93–103. [Google Scholar] [CrossRef]
- Hokkirigawa, K.; Kato, K.; Li, Z.Z. The effect of hardness on the transition of the abrasive wear mechanism of steels. Wear 1988, 123, 241–251. [Google Scholar] [CrossRef]
- Goddard, J.; Wilman, H. A Theory of Friction and Wear During the Abrasion of Metals. Wear 1962, 5, 114–135. [Google Scholar] [CrossRef]
- Sin, H.; Saka, N.; Suh, N.P. Abrasive wear mechanisms and the grit size effect. Wear 1979, 55, 163–190. [Google Scholar] [CrossRef]
- Subhash, G.; Zhang, W. Investigation of the overall friction coefficeint in single-pass scratch test. Wear 2002, 252, 123–134. [Google Scholar] [CrossRef]
- Axén, N.; Hutchings, I.M. Analysis of abrasive wear and friction behaviour of composites. Mater. Sci. Technol. 1996, 12, 757–765. [Google Scholar] [CrossRef]
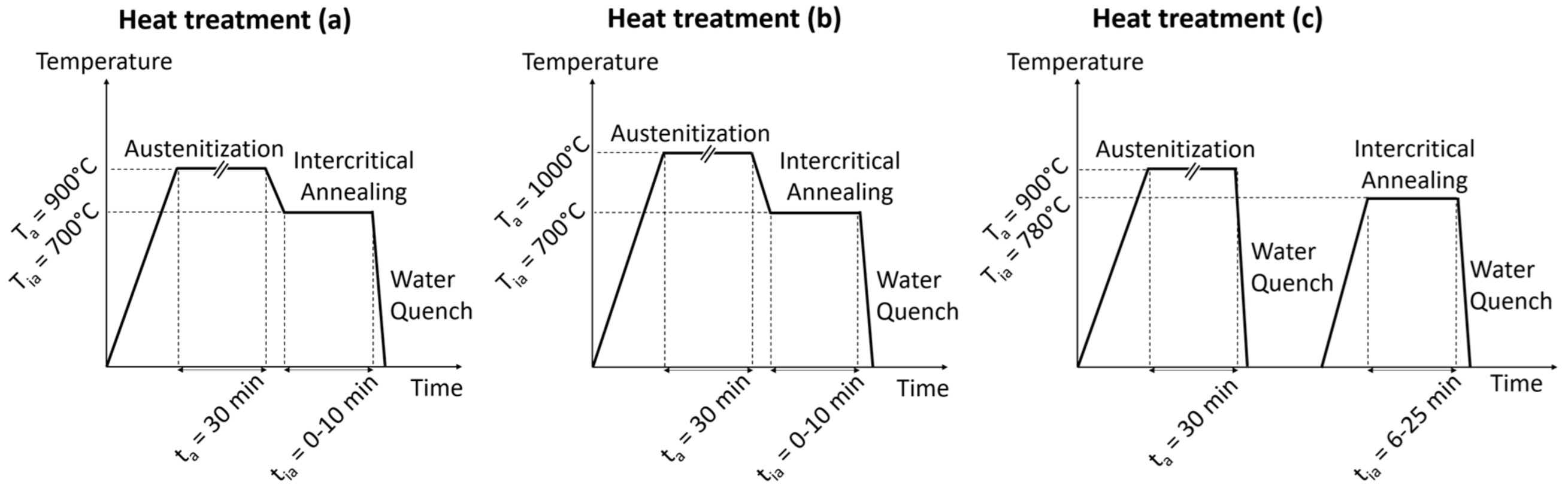
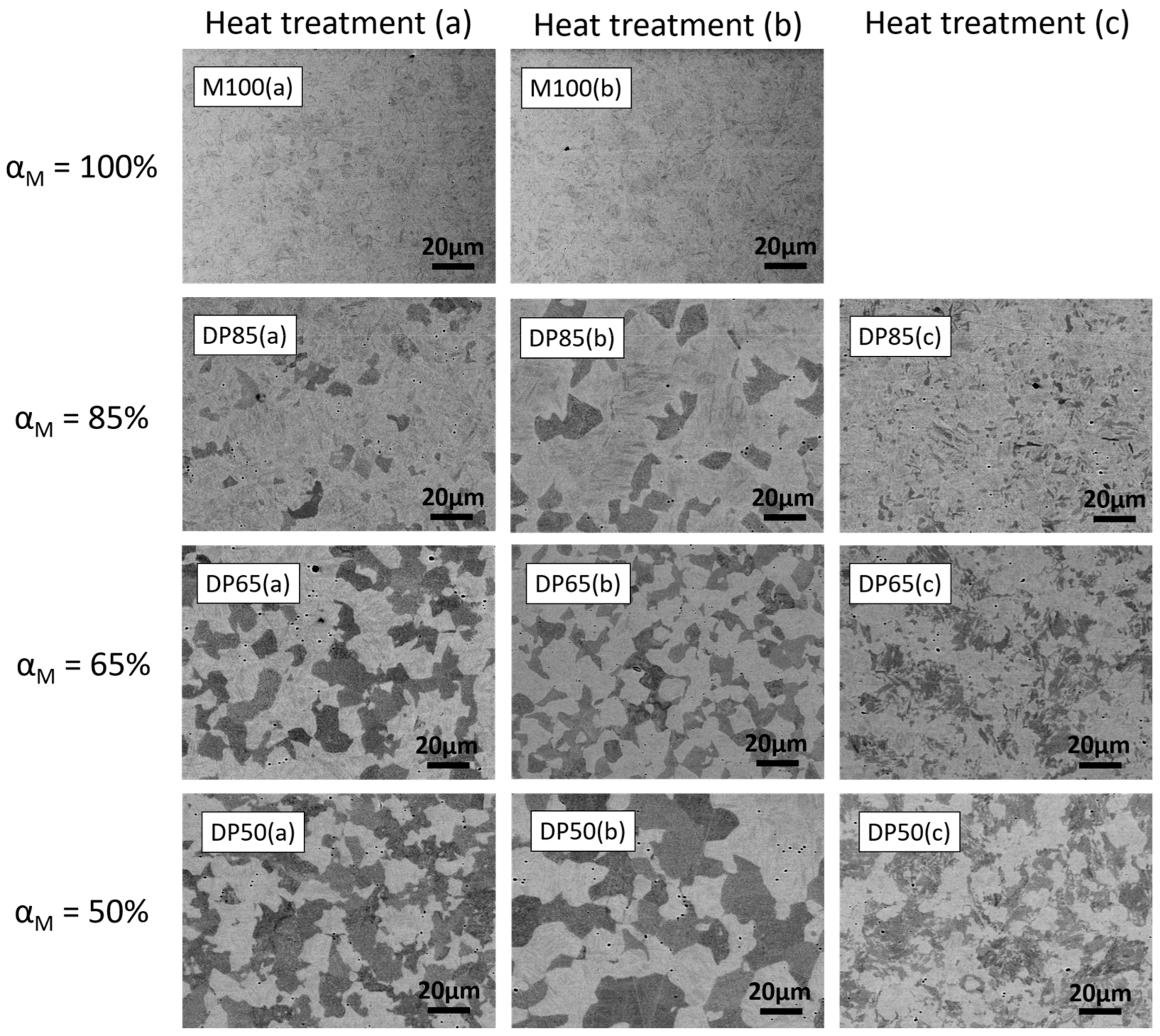

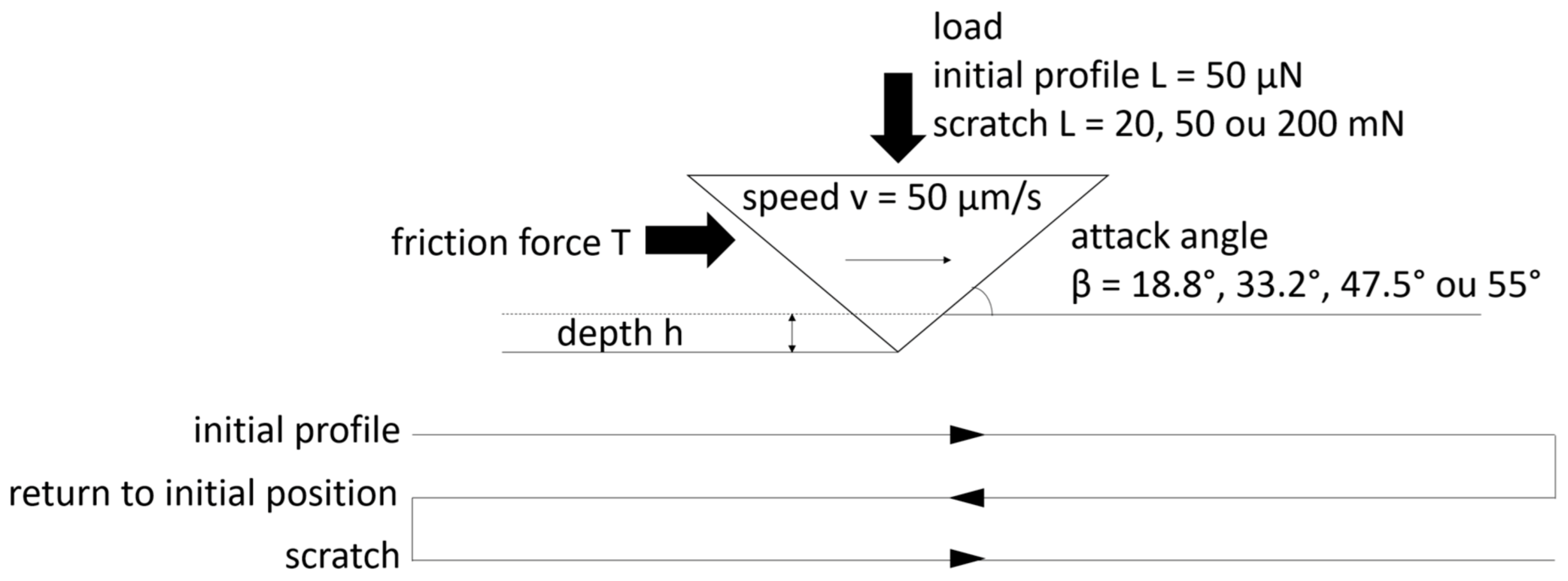
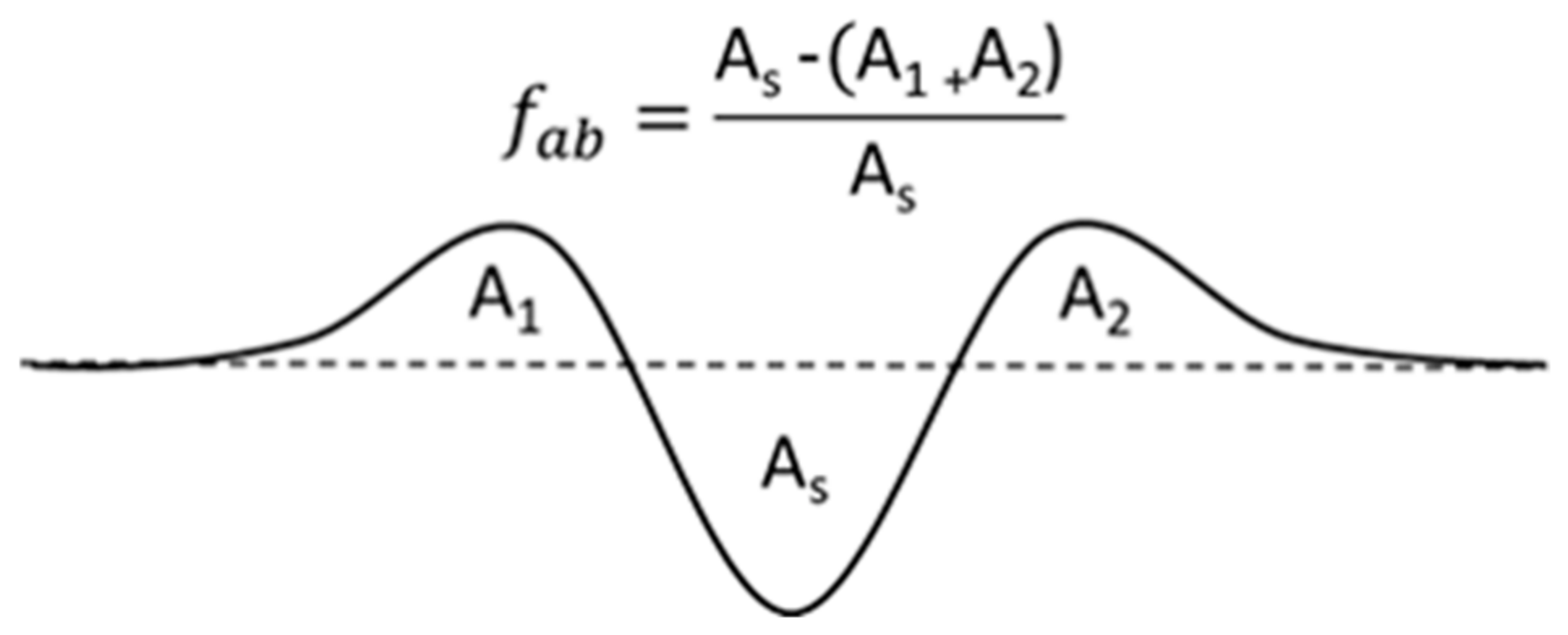
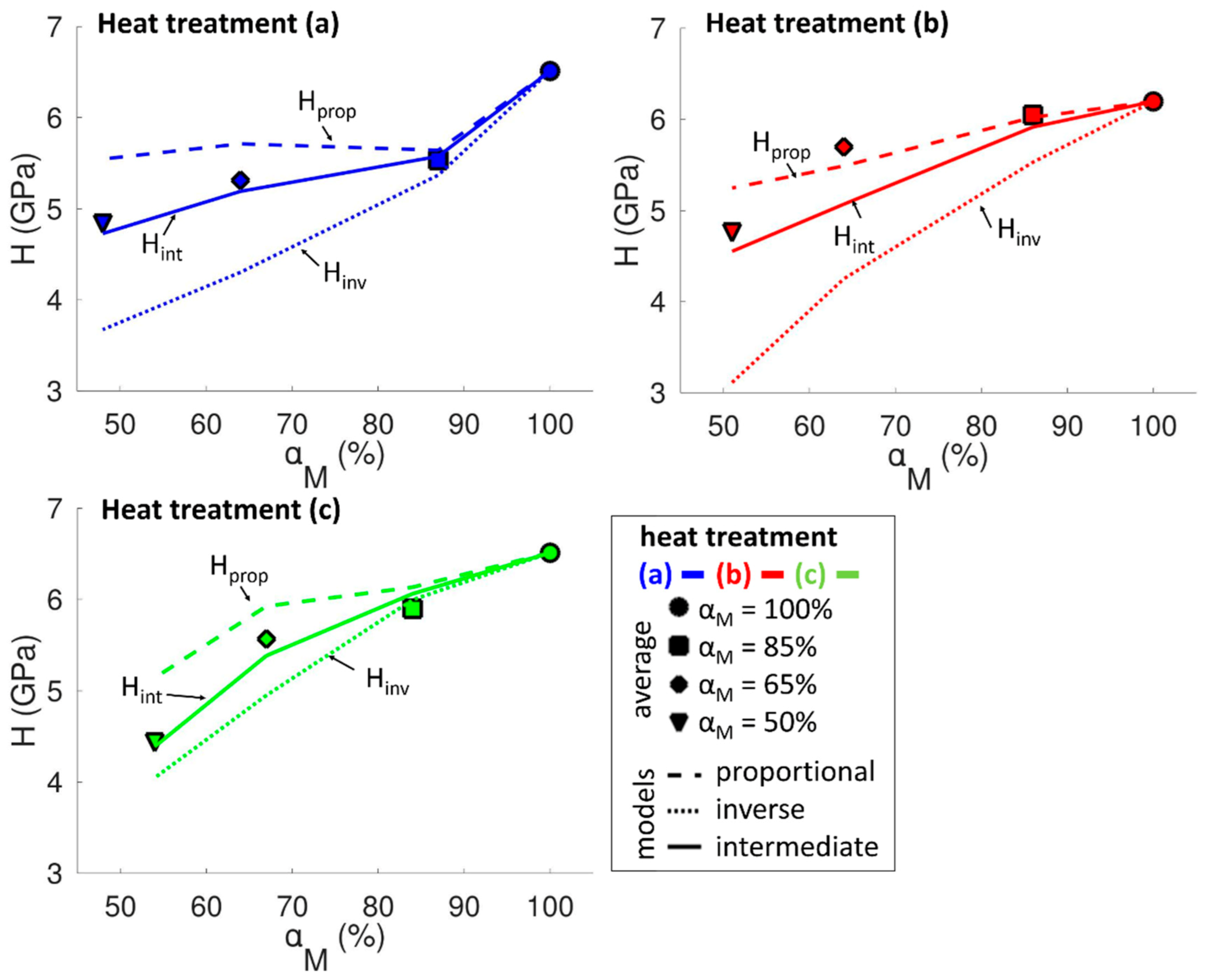
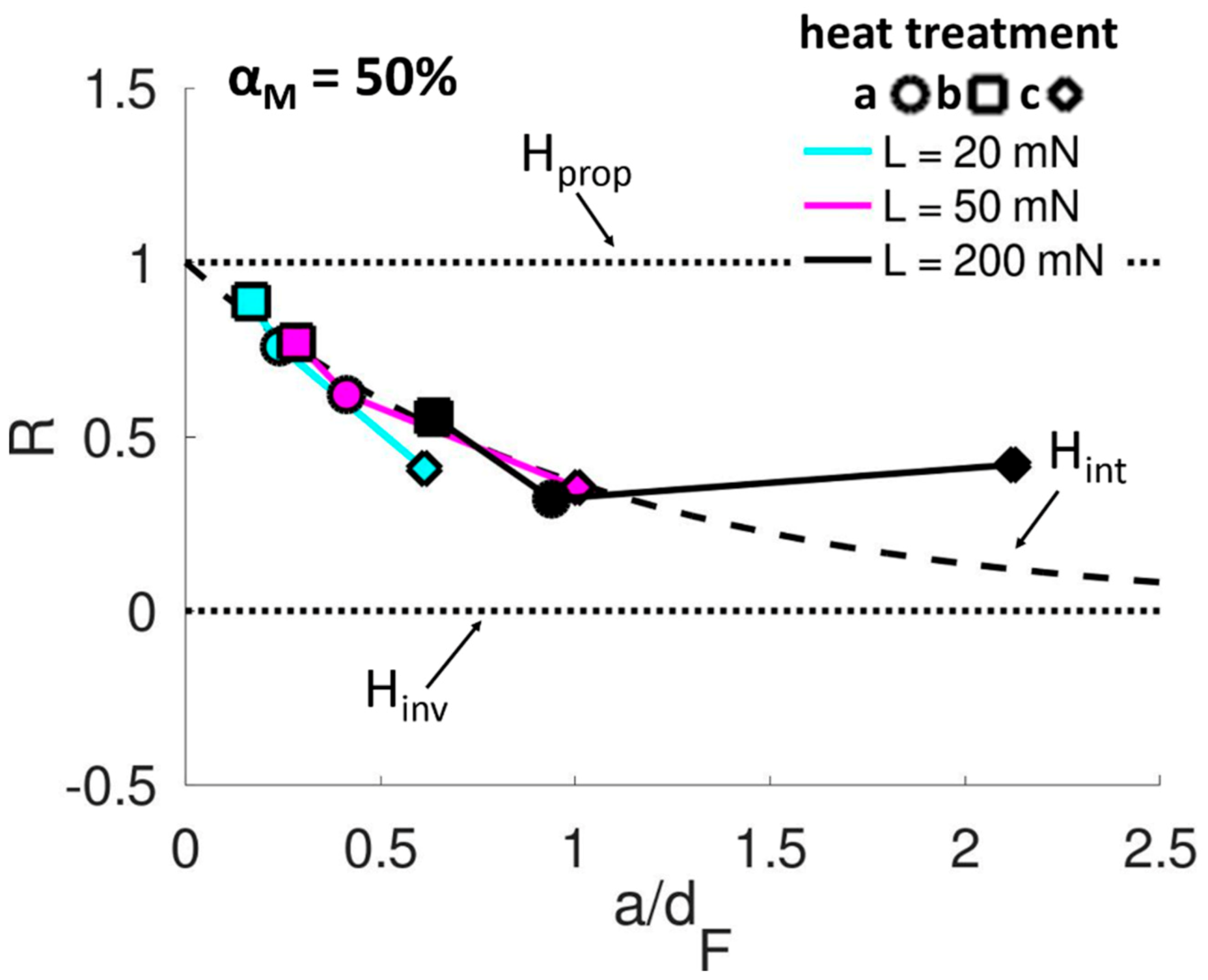
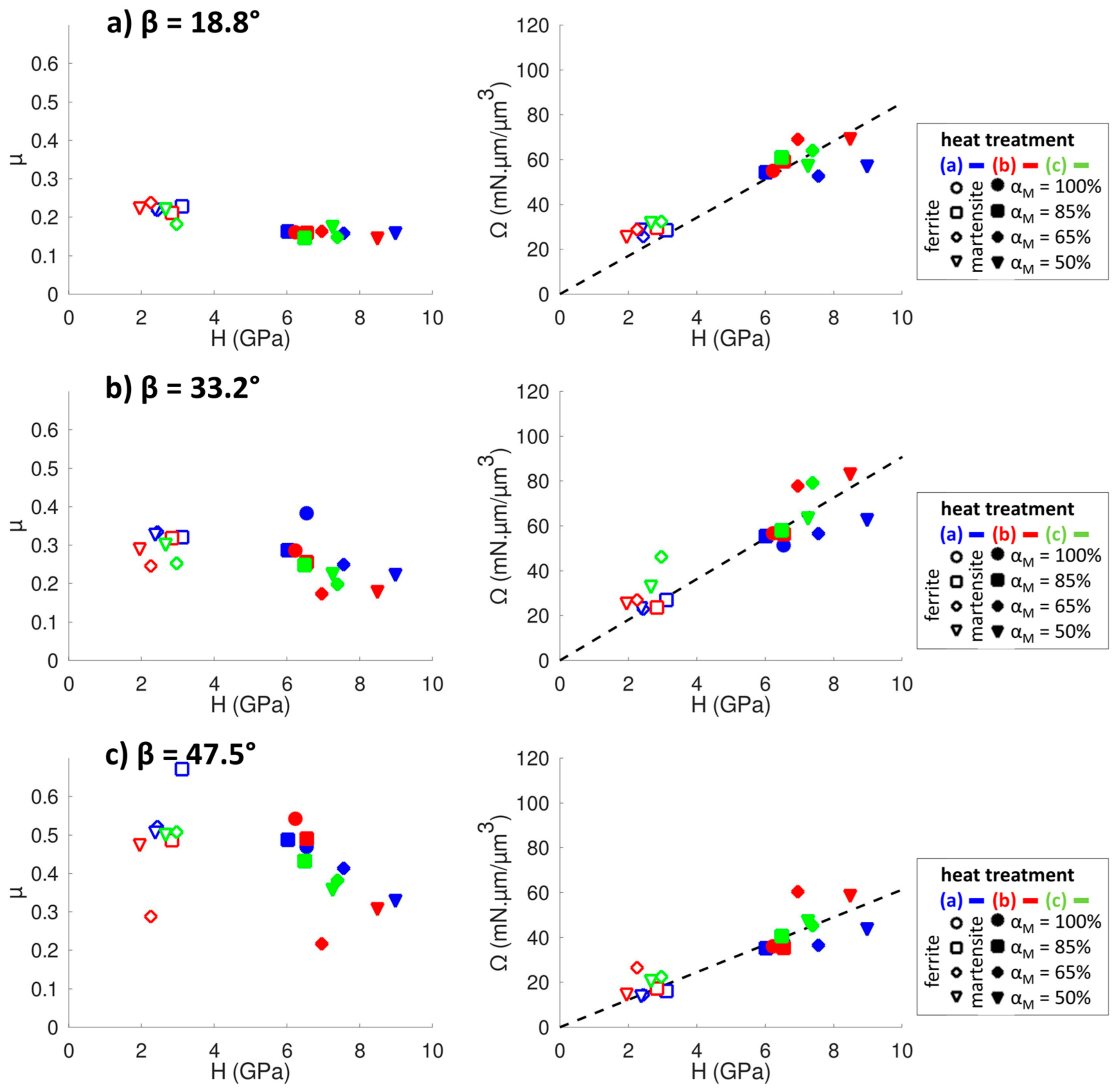

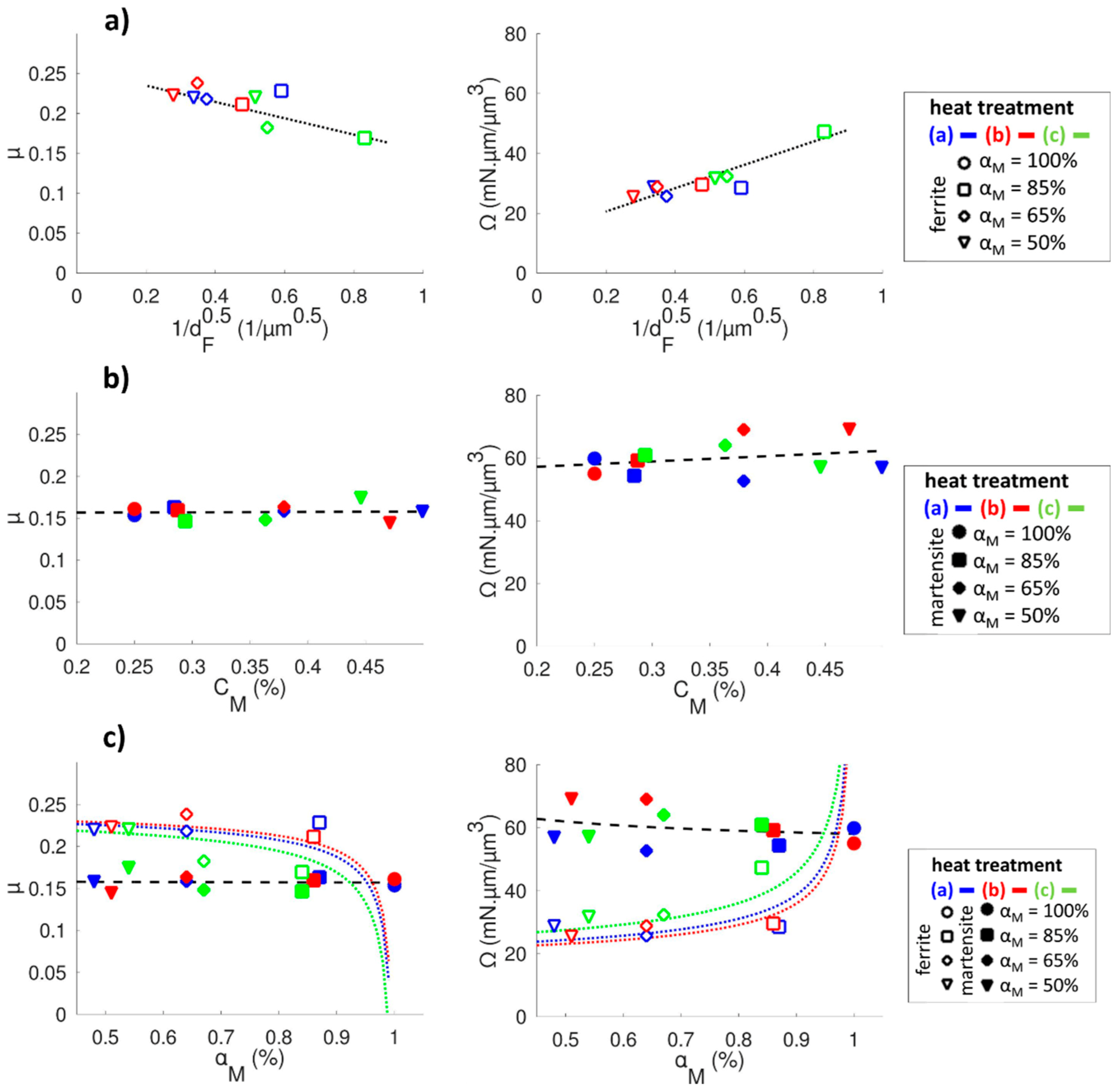

| C | Si | Mn | P | S | Cr | Mo | |
|---|---|---|---|---|---|---|---|
| wt% | 0.25 | <0.4 | 0.65 | <0.035 | <0.035 | 1.15 | 0.2 |
| Sample | Heat Treatment | tia (min) | αM (%) | CM (%) | dM (µm) | dF (µm) | HV2 |
|---|---|---|---|---|---|---|---|
| M100(a) | (a) | 0 | 100 ± 0 | 0.25 | N/A | N/A | 547 ± 8,6 |
| DP85(a) | (a) | 2 | 87 ± 1 | 0.28 | 24.63 ± 2.67 | 2.87 ± 0.38 | 452 ± 10.9 |
| DP65(a) | (a) | 4 | 64 ± 2 | 0.38 | 13.19 ± 0.59 | 7.12 ± 0.3 | 394 ± 18.7 |
| DP50(a) | (a) | 10 | 48 ± 3 | 0.5 | 8.02 ± 0.48 | 8.79 ± 0.5 | 336 ± 14.8 |
| M100(b) | (b) | 0 | 100 ± 0 | 0.25 | N/A | N/A | 530 ± 5.8 |
| DP85(b) | (b) | 3 | 86 ± 3 | 0.29 | 27.95 ± 4.77 | 4.39 ± 0.23 | 475 ± 15.7 |
| DP65(b) | (b) | 7 | 64 ± 5 | 0.38 | 14.58 ± 1.74 | 8.26 ± 0.95 | 410 ± 20 |
| DP50(b) | (b) | 10 | 51 ± 2 | 0.47 | 13.41 ± 0.81 | 12.88 ± 0.87 | 349 ± 12.9 |
| DP85(c) | (c) | 25 | 84 ± 2 | 0.29 | 7.08 ± 1.48 | 1.45 ± 0.05 | 443 ± 10.2 |
| DP65(c) | (c) | 7 | 67 ± 3 | 0.36 | 6.96 ± 0.37 | 3.31 ± 0.48 | 421 ± 10.9 |
| DP50(c) | (c) | 6 | 54 ± 2 | 0.44 | 4.29 ± 0.13 | 3.77 ± 0.15 | 355 ± 18.1 |
| Martensite | Ferrite | |||
|---|---|---|---|---|
| Load | aH (GPa/%) | bH (GPa) | H0 (GPa) | kH (GPa·µm1/2) |
| 20 mN | 11.46 | 3.57 | 1.38 | 3.22 |
| 50 mN | 9.65 | 3.73 | 0.92 | 3.89 |
| 200 mN | 5.02 | 4.40 | 1.33 | 2.68 |
| - | Martensite | Ferrite | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Load | β | K | aµ (/%) | bµ | aΩ (mN0·µm−2/%) | bΩ (mN·µm−2) | µ0 | kµ (µm1/2) | Ω0 (mN·µm−2) | kΩ (mN·µm−1.5) |
| 20 mN | 18.8° | 0.13 | −0.07 | 0.14 | 32.27 | 43.56 | 0.20 | −0.09 | 21.81 | 18.97 |
| 33.2° | 0.11 | −0.15 | 0.17 | 60.21 | 45.73 | 0.28 | −0.17 | 20.04 | 40.46 | |
| 47.5° | 0.13 | −0.29 | 0.25 | 64.46 | 31.48 | 0.35 | −0.26 | 12.71 | 40.10 | |
| 50 mN | 18.8° | 0.12 | −0.01 | 0.16 | 16.96 | 53.80 | 0.26 | −0.10 | 12.79 | 38.98 |
| 33.2° | 0.11 | −0.48 | 0.42 | 73.03 | 37.73 | 0.34 | −0.09 | 9.04 | 46.47 | |
| 47.5° | 0.16 | −0.83 | 0.70 | 63.97 | 20.59 | 0.50 | 0.00 | 8.39 | 20.13 | |
| 200 mN | 18.8° | 0.10 | 0.00 | 0.22 | −24.75 | 69.37 | 0.34 | −0.06 | 7.88 | 54.14 |
| 33.2° | 0.14 | −0.64 | 0.67 | −17.88 | 50.49 | 0.48 | 0.00 | 11.73 | 24.76 | |
| 47.5° | 0.26 | −0.36 | 0.82 | −16.17 | 29.88 | 0.99 | −0.21 | 2.12 | 19.96 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penfornis, C.; Jourani, A.; Mazeran, P.-E. Effect of Grain Sizes on the Friction and Wear Behavior of Dual-Phase Microstructures with Similar Macrohardness and Composition. Coatings 2023, 13, 533. https://doi.org/10.3390/coatings13030533
Penfornis C, Jourani A, Mazeran P-E. Effect of Grain Sizes on the Friction and Wear Behavior of Dual-Phase Microstructures with Similar Macrohardness and Composition. Coatings. 2023; 13(3):533. https://doi.org/10.3390/coatings13030533
Chicago/Turabian StylePenfornis, Corentin, Abdeljalil Jourani, and Pierre-Emmanuel Mazeran. 2023. "Effect of Grain Sizes on the Friction and Wear Behavior of Dual-Phase Microstructures with Similar Macrohardness and Composition" Coatings 13, no. 3: 533. https://doi.org/10.3390/coatings13030533
APA StylePenfornis, C., Jourani, A., & Mazeran, P.-E. (2023). Effect of Grain Sizes on the Friction and Wear Behavior of Dual-Phase Microstructures with Similar Macrohardness and Composition. Coatings, 13(3), 533. https://doi.org/10.3390/coatings13030533







