Thermal Case Study of Cilia Actuated Transport of Radiated Blood-Based Ternary Nanofluid under the Action of Tilted Magnetic Field

Abstract

Micro/nanoscale fabricated devices have widely been used in modern technology and bioengineering as they offer excellent heat transfer. Removal of excess heat, coolant selection, rapid mixing, and handling proportion of colloidal metallic nanogranules in the base fluid are the main challenges in micro/nanofluidic systems. To address these problems, the primary motivation of the intended mathematical flow problem is to investigate the thermal and flow aspects of blood-based ternary nanofluid in the presence of inclined magnetic field and thermal radiations through a microfluidic pump with elastic walls. Further, the pump inner surface is smeared with fabricated cilia. The embedded cilia blow in coordination to start metachronal travelling waves along the pump wall that assist homogenous mixing and manipulation. The entire analysis is conducted in moving frame and simplified under lubrication and Rosseland approximations. Numerical solution of various flow and thermal entities are computed via the shooting method and plotted for different values of the parameters of interest. A comparative glimpse allows us to conclude that the trimetallic blood-based nanofluid exhibits elevated heat transfer rate by 12–18%, bi-metallic by about 11–12%, and mono nanofluid by about 6% compared to the conventional blood model. The study also determines that the prolonged cilia commence augmentation in flowrate and pressure-gradient around the pump deep portion. Furthermore, the radiated ternary liquid under fragile magnetic field effects may contribute to the cooling process by eliminating unnecessary heat from the system. It is also noticed that around the ciliated wall, the heat transfer irreversibility effects are appreciable over the fluid frictional irreversibility.

1. Introduction

Microfluidics refers to the manipulation of liquids and suspended particles at the microlevel, which is related to a deep understanding of fluid behavior at this level and the engineering of micro-conduits. Recent developments in micro/nanofluidic devices and their enhanced accessibility in industrial and biomedical applications allowed several researchers to model, manufacture, and apply microfluidic techniques. For instance, remarkable applications of microfluidic pumping flows have been discussed in [1,2,3] for drug supply, in [4] for mixing, in [5] for Deoxyribonucleic acid (DNA) and protein analysis, in [6] for therapeutic procedures, and in [7,8,9] for various micropumps with potential uses and lab-on-chip devices, etc. Chaube et al. [10] investigated the peristaltic driven flow through a micro-electroosmotic pump with the lubrication approach. In this regard, a recent attempt elaborating the couple stress fluid transport through microfluidic rotating channel was presented by Siva et. [11]. They reported that inside the microchannel, the axial flow rate is a decreasing function of the rotating Reynolds number, and the flowrate attains a steady conduct under high electroosmotic effect. Some interesting mathematical models of biological flows through microchannels are reported as an application of microfluidic pump flows [12,13,14,15].

Accomplishing fluid motion in micro dimensions is exceptionally complicated due to the very high surface-to-volume ratio of microsystems and small inertial effects. To operate essential biophysical functions such as mixing and movement, in many microorganisms and cells, cilia and flagella beat together in complex pattern to create net fluid flow induced by metachronal waves. Based on this approach, different fabrication methods have been demonstrated to introduce artificial cilia capable of microfluidic pumping. In this regard, Saleem et al. [16] reported that the artificial cilia inserted inside the channel surface facilitate micro-mixing and manipulate fluid flow. An MHD biomimetic blood pump model was suggested by Ramesh et al. [17]. Ashraf et al. [18] and Riaz et al. [19] claimed that epic cilia length enhances fluid flow rate in cilia-assisted motion of viscous fluid and water-based nanofluid in symmetric shaped conduit.

Some interesting studies of fabricated cilia in the perception of microfluidic processing, instantaneous mixing and pumping are mentioned [16,17,18,19]. In this regime, Javid et al. [20] presented a mathematical model of pumping transport induced by cilia stimulated asymmetric metachronal waves and reported that prolonged cilia contribute to fluid flow enhancement. Abo-Elkhair [21] discussed the effect of a ciliated wall on the pumping motion of magneto viscous fluid. Recently, Saleem and Munawar [22] reported that appropriate mimetic cilia length is required to assist fluid motion and rapid mixing.

Magneto-fluidics at the microscale refers to the combination of magnetic field and fluid flows through microdevices. For the last few decades, the magnetohydrodynamic ciliary and peristaltic flows have attracted substantial attention from many researchers, especially in the context of biological flows through a microfluidic conduit. A mathematical model of a bio-magnetic fluid under ferro-hydrodynamics and magnetohydrodynamics principles was contributed by Tzirtzilakis [23]. Bansi et al. [24] reviewed the resistive nature of a magnetic field on radiated blood flow through the oscillatory artery. Saleem [25] investigated the effects of a magnetic field on ciliary transport of non-Newtonian fluid and reported that around the channel core part, compelling magnetic field effects undermine the fluid motion. Several studies [26,27,28,29] elaborate on the resistive nature of magnetic fields on pumping transport of various biological fluids.

Blood is a non-Newtonian fluid with shear-thinning properties. In microchannel flow, base fluids seem deficient in thermal conductance. With the passage of time, modern development in nanotechnology has led to new class of fluids named nanofluids. A nanofluid is obtained by the combination of one or more kind of metallic nanoparticle with superior thermal conductivity in base fluid. Thermo-flows in microchannels have been the subject of mounting interest for many researchers of this era due to the extensive industrial and scientific applications. Some essential applications are found in bio-engineered pumps thermal and drug delivery pumps [30,31], lubricants [32], micro-mixers [33], and cooling [34]. A pioneering study proposing the concept of nanofluids was put forward by Choi [35]. The idea of ternary fluids—that is, the dispersion of trimetallic nanoparticles with a base fluid—has been investigated in recent times. Experimental work [36,37] is noted to report the implication and extraordinary features of ternary nanofluids. Although only a small number of theoretical attempts have been introduced to highlight the favorable and perceptive role of ternary nanofluid in heat transfer amplification. In this respect, a theoretical trihybrid nanofluid model explaining improved heat transfer features was provided by Manjunatha et al. [38]. Elnaqeeb et al. [39] examined the impacts of stretching and suction on water-based ternary nanofluids. Recently, a thermal analysis of Williamson ternary nanofluid was performed by Munawar and Saleem [40], who stated that radiated ternary fluid gained improved heat transfer aspects compared to hybrid and mono nanofluids.

In thermos-flows, thermal management is a primary requirement. Accretion of excessive heat wastes unfavorably affect pump performance. Thus, to accomplish a preferred thermo-mechanical model with appropriate thermal supervision, excessive heat is desired to be reduced to its best level. Thus, it is vital to discover the methods that promote entropy minimization and flow optimization. There have been some exciting studies illustrating entropic analyses in microchannels [41,42,43]. A ground-breaking investigation concerning the entropy construction in a thermal system was contributed by Bejan [44]. Misra et al. [45] and Munawar et al. [46] proposed an optimal model of microchannel and wavy triangular cavity to decrease entropy formation.

A comprehensive review of the abovementioned literature mirrors the consideration of unary and hybrid nanofluid fluids in microdevices. The adaptation of trimetallic nanofluids in bio-liquids that are acknowledged to have considerable thermal performance is an obligation in modern developments towards recent microfluidic applications. The current work aims to fill this gap by considering cilia-regulated transport of a hyperbolic tangent ternary nanofluid through a symmetric microchannel with flexible walls. The ternary nanofluid is prepared by the merger of three metallic nanoparticles: titanium dioxide TiO₂, silicon dioxide SiO₂, and aluminum oxide Al₂O₃ in the base fluid (blood). The base fluid is modeled as hyperbolic tangent fluid due to its shear thinning properties. Moreover, the simultaneous effects of inclined magnetic field and thermal radiation are also considered. To the best of our understanding such flow setting has never been studied before now. The numerical solutions for flow and thermodynamical quantities were computed via the shooting method. A comparison between the thermal features of mono/hybrid/ternary nanofluids and traditional blood is presented. The anticipated study may offer a deep insight in bioengineering pump design to be utilized in drug delivery and thermal pipe heat sinks.

2. Mathematical Modelling and Governing Equations

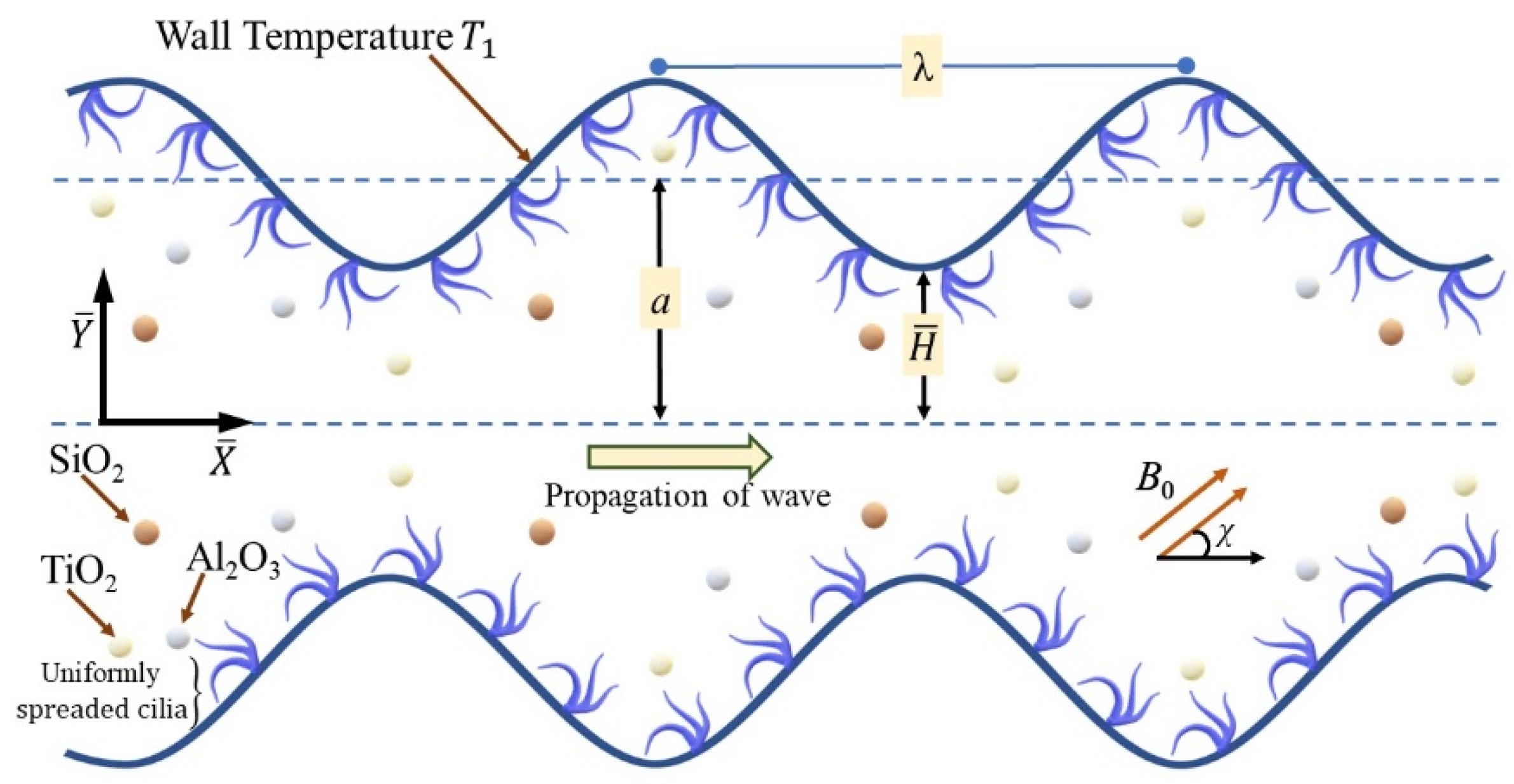
2.1. Problem Formulation

A two-dimensional pumping motion of blood-based trihybrid nanofluid was considered through a symmetric micropump under the action of a tilted magnetic field at an angle χ. The working ternary fluid flowing through the pump is assumed as TiO₂-SiO₂-Al₂O₃/blood that is acquired by the dispersion of 1% volume fraction of each tri-hybrid nanosized metallic particle of Titanium dioxide (TiO₂), silicon dioxide or silica (SiO₂), and Alumina (Al₂O₃) in conventional blood (base fluid) characterized by hyperbolic tangent fluid. Furthermore, the internal surface of the pump is imbedded with a layer of fabricated cilia that blow in organization to start a set of travelling waves moving with constant speed c along the pump wall, named as metachronal waves, as depicted in Figure 1. The present flow is modeled in a rectangular coordinate system in such a way that the wave propagation along the $\overline{X}$-axis and the $\overline{Y}$-axis is orthogonal to the motion.

The vertical position of cilia is formulated [47] by the explicit function of space variable $\overline{X}$ and time variable $\overline{t}$ as

$$\overline{H}\left(\overline{X},\overline{t}\right)=a+a\epsilon \cos \left(\frac{2\pi }{\lambda }\left(\overline{X}-c\overline{t}\right)\right).$$

(1)

The cilia blow in an elliptical shape and are horizontally located at [42]

$$\overline{G}\left(\overline{X},\overline{t}\right)=X_0+a\alpha \epsilon \sin \left(\frac{2\pi }{\lambda }\left(\overline{X}-c\overline{t}\right)\right).$$

(2)

The cilia velocity components along horizontal and vertical directions are calculated by Equations (1) and (2) as

$${\overline{U}}_0={\left(\frac{\partial \overline{G}}{\partial \overline{t}}\right)}_{X_0}=\frac{-\left(\frac{2\pi }{\lambda }\right)a\epsilon \alpha c\cos \left(\frac{2\pi }{\lambda }\left(\overline{X}-c\overline{t}\right)\right)}{1-\left(\frac{2\pi }{\lambda }\right)a\epsilon \alpha \cos \left(\frac{2\pi }{\lambda }\left(\overline{X}-c\overline{t}\right)\right)},$$

(3)

$$\overline{V_0}={\left(\frac{\partial \overline{H}}{\partial \overline{t}}\right)}_{X_0}=\frac{-\left(\frac{2\pi }{\lambda }\right)a\epsilon \alpha c\sin \left(\frac{2\pi }{\lambda }\left(\overline{X}-c\overline{t}\right)\right)}{1-\left(\frac{2\pi }{\lambda }\right)a\epsilon \alpha \sin \left(\frac{2\pi }{\lambda }\left(\overline{X}-c\overline{t}\right)\right)},$$

(4)

where a represents mean width of the pump, α signifies the measure of eccentricity of elliptical course, λ stands for the wavelength of propagating metachronal wave, ε is used for the height of inserted mimetic cilia, and X₀ is the location of nanofluid particle.

Since blood is considered as the base fluid, a pseudoplastic fluid model is assumed. The tangent hyperbolic fluid is a well-known pseudoplastic fluid model found in the literature [48], for which the extra stress tensor for a trihybrid nanofluid is given by

$$\overline{S}=\left[{\mu }_{\infty }+\left({\mu }_{thnf}+{\mu }_{\infty }\right)\tanh {\left(\mathsf{\Gamma }\dot{\gamma }\right)}^n\right]A_1,$$

(5)

where $A_1=\nabla V+{\left( \nabla V\right)}^T$ is the first Rivlin-Erickson tensor with the velocity vector $V=\left[\overline{U}\left(\overline{X},\overline{Y},\overline{t}\right), \overline{V}\left(\overline{X},\overline{Y},\overline{t}\right)\right]$; $\dot{\gamma }=\sqrt{\frac{1}{2}\sum _{\mathrm{i}}\sum _j{\dot{\gamma }}_{\mathrm{ij}}{\dot{\gamma }}_{\mathrm{ij}}}=\sqrt{\frac{\mathsf{\Pi }}{2}}$ is the shear rate, in which $\mathsf{\Pi }=\mathrm{trac}\left[A_1{}^2\right]$ defines the second invariant for strain tensor; n is the power law index; μ_∞ is the infinite shear rate viscosity; the effective viscosity for the ternary fluid is measured by μ_thnf at zero shear rate; and Γ is the time constant. Since the tangent hyperbolic fluid shows shear-thinning properties, it is supposed that μ_∞ is zero and Γ$\dot{\gamma }$ is smaller than 1; thus, Equation (5) leads to

$$\overline{S}={\mu }_{thnf}\left[1+n\left(\mathsf{\Gamma }\dot{\gamma }-1\right)\right]A_1.$$

(6)

The extra stress components of the hyperbolic tangent ternary nanofluid from Equation (6) can be calculated as

$${\overline{S}}_{XX}=2{\mu }_{thnf}\left[1+n\left(\mathsf{\Gamma }\dot{\gamma }-1\right)\right]\frac{\partial \overline{U}}{\partial \overline{X}},$$

(7)

$${\overline{S}}_{XY}={\mu }_{thnf}\left[1+n\left(\mathsf{\Gamma }\dot{\gamma }-1\right)\right]\left(\frac{\partial \overline{U}}{\partial \overline{Y}}+\frac{\partial \overline{V}}{\partial \overline{X}}\right),$$

(8)

$${\overline{S}}_{YY}={\mu }_{thnf} \left[1+n\left(\mathsf{\Gamma }\dot{\gamma }-1\right)\right]\left(\frac{\partial \overline{V}}{\partial \overline{Y}}\right),$$

(9)

in which $\dot{\gamma }={\left(2{\left(\frac{\partial U}{\partial X}\right)}^2+{\left(\frac{\partial U}{\partial Y}+\frac{\partial V}{\partial X}\right)}^2+2\frac{\partial V}{\partial Y}\right)}^{1/2}$. The considered blood-based ternary nanofluid model reduces to an aqueous-based ternary nanofluid when Γ = 0 or n = 1.

2.2. Governing Equations in Laboratory Frame

In the context of the laboratory frame, the conservation laws for mass, momentum, and energy under the action of uniform inclined magnetic field B = [B₀sin(χ), B₀cos(χ)] are given as [16,17,18]

$$\frac{\partial \overline{U}}{\partial \overline{X}}+\frac{\partial \overline{V}}{\partial \overline{Y}}=0,$$

(10)

$${\rho }_{thnf}\left(\frac{\partial \overline{U}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{U}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{U}}{\partial \overline{Y}}\right)=-\frac{\partial \overline{P}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{XX}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{XY}}{\partial \overline{Y}}-{\sigma }_{thnf}{B}_0^2\cos \left(\chi \right)\left(\overline{U}\cos \left(\chi \right)-\overline{V}\sin \left(\chi \right)\right),$$

(11)

$${\rho }_{thnf}\left(\frac{\partial \overline{V}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{V}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{V}}{\partial \overline{Y}}\right)=-\frac{\partial \overline{P}}{\partial \overline{Y}}+\frac{\partial {\overline{S}}_{XY}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{YY}}{\partial \overline{Y}}-{\sigma }_{thnf}{B}_0^2\sin \left(\chi \right)\left(\overline{U}\cos \left(\chi \right)-\overline{V}\sin \left(\chi \right)\right),$$

(12)

$$\begin{array}{c}{\left(\rho C_P\right)}_{thnf}\left(\frac{\partial \overline{T}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{T}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{T}}{\partial \overline{Y}}\right)=\hfill \\ k_{thnf}\left(\frac{{\partial }^2\overline{T}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{T}}{\partial {\overline{Y}}^2}\right)+{\overline{S}}_{XX}\frac{\partial \overline{U}}{\partial \overline{X}}+{\overline{S}}_{XY}\left(\frac{\partial \overline{U}}{\partial \overline{Y}}+\frac{\partial \overline{V}}{\partial \overline{X}}\right)+{\overline{S}}_{YY}\frac{\partial \overline{V}}{\partial \overline{Y}}-\left(\frac{\partial {\overline{q}}_r}{\partial \overline{X}}+\frac{\partial {\overline{q}}_r}{\partial \overline{Y}}\right)\hfill \\ +{\sigma }_{thnf}{B}_0^2\cos \left(\chi \right)\left({\overline{U}}^{ 2}\cos \left(\chi \right)-{\overline{V}}^{ 2}\sin \left(\chi \right)\right),\hfill \end{array}$$

(13)

where $\overline{U}$ and $\overline{V}$ correspond to the velocity components in the direction of $\overline{X}$ and $\overline{Y}$-axes, $\overline{P}$ denotes the trihybrid nanofluid pressure, and $\overline{T}$ is the fluid temperature.

All surfaces above 0 °C emit thermal radiation. According to Stefan–Boltzmann law, the thermal energy radiated per unit area from a blackbody is directly proportional to the fourth power of its temperature, with a constant of proportionality σ*, called the Stefan–Boltzmann constant. For a media that is optically thick for all wavelengths, one may use the Rosseland approximation [49,50], which gives the net radiation heat flux ${\overline{q}}_r$ [Wm⁻²] as

$${\overline{q}}_r=\frac{-4{\sigma }^{*}}{3K^{*}}\frac{\partial {\overline{T}}^4}{\partial \overline{Y}},$$

(14)

in which K* and σ* correspond to the absorption coefficient and the Stefan-Boltzmann constant, respectively. In modelling Equation (14), the magnitude of radiative heat flux is considered as insignificant along wave propagation direction $\overline{X}$ compared to its normal direction $\overline{Y}$. The Taylor series opening of $\overline{T}$⁴ about the temperature difference (∆T) in the occurrence of insignificant temperature gradient in the symmetric channel is written as ${\overline{T}}^4\cong 4\overline{T}$ (∆T)³ − 3(∆T)⁴. Consequently, Equation (14) leads to

$${\overline{q}}_r=\frac{-16{\sigma }^{*}{\left(\Delta \mathrm{T}\right)}^3}{3K^{*}}\frac{\partial \overline{T}}{\partial \overline{Y}}.$$

(15)

2.3. Thermophysical Features of Trihybrid Nanofluid (TiO₂-SiO₂-Al₂O₃/Blood)

It is deemed that the blood-based trihybrid nanofluid is a diluted colloidal mixture of trihybrid nanoparticles of Titania (TiO₂), Silox (SiO₂), and Alumina (Al₂O₃) mixed thoroughly in a base liquid, assumed to be pure blood. Titanium dioxide is an alkaline and highly corrosion-resistant coolant agent. It is harmless and is suitable for medical uses. Furthermore, silica and alumina are considered owing to their non-reactive nature and thermodynamical stability, respectively. At the reference temperature 25 °C, the numerical values of thermophysical properties for the trihybrid nanofluid are shown in

Table 1. Thermophysical properties of the blood-based trimetallic nanofluid [38,39,40].

Physical Entities	Base Fluid		Solid Nanogranules
	(Blood)	TiO2	SiO2	Al2O3
ρ (kgm−3)	1063	4250	2200	3970
σ (1/Ωm)	0.8	2.4 × 106	3.5 × 106	36.9 × 106
Cp (JK−1kg−1)	3594	686.2	754	765
k (Wm−1K−1)	0.492	8.9538	1.4013	40

.

The mathematical equations explaining the thermophysical properties of ternary fluids are quantified as [38,39]

$${\rho }_{thnf}=\left(1-{\varphi }_1\right)\left[\left(1-{\varphi }_2\right)\left\{\left(1-{\varphi }_3\right){\rho }_f+{\varphi }_3{\rho }_3\right\}+{\varphi }_2{\rho }_2\right]+{\varphi }_1{\rho }_1,$$

(16)

$${\left(\rho C_p\right)}_{thnf}=\left(1-{\varphi }_1-{\varphi }_2-{\varphi }_3\right){\left(\rho C_p\right)}_f+{\varphi }_1{\left(\rho C_p\right)}_1+{\varphi }_2{\left(\rho C_p\right)}_2+{\varphi }_3{\left(\rho C_p\right)}_3.$$

(17)

The effective electrical and thermal conductivities of ternary fluid (σ_thnf, and k_thnf) can be expressed, respectively, as [40]

$$\frac{{\sigma }_{thnf}}{{\sigma }_f}=\frac{\left(1+2{\varphi }_1\right){\sigma }_1+\left(1-2{\varphi }_1\right){\sigma }_{hnf}}{\left(1-{\varphi }_1\right){\sigma }_1+\left(1+{\varphi }_1\right){\sigma }_{hnf}},$$

(18)

with $\frac{{\sigma }_{hnf}}{{\sigma }_{nf}}=\frac{\left(1+2{\varphi }_2\right){\sigma }_2+\left(1-2{\varphi }_2\right){\sigma }_{nf}}{\left(1-{\varphi }_2\right){\sigma }_2+\left(1+{\varphi }_2\right){\sigma }_{nf}}$ and $\frac{{\sigma }_{nf}}{{\sigma }_f}=\frac{\left(1+2{\varphi }_3\right){\sigma }_3+\left(1-2{\varphi }_3\right){\sigma }_f}{\left(1-{\varphi }_3\right){\sigma }_3+\left(1+{\varphi }_3\right){\sigma }_f};$

$$\frac{k_{thnf}}{k_{hnf}}=\frac{k_1+2k_{hnf}-2{\varphi }_1\left(k_{hnf}-k_1\right)}{k_1+2k_{hnf}+{\varphi }_1\left(k_{hnf}-k_1\right)},$$

(19)

with $\frac{k_{hnf}}{k_{nf}}=\frac{k_2+2k_{nf}-2{\varphi }_2\left(k_{nf}-k_2\right)}{k_2+2k_{nf}+{\varphi }_2\left(k_{nf}-k_2\right)}$ and $\frac{k_{nf}}{k_f}=\frac{k_3+2k_f-2{\varphi }_3\left(k_f-k_3\right)}{k_3+2k_f+{\varphi }_3\left(k_f-k_3\right)}$; and the effective viscosity is given by

$$\frac{{\mu }_{thnf}}{{\mu }_f}=\frac{1}{{\left(1-{\varphi }_1\right)}^{5/2}{\left(1-{\varphi }_2\right)}^{5/2}{\left(1-{\varphi }_3\right)}^{5/2}},$$

(20)

where the subscripts 1, 2, and 3 correspond to the characteristics connected with nanoparticles of titanium oxide, silica, and Aluminum oxide, respectively. The alphabetical subscripts thnf, hnf, nf, and f correspondingly allude to the properties associated with trihybrid, bi-hybrid, mono nanofluid, and pure blood. The symbols ρ, ρC_p, σ, k, µ, and ϕ are used for the density, the effective heat capacity, the electrical conductivity, the thermal conductivity, the viscosity, and volume fraction of metallic nanogranules

2.4. Governing Equations in Wave Frame

The transformation between the laboratory frame and moving frame are described by the following equations:

$$\overline{x}=\overline{X}-c\overline{t}, \overline{y}=\overline{Y}, \overline{p}\left(\overline{x},\overline{y}\right)=\overline{P}\left(\overline{X},\overline{Y},\overline{t}\right), \overline{u}\left(\overline{x},\overline{y}\right)=\overline{U}\left(\overline{X},\overline{Y},\overline{t}\right)-c, \overline{v}\left(\overline{x},\overline{y}\right)=\overline{V}\left(\overline{X},\overline{Y},\overline{t}\right).$$

(21)

Subsequently, we can establish the following non-dimensional quantities to nondimensionalize the governing equations:

$$\begin{array}{c}x=\frac{\overline{x}}{\lambda }, y=\frac{\overline{y}}{a}, t=\frac{c\overline{t}}{a}, u=\frac{\overline{u}}{c}, v=\frac{\overline{v}}{\beta c}, p=\frac{\overline{p}{a}^2}{{\mu }_{f}c\lambda }, \\ \theta =\frac{\overline{T}-T_0}{T_1-T_0}, \beta =\frac{a}{\lambda }, S=\frac{\overline{S}a}{{\mu }_{f}c}, H=\frac{\overline{H}}{a}, \mathrm{Re}=\frac{{\rho }_{f}ac}{{\mu }_f}, \end{array}\}$$

(22)

We describe the stream function (Ψ) as

$$u=\frac{\partial \mathsf{\Psi }}{\partial y}, v=-\frac{\partial \mathsf{\Psi }}{\partial x},$$

(23)

Then, utilizing Equations (21)–(23) into Equations (10)–(13) and (15) and employing (β ≪ 1) and the small Reynolds number (Re ≈ 0) approximations, the dimensionless forms of the governing equations can be expressed as

$$\frac{\partial p}{\partial x}=\frac{{\mu }_{thnf}}{{\mu }_f}\left[\left(1-n\right)\frac{{\partial }^3\mathsf{\Psi }}{\partial y^3}+\frac{n\mathrm{We}}{2}\frac{\partial }{\partial y}\left\{{\left(\frac{{\partial }^2\mathsf{\Psi }}{\partial y^2}\right)}^2\right\}\right]-\frac{{\sigma }_{thnf}}{{\sigma }_f}{\mathrm{Ha}}^2{\cos }^2\left(\chi \right)\left(\frac{\partial \mathsf{\Psi }}{\partial y}+1\right),$$

(24)

$$\frac{\partial p}{\partial y}=0,$$

(25)

$$\begin{gathered} \left(\frac{k_{thnf}}{k_f}+R_n\right)\frac{{\partial }^2\theta }{\partial y^2}+\frac{{\mu }_{thnf}}{{\mu }_f}\mathrm{EcPr}\left[\left(1-n\right){\left(\frac{{\partial }^2\mathsf{\Psi }}{\partial y^2}\right)}^2+n\mathrm{We}{\left(\frac{{\partial }^2\mathsf{\Psi }}{\partial y^2}\right)}^3\right] \\ +\frac{{\sigma }_{thnf}}{{\sigma }_f}{\mathrm{PrEcHa}}^2{\cos }^2\left(\chi \right){\left(\frac{\partial \mathsf{\Psi }}{\partial y}+1\right)}^2=0. \end{gathered}$$

(26)

The cross-differentiation of Equations (24) and (25) takes the form of

$$\frac{{\mu }_{thnf}}{{\mu }_f}\left[\left(1-n\right)\frac{{\partial }^4\mathsf{\Psi }}{\partial y^4}+n\mathrm{We}\frac{{\partial }^2}{\partial y^2}\left\{{\left(\frac{{\partial }^2\mathsf{\Psi }}{\partial y^2}\right)}^2\right\}\right]+\frac{{\sigma }_{thnf}}{{\sigma }_f}{\mathrm{Ha}}^2{\cos }^2\left(\chi \right)\frac{{\partial }^2\mathsf{\Psi }}{\partial y^2}=0.$$

(27)

The corresponding boundary conditions are written as

$$\begin{array}{c}\mathsf{\Psi }=0,\frac{{\partial }^2\mathsf{\Psi }}{\partial y^2}=0,\frac{\partial \theta }{\partial y}=0,\frac{\partial \mathsf{\Phi }}{\partial y}=0,\mathrm{at}y=0,\\ \mathsf{\Psi }=\mathrm{F}, \frac{\partial \mathsf{\Psi }}{\partial y}=-1-\frac{2\pi \alpha \epsilon \beta \cos (2\pi x)}{1-2\pi \alpha \epsilon \beta \cos \left(2\pi x\right)}, \theta =1\mathrm{at}y=H,\end{array}\}$$

(28)

where Ha, We, Pr, Ec, and R_n are the Hartmann number, the Weissenberg number, the Prandtl number, the Eckert number, and the thermal radiation parameter, which are, respectively, defined as

$$\mathrm{Ha}=\sqrt{\frac{{\sigma }_f}{{\mu }_f}}{B}_{0}a, \mathrm{We}=\frac{\mathsf{\Gamma }c}{a}, \mathrm{Pr}=\frac{{\mu }_f{C}_P}{k_f}, \mathrm{Ec}=\frac{c^2}{C_P\Delta T}, {\mathrm{R}}_{\mathrm{n}}=\frac{16{\sigma }^{*}{\left(\Delta T\right)}^3}{3{\mu }_f{C}_P{K}^{*}}.$$

(29)

The inter-transformation for the dimensionless mean flow rate for the laboratory (Q) and the wave (F) settings can be written as

$$Q=1+F, \mathrm{where}F={{\displaystyle \int }}_0^H\left(\frac{\partial \mathsf{\Psi }}{\partial y}\right)dy.$$

(30)

2.5. Entropy Analysis

In the ciliated micropump, the essential components to generate entropy are heat transfer effects due to radiation and convection, fluid friction, and magnetic field. Hence, the entropy production equation for the proposed flow from the perspective of the second law of thermodynamics can be expressed as [44,45,46,47]

$$S_{gen}^{\prime \prime \prime }=\frac{1}{T_0^2}\left[k_{thnf}{\left(\nabla \overline{T}\right)}^2+\frac{16{\sigma }^{*}{\left(T_1-T_0\right)}^3}{3K^{*}}{\left(\nabla \overline{T}\right)}^2\right]+\frac{{\mu }_{thnf}}{T_0}\left[S·\nabla V\right]+\frac{{\sigma }_{thnf}}{T_0}{B}_0^2\cos \left(\chi \right)\left({\overline{U}}^{ 2}\cos \left(\chi \right)-{\overline{V}}^{ 2}\sin \left(\chi \right)\right).$$

(31)

Utilizing Equations (21) and (22) in Equation (31) and dividing by characteristic entropy S_G0 deliver the total entropy number N_S as

$$N_S=\underset{N_H}{\underbrace{\left(\frac{k_{thnf}}{k_f}+\frac{R_n}{\mathrm{Pr}}\right){\left(\frac{\partial \theta }{\partial y}\right)}^2}}+\underset{N_F}{\underbrace{\frac{{\mu }_{thnf}}{{\mu }_f}\frac{\mathrm{PrEc}}{\tau }\left[\left(1-n\right){\left(\frac{{\partial }^2\mathsf{\Psi }}{\partial y^2}\right)}^2+n\mathrm{We}{\left(\frac{{\partial }^2\mathsf{\Psi }}{\partial y^2}\right)}^3\right]}}+\underset{N_J}{\underbrace{\frac{{\sigma }_{thnf}}{{\sigma }_f}{\mathrm{PrEcHa}}^2{\left(\frac{\partial \mathsf{\Psi }}{\partial y}+1\right)}^2}}.$$

(32)

In Equation (32), the very first term ($N_H$) describes the heat transfer irreversibility owing to convection and radiation impacts, the second part ($N_F$) occurs owing to fluid friction irreversibility, and the last factor ($N_J$) depicts the entropy production because of the magnetic field. Furthermore, the dimensionless parameter τ (=∆T/T₀) is maintained as one.

The Bejan number for the present entropy generation number is identified as

$$\mathrm{Be}=\frac{N_H}{N_H+N_F+N_J}.$$

(33)

In the context of thermodynamics, the Bejan number belongs to [0, 1] and differentiates the heat transfer irreversibility and the system overall irreversibilities due to other reasons. The values of Be over 0.5 indicate substantial effects of heat transfer irreversibility over the total irreversibility of the flow system. The values of Be below 0.5 indicate domination of the system’s collective irreversibility due to the other sources such as fluid friction and magnetic field.

3. Solution of the Problem

The Numerical solution of Equations (24)–(27), with the help of the boundary conditions stated in Equation (28), were computed via the shooting method with the help of computational software Mathematica. The built-in numerical package “NDSolve” was utilized, in which the shooting method was called on. To validate the numerical results, we have calculated the analytical solutions by perturbation technique assuming We ≪ 1 as the perturbation parameter. The Taylor series expansion of dependent variables (Ψ and θ) are expanded as

$$\mathsf{\Psi }={\mathsf{\Psi }}_0+{\mathrm{We}\mathsf{\Psi }}_1+\mathrm{O}\left({\mathrm{We}}^2\right),$$

(34)

$$\mathsf{\theta }={\mathsf{\theta }}_0+{\mathrm{We}\mathsf{\theta }}_1+\mathrm{O}\left({\mathrm{We}}^2\right),$$

(35)

Ignoring the second- and higher-order terms, Equations (34) and (35) result in a coupled linear differential equation of zero and first orders. These linear differential equations can be solved exactly by the “DSolve” command of the software Mathematica. A comparison of results by numerical and analytical methods has been provided in

Table 2. The comparison of numerical values of axial velocity distribution (u(y)) near the pump center when We = 0.001, ε = 0.25, and n = 0.2.

Ha	Perturbation Solution	Numerical Solution
0.5	2.31025	2.31118
1	2.25681	2.28942
1.5	2.21310	2.25518
2	2.10603	2.21105
2.5	2.04358	2.16001

for the velocity profile. The table depicts good agreement between analytical and numerical results, which provides confidence on the legitimacy of the present solution.

4. Computational Results and Discussion

This section intends to interpret the graphical illustrations of the numerical results of the velocity profile (u), the streamline function (Ψ), pressure gradient (dp/dx), pressure rise per wavelength (Δp), the temperature distribution (θ), the entropy formation number (N_S), and the Bejan number (Be) for the trihybrid nanofluid. Different graphs for various values of the applicable parameters of interest are provided through Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. In the entire evaluation, the net volumetric proportion of metallic nanogranules, ϕ (=ϕ₁ + ϕ₂ + ϕ₃) scattered in the traditional base fluid is assumed as 3%. Therefore, the blood-based trihybrid nanofluid is deemed to be obtained by combining 1% fraction of each kind of metallic nanogranule (such as titanium dioxide, silicon dioxide, and alumina) in the hyperbolic tangent nanofluid. Since the current parametric study was conducted for pertinent parameters of interest, some of the parameters are assigned with fixed values, such as Ec = n = 0.2, α = 0.3, β = 0.006, and χ = π/3

4.1. Flow and Pumping Characteristics

To investigate the impact of the Weissenberg number (We) and the Hartmann number (Ha) on velocity distribution u(y) of the trihybrid nanofluid, Figure 2a,b is displayed. Near the pump core region, slight variations in fluid velocity are cited with respect to the Weissenberg number (We). Meanwhile, around the pump surface, effects of We on axial velocity are insignificant, as depicted through Figure 2a,b, which shows that close to the pump center, an impediment in trihybrid nanofluid flow is associated with large values of the Hartmann number (Ha). This dampening act of magnetic field on the fluid motion is predictable owing to the occurrence of electromotive force induced by the magnetic force. However, around the pump wall, an acceleration in fluid flow is seen for strong magnetic effects.

Figure 2. Alterations in the axial velocity distribution for distinct values of (a)Weissenberg number (We) and (b) the Hartmann number (Ha) at fixed values of ε = 0.2 and x = 0.6.

Figure 2. Alterations in the axial velocity distribution for distinct values of (a)Weissenberg number (We) and (b) the Hartmann number (Ha) at fixed values of ε = 0.2 and x = 0.6.

Figure 3a–c, respectively, demonstrates the variations in pressure gradient dp/dx versus axial distance x for different values of the Weissenberg number (We), the Hartmann number (Ha), and the cilia length parameter (ε). Figure 3a reveals that an augmentation in pressure gradient is viewed throughout the pump length for large values of the Weissenberg number (We). It is further observed that in the proximity of the pump deep zone, an appropriately elevated pressure gradient is needed to balance the same flux. A substantial decline in pressure gradient is observed throughout the channel when large values of the Hartmann number (Ha) are considered, as portrayed in Figure 3b. However, a significantly elevated pressure gradient is expected to maintain a similar flux in the pump narrow part. The precise length of cilia is required to commence desirable synchronization. Thus, the extended cilia communicate more profoundly than the shorter cilia. Consequently, the high values of cilia length induce an escalation in pressure gradient in the pump deep part, as revealed in Figure 3c.

Figure 3. Alterations in the pressure gradient profile for distinct values of (a) Weissenberg number (We), (b) Hartmann number (Ha), and (c) cilia length parameter (ε).

Figure 3. Alterations in the pressure gradient profile for distinct values of (a) Weissenberg number (We), (b) Hartmann number (Ha), and (c) cilia length parameter (ε).

In Figure 4a–c, the effects of the Weissenberg number (We), the Hartmann number (Ha), and the cilia length parameter (ε) on pressure rise per metachronal wavelength Δp are respectively plotted. Figure 4a exposes that in the ciliary pumping zone (Δp > 0), the high values of the Weissenberg number (We) induce an augmentation in Δp. In the meanwhile, in the augmented pumping zone (Δp < 0), the impact of We on Δp is observed to be reversed entirely. Figure 4b determines that for the large values of the Hartmann number (Ha), Δp enhances in the augmented pumping zone (Δp < 0) and decreases in the pumping region (Δp > 0). Further, in the free pumping zone (Δp = 0), effects of Ha on Δp are trivial. Figure 4c indicates that the prolonged cilia, respectively, generate an enrichment and deterioration in Δp in both the pumping (Δp > 0) and the augmented pumping zones (Δp < 0).

Figure 4. Alterations in pressure rise per metachronal wavelength for distinct values of (a) Weissenberg number (We), (b) Hartmann number (Ha), and (c) cilia length parameter (ε).

Figure 4. Alterations in pressure rise per metachronal wavelength for distinct values of (a) Weissenberg number (We), (b) Hartmann number (Ha), and (c) cilia length parameter (ε).

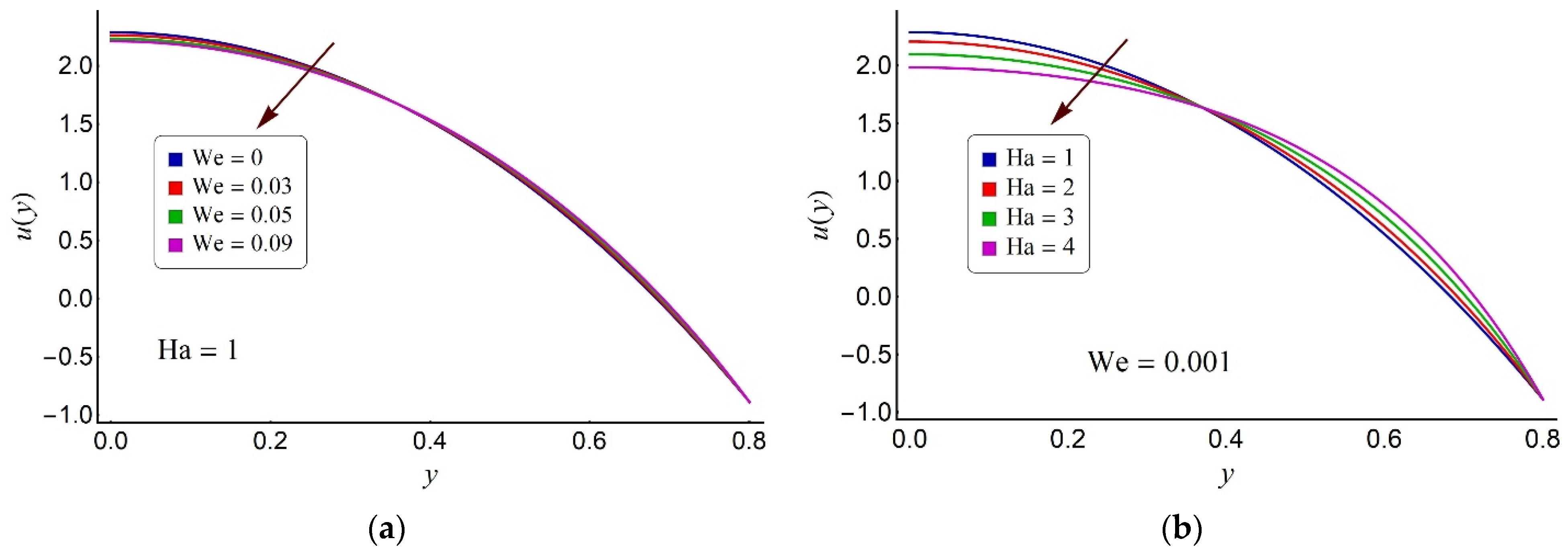
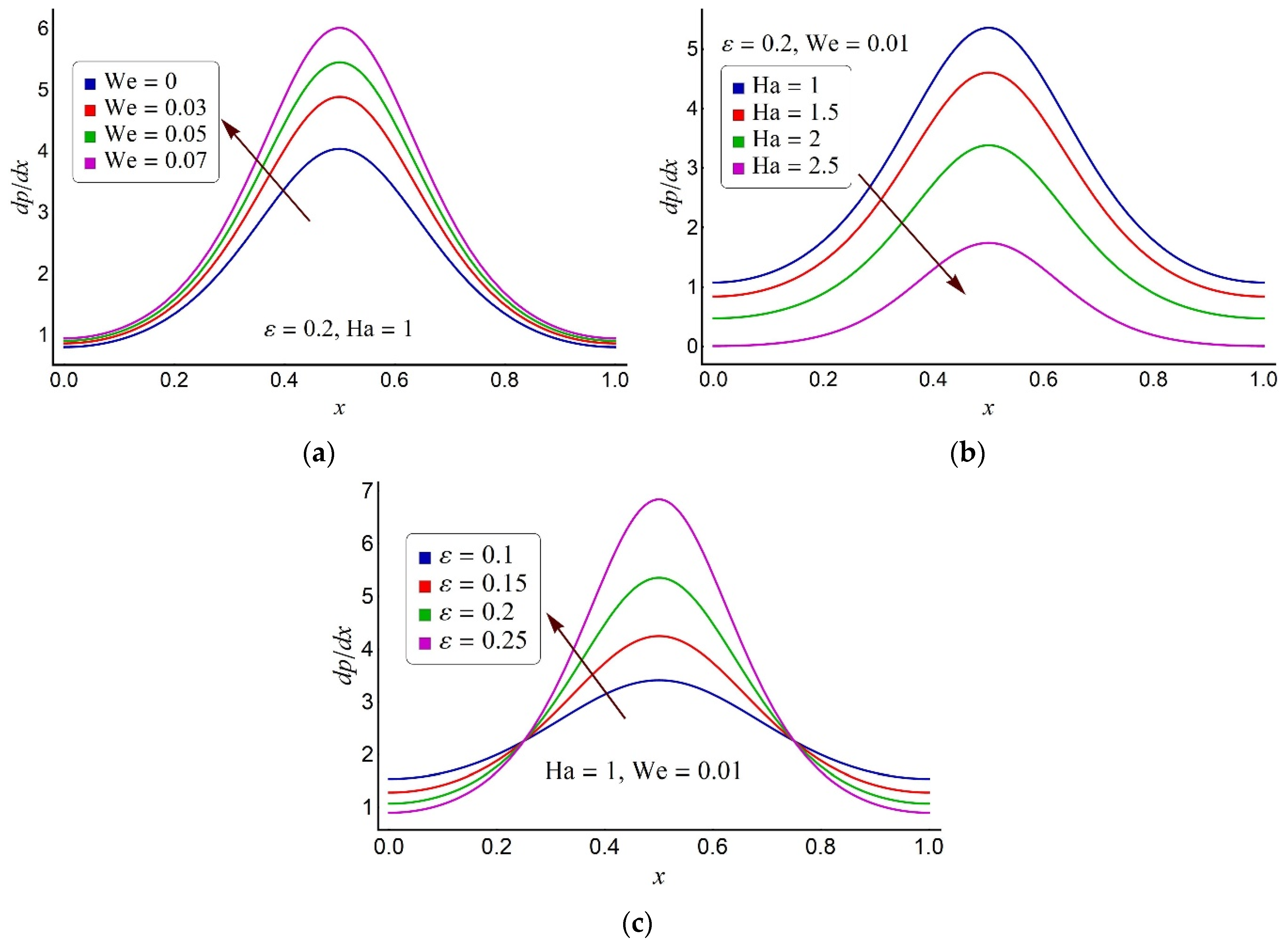
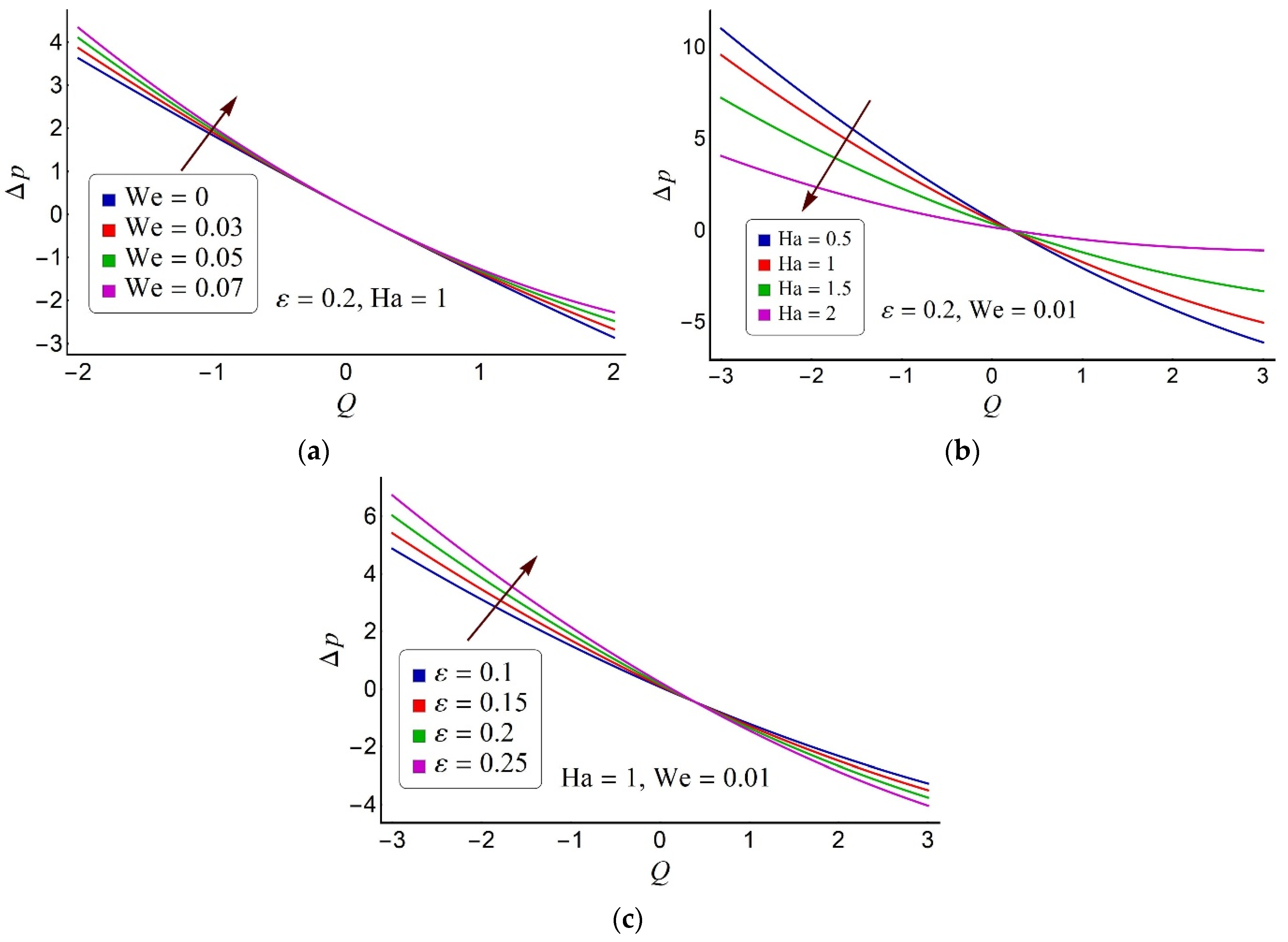
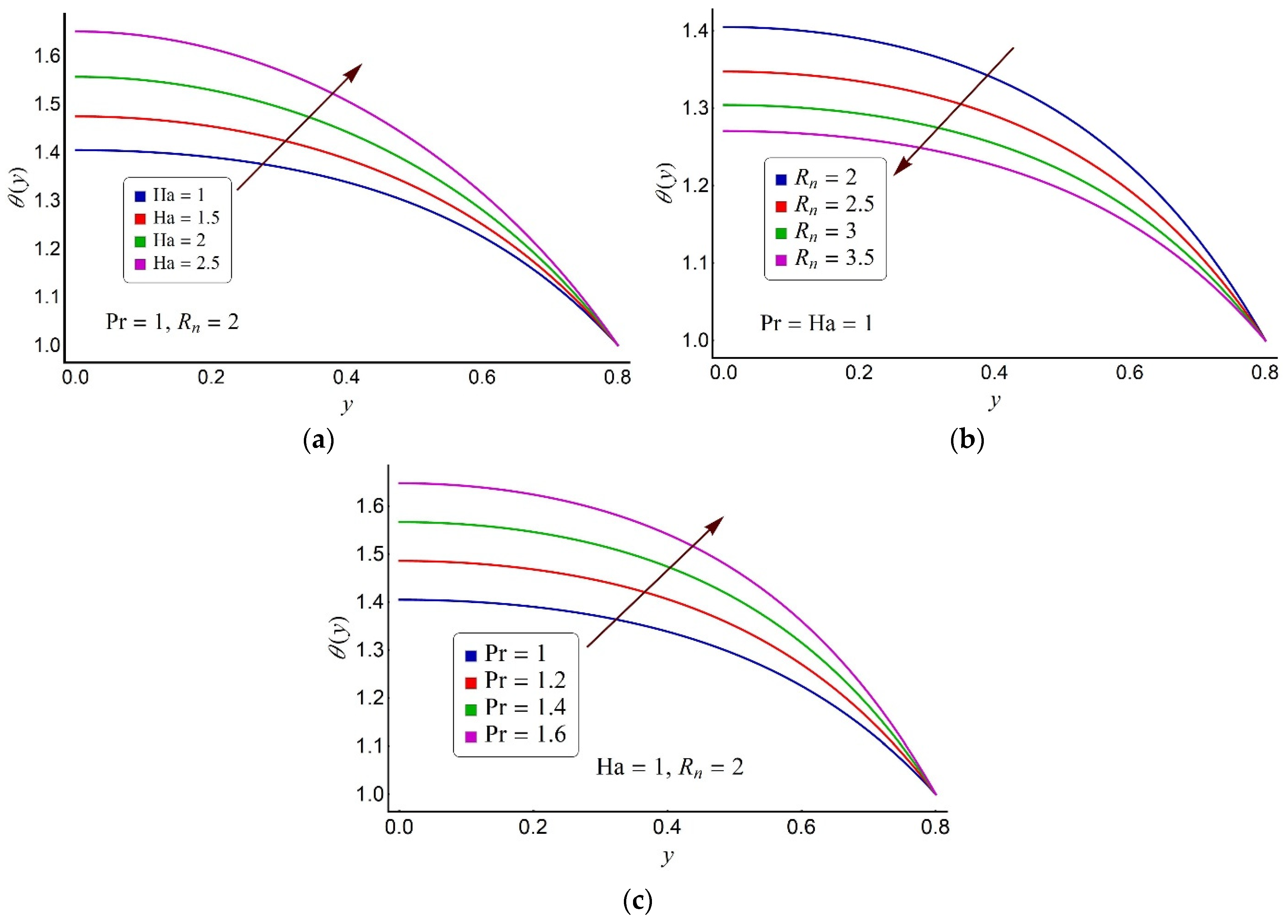
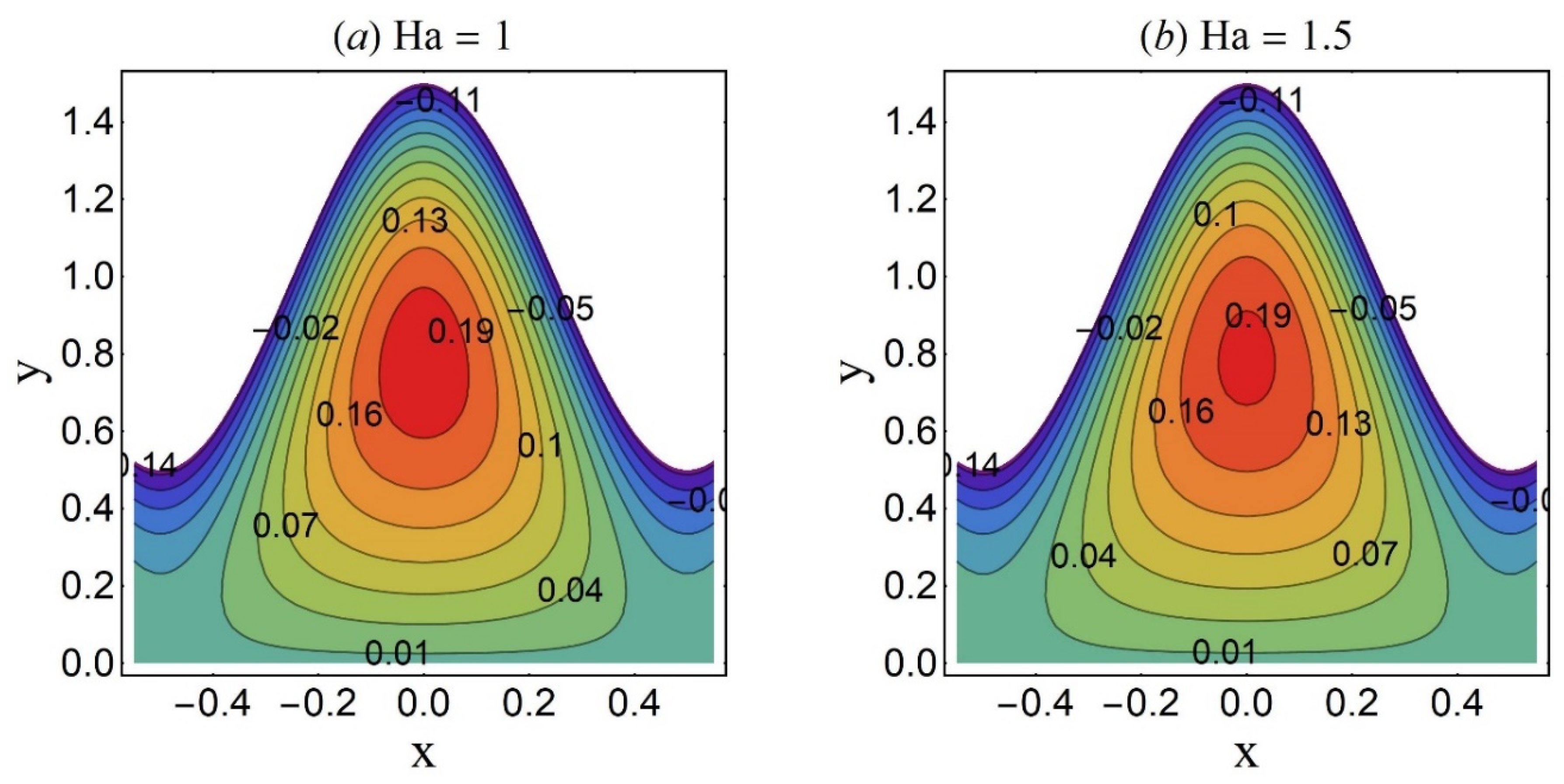
4.2. Thermal Characteristics of the Ternary Fluid

Figure 5a–c portrays the fluctuations in the temperature distribution of trihybrid nanofluid for the altered values of the Hartmann number (Ha), the thermal radiation number (R_n), and the Prandtl number (Pr). Figure 5a shows that the lofty values of the Hartmann number (Ha) engender an enrichment in ternary nanofluid temperature because of significant convection. This rise in temperature is more pronounced across the pump center than its peripheral area. Figure 5b demonstrates that the elevated values of the thermal radiation number (R_n) retain the capability to substantially drop the medium temperature. This assertion is elaborated since the converse relation between thermal radiation and heat conduction stimulates a cooling process in the medium by dropping the liquid temperature down. Consequently, the radiated nanofluid might be acknowledged as a more expedient cooling agent than the traditional fluid. Figure 5c investigates the consequence of the Prandtl number (Pr) on fluid temperature. In thermal flows, the Prandtl number monitors the comparative of consequence of momentum diffusive rate to the thermal diffusive rate. Small values of Pr indicate that the heat diffuses swiftly compared to velocity dispersion. The higher values of Pr indicate the rapid dispersion of momentum rather than heat. Therefore, a considerable increment in liquid temperature is seen for substantial values of Pr.

Figure 5. Alterations in temperature profile for various values of (a) the Hartmann number (Ha), (b) the thermal radiation number (R_n), and (c) the Prandtl number (Pr).

Figure 5. Alterations in temperature profile for various values of (a) the Hartmann number (Ha), (b) the thermal radiation number (R_n), and (c) the Prandtl number (Pr).

The degree of randomness and disarray in the system is characterized as entropy of the system. To accomplish enhanced proficiency for a thermal flow, heat losses should be reduced to the maximum extent. To discuss the variations in the entropy generation number N_s, Figure 6a–c is exhibited. Figure 6a determines that the elevated values of the Hartman number (Ha) lead to an enlargement in entropy formation near the pump boundary. Around the pump center, the alterations in entropy generation number are minimal. This fact can be confirmed from

Table 3. The heat transfer rate for blood, mono nanofluid, hybrid nanofluid, and tri-hybrid nanofluid at fixed values of Ec = 0.1, Pr = 1, and R_n = 1.

Ha	Blood	Mono Nanofluid	% Increase	Bi-Hybrid Nanofluid	% Increase	Ternary Nanofluid	% Increase
0.5	0.87458	0.92805	6.11	0.97141	11.07	1.03398	18.23
1	1.03909	1.10407	6.25	1.15685	11.33	1.21239	16.68
1.5	1.31190	1.39597	6.41	1.46436	11.62	1.50839	14.98
2	1.69127	1.80186	6.54	1.89194	11.86	1.92020	13.54
2.5	2.17514	2.31953	6.64	2.43729	12.05	2.44572	12.45

, which exhibits the comparative glimpse of heat transfer rate in ternary/binary/mono nanofluid and traditional blood for different values of Ha. From Table 3, it is noticed that around the pump surface, the heat transfer rate enhances for large values of Ha. At the same value of Ha, the heat transfer rate is maximum for the trihybrid nanofluid and minimum for blood model. For instance, at Ha = 0.5, the heat transfer rate is lifted to 6.11% for mono nanofluid, 11.07% for hybrid nanofluid, and 18.23% for trihybrid nanofluid compared to pure blood. Figure 6b communicates that the loft values of the thermal radiation number (R_n) curtail entropy generation around the peripheral zone of the micropump, whereas the effects of R_n near the pump center are negligible. Thus, it can be reported that the radiated ternary nanofluid may be considered as an important factor for the better the functioning of thermal system. Figure 6c conveys that the overall entropy production inside the micropump amplifies for large values of Pr.

Figure 6. Variations in entropy generation number distribution for different values of (a) the Hartmann number (Ha), (b) the thermal radiation number (R_n), and (c) the Prandtl number (Pr).

Figure 6. Variations in entropy generation number distribution for different values of (a) the Hartmann number (Ha), (b) the thermal radiation number (R_n), and (c) the Prandtl number (Pr).

The Bejan number proposes a clear perception about the discrimination in system irreversibilities due to various causes. In thermodynamics, the Bejan number is described as the fraction of irreversibility due to convection and conduction to total irreversibility of the system due to different causes such as fluid friction and magnetic field. The values of the Bejan number Be lie in [0, 1]. Be > 0.5 indicates the dominating effect of heat transfer irreversibility over the system’s overall irreversibility. Be < 0.5 indicates the leading effect of irreversibilities due to fluid friction and magnetic field over the heat transfer irreversibility owing to convection and radiation. Figure 7a shows that a sizeable raise in the Bejan number distribution of the trihybrid nanofluid can be observed for the higher values of Ha. Close to the pump center, the fluid frictional irreversibility leads over the heat transfer irreversibility, whereas around the pump peripheral part heat transfer irreversibility overlooks. Figure 7b shows that the elevated values of the radiation number (R_n) assist the leading effect of overall irreversibility of the system over the heat transfer irreversibility. Figure 7c illuminates that the Bejan number seems to be a boosting function of the Prandtl number (Pr). Near the pump center, the Bejan number moves to zero, which indicates the absence of heat transfer irreversibility effects, but close to the pump wall, the heat transfer effects are appreciable.

Figure 7. Alterations in the Bejan number distribution for distinct values of (a) the Hartmann number (Ha), (b) the thermal radiation number (R_n), and (c) the Prandtl number (Pr).

Figure 7. Alterations in the Bejan number distribution for distinct values of (a) the Hartmann number (Ha), (b) the thermal radiation number (R_n), and (c) the Prandtl number (Pr).

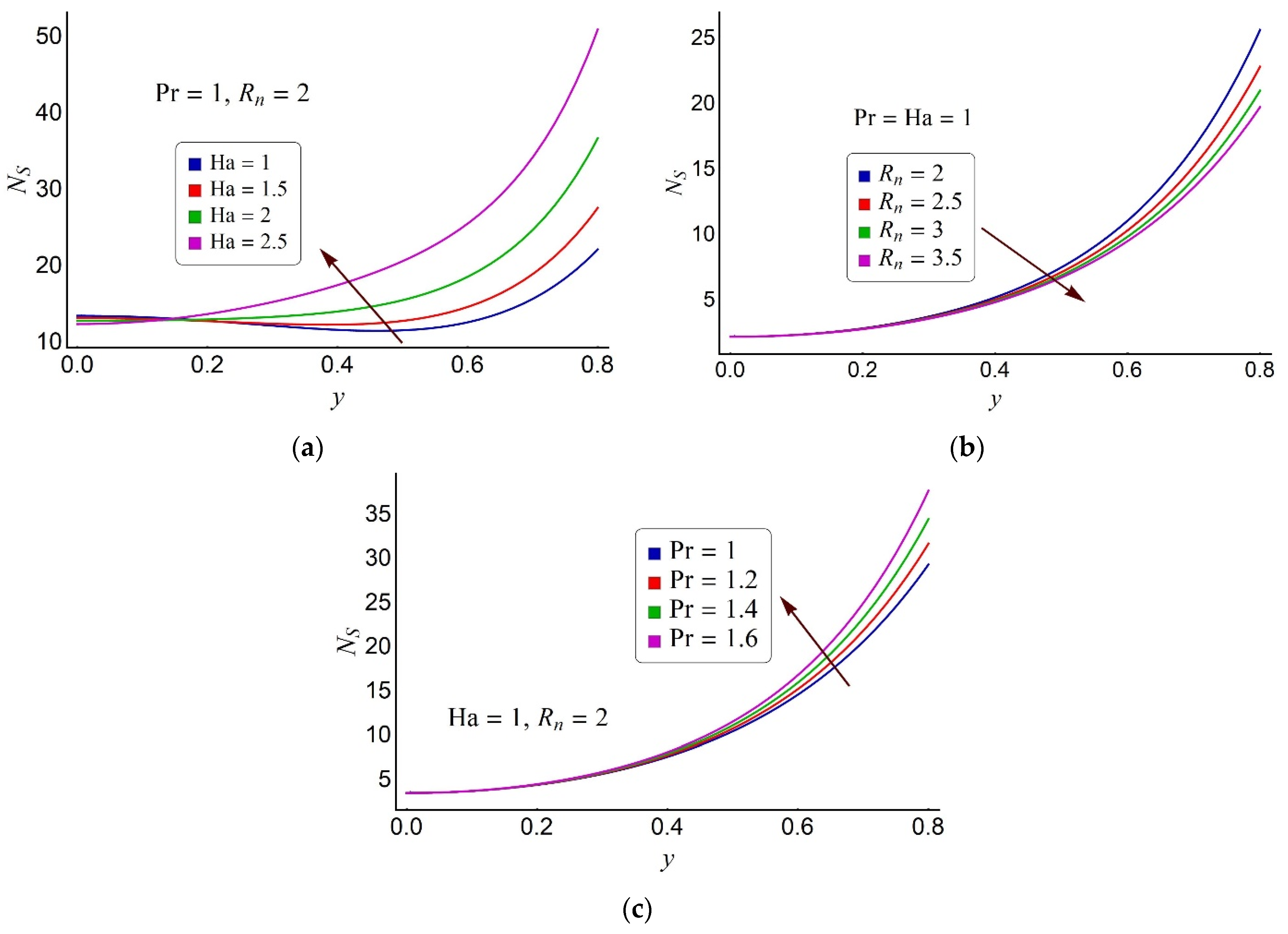
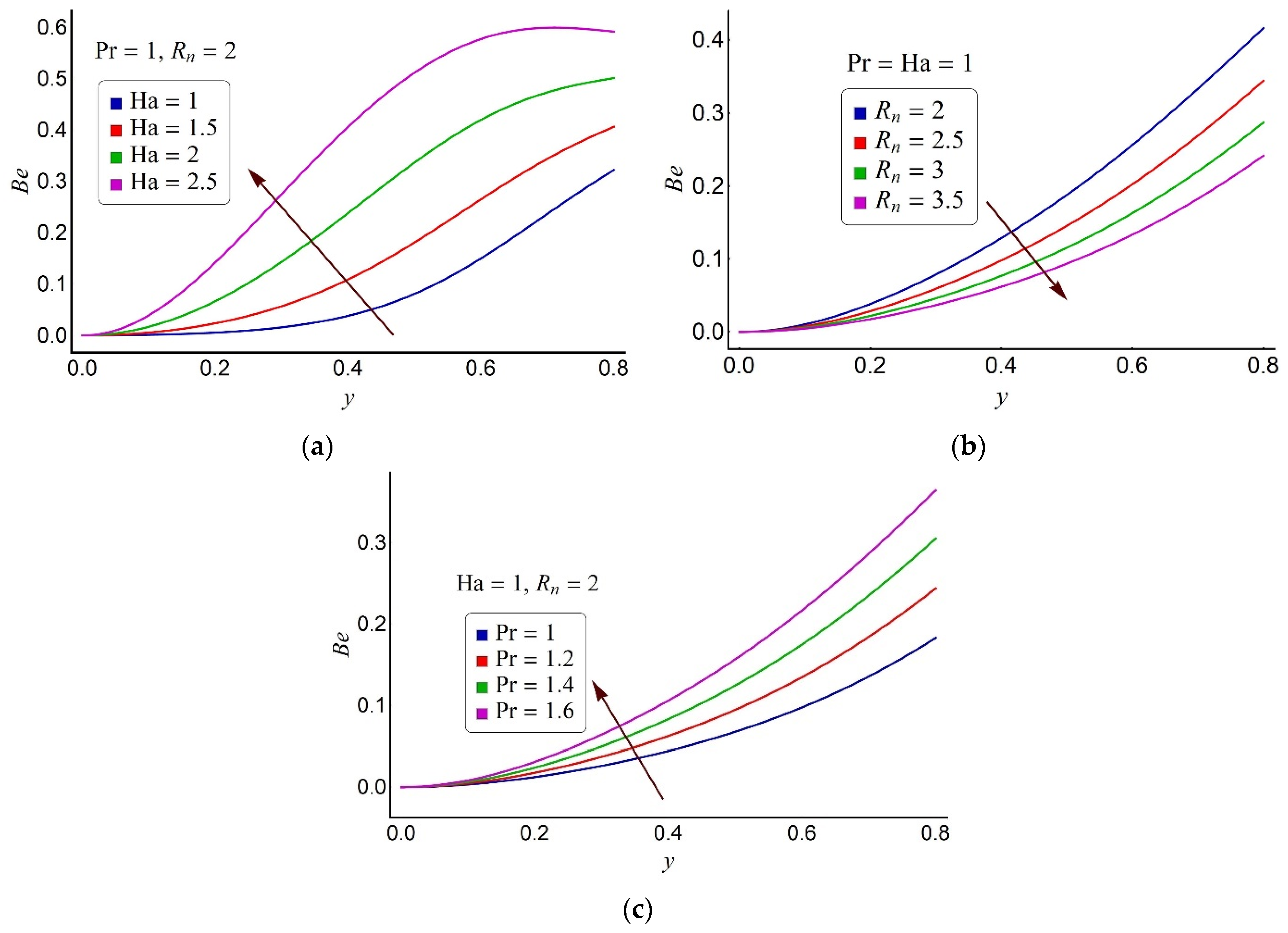
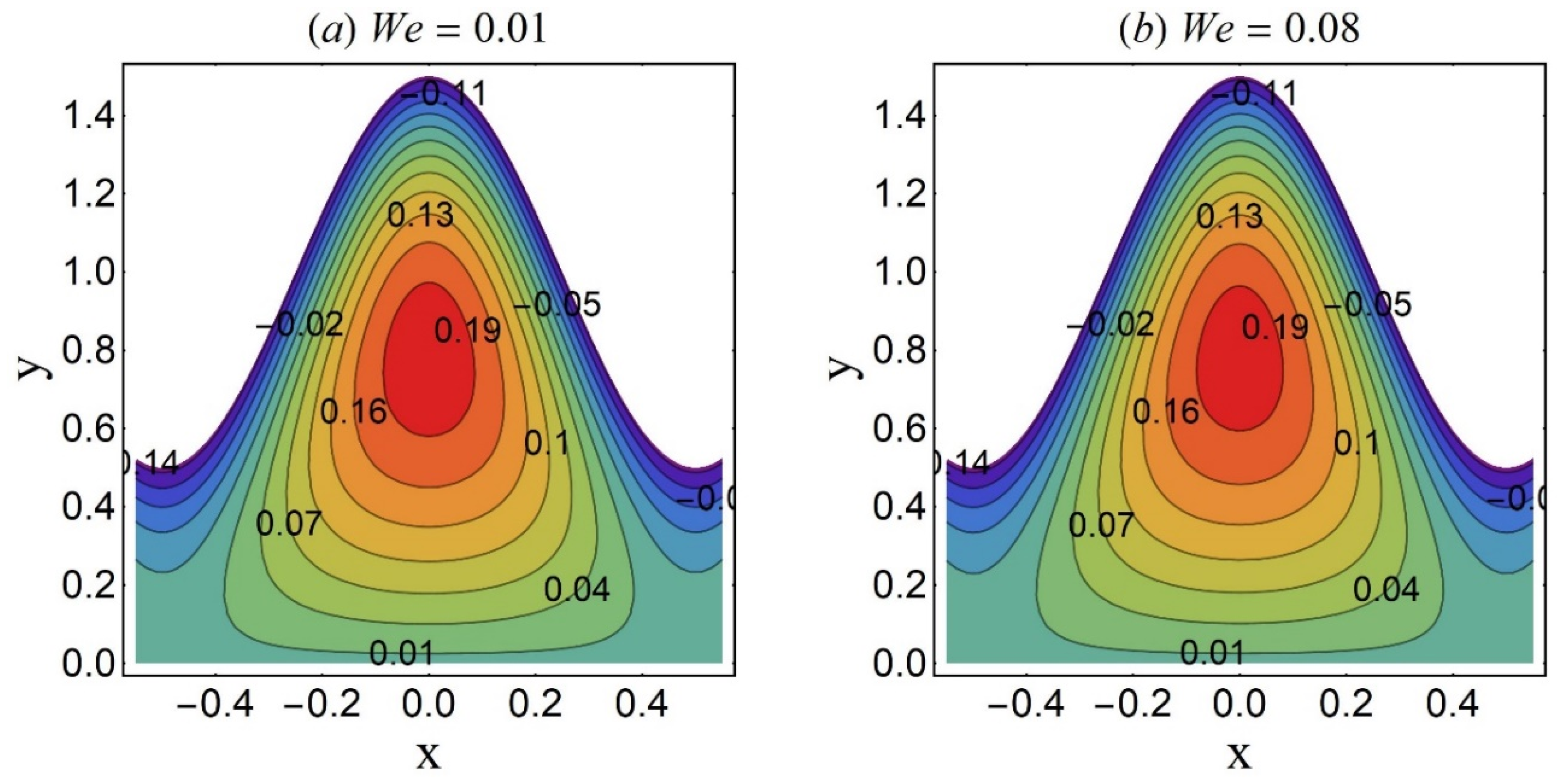
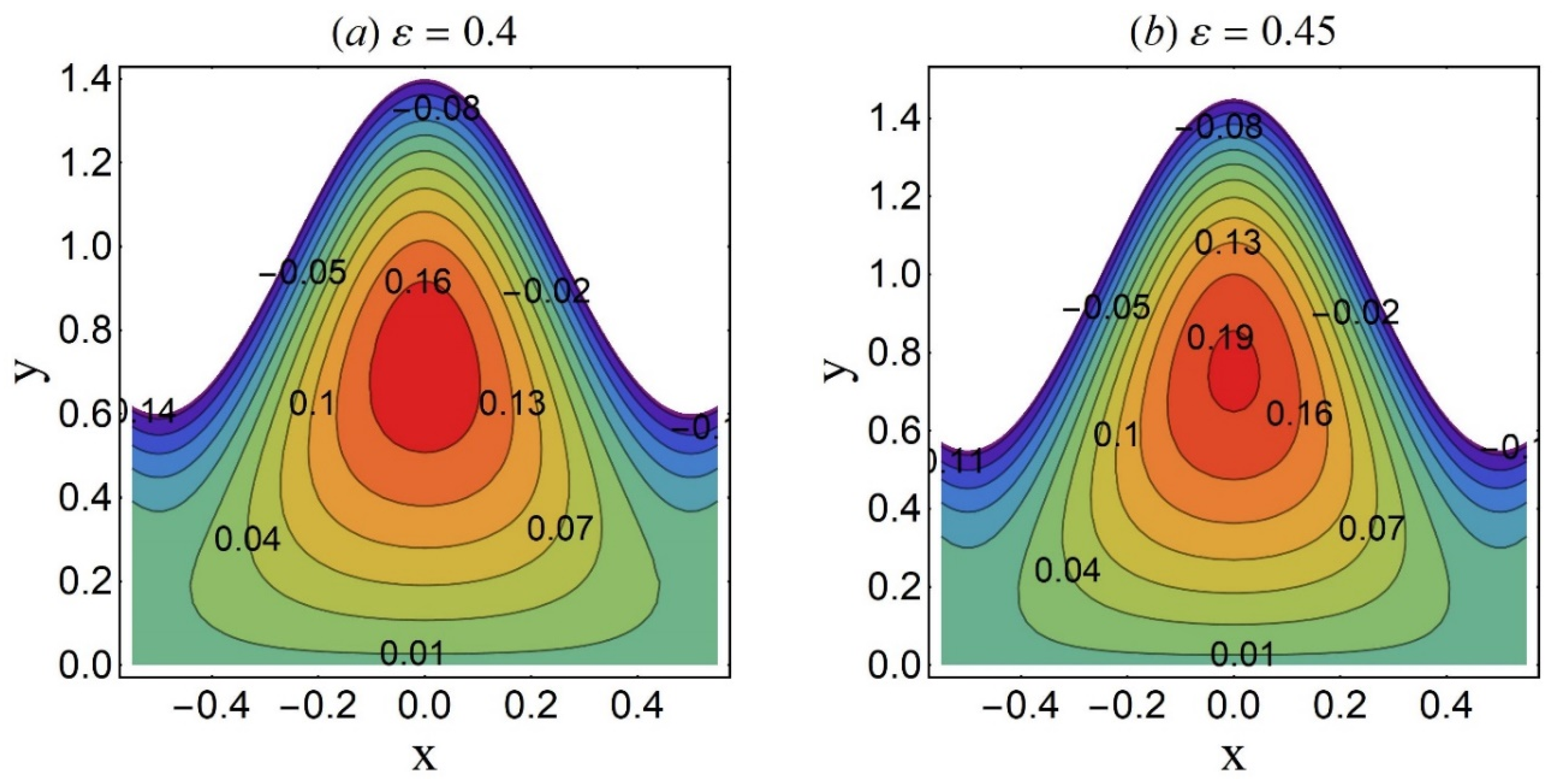
4.3. Streamline Pattern and Trapping Phenomenon

Trapping is regarded as an interesting aspect of pumping ciliary motion. At the sizable amplitude ratio and fixed stream rate, a group of closed streamlines separate to imprison a fluid mass named as trapped bolus that pushes forward with the speed of the metachronal wave. This trend is visualized through Figure 8, Figure 9 and Figure 10 for distinct values of the Weissenberg number (We), the Hartmann number (Ha), and cilia length parameter (ε). Figure 8a,b shows that the restrained bolus shrinks in size when the higher values of We are selected. Figure 9a,b shows that the trapped bolus inflates in size and a new bolus is generated when the large values of ε are taken into consideration. This enhancing trend in bolus size conveys the direct relationship of cilia length with fluid flow rate. Figure 10a,b reports that a significant reduction in bolus size can be observed at increasing values of Ha. This contraction in the imprisoned bolus size occurs because of the resistance of magnetic field to fluid flow rate.

Figure 8. Streamline pattern for (a) We = 0.01 and (b) We = 0.08 at fixed values of Ha = 1 and ε = 0.4.

Figure 8. Streamline pattern for (a) We = 0.01 and (b) We = 0.08 at fixed values of Ha = 1 and ε = 0.4.

Figure 9. Streamline pattern for (a) ε = 0.4 and (b) ε = 0.4 at fixed values of Ha = 1 and We = 0.01.

Figure 9. Streamline pattern for (a) ε = 0.4 and (b) ε = 0.4 at fixed values of Ha = 1 and We = 0.01.

Figure 10. Streamline pattern for (a) Ha = 1 and (b) Ha = 1.5 at fixed values of We = 0.01 and ε = 0.4.

Figure 10. Streamline pattern for (a) Ha = 1 and (b) Ha = 1.5 at fixed values of We = 0.01 and ε = 0.4.

5. Conclusions

The present study investigates the impact of tilted magnetic field and thermal radiation on pumping motion of ternary nanofluid flowing through an elastic micropump. To implement unidirectional motion and dynamic mixing, the internal side of the elastic pump contained mimicked cilia. The governing equations of the intended flow were modelled in moving frame and simplified under the lubrication and Rosseland approximation. The shooting technique was utilized to determine the numerical solutions of axial velocity, stream function, pressure gradient, pressure rise per metachronal wavelength, temperature, the entropy formation number, and the Bejan number. From the above analysis, the following conclusions are drawn:

• Around the pump surface, the exalted values of the Hartman number and the Weissenberg number induce an acceleration in fluid velocity.
• In the pump deep part, the ternary fluid pressure gradient enhances for the small values of the magnetic parameter and extended cilia.
• In the pumping zone, the pressure rise per metachronal wavelength in an escalating function of cilia length and small Hartmann number, whereas the same parameters induce a deceleration in pressure rise in the co-pumping zone.
• The temperature of the medium dampens down by contemplating the thermally radiated ternary fluid in a weak magnetic environment.
• Appropriately small values of the Hartmann number and substantially elevated values of the radiation number effectively contribute to entropy reduction in the micropump.
• Weak magnetic field and strong radiation effects assist with the domination of the fluid friction irreversibility over the heat transfer irreversibility.
• The small values of the magnetic parameter and prolonged cilia aids the fluid flow rate augmentation.
• The heat transfer rate is raised by about 6% in mono nanofluid, 11%–12% in bi-hybrid nanofluid, and 12%–18% in ternary fluid compared to conventional blood model for different values of the magnetic parameter.
• The present study may provide a profound perception in bioengineered medical instruments and thermal pipe heat sink. It can further assist with commencing a new course for the consideration of various other ternary nanofluids as desirable coolants under resistive forces, that is, electric and induced magnetic fields, porous media, and gravity effects. Such other possible future extensions may be the consideration of temperature and velocity jumps at the boundary, which could further explore the mechanism of thermo-microfluidics devices.