Spectral Relaxation Methodology for Chemical and Bioconvection Processes for Cross Nanofluid Flowing around an Oblique Cylinder with a Slanted Magnetic Field Effect
Abstract
1. Introduction
- In the whole literature, there are several studies which are related to a Cross fluid model attached with horizontal and vertical cylinders, but a Cross fluid model has not yet been used with an inclined cylinder. Therefore, this attempt is performed to carry out the results with Cross fluid along an inclined cylinder geometry.
- The spectral relaxation technique has not been utilized yet for the case of numerical computation of Cross nanofluid flow subjected to an elastic cylinder.
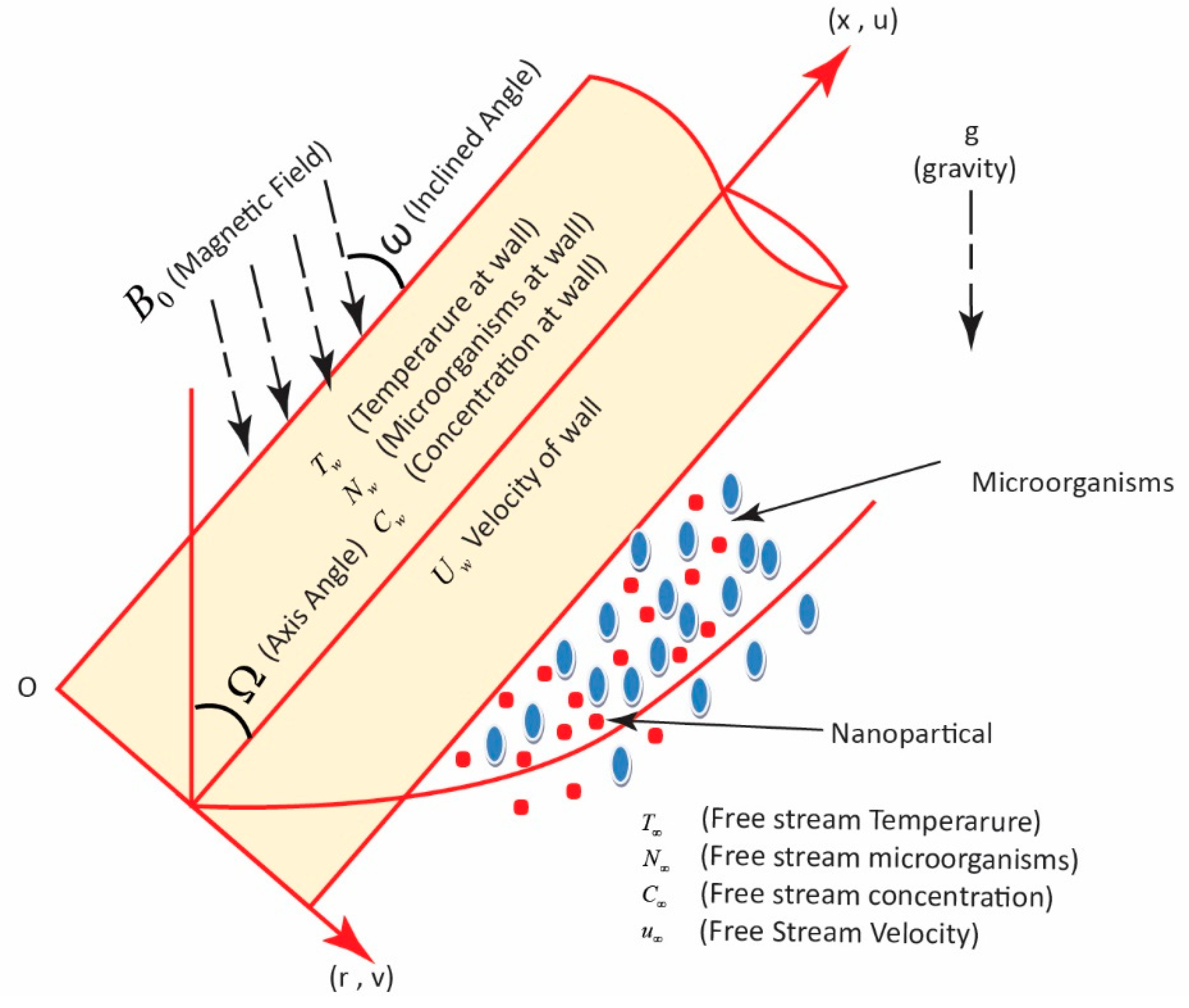
2. Flow Analysis
3. Rheology of Cross Fluid
4. Modeled Equations
5. Method of Solution
6. Numerical Procedure: Spectral Relaxation Technique
6.1. Advantages of Spectral Relaxation Technique
- Less expensive
- Easier to implement than finite element methods
- They shine best when high accuracy is sought
- They are useful in simple domains with smooth solutions.
6.2. Applied Spectral Relaxation Technique on Current Problem
7. Validness of Study
8. Data Description, Collection, Interpretation, and Discussion
8.1. Data Collection
8.2. Data Description
8.3. Data Handling
8.4. Interpretation of Numerically Outcomes
9. Results and Discussion
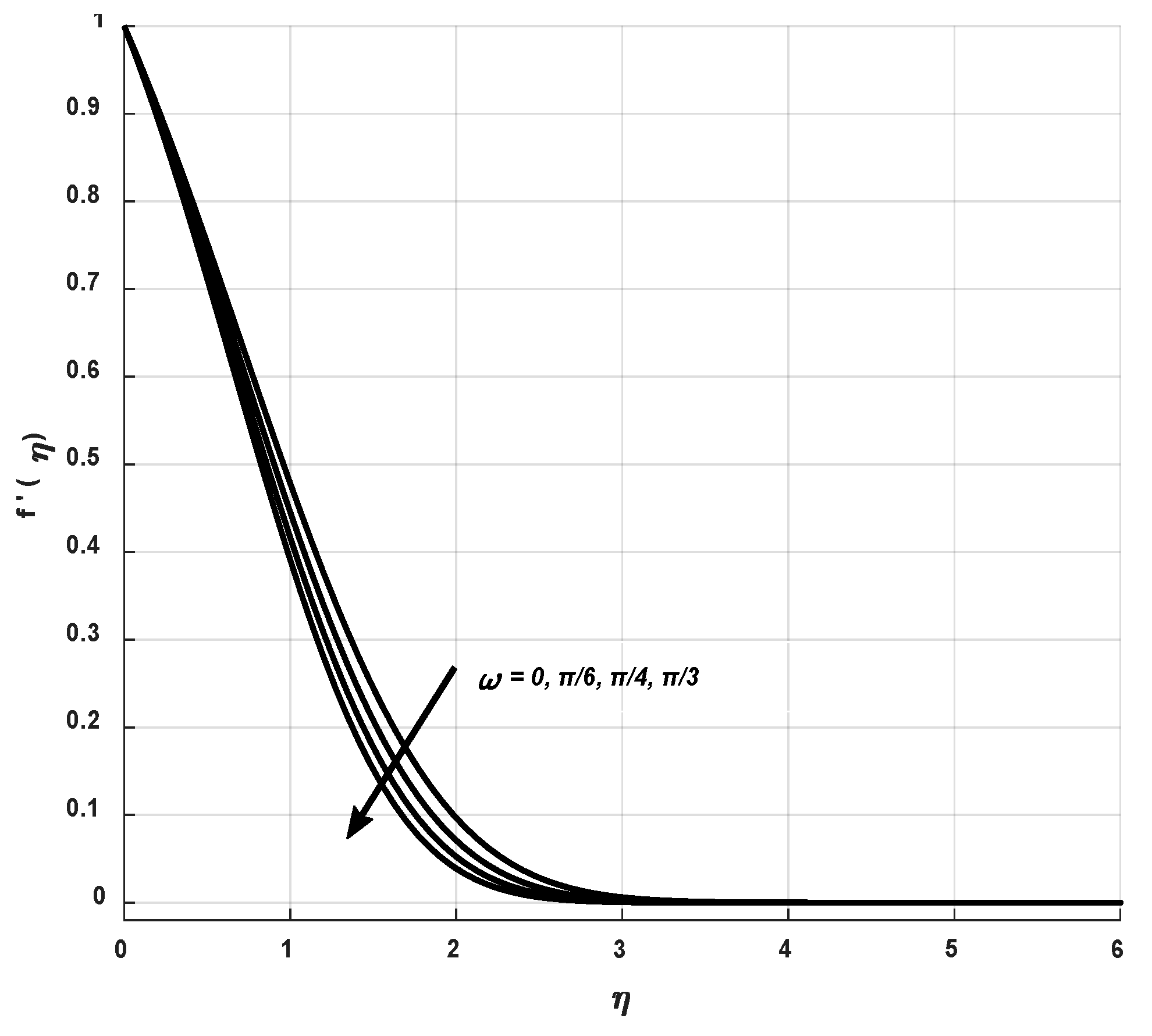
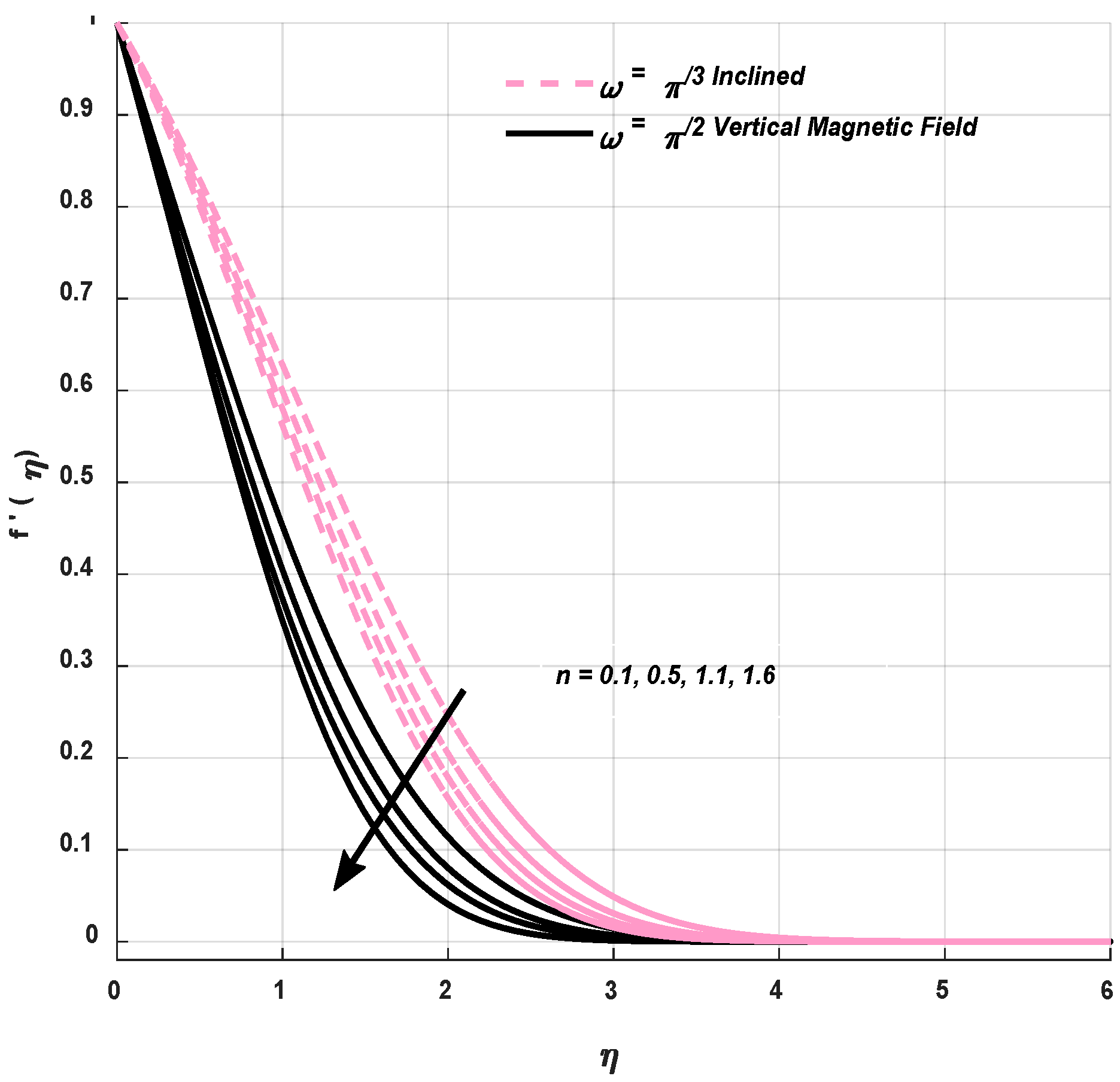
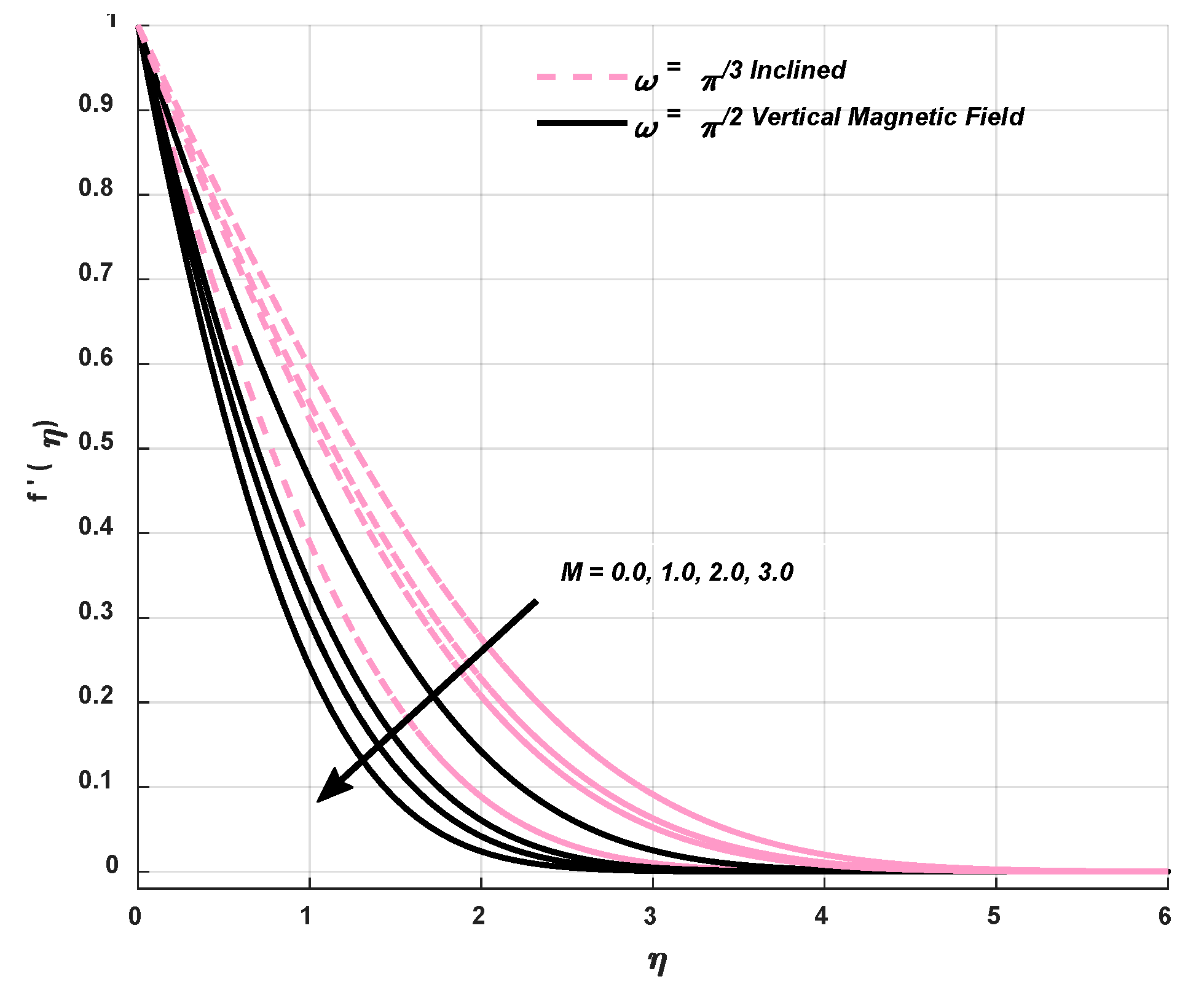
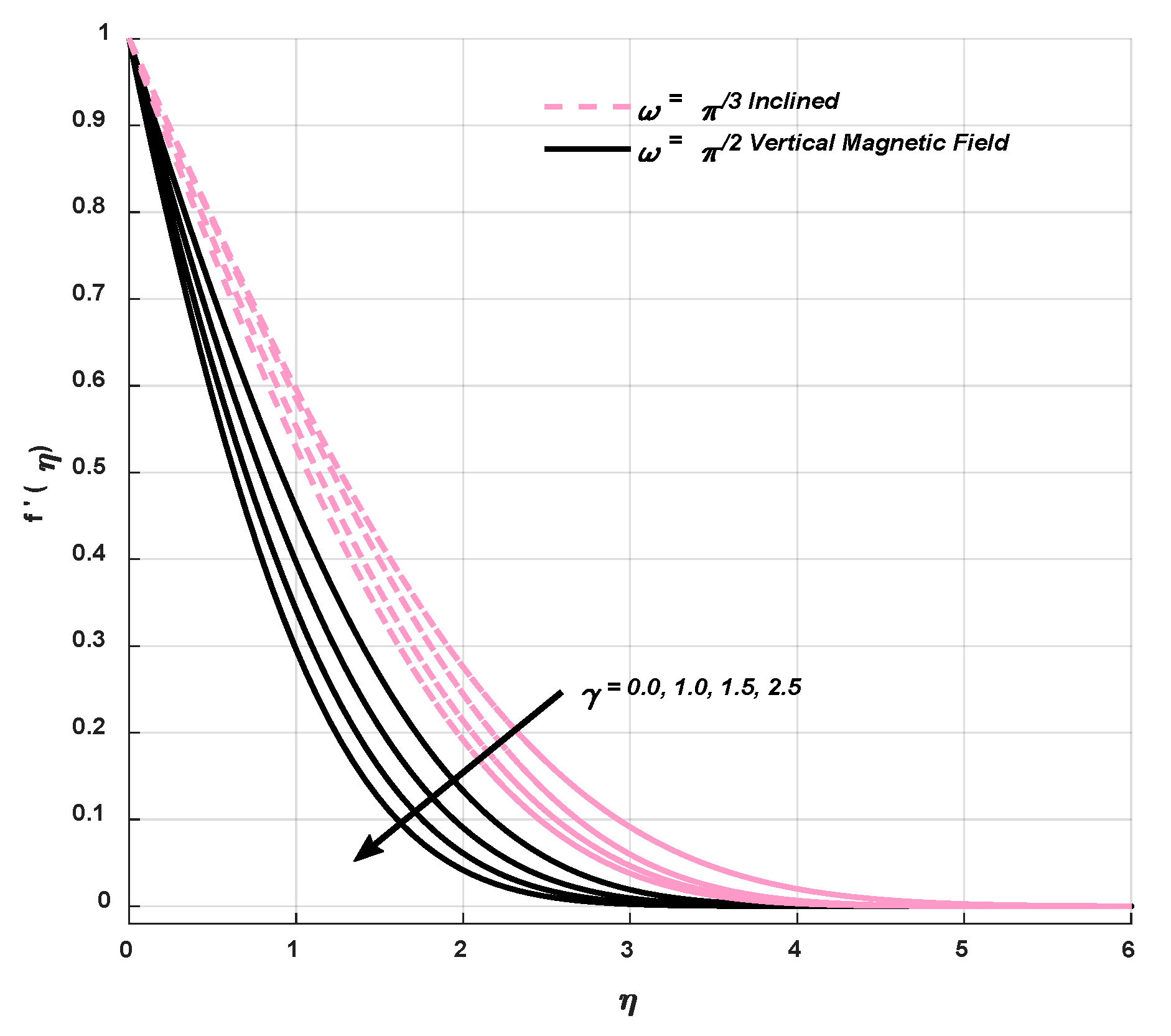
9.1. Velocity Profile
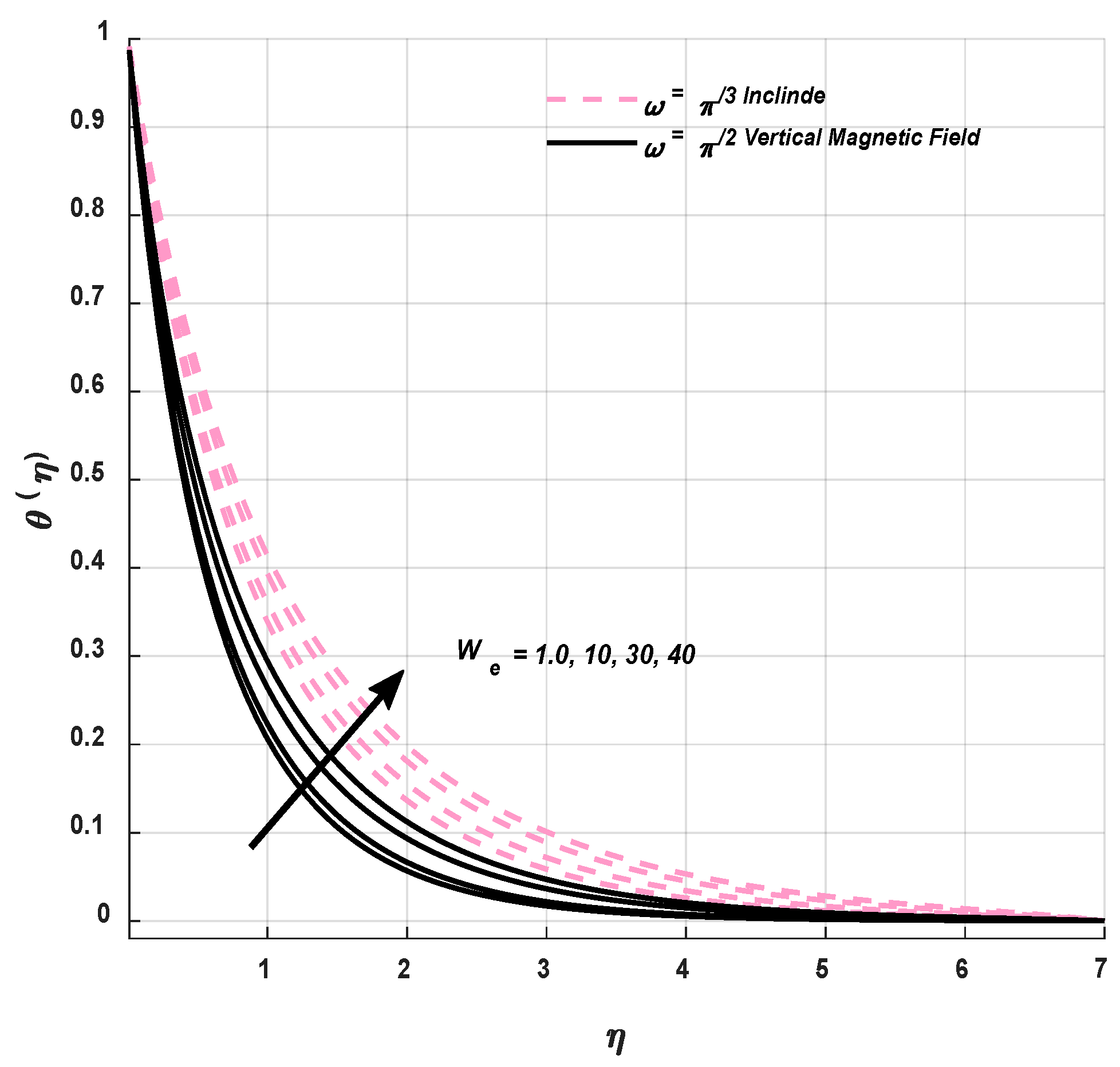
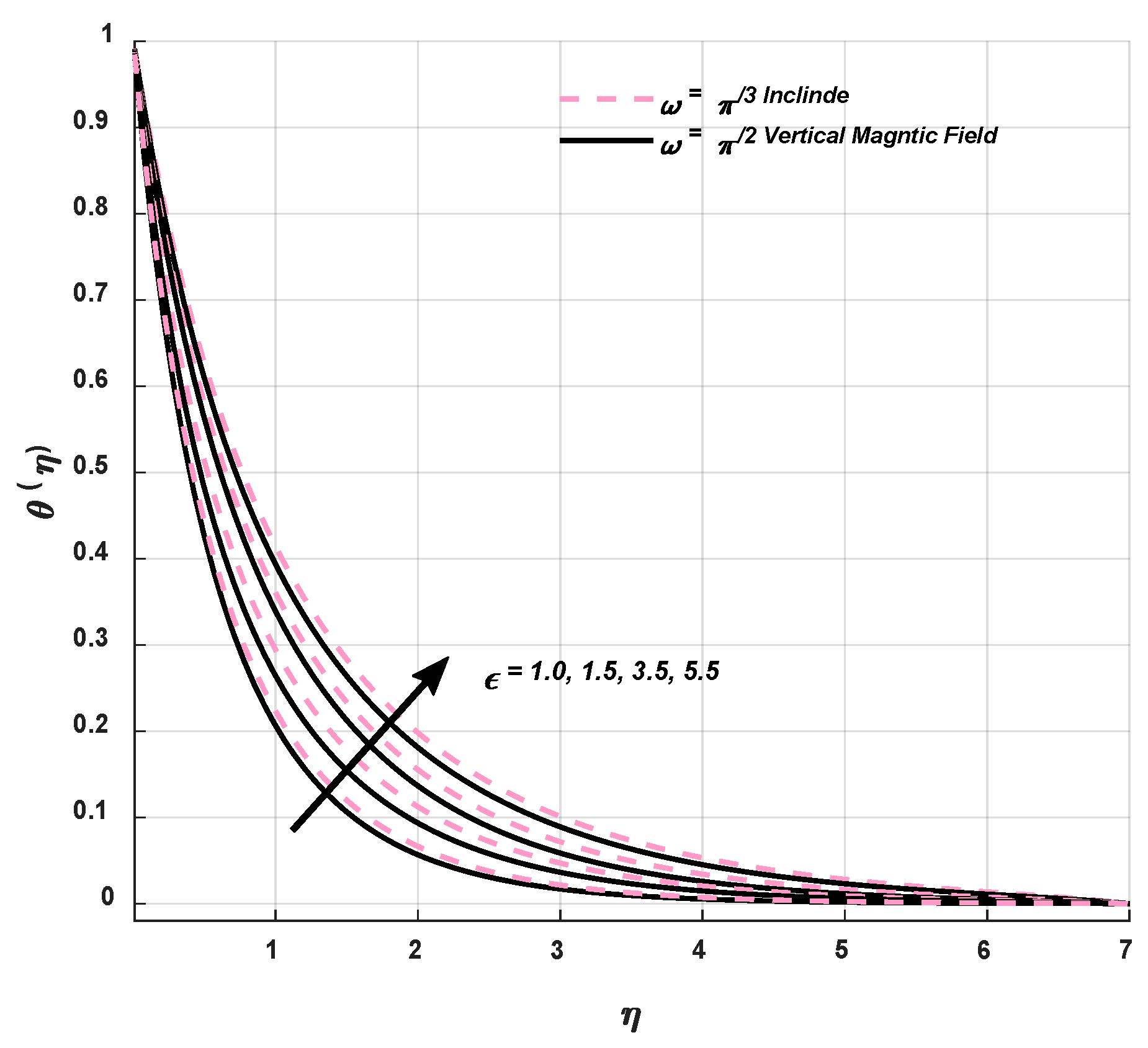
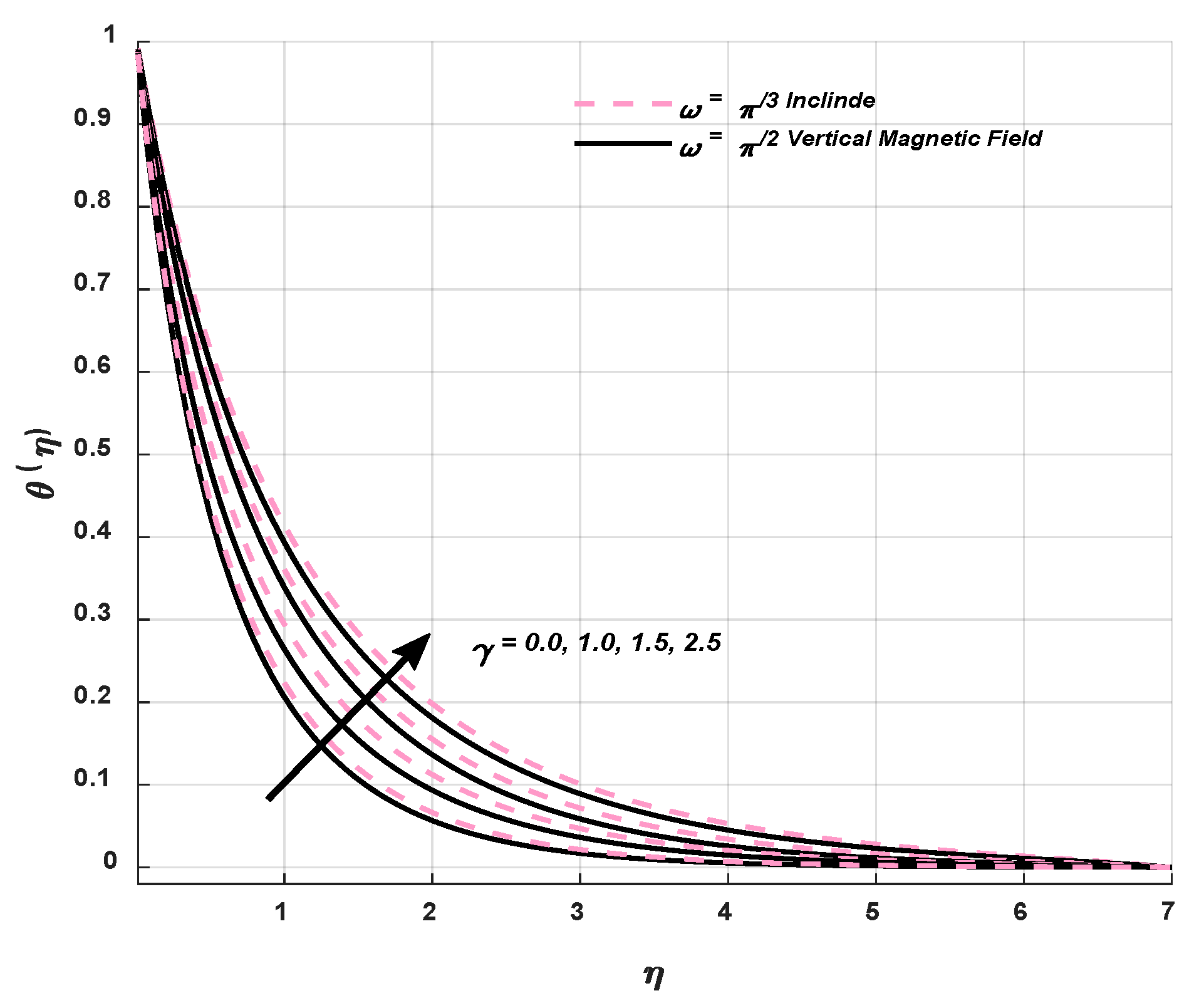
9.2. Temperature Profile
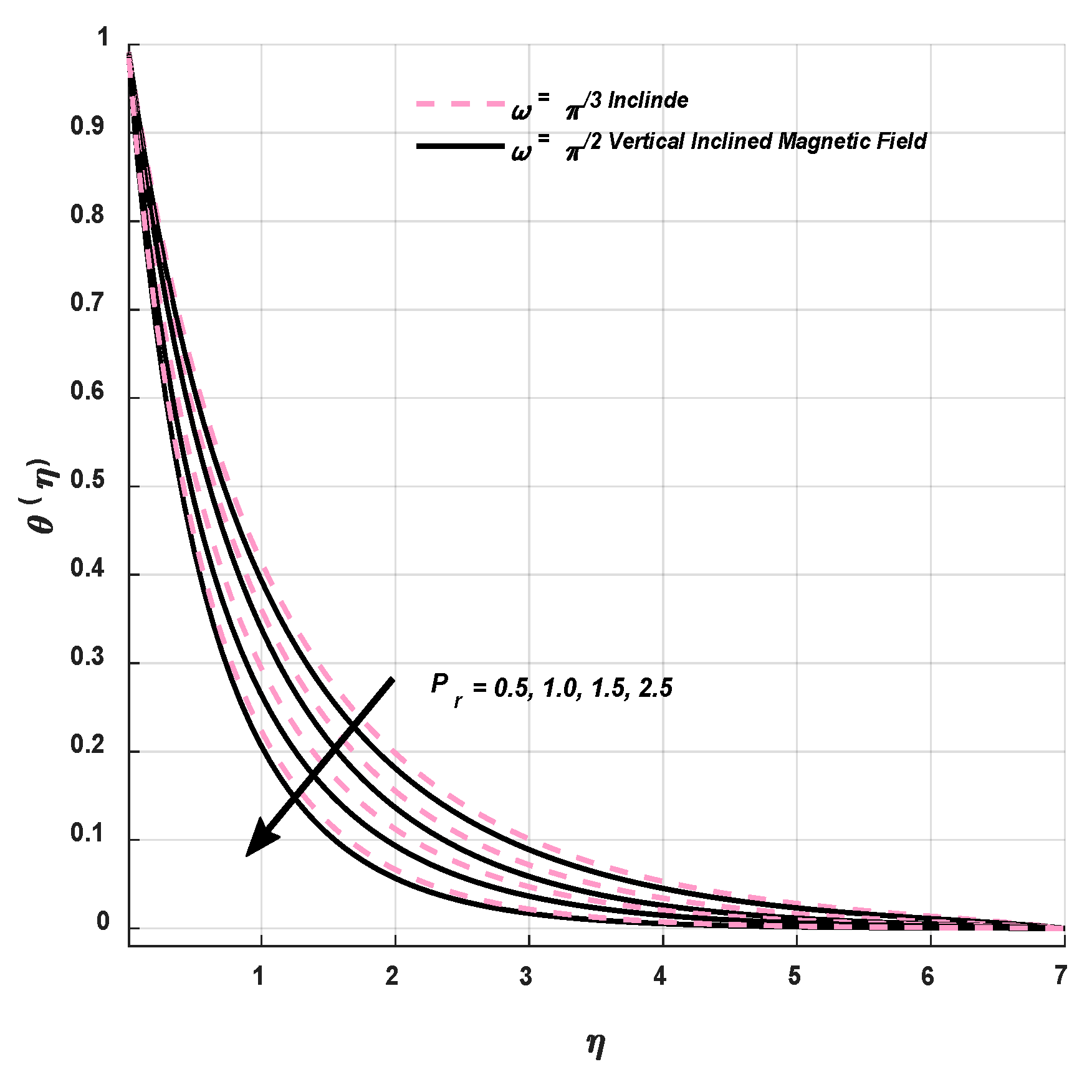
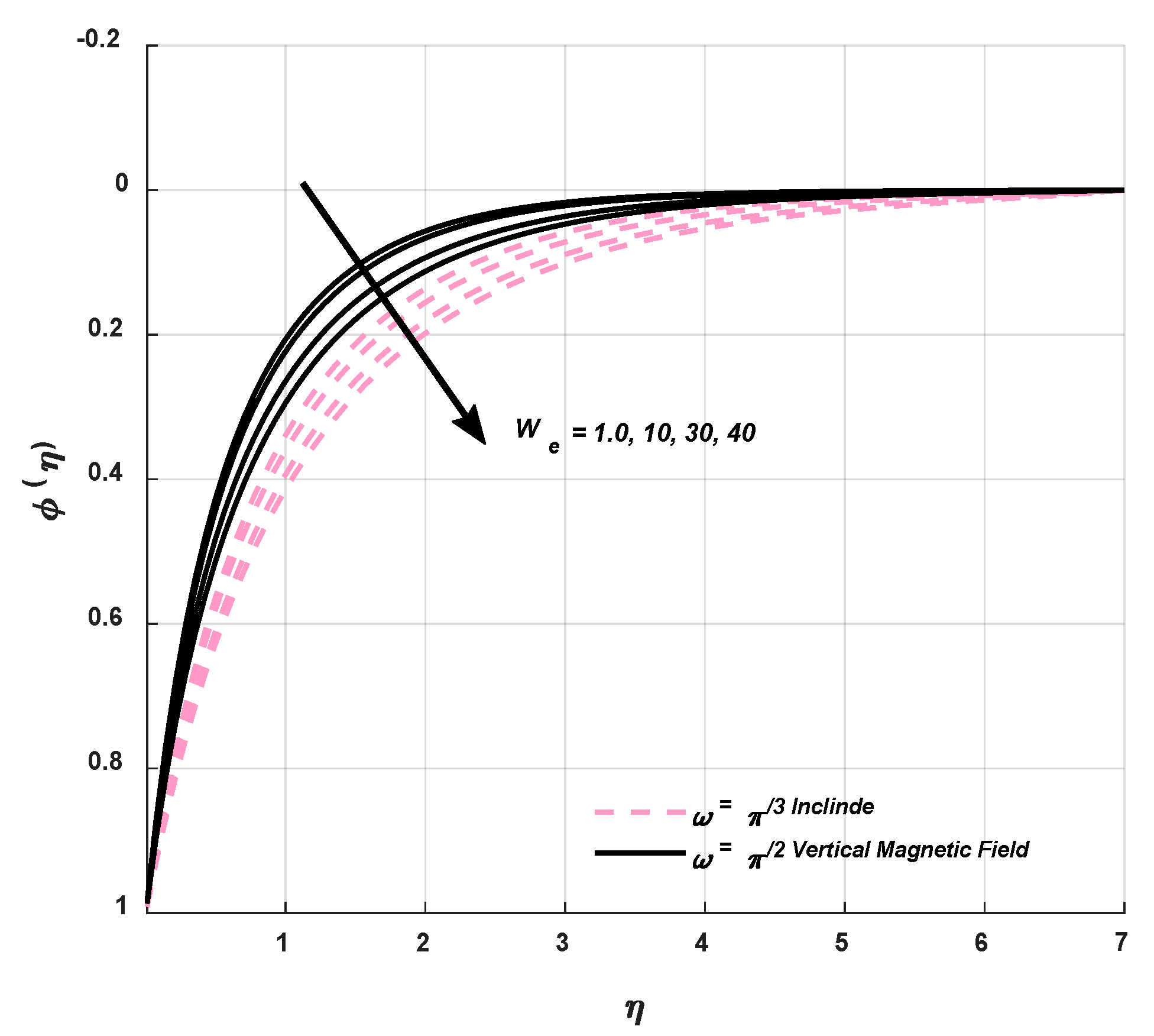
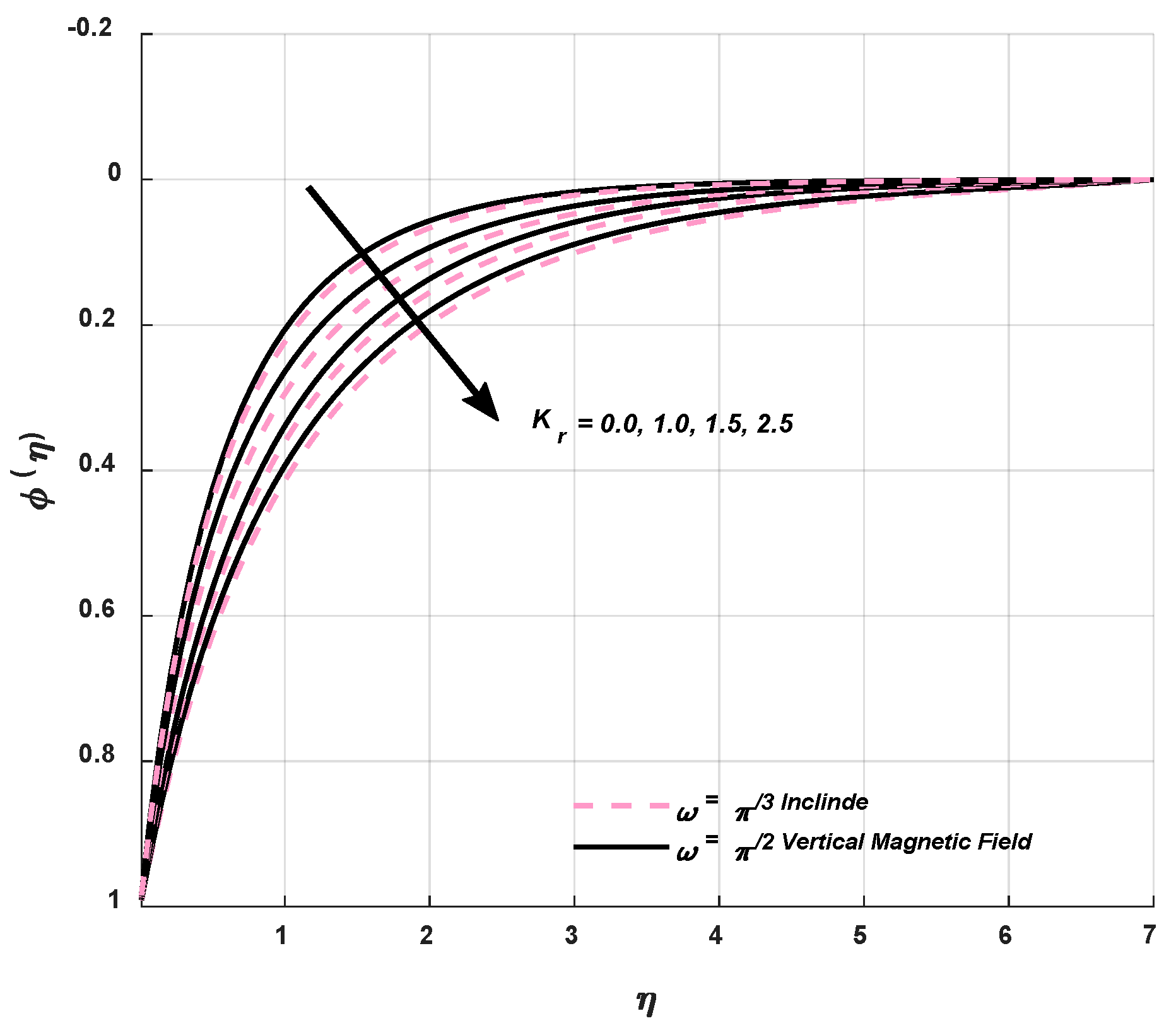
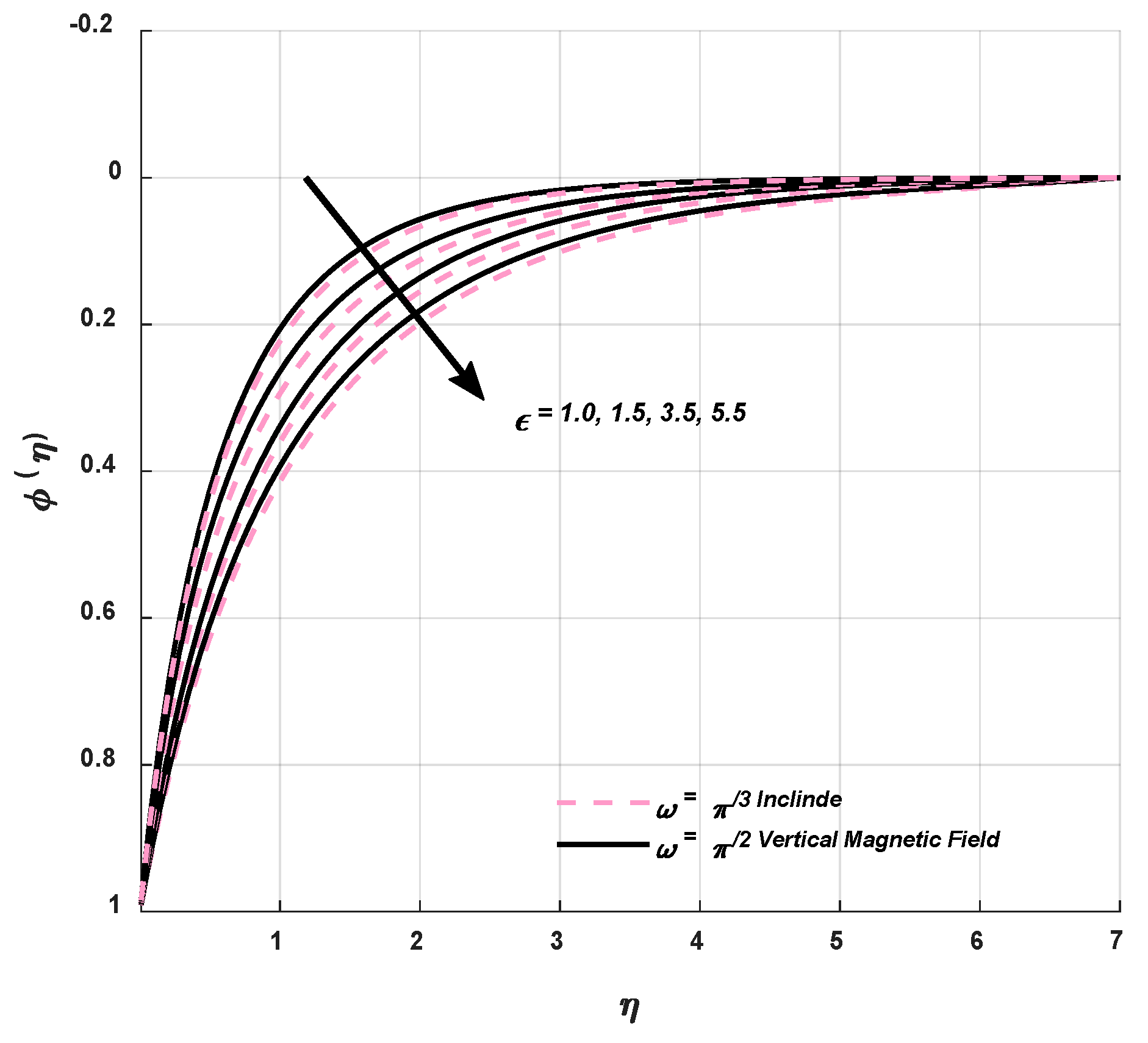
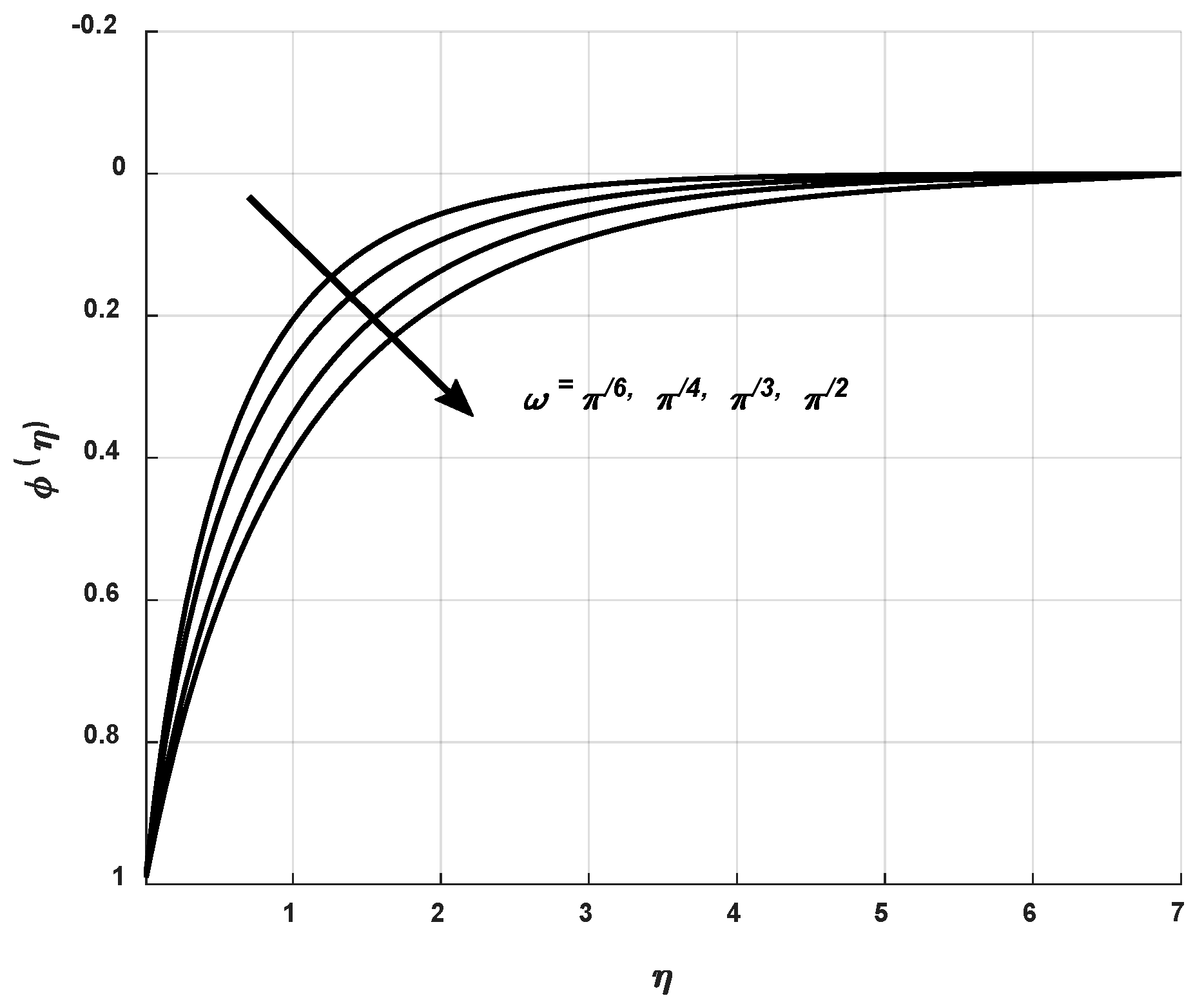
9.3. Concentration Profile
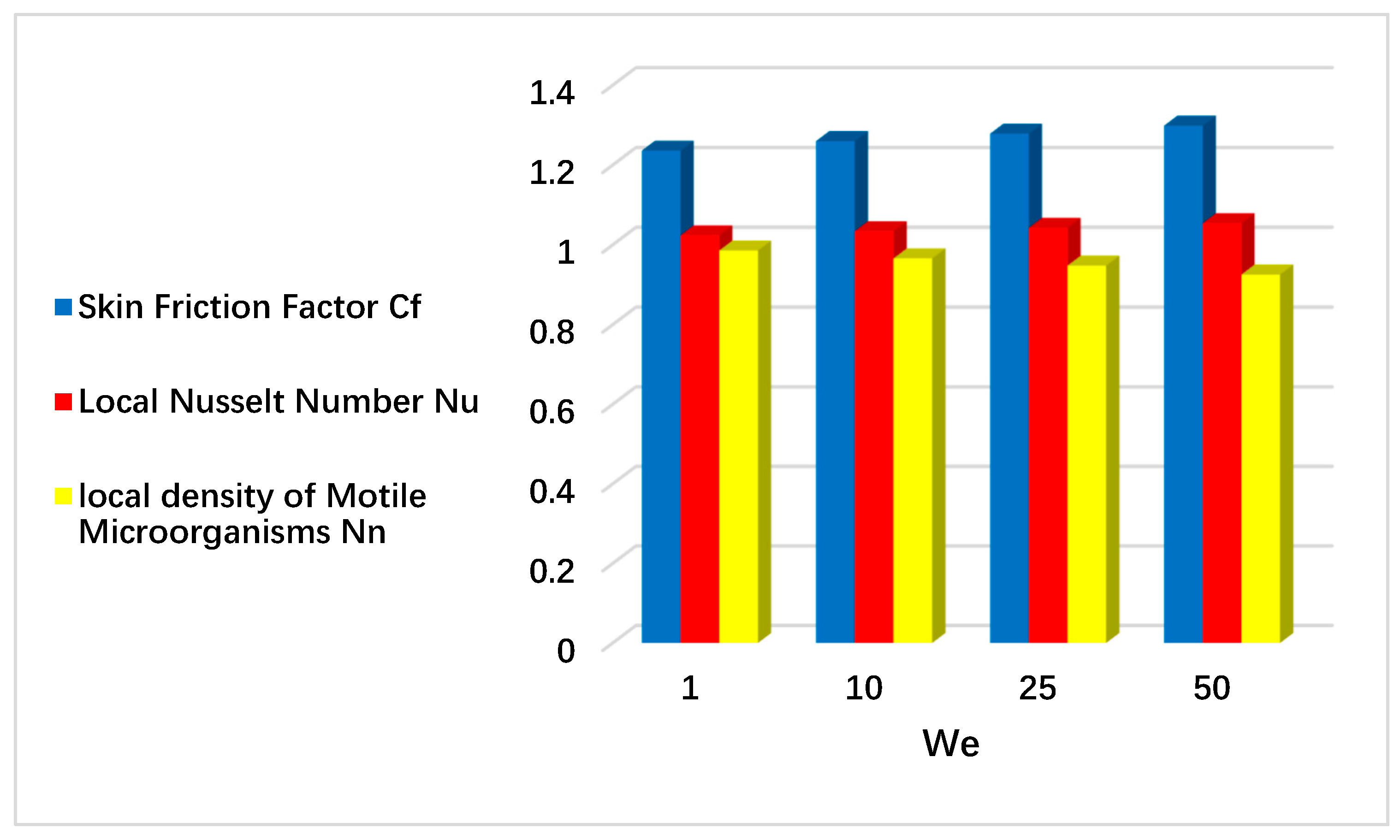
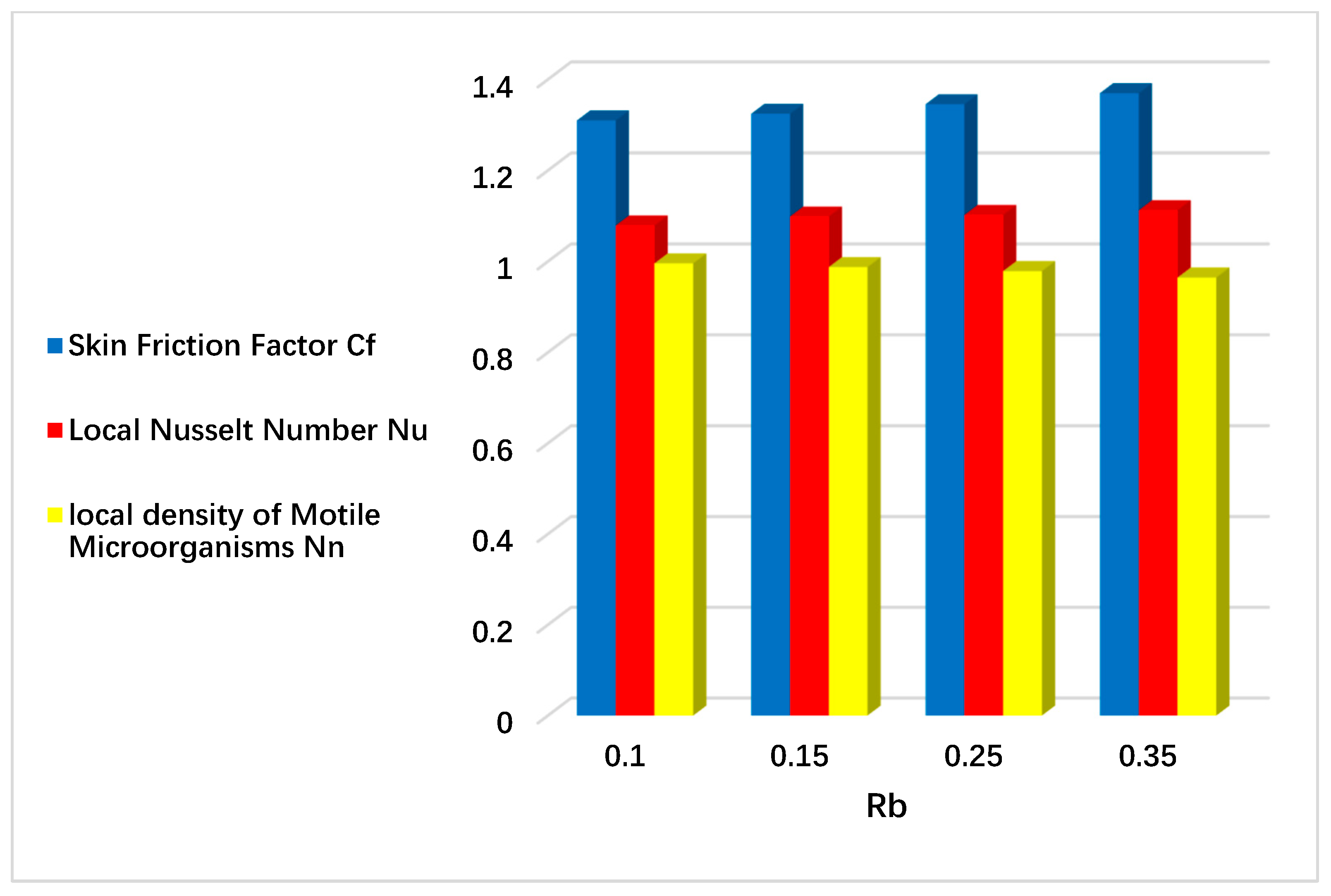
9.4. Statistical Graphs
10. Conclusions
- Shear thinning behavior is noticed as a result of a magnification in a Weissenberg number, which brings a decrement in fluid viscosity and amplifies velocity of the fluid flow.
- The fluid behavior is shear thickening owing to magnification in power law index n, which amplifies the fluid viscosity and velocity phenomenon.
- It is well-established that the molecules collide more randomly and exchange more KE with each other by virtue of a magnification in the thermal conductivity parameter which provides an amplification in the temperature field.
- It is observed that the microorganism swimming speed amplifies as a result of an augmentation in w, which brings about an increment in the microorganisms flow field.
- Transport of heat is rapid on a cylinder as compared to a flat surface. Molecules collide more randomly and enhance K.E in the case of cylindrical surface in contrast to elastic surface.
- The drag friction phenomenon is inversely related to the fluid flow motion. Amplification in We amplifies and encourages the viscosity phenomenon, which diminishes the fluid velocity and escalates the drag friction phenomenon.
- Viscosity is inversely linked with temperature. Amplification in Weissenberg number We and power law index n amplifies the fluid viscosity, which diminishes the fluid velocity and amplifies temperature.
- A positive variation in M encourages the resistive force, called Lorentz force, which provides hurdle to the fluid flow and diminishes the velocity phenomenon, but a magnification M provides a substantial heat to the fluid flow subjected to a cylinder.
- From the obtained results, it is revealed that more heat is produced in the case of nanofluid in contrast to simple base fluid.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Parameters | Units | Parameters | Units |
| Gravity (g) | Activation energy (E) | Kg∙J∙mol−1 | |
| material constant | N∙m−2 | Power law index (n) | N∙m−2 |
| Magnetic field () | Kg∙s−2∙A_1 | cell swimming speed (Wc) | m∙s−1 |
| Density () | Kg∙m-−3 | Temperature (T) | K |
| Angles () | Radian | Concentration (C) | Mol∙m−3 |
| Thermal conductivity () | W∙m−1∙k−1 | microorganisms concentration (N) | Mol∙m−3 |
| Thermophoresis diffusion (D) | m2∙s−1 | curvature parameter (γ) | m−1 |
| Brownian diffusion | m2∙s−1 | An unsteadiness parameter (A) | m∙s−1 |
| Heat capacity () | J∙Kg−1∙K−1 | Buoyancy force (Nr) | Kg∙m2 |
| Reaction rate | mol∙s−1 | Electrical conductivity () | Sem∙m−1 |
| Temperature difference (δ) | K | - | - |
References
- Nabwey Hossam, A.; Alshber, S.I.; Rashad, A.M.; Mahdy, A.E.N. Influence of bioconvection and chemical reaction on magneto—Carreau nanofluid flow through an inclined cylinder. Mathematics 2022, 10, 504. [Google Scholar] [CrossRef]
- Ayub, A.; Sabir, Z.; Shah, S.Z.H.; Wahab, H.A.; Sadat, R.; Ali, M.R. Effects of homogeneous-heterogeneous and Lorentz forces on 3-D radiative magnetized cross nanofluid using two rotating disks. Int. Commun. Heat Mass Transf. 2022, 130, 105778. [Google Scholar] [CrossRef]
- Shah, S.L.; Ayub, A.; Dehraj, S.; Wahab, H.A.; Sagayam, K.M.; Ali, M.R.; Sadat, R.; Sabir, Z. Magnetic dipole aspect of binary chemical reactive Cross nanofluid and heat transport over composite cylindrical panels. Waves Random Complex Media 2022, 1–24. [Google Scholar] [CrossRef]
- Ayub, A.; Sabir, Z.; Wahab, H.A.; Balubaid, M.; Mahmoud, S.R.; Ali, M.R.; Sadat, R. Analysis of the nanoscale heat transport and Lorentz force based on the time-dependent Cross nanofluid. Eng. Comput. 2022, 1–20. [Google Scholar]
- Imran, M.; Farooq, U.; Waqas, H.; Anqi, A.E.; Safaei, M.R. Numerical performance of thermal conductivity in Bioconvection flow of cross nanofluid containing swimming microorganisms over a cylinder with melting phenomenon. Case Stud. Therm. Eng. 2021, 26, 101181. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Roghani, S.; Mogharrebi, A.; Asadi, A.; Waqas, M.; Ganji, D. Investigation of cross-fluid flow containing motile gyrotactic microorganisms and nanoparticles over a three-dimensional cylinder. Alex. Eng. J. 2020, 59, 3297–3307. [Google Scholar] [CrossRef]
- Ali, M.; Sultan, F.; Khan, W.A.; Shahzad, M.; Arif, H. Important features of expanding/contracting cylinder for Cross magneto-nanofluid flow. Chaos Solitons Fractals 2020, 133, 109656. [Google Scholar] [CrossRef]
- Khan, N.S.; Humphries, U.W.; Kumam, W.; Kumam, P.; Muhammad, T. Bioconvection Casson nanoliquid film sprayed on a stretching cylinder in the portfolio of homogeneous—Heterogeneous chemical reactions. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Mech. 2022, 102, e202000222. [Google Scholar] [CrossRef]
- Gopal, D.; Munjam, S.R.; Kishan, N. Analytical impact of Carreau nanofluid model under the influence of chemical reaction, Soret and Dufour over inclined stretching cylinder. Int. Commun. Heat Mass Transf. 2022, 135, 106148. [Google Scholar] [CrossRef]
- Khan, M.; Yasir, M.; Alshomrani, A.S.; Sivasankaran, S.; Aladwani, Y.R.; Ahmed, A. Variable heat source in stagnation-point unsteady flow of magnetized Oldroyd-B fluid with cubic autocatalysis chemical reaction. Ain Shams Eng. J. 2022, 13, 101610. [Google Scholar] [CrossRef]
- Lim, Y.J.; Shafie, S.; Isa, S.M.; Rawi, N.A.; Mohamad, A.Q. Impact of chemical reaction, thermal radiation and porosity on free convection Carreau fluid flow towards a stretching cylinder. Alex. Eng. J. 2022, 61, 4701–4717. [Google Scholar] [CrossRef]
- Liu, C.; Khan, M.U.; Ramzan, M.; Chu, Y.M.; Kadry, S.; Malik, M.Y.; Chinram, R. Nonlinear radiative Maxwell nanofluid flow in a Darcy–Forchheimer permeable media over a stretching cylinder with chemical reaction and bioconvection. Sci. Rep. 2021, 11, 9391. [Google Scholar] [CrossRef] [PubMed]
- Alarabi, T.H.; Rashad, A.M.; Mahdy, A. Homogeneous–heterogeneous chemical reactions of radiation hybrid nanofluid flow on a cylinder with joule heating: Nanoparticles shape impact. Coatings 2021, 11, 1490. [Google Scholar] [CrossRef]
- Shahid, A.; Bhatti, M.M.; Ellahi, R.; Mekheimer, K.S. Numerical experiment to examine activation energy and bi-convection Carreau nanofluid flow on an upper paraboloid porous surface: Application in solar energy. Sustain. Energy Technol. Assess. 2022, 52, 102029. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; Shankar, B.M.; Ramadan, S.F.; Mallik, H.E.; Mohamed, M.S. On the stability of convection in a non-newtonian vertical fluid layer in the presence of gold nanoparticles: Drug agent for thermotherapy. Mathematics 2021, 9, 1302. [Google Scholar] [CrossRef]
- Zaher, A.Z.; Ali, K.K.; Mekheimer, K.S. Electroosmosis forces EOF driven boundary layer flow for a non-Newtonian fluid with planktonic microorganism: Darcy Forchheimer model. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2534–2559. [Google Scholar] [CrossRef]
- Elogail, M.A.; Mekheimer, K.S. Modulated viscosity-dependent parameters for MHD blood flow in microvessels containing oxytactic microorganisms and nanoparticles. Symmetry 2020, 12, 2114. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; Ramadan, S.F. New insight into gyrotactic microorganisms for bio-thermal convection of Prandtl nanofluid over a stretching/shrinking permeable sheet. SN Appl. Sci. 2020, 2, 450. [Google Scholar] [CrossRef]
- Aly, M.A.; El-Sapa, S. Effects of Soret and Dufour numbers on MHD thermosolutal convection of a nanofluid in a finned cavity including rotating circular cylinder and cross shapes. Int. Commun. Heat Mass Transf. 2022, 130, 105819. [Google Scholar] [CrossRef]
- Zeeshan, A.; Mehmood, O.U.; Mabood, F.; Alzahrani, F. Numerical analysis of hydromagnetic transport of Casson nanofluid over permeable linearly stretched cylinder with Arrhenius activation energy. Int. Commun. Heat Mass Transf. 2022, 130, 105736. [Google Scholar] [CrossRef]
- Ramzan, M.; Shaheen, N.; Chung, J.D.; Kadry, S.; Chu, Y.M.; Howari, F. Impact of Newtonian heating and Fourier and Fick’s laws on a magnetohydrodynamic dusty Casson nanofluid flow with variable heat source/sink over a stretching cylinder. Sci. Rep. 2021, 11, 2357. [Google Scholar] [CrossRef] [PubMed]
- Poply, V.; Devi, R. A two—Component modeling for free stream velocity in magnetohydrodynamic nanofluid flow with radiation and chemical reaction over a stretching cylinder. Heat Transf. 2021, 50, 3603–3619. [Google Scholar]
- Ibrahim, W.; Negera, M. Viscous dissipation effect on mixed convective heat transfer of MHD flow of Williamson nanofluid over a stretching cylinder in the presence of variable thermal conductivity and chemical reaction. Heat Transf. 2021, 50, 2427–2453. [Google Scholar] [CrossRef]
- Gharami, P.P.; Arifuzzaman, S.M.; Khan, M.; Sarkar, T.; Ahmmed, S.F. MHD effect on unsteady flow of tangent hyperbolic nano-fluid past a moving cylinder with chemical reaction. SN Appl. Sci. 2020, 2, 1256. [Google Scholar] [CrossRef]
- Xiong, P.Y.; Hamid, A.; Chu, Y.M.; Khan, M.I.; Gowda, R.J.; Kumar, R.N.; Prasannakumara, B.C.; Qayyum, S. Dynamics of multiple solutions of Darcy–Forchheimer saturated flow of Cross nanofluid by a vertical thin needle point. Eur. Phys. J. Plus 2021, 136, 345. [Google Scholar] [CrossRef]
- Punith Gowda, R.J.; Naveen Kumar, R.; Jyothi, A.M.; Prasannakumara, B.C.; Sarris, I.E. Impact of binary chemical reaction and activation energy on heat and mass transfer of marangoni driven boundary layer flow of a non-Newtonian nanofluid. Processes 2021, 9, 702. [Google Scholar] [CrossRef]
- Gowda, R.P.; Kumar, R.N.; Aldalbahi, A.; Issakhov, A.; Prasannakumara, B.C.; Rahimi-Gorji, M.; Rahaman, M. Thermophoretic particle deposition in time-dependent flow of hybrid nanofluid over rotating and vertically upward/downward moving disk. Surf. Interfaces 2021, 22, 100864. [Google Scholar] [CrossRef]
- Varun Kumar, R.S.; Gunderi Dhananjaya, P.; Naveen Kumar, R.; Punith Gowda, R.J.; Prasannakumara, B.C. Modeling and theoretical investigation on Casson nanofluid flow over a curved stretching surface with the influence of magnetic field and chemical reaction. Int. J. Comput. Methods Eng. Sci. Mech. 2022, 23, 12–19. [Google Scholar] [CrossRef]
- Sabir, Z.; Ayub, A.; Guirao, J.L.; Bhatti, S.; Shah, S.Z.H. The effects of activation energy and thermophoretic diffusion of nanoparticles on steady micropolar fluid along with Brownian motion. Adv. Mater. Sci. Eng. 2020, 2020, 2010568. [Google Scholar] [CrossRef]
- Shah SZ, H.; Ayub, A.; Sabir, Z.; Adel, W.; Shah, N.A.; Yook, S.J. Insight into the dynamics of time-dependent cross nanofluid on a melting surface subject to cubic autocatalysis. Case Stud. Therm. Eng. 2021, 27, 101227. [Google Scholar] [CrossRef]
- Kumar, R.N.; Gowda, R.P.; Alam, M.M.; Ahmad, I.; Mahrous, Y.M.; Gorji, M.R.; Prasannakumara, B.C. Inspection of convective heat transfer and KKL correlation for simulation of nanofluid flow over a curved stretching sheet. Int. Commun. Heat Mass Transf. 2021, 126, 105445. [Google Scholar] [CrossRef]
- Darvesh, A.; Sajid, T.; Jamshed, W.; Ayub, A.; Shah, S.Z.; Eid, M.R.; Hussain, S.M.; Akram, M.; Hafeez, M.B.; Krawczuk, M. Rheology of Variable Viscosity-Based Mixed Convective Inclined Magnetized Cross Nanofluid with Varying Thermal Conductivity. Appl. Sci. 2022, 12, 9041. [Google Scholar] [CrossRef]
- Varun Kumar, R.S.; Alhadhrami, A.; Punith Gowda, R.J.; Naveen Kumar, R.; Prasannakumara, B.C. Exploration of Arrhenius activation energy on hybrid nanofluid flow over a curved stretchable surface. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Mech. 2021, 101, e202100035. [Google Scholar] [CrossRef]
- Ayub, A.; Wahab, H.A.; Shah, S.Z.; Shah, S.L.; Darvesh, A.; Haider, A.; Sabir, Z. Interpretation of infinite shear rate viscosity and a nonuniform heat sink/source on a 3D radiative cross nanofluid with buoyancy assisting/opposing flow. Heat Transf. 2021, 50, 4192–4232. [Google Scholar] [CrossRef]
- Ayub, A.; Sabir, Z.; Altamirano, G.C.; Sadat, R.; Ali, M.R. Characteristics of melting heat transport of blood with time-dependent cross-nanofluid model using Keller–Box and BVP4C method. Eng. Comput. 2022, 38, 3705–3719. [Google Scholar] [CrossRef]
- Jyothi, A.M.; Kumar, R.N.; Gowda, R.P.; Prasannakumara, B.C. Significance of Stefan blowing effect on flow and heat transfer of Casson nanofluid over a moving thin needle. Commun. Theor. Phys. 2021, 73, 095005. [Google Scholar] [CrossRef]
- Sarada, K.; Gamaoun, F.; Abdulrahman, A.; Paramesh, S.O.; Kumar, R.; Prasanna, G.D.; Gowda, R.P. Impact of exponential form of internal heat generation on water-based ternary hybrid nanofluid flow by capitalizing non-Fourier heat flux model. Case Stud. Therm. Eng. 2022, 38, 102332. [Google Scholar]
- Kumar, R.N.; Gamaoun, F.; Abdulrahman, A.; Chohan, J.S.; Gowda, R.P. Heat transfer analysis in three-dimensional unsteady magnetic fluid flow of water-based ternary hybrid nanofluid conveying three various shaped nanoparticles: A comparative study. Int. J. Mod. Phys. B 2022, 36, 2250170. [Google Scholar] [CrossRef]
- Ayub, A.; Sajid, T.; Jamshed, W.; Zamora, W.R.; More, L.A.; Talledo, L.M.; Rodríguez Ortega de Peña, N.I.; Hussain, S.M.; Hafeez, M.B.; Krawczuk, M. Activation Energy and Inclination Magnetic Dipole Influences on Carreau Nanofluid Flowing via Cylindrical Channel with an Infinite Shearing Rate. Appl. Sci. 2022, 12, 8779. [Google Scholar] [CrossRef]
- Ali, A.; Sarkar, S.; Das, S.; Jana, R.N. A report on entropy generation and Arrhenius kinetics in magneto-bioconvective flow of Cross nanofluid over a cylinder with wall slip. Int. J. Ambient. Energy 2022, 1–16. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, X.; Rehman, M.I.U.; Hamid, A. Thermal radiation aspect of bioconvection flow of magnetized Sisko nanofluid along a stretching cylinder with swimming microorganisms. Case Stud. Therm. Eng. 2022, 30, 101771. [Google Scholar] [CrossRef]
- Ramzan, M.; Shahmir, N.; Ghazwani, H.A. Stefan blowing impact on bioconvective Maxwell nanofluid flow over an exponentially stretching cylinder with variable thermal conductivity. Waves Random Complex Media 2022, 1–16. [Google Scholar] [CrossRef]
- Abdelmalek, Z.; Khan, S.U.; Waqas, H.; Riaz, A.; Khan, I.A.; Tlili, I. A mathematical model for bioconvection flow of Williamson nanofluid over a stretching cylinder featuring variable thermal conductivity, activation energy and second-order slip. J. Therm. Anal. Calorim. 2021, 144, 205–217. [Google Scholar] [CrossRef]
- Benos, L.T.; Karvelas, E.G.; Sarris, I.E. A theoretical model for the magnetohydrodynamic natural convection of a CNT-water nanofluid incorporating a renovated Hamilton-Crosser model. Int. J. Heat Mass Transf. 2019, 135, 548–560. [Google Scholar] [CrossRef]
- Sarris, I.E.; Kassinos, S.C.; Carati, D. Large-eddy simulations of the turbulent Hartmann flow close to the transitional regime. Phys. Fluids 2007, 19, 085109. [Google Scholar] [CrossRef]
- Sarris, I.; Tsiakaras, P.; Song, S.; Vlachos, N. A three-dimensional CFD model of direct ethanol fuel cells: Anode flow bed analysis. Solid State Ion. 2006, 177, 2133–2138. [Google Scholar] [CrossRef]
- Karvelas, E.; Liosis, C.; Benos, L.; Karakasidis, T.; Sarris, I. Micromixing efficiency of particles in heavy metal removal processes under various inlet conditions. Water 2019, 11, 1135. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Pop, I. Numerical exploration of a non-Newtonian Carreau fluid flow driven by catalytic surface reactions on an upper horizontal surface of a paraboloid of revolution, buoyancy and stretching at the free stream. Alex. Eng. J. 2017, 56, 647–658. [Google Scholar] [CrossRef]
- Muhammad, T.; Alamri, S.Z.; Waqas, H.; Habib, D.; Ellahi, R. Bioconvection flow of magnetized Carreau nanofluid under the influence of slip over a wedge with motile microorganisms. J. Therm. Anal. Calorim. 2021, 143, 945–957. [Google Scholar] [CrossRef]
- Shafique, Z.; Mustafa, M.; Mushtaq, A. Boundary layer flow of Maxwell fluid in rotating frame with binary chemical reaction and activation energy. Results Phys. 2016, 6, 627–633. [Google Scholar] [CrossRef]
- Mahdy, A.; Hady, F.M.; Mohamed, R.A.; Abo-zaid, O.A. Activation energy effectiveness in dusty Carreau fluid flow along a stretched cylinder due to nonuniform thermal conductivity property and temperature—Dependent heat source/sink. Heat Transf. 2021, 50, 5760–5778. [Google Scholar] [CrossRef]
- Mahdy, A. Natural convection boundary layer flow due to gyrotactic microorganisms about a vertical cone in porous media saturated by a nanofluid. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 67–76. [Google Scholar] [CrossRef]
- Yusuf, T.A.; Mabood, F.; Prasannakumara, B.C.; Sarris, I.E. Magneto-bioconvection flow of Williamson nanofluid over an inclined plate with gyrotactic microorganisms and entropy generation. Fluids 2021, 6, 109. [Google Scholar] [CrossRef]
- Jamshed, W.; Aziz, A. Entropy Analysis of TiO2-Cu/EG Casson Hybrid Nanofluid via Cattaneo-Christov Heat Flux Model. Appl. Nanosci. 2018, 8, 1–14. [Google Scholar]
- Jamshed, W.; Nisar, K.S. Computational single phase comparative study of Williamson nanofluid in parabolic trough solar collector via Keller box method. Int. J. Energy Res. 2021, 45, 10696–10718. [Google Scholar] [CrossRef]
- Pasha, A.A.; Islam, N.; Jamshed, W.; Alam, M.I.; Jameel, A.G.A.; Juhany, K.A.; Alsulami, R. Statistical analysis of viscous hybridized nanofluid flowing via Galerkin finite element technique. Int. Commun. Heat Mass Transf. 2022, 137, 106244. [Google Scholar] [CrossRef]
- Hussain, S.M.; Jamshed, W.; Pasha, A.A.; Adil, M.; Akram, M. Galerkin finite element solution for electromagnetic radiative impact on viscid Williamson two-phase nanofluid flow via extendable surface. Int. Commun. Heat Mass Transf. 2022, 137, 106243. [Google Scholar] [CrossRef]
- Akram, M.; Jamshed, W.; Goud, B.S.; Pasha, A.A.; Sajid, T.; Rahman, M.M.; Arshad, M.; Weera, W. Irregular heat source impact on Carreau nanofluid flowing via exponential expanding cylinder: A thermal case study. Case Stud. Therm. Eng. 2022, 36, 102190. [Google Scholar] [CrossRef]
- Khan, M.; Saleh Alshomrani, A. Characteristics of melting heat transfer during flow of Carreau fluid induced by a stretching cylinder. Eur. Phys. J. E 2017, 40, 8. [Google Scholar]
- Rangi, R.R.; Ahmad, N. Boundary Layer Flow past a Stretching Cylinder and Heat Transfer with Variable Thermal Conductivity. Appl. Math. 2012, 3, 205–209. [Google Scholar] [CrossRef]




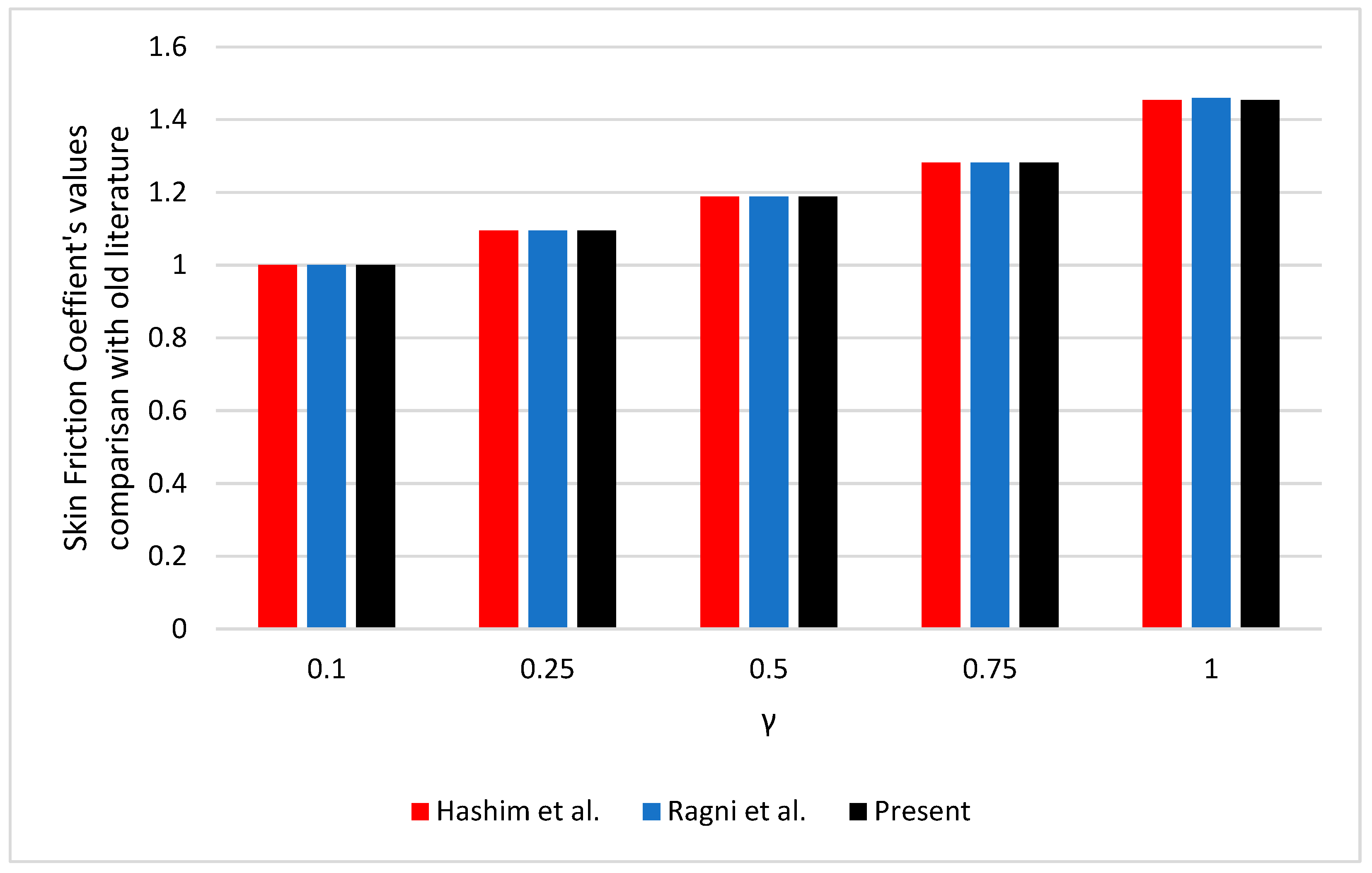
| Γ | Khan and Alshomrani [59] | Ragni et al. [60] | Present |
|---|---|---|---|
| 0.10 | 1.0000000 | 1.0000000 | 1.0000000 |
| 0.25 | 1.0943730 | 1.0943780 | 1.0943770 |
| 0.50 | 1.1887270 | 1.1887150 | 1.1887291 |
| 0.75 | 1.2818190 | 1.2818330 | 1.2818263 |
| 1.00 | 1.4533730 | 1.4593080 | 1.4533642 |
| We | Rb | N | Γ | M | A | Surface Drag Friction Cf | Heat Transfer Nu | Microorganisms’ Density Nn |
|---|---|---|---|---|---|---|---|---|
| 1.0 | - | - | - | - | - | 1.235892 | 1.02357 | 0.985636 |
| 10.0 | - | - | - | - | - | 1.259863 | 1.033987 | 0.965874 |
| 25.0 | - | - | - | - | - | 1.278524 | 1.042548 | 0.947865 |
| 50.0 | - | - | - | - | - | 1.298552 | 1.053952 | 0.925479 |
| - | 0.10 | - | - | - | - | 1.309874 | 1.07899 | 0.995687 |
| - | 0.15 | - | - | - | - | 1.324587 | 1.098745 | 0.987541 |
| - | 0.25 | - | - | - | - | 1.345469 | 1.102155 | 0.978745 |
| - | 0.35 | - | - | - | - | 1.369874 | 1.112548 | 0.964587 |
| - | - | 0.50 | - | - | - | 1.121548 | 1.087855 | 1.124579 |
| - | - | 0.80 | - | - | - | 1.102545 | 1.103215 | 1.112459 |
| - | - | 1.10 | - | - | - | 1.087854 | 1.125449 | 1.101255 |
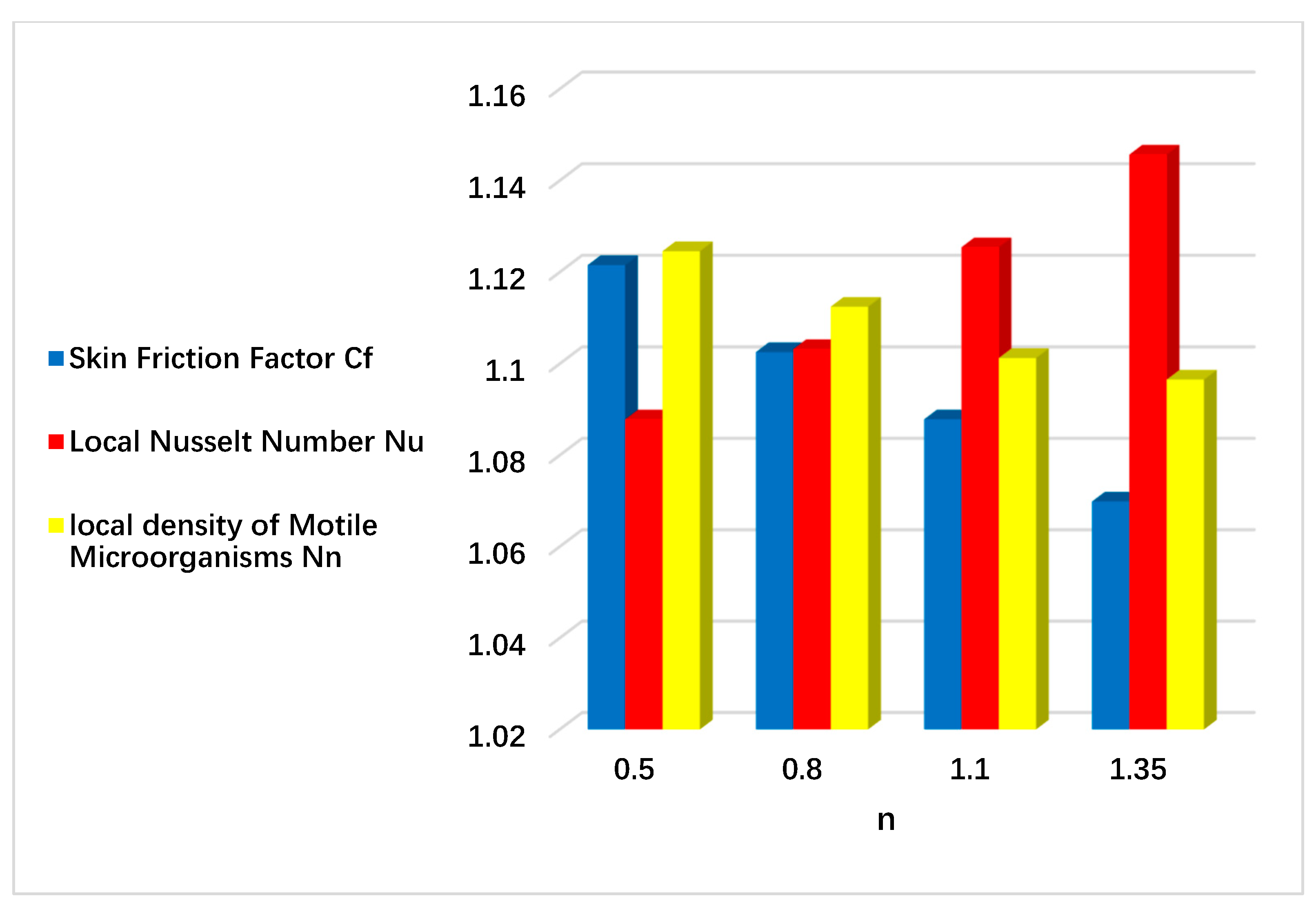
| - | - | 1.35 | - | - | - | 1.069874 | 1.145687 | 1.096548 |
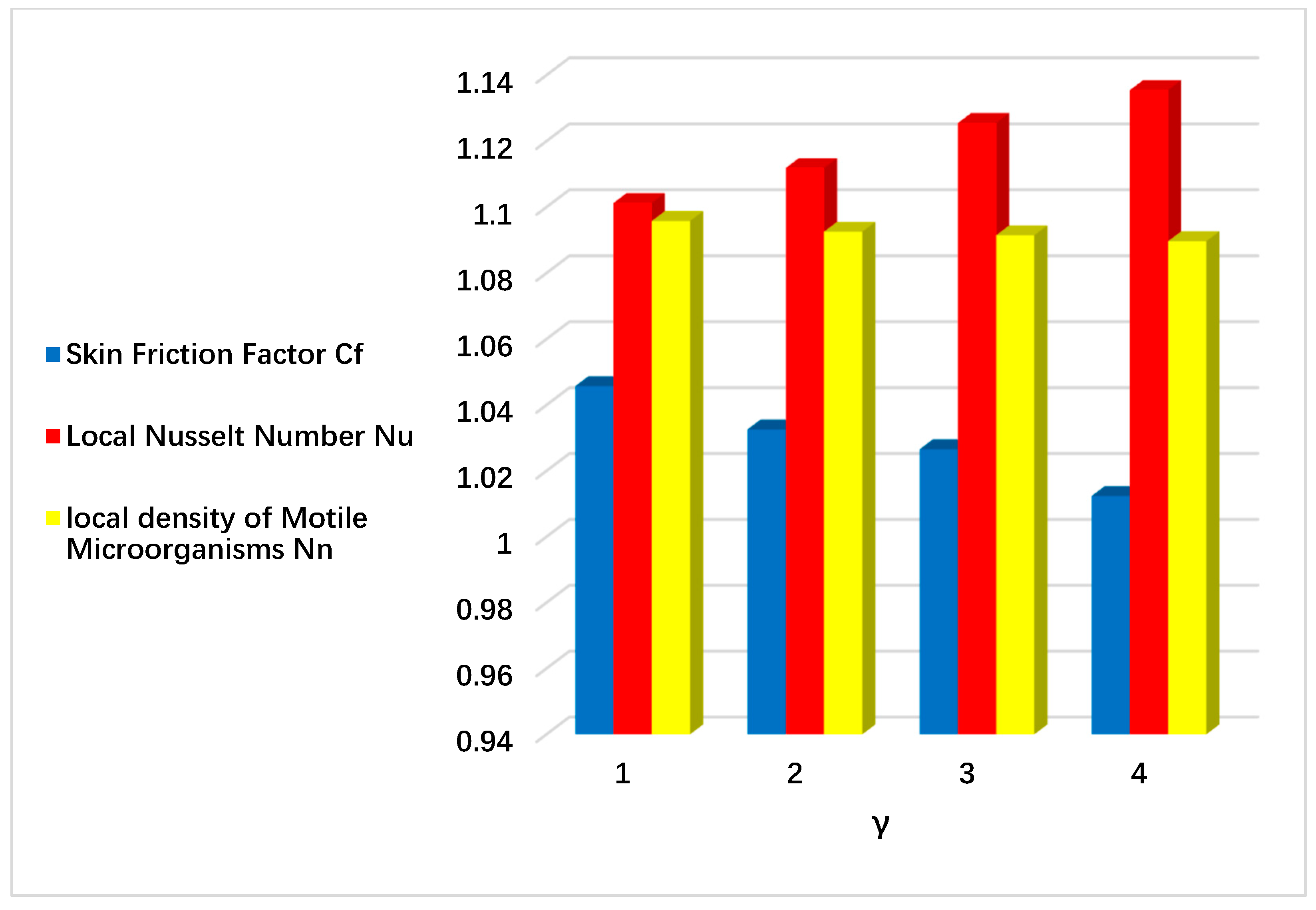
| - | - | - | 1.0 | - | - | 1.045698 | 1.101255 | 1.095785 |
| - | - | - | 2.0 | - | - | 1.032578 | 1.111854 | 1.092549 |
| - | - | - | 3.0 | - | - | 1.026548 | 1.125487 | 1.091458 |
| - | - | - | 4.0 | - | - | 1.01236 | 1.135459 | 1.089652 |
| - | - | - | - | 0.10 | - | 1.894521 | 1.884579 | 1.884578 |
| - | - | - | - | 0.50 | - | 1.890023 | 1.889578 | 1.874578 |
| - | - | - | - | 1.00 | - | 1.880457 | 1.890022 | 1.86458 |
| - | - | - | - | 1.12 | - | 1.874587 | 1.898453 | 1.846578 |
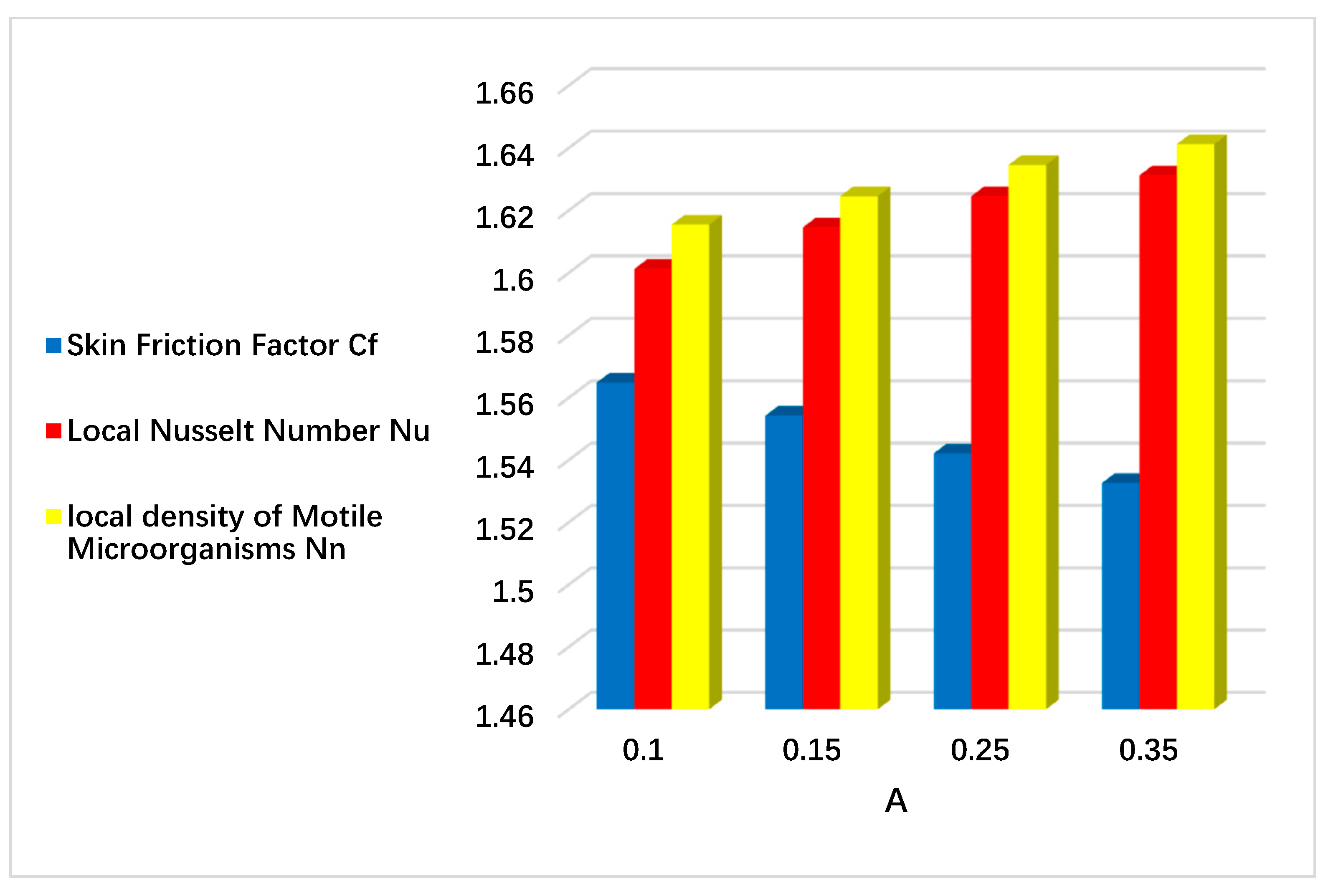
| - | - | - | - | - | 0.10 | 1.564874 | 1.601254 | 1.615458 |
| - | - | - | - | - | 0.15 | 1.554248 | 1.614588 | 1.624578 |
| - | - | - | - | - | 0.25 | 1.542154 | 1.624574 | 1.634588 |
| - | - | - | - | - | 0.35 | 1.532645 | 1.631246 | 1.641249 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasool, G.; Shah, S.Z.H.; Sajid, T.; Jamshed, W.; Cieza Altamirano, G.; Keswani, B.; Artidoro Sandoval Núñez, R.; Sánchez-Chero, M. Spectral Relaxation Methodology for Chemical and Bioconvection Processes for Cross Nanofluid Flowing around an Oblique Cylinder with a Slanted Magnetic Field Effect. Coatings 2022, 12, 1560. https://doi.org/10.3390/coatings12101560
Rasool G, Shah SZH, Sajid T, Jamshed W, Cieza Altamirano G, Keswani B, Artidoro Sandoval Núñez R, Sánchez-Chero M. Spectral Relaxation Methodology for Chemical and Bioconvection Processes for Cross Nanofluid Flowing around an Oblique Cylinder with a Slanted Magnetic Field Effect. Coatings. 2022; 12(10):1560. https://doi.org/10.3390/coatings12101560
Chicago/Turabian StyleRasool, Ghulam, Syed Zahir Hussain Shah, Tanveer Sajid, Wasim Jamshed, Gilder Cieza Altamirano, Bright Keswani, Rafaél Artidoro Sandoval Núñez, and Manuel Sánchez-Chero. 2022. "Spectral Relaxation Methodology for Chemical and Bioconvection Processes for Cross Nanofluid Flowing around an Oblique Cylinder with a Slanted Magnetic Field Effect" Coatings 12, no. 10: 1560. https://doi.org/10.3390/coatings12101560
APA StyleRasool, G., Shah, S. Z. H., Sajid, T., Jamshed, W., Cieza Altamirano, G., Keswani, B., Artidoro Sandoval Núñez, R., & Sánchez-Chero, M. (2022). Spectral Relaxation Methodology for Chemical and Bioconvection Processes for Cross Nanofluid Flowing around an Oblique Cylinder with a Slanted Magnetic Field Effect. Coatings, 12(10), 1560. https://doi.org/10.3390/coatings12101560