Bi Layer Properties in the Bi–FeNi GMR-Type Structures Probed by Spectroscopic Ellipsometry
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Atomic Force Microscopy Study
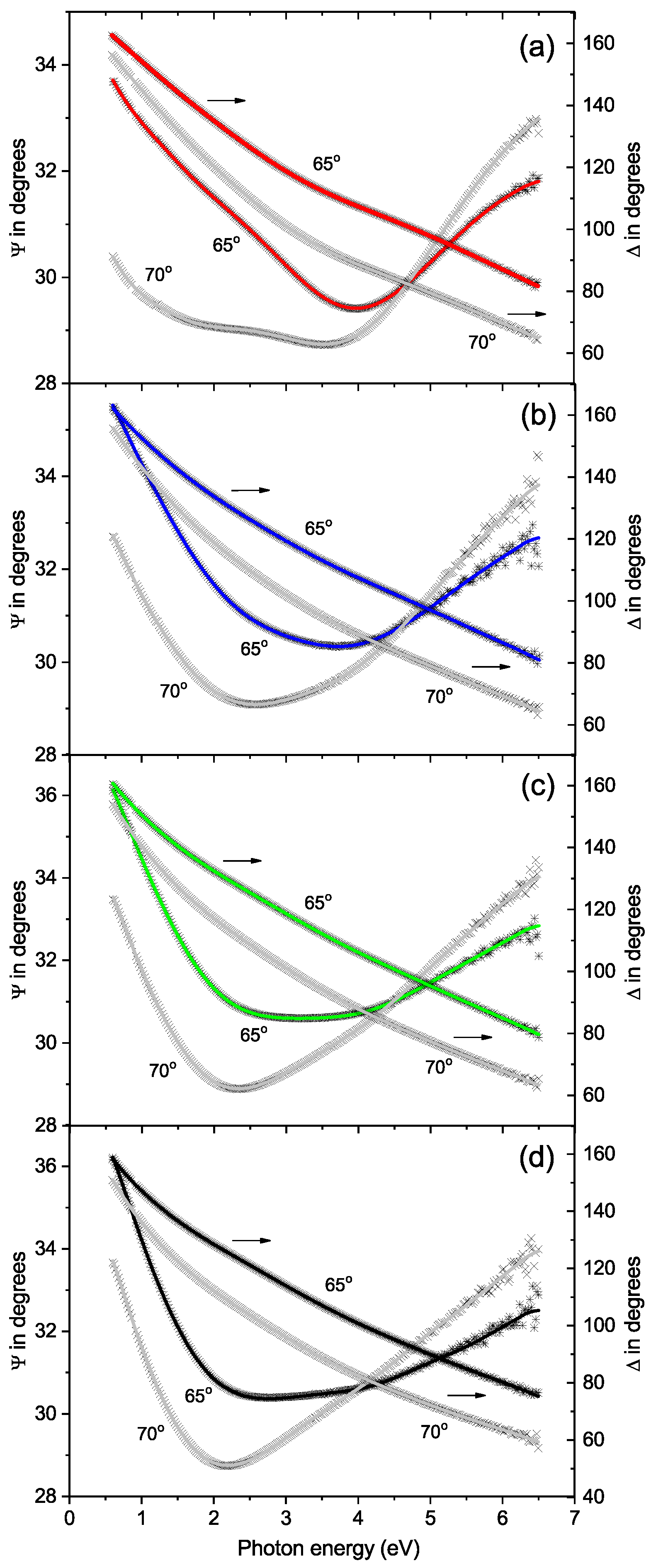
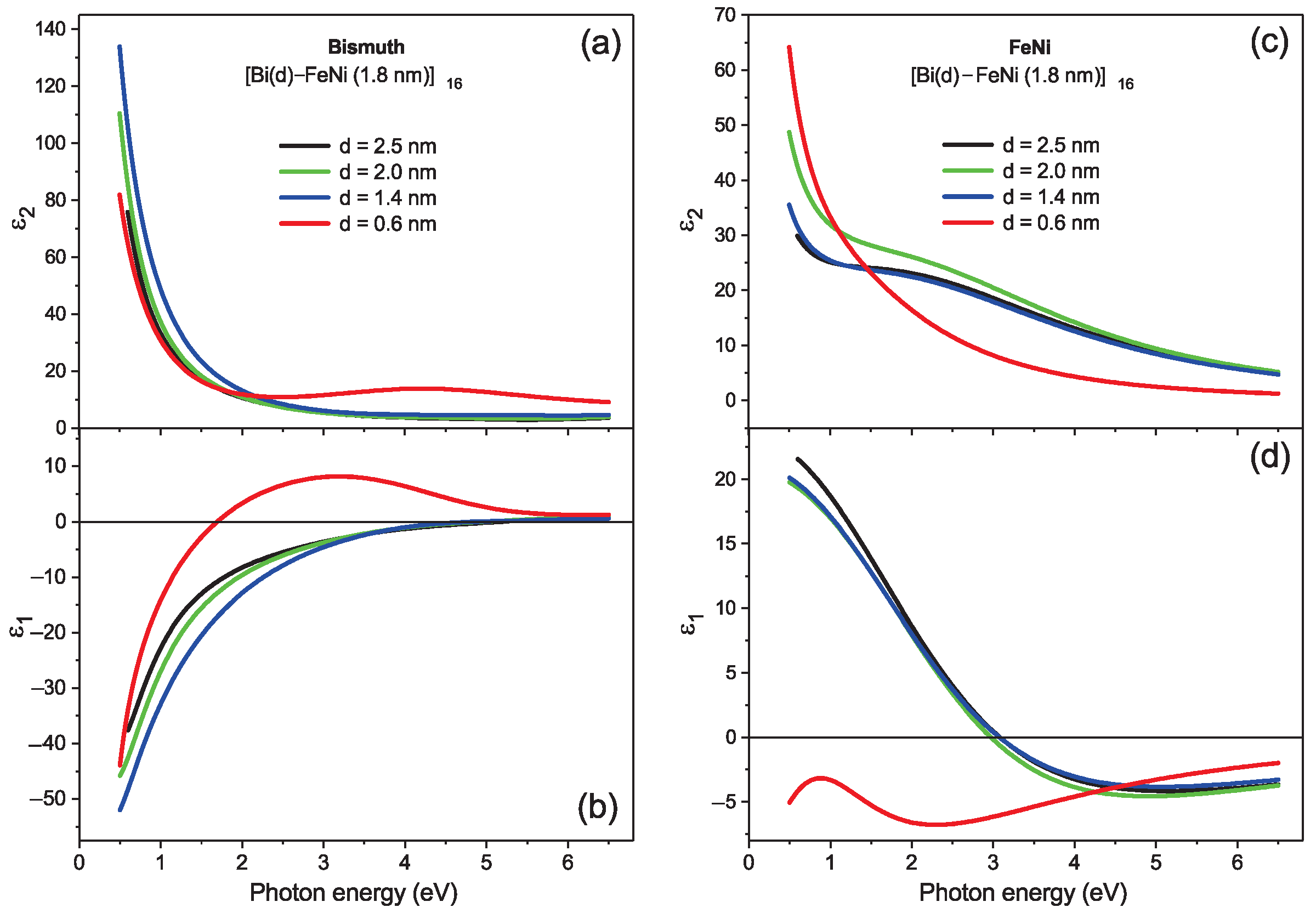
3.2. Spectroscopic Ellipsometry Study of the Ultrathin Bi–FeNi Multilayer Film Samples
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| GMR | Giant magnetoresistance |
| SOC | Spin–orbit coupling |
| TI | Topological insulator |
| MLF | Multilayered film |
| SE | Spectroscopic ellipsometry |
| AFM | Atomic force microscopy |
| FM | Ferromagnetic |
| XRD | X-ray diffraction |
| XRR | X-ray reflectivity |
References
- Bychkov, Y.A.; Rashba, E.I. Properties of a 2D electron gas with lifted spectral degeneracy. JETP Lett. 1984, 39, 78–81. [Google Scholar]
- Golin, S. Band Structure of Bismuth: Pseudopotential Approach. Phys. Rev. B 1968, 166, 643–651. [Google Scholar] [CrossRef]
- Gonze, X.; Michenaud, J.-P.; Vigneron, J.-P. First-principles study of As, Sb, and Bi electronic properties. Phys. Rev. B 1990, 41, 11827–11836. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Allen, R.E. Electronic structure of the semimetals Bi and Sb. Phys. Rev. B 1995, 52, 1566–1577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hofmann, P. The surfaces of bismuth: Structural and electronic properties. Prog. Surf. Sci. 2006, 81, 191–245. [Google Scholar] [CrossRef]
- Yokota, Y.; Takeda, J.; Dang, C.; Han, G.; McCarthy, D.N.; Nagao, T.; Hishita, S.; Kitajima, K.; Katayama, I. Surface metallic states in ultrathin Bi(001) films studied with terahertz time-domain spectroscopy. Appl. Phys. Lett. 2012, 100, 251605. [Google Scholar] [CrossRef]
- Hoffman, C.A.; Meyer, J.R.; Bartoli, F.J. Semimetal-to-semiconductor transition in Bismuth thin films. Phys. Rev. B 1993, 48, 11431–11434. [Google Scholar] [CrossRef]
- Koroteev, Y.M.; Bihlmayer, G.; Chulkov, E.V.; Blugel, S. First-principles investigation of structural and electronic properties of ultrathin Bi films. Phys. Rev. B 2008, 77, 045428. [Google Scholar] [CrossRef] [Green Version]
- Wada, M.; Murakami, S.; Freimuth, F.; Bihlmayer, G. Localized edge states in two-dimensional topological insulators: Ultrathin Bi films. Phys. Rev. B 2011, 83, 121310(R). [Google Scholar] [CrossRef] [Green Version]
- Murakami, S. Quantum Spin Hall Effect and Enhanced Magnetic Response by Spin-Orbit Coupling. Phys. Rev. Lett. 2006, 97, 236805. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Kane, C.L.; Mele, E.J. Topological Insulators in Three Dimensions. Phys. Rev. Lett. 2007, 98, 106803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Z.; Liu, C.-X.; Wu, Y.-S.; Duan, W.-H.; Liu, F.; Wu, J. Stable nontrivial Z2 topology in ultrathin Bi(111) films: A first principles study. Phys. Rev. Lett. 2011, 107, 136805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kovaleva, N.N.; Chvostova, D.; Pacherova, O.; Muratov, A.V.; Fekete, L.; Sherstnev, I.A.; Kugel, K.I.; Pudonin, F.A.; Dejneka, A. Bismuth layer properties in the ultrathin Bi–FeNi multilayer films probed by spectroscopic ellipsometry. Appl. Phys. Lett. 2021, 119, 183101. [Google Scholar] [CrossRef]
- Sherstnev, I.A. Electronic Transport and Magnetic Structure of Nanoisland Ferromagnetic Systems. Ph.D. Thesis, P.N. Lebedev Physical Institute, Moscow, Russia, 2014. [Google Scholar]
- Boltaev, A.P.; Pudonin, F.A.; Shertnev, I.A.; Egorov, D.A. Detection of the metal-insulator transition in disordered systems of magnetic nanoislands. JETP 2017, 125, 465–468. [Google Scholar] [CrossRef]
- Woollam, J.A. VASE Spectroscopic Ellipsometry Data Analysis Software; J.A. Woollam, Co.: Lincoln, NE, USA, 2010. [Google Scholar]
- Stupakov, A.; Bagdinov, A.V.; Prokhorov, V.V.; Bagdinova, A.N.; Demikhov, E.I.; Dejneka, A.; Kugel, K.I.; Gorbatsevich, A.A.; Pudonin, F.A.; Kovaleva, N.N. Out-of-plane and in-plane magnetization behaviour of dipolar interacting FeNi nanoislands around the percolation threshold. J. Nanomater. 2016, 3190260. [Google Scholar] [CrossRef]
- Kovaleva, N.N.; Chvostova, D.; Bagdinov, A.V.; Petrova, M.G.; Demikhov, E.I.; Pudonin, F.A.; Dejneka, A. Interplay of electronic correlation and localization in disordered β-tantalum films: Evidence from dc transport and spectroscopic ellipsometry study. Appl. Phys. Lett. 2015, 106, 051907. [Google Scholar] [CrossRef]
- Kovaleva, N.; Chvostova, D.; Dejneka, A. Localization phenomena in disordered tantalum films. Metals 2017, 7, 257. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Elsevier Science: San Diego, CA, USA, 1991. [Google Scholar]
- Hütten, A.; Mrozek, S.; Heitmann, S.; Hempel, T.; Brückl, H.; Reiss, G. Evolution of the GMR-Effect Amplitude in Copper-Permalloy-Multilayered Thin Films. Acta Mater. 1999, 47, 4245–4252. [Google Scholar] [CrossRef]
- Mathon, J. Exchange Interactions and Giant Magnetoresistance in Magnetic Multilayers. Contemp. Phys. 1991, 32, 143–156. [Google Scholar] [CrossRef]
- Nagao, T.; Sadowski, J.T.; Saito, M.; Yaginuma, S.; Fujikawa, Y.; Kogure, T.; Ohno, T.; Hasegawa, S.; Sakurai, T. Nanofilm allotrope and phase transformation of ultrathin Bi film on Si(111) − 7 × 7. Phys. Rev. Lett. 2004, 93, 105501. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.Y.; Jain, A.L. Modulated Piezoreflectance in Bismuth. Phys. Rev. B 1970, 2, 2978–2983. [Google Scholar] [CrossRef]
- Lenham, A.P.; Treherne, D.M.; Metcalfe, R.J. Optical Properties of Antimony and Bismuth Crystals. J. Opt. Soc. Am. 1965, 55, 1072–1074. [Google Scholar] [CrossRef]
- Hunderi, O. Optical properties of crystalline and amorphous bismuth films. J. Phys. F 1975, 5, 2214–2225. [Google Scholar] [CrossRef]
- Toudert, J.; Serna, R. Interband transitions in semi-metals, semiconductors, and topological insulators: A new driving force for plasmonics and nanophotonics [Invited]. Opt. Mater. Express 2017, 7, 2299–2325. [Google Scholar] [CrossRef]
- Kovaleva, N.N.; Kusmartsev, F.V.; Mekhiya, A.B.; Trunkin, I.N.; Chvostova, D.; Davydov, A.B.; Oveshnikov, L.N.; Pacherova, O.; Sherstnev, I.A.; Kusmartseva, A.; et al. Control of Mooij correlations at the nanoscale in the disordered metallic Ta-nanoisland FeNi multilayers. Sci. Rep. 2020, 10, 21172. [Google Scholar] [CrossRef] [PubMed]
- Suslov, A.V.; Davydov, A.B.; Oveshnikov, L.N.; Morgun, L.A.; Kugel, K.I.; Zakhvalinskii, V.S.; Pilyuk, E.A.; Kochura, A.V.; Kuzmenko, A.P.; Pudalov, V.M.; et al. Observation of subkelvin superconductivity in Cd3As2 thin films. Phys. Rev. B 2019, 99, 094512. [Google Scholar] [CrossRef] [Green Version]
- Kochura, A.V.; Zakhvalinskii, V.S.; Htet, A.Z.; Ril’, A.I.; Pilyuk, E.A.; Kuz’menko, A.P.; Aronzon, B.A.; Marenkin, S.F. Growth of thin cadmium arsenide films by magnetron sputtering and their structure. Inorg. Mater. 2019, 55, 879–886. [Google Scholar] [CrossRef]
- Kovaleva, N.; Chvostova, D.; Fekete, L.; Muratov, A. Morphology and Optical Properties of Thin Cd3As2 Films of a Dirac Semimetal Compound. Metals 2020, 10, 1398. [Google Scholar] [CrossRef]


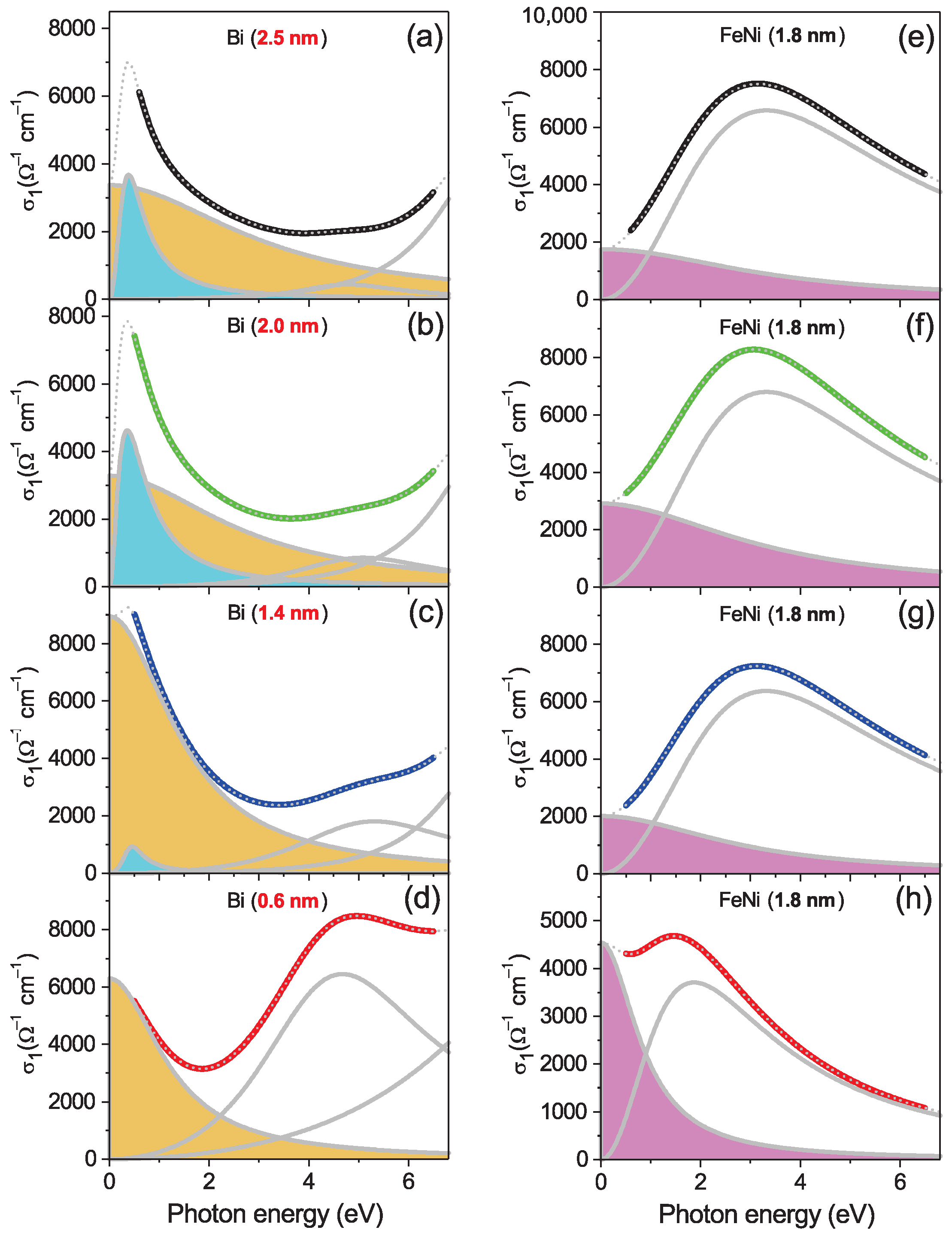
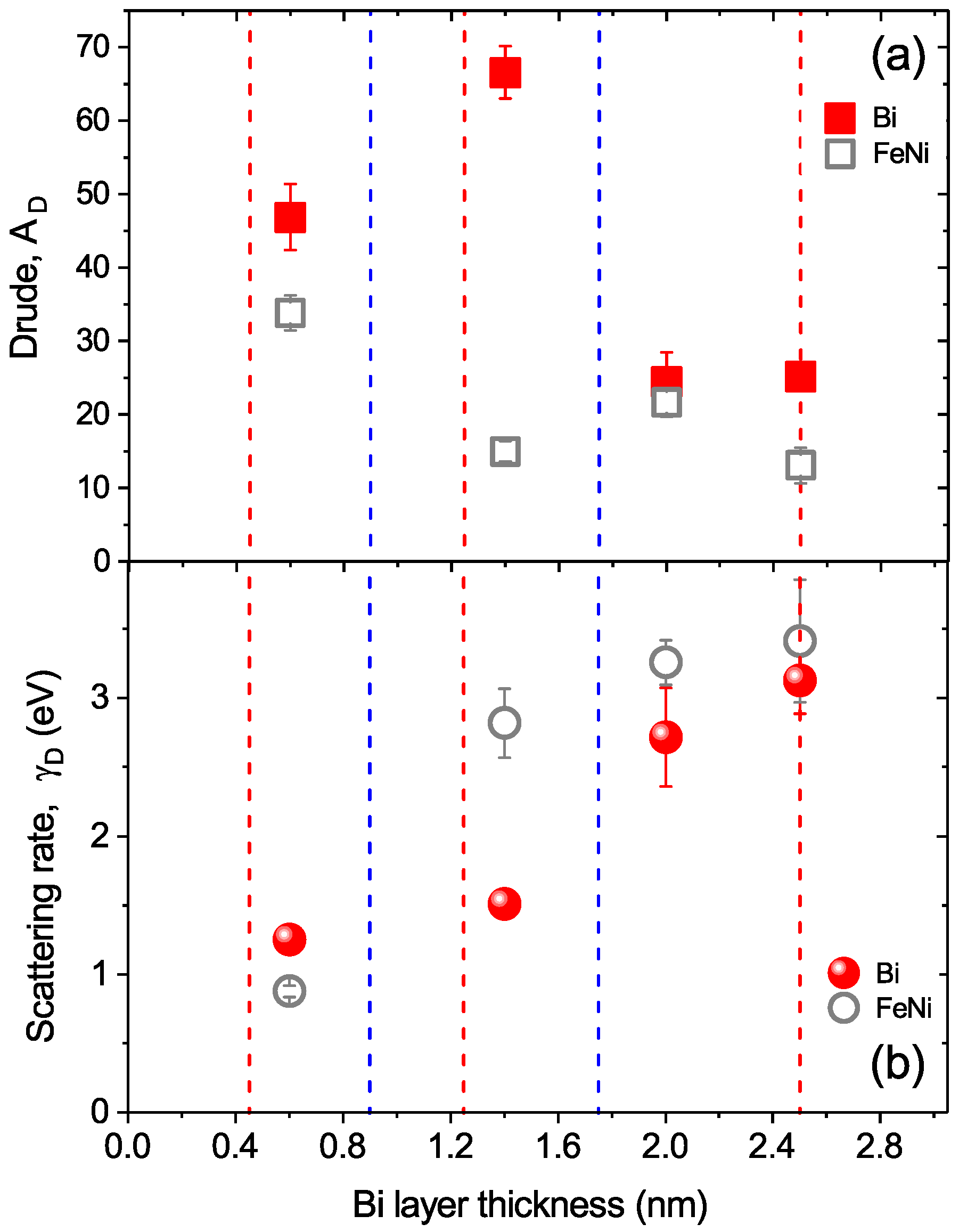
| Parameters | 0.6 nm | 1.4 nm | 2.0 nm | 2.5 nm | |
|---|---|---|---|---|---|
| Drude | 46.(9) ± 4 | 66.(7) ± 4 | 24.(5) ± 4 | 25.(1) ± 2 | |
| 1.2(5) ± 0.09 | 1.51(0) ± 0.06 | 2.7(2) ± 0.4 | 3.1(3) ± 0.2 | ||
| 6300 ± 540 | 8970 ± 540 | 3290 ± 540 | 3370 ± 270 | ||
| Lorentz | – | 0.45(8) ± 0.05 | 0.35(9) ± 0.01 | 0.38(6) ± 0.004 | |
| oscillator | – | 15.(0) ± 6 | 96.(0) | 70.(8) ± 2 | |
| – | 0.52(6) ± 0.09 | 0.79(1) ± 0.02 | 0.67(6) | ||
| Lorentz | 4.67 | 5.31(5) ± 0.03 | 5.08(7) ± 0.04 | 4.77(5) ± 0.04 | |
| oscillator | 10.2(7) ± 0.6 | 2.53(2) ± 0.05 | 1.2(5) ± 0.1 | 0.67(6) ± 0.08 | |
| 4.2(1) ± 0.07 | 3.99(3) ± 0.07 | 3.4(7) ± 0.2 | 2.5(5) ± 0.2 | ||
| Lorentz | 11.1 | 7.8 | 7.7 | 7.7 | |
| oscillator | 7.2 | 4.1 | 4.1 | 4.1 | |
| 8.9 | 2.8 | 2.8 | 2.8 |
| Parameters | 0.6 nm | 1.4 nm | 2.0 nm | 2.5 nm | |
|---|---|---|---|---|---|
| Drude | 33.(8) ± 2 | 15.(0) ± 1 | 21.(7) ± 2 | 13.(1) ± 2 | |
| 0.876(5) ± 0.04 | 2.8(2) ± 0.3 | 3.4(2) ± 0.4 | 3.1(3) ± 0.2 | ||
| 4540 ± 270 | 2020 ± 130 | 2920 ± 270 | 1760 ± 270 | ||
| Lorentz | 1.87 | 3.32 | 3.32 | 3.32 | |
| oscillator | 14.76 | 14.28 | 15.23 | 14.74 | |
| 3.62 | 5.88 | 5.65 | 5.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovaleva, N.; Chvostova, D.; Fekete, L.; Dejneka, A. Bi Layer Properties in the Bi–FeNi GMR-Type Structures Probed by Spectroscopic Ellipsometry. Coatings 2022, 12, 872. https://doi.org/10.3390/coatings12060872
Kovaleva N, Chvostova D, Fekete L, Dejneka A. Bi Layer Properties in the Bi–FeNi GMR-Type Structures Probed by Spectroscopic Ellipsometry. Coatings. 2022; 12(6):872. https://doi.org/10.3390/coatings12060872
Chicago/Turabian StyleKovaleva, Natalia, Dagmar Chvostova, Ladislav Fekete, and Alexandr Dejneka. 2022. "Bi Layer Properties in the Bi–FeNi GMR-Type Structures Probed by Spectroscopic Ellipsometry" Coatings 12, no. 6: 872. https://doi.org/10.3390/coatings12060872
APA StyleKovaleva, N., Chvostova, D., Fekete, L., & Dejneka, A. (2022). Bi Layer Properties in the Bi–FeNi GMR-Type Structures Probed by Spectroscopic Ellipsometry. Coatings, 12(6), 872. https://doi.org/10.3390/coatings12060872







