Prediction of Mechanical Properties of Thin-Walled Bar with Open Cross-Section under Restrained Torsion
Abstract
:1. Introduction
2. Theoretical Analysis in Free Torsion
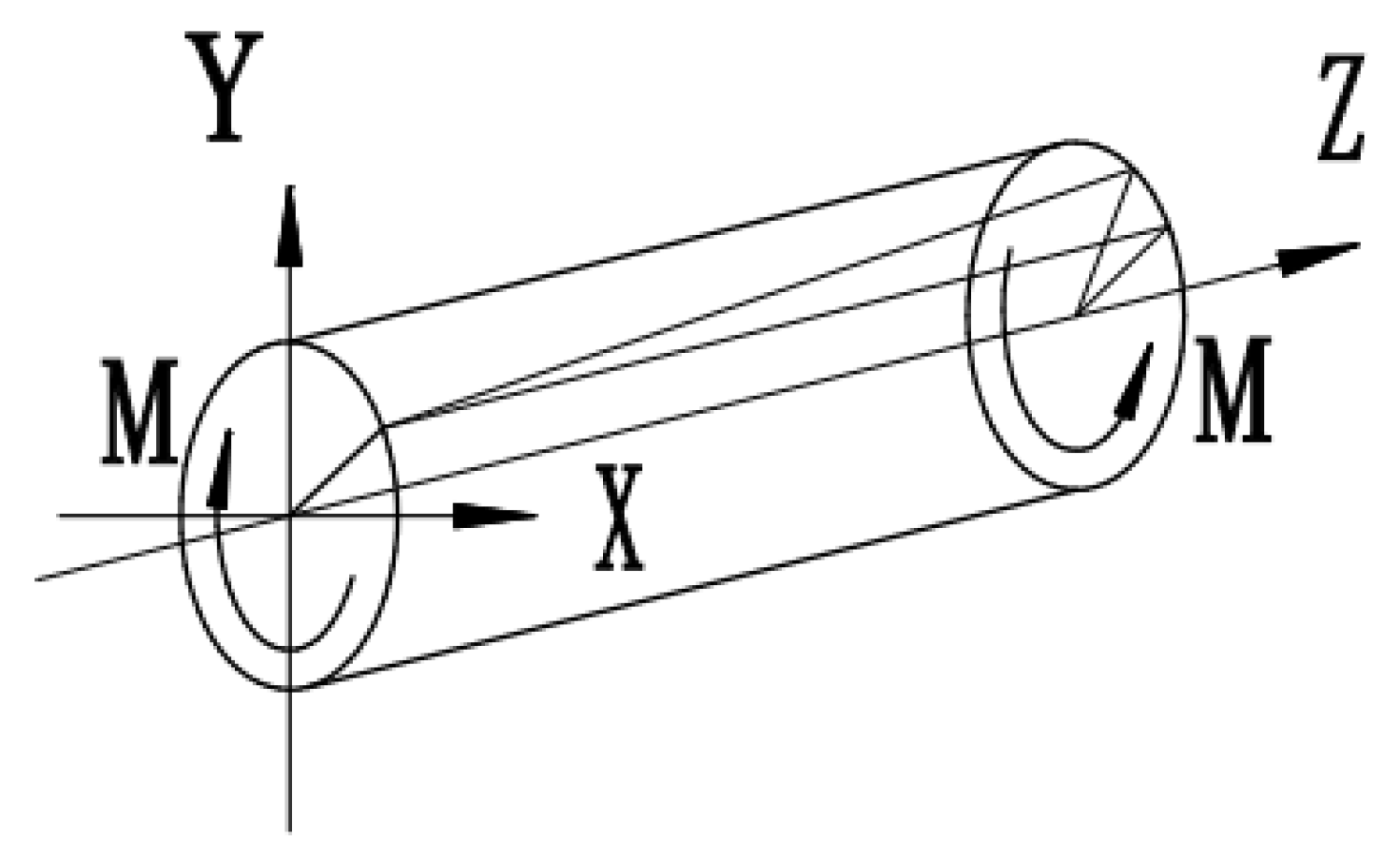
2.1. Saint-Venant’s Fundamental Equation
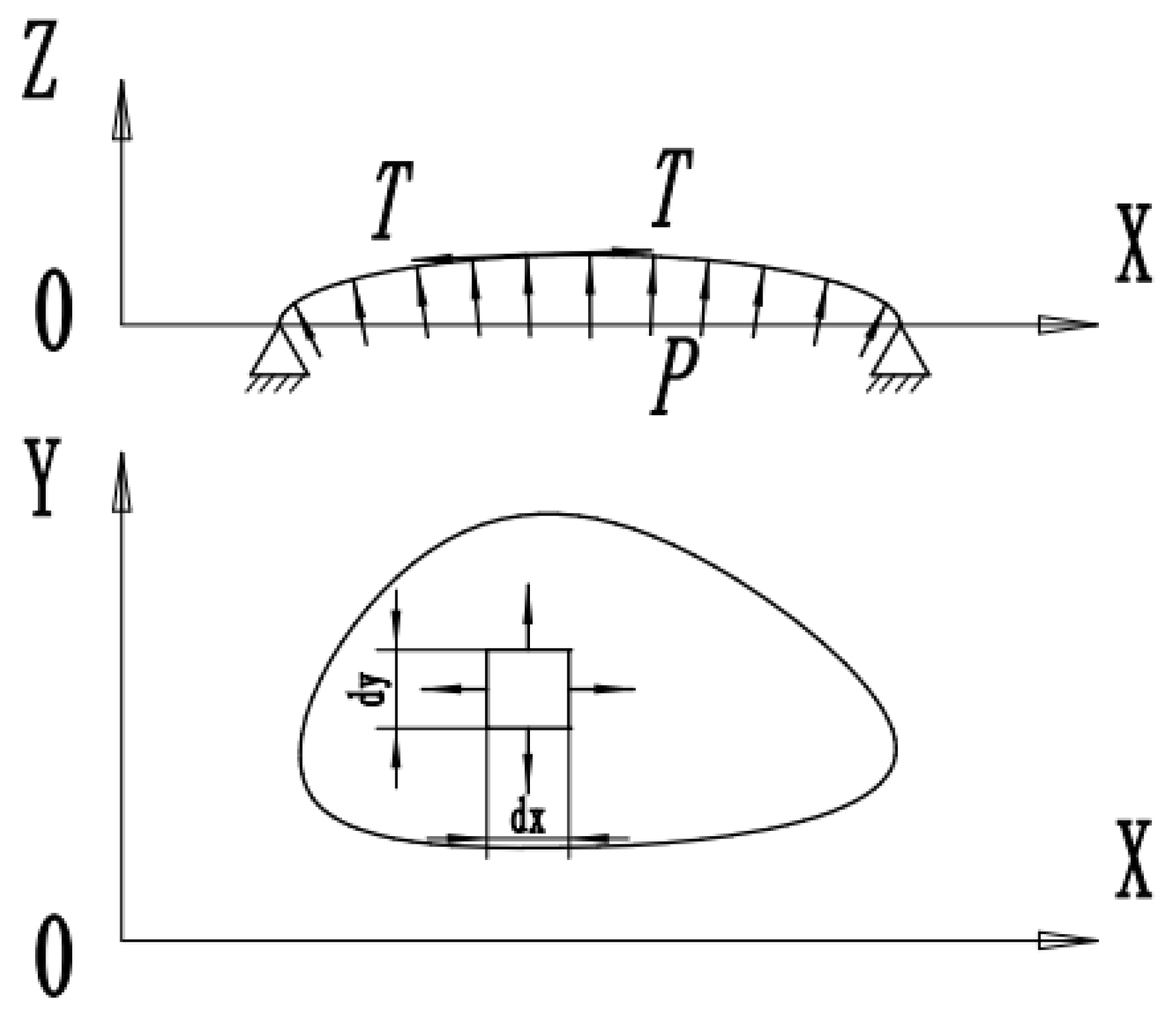
2.2. Membrane Analogy Theory in Torsion
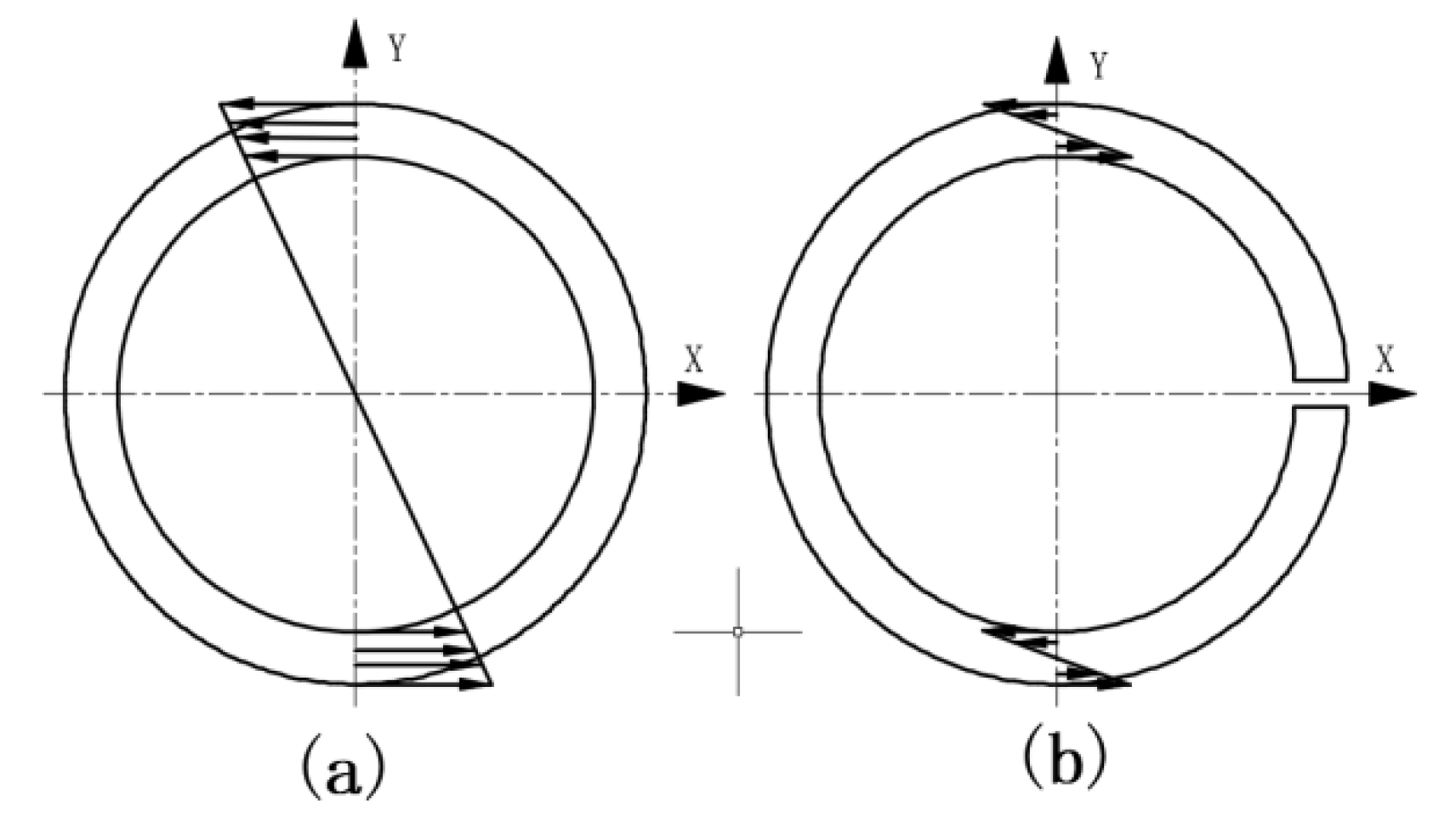
2.3. Torsional Properties of Thin-Walled Bars with Open and Closed Cross-Section
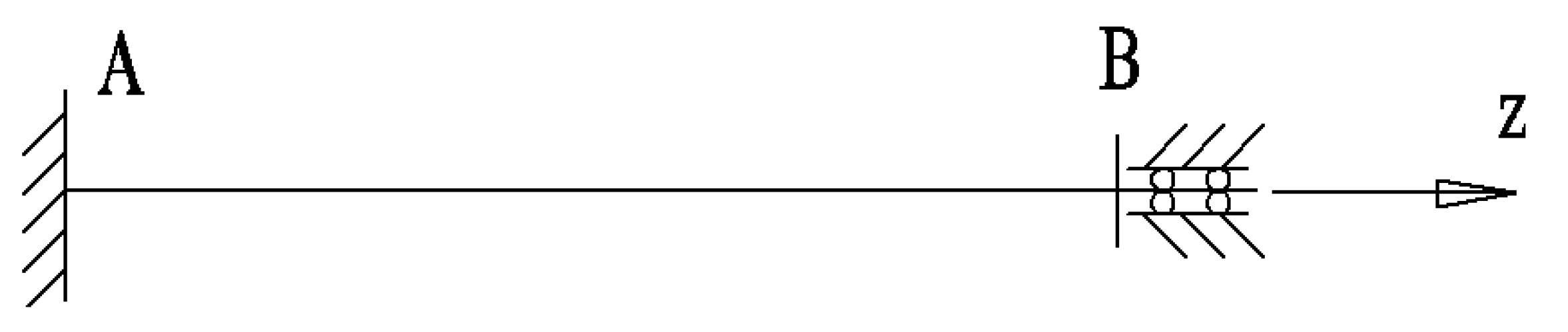
3. Theoretical Analysis in Constrained Torsion
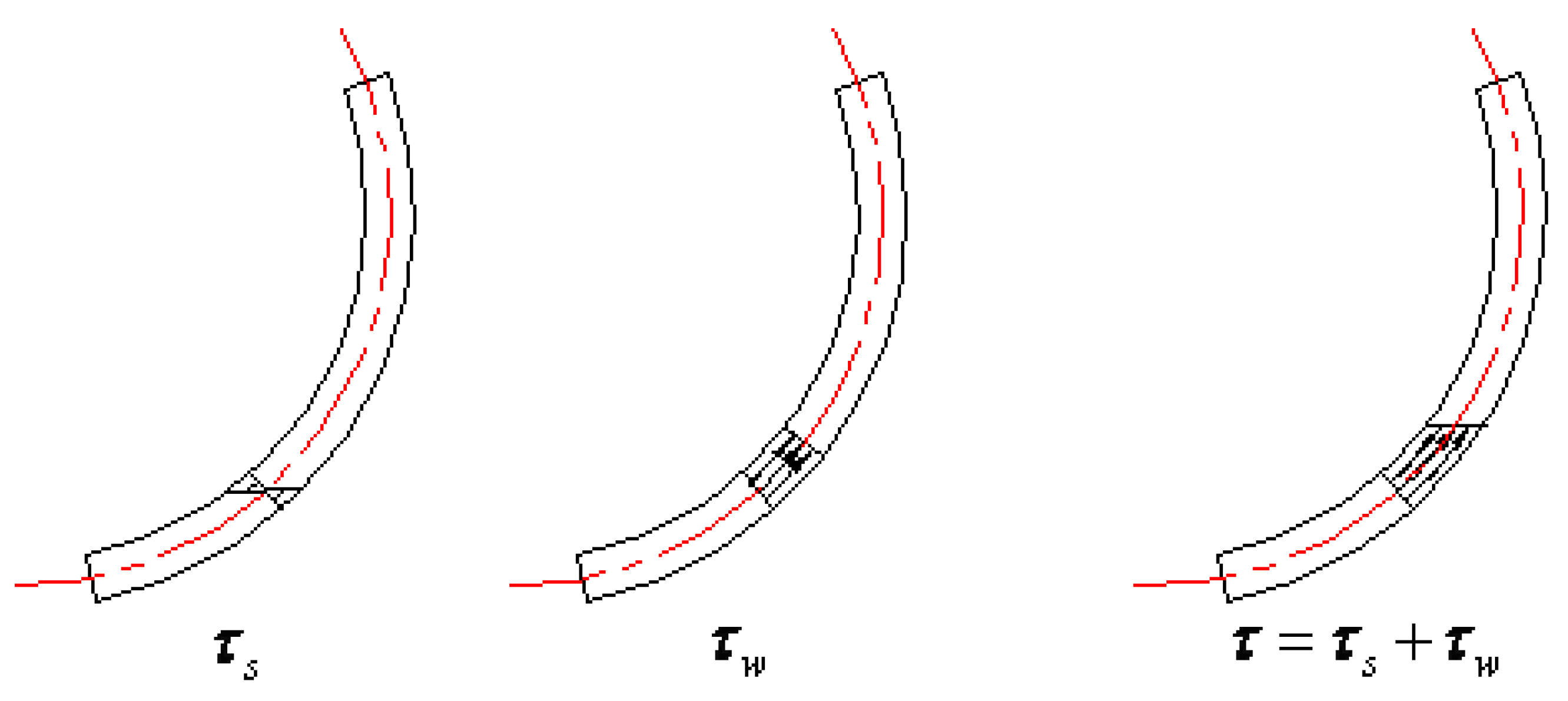
3.1. Differential Equation of Constrained Torsion in Thin-Walled Bar with Open Cross-Section
3.2. Initial Parameter Method for Constrained Torsion Differential Equations
3.3. Constrained Torsion Problem of Thin-Walled Bar with Open Cross-Section
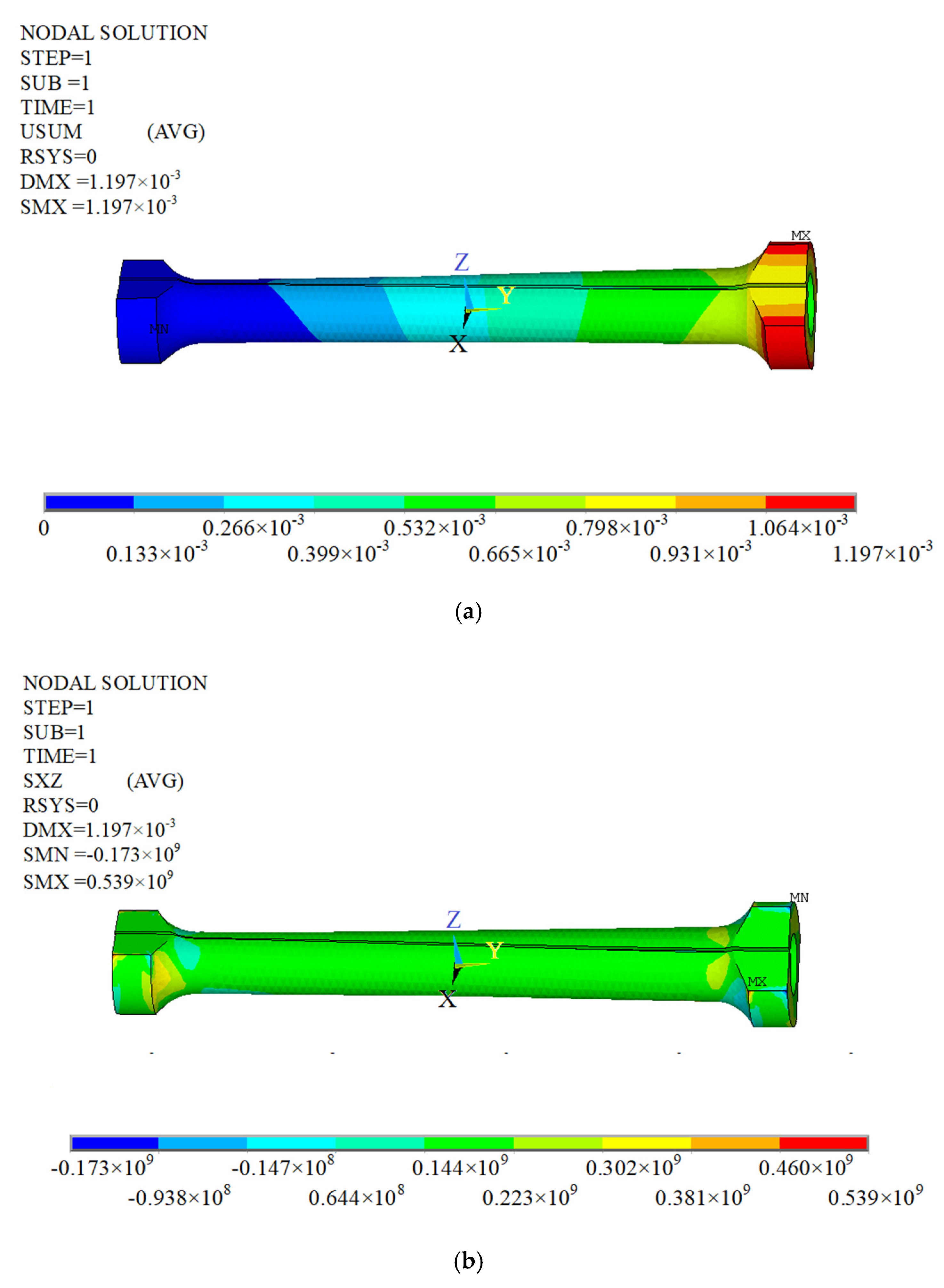
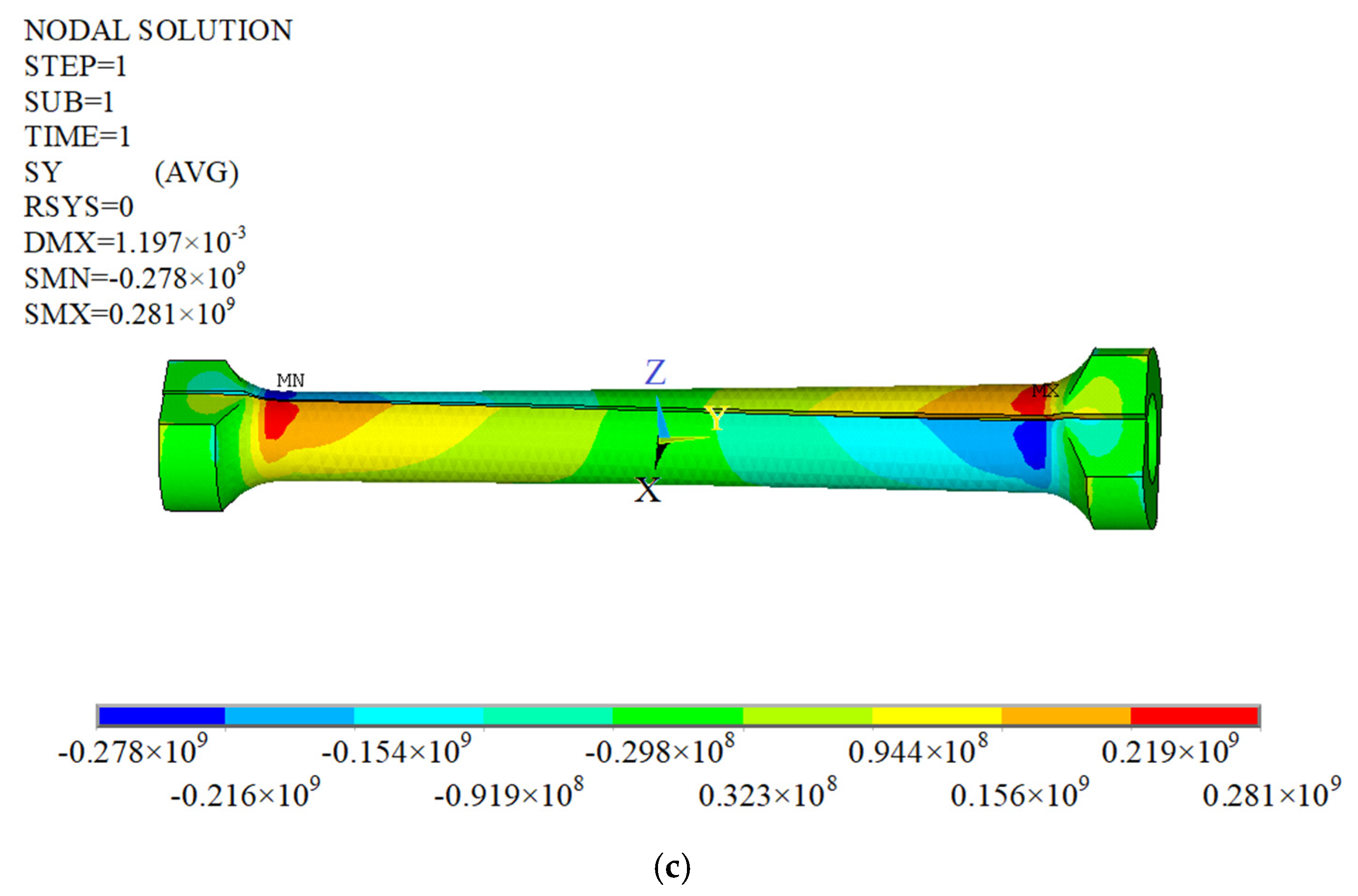
4. Experiment and Numerical Modeling Validation
5. Conclusions
- (1)
- The elastic properties of the thin-walled bar with open and closed cross-sections were compared on the basis of Saint-Venant’s theory, and the special properties of the thin-walled bar with an open cross-section were determined. Compared to the closed thin-walled bar, the thin-walled bar with an open cross-section can support a larger percentage of torsion and is more appropriate for the elastic structures where large deformation is needed.
- (2)
- The mechanical characteristic equation of the thin-walled bar with an open cross-section was established by means of small deformation theory, which can be used for predicting the analytical solution of the torsion angle and distribution of stress for the thin-walled bar with an open cross-section under restrained torsion.
- (3)
- The mechanical properties of the thin-walled bar with an open cross-section were studied through an experimental test and mathematical analysis. The values of torsion angle and normal stress observed from FE simulations and experimental tests were similar to those of the theoretical solution (the error was less than 10%). The predictions of the current work can be regarded as the basic reference for the design of a thin-walled bar with an open cross-section.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alam, M.I.; Kanagarajan, B.; Jana, P. Optimal design of thin-walled open cross-section column for maximum buckling load. Thin Walled Struct. 2019, 141, 423–434. [Google Scholar] [CrossRef]
- Sapountzakis, E.J. Torsional vibrations of composite bars by BEM. Compos. Struct. 2005, 70, 229–239. [Google Scholar] [CrossRef]
- Zaczynska, M.; Kazmierczyk, F. Multi-Mode Buckling Analysis of FGM Channel Section Beams. Materials 2020, 13, 2567. [Google Scholar] [CrossRef]
- Szychowski, A. A theoretical analysis of the local buckling in thin-walled bars with open cross-section subjected to warping torsion. Thin Walled Struct. 2014, 76, 42–55. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Kim, N.I.; Lee, J. Analysis of thin-walled open-section beams with functionally graded materials. Compos. Struct. 2016, 138, 75–83. [Google Scholar] [CrossRef]
- Christiansen, S. A review of some integral equations for solving the Saint-Venant torsion problem. J. Elast. 1978, 8, 1–20. [Google Scholar] [CrossRef]
- Manta, D.; Gonçalves, R.; Camotim, D. Combining shell and GBT-based finite elements: Vibration and dynamic analysis. Thin Walled Struct. 2021, 167, 108187. [Google Scholar] [CrossRef]
- Murray, N.W.; Lau, Y.C. The behaviour of a channel cantilever under combined bending and torsional loads. Thin Walled Struct. 1983, 1, 55–74. [Google Scholar] [CrossRef]
- Plaut, R.H.; Moen, C.D. Lateral-torsional deformations of single-span and two-span thin-walled beams with continuous bracing. J. Constr. Steel Res. 2021, 179, 106534. [Google Scholar] [CrossRef]
- Plaut, R.H.; Moen, C.D. Flexural-torsional deformations of imperfect thin-walled columns with discrete bracing. Thin Walled Struct. 2020, 154, 106897. [Google Scholar] [CrossRef]
- Pham, C.H.; Hancock, G.J. Shear tests and design of cold-formed steel channels with central square holes. Thin Walled Struct. 2020, 149, 106650. [Google Scholar] [CrossRef]
- Wang, X.; Xia, P.; Masarati, P. Optimal Control of Pretwisted Rotating Thin-Walled Beams via Piezoelectrically Induced Couplings. AIAA J. 2019, 57, 1–17. [Google Scholar] [CrossRef]
- Yu, J.; Sun, W.; Huang, H.; Huang, Y. Study on the deformation control and microstructures of thin-walled parts repaired by laser cladding. Coatings 2020, 10, 369. [Google Scholar] [CrossRef] [Green Version]
- Troyani, N.; Perez, A.; Gomes, C.; Baiz, P.; Fonseca, Z.D. Selective finite element refinement in torsional problems based on the membrane analogy. Finite Elem. Anal. Des. 2009, 45, 547–554. [Google Scholar] [CrossRef]
- Aronov, B.; Sharir, M. On a Procedure for analyzing Saint-Venant torsional stresses by means of membrane analogy. J. Jpn. Soc. Exp. Mech. 1990, 10, 137–173. [Google Scholar] [CrossRef]
- Obst, M.; Kurpisz, D.; Paczos, P. The experimental and analytical investigations of torsion phenomenon of thin-walled cold formed channel beams subjected to four-point bending. Thin Walled Struct. 2016, 106, 179–186. [Google Scholar] [CrossRef]
- Prisekin, V.L.; Rastorguev, G.I. Bending and cramped torsion of thin-walled rods. Mech. Solids 2019, 54, 1030–1041. [Google Scholar] [CrossRef]
- Lanoye, E.; Dormieux, L.; Kondo, D. A micromechanical-based damage analysis of a cylindrical bar under torsion: Theoretical results, finite elements verification and application. Theor. Appl. Fract. Mech. 2014, 74, 116–125. [Google Scholar] [CrossRef]
- Erkmen, R.E.; Mohareb, M. Torsion analysis of thin-walled beams including shear deformation. Thin Walled Struct. 2008, 44, 1096–1108. [Google Scholar] [CrossRef]
- Janarthanan, B.; Mahendran, M. Behaviour and strength of unlipped channel sections under combined bending and torsion. J. Constr. Steel Res. 2021, 182, 106648. [Google Scholar] [CrossRef]
- Wan, H.X.; Huang, B.; Mahendran, M. Experiments and numerical modelling of cold-formed steel beams under bending and torsion. Thin Walled Struct. 2021, 161, 107424. [Google Scholar] [CrossRef]

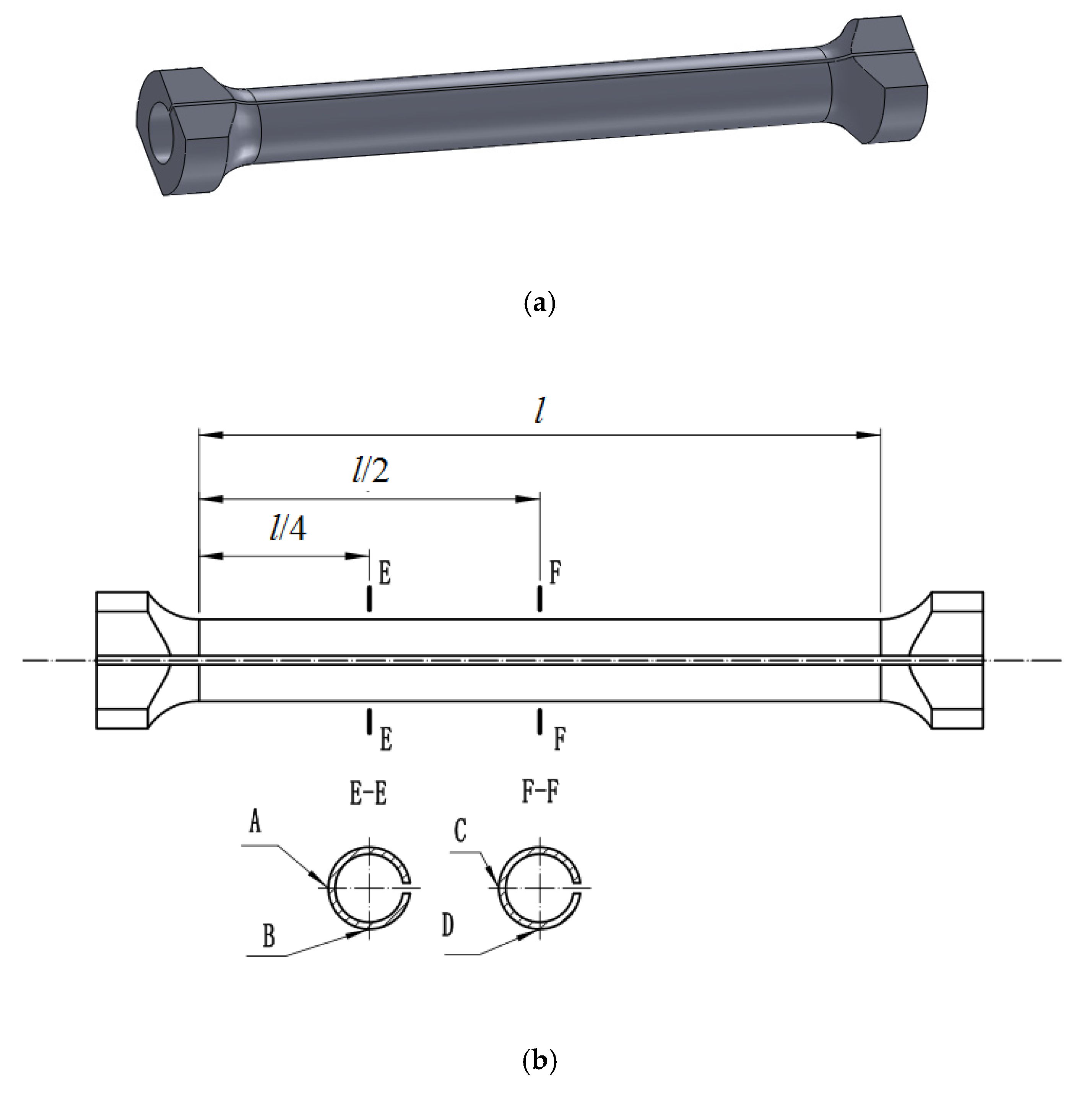

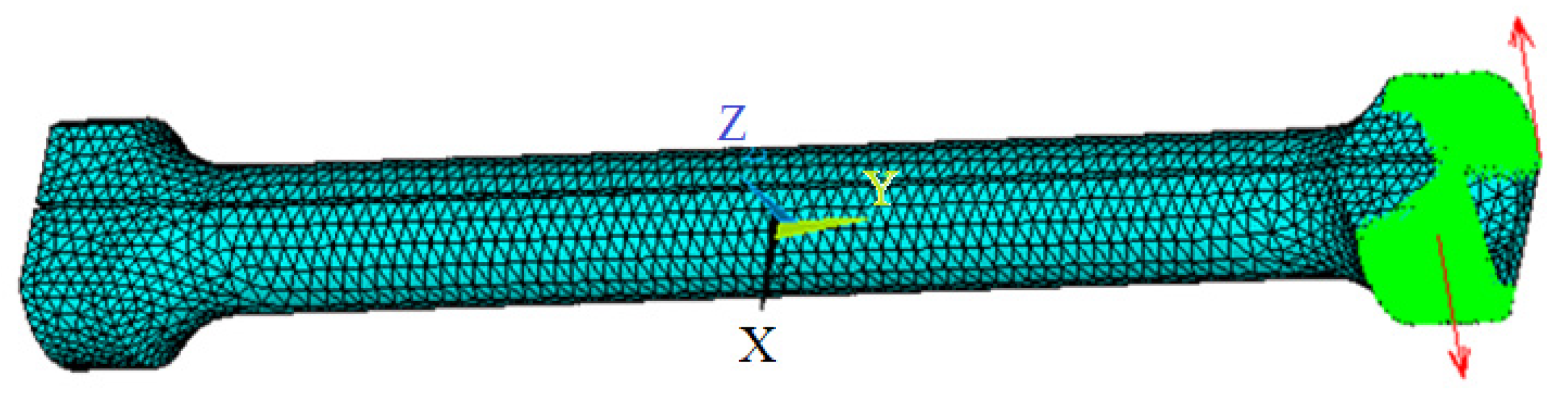
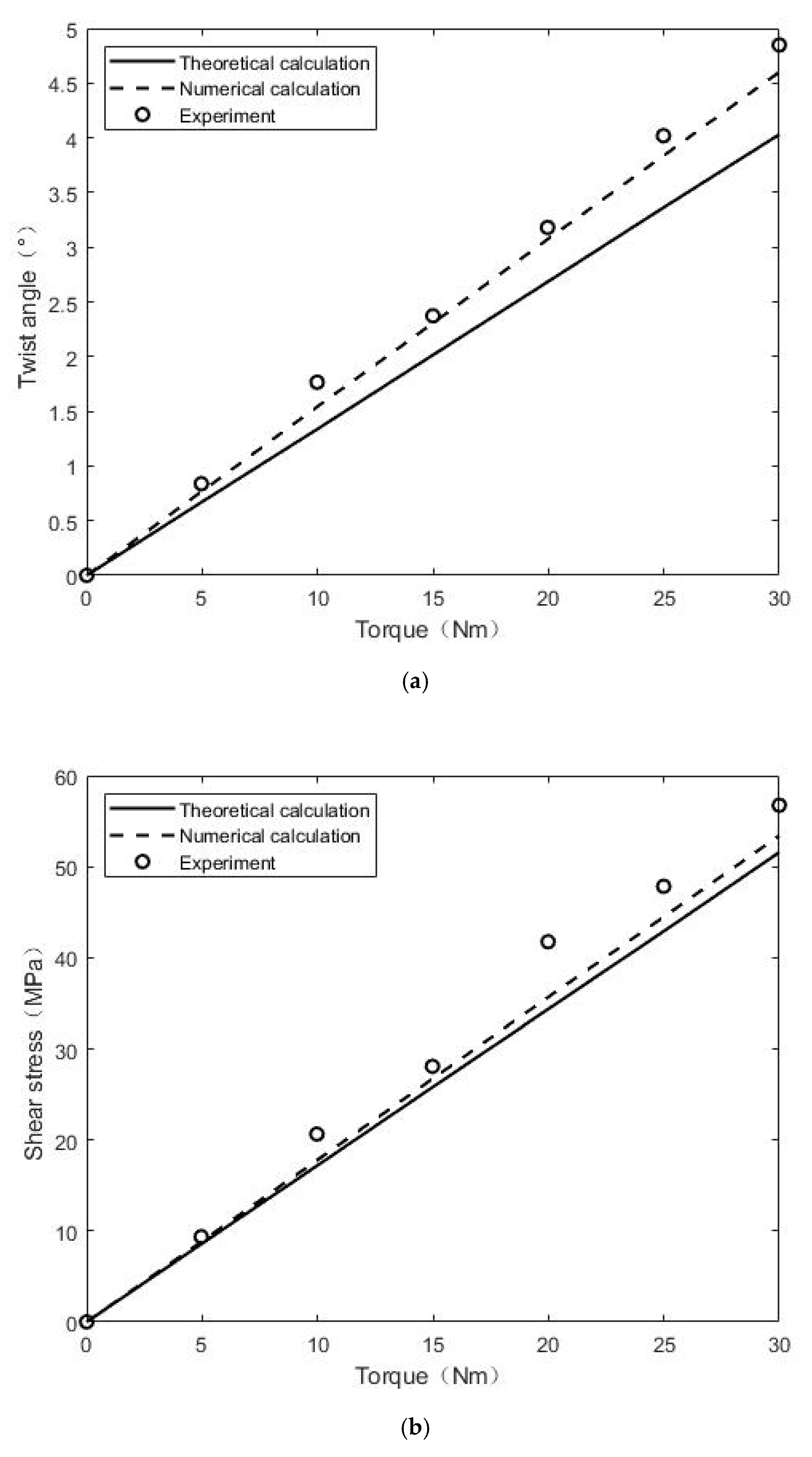
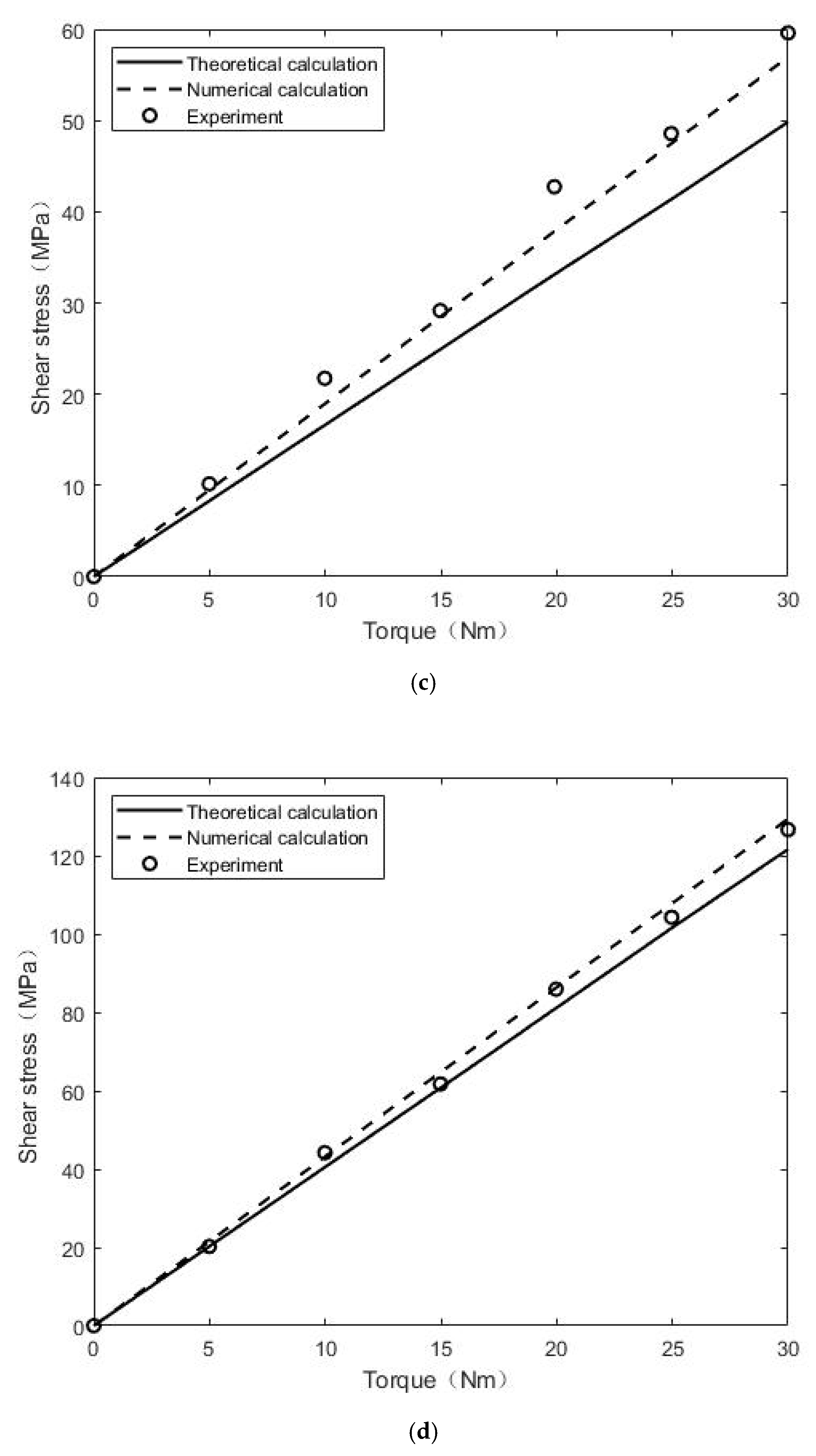
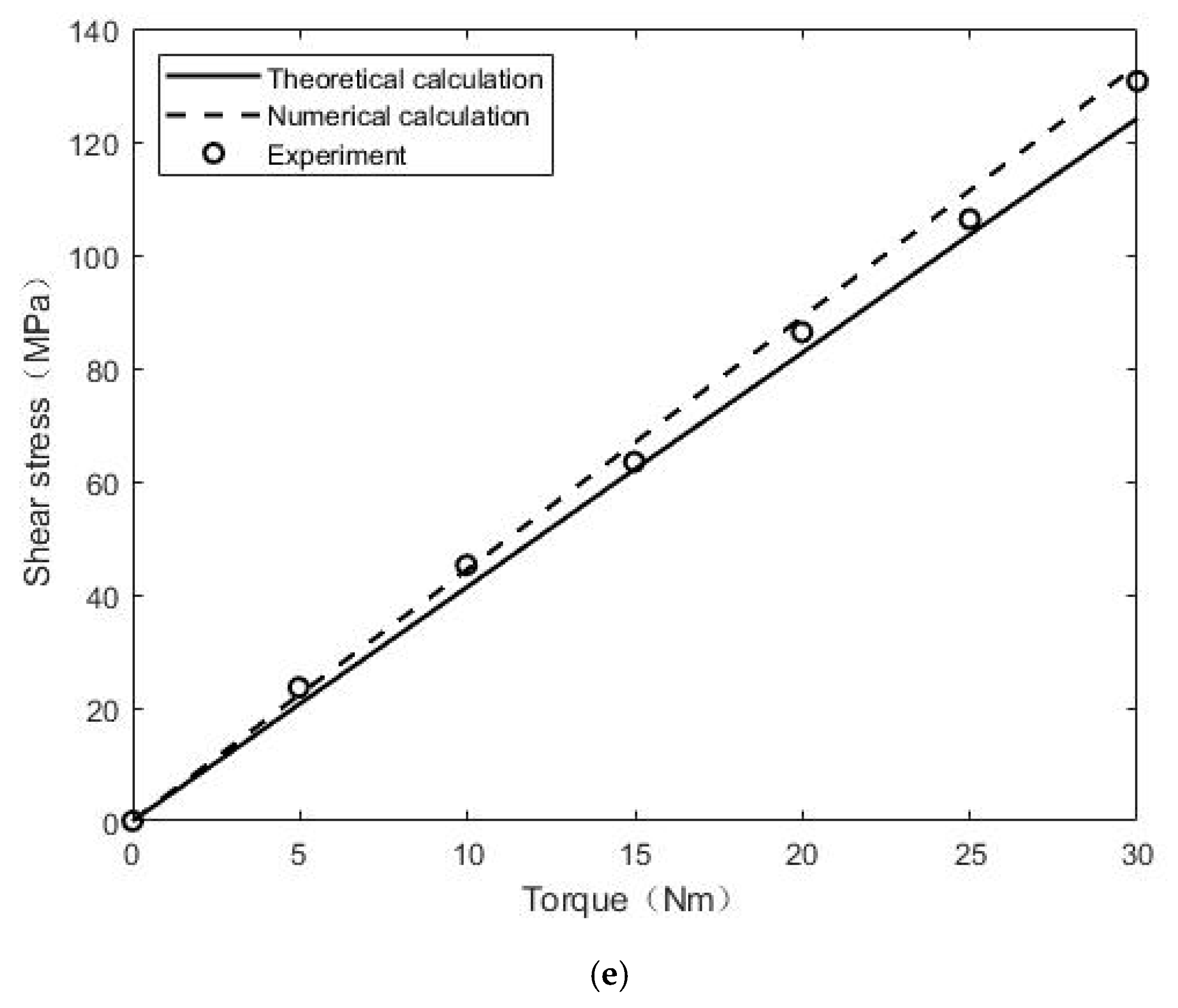
| Load (Nm) | Angle of Rotation (°) | Shear Stress of Point A (Mpa) | Shear Stress of Point B (Mpa) | Shear Stress of Point C (Mpa) | Shear Stress of Point D (Mpa) | |
|---|---|---|---|---|---|---|
| Theoretical calculation | 5 | 0.67 | 8.31 | 8.55 | 20.25 | 20.58 |
| 10 | 1.34 | 16.61 | 17.16 | 40.50 | 41.25 | |
| 15 | 2.02 | 24.92 | 25.79 | 60.75 | 62.07 | |
| 20 | 2.68 | 33.22 | 34.34 | 81.06 | 82.65 | |
| 25 | 3.36 | 41.36 | 42.89 | 101.50 | 103.57 | |
| 30 | 4.03 | 49.83 | 51.58 | 121.64 | 124.14 | |
| Numerical calculation | 5 | 0.77 | 9.49 | 8.82 | 21.50 | 22.27 |
| 10 | 1.54 | 18.94 | 17.76 | 43.14 | 44.33 | |
| 15 | 2.31 | 28.48 | 26.71 | 64.75 | 66.79 | |
| 20 | 3.07 | 37.95 | 35.66 | 86.25 | 88.94 | |
| 25 | 3.84 | 47.46 | 44.47 | 107.75 | 111.33 | |
| 30 | 4.61 | 56.95 | 53.42 | 129.40 | 133.49 | |
| Experiment | 5 | 0.84 | 10.17 | 9.37 | 20.24 | 23.59 |
| 10 | 1.77 | 21.74 | 20.65 | 44.20 | 45.22 | |
| 15 | 2.37 | 29.17 | 28.08 | 61.75 | 63.45 | |
| 20 | 3.18 | 42.74 | 41.75 | 85.90 | 86.34 | |
| 25 | 4.02 | 48.57 | 47.84 | 104.25 | 106.30 | |
| 30 | 4.85 | 59.66 | 56.75 | 126.64 | 130.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Huang, Z.; Guo, Y.; Li, G. Prediction of Mechanical Properties of Thin-Walled Bar with Open Cross-Section under Restrained Torsion. Coatings 2022, 12, 562. https://doi.org/10.3390/coatings12050562
Chen Z, Huang Z, Guo Y, Li G. Prediction of Mechanical Properties of Thin-Walled Bar with Open Cross-Section under Restrained Torsion. Coatings. 2022; 12(5):562. https://doi.org/10.3390/coatings12050562
Chicago/Turabian StyleChen, Zhewu, Zhanda Huang, Yong Guo, and Guibing Li. 2022. "Prediction of Mechanical Properties of Thin-Walled Bar with Open Cross-Section under Restrained Torsion" Coatings 12, no. 5: 562. https://doi.org/10.3390/coatings12050562
APA StyleChen, Z., Huang, Z., Guo, Y., & Li, G. (2022). Prediction of Mechanical Properties of Thin-Walled Bar with Open Cross-Section under Restrained Torsion. Coatings, 12(5), 562. https://doi.org/10.3390/coatings12050562





