Abstract
The present study’s main focus is regarding the physical properties of a two-dimensional (2D) magneto-hydrodynamic boundary layer non-Newtonian Casson fluid flow that moves due to an exponentially expanding surface with a mixed convection heat transfer mechanism. In the hydrodynamic flow and heat transmission process, the combined impact of thermal radiation and magnetic field influence is explored. The internal heat generation owing to the fluid motion or a very fluid viscosity is not taken into account. The Chebyshev spectral method (CSM) is employed in this work due to its ability, accuracy, and ease of obtaining the solution for non-linear system of ordinary differential equations (ODEs). This method is an approximate method that can usually obtain the solution in a series form. The mixed convection impact is incorporated in our problem. The results are graphed to help comprehend the many physical parameters that arise in the problem. Graphical results uncover that the speed liquid stream is lessened when reinforcing both the Casson boundary and the Hartmann number, while converse attributes are applied for the Grashof number and the radiation boundary. Finally, a comparison of our current results with previously published work on several particular situations of the problem reveals that they are in excellent agreement.
MSC:
MSC 2010 No.: 65M60; 76F12; 41A30; 65N12
1. Introduction
Research issues in regards to the non-Newtonian fluid movement and heat transport in the Casson model as a result of an extending surface with a given temperature have an assortment of uses in the design and a few modern assembly processes, particularly in the most recent couple of years. A non-Newtonian fluid with yield stress is known as a Casson fluid [1,2,3,4]. These manufacturing processes may include hot rolling, glass fiber, wire drawing, the expulsion of plastic sheets, extraction of raw petroleum from oil-based commodities and paper creation. Hence, studies of the non-Newtonian Casson fluid have their importance in engineering, as well as in scientific areas [5,6,7,8,9,10]. Most of the related studies look at heat transfer mechanisms as well as mass transfer aspects and their importance in engineering fields using various types of fluids, such as the viscoelastic nanofluid, ferrofluid, non-Newtonian blood fluid, the flow of copper oxide nanoparticles, Bingham fluid, Jeffrey fluid, micropolar fluid, Newtonian and non-Newtonian nanofluid [11,12,13,14,15,16,17,18,19,20,21].
Because Fourier transforms for Chebyshev multinomials are available to properly compute matrix–vector products, they have been more widely employed than additional groups of orthogonal polynomials. The linear and non-linear differential equations, the integral equations, and the integro-differential equations have all been solved using these polynomials [22]. This method is also widely used to explain the fractional diffusion equation [23], fractional-order integro-differential equations and others ([24,25,26,27]). The key benefit of this strategy is that it can obtain correct results by using only a few terms from the series solution. The proposed method is significantly faster than the alternatives. Chebyshev’s functions are commonly utilized in function approximation because of their good features. Spurred by the above significant examinations, the current exploration is centered around the investigation of the mathematical arrangement by the CSM for the MHD fluid flow and heat transfer for the non-Newtonian Casson liquid over an extending surface with viscous dissipation and thermal radiation.
2. Governing Equations
In this section, we investigated the influence of heat radiation on the non-Newtonian Casson model, which could be described as follows, based on the model provided previously by Pal [28]:
with the following set of constraints:
where f represents the dimensionless stream function, represents the dimensionless velocity, represents the dimensionless temperature, represents the Casson parameter and X represents the dimensionless location along the plate. Additionally, the governing parameters , , R, , , a, and can be defined as the thermal buoyancy parameter, the Hartmann number, the radiation parameter, the Reynolds number, the Prandtl number, the parameter of the temperature distribution in the stretching surface, the dimensionless heat generation/absorption parameter and the Eckert number, respectively.
3. Implementation of the Proposed Numerical Method
In this section, we treated the obtained non-linear system of ODEs (1) and (2) with the corresponding boundary conditions (3) and (4) with the help of implementing the CSM. We applied this procedure with help from the following items:
- We implemented the proposed technique by using a Chebyshev function to approximate , , , and by taking and and the integration as follows:
- We implemented the boundary conditions (7) to find the values of (the constants of integration) as follows:
4. Numerical Method Verification
To ensure the correctness and validity of the data acquired through the use of the Chebyshev spectral method, the numerical values of the Nusselt number estimated by the present approach for and were compared to those of Pal [28]. As can be seen from Table 1, the current results agreed quite well with those produced by Pal [28], emphasizing the precision of the numerical method used.

Table 1.
Comparison of Nusselt number calculated by Pal [28] with and for various values of a and .
5. Results and Discussion
The system of ODEs (1) and (2) dependents upon the conditions (3) and (4) was solved numerically after utilizing the Chebyshev spectral method. To obtain an actual understanding, a parametric report was generated for the current physical problem, and the mathematical results were displayed using graphical outlines. Diagrams in Figure 1 show the variety of velocity and the variety of temperature for distinct values of the Casson parameter . It was noted that the impact of the Casson parameter played a prominent feature for both the velocity fluid flow and heat transfer. It very well may be seen from these figures that both the temperature and the velocity profiles decreased when expanding the value of the Casson parameter. Furthermore, the Casson parameter with the smallest value provided the most notable liquid velocity and the highest liquid temperature.

Figure 1.
(a) Impact of on ; (b) impact of on .
Figure 2a,b shows the influence of the velocity profile and the temperature profile in the momentum and thermal boundary layers for various Hartmann numbers. It was noted that the impact of the Hartmann number played a prominent feature in the velocity fluid flow. The Hartmann number had the effect of decreasing the value of velocity profiles throughout the boundary layer, while the temperature diagram had the reverse effect.
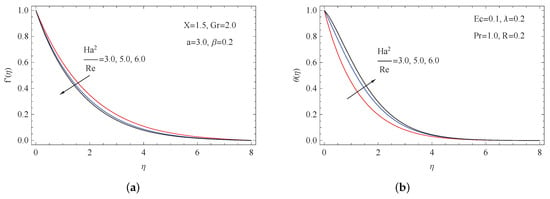
Figure 2.
(a) Impact of on ; (b) impact of on .
To display the impacts of the Grashof number on both the velocity and the temperature fields, we plotted Figure 3a,b. It was found that both the velocity and the temperature of the fluid increased for the Grashof number. Furthermore, we can see that the impact of this parameter had a prime role near the stretching sheet. It is worth noting that the Hartmann number and the Grashof number exhibited opposite characteristics when it came to the velocity (see Figure 3a,b).
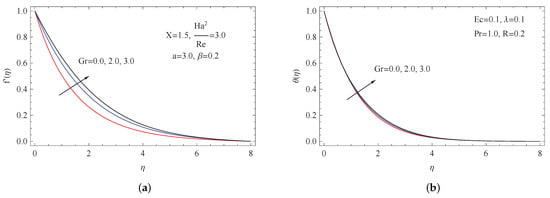
Figure 3.
(a) Impact of on ; (b) impact of on .
Figure 4 is a plot for both the non-dimensional velocity and the non-dimensional temperature , with for different upsides for X. From this plot, it was fascinating to see that as the value of X enhanced, the velocity of the non-Newtonian fluid increased, while the converse was noticed for . The impact of the dimensionless coordinate parameter X represented a critical role in both the hydrodynamic boundary layer and the velocity field.
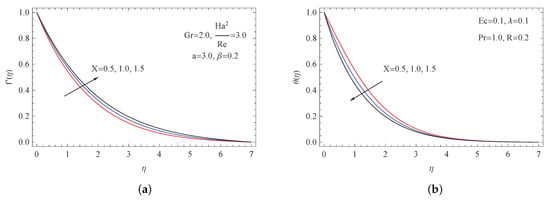
Figure 4.
(a) Impact of X on ; (b) impact of X on .
Figure 5a,b shows the effect of the thermal radiation parameter R on the velocity and temperature curves. It was observed that both the hydro-dynamical momentum layer and the thermal layer were increased when enhancing R. Physically, this was due to the radiation energy enlivening the related development of the boundary layer.
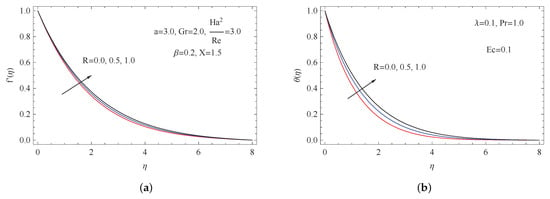
Figure 5.
(a) Impact of R on ; (b) impact of R on .
The graph in Figure 6 illustrates the variation of temperature for distinct values of the heat generation/absorption parameter . Figure 6 shows, as expected, that the escalation of the heat generation (absorption) parameter prompted an ascent of the temperature . We also saw that when grew, the thermal thickness increased.
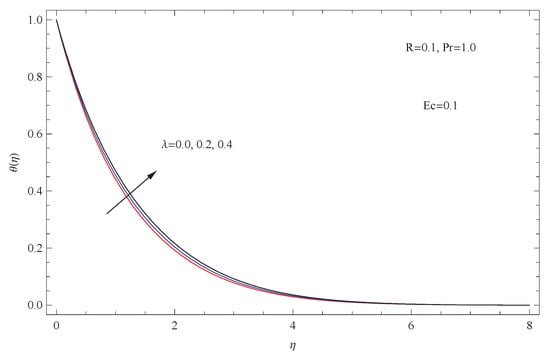
Figure 6.
Impact of on .
6. Conclusions
We demonstrated a numerical simulation of the non-Newtonian MHD Casson fluid flow and heat transfer due to an extensible sheet with thermal radiation. The current study looked into how heat transfer devices rely on temperature, which could signal that the Casson fluid’s upgrading qualities are improving, making it more appealing for applications. The proposed ODEs were numerically solved after employing the Chebyshev spectral technique. The influence of various physical parameters on the velocity and temperature profiles was visually depicted and explained in detail. A portion of the significant findings of our examination was acquired by a graphical portrayal. Finally, the precious obtained results, which were confirmed through a validation of our data, reflected the reliability and the trust of the CSM, especially in this type of highly nonlinear ODEs that can be applied in the field of technological and industrial engineering.
Author Contributions
Conceptualization, M.M.K. and A.M.M.; methodology, M.M.B.; software, M.M.K.; validation, M.M.K., A.M.M. and M.M.B.; formal analysis, A.M.M.; investigation, M.M.K.; resources, A.M.M.; data curation, M.M.K.; writing—original draft preparation, M.M.B.; writing—review and editing, M.M.K., A.M.M.; supervision, M.M.K.; project administration, M.M.K.; funding acquisition, M.M.B., and M.M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research at the Imam Mohammad Ibn Saud Islamic University through the research group No. RG-21-09-06.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at the Imam Mohammad Ibn Saud Islamic University for funding this work through the research group No. RG-21-09-06.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Akbar, N. Influence of magnetic field on peristaltic flow of a Casson fluid in an asymmetric channel: Application in crude oil refinement. J. Magnet. Magnet. Mater. 2015, 378, 463–468. [Google Scholar] [CrossRef]
- Hayat, T.; Shehzad, S.A.; Alsaedi, A. Soret and Dufour effects on magnetohydrodynamic (MHD) flow of Casson fluid. Appl. Math. Mech. 2012, 33, 1301–1312. [Google Scholar] [CrossRef]
- Hussanan, A.; Zuki Salleh, M.; Tahar, R.M.; Khan, I. Unsteady boundary layer flow and heat transfer of a Casson fluid past an oscillating vertical plate with Newtonian heating. PLoS ONE 2014, 9, e108763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kameswarani, P.K.; Shaw, S.; Sibanda, P. Dual solutions of Casson fluid flow over a stretching or shrinking sheet. Sadhana 2014, 39, 1573–1583. [Google Scholar] [CrossRef] [Green Version]
- Kirubhashankar, C.K.; Ganesh, S.; Mohamed Ismail, A. Casson fluid flow and heat transfer over an unsteady porous stretching surface. Appl. Math. Sci. 2015, 9, 345–351. [Google Scholar] [CrossRef]
- Megahed, A.M. Heat flux and variable rhermal conductivity effects on Casson flow and heat transfer due to an exponentially stretching sheet with viscous dissipation and heat generation. Int. J. Chem. React. Eng. 2016, 14, 167–174. [Google Scholar] [CrossRef]
- Mahmoud, M.A.A.; Megahed, A.M. MHD Flow and heat transfer characteristics in a Casson liquid film towards an unsteady stretching sheet with temperature-dependent thermal conductivity. Braz. J. Phys. 2017, 47, 512–523. [Google Scholar] [CrossRef]
- Elham, A.; Megahed, A.M. MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon. Nanotechnol. Rev. 2022, 11, 463–472. [Google Scholar]
- Nadeem, S.; Haq, R.L.; Akbar, N.S. MHD three-dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary conditions. IEEE Trans. Nanotechnol. 2014, 13, 109–115. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.L.; Akbar, N.S.; Khan, Z.H. MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alex. Eng. J. 2013, 52, 577–582. [Google Scholar] [CrossRef]
- Hussain, A.; Sarwar, L.; Akbar, S.; Nadeem, S.; Jamal, S. Numerical investigation of viscoelastic nanofluid flow with radiation effects. Proc. Inst. Mech. Eng. Part J. Nanomater. Nanoeng. Nanosyst. 2019, 233, 87–96. [Google Scholar] [CrossRef]
- Vo, D.D.; Saleem, S.; Alderremy, A.A.; Nguyen, T.K. Heat transfer enhancement and migration of ferrofluid due to electric force inside a porous medium with complex geometry. Phys. Scr. 2019, 94, 115218. [Google Scholar] [CrossRef]
- Saleem, A.; Akhtar, S.; Nadeem, S.; Issakhov, A.; Ghalambaz, M. Blood Flow Through a Catheterized Artery Having a Mild Stenosis at the Wall with a Blood Clot at the Centre. Comput. Model. Eng. Sci. 2020, 125, 565–577. [Google Scholar] [CrossRef]
- Rehman, A.U.; Abbas, N.; Nadeem, S.; Saleem, A. Significance of Coriolis force on the dynamics of water conveying copper and copper oxide nanoparticles. Phys. Scr. 2020, 95, 115706. [Google Scholar] [CrossRef]
- Saleem, A.; Kiani, M.N.; Nadeem, S.; Issakhov, A. Heat transfer and Helmholtz-Smoluchowski velocity in Bingham fluid flow. Appl. Math. Mech. 2020, 41, 1167–1178. [Google Scholar] [CrossRef]
- Nadeem, S.; Khan M., N.; Abbas, N. Transportation of slip effects on nanomaterial micropolar fluid flow over exponentially stretching. Alex. Eng. J. 2020, 59, 3443–3450. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Malik, M.Y. Heat transport in CNTs based nanomaterial flow of non-Newtonian fluid having electro magnetize plate. Alex. Eng. J. 2020, 59, 3431–3442. [Google Scholar] [CrossRef]
- Nadeem, S.; Ahmad, S.; Muhammad, N. Analysis of ferrite nanoparticles in liquid. Pramana 2020, 94, 1–9. [Google Scholar] [CrossRef]
- Nadeem, S.; Ijaz, M.; El-Kott, A.; Ayub, M. Rosseland analysis for ferromagnetic fluid in presence of gyrotactic microorganisms and magnetic dipole. Ain Shams Eng. J. 2020, 11, 1295–1308. [Google Scholar] [CrossRef]
- Nadeem, S.; Akhtar, S.; Saleem, A. Peristaltic flow of a heated Jeffrey fluid inside an elliptic duct: Streamline analysis. Appl. Math. Mech. 2021, 42, 583–592. [Google Scholar] [CrossRef]
- Saleem, S.; Akhtar, S.; Nadeem, S.; Saleem, A.; Ghalambaz, M.; Issakhov, A. Mathematical study of electroosmotically driven peristaltic flow of Casson fluid inside a tube having systematically contracting and relaxing sinusoidal heated walls. Chin. Phys. 2021, 71, 300–311. [Google Scholar] [CrossRef]
- El-Gendi, S.E. Chebyshev solution of differential, integral and integro-differential equations. Comput. J. 1696, 12, 282–287. [Google Scholar] [CrossRef] [Green Version]
- Khader, M.M.; Ahmed, M. Megahed, Differential transformation method for studying flow and heat transfer due to a stretching sheet embedded in a porous medium with variable thickness, variable thermal conductivity and thermal radiation. Appl. Math. Mech. 2014, 35, 1387–1400. [Google Scholar] [CrossRef]
- Khader, M.M. Mittag–Leffler collocation optimization method for studying a physical problem in fluid flow with fractional derivatives. Math. Methods Appl. Sci. 2022, 7763, 1–15. [Google Scholar] [CrossRef]
- Khader, M.M. Numerical study of the nanofluid thin film flow past an unsteady stretching sheet with fractional derivatives using the spectral collocation Chebyshev approximation. Int. J. Mod. Phys. C 2021, 32, 1–14. [Google Scholar] [CrossRef]
- Khader, M.M. On the numerical solutions for the fractional diffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2535–2542. [Google Scholar] [CrossRef]
- Khader, M.M.; Sharma, R.P. Evaluating the unsteady MHD micropolar fluid flow past stretching/shirking sheet with heat source and thermal radiation: Implementing fourth order predictor-corrector FDM. Math. Comput. Simul. 2021, 181, 333–350. [Google Scholar] [CrossRef]
- Pal, D. Mixed convection heat transfer in the boundary layers on an exponentially stretching surface with magnetic field. Appl. Math. Comput. 2010, 217, 2356–2369. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).