Growth and Optical Properties of Ga₂O₃ Layers of Different Crystalline Modifications

Abstract

In the present work, a new method of growing layers of three main crystal modifications of Ga₂O₃, namely α-phase, ε-phase, and β-phase, with thickness of 1 µm or more was developed. The method is based on the use of two approaches, namely a combination of Ga₂O₃ growth using the hydride vapor-phase epitaxy (HVPE) method and the use of a silicon crystal with a buffer layer of dislocation-free silicon carbide as a substrate. As a result, Ga₂O₃ gallium oxide layers of three major Ga₂O₃ crystal modifications were grown, namely, α-phase, ε-phase, and β-phase. The substrate temperatures and precursor flux values at which it is possible to grow only α-phase, only ε-phase, or only β-phase without a mixture of these phases were established. It was found that the metastable α- and ε-phases change into the stable β-phase when heated above 900 °C. Experimentally obtained Raman and ellipsometric spectra of α-phase, ε-phase, and β-phase of Ga₂O₃ are presented. The theoretical study of the Raman spectra and the dependences of dielectric function on photon energy for all three phases was carried out. The vibrations of Ga₂O₃ atoms corresponding to the main lines of the Raman spectrum of the α-phase, ε-phase, and β-phase were simulated by density functional methods.

1. Introduction

In recent years, there has been a great interest in the growth of the so-called transparent conductors, which are often represented by metal oxides, such as zinc oxide ZnO, magnesium oxide MgO, gallium oxide Ga₂O₃ and some other oxides [1]. Among these materials, gallium oxide Ga₂O₃ excels [2]: first, it is a semiconductor with a large bandgap of $~$5 eV; second, it has a very high breakdown voltage of $~$8 ${\mathrm{MV} \mathrm{cm}}^{-1}$; third, it is easily doped, which makes it very promising for applications in micro- and optoelectronics. In addition, it is easily mixed with the Cr₂O₃ magnetic material, which makes it promising for spintronics. Another important feature of Ga₂O₃ is that it can be in several crystalline modifications. Reviews [2,3,4] indicate five phases as the main ones, namely, the stable $\beta$ phase with the monoclinic structure $C2/m$, and the metastable phases: $\epsilon$ phase, with the orthorhombic structure $Pna{2}_1$; $\alpha$ phase, with the rhombohedral structure $R\overline{3}c$ (corundum structure); $\delta$ phase, with the body-centered cubic structure $la\overline{3}$; and $\gamma$ phase, with the cubic structure $Fd\overline{3}m$. At present there is also great interest in modeling the properties of Ga₂O₃, which is related to the prospects of using Ga₂O₃ in various microelectronic devices [3,4,5,6,7]. In particular, the influence of point defects on the electrical and optical properties of Ga₂O₃ has been investigated in [8,9,10]. Despite quite a large number of metastable phases, it is extremely difficult to obtain them, because generally only the stable $\beta$ phase grows. At present, a sufficiently large number of methods to grow Ga₂O₃ have been developed [1,2,3,4]. These are various volumetric growth technologies, molecular-beam epitaxy (MBE), chemical vapor deposition (CVD), metal-organic chemical vapor deposition (MOCVD), as well as hydride vapor-phase epitaxy (HVPE) methods [7,11]. To grow Ga₂O₃ layers, as a rule, different orientations of sapphire Al₂O₃ crystals, as well as silicon in the (100) orientation, are used as substrates [2,3,4]. Both sapphire and silicon have a number of well-known drawbacks. Sapphire is a dielectric, which substantially limits the application of the resulting layers in microelectronics; moreover, it is hard to etch out and process it. Silicon can conduct electric current, and it is much easier to etch out and process, but Ga₂O₃ grows significantly worse on it [2]. First, silicon badly orients the growing layers of Ga₂O₃; second, oxygen O₂ and water H₂O, which are used as reagents to obtain Ga₂O₃, react with silicon to form amorphous silicon dioxide SiO₂, which further worsens the epitaxy of Ga₂O₃ [7].

In this work, it is proposed to grow Ga₂O₃ layers not just on silicon, but on silicon Si(111) with a dislocation-free silicon carbide SiC buffer layer grown by the method of coordinated substitution of atoms (MCSA) [12,13]. The SiC(111) buffer layer protects silicon from oxidation and significantly improves the orientation of the growing Ga₂O₃ layers [7]. It is very likely that one of the reasons for this is the oxide layer on Si, which is impossible to get rid of when growing Ga₂O₃. If a SiC layer is simply deposited on a silicon substrate, for example, by the CVD method, then it will be even worse than without SiC, because a huge number of misfit dislocations at the Si/SiC interface (lattice misfit parameter is 20%) are formed, which then sprout into Ga₂O₃ and degrade its quality. In a series of papers [14,15,16,17], the MCSA was developed to obtain dislocation-free layers of silicon carbide of the cubic 3C-SiC polytype on silicon by a chemical reaction of silicon with carbon monoxide CO gas. This substitution reaction replaces half of the Si atoms in the diamond-like silicon lattice with C atoms in a coordinated manner. The term “coordinated” means that the removal of the Si atom from the lattice and the incorporation of the C atom in its place by the chemical reaction occur simultaneously [13,15].

2Si (crystal) + CO (gas) = SiC (crystal) + SiO (gas) ↑

(1)

The oxygen atom plays here the role of a catalyst for the substitution reaction. A transition state of reaction (1), corresponding to the energy maximum along the reaction path, is represented by an almost equilateral triangle with Si, C, and O atoms at its vertices [15]. After overcoming this barrier with a height of 1.2 eV, the SiO molecule leaves the system. Such a mechanism of the coordinated substitution preserves the structure of the initial Si cubic lattice, which ensures the growth of the cubic 3C-SiC polytype, exclusively [12,13]. This mechanism is realized on the Si surface of any orientation, but a particularly high quality of the interface between Si and SiC is found on the (111) surface [12]. Numerous microscopic studies have shown that the 3C-SiC(111)/Si(111) interface formed by the MCSA does not contain lattice misfit dislocations [12,13], because 5 cells of 3C-SiC almost perfectly match with 4 cells of Si. Only various stacking faults are formed, in particular, twins [12], which fundamentally distinguishes the MCSA from traditional growth methods, such as the CVD, where numerous lattice misfit dislocations are formed [1]. A detailed comparison of the MCSA method with others was made in a recent review [13].

The purpose of this work is to produce high-quality Ga₂O₃ layers of various crystalline modifications on the 3C-SiC(111)/Si(111) hybrid substrates by the HVPE method in a wide temperature range of 500–1000 °C and to study the Raman and ellipsometric spectra (dielectric function) of the obtained phases.

2. Materials and Methods

Ga₂O₃ layers were grown on standard silicon 3-inch wafers oriented with a declination of 4° from the base (111) orientation towards the (110) direction. Silicon was doped with phosphorus, resistivity $>{10}^3 \mathsf{\Omega } \mathrm{cm}$. First, dislocation-free 3C-SiC(111) buffer layers of 60–100 nm thickness were grown on silicon by the MCSA by chemical reaction (1). The temperature of the SiC synthesis was 1300 °C, pressure of CO gas was 100 Pa, synthesis time was 10 min. Technical details of the SiC synthesis by the MCSA method are given in reviews [12,13]. A typical X-ray diffraction (XRD) spectrum of a 3C-SiC(111)/Si(111) hybrid substrate produced this way is shown in Figure 1a.

It is clearly seen that only the peaks corresponding to the (111) orientation are presented in the spectrum; i.e., the silicon substrate completely orients the growing 3C-SiC layer obtained by the MCSA [12,13]. The Raman spectrum of a 3C-SiC(111)/Si(111) hybrid substrate obtained this way is shown in Figure 1b. It is just a combination of Si lines and two standard cubic SiC lines (798 cm⁻¹ and 970 cm⁻¹) [13].

An ellipsometric spectrum of the SiC-3C(111)/Si(111) hybrid substrate measured by the VUV-VASE ultraviolet rotating-analyzer ellipsometer (J.A. Woollam Co., Lincoln, Dearborn, MI, USA) in the photon energy range 0.5–9.3 eV, is shown in Figure 2. To analyze this dependence, it is sufficient to use the simplest single-layer ellipsometric model [18] consisting of a substrate containing Si, SiC, pores, and a SiC layer with roughness on its surface. This model gives a thickness of the SiC layer of $~$80 nm.

Ga₂O₃ layers were grown on the 3C-SiC(111)/Si(111) hybrid substrate by HVPE by the following chemical reaction:

$$2\mathrm{GaCl}+\frac{3}{2} {\mathrm{O}}_2={\mathrm{Ga}}_2{\mathrm{O}}_3+{\mathrm{Cl}}_2$$

(2)

Gallium chloride was synthesized directly in the source zone of the reactor with gaseous hydrogen chloride (HCl 99.999%) passing over metallic gallium (Ga 99.9999%). The yield of the GaCl synthesis reaction was about 85%. The oxygen required for the formation of gallium oxide was supplied in a mixture with argon (20% oxygen, 80% argon). The synthesis of gallium oxide was carried out under conditions of excess oxygen flow. The ratio of the components of the VI/III groups was in the range of 3–5. The Ga₂O₃ deposition rate was determined by the HCl flow through the gallium source and depended on the deposition temperature, which varied over a wide range of 500–1000 °C. With a total gas flow of $~$5 slm, the rate of Ga₂O₃ deposition started from approximately $0.4–0.5 \mathsf{\mu }\mathrm{m}/\min$ at 500 °C and ended with values of $0.8–1.0 \mathsf{\mu }\mathrm{m}/\min$ at 1000 °C. The deposition time was chosen to be approximately $1–2 \min$ in order to obtain a Ga₂O₃ layer with a thickness of approximately $~1 \mathsf{\mu }\mathrm{m}$. After the end of the growth, the substrate was cooled in an argon flow to room temperature.

In order to find out the nature of oscillations corresponding to each line of the Raman spectrum, this spectrum was calculated by methods of the density-functional theory (DFT) by utilizing the Quantum Espresso code [19]. In all calculations periodic boundary conditions in all three dimensions were considered, the exchange-correlation contribution was calculated using the GGA-PBESol functional [20]. To integrate over the Brillouin zone, a grid of k-points was generated by the Monkhorst–Pack scheme so that the distance between them was no more than 0.25 ${\AA }^{-1}$. All calculations used the norm-conserving pseudopotentials ONCVPSP v0.4.1 (stringent) (http://www.pseudo-dojo.org/ (accessed on 20 November 2022)) and the cutoff energy of plane waves of 850 eV corresponding to the highest available accuracy.

3. Results

The research has shown that different temperatures of the synthesis produce different phases of Ga₂O₃.

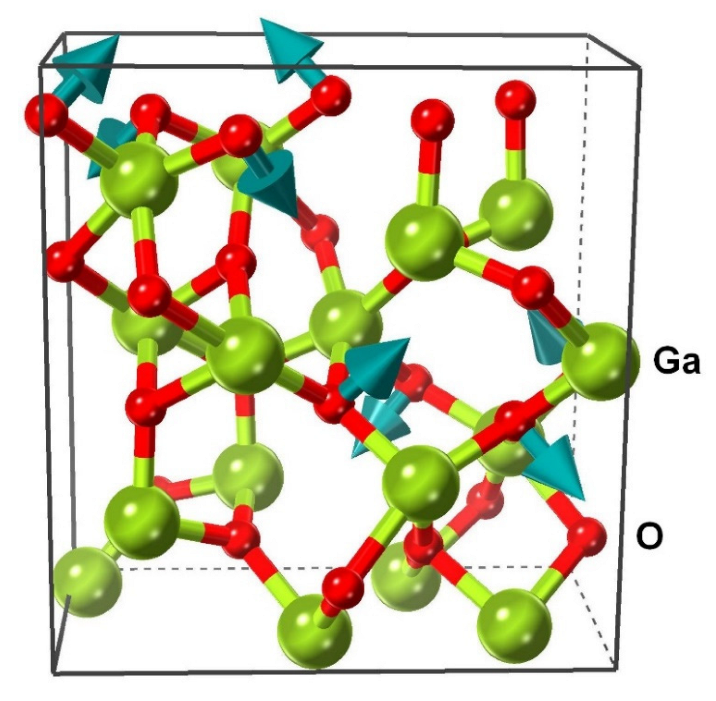
3.1. Stable $\beta$ Phase with Monoclinic Structure $C2/m$

At a temperature of 800–1000 °C, the deposition of Ga₂O₃ resulted in the stable $\beta$ phase, as in the vast majority of other experiments [2,4,21]. Figure 3 shows a typical XRD spectrum of a Ga₂O₃ sample grown on the 3C-SiC(111)/Si(111) hybrid substrate at 900 °C. It can be seen that there is only the $\beta$ phase, and its <$\overline{2}01$> direction is oriented upwards.

A configuration of atoms in $\beta$-Ga₂O₃ with the <$\overline{2}01$> direction oriented upwards is shown in Figure 4.

It is well known that $\beta$-Ga₂O₃ has birefringent monoclinic structure $C2/m$. That is why light polarization inside the crystal where scattering occurs is generally elliptical and differs from the incident and reflected polarizations. Thus, an analysis of the Raman scattering for a monoclinic structure can be quite complicated [6]. However, if the polarization of the detected signal is not changed, then the situation becomes much simpler. Figure 5a shows the Raman spectrum of this Ga₂O₃/SiC/Si sample, obtained in confocal geometry excluding birefringence. Three lines of this spectrum indicate silicon, the remaining lines indicate $\beta$-Ga₂O₃, characterized by four lines in the range of 100–200 ${\mathrm{cm}}^{-1}$ with $A_g^{\left(3\right)}$ being the highest, and by the second- highest line being $A_g^{\left(6\right)}$ at $~$420 ${\mathrm{cm}}^{-1}$ (Figure 5a).

Figure 5b shows the theoretical Raman spectrum of $\beta$-Ga₂O₃, where each line has a thickness of 5 ${\mathrm{cm}}^{-1}$. It can be seen that this spectrum agrees very well with the experimental one in Figure 5a; there is only a minor difference in the position and height of the lines, but all the characteristic lines are present. The frequencies of the main lines coincide very well with a similar result obtained with the hybrid B3LYP functional [6]; it is very difficult to compare the amplitudes because of the birefringence. The data on the main Raman lines of all three phases are given in a single table in Section 4. Figure 6 shows directions and relative amplitudes of oscillations of $\beta$-Ga₂O₃ atoms, as calculated by the DFT method for two main lines of the Raman spectrum. It can be seen that only four oxygen atoms oscillate in both cases, the other six atoms of the primitive cell are practically immobile.

The ordinary dielectric function of the produced $\beta$-Ga₂O₃ sample has been measured as a function of the photon energy. For this, the M-2000D rotating-compensator ellipsometer (J.A. Woollam Co.), working in the range of 0.7–6.5 eV, was used. Due to a significant roughness of this sample, it was not possible to measure the dielectric function with the VUV-VASE ultraviolet rotating-analyzer ellipsometer (J.A. Woollam Co., Dearborn, MI, USA) operating in a wider photon energy range of 0.5–9.3 eV. Figure 7 shows the resulting dependence of the dielectric function on the photon energy, which was derived from the experimental dependence by subtracting the roughness. Anisotropy of the dielectric function [22] was not taken into account.

Comparing the theoretical dependence [5] with the obtained experimental one, we can conclude that there is a qualitative agreement between them.

3.2. Metastable $\epsilon$ Phase Ga₂O₃ with Orthorhombic Structure $Pna{2}_1$

At a synthesis temperature of 550–600 °C, the deposition of Ga₂O₃ resulted in the metastable $\epsilon$ phase. Figure 8 shows a typical XRD spectrum of a Ga₂O₃ sample grown on the 3C-SiC(111)/Si(111) hybrid substrate at 570 °C. It can be seen that there is only the $\epsilon$ phase, which is oriented upwards mostly by the <001> direction, although there are small peaks from other planes too.

A configuration of atoms in $\epsilon$-Ga₂O₃ with the <001> direction oriented upwards is shown in Figure 9. The metastable $\epsilon$-Ga₂O₃ has the orthorhombic structure $Pna{2}_1$, so the peaks of the Raman spectrum differ from the peaks of the stable $\beta$ phase.

Since the $Pna{2}_1$ symmetry is much weaker than the $C2/m$ symmetry, the $\epsilon$ phase has many more lines of the Raman spectrum than the $\beta$ phase [23]. The five highest lines of the spectrum are observed in the range of 80–260 ${\mathrm{cm}}^{-1}$ (there is also a high line at 685 ${\mathrm{cm}}^{-1}$), i.e., before the first silicon line corresponding to 300 ${\mathrm{cm}}^{-1}$. That is why Figure 10a shows the Raman spectrum of the Ga₂O₃/SiC/Si sample, obtained in the confocal geometry of scattering (i.e., excluding birefringence), only in the range up to 300 ${\mathrm{cm}}^{-1}$.

The five highest lines of the spectrum are numerated and correspond to the following frequencies: 86, 117, 131, 150, and 253 ${\mathrm{cm}}^{-1}$. In order to find out the nature of oscillations corresponding to each line of the Raman spectrum, this spectrum was calculated by the DFT methods by utilizing the Quantum Espresso code [19] and the GGA-PBESol functional [20] in the same approximations as for the $\beta$ phase. The resulting theoretical spectrum is shown in Figure 10b. The numbers here indicate the lines corresponding to the following frequencies: 91, 128, 152, 175, and 245 ${\mathrm{cm}}^{-1}$. One can see the qualitative agreement between the theoretical and experimental data. The data on the main Raman lines of all three phases are given in a single table in Section 4. An analysis has shown that the collective motion of atoms, corresponding to the lines of the Raman spectrum, is very complex, which is obviously caused by the weakness of the $Pna{2}_1$ symmetry [23]. The only exception is line No. 5, which is the main line of the Raman spectrum of the metastable $\epsilon$-Ga₂O₃. Figure 11 shows directions and relative amplitudes of oscillations of $\epsilon$-Ga₂O₃ atoms, as calculated in the DFT framework for the main line No. 5 of the Raman spectrum.

It can be seen that only eight oxygen atoms out of 40 atoms in the cell move. The dielectric function of the produced $\epsilon$-Ga₂O₃ sample has been measured as a function of the photon energy. For this, the M-2000D rotating-compensator ellipsometer (J.A. Woollam Co., Dearborn, MI, USA) working in the range of 0.7–6.5 eV was used. Due to a significant roughness of this sample, it was not possible to measure the dielectric function with the VUV-VASE ultraviolet rotating-analyzer ellipsometer (J.A. Woollam Co.) operating in a wider photon energy range of 0.5–9.3 eV. Figure 12 shows the resulting dependence of the dielectric function on the photon energy, which was derived from the experimental dependence by subtracting the roughness.

Anisotropy of the dielectric function was not taken into account. Comparing the theoretical dependence [5] with the obtained experimental one, we can conclude that there is a qualitative agreement between them.

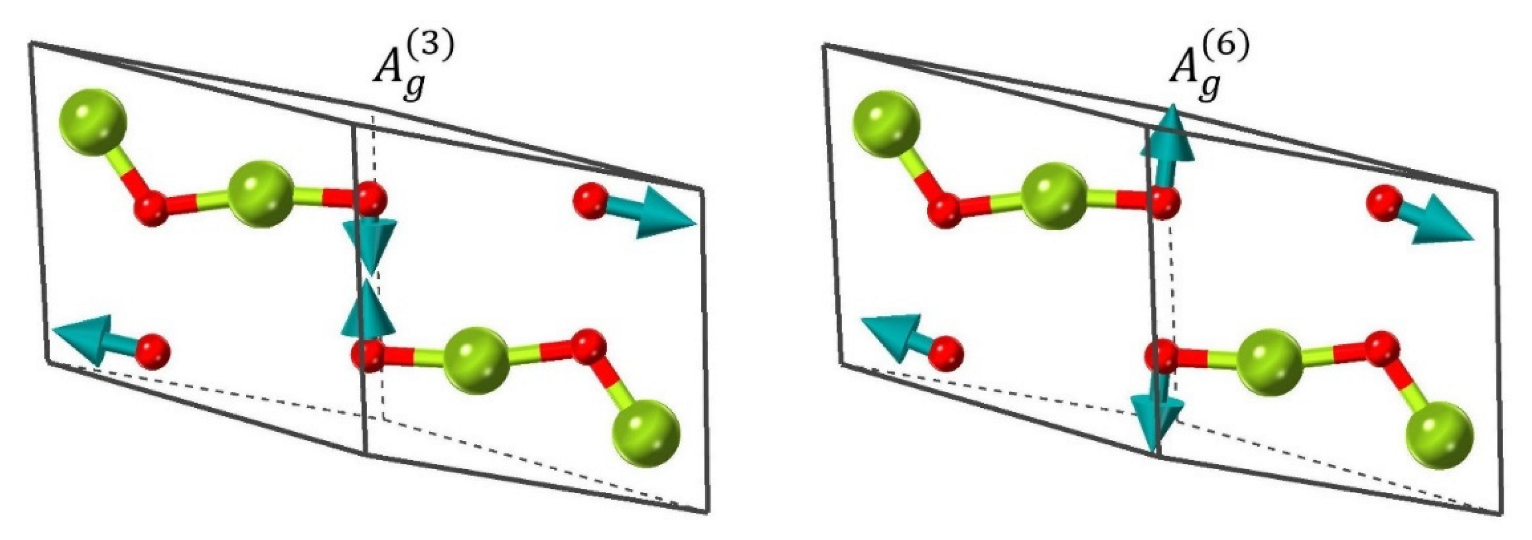
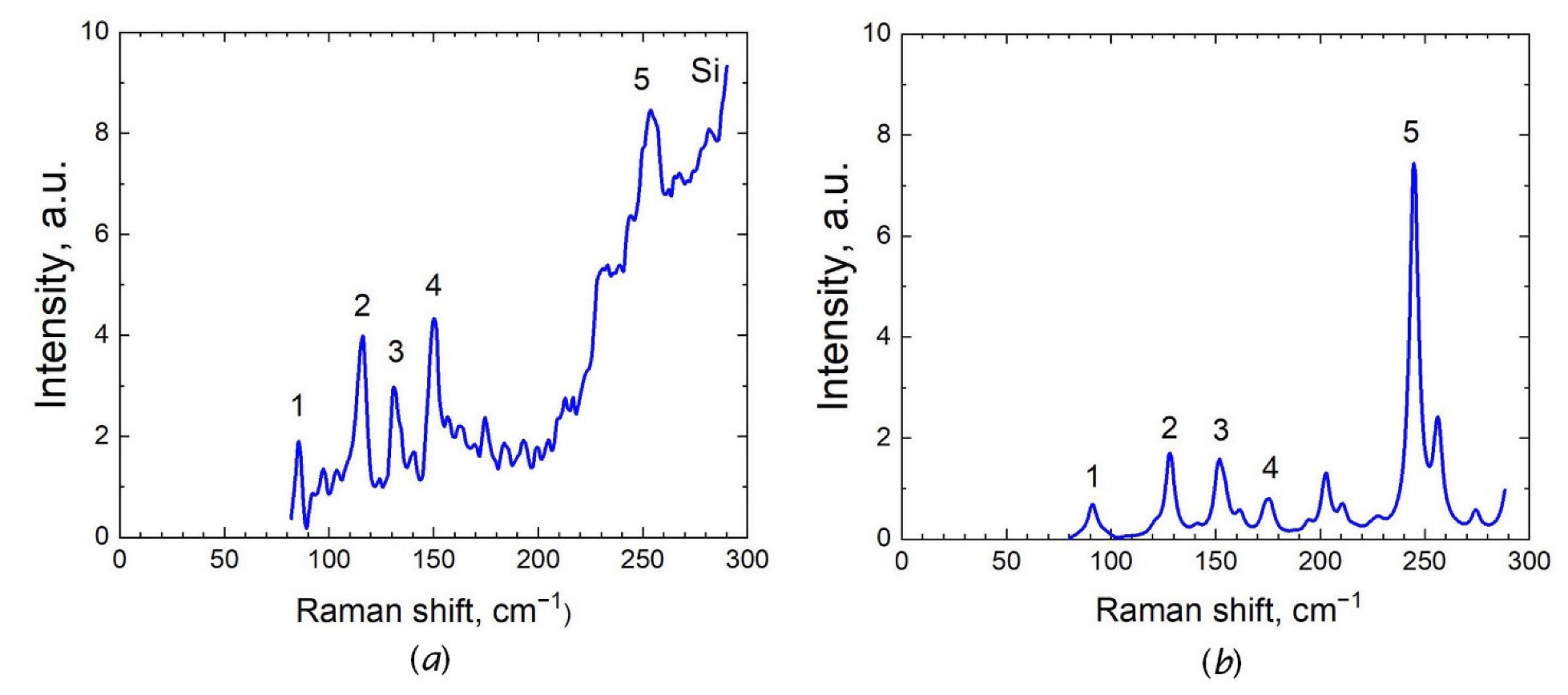
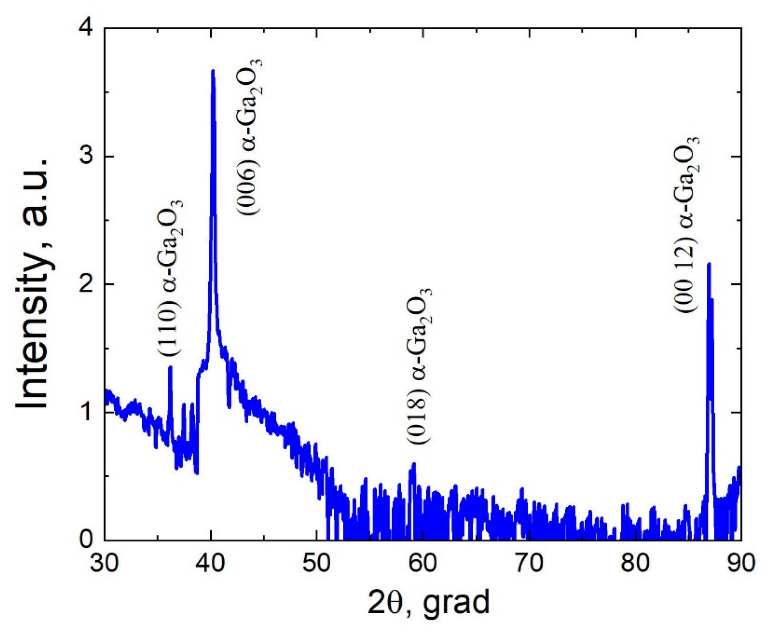
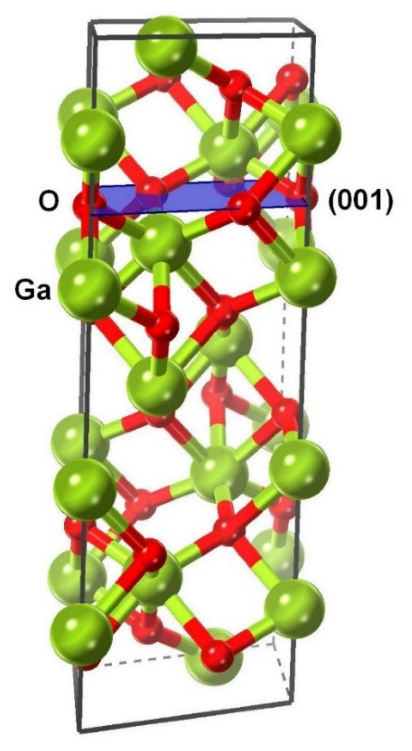
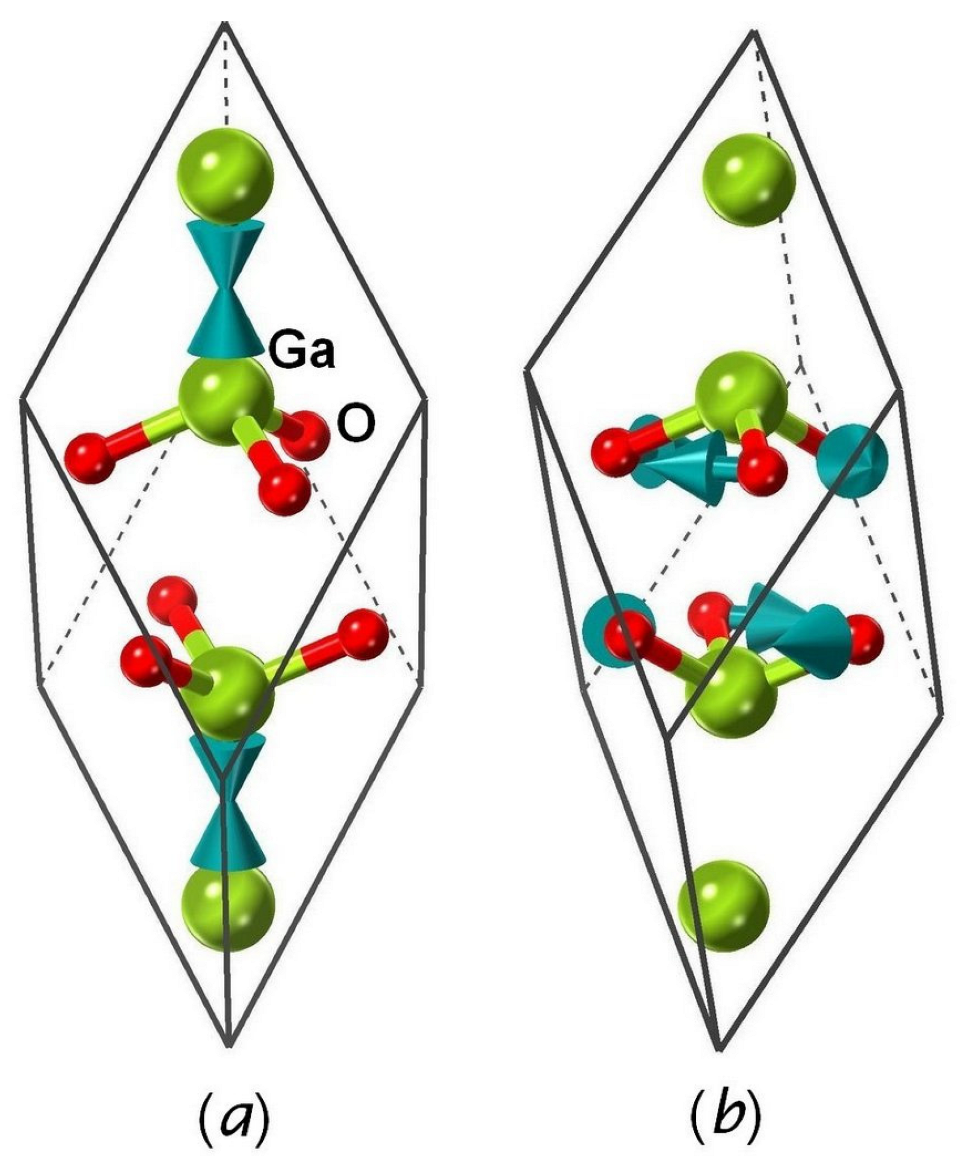
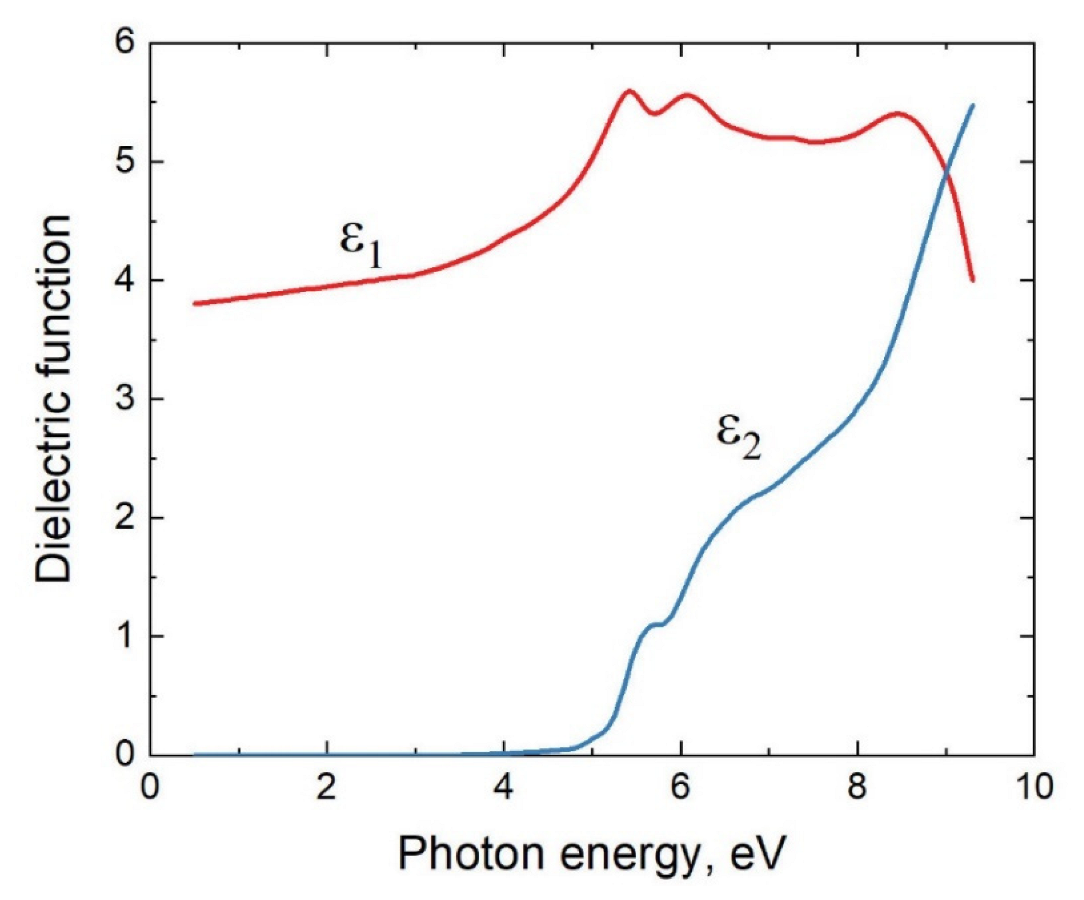
3.3. Metastable $\alpha$ Phase of Ga₂O₃ with Trigonal Structure $R\overline{3}c$

At a synthesis temperature of 500–520 °C, the deposition of Ga₂O₃ resulted in the metastable $\alpha$ phase. Figure 13 shows a typical XRD spectrum of a Ga₂O₃ sample grown on the hybrid substrate 3C-SiC(111)/Si(111) at 510 °C. It is seen that only the $\alpha$ phase is present, and its <001> direction is oriented upwards, although there are also small peaks corresponding to the (011), (018) planes. A configuration of atoms in $\alpha$-Ga₂O₃ with the <001> direction oriented upwards is shown in Figure 14. $\alpha$-Ga₂O₃ has a very symmetrical trigonal structure $R\overline{3}c$ (corundum structure).

The DFT calculations with the use of the SCAN meta-GGA functional [24] show that, among all phases of Ga₂O₃, the $\beta$ phase is the most energetically favorable, the $\epsilon$ phase is less favorable by 0.084 eV per structural unit, while the $\alpha$ phase is less favorable than the $\beta$ phase by 0.097 eV per structural unit.

The $\beta$ phase has the lowest density (5.9 $\mathrm{g}/{\mathrm{cm}}^3$), then comes the $\epsilon$ phase (6.1 $\mathrm{g}/{\mathrm{cm}}^3$), and the $\alpha$ phase has the highest density (6.5 $\mathrm{g}/{\mathrm{cm}}^3$). Thus, there is nothing surprising in the fact that, as the synthesis temperature decreases, the phases proceed in the sequence $\beta \to \epsilon \to \alpha$. Since $\alpha$ phase is the most symmetrical, the Raman spectrum of metastable $\alpha$-Ga₂O₃ contains the smallest number of lines. Figure 15 shows that one line of silicon and six lines corresponding to $\alpha$-Ga₂O₃ are visible (only line $E_{g,1}$ at 240 ${\mathrm{cm}}^{-1}$ [25] is not visible).

This spectrum was also calculated by the DFT methods by utilizing the Quantum Espresso code [19] and the GGA-PBESol functional [20] in the same approximations as before. The resulting theoretical spectrum is shown in Figure 15b. It can be seen that this spectrum agrees very well with the experimental one. Collective motions of atoms in $\alpha$-Ga₂O₃, corresponding to each line of the Raman spectrum, have been also calculated by the DFT method. The most interesting are the motions of atoms, which correspond to lines A_1g,1 and A_1g,2; they are shown in Figure 16.

In the case of line A_1g,1, only Ga atoms move, towards each other (Figure 16a). This happens very rarely, since, as a rule, mainly O atoms move, because they are lighter (Figure 6, Figure 11 and Figure 16b). In the case of line A_1g,2, O atoms move in a circle in the same direction (Figure 16b). In the case of lines E_g,4, E_g,5, only O atoms move as well, but their motion is less symmetrical. Since the surface of the $\alpha$-Ga₂O₃ sample is much smoother than that of the $\beta$- and $\epsilon$-phase samples, it reflects light better, so it becomes possible to measure the ordinary dielectric function of this sample with the VUV-VASE ultraviolet rotating-analyzer ellipsometer (J.A. Woollam Co., Dearborn, MI, USA) in the photon energy range of 0.5–9.3 eV. Figure 17 shows the resulting dependence of the dielectric function on the photon energy, which was derived from the experimental dependence by subtracting the roughness. Anisotropy of the dielectric function was not taken into account.

While there are very few experimental data on the dielectric function for the $\beta$ phase and the $\epsilon$ phase (which, apparently, can be explained by the roughness of these phases), there are such data for the $\alpha$ phase. In particular, in the work [26] such a spectrum was measured on the synchrotron ellipsometer in the MLS, Berlin, in the region from 0.04 to 20 eV. The agreement of the data obtained in the present work with the data [26] is very good, despite the significant difference in the growth technique of Ga₂O₃. The method used was ultrasonic mist chemical vapor epitaxy on (0001) α- Al₂O₃ substrate. Comparing the theoretical dependence [5] with the obtained experimental one, it can be concluded that there is also a good agreement between them.

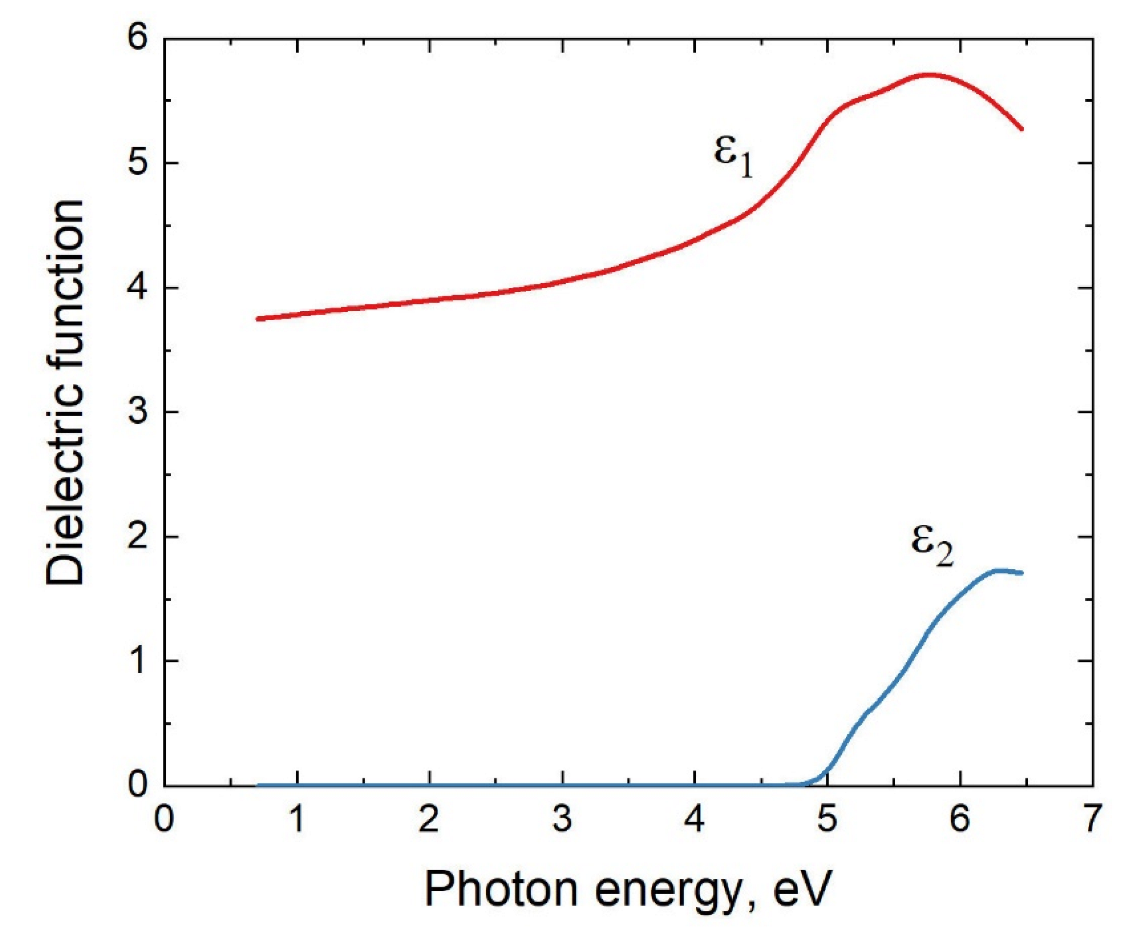
4. Discussion

Hence, it has been determined that by changing the synthesis temperature, it is possible to grow, by the HVPE method, Ga₂O₃ layers of three crystalline modifications on the 3C-SiC(111)/Si(111) hybrid substrates. Namely, the stable and least dense ($\rho$ = 5.9 $\mathrm{g}/{\mathrm{cm}}^3$) $\beta$ phase grows at a temperature of 800–1000 °C, the metastable $\epsilon$ phase with a density of $\rho$ = 6.1 $\mathrm{g}/{\mathrm{cm}}^3$ grows at a temperature of 550–600 °C, the densest ($\rho$ = 6.5 $\mathrm{g}/{\mathrm{cm}}^3$) and most symmetrical $\alpha$ phase grows at a temperature of 500–520 °C. The density values have been calculated by the DFT method using the SCAN meta-GGA functional, which gives the most accurate results on the geometric configuration of atoms [24]. It should also be emphasized that the $\alpha$ phase grows very smoothly (the roughness is no more than 5 nm), while the $\epsilon$ and $\beta$ phases have an order of magnitude greater roughness. At intermediate temperatures, a mixture of different phases grows. When heated to 900 °C for 10–15 min, the layers of the metastable $\alpha$ and $\epsilon$ phases completely transform into the stable $\beta$ phase. This indicates that the value of the potential barrier of phase transitions in this case is small. It should be noted that the Raman spectrum of the $\alpha$ phase contains only seven lines, which is much less than the number of lines in the Raman spectrum of the $\beta$ phase and, especially, the $\epsilon$. phase. This is obviously due to the fact that the $\alpha$ phase is the most symmetrical and has the structure of corundum. Therefore, the band structure of the $\alpha$ phase is the simplest [5]. The data on the main Raman lines of all three phases are given in

Table 1. The values of the frequencies of the main Raman peaks of all three phases, by which they can be identified.

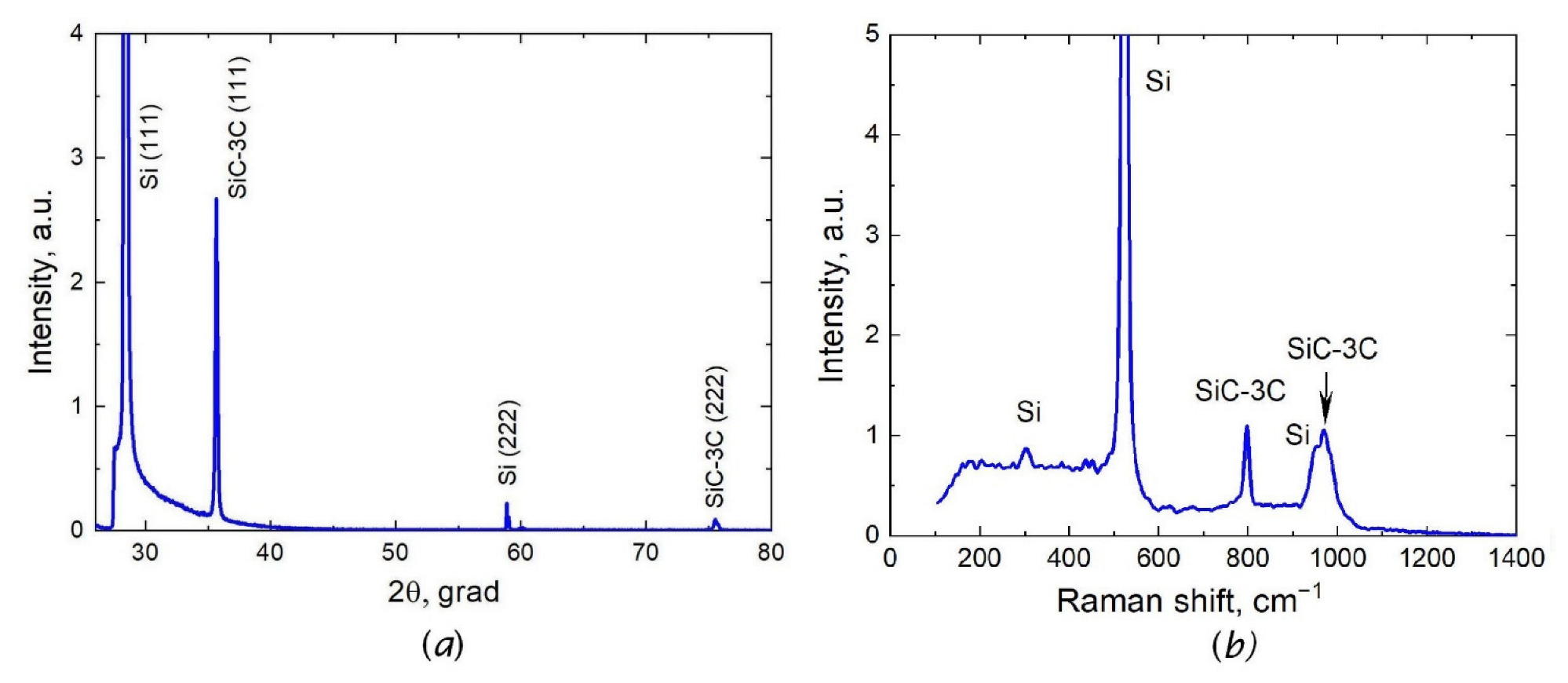
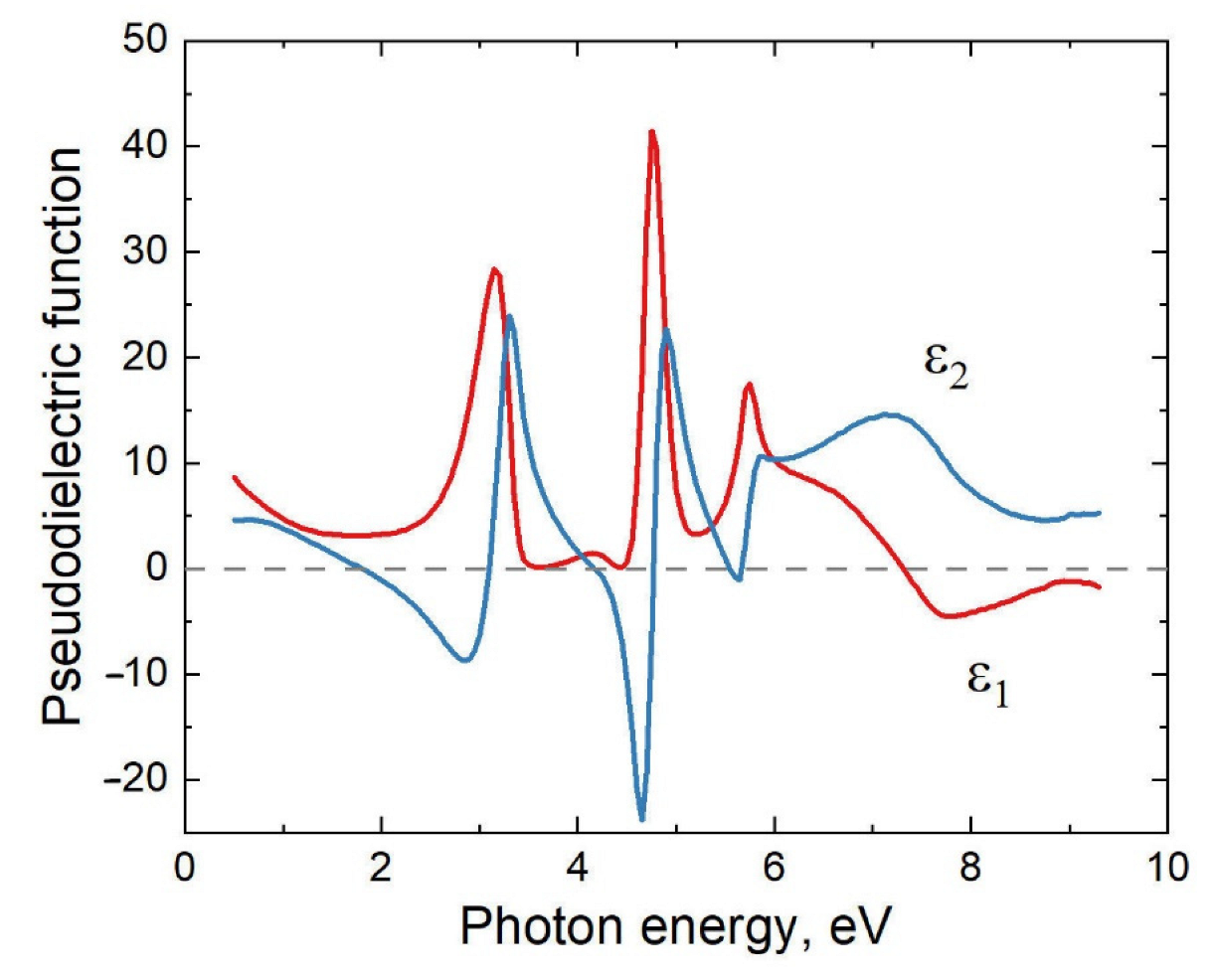
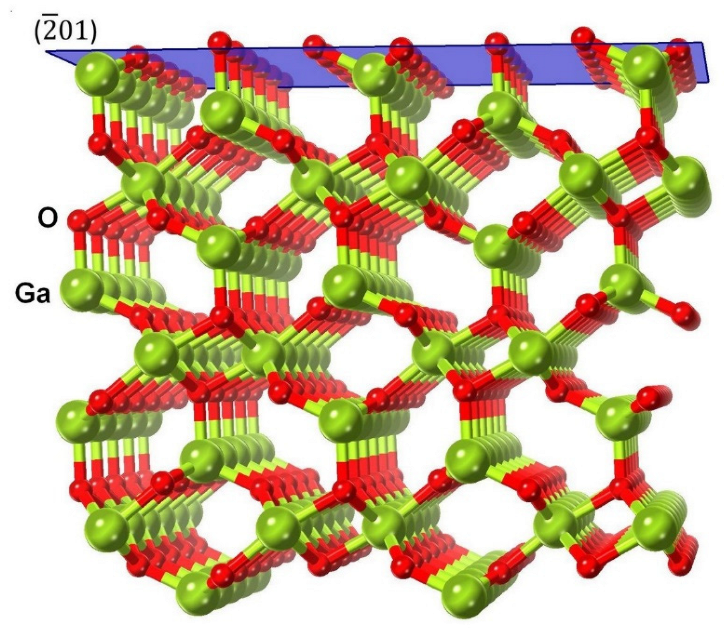
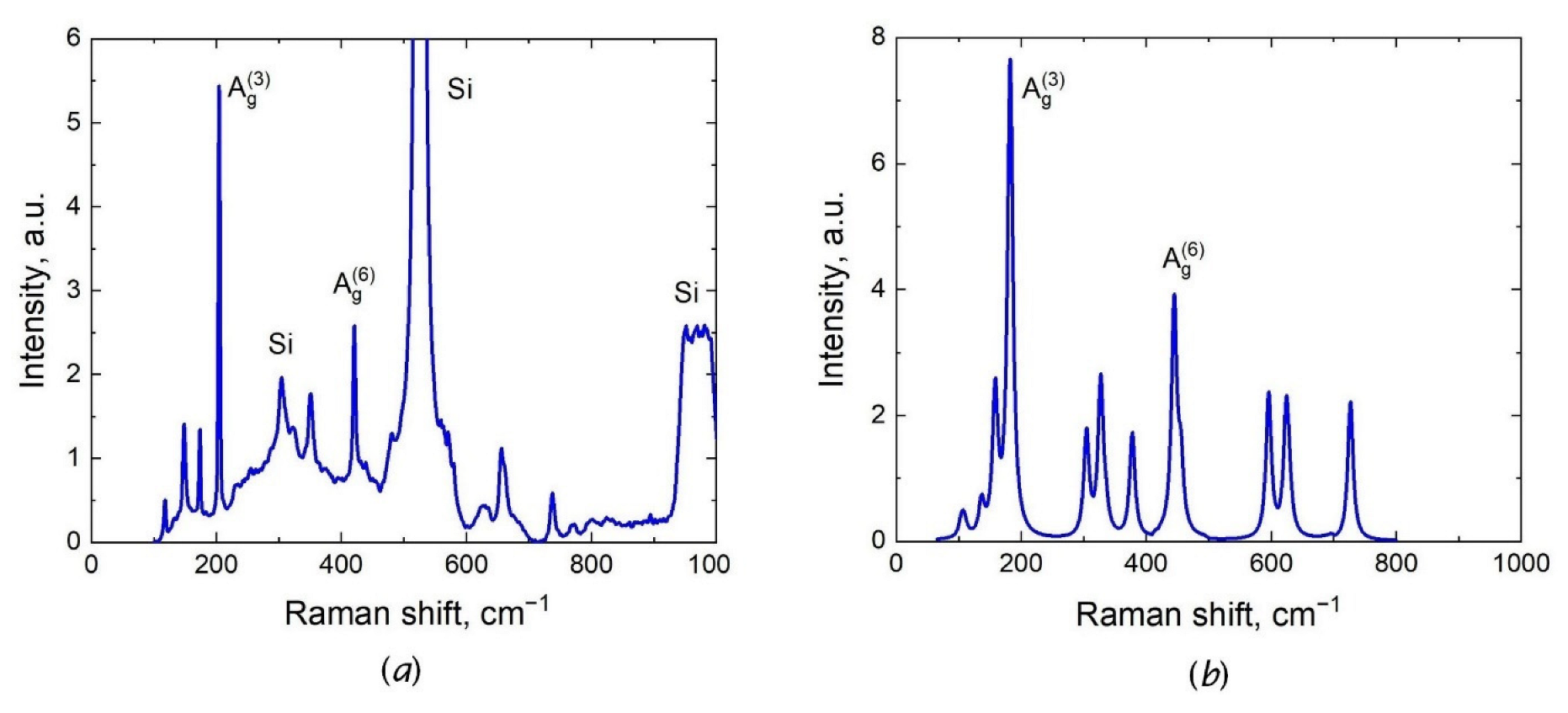
Phase of Ga2O3	Peaks	Freq., cm−1, Exp., This Work	Freq., cm−1, Theor., This Work	Freq., cm−1, Exp., [6,23,25]
$\alpha$-phase	A1g,1	221	216	217
	Eg,2	289	291	285
	Eg,3	332	319	327
	Eg,4	435	449	430
	A1g,2	576	577	570
	Eg,5	691	695	688
$\beta$-phase	$B_g^{\left(1\right)}$	117	108	115
	$B_g^{\left(2\right)}$	149	137	145
	$A_g^{\left(2\right)}$	174	159	170
	$A_g^{\left(3\right)}$	205	182	200
	$A_g^{\left(6\right)}$	421	445	416
$\epsilon$-phase	1	86	91	82
	2	117	128	113
	3	131	152	128
	4	150	175	147
	5	253	245	249

. It is easy to see that the Raman lines of the Ga₂O₃ samples grown on SiC/Si are shifted on average by 3.5 cm⁻¹ upwards (except for the E_g,5 of $\alpha -$ phase line). The most likely explanation for this result is that all Ga₂O₃ phases grown on SiC/Si are compressed compared to free Ga₂O₃. The compression value can be estimated as 0.1 GPa. This once again proves the ordering effect of SiC on Ga₂O₃. Measurements of the dielectric function have shown that the $\alpha$ phase is the most transparent, which is clearly due to the fact that the bandgap of the $\alpha$ phase is larger than that of the other phases. Estimates that have been made using the DFT methods show that the bandgap of the $\alpha$ phase is 0.4 eV larger than that of the $\beta$ phase. All this, along with the high mobility of charge carriers, makes $\alpha$-Ga₂O₃ a very promising material for microelectronics, especially as a transparent conductor. Until now, it was believed that the metastable $\alpha$ phase grows very badly, but in this work it has been shown that, at low temperatures of 500–520 °C, it grows very steadily on the 3C-SiC(111)/Si(111) hybrid substrates. At temperatures below 550 °C, the $\alpha$ phase does not transform into any other phase.

5. Conclusions

In this work, a technique to grow three different phases of Ga₂O₃ on the hybrid 3C-SiC(111)/Si(111) substrates has been developed. The layers thicker than 1 μm have been grown by the HVPE method. It has been found that the type of crystal structure in this case depends on the temperature of Ga₂O₃ synthesis. At low temperatures, the most symmetric $\alpha$ phase of the corundum structure grows, which has been successfully obtained only on rare occasions until now. As the temperature rises, the growth of the $\alpha$ phase is transformed into the growth of the $\epsilon$ phase, which is the least symmetric of all. With a further increase in temperature, the growth switches to the growth of the stable $\beta$ phase, which then remains steady. The Raman and ellipsometric spectra of all three phases have been studied, which makes it now easy to identify the phase by the Raman spectroscopy. Oscillations of atoms in Ga₂O₃, corresponding to the main lines of the Raman spectra of all three phases, have been modeled by the DFT methods.