Heat Transfer in Nanomaterial Suspension (CuO and Al₂O₃) Using KKL Model

Abstract

Novel nonlinear power-law flux models were utilized to model the heat transport phe-nomenon in nano-micropolar fluid over a flexible surface. The nonlinear conservation laws (mass, momentum, energy, mass transport and angular momentum) and KKL cor-relations for nanomaterial under novel flux model were solved numerically. Computed results were used to study the shear-thinning and shear-thickening nature of nano pol-ymer suspension by considering n-diffusion theory. Normalized velocity, temperature and micro-rotation profiles were investigated under the variation of physical parame-ters. Shear stresses at the wall for nanoparticles (CuO and Al₂O₃) were recorded and dis-played in the table. Error analyses for different physical parameters were prepared for various parameters to validate the obtained results.

1. Introduction

Polymer liquids like suspensions are non-Newtonian liquids containing solid-like microstructure. The rheology of such suspensions is characterized by two types of stress–strain correlations (i) the stress–strain correlations associated with macromotion caused by the body and surface forces and (ii) couple stress–strain constitutive equations based on micro-rotations of solid structures immersed in the suspension. Eringen [1] was the first to introduce the theory of such fluids and named them “micropolar fluids” (MF). After Eringen, many investigations were carried out to analyze several phenomena like heat transfer [2,3], mass transfer [4,5], viscous dissipation [6,7], Joule heating [8], Hall and ion slip effects [9], the effect of dispersion of nanoparticles [10,11], Soret and Dufour effects [12], using MF theory. The studies mentioned in refs. [13,14] are based on classical linear flux models, which assume that the diffusion coefficients are constant. However, Peter et al. [15] showed that the spinning of solid particles immersed in base liquid has a significant effect on viscosity effectiveness. This development motivated the researchers to establish novel nonlinear constitutive models for MF and, in view of suggestions by Peter et al. [15] and Sui et al. [16], proposed a novel similar nonlinear fluidic system. The generalized n- diffusion theory [17] is utilized by Sui et al. [16] to capture shear-thinning and shear-thickening performances. For more clarity, the following Table 1 is given for the comparison between classical and novel flux models.

Table 1. Comparison between classical and novel models.

Classical Models	Novel Models
classical Fourier law of heat flux ${\mathsf{q}}_{heat}=-k\nabla T$	novel Fourier law of heat flux ${\mathsf{q}}_{heat}=-k{\left|N\right|}^{n-1}\nabla T$
classical stress–strain model ${\tau }_{yx}=\mu \frac{\partial u}{\partial y}$	novel stress–strain model ${\tau }_{yx}=\mu {\left|N\right|}^{n-1}\frac{\partial u}{\partial y}+k_0\frac{\partial }{\partial y}\left({\left|N\right|}^{n-1}N\right)$

The expression $k{\left|N\right|}^{n-1},$ $\mu {\left|N\right|}^{n-1}$ and $k_0{\left|N\right|}^{n-1}$ are termed apparent thermal conductivity, apparent dynamic viscosity & apparent vortex viscosity, respectively. Further, for $n<1$ is the case of the shear-thinning nature of the liquid. It is noted that for the power index, $n=1,$ the novel flux models reduce to the classical Fourier law of heat conduction and classical stress–strain relations for MF. Moreover $n>1$ , the novel models capture shear-thickening behavior. Theoretical and experimental works on an enhancement of heat transfer through the dispersion of nanosolid particles in liquids motivated researchers and to invent several correlations for effective (viscosity, thermal properties and thermal conductivity etc.,) Among them example, the latest model is by Koo, Kleinstreuer and Li (KKL). Researchers have studied this model in recent years to present and analyze several applications in the field of science and technology. For instance, Kandelousi [18] and Haq et.al. [19] presented applications of KKL model in different geometries, while Alsagri and Moradi [20] presented some applications of the KKL nanoliquid model. They discussed some applications of nanofluid in heat transfer problems between rotary tubes. Rana and Nawaz [21] investigated the enhancement of heat transfer in Sutterby nanoliquid by analyzing the Koo–Kleinstreuer and Li (KKL) correlations. They also studied the generalized heat fluxes via Cattaneo–Christov heat flux model. An optimization via a numerical approach of microchannel heat sink (MCHS) performance utilizing the KKL theory has been analyzed by Pourmehran et al. [22]. Vijaybabu [23] computed the entropy generation and influence of permeable circular geometry by considering the nanofluids through KKL theory. Haq and Aman [24] analyzed the heated trapezoidal cavity with inner-heated obstacles with the KKL nanoliquid model. Multiple results for hydromagnetic Jeffery–Hamel flow utilizing KKL nanofluid model is studied by Rana et al. [25] Sheikholeslami and Mahian [26] presented application in energy storage through KKL theory by studying the enhancement of PCM solidification using inorganic nanomaterial. Mehmood et al. [27] studied simulations of hydromagnetic convective rheology in a square porous cavity using the KKL model. Li et al. [28] presented the applications of CVFEM for nanofluid heat transfer intensification by studying the KKL nano liquid model. Computational modeling of curved geometry with Koo–Kleinstreuer and Li (KKL) correlation model has been studied by Gowda et al. [29]. The relations utilized are:

$${\rho }_{nf}=(1-\varphi ){\rho }_f+\varphi {\rho }_s,{(\rho c_p)}_{nf}=(1-\varphi ){(\rho c_p)}_f+\varphi {(\rho c_p)}_s,$$

(1)

$${\sigma }_{nf}={\sigma }_f(1+\frac{3(\sigma -1)\varphi }{\sigma +2-(\sigma -1)\varphi }),\sigma =\frac{{\sigma }_s}{{\sigma }_f},$$

(2)

$$\frac{k_{static}}{k_f}=1+\frac{3\varphi (\frac{k_p}{k_f}-1)}{(\frac{k_p}{k_f}+2)-(\frac{k_p}{k_f}-1)\varphi },k_{eff}=k_{static}+k_{Brownian},$$

(3)

$$k_{eff}=1+\frac{3\varphi (\frac{k_p}{k_f}-1)}{(\frac{k_p}{k_f}+2)-(\frac{k_p}{k_f}-1)\varphi }+5\times {10}^4{g}^{\prime }(\varphi ,T,d_p)\varphi {\rho }_f{(c_p)}_f\sqrt{\frac{{\kappa }_{b}T}{d_p{\rho }_p}}$$

(4)

$$R_f=4\times {10}^{-8}k{m}^2/W,R_f=-d_p(1/k_p-1/k_{p,eff}),$$

(5)

$$g^{\prime }(\varphi ,T,d_p)=\left.\begin{array}{c}Ln(T)\left(\begin{array}{c}{a}_1+a_{3}Ln(\varphi )+a_{2}Ln(d_p)+a_{5}Ln{(d_p)}^2\\ +a_{4}Ln(d_p)Ln(\varphi )\end{array}\right)\\ +\left(\begin{array}{c}{a}_6+a_{8}Ln(\varphi )+a_{7}Ln(d_p)+a_{10}Ln{(d_p)}^2\\ +a_{9}Ln(\varphi )Ln(d_p)\end{array}\right),\end{array}\right)$$

(6)

$$k_{Brownian}=5\times {10}^4{g}^{\prime }(\varphi ,T,d_p)\varphi {\rho }_f{(c_p)}_f\sqrt{\frac{{\kappa }_{b}T}{d_p{\rho }_p}},300K<T<325K,$$

(7)

$${\mu }_{nf}=\frac{{\mu }_f}{{(1-\varphi )}^{2.5}}+\frac{k_{Brownian}}{k_f}\times \frac{{\mu }_f}{{\mathrm{Pr}}_f}.$$

(8)

Thermophysical properties of water and two types of metallic nanoparticles, which are used by Sheikholeslami [30], are given in Table 2.

Table 2. Thermophysical properties of water and nanoparticles.

Physical Property	Water/Base Fluid	$\mathit{C}\mathit{u}\mathit{O}$	$\mathit{A}{\mathit{l}}_2{\mathit{O}}_3$
$\rho \left(\mathrm{kg}{.\mathrm{m}}^{-3}\right)$	997.1	8933	3970
$C_p\left(\mathrm{J}{.\mathrm{kg}}^{-1}.{\mathrm{K}}^{-1}\right)$	4179	385	765
$k\left(\mathrm{W}{.\mathrm{m}}^{-1}.{\mathrm{K}}^{-1}\right)$	0.613	401	25
$d_p\left(\mathrm{nm}\right)$	-	40	47
$\sigma \left(\mathrm{S}{.\mathrm{m}}^{-1}\right)$	0.05	5.96 × 1007	3.69 × 10 07

2. Physical Situation

We investigated the effects of dispersion of nanoparticles (CuO and Al₂O₃) on the performance of thermal conductivity and viscosity using the KKL model. Mass, linear momentum, angular momentum and thermal diffusion, and boundary layers models are:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(9)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\left(\frac{{\mu }_{nf}-k_0}{{\rho }_{nf}}\right)\frac{\partial }{\partial y}\left({\left|N\right|}^{n-1}\frac{\partial u}{\partial y}\right)+\frac{k}{{\rho }_{nf}}\frac{\partial }{\partial y}\left({\left|N\right|}^{n-1}N\right),$$

(10)

$${\rho }_{nf}j\left(u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial y}\right)=\frac{\partial }{\partial y}\left(\gamma \frac{\partial N}{\partial y}\right)-k_0{\left|N\right|}^{n-1}\left(2N+\frac{\partial u}{\partial y}\right),$$

(11)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{{\lambda }_0}{{(\rho c_p)}_{nf}}\frac{\partial }{\partial y}\left({\left|N\right|}^{n-1}\frac{\partial T}{\partial y}\right)$$

(12)

where $[u,v,0]$ is for the velocity of the fluid, $[0,N,0]$ is for the microrotations or angular velocity in the xy plane, and T is for the temperature of the fluid. The other physical quantities ${\rho }_{nf}$ and ${\lambda }_0$ are the density and thermal conductivity, respectively. In this study, the Spin gradient viscosity $\gamma$ is defined as $\gamma =\left({\mu }_{nf}-k_0/2\right){\left|N\right|}^{n-1}={\mu }_{nf}{\left|N\right|}^{n-1}\left(1+K/2\right)j$ such that $j={\left(U_w^{n-2}x{\mu }_{nf}/{\rho }_{nf}\right)}^{\frac{2}{n+1}}$ where $K=k_0/{\mu }_{nf}.$

The following boundary conditions:

$$\left.\begin{array}{c}u=U_w,v=0,N=-m\frac{\partial u}{\partial y},T=T_w,\mathrm{at}y=0\\ u=v=N\to 0,T\to T_{\infty } as y\to \infty .\end{array}\right\}$$

(13)

are implemented for the solution of modeled boundary problems.

Normalization of equations: Diffusion Equations (9)–(12) and initial and boundary conditions (8a) are made dimensionless using the following transformations:

$$\left.\begin{array}{c}u=\frac{\partial \psi }{\partial y},v=-\frac{\partial \psi }{\partial x},\psi (x,y)={\left(\frac{U_w^{2n-1}x{\mu }_{nf}}{{\rho }_{nf}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$1+n$}\right.}f(\eta ),\\ N={\left(\frac{U_w^3{\rho }_{nf}}{x{\mu }_{nf}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$1+n$}\right.}R(\eta ),\theta (\eta )=\frac{T-T_{\infty }}{T_w-T_{\infty }},\eta ={\left(\frac{U_w^{2-n}{\rho }_{nf}}{x{\mu }_{nf}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$1+n$}\right.}y,\end{array}\right)$$

(14)

and hence we get the following boundary value problems:

$$\left.\begin{array}{c}(1+K)({\left|R\right|}^{n-1}{f}^{″}{)}^{\prime }+K({\left|R\right|}^{n-1}R{)}^{\prime }+\frac{A_1}{A_3}\frac{1}{n+1}f{f}^{″}=0,\\ f^{\prime }(0)=1,f(0)=0\end{array}\right\}$$

(15)

$$\left.\begin{array}{c}(1+\frac{K}{2})({\left|R\right|}^{n-1}{R}^{\prime }{)}^{\prime }-K{\left|R\right|}^{n-1}\left[2R+f^{″}\right]+\frac{A_1}{A_3}\left(R{f}^{\prime }+f{R}^{\prime }\right)=0,\\ R(0)=-\frac{1}{2}{f}^{″}(0),R(\infty )=0\end{array}\right\}$$

(16)

$$\left.\begin{array}{c}{\left({\left|R\right|}^{n-1}{\theta }^{\prime }\right)}^{\prime }+A_2\mathrm{Pr}\frac{1}{n+1}f{\theta }^{\prime }=0,\\ \theta (0)=1,\theta \to 0\mathrm{as}\eta \to \infty ,\end{array}\right\}$$

(17)

where:

$$\begin{array}{c}{A}_1=\frac{{\rho }_{nf}}{{\rho }_f},A_2=\frac{{(\rho c_p)}_{nf}}{{(\rho c_p)}_f},A_3=\frac{{\mu }_{nf}}{{\mu }_f},A_4=\frac{k_{eff}}{k_f},A_5=\frac{{\sigma }_{nf}}{{\sigma }_f},\mathrm{Pr}=\frac{{\mu }_f{(c_p)}_f}{k_f}.\end{array}$$

(18)

Expressions for the wall skin friction and Nusselt number are given below:

$$C_{fx}=-\frac{2{\tau }_w}{{\rho }_{nf}{u}_w^2}=2^{n-2}(1+\frac{K}{2}){\left|f^{″}(0)\right|}^{n-1}{f}^{″}(0),$$

(19)

where:

$${\tau }_w={\left[({\mu }_{nf}+k_0){\left|N\right|}^{n-1}\partial u/\partial y+k_0{\left|N\right|}^{n-1}N\right]}_{y=0}$$

(20)

$$\mathrm{R}{\mathrm{e}}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}Nu=\frac{x{q}_w}{{\lambda }_w(T_w-T_{\infty })}=-{\theta }^{\prime }(0),$$

(21)

$$q_w=-{\lambda }_0{\left[{\left|N\right|}^{n-1}\partial T/\partial y\right]}_{y=0}.$$

(22)

3. Numerical Procedure

Here, a brief and complete description of the numerical approaches Adams and explicit Runge–Kutta (RK) methods to solve heat transport phenomenon in nano-micropolar polymer over a flexible surface (15)–(17) is presented.

Adam Predictor—Corrector Solver

The heat transport phenomenon in nano-micropolar polymer over a flexible surface is represented in Equations (15)–(17) and is transformed in to equivalent first-order differential system along with boundary conditions in terms of the velocity field $f\left(\eta \right)$, $R\left(\eta \right)$, temperature profile $\theta \left(\eta \right)$.

Generic representations of a derived first-order system for $f\left(\eta \right)$, $R\left(\eta \right)$ and $\theta \left(\eta \right)$ are given, respectively, as follows:

$$\frac{df}{d\eta }=b(\eta ,f),f({\eta }_0)=f_0,$$

(23)

$$\frac{dR}{d\eta }=b(\eta ,R),R({\eta }_0)=R_0,$$

(24)

$$\frac{d\theta }{d\eta }=b(\eta ,\theta ),\theta ({\eta }_0)={\theta }_0,$$

(25)

The generalized expressions for two-stage Adams predictor–corrector technique [31,32,33,34,35,36] for $f\left(\eta \right)$, $R\left(\eta \right)$ and $\theta \left(\eta \right)$ are given, respectively, as follows:

$$f_{k+1}=f_k+\frac{h}{2}\left(3w({\eta }_k,f_k)-w({\eta }_{k-1},f_{k-1})\right),$$

(26)

$$R_{k+1}=R_k+\frac{h}{2}\left(3w({\eta }_k,R_k)-w({\eta }_{k-1},R_{k-1})\right),$$

(27)

$${\theta }_{k+1}={\theta }_k+\frac{h}{2}\left(3w({\eta }_k,{\theta }_k)-w({\eta }_{k-1},{\theta }_{k-1})\right),$$

(28)

where h is a step size parameter. Accordingly, standard multi-stage Adams predictor-corrector expressions for $f\left(\eta \right)$, $R\left(\eta \right)$ and $\theta \left(\eta \right)$ are illustrated, respectively, as follows:

$$f_{k+1}=f_k+\frac{h}{2}\left(w({\eta }_{k+1},f_{k+1})-w\left({\eta }_k,f_k\right)\right),$$

(29)

$$R_{k+1}=R_k+\frac{h}{2}\left(w({\eta }_{k+1},R_{k+1})-w\left({\eta }_k,R_k\right)\right),$$

(30)

$${\theta }_{k+1}={\theta }_k+\frac{h}{2}\left(w({\eta }_{k+1},{\theta }_{k+1})-w\left({\eta }_k,{\theta }_k\right)\right),$$

(31)

4. Results and Discussion

In this section, we present and discuss the behavior of several involved physical quantities on the flow field by utilizing the numerical values given in Table 3. Several graphs were prepared to analyze the absolute error in computation. Moreover, a comparison of obtained solutions via the Adams method and explicit Runge–Kutta method is also presented. A good agreement between the solutions is noted, which validates the precision of obtained results. The graphical and tabular results are presented to show the effects of physical parameters. In this regard, Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 were plotted to analyze the effects of the involved physical parameter when CuO nanoparticles are suspended in the base fluid. Figure 1 presents the effects of k₀ on the velocity profile $f^{\prime }$. It is noted that velocity field retard for positive values of k₀. The momentum boundary layer also decreases with an increase in k₀. The solid curves present the solutions via the Adams method, whereas bullets represent the results for the explicit Runge–Kutta method. Both solutions were found to be in good agreement.

Table 3. The coefficient values of CuO and Al₂O₃ nanofluids.

Coefficient Values	CuO-Water [37]	Al2O3-Water
a1	−26.593310846	52.813488759
a2	−0.403818333	6.115637295
a3	−33.3516805	0.6955715084
a4	−1.915825591	4.17455552786 × 10−2
a5	6.42185846658 × 10−2	0.176919300241
a6	48.40336955	−298.19819084
a7	−9.787756683	−34.532716906
a8	190.245610009	−3.9225289283
a9	10.9285386565	−0.2354329626
a10	−0.72009983664	−0.999063481

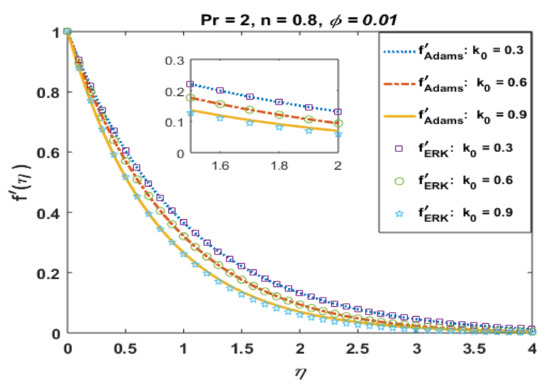
Figure 1. Effects of k₀ on $f^{\prime }\left(\eta \right)$.

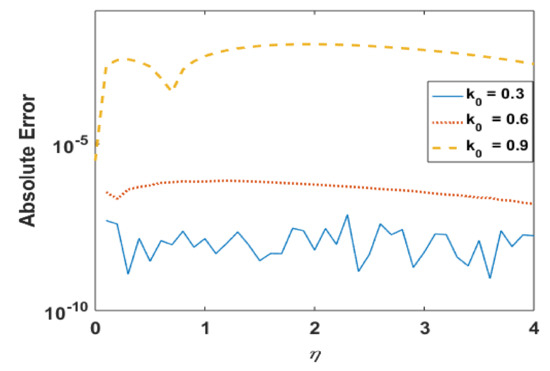
Figure 2. Absolute error in $f^{\prime }\left(\eta \right)$ for different k₀.

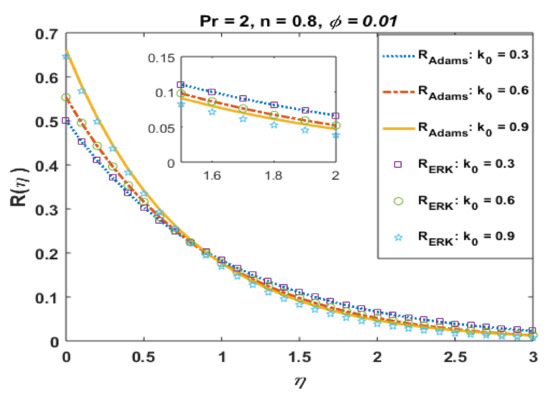
Figure 3. Effects of k₀ on $R\left(\eta \right)$.

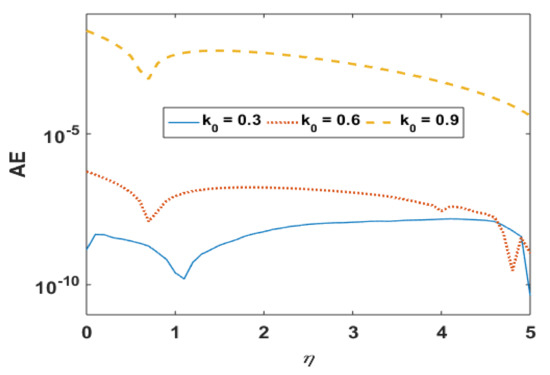
Figure 4. Absolute error in $R\left(\eta \right)$ on different k₀.

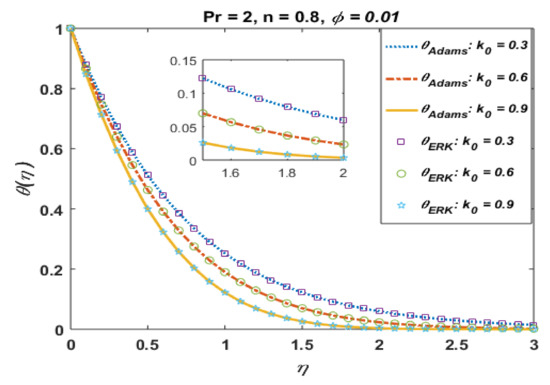
Figure 5. Effects of k₀ on $\theta \left(\eta \right)$.

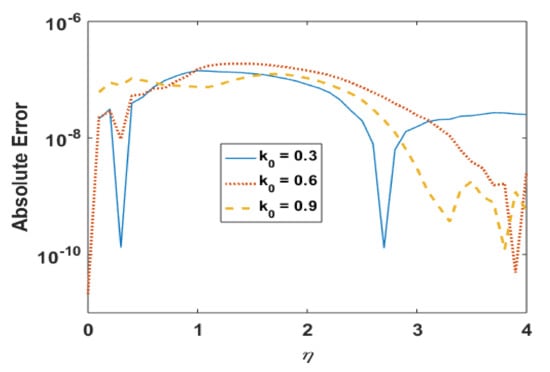
Figure 6. Absolute error in $\theta \left(\eta \right)$ for different k₀.

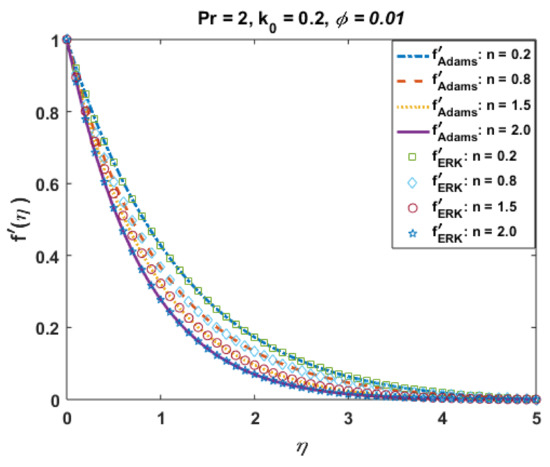
Figure 7. Effects of n on $f^{\prime }\left(\eta \right)$.

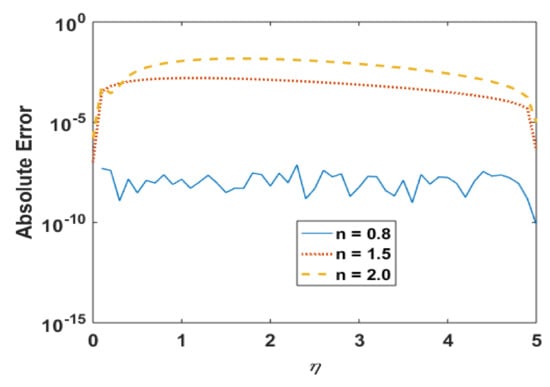
Figure 8. Absolute error in $f^{\prime }\left(\eta \right)$ for different n.

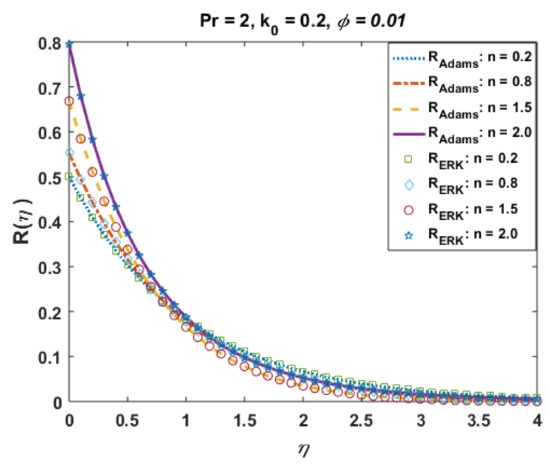
Figure 9. Effects of n on $R\left(\eta \right)$.

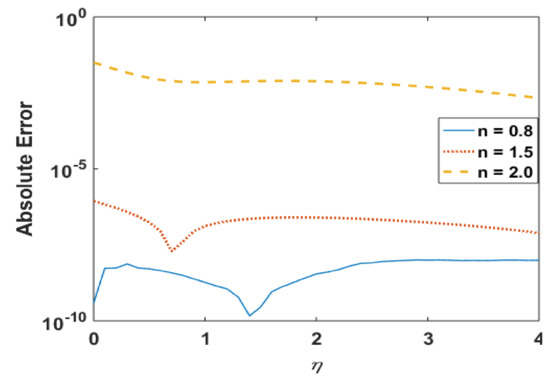
Figure 10. Absolute error in $R\left(\eta \right)$ for different n.

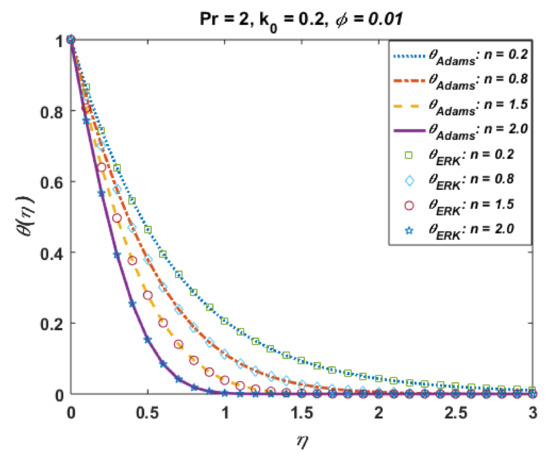
Figure 11. Influence of n on $\theta \left(\eta \right)$.

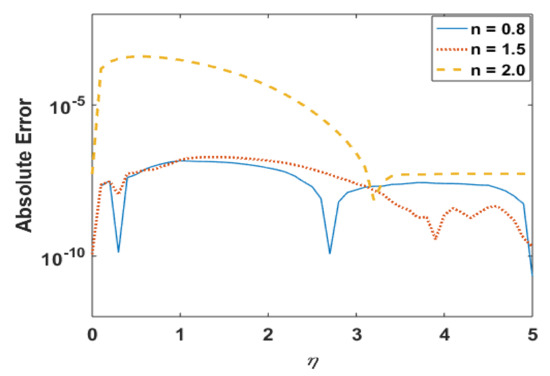
Figure 12. Absolute error in $\theta \left(\eta \right)$ for different n.

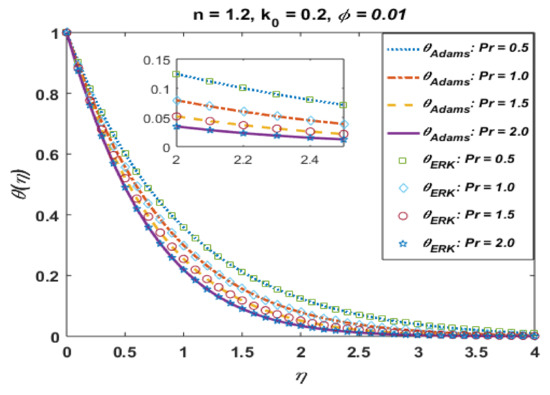
Figure 13. Effects of Pr on $\theta \left(\eta \right)$.

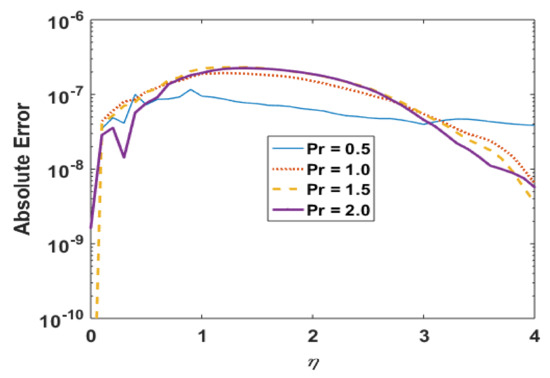
Figure 14. Absolute error in $\theta \left(\eta \right)$ for different Pr.

Figure 2 presents the absolute error $f^{\prime }\left(\eta \right)$ for different values of k₀. It is noted that the error in computations is approximately 10⁻⁸. Figure 3 portrays the effects of k₀ on R. It is noted the profile R decreases near the boundary but demonstrates the opposite trend away from the wall. This is obvious to obey the mass conservation constraint. The absolute error in profile R is presented in Figure 4, which confirmations that the error is minimum to the tolerance level.

Figure 5 and Figure 6 present the effects of k₀ on temperature profile $\theta$ and the absolute error in computations. It is observed that the temperature profile was found to decrease with an increase in k₀. Moreover, solutions obtained via the Adams method and explicit Runge–Kutta is also in good agreement, and the absolute error is also found to be negligible.

Figure 7 portrays the effects of shear-thinning/thickening parameter “n” on the velocity profile $f^{\prime }$. The case (n < 1.0) represents the reduction in viscosity with the shear rate or shear-thinning effects, whereas the case (n > 1.0) shows the increase in viscosity with the shear rate or shear-thickening effect. The plot elucidates that the velocity field $f^{\prime }$ increases for the case when n decreases from numerical value 1.0, whereas $f^{\prime }$ it decreases for the case when n increases from numerical value 1.0.

Such outcomes illustrate that the more shear-thinning/thickening effects will be observed when the values different from n = 1.0 are considered. From a physical point of view, it is clear that an apparent decrease/increase in viscosity of the suspended micropolar material is accredited to the rotation of particles and for increasing/decreasing values of “n”, the shear-thinning/thickening effects due to the microparticle rotation represents the layer-by-layer fluid separation, which results in the momentum boundary layer thinned/thickened for different n. The solutions via Adam and explicit RK are also in good agreement, and the absolute error (Figure 8) is also negligible.

Figure 9 presents the effects of “n” on profile micro-rotation velocity field R via Adams and explicit RK since the particle angular velocity distribution profiles is a significant factor in micropolar fluid rheology. This plot signifies the exclusive micro-rotation velocity profiles for the shear-thinning/thickening phenomenon portrayed by “n”. It is also observed that the microrotation velocity field retards at the boundary and reaches the numerical values of 0.0 at the boundary layer. The profiles consequently overlap each other, as noted in the figure. The granular velocity decreasing rate is minor near the wall and signifies the boundary layer. The absolute error plot (Figure 10) also shows negligible error up to the tolerance level.

Figure 11 presents the effects of n on the temperature profile $\theta$. This plot shows that the temperature profile decays with an increase in n. The temperature field thickens for smaller values of “n”, which not only be contingent on heat conduction performance of micropolar fluid demonstrated by reformed thermal conductivity properties but also to a great magnitude on the shear-thinning consequence as a dynamical property in shear flow. Moreover, solutions via Adams and explicit RK are also in good agreement. Figure 12 portrays the absolute error is computed results for different values and noted that error is negligible. Figure 13 is prepared to interpret the effects of the Prandtl number Pr on the temperature profile. This graph shows that temperature retards for positive values of Pr. Moreover, absolute error (Figure 14) is also found to be negligible. Table 4 is prepared to analyze the values for skin friction and the local Nusselt number for different physical quantities.

Table 4. Behavior of skin friction and Nusselt number when $\varphi =0.04,\mathrm{Pr}=2.73$ and $K=0.1$.

Index	Case	$\mathit{C}\mathit{u}\mathit{o}$		$\mathit{A}{\mathit{l}}_2{\mathit{O}}_3$
		$-{\left(\mathrm{Re}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{C}_f$	${\left(\mathrm{Re}\right)}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}Nu$	$-{\left(\mathrm{Re}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{C}_f$	${\left(\mathrm{Re}\right)}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}Nu$
$K$	0	2.6727	1.7826	2.6976	1.7774
	0.1	3.3973	1.7291	3.4293	1.7233
	0.2	4.2556	1.6664	4.2897	1.6604
	0.3	5.2086	1.5909	5.2426	1.5847
$\mathrm{Pr}$	1.5	7.2436	1.1847	7.3631	1.1700
	2.73	7.3249	1.3146	7.3596	1.3038
	3.2	7.3394	1.3587	7.3590	1.3502
	4.0	7.3562	1.4205	7.3583	1.4179
$\phi$	0.01	3.4186	1.7298	7.3515	1.3084
	0.04	3.3973	1.7291	7.3596	1.3038
	0.10	3.2506	1.7377	7.3582	1.2996
	0.15	2.9983	1.7575	7.3419	1.3001

Figure 15 presents the effects of k₀ on the velocity profile for the suspension of alumina nanoparticles. It is observed that velocity profiles accelerate for the positive values of k₀. Moreover, thermal boundary layers also increase with an increase in k₀. The solutions obtained via the Adams method are in good agreement with the results of ERK. The effects of k₀ on R are portrayed in Figure 16. It is noted that jump effects were noted at the wall for positive values of k₀, whereas an opposite trend is noted after the region $\eta >1$.

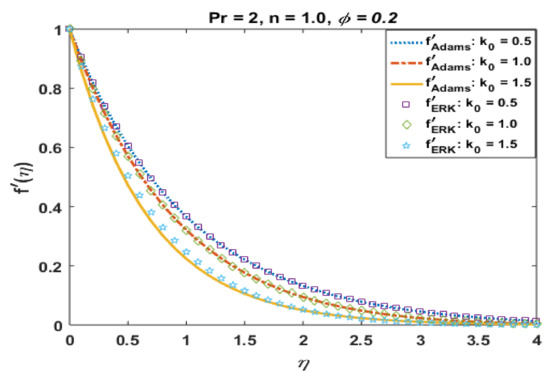
Figure 15. Effects of k₀ on $f^{\prime }\left(\eta \right)$.

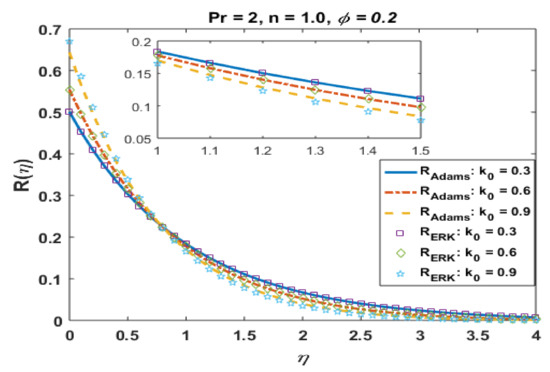
Figure 16. Effects of k₀ on $R\left(\eta \right)$.

The effects of k₀ on temperature profile $\theta$ are elucidated in Figure 17. It is observed that temperature and thermal boundary layer reduced with an increase in k₀. The micro-rotation parameter “n” retards the flow and boundary layer, as noted in Figure 18. The results for CuO and Al₂O₃ are qualitatively similar.

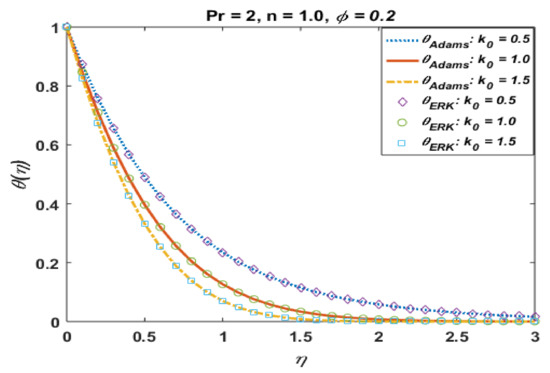
Figure 17. Effects of k₀ on $\theta$.

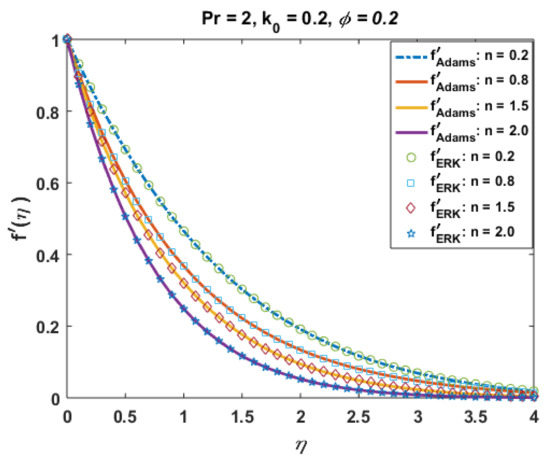
Figure 18. Effects of n on $f^{\prime }\left(\eta \right)$.

Effects of n on profiles R and $\theta$ are portrayed in Figure 19 and Figure 20. From these plots, one can see the jump effects are noted for larger values of n against R and the opposite trend is noted far from the surface, whereas temperature and thermal boundary layer retards for positive values of n. The effects of the Prandtl number Pr on temperature are presented in Figure 21. It is noted that the temperature and thermal boundary layer decrease with an increase in Pr. From the plotted graphs, it is noted that the results of CuO suspension are qualitatively similar to those of Al₂O₃.

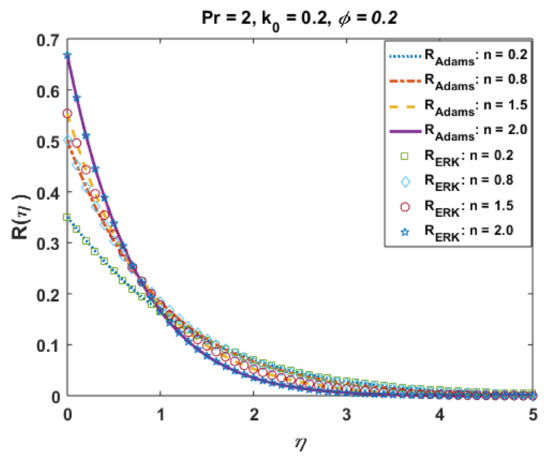
Figure 19. Effects of n on $R\left(\eta \right)$.

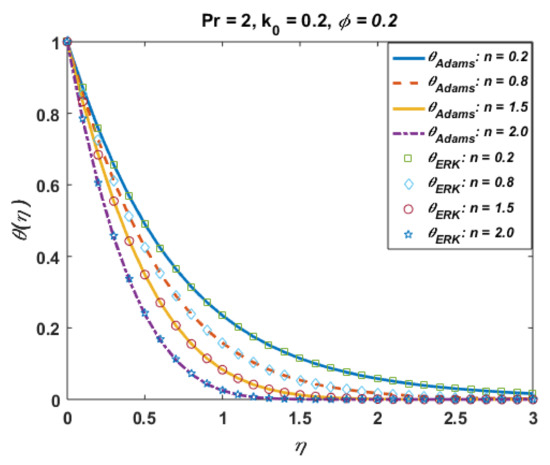
Figure 20. Effects of n on $\theta \left(\eta \right)$.

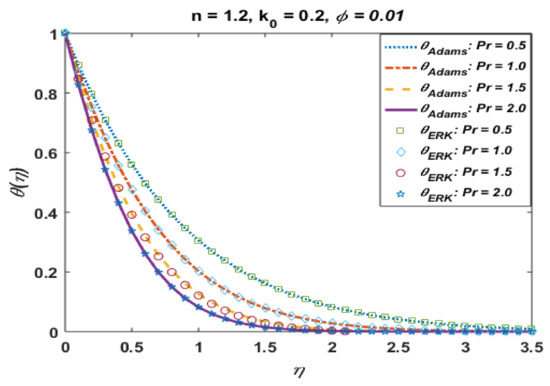
Figure 21. Effects of Pr on $\theta \left(\eta \right)$.

We further analyzed the comparative study of different numerical methods, including Adam method, backward difference method (BDF), explicit Runge–Kutta (ERK), implicit Runge–Kutta (IRK) and extrapolation (ET) for CuO and Al₂O₃.based metallic nano polymeric suspension in the KKL fluidic model. Results for Adam, BDF, ERK, IRK and ET both types of suspension are presented in Table 5 in terms of computational time consumed, number of steps, ODE evaluations and different accuracy goals. Time and space accuracy for proposed numerical approaches were validated through numerical data provided in Table 5. Furthermore, one may see that accuracy convergence, stability of all numerical approaches was validated for all four different levels of accuracy goals, i.e., 10⁻⁷, 10⁻¹⁵, 10⁻²² and 10⁻³⁰. However, the complexity of all algorithms increased for more stiff levels of accuracy goals. The performance of computational time complexity, as well as numbers of evaluation, were generally found best for Adam numerical method in the case of CuO and Al₂O₃.based metallic nano polymeric suspension in the KKL fluidic model for a scenario based on k₀ = 0.6. The results were omitted for other scenarios due to similar trends inferences of accuracy, convergence, stability and complexity for all other cases of the KKL fluidic model.

Table 5. Convergence and complexity test for $k_0=0.6$.

Method	Accuracy Goal	$\mathit{C}\mathit{u}\mathit{o}$			$\mathit{A}{\mathit{l}}_2{\mathit{O}}_3$
		Time	Steps	Evaluation	Time	Steps	Evaluation
Adams	${10}^{-30}$	0.92875	177	395	1.675	184	398
	${10}^{-22}$	0.765625	162	374	1.37	172	384
	${10}^{-15}$	0.8125	149	360	1.25	158	342
	${10}^{-07}$	0.296875	64	145	0.39062	62	135
BDF	${10}^{-30}$	1.6875	243	657	1.95313	284	724
	${10}^{-22}$	1.60938	237	633	1.70313	249	681
	${10}^{-15}$	1.32813	227	600	1.23438	219	575
	${10}^{-07}$	0.4375	108	291	0.671875	105	291
ERK	${10}^{-30}$	3.45313	115	1837	3.9875	116	1853
	${10}^{-22}$	2.6875	84	1341	3.84375	84	1341
	${10}^{-15}$	0.359375	67	675	0.359375	34	649
	${10}^{-07}$	0.28125	21	212	0.28125	19	193
IRK	${10}^{-30}$	7.51563	145	2041	53.5	141	1968
	${10}^{-22}$	4.32813	113	1716	46.9375	97	1456
	${10}^{-15}$	3.45313	96	1563	14.4688	89	1622
	${10}^{-07}$	0.21875	39	641	12.5	41	670
ET	${10}^{-30}$	0.984375	199	420	1.88125	203	428
	${10}^{-22}$	0.87375	171	388	1.84375	183	387
	${10}^{-15}$	0.828125	152	367	1.38264	174	363
	${10}^{-07}$	0.467835	92	205	0.884375	98	183