Exchange Bias in Thin Films—An Update
Abstract
1. Introduction
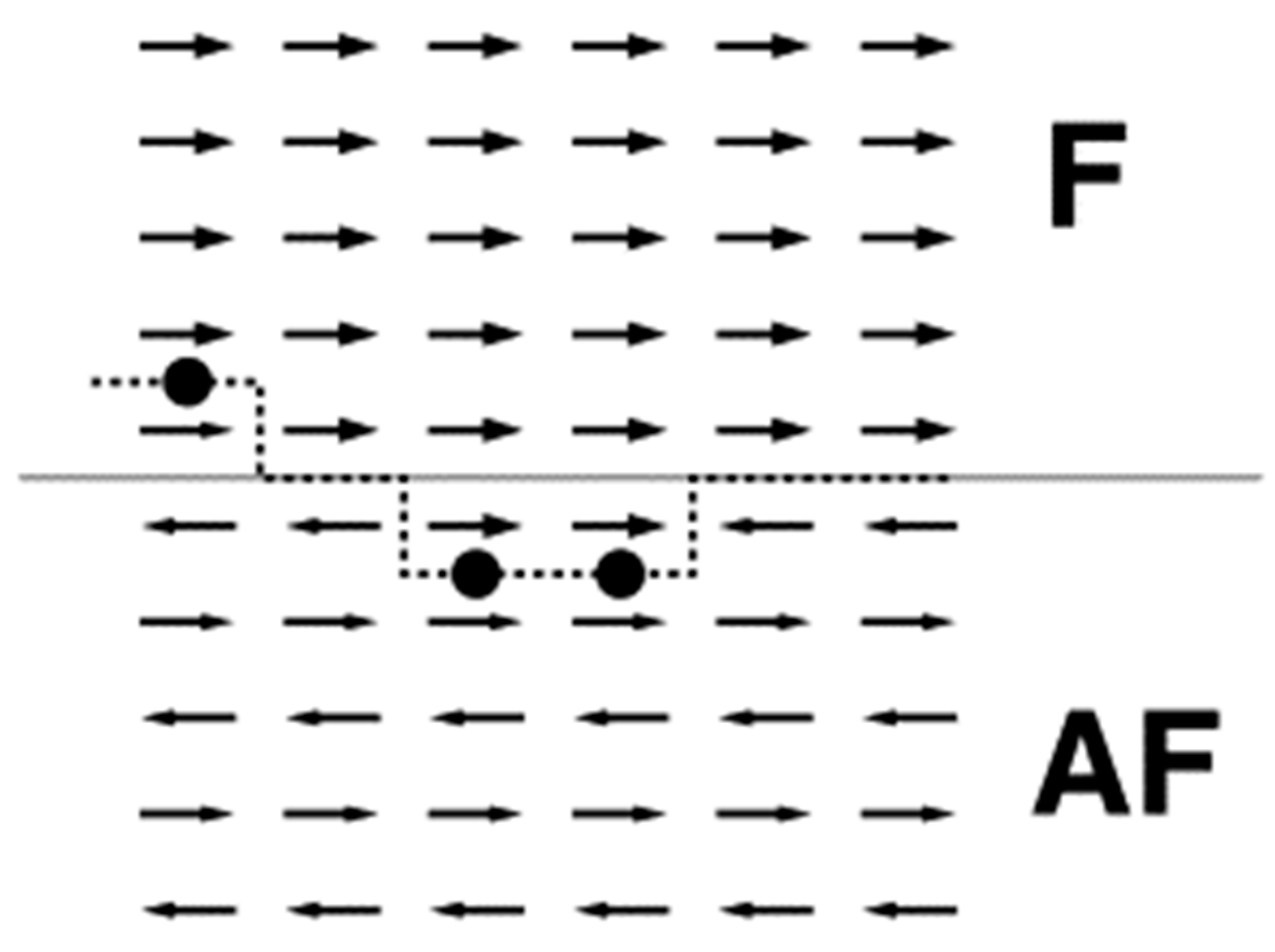
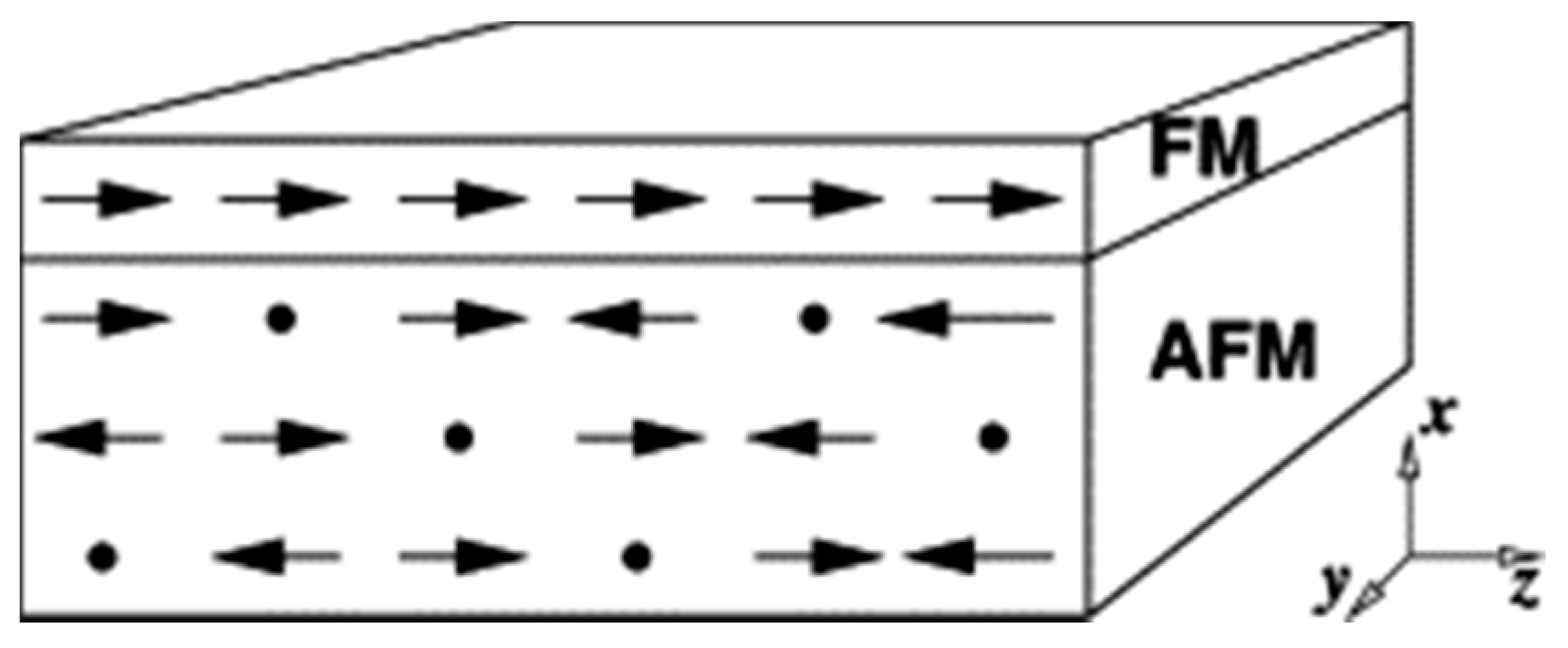
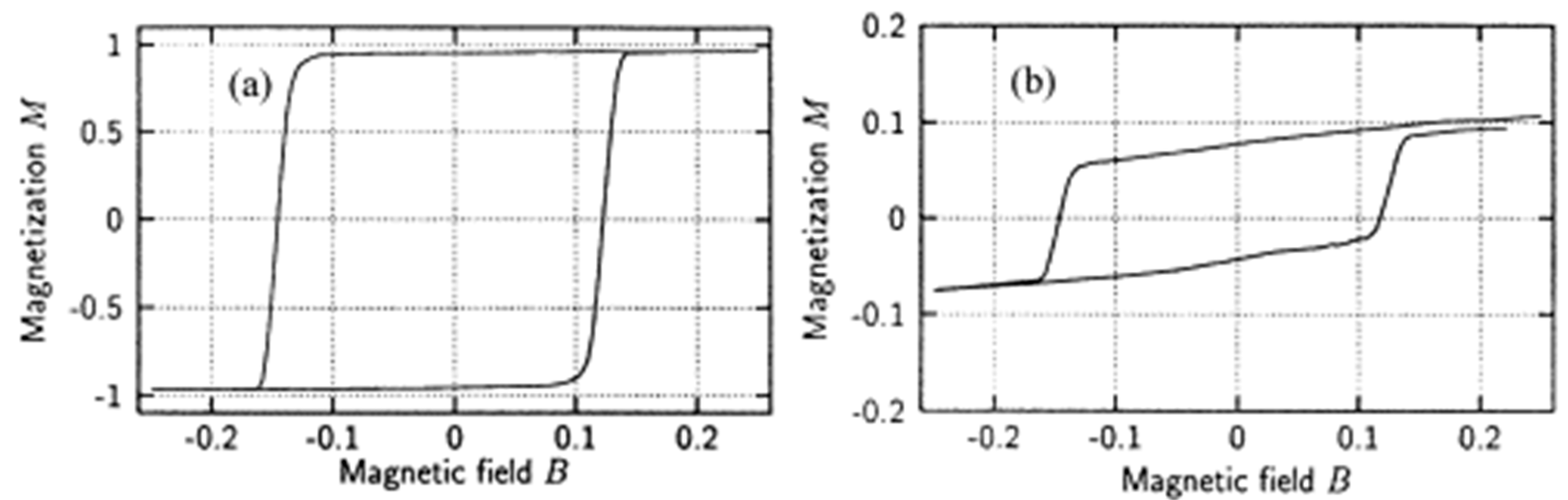
2. Properties of Exchange Bias Systems
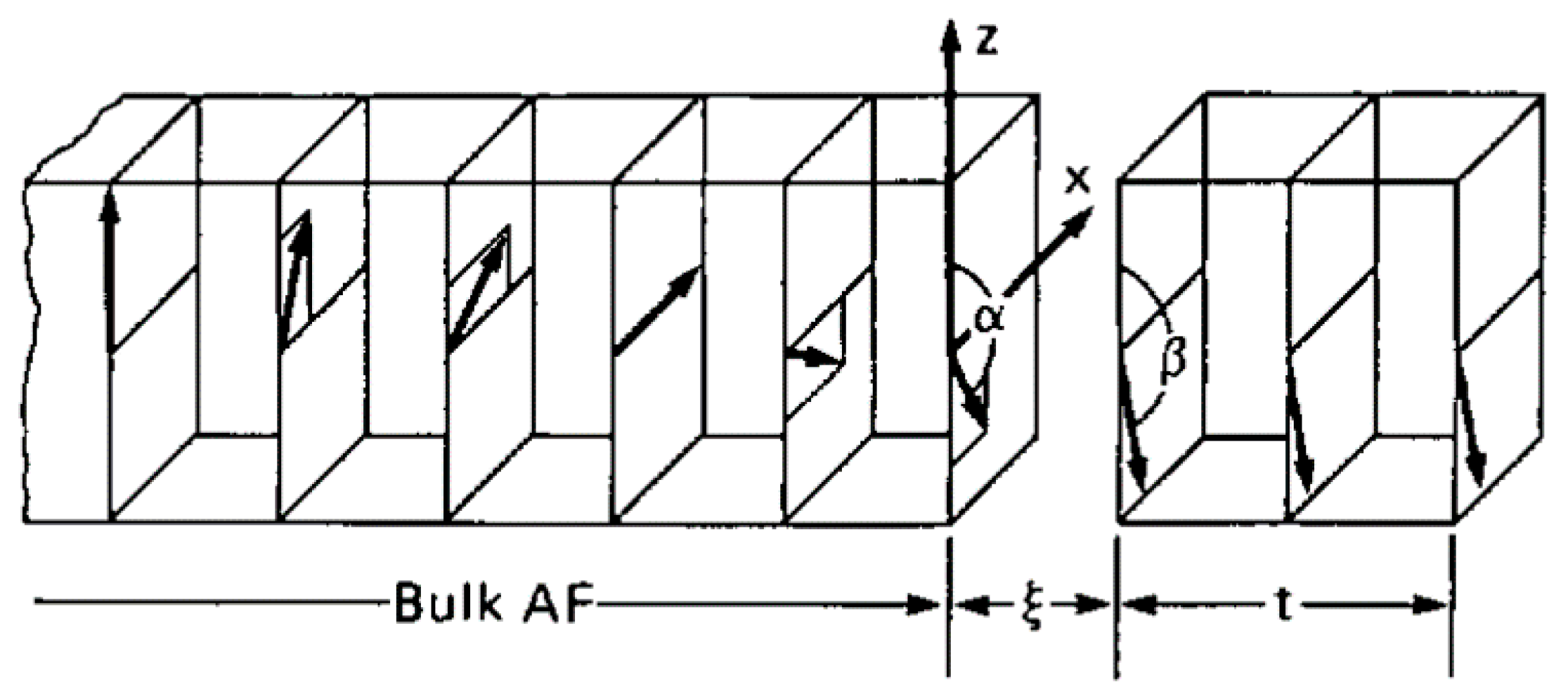
3. Modeling the Exchange Bias
4. Traditional Thin Film Systems
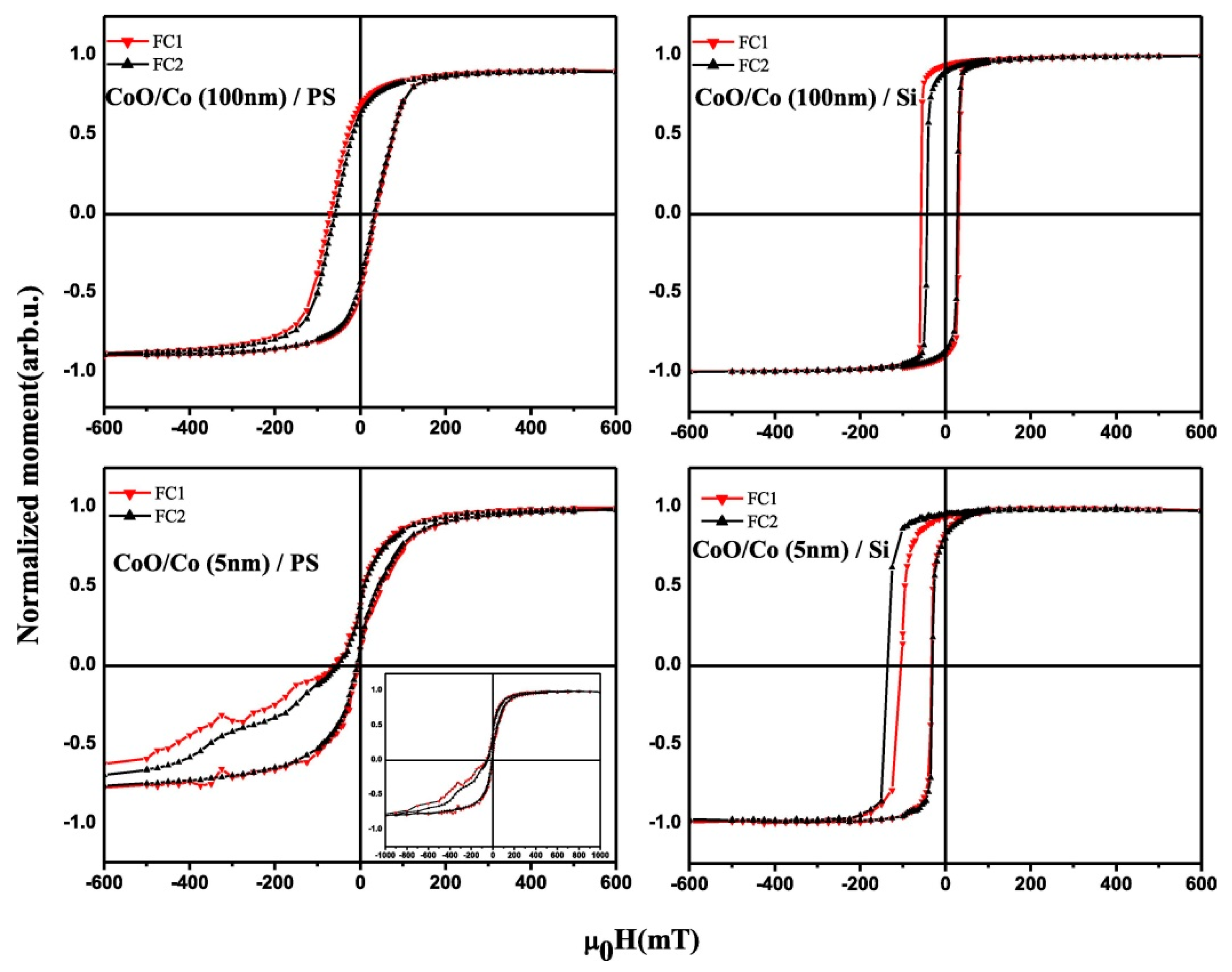
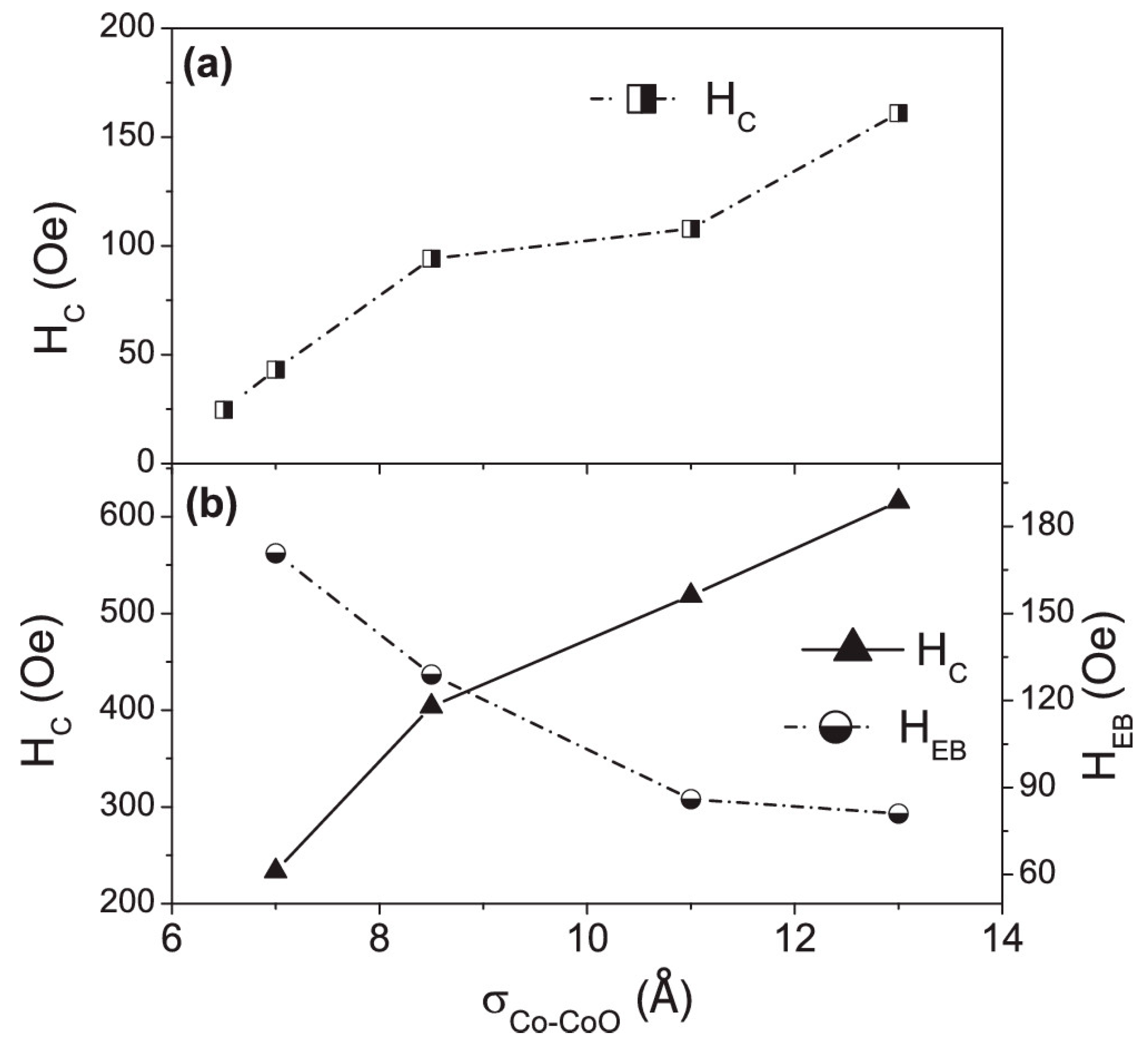
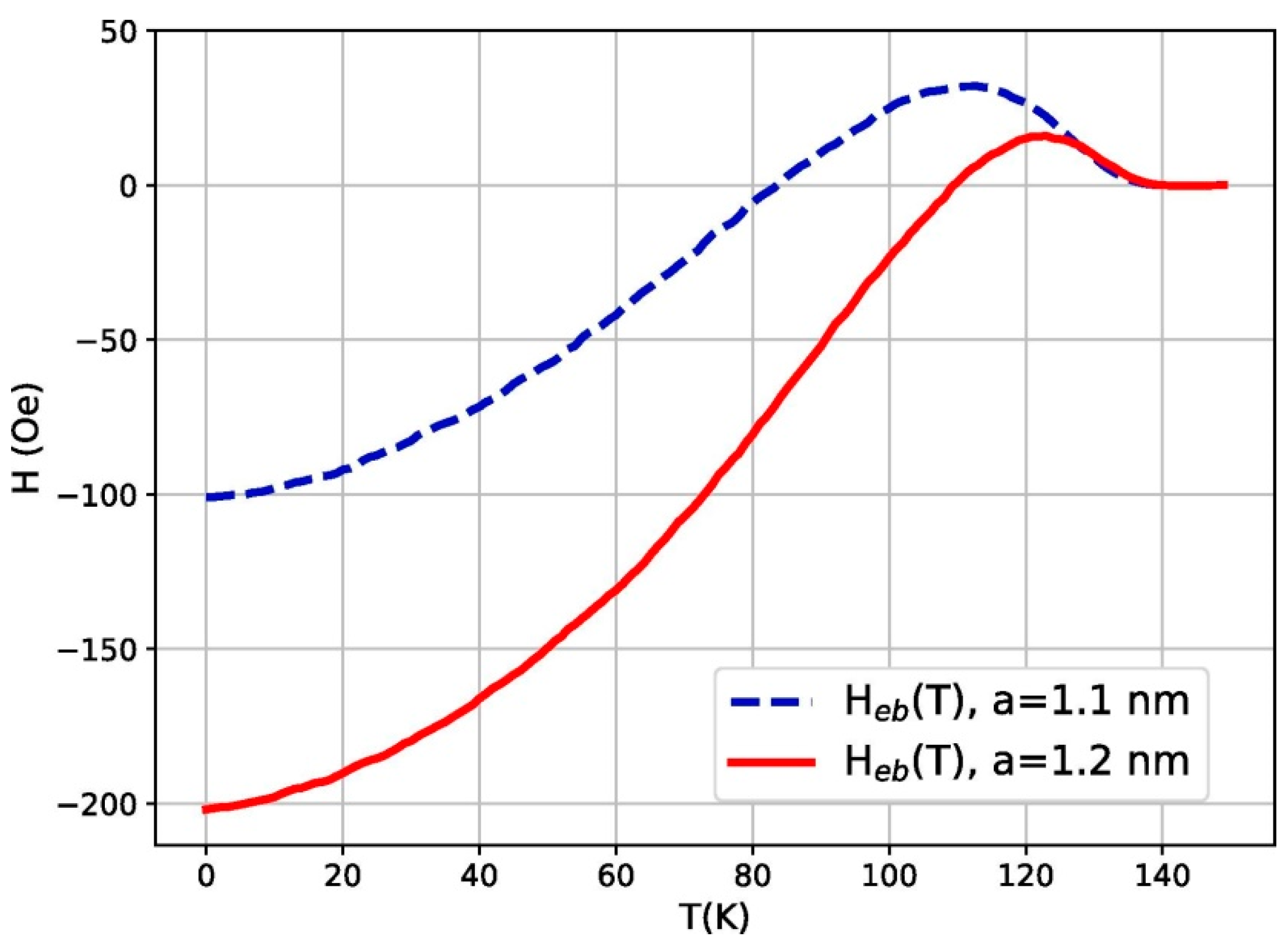
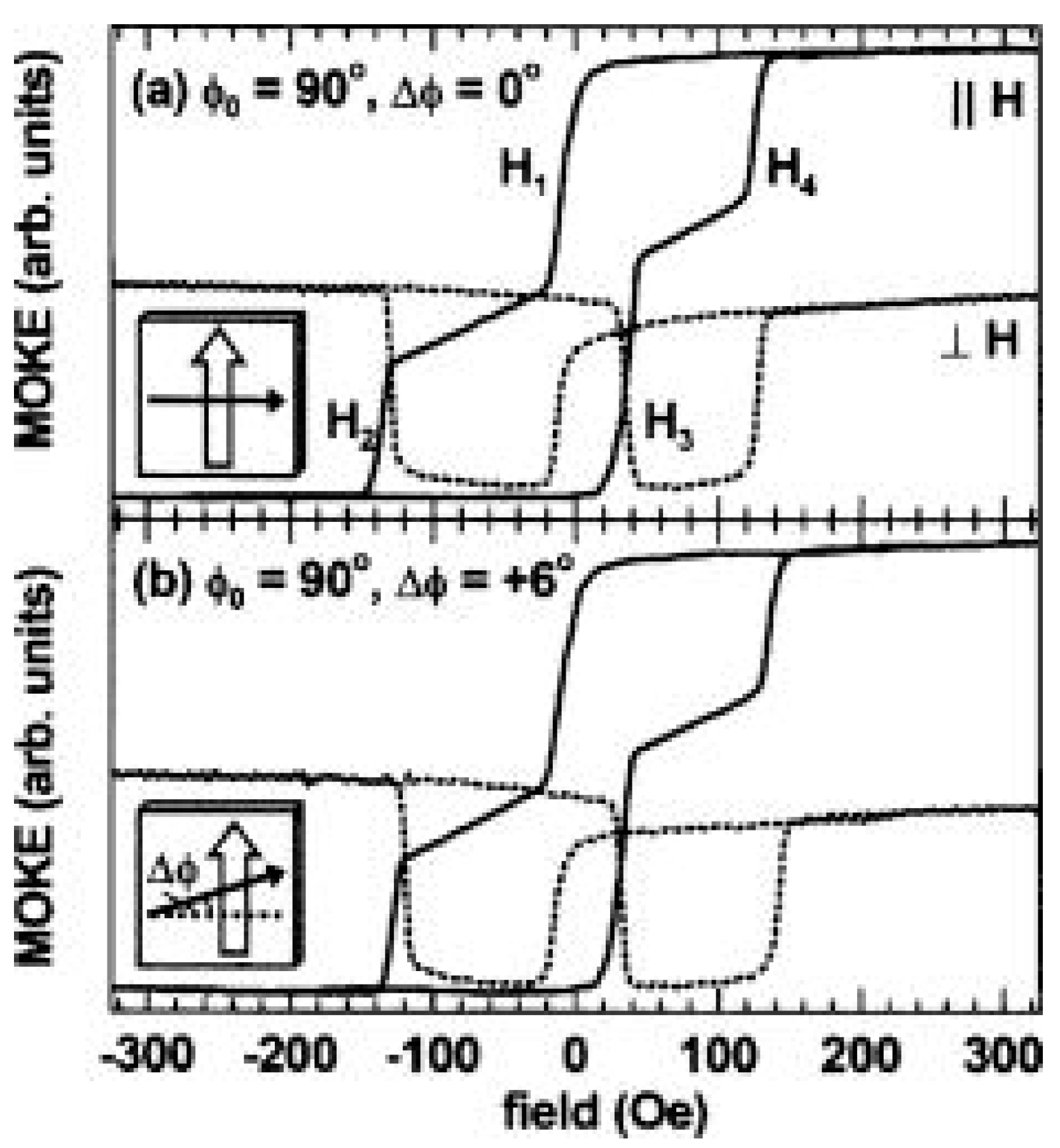
4.1. Co/CoO Thin Film Systems
4.2. Ni/NiO Thin Film Systems
4.3. Fe/FeF2 Thin Film Systems
4.4. Fe/MnF2 Thin Film Systems
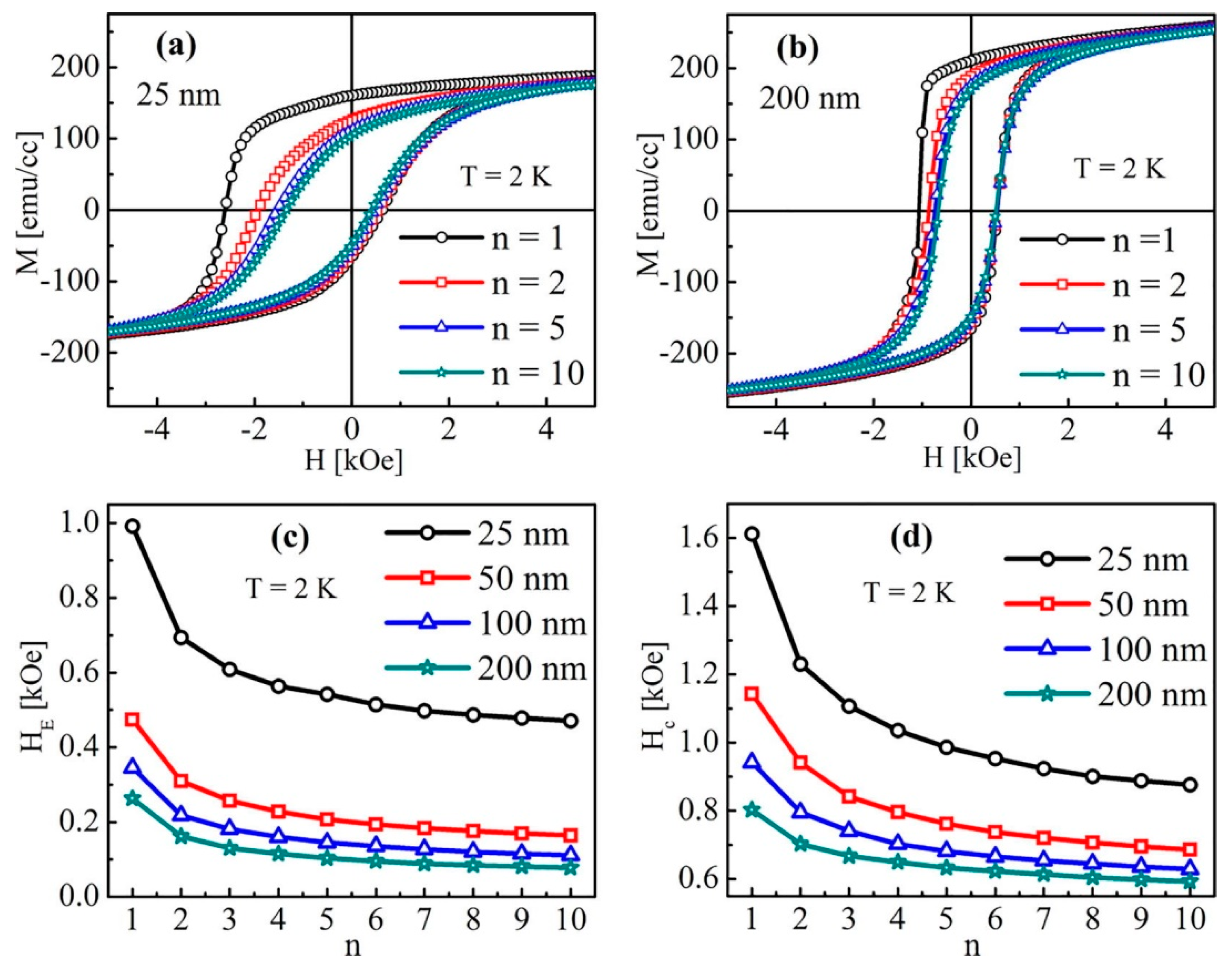
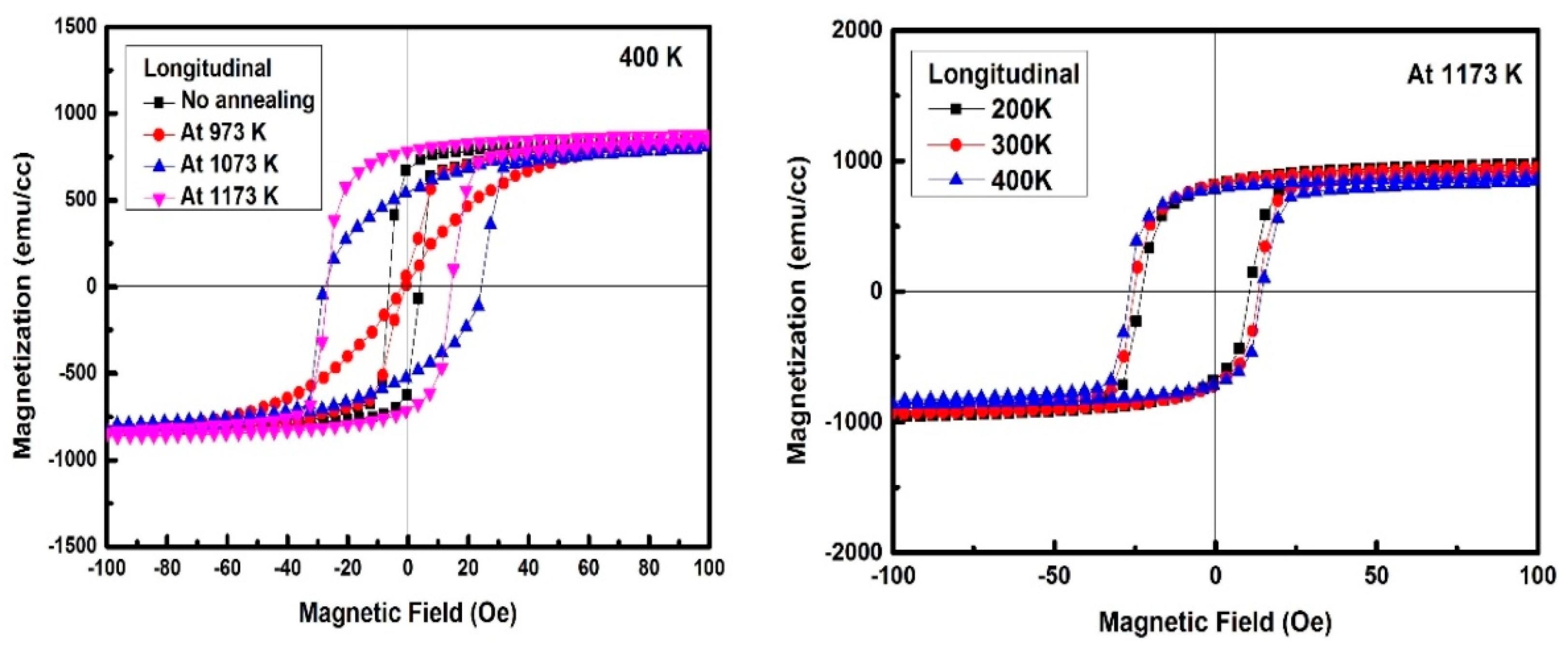
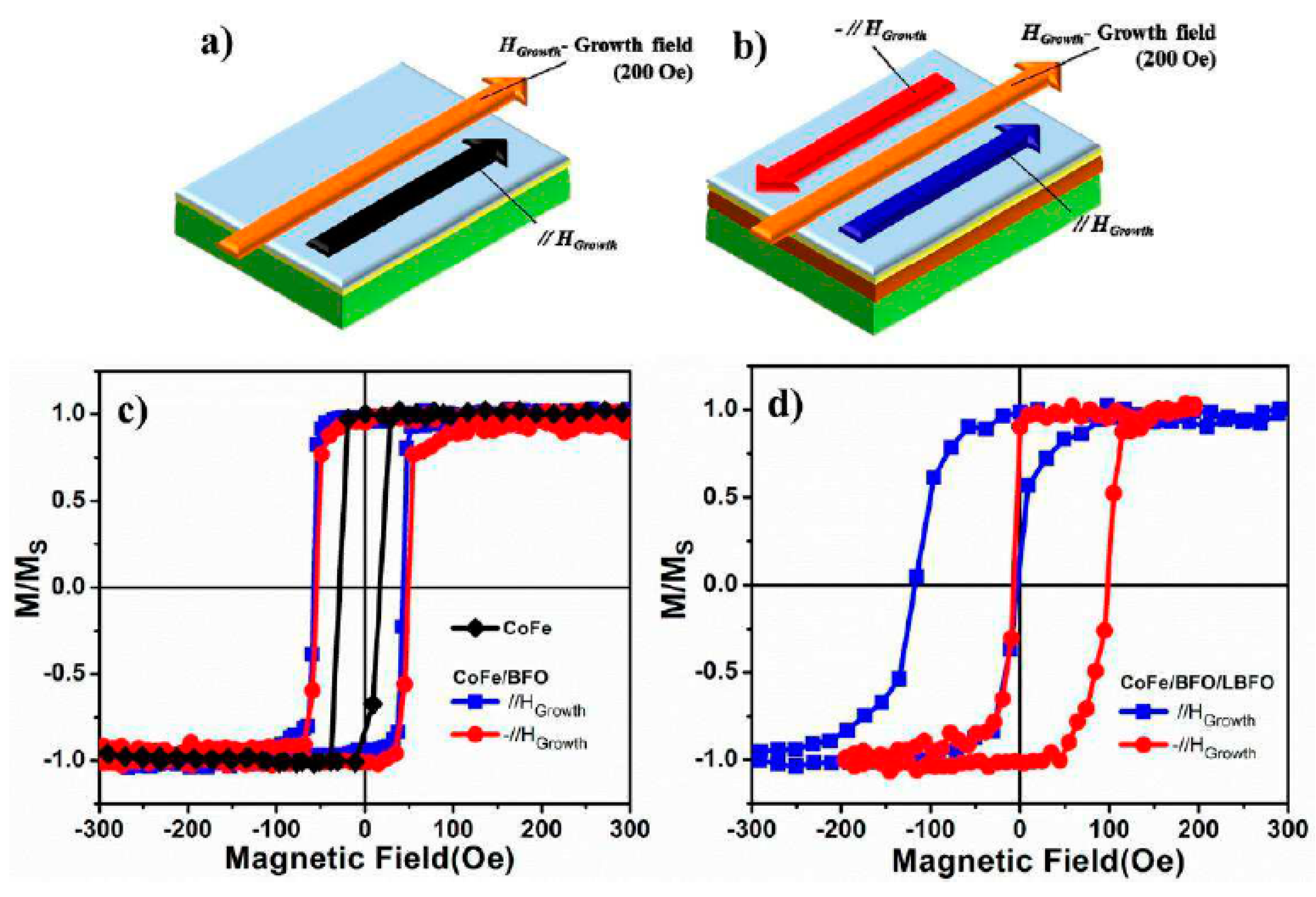
5. Thin Film Systems from Other Materials
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meiklejohn, W.H.; Bean, C.P. New magnetic anisotropy. Phys. Rev. 1956, 102, 1413–1414. [Google Scholar] [CrossRef]
- Nogués, J.; Moran, T.J.; Lederman, D.; Schuller, I.K.; Rao, K.V. Role of interfacial structure on exchange-biased FeF2-Fe. Phys. Rev. B 1999, 59, 6984–6993. [Google Scholar] [CrossRef]
- Blachowicz, T.; Tillmanns, A.; Fraune, M.; Beschoten, B.; Güntherodt, G. Exchange-bias in (110)-oriented CoO/Co bilayers with different magnetocrystalline anisotropies. Phys. Rev. B 2007, 75, 054425. [Google Scholar] [CrossRef]
- Schneider, V.; Reinholdt, A.; Kreibig, U.; Weirich, T.; Güntherodt, G.; Beschoten, B.; Tillmanns, A.; Krenn, H.; Rumpf, K.; Granitzer, P. Structural and Magnetic Properties of Ni/NiOxide and Co/CoOxide Core/Shell Nanoparticles and their possible Use for Ferrofluids. Z. Phys. Chem. 2006, 220, 173–187. [Google Scholar] [CrossRef]
- Tillmanns, A.; Oertker, S.; Beschoten, B.; Güntherodt, G.; Eisenmenger, J.; Schuller, I.K. Angular dependence and origin of asymmetric magnetization reversal in exchange-biased Fe/FeF2(110). Phys. Rev. B 2008, 78, 012401. [Google Scholar] [CrossRef]
- Eisenmenger, J.; Li, Z.-P.; Macedo, W.A.A.; Schuller, I.K. Exchange bias and asymmetric reversal in nanostructures dot arrays. Phys. Rev. Lett. 2005, 94, 057203. [Google Scholar] [CrossRef] [PubMed]
- Macedo, W.A.A.; Sahoo, B.; Kuncser, V.; Eisenmenger, J.; Felner, I.; Nogués, J.; Liu, K.; Keune, W.; Schuller, I.K. Changes in ferromagnetic spin structure induced by exchange bias in Fe/MnF2 films. Phys. Rev. B 2004, 70, 224414. [Google Scholar] [CrossRef]
- Tillmanns, A.; Oertker, S.; Beschoten, B.; Güntherodt, G.; Leighton, C.; Schuller, I.K.; Nogués, J. Magneto-optical study of magnetization reversal asymmetry in exchange bias. Appl. Phys. Lett. 2006, 89, 202512. [Google Scholar] [CrossRef]
- Hussain, Z.; Bera, A.K.; Dev, A.S.; Kumar, D.; Reddy, V.R. Exchange bias effect in Fe/LaAlO3: An interface induced effect. J. Alloys Comp. 2020, 849, 156484. [Google Scholar] [CrossRef]
- Zhang, B.M. Correlation of microstructure with magnetic properties in Pr0.67Sr0.33MnO3 thin films. J. Mater. Sci. Mater. Electron. 2020, 31, 19875–19882. [Google Scholar] [CrossRef]
- Nogués, J.; Sort, J.; Langlais, V.; Skumryev, V.; Surinach, S.; Munoz, J.S.; Baró, M.D. Exchange bias in nanostructures. Phys. Rep. 2005, 422, 65–117. [Google Scholar] [CrossRef]
- Laureti, S.; Suck, S.Y.; Haas, H.; Prestat, E.; Bourgeouis, O.; Givord, D. Size dependence of exchange bias in Co/CoO nanostructures. Phys. Rev. Lett. 2012, 108, 077205. [Google Scholar] [CrossRef] [PubMed]
- Javed, K.; Li, W.J.; Ali, S.S.; Shi, D.W.; Khan, U.; Riaz, S.; Han, X.F. Enhanced exchange bias and improved ferromagnetic properties in Permalloy–BiFe0.95Co0.05O3 core–shell nanostructures. Sci. Rep. 2016, 5, 18203. [Google Scholar] [CrossRef] [PubMed]
- Barreto, P.G.; Sousa, M.A.; Pelegrini, F.; Alayo, W.; Litterst, F.J.; Baggio-Saitovitch, E. Ferromagnetic resonance study of the misalignment between anisotropy axes in exchange-biased NiFe/FeMn/Co trilayers. Appl. Phys. Lett. 2014, 104, 202403. [Google Scholar] [CrossRef]
- Sing, S.; Kumar, P.; Gupta, A.; Kumar, D. In-situ study of exchange-bias in interlayer coupled Co/CoO/Co trilayer structure. J. Magn. Magn. Mater. 2020, 513, 167186. [Google Scholar] [CrossRef]
- Nogués, J.; Schuller, I.K. Exchange bias. J. Magn. Magn. Mat. 1999, 192, 203. [Google Scholar] [CrossRef]
- Thomas, S.; Reethu, K.; Thanveer, T.; Myint, M.T.Z.; Al-Harthi, S.H. Effect of shell thickness on the exchange bias blocking temperature and coercivity in Co-CoO core-shell nanoparticles. J. Appl. Phys. 2017, 122, 063902. [Google Scholar] [CrossRef]
- Ali, M.; Adie, P.; Marrows, C.H.; Greig, D.; Hickey, B.J.; Stamps, R.L. Exchange bias using a spin glass. Nat. Mater. 2007, 6, 70–75. [Google Scholar] [CrossRef]
- Moran, T.J.; Schuller, I.K. Effects of cooling field strength on exchange anisotropy at permalloy/CoO interfaces. J. Appl. Phys. 1996, 79, 5109. [Google Scholar] [CrossRef]
- Nogués, J.; Lederman, D.; Moran, T.J.; Schuller, I.K. Positive exchange bias in Fe–Fe2 bilayers. Phys. Rev. Lett. 1996, 76, 4624. [Google Scholar] [CrossRef]
- Nogués, J.; Leighton, C.; Schuller, I.K. Correlation between antiferromagnetic interface coupling and positive exchange bias. Phys. Rev. B 2000, 61, 1315. [Google Scholar] [CrossRef]
- Ambrose, T.; Chien, C.L. Dependence of exchange field and coercitivity on cooling field in NiFe/CoO bilayers. J. Appl. Phys. 1998, 83, 7222. [Google Scholar] [CrossRef]
- Leighton, C.; Nogués, J.; Suhl, H.; Schuller, I.K. Competing interfacial exchange and Zeeman energies in exchange biases bilayers. Phys. Rev. B 1999, 60, 12837. [Google Scholar] [CrossRef]
- Hwang, D.G.; Lee, S.S.; Park, C.M. Effect of roughness slope on exchange biasing in NiO spinvalves. Appl. Phys. Lett. 1998, 72, 2162. [Google Scholar] [CrossRef]
- Moran, T.J.; Gallego, J.M.; Schuller, I.K. Increased exchange anisotropy due to disorder at permalloy/CoO interfaces. J. Appl. Phys. 1995, 78, 1887. [Google Scholar] [CrossRef]
- Polisetty, S.; Sahoo, S.; Binek, C. Scaling behavior of the exchange-bias training effect. Phys. Rev. B 2007, 76, 184423. [Google Scholar] [CrossRef]
- Qiu, X.P.; Yang, D.Z.; Zhou, S.M.; Chantrell, R.; O’Grady, K.; Nowak, U.; Du, J.; Bai, X.J.; Sun, L. Rotation of the pinning direction in the exchange bias training effect in polycrystalline NiFe/FeMn bilayers. Phys. Rev. Lett. 2008, 101, 147207. [Google Scholar] [CrossRef]
- Brems, S.; Temst, K.; van Haesendonk, C. Origin of the training effect and asymmetry of the magnetization in polycrystalline exchange bias systems. Phys. Rev. Lett. 2007, 99, 067201. [Google Scholar] [CrossRef]
- Binek, C.; Polisetty, S.; He, X.; Berger, A. Exchange bias training effect in coupled all ferromagnetic bilayer structures. Phys. Rev. Lett. 2006, 96, 067201. [Google Scholar] [CrossRef]
- Brück, S.; Schütz, G.; Goering, E.; Ji, X.S.; Krishnan, K.M. Uncompensated moments in the MnPd/Fe exchange bias system. Phys. Rev. Lett. 2008, 101, 126402. [Google Scholar] [CrossRef]
- Meiklejohn, W.H. Exchange anisotropy—A review. J. Appl. Phys. 1962, 33, 1328–1335. [Google Scholar] [CrossRef]
- Néel, L. Étude théorique du couplage ferro-antiferromagnétique dans les couches minces. Ann. Phys. 1967, 14, 61–80. [Google Scholar] [CrossRef]
- Kiwi, M. Exchange bias theory. J. Magn. Magn. Mater. 2001, 234, 584–595. [Google Scholar] [CrossRef]
- Malozemoff, A.P. Random-field model of exchange bias anisotropy at rough ferromagnetic-antiferromagnetic interfaces. Phys. Rev. B 1987, 35, 3679. [Google Scholar] [CrossRef]
- Malozemoff, A.P. Mechanisms of exchange anisotropy. J. Appl. Phys. 1988, 63, 3874–3879. [Google Scholar] [CrossRef]
- Malozemoff, A.P. Heisenberg to Ising crossover in a random-field model with uniaxial anisotropy. Phys. Rev. B 1998, 37, 7673. [Google Scholar] [CrossRef] [PubMed]
- Mauri, D.; Siegmann, H.C.; Bagus, P.S.; Kay, E. Simple model for thin ferromagnetic films exchange coupled to an antiferromagnetic substrate. J. Appl. Phys. 1987, 62, 3047–3049. [Google Scholar] [CrossRef]
- Meiklejohn, W.H.; Bean, C.P. New magnetic anisotropy. Phys. Rev. 1957, 105, 904. [Google Scholar] [CrossRef]
- Schulthess, T.C.; Butler, W.H. Consequences of spin-flop coupling in exchange biased films. Phys. Rev. Lett. 1998, 81, 4516. [Google Scholar] [CrossRef]
- Schulthess, T.C.; Butler, W.H. Coupling mechanisms in exchange biased films. J. Appl. Phys. 1999, 85, 5510. [Google Scholar] [CrossRef]
- Takano, K.; Kodama, R.H.; Berkowitz, A.E.; Cao, W.; Thomas, G. Interfacial uncompensated antiferromagnetic spins: Role in unidirectional anisotropy in polycrystalline Ni81F19/CoO bilayers. Phys. Rev. Lett. 1997, 79, 1130. [Google Scholar] [CrossRef]
- Takano, K.; Kodama, R.H.; Berkowitz, A.E.; Cao, W.; Thomas, G. Role of interfacial uncompensated antiferromagnetic spins in unidirectional anisotropy in Ni81F19/CoO bilayers. J. Appl. Phys. 1998, 83, 6888. [Google Scholar] [CrossRef]
- Stiles, M.D.; McMichael, R.D. Model for exchange bias in polycrystalline ferromagnet-antiferromagnet bilayers. Phys. Rev. B 1999, 59, 3722. [Google Scholar] [CrossRef]
- Miltényi, P.; Gierlings, M.; Keller, M.; Beschoten, B.; Güntherodt, G.; Nowak, U.; Usadel, K.D. Diluted antiferromagnets in exchange bias: Proof of the domain state model. Phys. Rev. Lett. 2000, 84, 4224. [Google Scholar] [CrossRef] [PubMed]
- Nowak, U.; Usadel, K.D.; Keller, J.; Miltényi, P.; Beschoten, B.; Güntherodt, G. Domain state model for exchange bias. I. Theory. Phys. Rev. B 2002, 66, 014430. [Google Scholar] [CrossRef]
- Keller, J.; Miltényi, P.; Beschoten, B.; Güntherodt, G.; Nowak, U.; Usadel, K.D. Domain state model for exchange bias. II. Experiments. Phys. Rev. B 2002, 66, 014431. [Google Scholar] [CrossRef]
- Beschoten, B.; Keller, J.; Tillmanns, A.; Miltényi, P.; Güntherodt, G. Domain state model for exchange bias: Training effect of diluted Co1-yO on exchange bias in Co/CoO. IEEE Trans. Magn. 2002, 38, 2744. [Google Scholar] [CrossRef]
- Nowak, U.; Misra, A.; Usadel, K.D. Modeling exchange bias microscopically. J. Magn. Magn. Mater. 2002, 240, 243–247. [Google Scholar] [CrossRef]
- Nowak, U.; Misra, A.; Usadel, K.D. Domain staate model for exchange bias. J. Appl. Phys. 2001, 89, 7269–7271. [Google Scholar] [CrossRef]
- Kiwi, M.; Mejía-López, J.; Portugal, R.D.; Ramírez, R. Exchange bias model for Fe/FeF2: Role of domains in the ferromagnet. Europhys. Lett. 1999, 48, 573–579. [Google Scholar] [CrossRef]
- Kiwi, M.; Mejía-López, J.; Portugal, R.D.; Ramírez, R. Exchange-bias systems with compensated interfaces. Appl. Phys. Lett. 1999, 75, 3995–3997. [Google Scholar] [CrossRef]
- Kiwi, M.; Mejía-López, J.; Portugal, R.D.; Ramírez, R. Positive exchange bias model: Fe/FeF2 and Fe/MnF2 bilayers. Solid State Comm. 2000, 116, 315–319. [Google Scholar] [CrossRef]
- Nolting, F.; Scholl, A.; Stöhr, J.; Seo, J.W.; Fompeyrine, J.; Siegwart, H.; Locquet, J.-P.; Anders, S.; Lüning, J.; Fullerton, E.E.; et al. Direct observation of the alignment of ferromagnetic spins by antiferromagnetic spins. Nature 2000, 405, 767–769. [Google Scholar] [CrossRef] [PubMed]
- Matsuyama, H.; Haginoya, C.; Koike, K. Microscopic imaging of Fe magnetic domains exchange coupled with those in a NiO(001) surface. Phys. Rev. Lett. 2000, 85, 646–649. [Google Scholar] [CrossRef] [PubMed]
- Radu, F.; Westphalen, A.; Theis-Bröhl, K.; Zabel, H. Quantitative description of the azimuthal dependence of the exchange bias effect. J. Phys. Condens. Matter 2006, 18, L29–L36. [Google Scholar] [CrossRef]
- Harres, A.; Geshev, J. A polycrystalline model for magnetic exchange bias. J. Phys. Condens. Matter 2012, 24, 326004. [Google Scholar] [CrossRef] [PubMed]
- Saha, J.; Victora, R.H. Large scale micromagnetic simulation for the exchange interaction between a polycrystalline antiferromagnet and a ferromagnet. Phys. Rev. B 2006, 73, 104433. [Google Scholar] [CrossRef]
- Choo, D.; Chantrell, R.W.; Lamberton, R.; Johnston, A.; O’Grady, K. A model of the magnetic properties of coupled ferromagnetic/antiferromagnetic bilayers. J. Appl. Phys. 2007, 101, 09E521. [Google Scholar] [CrossRef]
- O’Grady, K.; Fernandez-Outon, L.E.; Vallejo-Fernandez, G. A new paradigm for exchange bias in polycrystalline thin films. J. Magn. Magn. Mater. 2010, 322, 883–899. [Google Scholar] [CrossRef]
- Mangin, S.; Montaigne, F.; Schuhl, A. Interface domain wall and exchange bias phenomena in ferrimagnetic/ferrimagnetic bilayers. Phys. Rev. B 2003, 68, 140404. [Google Scholar] [CrossRef]
- Fullerton, E.E.; Jiang, J.S.; Grimsditch, M.; Sowers, C.H.; Bader, S.D. Exchange-spring behavior in epitaxial hard/soft magnetic bilayers. Phys. Rev. B 1998, 58, 12193. [Google Scholar] [CrossRef]
- Montaigne, F.; Mangin, S.; Henry, Y. Transitions of magnetic configuration at the interface of exchange-coupled bilayers: TbFe/GdFe as a model system. Phys. Rev. B 2003, 67, 144412. [Google Scholar] [CrossRef]
- Stamps, R.L. Mechanism of exchange bias: Partial wall pinning, and fluctuations. J. Magn. Magn. Mater. 2002, 242–245, 139–145. [Google Scholar] [CrossRef]
- Morales, R.; Basaran, A.C.; Villegas, J.E.; Navas, D.; Soriano, N.; Mora, B.; Redondo, C.; Batlle, X.; Schuller, I.K. Exchange-bias phenomenon: The role of the ferromagnetic spin structure. Phys. Rev. Lett. 2015, 114, 097202. [Google Scholar] [CrossRef] [PubMed]
- Dimitriadis, V.; Kechrakos, D.; Chubykalo-Fesenko, O.; Tsiantos, V. Shape-dependent exchange bias effect in magnetic nanoparticles with core-shell morphology. Phys. Rev. B 2015, 92, 064420. [Google Scholar] [CrossRef]
- Iglesias, Ò.; Labarta, A.; Batlle, X. Exchange bias phenomenology and models of core/shell nanoparticles. J. Nanosci. Nanotechnol. 2008, 8, 2761–2780. [Google Scholar] [CrossRef]
- Simon, E.; Yanes, R.; Khmelevskyi, S.; Palotás, K.; Szunyogh, L.; Nowak, U. Magnetism and exchange-bias effect at the MnN/Fe interface. Phys. Rev. B 2018, 98, 094415. [Google Scholar] [CrossRef]
- Khan, R.A.; Nembach, H.T.; Ali, M.; Shaw, J.M.; Marrows, C.H.; Moore, T.A. Magnetic domain texture and the Dzyaloshinskii-Moriya interaction in Pt/Co/IrMn and Pt/Co/FeMn thin films with perpendicular exchange bias. Phys. Rev. B 2018, 98, 064413. [Google Scholar] [CrossRef]
- Kolesnikov, A.G.; Stebliy, M.E.; Davydenko, A.V.; Kozlov, A.G.; Osmushko, I.S.; Korochentsev, V.V.; Ognev, A.V.; Gerasimenko, A.V.; Sadovnikov, A.V.; Gubanov, V.A.; et al. Magnetic properties and the interfacial Dzyaloshinskii-Moriya interaction in exchange biased Pt/Co/NixOy films. Appl. Surf. Sci. 2021, 543, 148720. [Google Scholar] [CrossRef]
- Fita, I.; Markovich, V.; Moskvin, A.S.; Wisniewski, A.; Puzniak, R.; Iwanowski, P.; Martin, C.; Maignan, A.; Carbonio, R.E.; Gutowska, M.U.; et al. Reversed exchange-bias effect associated with magnetism reversal in the weak ferrimagnet LuFe0.5Cr0.5O3. Phys. Rev. B 2018, 97, 104416. [Google Scholar] [CrossRef]
- Manipatruni, S.; Nikonov, D.E.; Lin, C.-C.; Prasad, B.; Huang, Y.-L.; Damodaran, A.R.; Chen, Z.H.; Ramesh, R.; Young, I.A. Voltage control of unidirectional anisotropy in ferromagnet-multiferroic system. Sci. Adv. 2018, 4, eaat4229. [Google Scholar] [CrossRef]
- Albisetti, E.; Petti, D.; Sala, G.; Silvani, R.; Tacchi, S.; Finizio, S.; Wintz, S.; Calò, A.; Zheng, X.R.; Raabe, J.; et al. Nanoscale spin-wave circuits based on engineered reconfigurable spin-textures. Comm. Phys. 2018, 1, 56. [Google Scholar] [CrossRef]
- González, J.A.; Andrés, J.P.; López Antón, R.; de Toro, J.A.; Normile, P.S.; Muniz, P.; Riveiro, J.M.; Nogués, J. Maximizing exchange bias in Co/CoO core/shell nanoparticles by lattice matching between the shell and the embedding matrix. Chem. Mater. 2017, 29, 5200–5206. [Google Scholar] [CrossRef]
- Xing, Q.X.; Han, Z.L.; Zhao, S.F. Exchange bias of nanostructured films assembled with Co/CoO core–shell clusters. Mater. Lett. 2017, 188, 103–106. [Google Scholar] [CrossRef]
- Guo, B.B.; Xu, Y.L.; Zhou, S.M. Morphology dependence of low temperatures exchange bias Co/CoO core-shell nanoparticles/spheres by eco-friendly solvothermal route. AIP Adv. 2018, 8, 115115. [Google Scholar] [CrossRef]
- Salazar-Alvarez, G.; Geshev, J.; Agramunt-Puig, S.; Navau, C.; Sanchez, A.; Sort, J.; Nogués, J. Tunable high-field magnetization in strongly exchange-coupled freestanding Co/CoO core/shell coaxial nanowires. ACS Appl. Mater. Interfaces 2016, 8, 22477–22483. [Google Scholar] [CrossRef] [PubMed]
- Gandha, K.; Chaudhary, R.P.; Mohapatra, J.; Koymen, A.R.; Liu, J.P. Giant exchange bias and its angular dependence in Co/CoO core-shell nanowire assemblies. Phys. Lett. A 2017, 381, 2092–2096. [Google Scholar] [CrossRef]
- Morales, R.; Flores, A.N.; Vargas, N.M.; Giuliani, J.; Schuller, I.K.; Monton, C. Ultradense arrays of sub-100 nm Co/CoO nanodisks for spintronics applications. ACS Appl. Nano Mater. 2020, 3, 4037–4044. [Google Scholar] [CrossRef]
- Sharma, A.; Tripathi, J.; Tripathi, S.; Kumar, Y.; Ugochukwu, K.C.; Kumar, D.; Gupta, M.; Chaudhary, R.J. Exchange bias in Co/CoO thin films deposited onto self-assembled nanosphere arrays. J. Magn. Magn. Mater. 2020, 510, 166599. [Google Scholar] [CrossRef]
- López Antón, R.; González, J.A.; Andrés, J.P.; Normile, P.; Canales-Vázquez, J.; Muniz, P.; Riveiro, J.M.; de Toro, J.A. Exchange Bias Optimization by Controlled Oxidation of Cobalt Nanoparticle Films Prepared by Sputter Gas Aggregation. Nanomaterials 2017, 7, 61. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T. Angle and rotational direction dependent horizontal loop shift in epitaxial Co/CoO bilayers on MgO(100). AIP Adv. 2017, 7, 115223. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T. Asymmetric hysteresis loops in Co thin films. Condens. Matter 2020, 5, 71. [Google Scholar] [CrossRef]
- Jochum, J.K.; Saerbeck, T.; Lazenka, V.; Joly, V.; Shan, S.C.; Boyen, H.-G.; Ternst, K.; Vantomme, A.; van Bael, M.J. Magnetic characterization of oblique angle deposited Co/CoO on gold nanoparticles. J. Magn. Magn. Mater. 2019, 483, 76–82. [Google Scholar] [CrossRef]
- Ovejero, J.G.; Godinho, V.; Lacroix, B.; García, M.A.; Hernando, A.; Fernández, A. Exchange bias and two steps magnetization reversal in porous Co/CoO layer. Mater. Des. 2019, 171, 107691. [Google Scholar] [CrossRef]
- Hussain, Z.; Reddy, V.R. Kerr microscopy study of thermal and athermal training effects in a C/CoO exchange bias system. J. Appl. Phys. 2017, 122, 103903. [Google Scholar] [CrossRef]
- Hussain, Z.; Reddy, V.R. Role of anti-ferromagnetic layer thickness in exchange bias: Case study of Co/CoO with Kerr microscopy. Mater. Res. Expr. 2019, 6, 066109. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, S.; Gupta, A. Effect of interface roughness on exchange coupling in polycrystalline Co/CoO bilayer structure: An in-situ investigation. J. Appl. Phys. 2016, 120, 085307. [Google Scholar] [CrossRef]
- Dobrynin, A.N.; Warin, P.; Vorobiev, A.; Givord, D. On the origin of positive exchange bias and coercivity enhancement in proximity to the blocking temperature. J. Magn. Magn. Mater. 2021, 520, 166707. [Google Scholar] [CrossRef]
- Menéndez, E.; Silva, L.E.S.; Johann, G.; Sort, J.; Dias, T. Unraveling the origin of training in granular Co-CoO exchange bias systems with buried antiferromagnetic constituents. J. Magn. Magn. Mater. 2019, 478, 170–174. [Google Scholar] [CrossRef]
- Roy, A.; de Toro, J.A.; Amaral, V.S.; Muniz, P.; Riveiro, J.M.; Ferreira, J.M.F. Exchange bias beyond the superparamagnetic blocking temperature of the antiferromagnet in a Ni-NiO nanoparticulate system. J. Appl. Phys. 2015, 115, 073904. [Google Scholar] [CrossRef]
- Chaghouri, H.L.; Tuna, F.; Santhosh, P.N.; Thomas, P.J. Tiny Ni–NiO nanocrystals with exchange bias induced room temperature ferromagnetism. Solid State Comm. 2016, 230, 11–15. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, Z.W.; Xu, Y.H.; Liu, Y.; Li, W.J.; Nie, Y.; Zhang, X.; Xiang, G. Exchange bias coupling in NiO/Ni bilayer tubular nanostructures synthetized by electrodeposition and thermal oxidation. J. Magn. Magn. Mater. 2017, 429, 74–78. [Google Scholar] [CrossRef]
- Amemiya, K.; Sakamaki, M. Effect of electric field on magnetism of Ni thin films via antiferromagnetic NiO. E J. Surf. Sci. Nanotech. 2018, 16, 186–189. [Google Scholar] [CrossRef]
- De los Santos Valladares, L.; Ionescu, A.; Holmes, S.; Barnes, C.H.W.; Bustamante Domınguez, A.; Avalos Quispe, O.; Gonzalez, J.C.; Milana, S.; Barbone, M.; Ferrari, A.C.; et al. Characterization of Ni thin films following thermal oxidation in air. J. Vac. Sci. Technol. B 2014, 32, 051808. [Google Scholar] [CrossRef]
- Raghavan, L.; Ojha, S.; Sulania, I.; Mishra, N.C.; Ranjith, K.M.; Baenitz, M.; Kanjilal, D. Thermal annealing induced competition of oxidation and grain growth in nickel thin films. Thin Solid Films 2019, 680, 40–47. [Google Scholar] [CrossRef]
- Ravikumar, P.; Taparia, D.; Alagarsamy, P. Thickness-dependent thermal oxidation of Ni into NiO thin films. J. Supercond. Novel Magn. 2018, 31, 3761–3775. [Google Scholar] [CrossRef]
- Ravikumar, P.; Kisan, B.; Perumal, A. Thickness dependent ferromagnetism in thermally decomposed NiO thin films. J. Magn. Magn. Mater. 2016, 418, 86–91. [Google Scholar] [CrossRef]
- Raghavan, L.; Ranjith, K.M.; Baenitz, M.; Kanjilal, D. Control of exchange bias by modifying the antiferromagnet and ferromagnet-antiferromagnet interface. Europhys. Lett. 2020, 130, 67006. [Google Scholar] [CrossRef]
- Anyfantis, D.I.; Sarigiannidou, E.; Rapenne, L.; Stamatelatos, A.; Ntemogiannis, D.; Kapaklis, V.; Poulopoulos, P. Unexpected development of perpendicular magnetic anisotropy in Ni/NiO multilayers after mild thermal annealing. IEEE Magn. Lett. 2019, 10, 6104105. [Google Scholar] [CrossRef]
- Zhang, Y.-J.; Chen, J.-H.; Li, L.-L.; Ma, J.; Nan, C.-W.; Lin, Y.-H. Ferroelectric strain modulation of antiferromagnetic moments in Ni/NiO ferromagnet/antiferromagnet heterostructures. Phys. Rev. B 2017, 95, 174420. [Google Scholar] [CrossRef]
- You, W.B.; Che, R.C. Excellent NiO-Ni nanoplate microwave absorber via pinning effect of antiferromagnetic-ferromagnetic interface. ACS Appl. Mater. Interfaces 2018, 10, 15104–15111. [Google Scholar] [CrossRef] [PubMed]
- Fitzsimmons, M.R.; Leighton, C.; Nogués, J.; Hoffmann, A.; Liu, K.; Majkrzak, C.K.; Dura, J.A.; Groves, J.R.; Springer, R.W.; Arendt, P.N.; et al. Influence of in-plane crystalline quality of an antiferromagnet on perpendicular exchange coupling and exchange bias. Phys. Rev. B 2002, 65, 134436. [Google Scholar] [CrossRef]
- Moran, T.J.; Nogués, J.; Lederman, D.; Schuller, I.K. Perpendicular coupling at Fe–FeF2 interfaces. Appl. Phys. Lett. 1998, 72, 617. [Google Scholar] [CrossRef]
- Fitzsimmons, M.R.; Yashar, P.; Leighton, C.; Schuller, I.K.; Majkrzak, C.F.; Dura, J.A. Asymmetric magnetization reversal in exchange-biased hysteresis loops. Phys. Rev. Lett. 2000, 84, 3986. [Google Scholar] [CrossRef] [PubMed]
- Dahlberg, E.D.; Miller, B.; Hill, B.; Jonsson, B.J.; Strom, V.; Rao, K.V.; Nogués, J.; Schuller, I.K. Measurements of the ferromagnetic/antiferromagnetic interfacial exchange energy in CO/CoO and Fe/FeF2 layers (invited). J. Appl. Phys. 1998, 83, 6893–6895. [Google Scholar] [CrossRef]
- Olamit, J.; Li, Z.-P.; Schuller, I.K.; Liu, K. Angular dependence of exchange anisotropy on the cooling field in ferromagnet/fluoride thin films. Phys. Rev. B 2006, 73, 024413. [Google Scholar] [CrossRef]
- Velasquez, E.A.; Mazo-Zuluaga, J.; Tangarife, E.; Mejia-Lopez, J. Structural relaxation and crystalline phase effects on the exchange bias phenomenon in FeF2/Fe core/shell nanoparticles. Adv. Mater. Interfaces 2020, 7, 2000862. [Google Scholar] [CrossRef]
- Tangarife, E.; Romero, A.H.; Mejía-López, J. A charge optimized many-body potential for iron/iron-fluoride systems. Phys. Chem. Chem. Phys. 2019, 21, 20118–20131. [Google Scholar] [CrossRef]
- Pechan, M.J.; Bennett, D.; Teng, N.; Leighton, C.; Nogués, J.; Schuller, I.K. Induced anisotropy and positive exchange bias: A temperature, angular, and cooling field study by ferromagnetic resonance. Phys. Rev. B 2002, 65, 064410. [Google Scholar] [CrossRef]
- Leighton, C.; Fitzsimmons, M.R.; Hoffmann, A.; Dura, J.; Majkrzak, C.F.; Lund, M.S.; Schuller, I.K. Thickness-dependent coercive mechanisms in exchange-biased bilayers. Phys. Rev. B 2002, 65, 064403. [Google Scholar] [CrossRef]
- Arenholz, E.; Liu, K. Angular dependence of the magnetization reversal in exchange-biased Fe/MnF2. Appl. Phys. Lett. 2005, 87, 132501. [Google Scholar] [CrossRef]
- Sudsom, D.; Blachowicz, T.; Hahn, L.; Ehrmann, A. Vortex nucleation and propagation in magnetic double-wedges and semi-squares for reliable quaternary storage systems. J. Magn. Magn. Mater. 2020, 514, 167294. [Google Scholar] [CrossRef]
- Shameem, P.V.M.; Kumar, M.S. Training effect of the exchange bias in sputter deposited Fe3O4 thin films with varying thickness. J. Magn. Magn. Mater. 2018, 458, 241–252. [Google Scholar] [CrossRef]
- Lee, C.-H.; Anbalagan, A.K.; Chang, T.-W.; Fan, C.-L.; Chung, J.-C.; Chien, S.-C. The exchange bias effect on single layer of Fe-rich FeRh thin film. Mater. Lett. 2019, 254, 309–311. [Google Scholar] [CrossRef]
- Fan, R.; Kinane, C.J.; Charlton, T.R.; Dorner, R.; Ali, M.; de Vries, M.A.; Brydson, R.M.D.; Marrows, C.H.; Hickey, B.J.; Arena, D.A.; et al. Ferromagnetism at the interfaces of antiferromagnetic FeRh epilayers. Phys. Rev. B 2010, 82, 184418. [Google Scholar] [CrossRef]
- Mallick, K.; Kumar, P.S.A. Crystallite size dependent exchange bias in MgFe2O4 thin films on Si(100). J. Appl. Phys. 2018, 124, 053901. [Google Scholar] [CrossRef]
- Ling, Y.C.; Liu, R.B.; Wang, H.B.; Xiao, S.Y.; Qu, D.Q.; Wang, G.G.; Han, Z.D.; Du, J.; Xu, Q.Y. Martensitic transformation and large exchange bias in Mn-rich Ni–Mn–Sn thin films on mica substrates. J. Alloys Comp. 2020, 827, 154303. [Google Scholar] [CrossRef]
- Khan, M.; Dubenko, I.; Stadler, S.; Ali, N. Exchange bias in bulk Mn rich Ni–Mn–Sn Heusler alloys. J. Appl. Phys. 2007, 102, 113914. [Google Scholar] [CrossRef]
- Sánchez Llamazares, J.L.; Flores-Zúniga, H.; Ríos-Jara, D.; Sánchez-Valdes, C.F.; García-Fernández, T.; Ross, C.A.; García, C. Structural and magnetic characterization of the intermartensitic phase transition in NiMnSn Heusler alloy ribbons. J. Appl. Phys. 2013, 113, 17A948. [Google Scholar] [CrossRef]
- Giri, S.K.; Sahoo, R.C.; Dasgupta, P.; Poddar, A.; Nath, T.K. Giant spontaneous exchange bias effect in Sm1.5Ca0.5CoMnO6 perovskite. J. Phys. D Appl. Phys. 2016, 49, 165002. [Google Scholar] [CrossRef]
- Sahoo, R.C.; Das, S.; Giri, S.K.; Paladhi, D.; Nath, T.K. Size modulated Griffiths phase and spin dynamics in double perovskite Sm1.5Ca0.5CoMnO6. J. Magn. Magn. Mater. 2019, 469, 161–170. [Google Scholar] [CrossRef]
- Panchal, G.; Choudhary, R.J.; Kumar, M.; Phase, D.M. Interfacial spin glass mediated spontaneous exchange bias effect in self-assembled La0.7Sr0.3MnO3:NiO nanocomposite thin films. J. Alloys Comp. 2019, 796, 196–202. [Google Scholar] [CrossRef]
- Wu, Y.J.; Wang, Z.J.; Bai, Y.; Liang, Y.M.; Ning, X.K.; Wang, Q.; Liu, W.; Zhang, Z.D. Transition of the exchange bias effect from in-plane to out-of-plane in La0.7Sr0.3MnO3:NiO nanocomposite thin films. J. Mater. Chem. C 2019, 7, 6091–6098. [Google Scholar] [CrossRef]
- Khadka, D.; Thapaliya, T.R.; Wen, J.J.; Need, R.F.; Huang, S.X. High quality epitaxial thin films and exchange bias of antiferromagnetic Dirac semimetal FeSn. Appl. Phys. Lett. 2020, 117, 032403. [Google Scholar] [CrossRef]
- Chen, D.Y.; Chen, Z.H.; He, Q.; Clarkson, J.D.; Serrao, C.R.; Yadav, A.K.; Nowakowski, M.E.; Fan, Z.; You, L.; Gao, X.S.; et al. Interface engineering of domain structures in biFeO3 thin films. Nano Lett. 2017, 17, 486–493. [Google Scholar] [CrossRef]
- Jiang, S.W.; Shan, J.; Mak, K.F. Electric-field switching of two-dimensional van der Waals magnets. Nat. Mater. 2018, 17, 406–410. [Google Scholar] [CrossRef]
- Fukami, S.; Zhang, C.L.; DuttaGupta, S.; Kurenkov, A.; Ohno, H. Magnetization switching by spin-orbit torque in an antiferromagnet-ferromagnet bilayer system. Nat. Mater. 2016, 15, 535–541. [Google Scholar] [CrossRef]
- Borders, W.A.; Akima, H.; Fukami, S.; Moriya, S.; Kurihara, S.; Horio, Y.; Sato, S.; Ohno, H. Analogue spin-orbit torque device for artificial-neural-network-based associative memory operations. Appl. Phys. Express 2017, 10, 013007. [Google Scholar] [CrossRef]
- Polewczyk, V.; Dumesnil, K.; Lacour, D.; Moutaouekkil, M.; Mjahed, H.; Tiercelin, N.; Petit Watelot, S.; Mishra, H.; Dusch, Y.; Hage-Ali, S.; et al. Unipolar and bipolar high-magnetic-field sensors based on surface acoustic wave resonators. Phys. Rev. Appl. 2017, 8, 024001. [Google Scholar] [CrossRef]
- Wang, G.P.; Chen, Z.Z.; He, H.C.; Meng, D.C.; Yang, H.; Mao, X.Y.; Pan, Q.; Chu, B.J.; Zuo, M.; Sun, Z.H.; et al. Room temperature exchange bias in structure-modulated single-phase multiferroic materials. Chem. Mater. 2018, 30, 6156–6163. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blachowicz, T.; Ehrmann, A. Exchange Bias in Thin Films—An Update. Coatings 2021, 11, 122. https://doi.org/10.3390/coatings11020122
Blachowicz T, Ehrmann A. Exchange Bias in Thin Films—An Update. Coatings. 2021; 11(2):122. https://doi.org/10.3390/coatings11020122
Chicago/Turabian StyleBlachowicz, Tomasz, and Andrea Ehrmann. 2021. "Exchange Bias in Thin Films—An Update" Coatings 11, no. 2: 122. https://doi.org/10.3390/coatings11020122
APA StyleBlachowicz, T., & Ehrmann, A. (2021). Exchange Bias in Thin Films—An Update. Coatings, 11(2), 122. https://doi.org/10.3390/coatings11020122





