Fracture Properties of α– and ĸ–Al2O3 Hard Coatings Deposited by Chemical Vapor Deposition
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
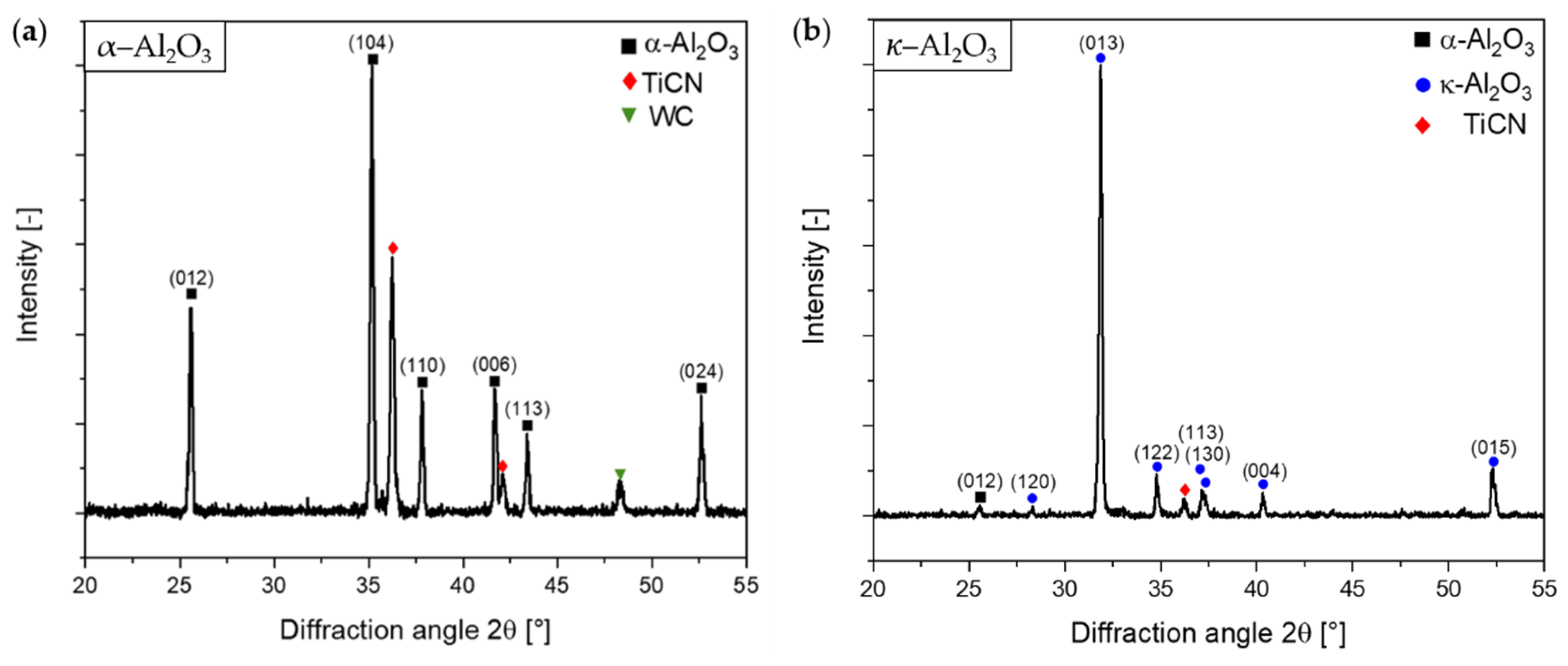
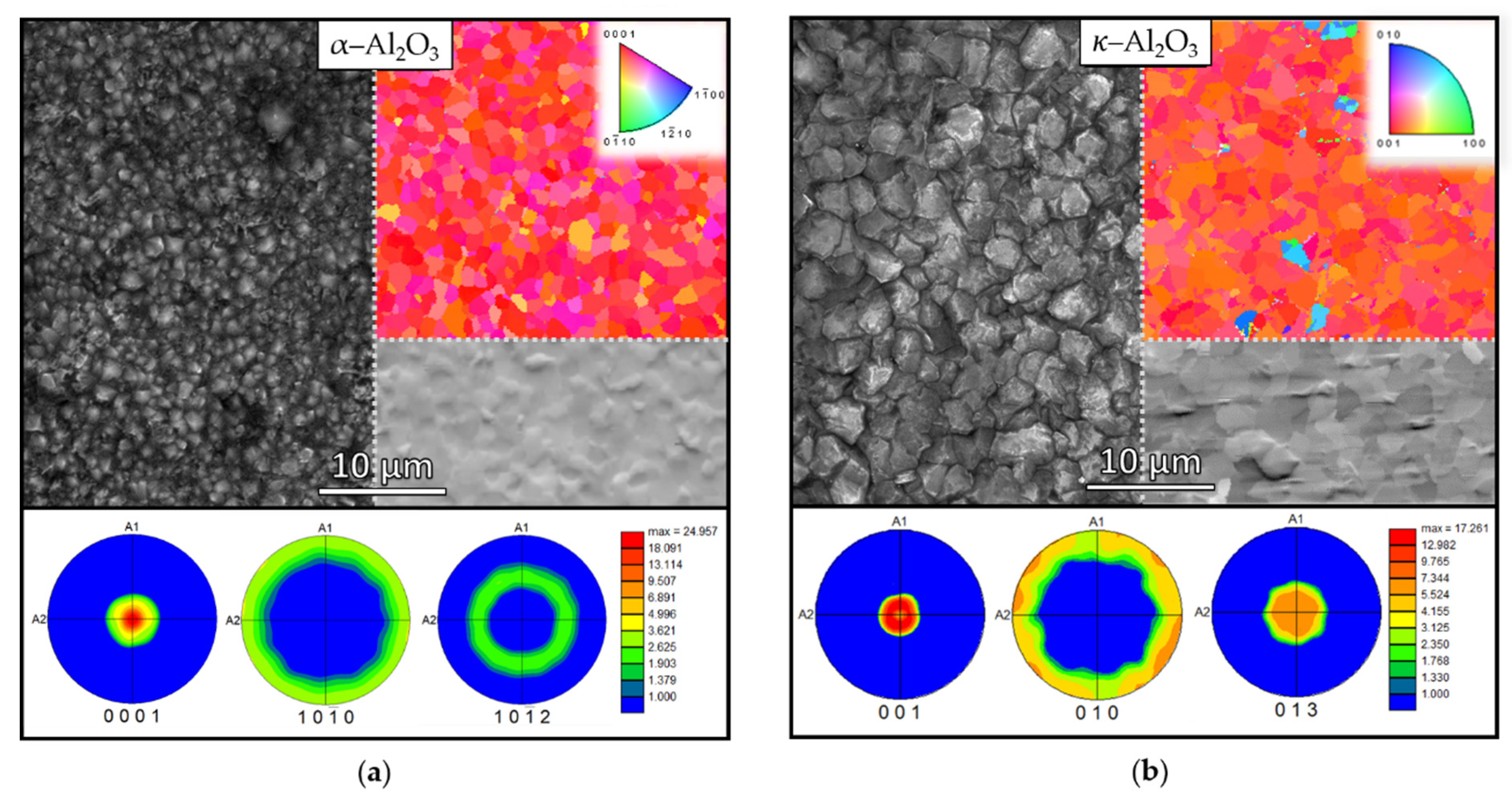
3.1. Microstructure
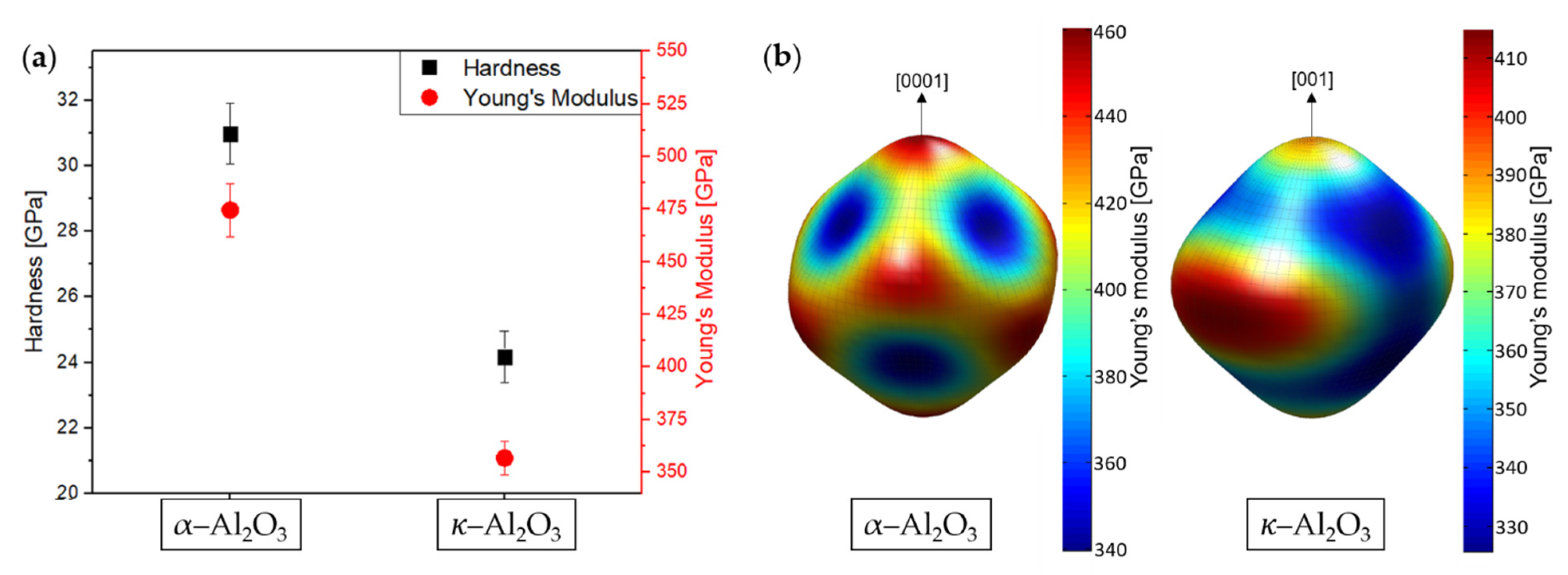
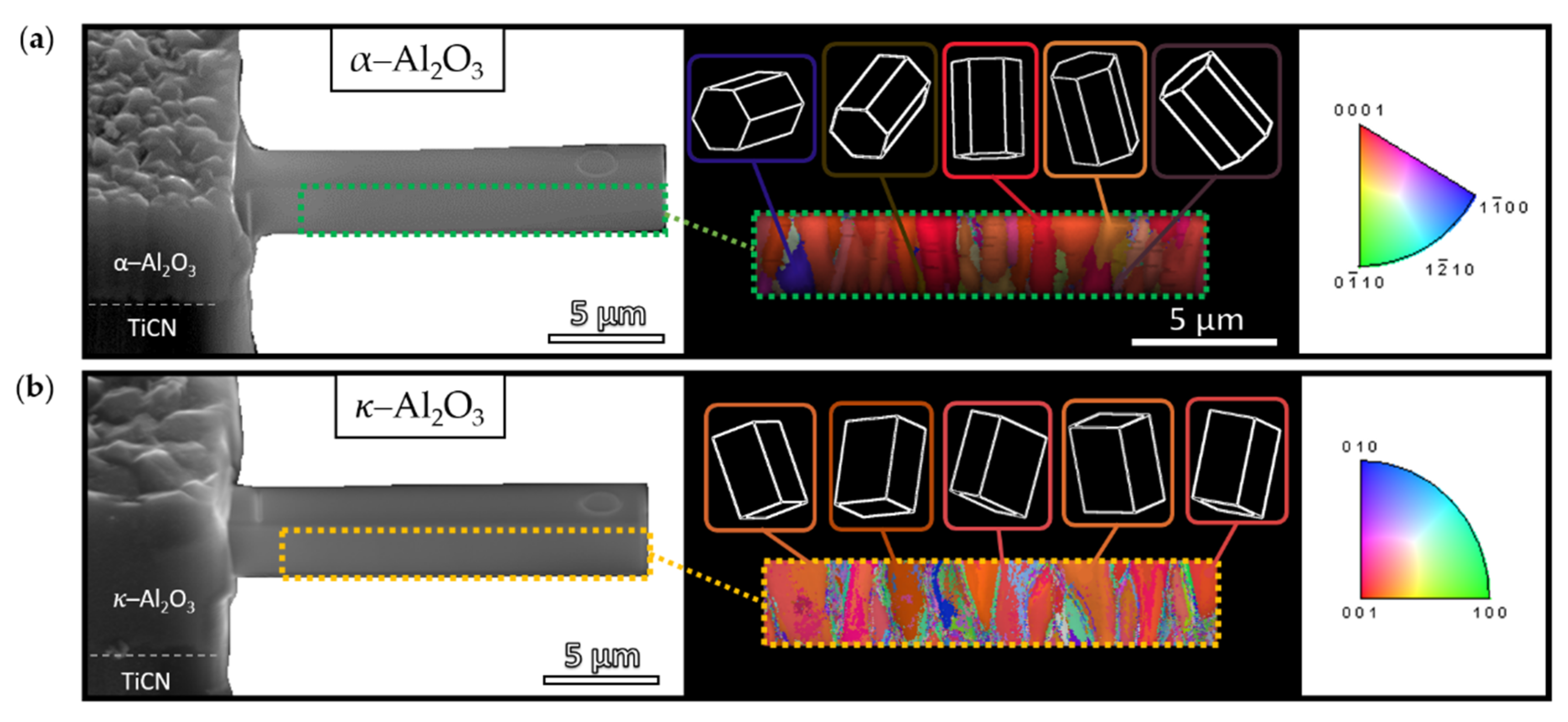
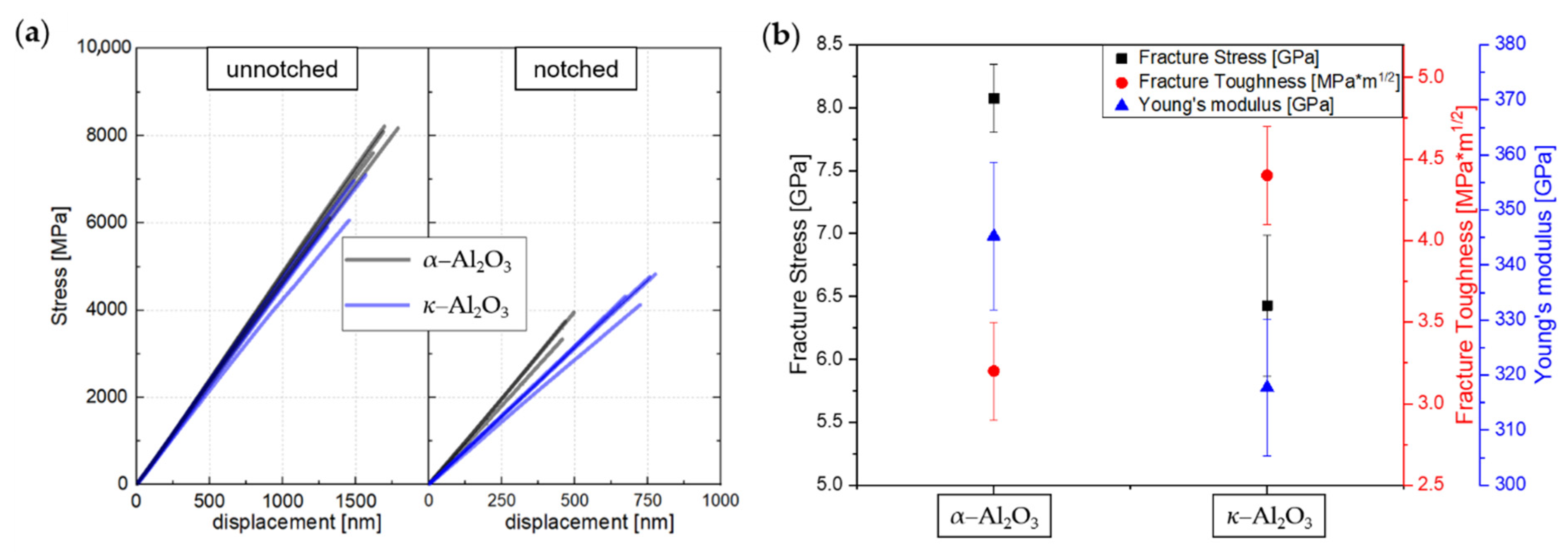
3.2. Mechanical Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mitterer, C. PVD and CVD Hard Coatings; Elsevier Ltd.: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Schleinkofer, U.; Czettl, C.; Michotte, C. Coating Applications for Cutting Tools; Elsevier Ltd.: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Garcia, J.; Pitonak, R.; Weißenbacher, R.; Köpf, A.; Soldera, F.; Suarez, S.; Miguel, F.; Pinto, H.; Kostka, A.; Mücklich, F. Design and characterization of novel wear resistant multilayer CVD coatings with improved adhesion between Al2O3 and Ti(C,N). Adv. Eng. Mater. 2010, 12, 929–934. [Google Scholar] [CrossRef]
- Ruppi, S.; Larsson, A.; Flink, A. Nanoindentation hardness, texture and microstructure of α-Al2O3 and κ-Al2O3 coatings. Thin Solid Films 2008, 516, 5959–5966. [Google Scholar] [CrossRef]
- Levin, I.; Brandon, D. Metastable alumina polymorphs: Crystal structures and transition sequences. J. Am. Ceram. Soc. 2005, 81, 1995–2012. [Google Scholar] [CrossRef]
- Ruppi, S. Advances in chemically deposited wear resistant coatings. J. Phys. IV 2001, 11, 847–859. [Google Scholar] [CrossRef]
- Ruppi, S.; Larsson, A. Chemical vapour deposition of κ-Al2O3. Thin Solid Films 2001, 388, 50–61. [Google Scholar] [CrossRef]
- Larsson, A.; Ruppi, S. Microstructure and properties of CVD γ-Al2O3 coatings. Int. J. Refract. Met. Hard Mater. 2001, 19, 515–522. [Google Scholar] [CrossRef]
- Hochauer, D.; Mitterer, C.; Penoy, M.; Michotte, C.; Martinz, H.; Kathrein, M. Thermal stability of doped CVD κ-Al2O3 coatings. Surf. Coat. Technol. 2010, 204, 3713–3722. [Google Scholar] [CrossRef]
- Skogsmo, J.; Halvarsson, M.; Vuorinen, S. Microstructural study of the κ-Al2O3 → α-Al2O3 transformation in CVD κ-Al2O3. Surf. Coat. Technol. 1992, 54–55, 186–192. [Google Scholar] [CrossRef]
- Moreno, M.; El Azhari, I.; Apel, D.; Meixner, M.; Wan, W.; Pinto, H.; Soldera, F.; Müklich, F.; Garcia, J. Design of comb crack resistant milling inserts: A comparison of stresses, crack propagation, and deformation behavior between Ti(C,N)/α-Al2O3 and Zr(C,N)/α-Al2O3 CVD coatings. Crystals 2021, 11, 493. [Google Scholar] [CrossRef]
- Hansson, P.; Halvarsson, M.; Vuorinen, S. Characterisation of the κ-Al2O3→α-Al2O3 transformation in different single layer coatings of CVD κ-Al2O3. Surf. Coat. Technol. 1995, 76–77, 256–264. [Google Scholar] [CrossRef]
- Osada, A.; Nakamura, E.; Homma, H.; Hayahi, T.; Oshika, T. Wear mechanism of thermally transformed CVD Al2O3 layer. Int. J. Refract. Met. Hard Mater. 2006, 24, 387–391. [Google Scholar] [CrossRef]
- Ruppi, S. Deposition, microstructure and properties of texture-controlled CVD α-Al2O3 coatings. Int. J. Refract. Met. Hard Mater. 2005, 23, 306–316. [Google Scholar] [CrossRef]
- Ruppi, S. Enhanced performance of α-Al2O3 coatings by control of crystal orientation. Surf. Coat. Technol. 2008, 202, 4257–4269. [Google Scholar] [CrossRef]
- Hochauer, D.; Mitterer, C.; Penoy, M.; Michotte, C.; Martinz, H.; Kathrein, M. Titanium doped CVD alumina coatings. Surf. Coat. Technol. 2008, 203, 350–356. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Manns, T.; Scholtes, B. DECcalc—A program for the calculation of diffraction elastic constants from single crystal coefficients. Mater. Sci. Forum 2011, 681, 417–419. [Google Scholar] [CrossRef]
- Gladden, J.R.; So, J.H.; Maynard, J.D.; Saxe, P.; Le Page, Y. Reconciliation of ab initio theory and experimental elastic properties of Al2O3. Appl. Phys. Lett. 2004, 85, 392. [Google Scholar] [CrossRef] [Green Version]
- Holm, B.; Ahuja, R.; Yourdshahyan, Y.; Johansson, B.; Lundqvist, B.I. Elastic and optical properties ofα- andκ−Al2O3. Phys. Rev. B 1999, 59, 12777–12787. [Google Scholar] [CrossRef]
- Matoy, K.; Schönherr, H.; Detzel, T.; Schöberl, T.; Pippan, R.; Motz, C.; Dehm, G. A comparative micro-cantilever study of the mechanical behavior of silicon based passivation films. Thin Solid Films 2009, 518, 247–256. [Google Scholar] [CrossRef]
- Gere, J.M.; Timoshenko, S.P. Mechanics of Materials, 3rd ed.; Springer-Science-Business Media, B.V.: Berlin/Heidelberg, Germany, 1991. [Google Scholar] [CrossRef]
- Gates-Rector, S.; Blanton, T. The powder diffraction file: A quality materials characterization database. Powder Diff. 2019, 34, 352–360. [Google Scholar] [CrossRef] [Green Version]
- Stylianou, R.; Tkadletz, M.; Schalk, N.; Penoy, M.; Czettl, C.; Mitterer, C. Effects of reference materials on texture coefficients determined for a CVD α-Al2O3 coating. Surf. Coat. Technol. 2019, 359, 314–322. [Google Scholar] [CrossRef]
- Chien, H.; Gao, M.C.; Miller, H.M.; Rohrer, G.S.; Ban, Z.; Prichard, P.; Liu, Y. Microtexture and hardness of CVD deposited α-Al2O3 and TiCxN1−x coatings. Int. J. Refract. Met. Hard Mater. 2009, 27, 458–464. [Google Scholar] [CrossRef]
- Shoja, S.; Mortazavi, N.; Lindahl, E.; Norgren, S.; Bäcke, O.; Halvarsson, M. Microstructure investigation of textured CVD alumina coatings. Int. J. Refract. Met. Hard Mater. 2020, 87, 105125. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Introduction to Contact Mechanics, 2nd ed.; Springer: New South Wales, Australia, 2007. [Google Scholar]
- Norton, A.; Falco, S.; Young, N.; Severs, J.; Todd, R. Microcantilever investigation of fracture toughness and subcritical crack growth on the scale of the microstructure in Al2O3. J. Eur. Ceram. Soc. 2015, 35, 4521–4533. [Google Scholar] [CrossRef]
- Zhang, P.; Li, S.; Zhang, Z. General relationship between strength and hardness. Mater. Sci. Eng. A 2011, 529, 62–73. [Google Scholar] [CrossRef]
- Ritchie, R. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef]
- Daniel, R.; Meindlhumer, M.; Zalesak, J.; Baumegger, W.; Todt, J.; Ziegelwanger, T.; Keckes, J.F.; Mitterer, C.; Keckes, J. Multi-scale interface design of strong and damage resistant hierarchical nanostructured materials. Mater. Des. 2020, 196, 109169. [Google Scholar] [CrossRef]
- Konstantiniuk, F.; Tkadletz, M.; Kainz, C.; Czettl, C.; Schalk, N. Mechanical properties of single and polycrystalline α-Al2O3 coatings grown by chemical vapor deposition. Surf. Coat. Technol. 2021, 410, 126959. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konstantiniuk, F.; Tkadletz, M.; Czettl, C.; Schalk, N. Fracture Properties of α– and ĸ–Al2O3 Hard Coatings Deposited by Chemical Vapor Deposition. Coatings 2021, 11, 1359. https://doi.org/10.3390/coatings11111359
Konstantiniuk F, Tkadletz M, Czettl C, Schalk N. Fracture Properties of α– and ĸ–Al2O3 Hard Coatings Deposited by Chemical Vapor Deposition. Coatings. 2021; 11(11):1359. https://doi.org/10.3390/coatings11111359
Chicago/Turabian StyleKonstantiniuk, Fabian, Michael Tkadletz, Christoph Czettl, and Nina Schalk. 2021. "Fracture Properties of α– and ĸ–Al2O3 Hard Coatings Deposited by Chemical Vapor Deposition" Coatings 11, no. 11: 1359. https://doi.org/10.3390/coatings11111359
APA StyleKonstantiniuk, F., Tkadletz, M., Czettl, C., & Schalk, N. (2021). Fracture Properties of α– and ĸ–Al2O3 Hard Coatings Deposited by Chemical Vapor Deposition. Coatings, 11(11), 1359. https://doi.org/10.3390/coatings11111359




