Theoretical Analysis of Roll-Over-Web Surface Thin Layer Coating
Abstract
1. Introduction
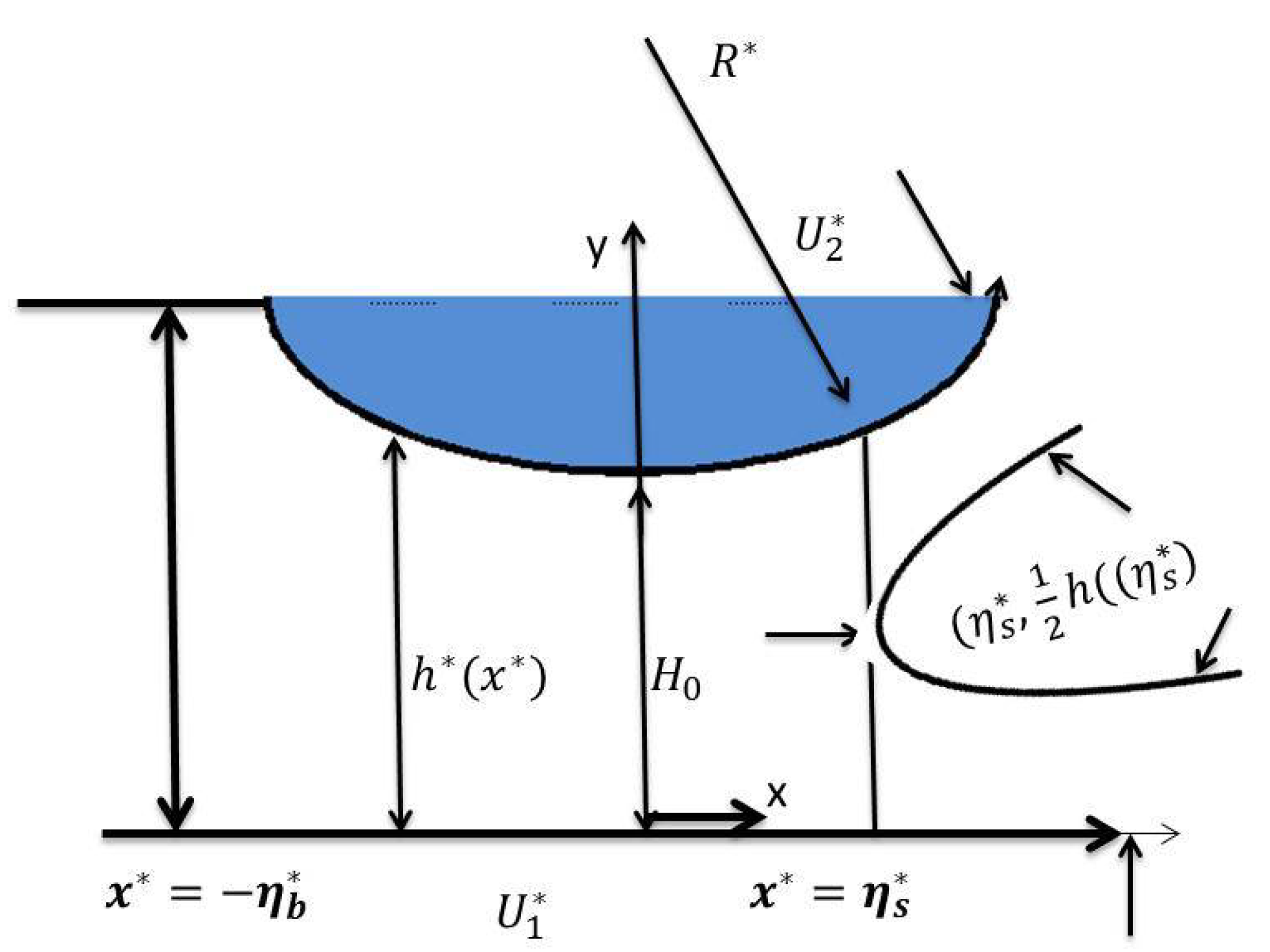
2. Materials and Methods
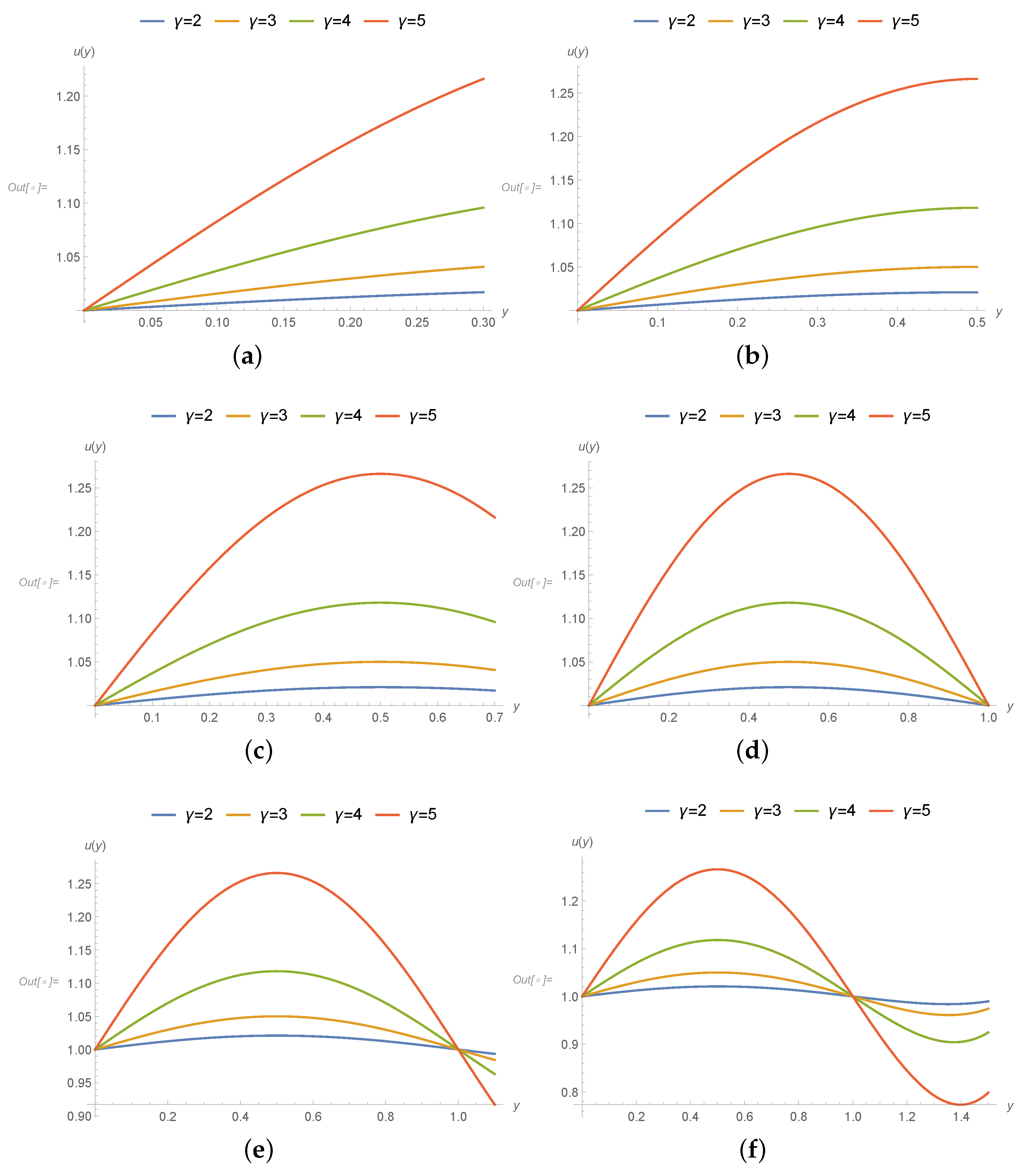
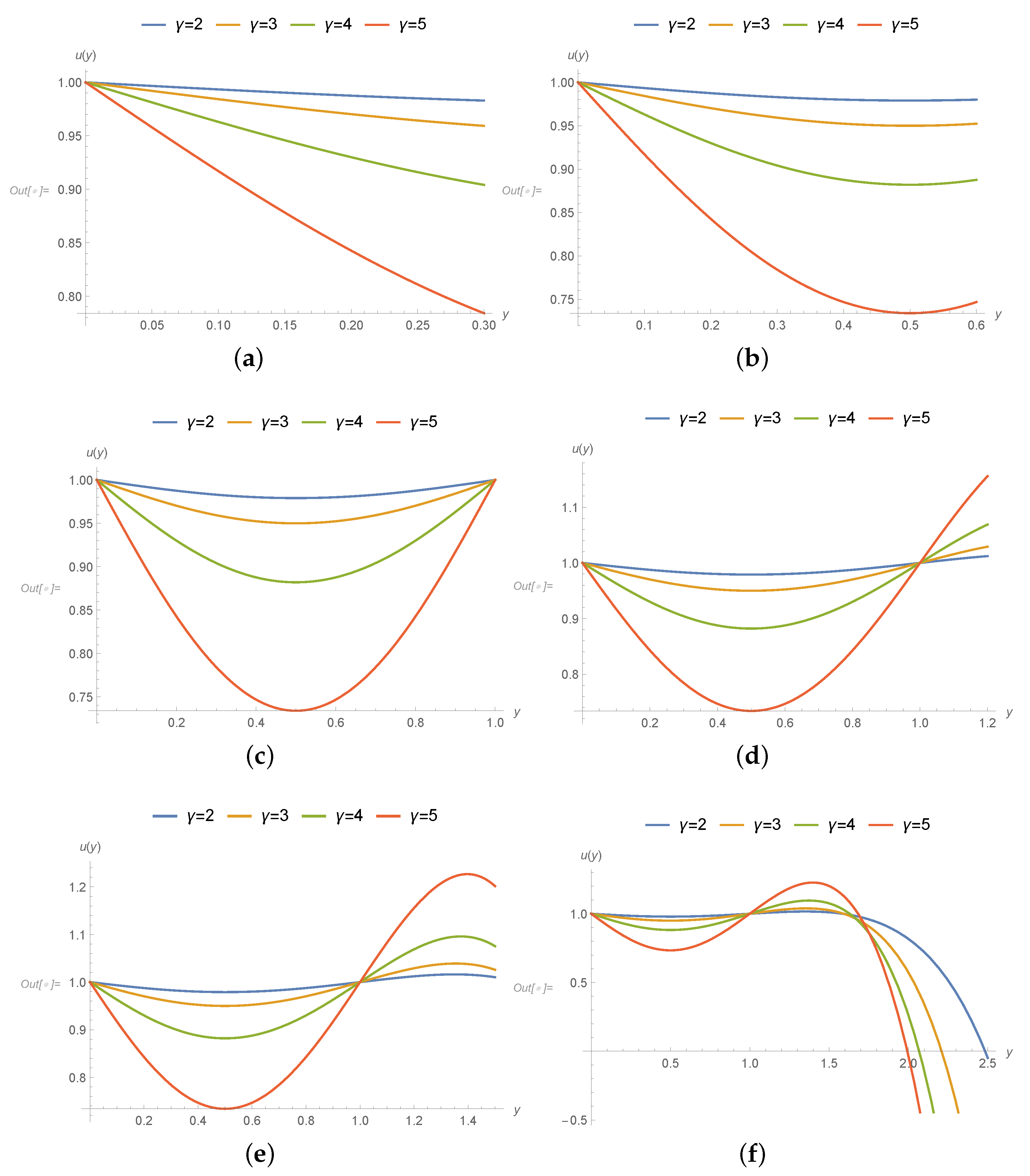
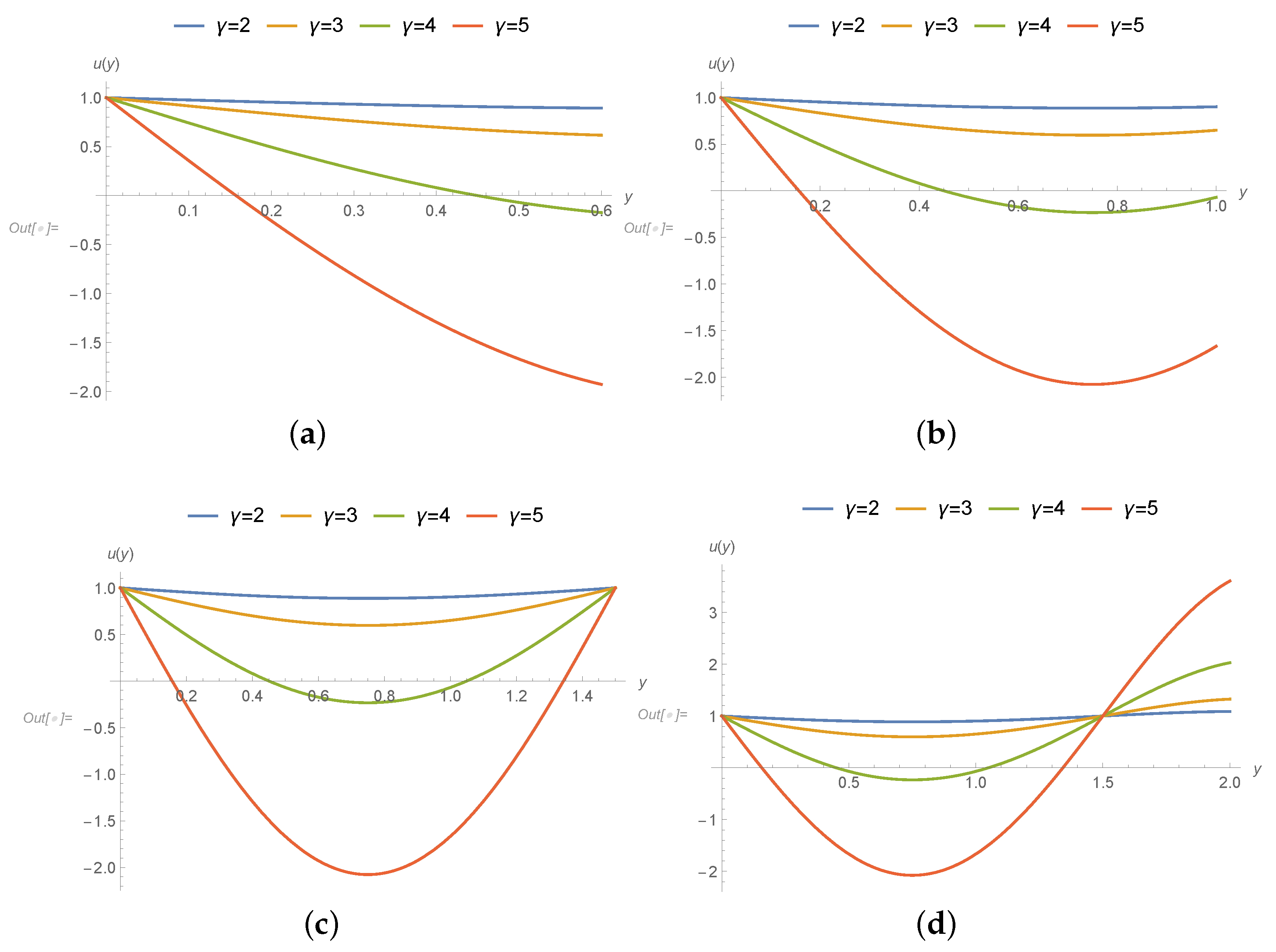
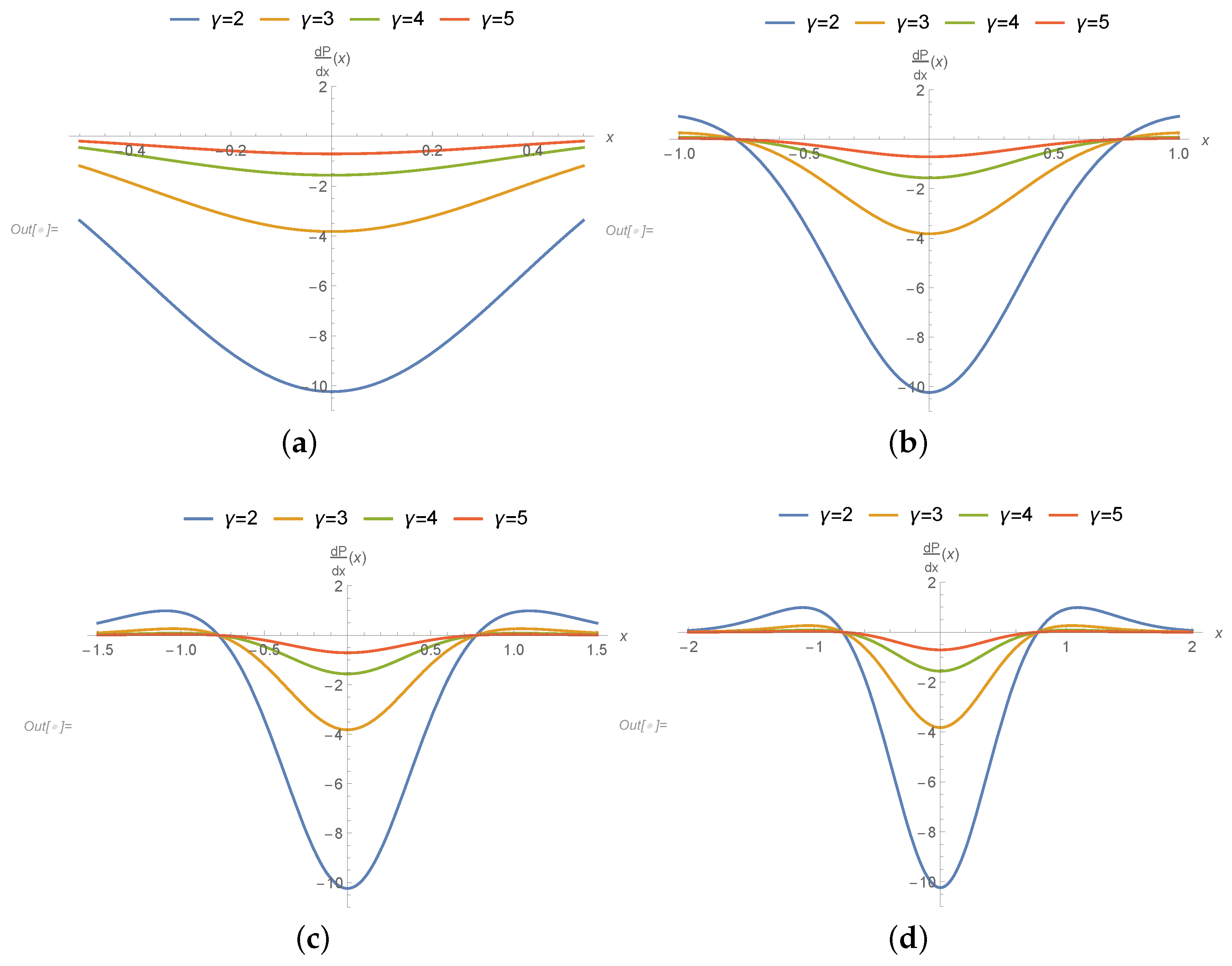
3. Results
4. Conclusions
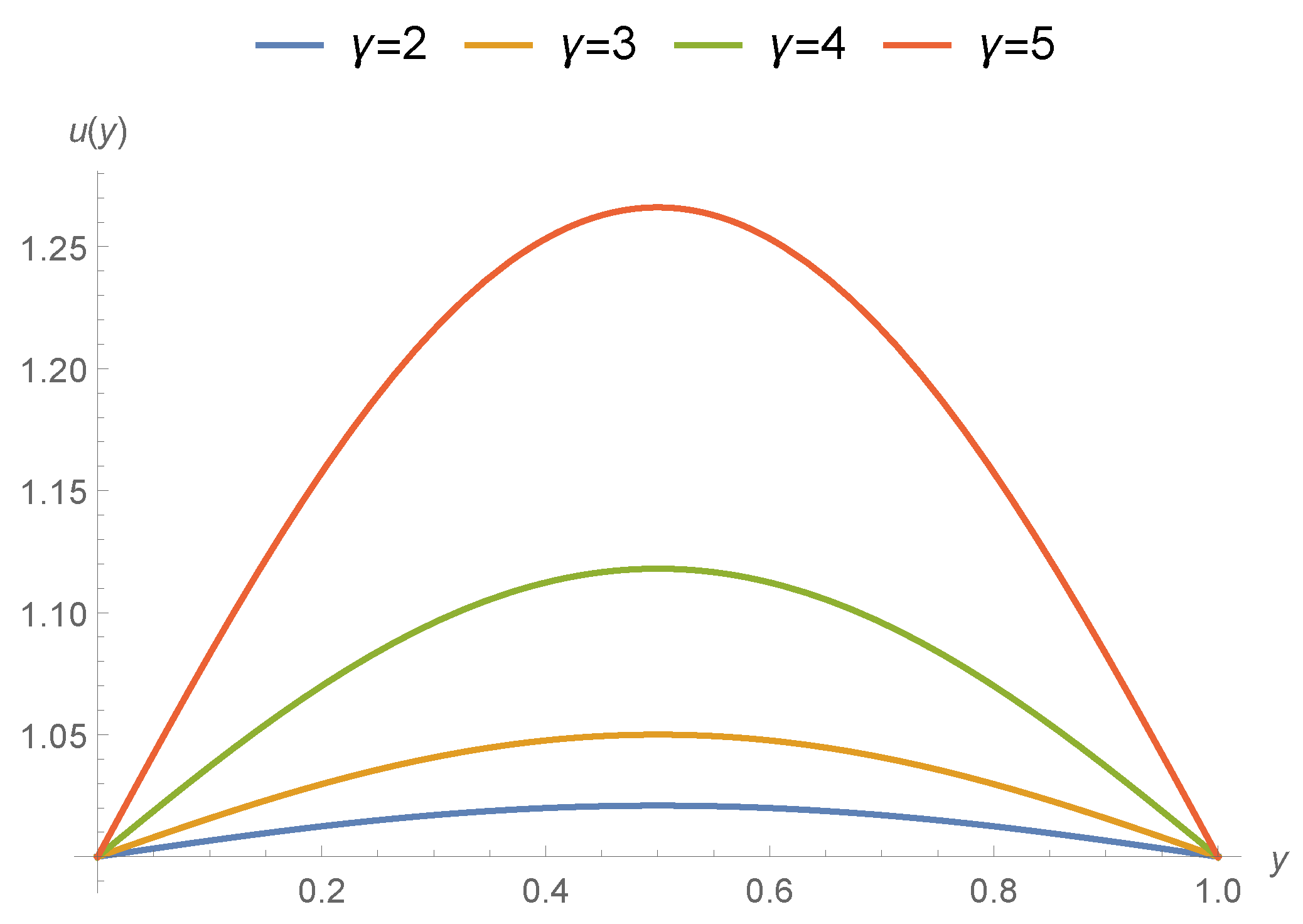
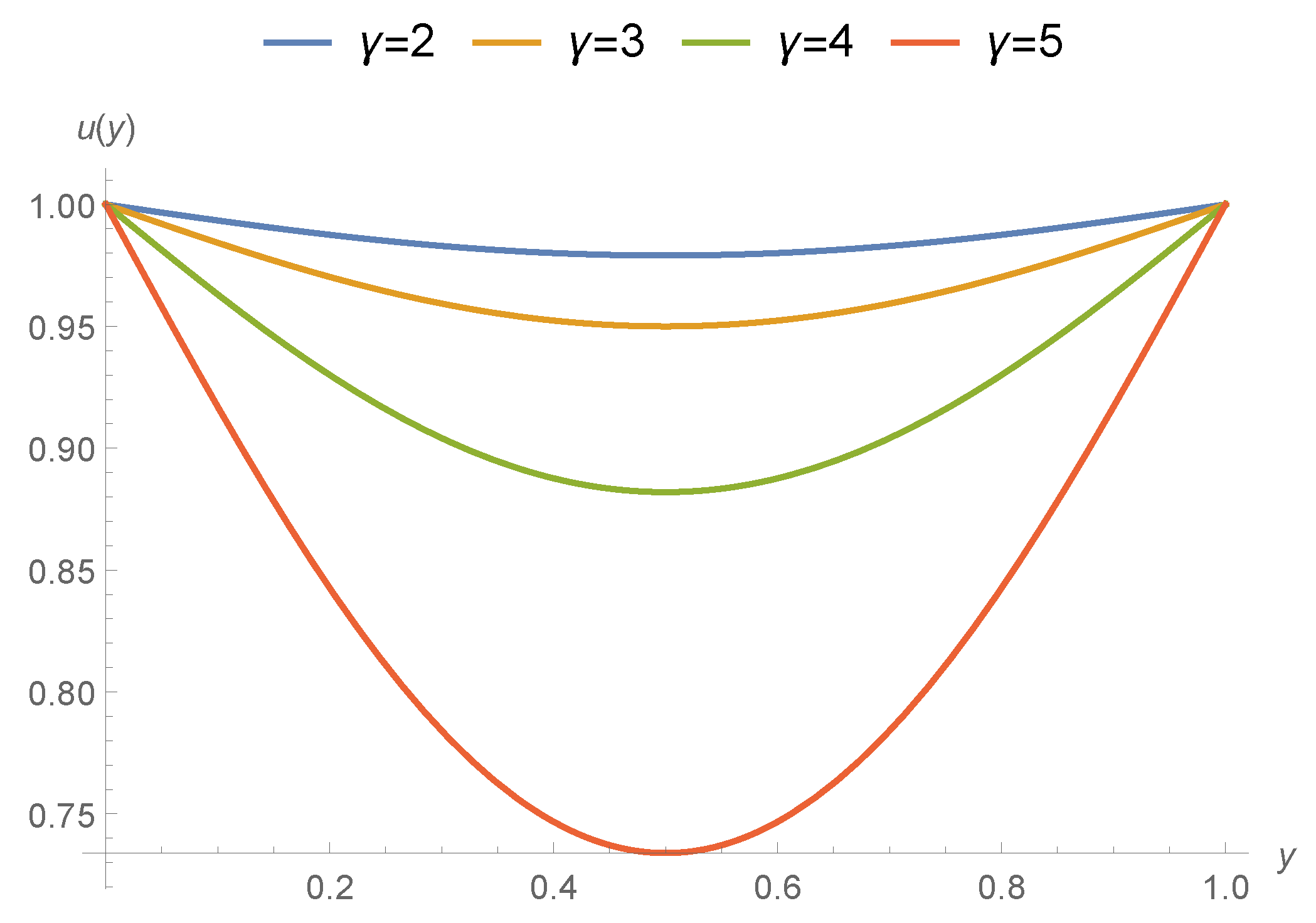
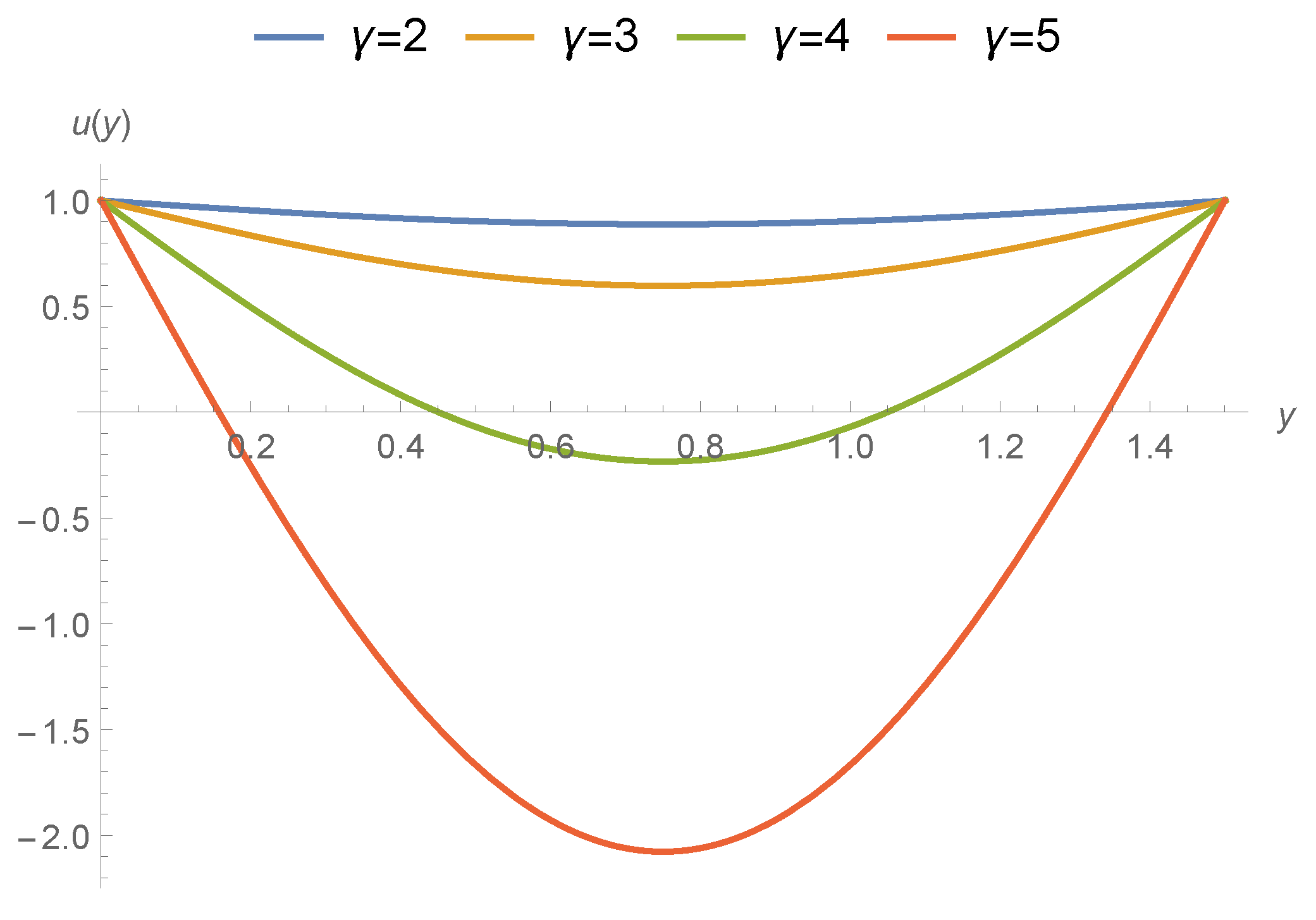
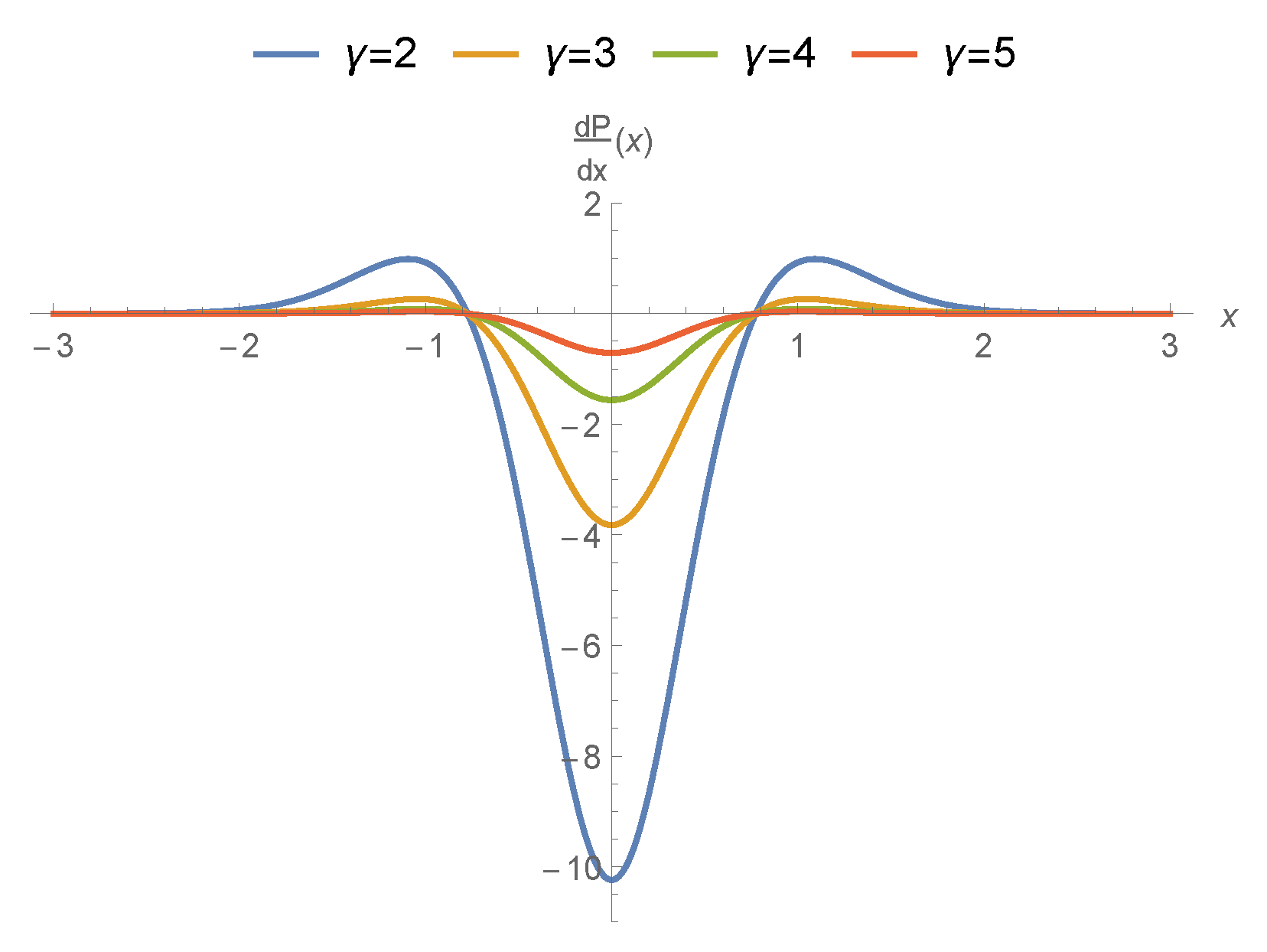
- The transport properties are affected due to coupled-stress and velocity decreases because of increase in applied couple stress.
- The gradients of pressures in the mid region are going up because of sturdy applied stress.
- In the upper stream and downwards sections of graphs, velocity and transport properties have been influenced and affected largely in the middle nip section the drag flow is supported due to the poignant roller and sheet.
- The support or disagreement enhances as coupled stress rises. So the speed of coating at this position exceeds one over the whole cross-section.
- Pressure slope is upbeat and as a consequence the speed at this position is utmost at the joining section of roller and leaf. It is interesting to say that axial position is less affected due to applied stresses and speed of roller.
Author Contributions
Funding
Conflicts of Interest
References
- Middleman, S. Fundamentals of Polymer Processing; McGraw-Hill: New York, NY, USA, 1977. [Google Scholar]
- Bird, R.B.; Dai, G.C.; Yarusso, B.J. The rheology and flow of viscoplastic materials. Rev. Chem. Eng. 1983, 1, 1–70. [Google Scholar] [CrossRef]
- Greener, Y.; Middleman, S. A theory of roll coating of viscous and viscoelastic fluids. Polym. Eng. Sci. 1975, 15, 1–10. [Google Scholar] [CrossRef]
- Coyle, D.J.; Macosko, C.W.; Scriven, L.E. Film-splitting flows in forward roll coating. J. Fluid Mech. 1986, 171, 183–207. [Google Scholar] [CrossRef]
- Hintermaier, J.C.; White, R.E. The splitting of a water film between rotating rolls. TAPPI J. 1965, 48, 617–625. [Google Scholar]
- Benkreira, H.; Patel, R.; Edwards, M.F.; Wilkinson, W.L. Classification and analyses of coating flows. J. Non-Newton. Fluid Mech. 1994, 54, 437–447. [Google Scholar] [CrossRef]
- Benkreira, H.; Edwards, M.F.; Wilkinson, W.L. Roll coating of purely viscous liquids. Chem. Eng. Sci. 1981, 36, 429–434. [Google Scholar] [CrossRef]
- Benkreira, H.; Edwards, M.F.; Wilkinson, W.L. Roll coating operations. J. Non-Newton. Fluid Mech. 1984, 14, 377–389. [Google Scholar] [CrossRef]
- Benkreira, H.; Edwards, M.F.; Wilkinson, W.L. A semi-empirical model of the forward roll coating flow of Newtonian fluids. Chem. Eng. Sci. 1981, 36, 423–427. [Google Scholar] [CrossRef]
- Sofou, S.; Mitsoulis, E. Roll-over-web coating of pseudoplastic and viscoplastic sheets using the lubrication approximation. J. Plast. Film Sheet. 2005, 21, 307–333. [Google Scholar] [CrossRef]
- Zahid, M.; Haroon, T.; Rana, M.A.; Siddiqui, A.M. Roll coating analysis of a third grade fluid. J. Plast. Film Sheet. 2017, 33, 72–91. [Google Scholar] [CrossRef]
- Zahid, M.; Rana, M.A.; Siddiqui, A.M. Roll coating analysis of a second-grade material. J. Plast. Film Sheet. 2018, 34, 232–255. [Google Scholar] [CrossRef]
- Ali, N.; Atif, H.M.; Javed, M.A.; Sajid, M. A theoretical analysis of roll-over-web coating of couple stress fluid. J. Plast. Film Sheet. 2018, 34, 43–59. [Google Scholar] [CrossRef]
- Gaskell, P.H.; Savage, M.D.; Summers, J.L.; Thompson, H.M. Modelling and analysis of meniscus roll coating. J. Fluid Mech. 1995, 298, 113–137. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. Determination of periodic solutions for the motion of a particle on a rotating parabola by means of the optimal homotopy asymptotic method. J. Sound Vib. 2010, 329, 1450–1459. [Google Scholar] [CrossRef]
- Iqbal, S.; Idrees, M.; Siddiqui, A.M.; Ansari, A.R. Some solutions of the linear and nonlinear Klein–Gordon equations using the optimal homotopy asymptotic method. Appl. Math. Comput. 2010, 216, 2898–2909. [Google Scholar] [CrossRef]
- Iqbal, S.; Javed, A. Application of optimal homotopy asymptotic method for the analytic solution of singular Lane–Emden type equation. Appl. Math. Comput. 2011, 217, 7753–7761. [Google Scholar] [CrossRef]
- Iqbal, S.; Ansari, A.R.; Siddiqui, A.M.; Javed, A. Use of optimal homotopy asymptotic method and Galerkin’s finite element formulation in the study of heat transfer flow of a third grade fluid between parallel plates. J. Heat Transf. 2011, 133, 091702. [Google Scholar] [CrossRef]
- Hashmi, M.S.; Khan, N.; Iqbal, S. Numerical solutions of weakly singular Volterra integral equations using the optimal homotopy asymptotic method. Comput. Math. Appl. 2012, 64, 1567–1574. [Google Scholar] [CrossRef][Green Version]
- Hashmi, M.S.; Khan, N.; Iqbal, S. Optimal homotopy asymptotic method for solving nonlinear Fredholm integral equations of second kind. Appl. Math. Comput. 2012, 218, 10982–10989. [Google Scholar] [CrossRef]
- Khaliq, S.; Abbas, Z. A theoretical analysis of roll-over-web coating assessment of viscous nanofluid containing Cu-water nanoparticles. J. Plast. Film Sheet. 2020, 36, 55–75. [Google Scholar] [CrossRef]
- Atif, H.M.; Ali, N.; Javed, M.A.; Abbas, F. Theoretical analysis of roll-over-web coating of a micropolar fluid under lubrication approximation theory. J. Plast. Film Sheet. 2018, 34, 418–438. [Google Scholar] [CrossRef]
- Bhatti, S.; Zahid, M.; Rana, M.A.; Siddiqui, A.M.; Abdul Wahab, H. Numerical analysis of blade coating of a third-order fluid. J. Plast. Film Sheet. 2019, 35, 157–180. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Zahid, M.; Rana, M.A.; Haroon, T. Calendering analysis of a third-order fluid. J. Plast. Film Sheet. 2014, 30, 345–368. [Google Scholar] [CrossRef]
- Singh, B. Wave propagation in a generalized thermoelastic material with voids. Appl. Math. Comput. 2007, 189, 698–709. [Google Scholar] [CrossRef]
- Mallik, S.H.; Kanoria, M. Generalized thermoelastic functionally graded solid with a periodically varying heat source. Int. J. Solids Struct. 2007, 44, 7633–7645. [Google Scholar] [CrossRef]
- Blake, T.D.; Ruschak, K.J.; Kistler, S.F.; Schweizer, P.M. Liquid Film Coating; Chapman and Hall: London, UK, 1997. [Google Scholar]
- Hayat, T.; Farooq, S.; Alsaedi, A.; Ahmad, B. Numerical study for Soret and Dufour effects on mixed convective peristalsis of Oldroyd 8-constants fluid. Int. J. Therm. Sci. 2017, 112, 68–81. [Google Scholar] [CrossRef]
- Hwang, S.S. Non-Newtonian liquid blade coating process. J. Fluids Eng. 1982, 104, 469–474. [Google Scholar] [CrossRef]
- Ruschak, K.J. Coating flows. Annu. Rev. Fluid Mech. 1985, 17, 65–89. [Google Scholar] [CrossRef]
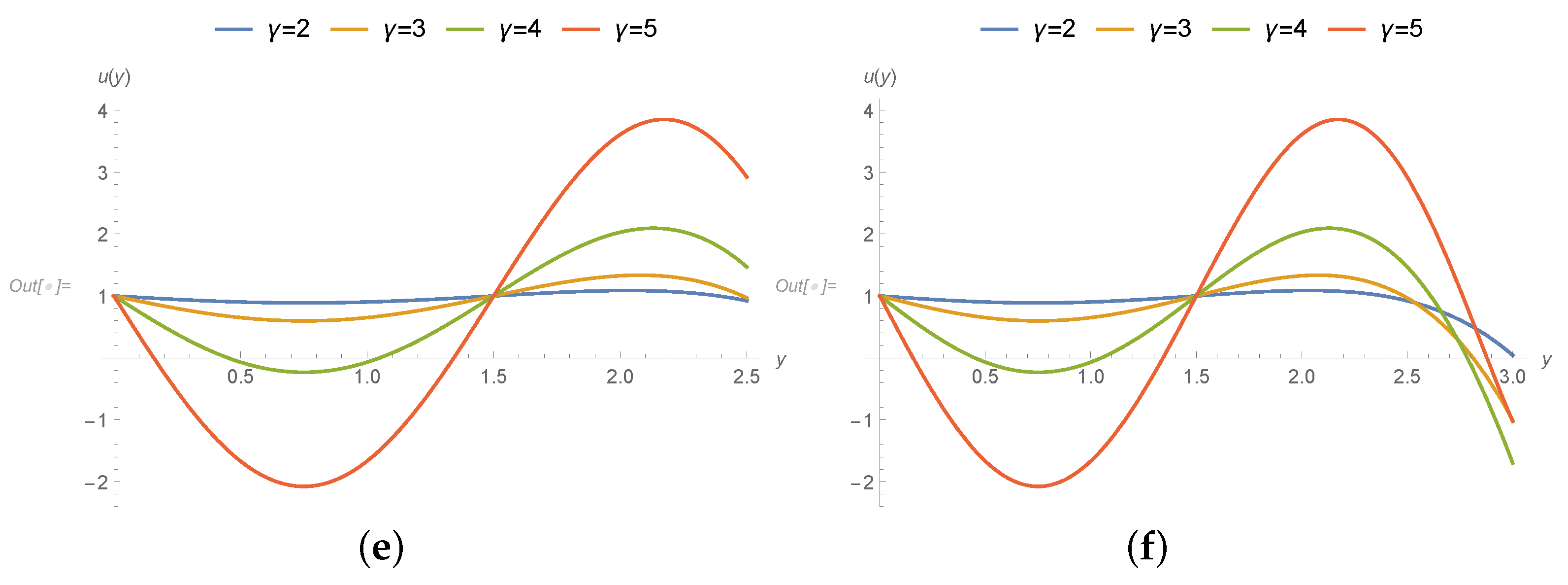
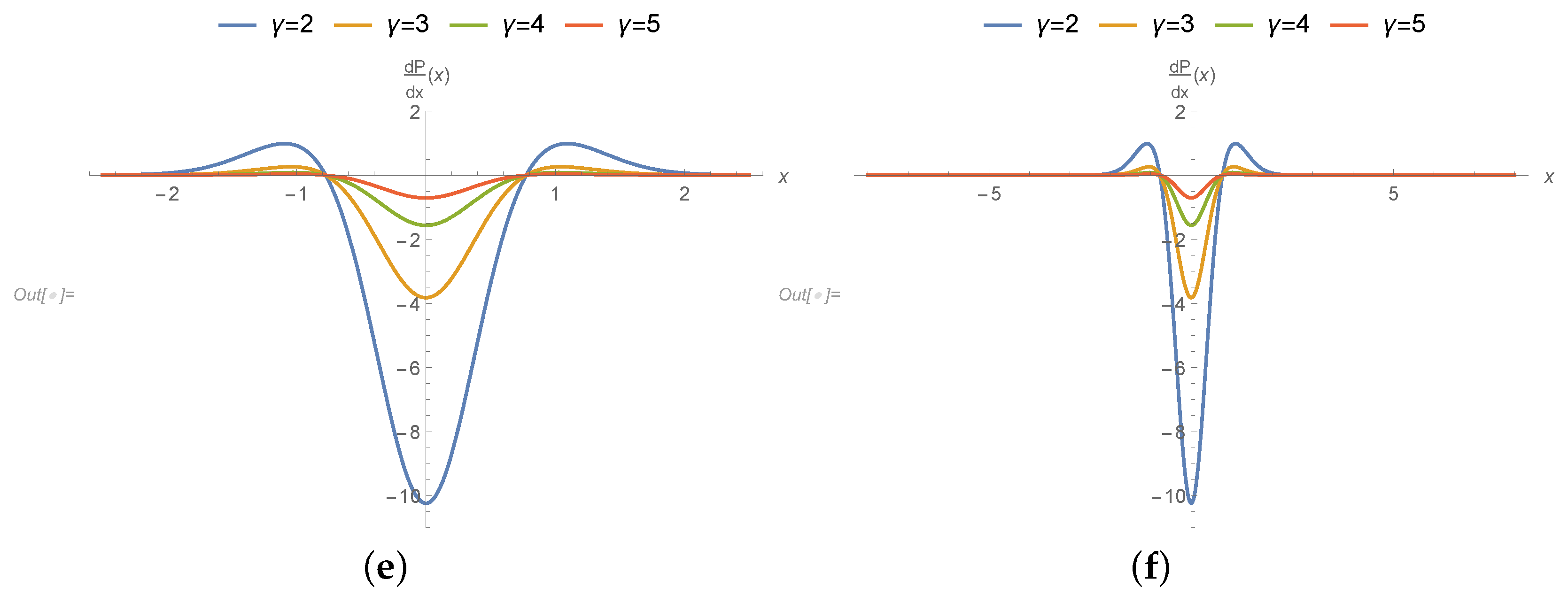
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manzoor, T.; Zafar, M.; Iqbal, S.; Nazar, K.; Ali, M.; Saleem, M.; Manzoor, S.; Kim, W.Y. Theoretical Analysis of Roll-Over-Web Surface Thin Layer Coating. Coatings 2020, 10, 691. https://doi.org/10.3390/coatings10070691
Manzoor T, Zafar M, Iqbal S, Nazar K, Ali M, Saleem M, Manzoor S, Kim WY. Theoretical Analysis of Roll-Over-Web Surface Thin Layer Coating. Coatings. 2020; 10(7):691. https://doi.org/10.3390/coatings10070691
Chicago/Turabian StyleManzoor, Tareq, Muhammad Zafar, Shaukat Iqbal, Kashif Nazar, Muddassir Ali, Mahmood Saleem, Sanaullah Manzoor, and Woo Young Kim. 2020. "Theoretical Analysis of Roll-Over-Web Surface Thin Layer Coating" Coatings 10, no. 7: 691. https://doi.org/10.3390/coatings10070691
APA StyleManzoor, T., Zafar, M., Iqbal, S., Nazar, K., Ali, M., Saleem, M., Manzoor, S., & Kim, W. Y. (2020). Theoretical Analysis of Roll-Over-Web Surface Thin Layer Coating. Coatings, 10(7), 691. https://doi.org/10.3390/coatings10070691