Structure of DPPC Monolayers at the Air/Buffer Interface: A Neutron Reflectometry and Ellipsometry Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Surface Pressure-Area Isotherm
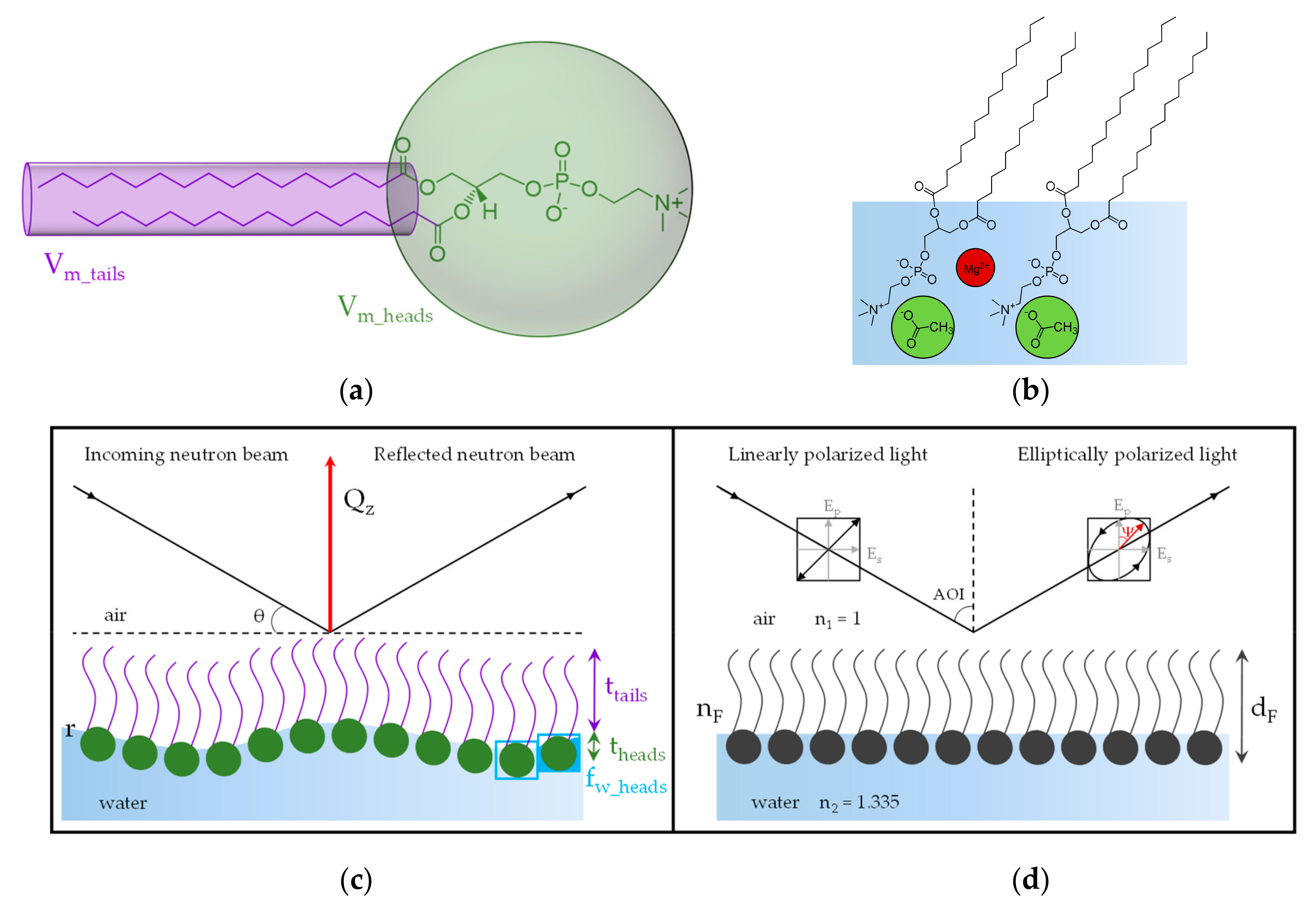
2.3. Neutron Reflectometry Data Acquisition
2.4. NR Data Modeling
2.5. Ellipsometry
3. Results
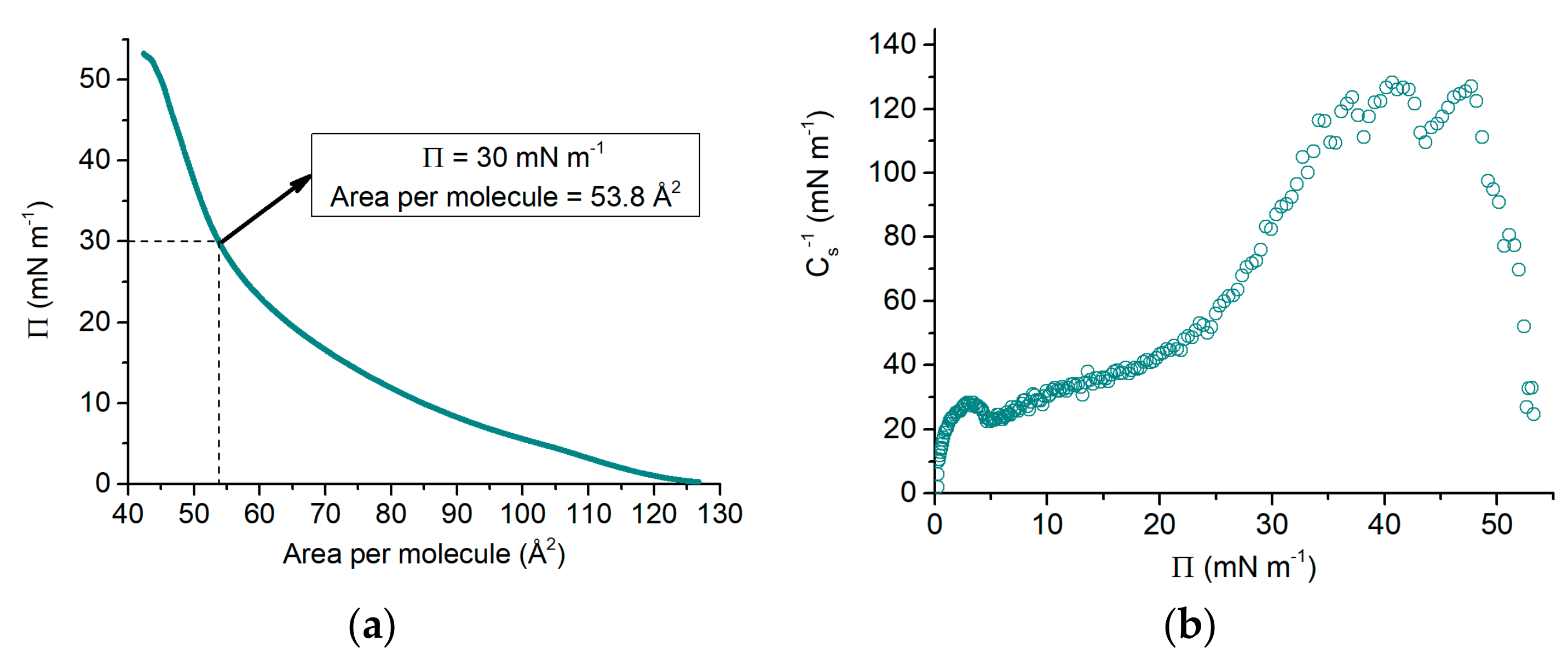
3.1. Π-A Isotherm
3.2. NR Results
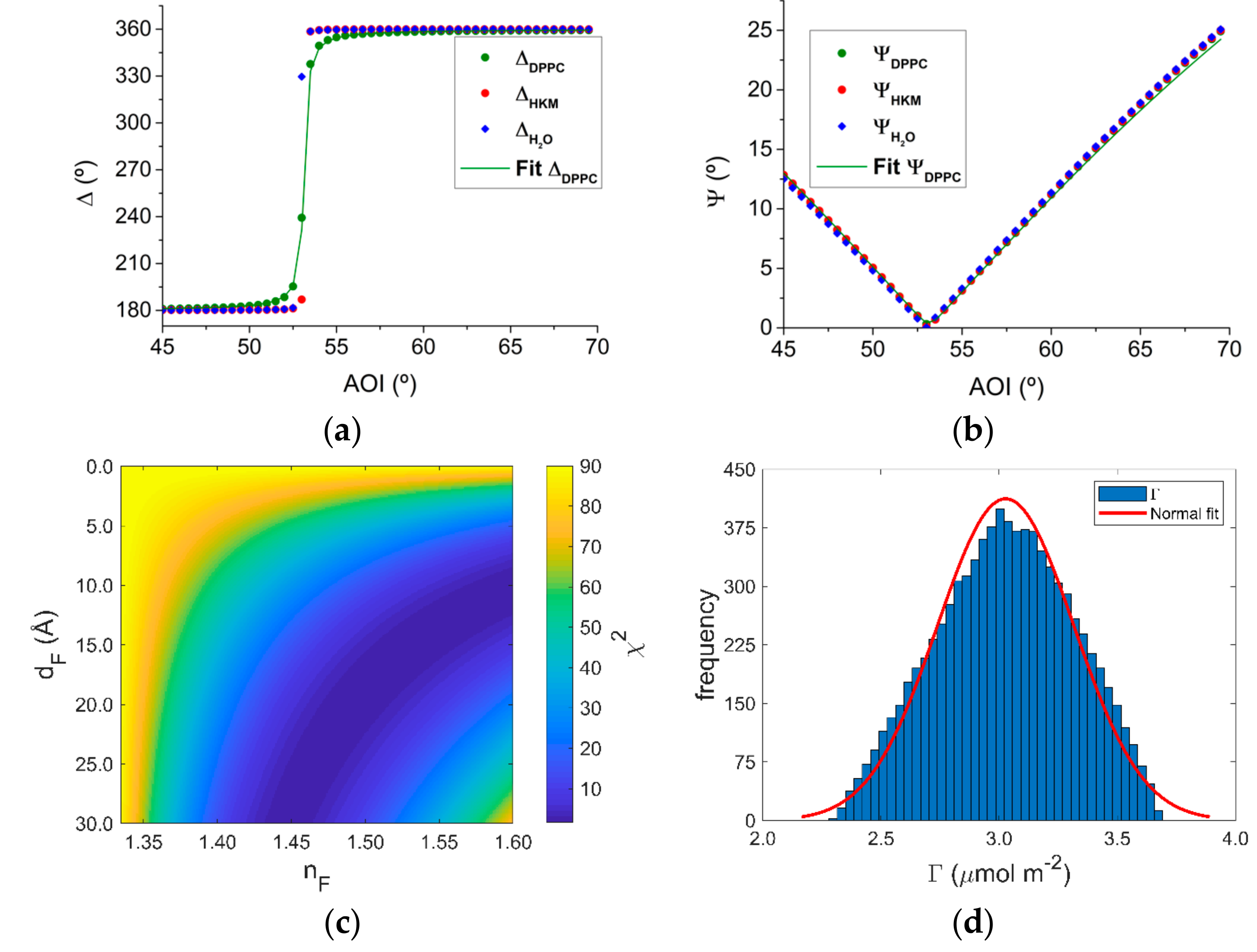
3.3. Ellipsometry
4. Discussion
4.1. Effect of HKM Buffer on the DPPC Monolayer Π-A Isotherm
4.2. Influence of HKM Buffer on the Structural Parameters of DPPC Monolayers at the LC Phase
4.3. Combining Neutron Reflectometry and Ellipsometry Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lodish, H.; Berk, A.; Zipursky, S.L.; Matsudaira, P.; Baltimore, D.; Darnell, J. Biomembranes: Structural organization and basic functions. In Molecular Cell Biology; Freeman, W.H.: New York, NY, USA, 2000; ISBN 978-0-7167-3136-8. [Google Scholar]
- Cooper, G.M. Structure of the Plasma Membrane. In The Cell: A Molecular Approach; Sunderland, Mass. Sinauer Associates: Washington, DC, USA, 2000. [Google Scholar]
- Vacklin, H.P.; Tiberg, F.; Fragneto, G.; Thomas, R.K.; Park, I.S.; Lund, S. Phospholipase A2 hydrolysis of supported phospholipid bilayers: A neutron reflectivity and ellipsometry study. Biochemistry 2005, 44, 2811–2821. [Google Scholar] [CrossRef]
- Bartkowiak, A.; Rojewska, M.; Prochaska, K. Study of mucin interaction with model phospholipid membrane at the air–water interface. Colloids Surfaces A Physicochem. Eng. Asp. 2019, 578, 123587. [Google Scholar] [CrossRef]
- Puglisi, G.; Fresta, M.; Pignatello, R. Synthesis of methotrexate α,γ-bis(amides) and correlation of thermotropic and DPPC biomembrane interaction parameters with their anticancer activity. Drug Dev. Res. 1998, 44, 62–69. [Google Scholar] [CrossRef]
- Caseli, L.; Sakai, A.; de Sousa Mesquita, A.P.; Nader, H.B.; Lopes, C.C.; Nakanishi, W.; Ariga, K. Thermodynamic and morphological properties of trastuzumab regulated by the lipid composition of cell membrane models at the air-water interface. Biophys. J. 2020, 118, 77a. [Google Scholar] [CrossRef]
- Zhao, L.; Feng, S.S.; Go, M.L. Investigation of Molecular interactions between paclitaxel and DPPC by langmuir film balance and differential scanning calorimetry. J. Pharm. Sci. 2004, 93, 86–98. [Google Scholar] [CrossRef]
- Sakai, A.; de Sousa Mesquista, A.P.; Nader, H.B.; Lopes, C.C.; Nakanishi, W.; Ariga, K.; Caseli, L. The lipid composition affects Trastuzumab adsorption at monolayers at the air-water interface. Chem. Phys. Lipids 2020, 227, 104875. [Google Scholar] [CrossRef]
- Deleu, M.; Paquot, M.; Nylander, T. Fengycin interaction with lipid monolayers at the air–aqueous interface—Implications for the effect of fengycin on biological membranes. J. Colloid Interface Sci. 2005, 283, 358–365. [Google Scholar] [CrossRef]
- Simons, K.; Vaz, W.L.C. Model systems, lipid rafts, and cell membranes. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 269–295. [Google Scholar] [CrossRef]
- Aleskndrany, A.; Sahin, I. The effects of Levothyroxine on the structure and dynamics of DPPC liposome: FTIR and DSC studies. Biochim. Biophys. Acta Biomembr. 2020, 183254. [Google Scholar] [CrossRef]
- Ortiz-Collazos, S.; Picciani, P.H.S.; Oliveira, O.N.; Pimentel, A.S.; Edler, K.J. Influence of levofloxacin and clarithromycin on the structure of DPPC monolayers. Biochim. Biophys. Acta Biomembr. 2019, 1861, 182994. [Google Scholar] [CrossRef]
- Vaknin, D.; Kjaer, K.; Als-Nielsen, J.; Lösche, M. Structural properties of phosphatidylcholine in a monolayer at the air/water interface: Neutron reflection study and reexamination of x-ray reflection measurements. Biophys. J. 1991, 59, 1325–1332. [Google Scholar] [CrossRef]
- Didcot, C.; Ox, O. Hydration of DPPC monolayers at the air/water interface and its modulation by the nonionic surfactant C12E4: A neutron reflection study. Langmuir 1996, 11, 3948–3952. [Google Scholar]
- Adams, E.M.; Casper, C.B.; Allen, H.C. Effect of cation enrichment on dipalmitoylphosphatidylcholine (DPPC) monolayers at the air-water interface. J. Colloid Interface Sci. 2016, 478, 353–364. [Google Scholar] [CrossRef] [PubMed]
- Guzmán, E.; Liggieri, L.; Santini, E.; Ferrari, M.; Ravera, F. Mixed DPPC-cholesterol Langmuir monolayers in presence of hydrophilic silica nanoparticles. Colloids Surfaces B Biointerfaces 2013, 105, 284–293. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-López, R.; Guzmán, E.; Velázquez, M.M.; Fernández-Peña, L.; Merchán, M.D.; Maestro, A.; Ortega, F.; Rubio, R.G. Influence of carbon nanosheets on the behavior of 1,2-Dipalmitoyl-sn-glycerol-3-phosphocholine Langmuir monolayers. Processes 2020, 8, 94. [Google Scholar] [CrossRef]
- Kent, M.S.; Murton, J.K.; Sasaki, D.Y.; Satija, S.; Akgun, B.; Nanda, H.; Curtis, J.E.; Majewski, J.; Morgan, C.R.; Engen, J.R. Neutron reflectometry study of the conformation of HIV Nef bound to lipid membranes. Biophys. J. 2010, 99, 1940–1948. [Google Scholar] [CrossRef]
- Ege, C.; Lee, K.Y.C. Insertion of Alzheimer’s Aβ40 peptide into lipid monolayers. Biophys. J. 2004, 87, 1732–1740. [Google Scholar] [CrossRef]
- Kienle, D.F.; De Souza, J.V.; Watkins, E.B.; Kuhl, T.L. Thickness and refractive index of DPPC and DPPE monolayers by multiple-beam interferometry. Anal. Bioanal. Chem. 2014, 406, 4725–4733. [Google Scholar] [CrossRef]
- Pusterla, J.M.; Malfatti-Gasperini, A.A.; Puentes-Martinez, X.E.; Cavalcanti, L.P.; Oliveira, R.G. Refractive index and thickness determination in Langmuir monolayers of myelin lipids. Biochim. Biophys. Acta Biomembr. 2017, 1859, 924–930. [Google Scholar] [CrossRef]
- Erbe, A.; Sigel, R. Tilt angle of lipid acyl chains in unilamellar vesicles determined by ellipsometric light scattering. Eur. Phys. J. E 2007, 22, 303–309. [Google Scholar] [CrossRef]
- Ducharme, D.; Max, J.J.; Salesse, C.; Leblanc, R.M. Ellipsometric study of the physical states of phosphatidylcholines at the air-water interface. J. Phys. Chem. 1990, 94, 1925–1932. [Google Scholar] [CrossRef]
- Ehlers, J. X-ray and Neuron Reflectivity: Principles and Applications; Springer: Berlin/Heidelberg, Germany, 1999; ISBN 3540661956. [Google Scholar]
- Zhou, X.L.; Chen, S.H. Theoretical foundation of X-ray and neutron reflectometry. Phys. Rep. 1995, 257, 223–348. [Google Scholar] [CrossRef]
- Cousin, F.; Chennevière, A. Neutron reflectivity for soft matter. EPJ Web Conf. 2018, 188, 04001. [Google Scholar] [CrossRef][Green Version]
- Campbell, R.A.; Saaka, Y.; Shao, Y.; Gerelli, Y.; Cubitt, R.; Nazaruk, E.; Matyszewska, D.; Lawrence, M.J. Structure of surfactant and phospholipid monolayers at the air/water interface modeled from neutron reflectivity data. J. Colloid Interface Sci. 2018, 531, 98–108. [Google Scholar] [CrossRef] [PubMed]
- Azzam, R.M.A.; Bashara, N.M. Ellipsometry and Polarized Light; North-Holland Publishing Company: New York, NY, USA, 1977; ISBN 0720406943. [Google Scholar]
- Motschmann, H.; Teppner, R. Ellipsometry in interface science. Stud. Interface Sci. 2001, 11, 1–42. [Google Scholar]
- Reiter, R.; Motschmann, H.; Knoll, W. Ellipsometric Characterization of Streptavidin Binding to Biotin-Functionalized Lipid Monolayers at the Water/Air Interface. Langmuir 1993, 9, 2430–2435. [Google Scholar] [CrossRef]
- Campbell, R.A.; Tummino, A.; Varga, I.; Milyaeva, O.Y.; Krycki, M.M.; Lin, S.Y.; Laux, V.; Haertlein, M.; Forsyth, V.T.; Noskov, B.A. Adsorption of denaturated lysozyme at the air-water interface: Structure and morphology. Langmuir 2018, 34, 5020–5029. [Google Scholar] [CrossRef]
- Tatur, S.; Badia, A. Influence of hydrophobic alkylated gold nanoparticles on the phase behavior of monolayers of DPPC and clinical lung surfactant. Langmuir 2012, 28, 628–639. [Google Scholar] [CrossRef]
- Maestro, A.; Deshmukh, O.S.; Mugele, F.; Langevin, D. Interfacial assembly of surfactant-decorated nanoparticles: On the rheological description of a colloidal 2D glass. Langmuir 2015, 31, 6289–6297. [Google Scholar] [CrossRef]
- Nestler, P.; Helm, C.A. Determination of refractive index and layer thickness of nm-thin films via ellipsometry. Opt. Express 2017, 25, 321–327. [Google Scholar] [CrossRef]
- Thoma, M.; Schwendler, M.; Baltes, H.; Helm, C.A.; Pfohl, T.; Riegler, H.; Mo, H. Ellipsometry and X-ray reflectivity studies on monolayers of phosphatidylethanolamine and phosphatidylcholine in contact with n-dodecane, n-hexadecane, and bicyclohexyl. Langmuir 1996, 12, 1722–1728. [Google Scholar] [CrossRef]
- Richter, R.P.; Brisson, A.R. Following the formation of supported lipid bilayers on Mica: A study combining AFM, QCM-D, and ellipsometry. Biophys. J. 2005, 88, 3422–3433. [Google Scholar] [CrossRef]
- Benjamins, J.; Thuresson, K.; Nylander, T. Ellipsometry studies of nonionic surfactant adsorption at the oil-water interface. Langmuir 2005, 21, 149–159. [Google Scholar] [CrossRef]
- Duncan, S.L.; Larson, R.G. Comparing experimental and simulated pressure-area isotherms for DPPC. Biophys. J. 2008, 94, 2965–2986. [Google Scholar] [CrossRef] [PubMed]
- Campbell, R.A.; Wacklin, H.P.; Sutton, I.; Cubitt, R.; Fragneto, G. FIGARO: The new horizontal neutron reflectometer at the ILL. Eur. Phys. J. Plus 2011, 126, 1–22. [Google Scholar] [CrossRef]
- Braun, L.; Uhlig, M.; von Klitzing, R.; Campbell, R.A. Polymers and surfactants at fluid interfaces studied with specular neutron reflectometry. Adv. Colloid Interface Sci. 2017, 247, 130–148. [Google Scholar] [CrossRef]
- Gutfreund, P.; Saerbeck, T.; Gonzalez, M.A.; Pellegrini, E.; Laver, M.; Dewhurst, C.; Cubitt, R. Towards generalized data reduction on a chopperbased time-of-flight neutron reflectometer. J. Appl. Crystallogr. 2018. [Google Scholar] [CrossRef]
- Gerelli, Y. Aurore: New software for neutron reflectivity data analysis. J. Appl. Crystallogr. 2016, 49, 330–339. [Google Scholar] [CrossRef]
- Sun, W.J.; Suter, R.M.; Knewtson, M.A.; Worthington, C.R.; Tristram-Nagle, S.; Zhang, R.; Nagle, J.F. Order and disorder in fully hydrated unoriented bilayers of gel-phase dipalmitoylphosphatidylcholine. Phys. Rev. E 1994, 49, 4665–4676. [Google Scholar] [CrossRef]
- Nagle, J.F.; Tristram-Nagle, S. Structure of lipid bilayers. Biochim. Biophys. Acta Rev. Biomembr. 2000, 1469, 159–195. [Google Scholar] [CrossRef]
- Braslau, A.; Deutsch, M.; Pershan, P.S.; Weiss, A.H.; Als-Nielsen, J.; Bohr, J. Surface roughness of water measured by x-ray reflectivity. Phys. Rev. Lett. 1985, 54, 114–117. [Google Scholar] [CrossRef]
- Sinha, S.K.; Sirota, E.B.; Garoff, S.; Stanley, H.B. X-ray and neutron scattering from rough surfaces. Phys. Rev. B 1988, 38, 2297–2311. [Google Scholar] [CrossRef]
- Maranville, B.B.; Green, A.; Kienzle, P.A. Distributed error-function roughness in refl1d reflectometry fitting program. arXiv 2018, arXiv:1801.04975. [Google Scholar]
- Szczepanowicz, K.; Bazylińska, U.; Pietkiewicz, J.; Szyk-Warszyńska, L.; Wilk, K.A.; Warszyński, P. Biocompatible long-sustained release oil-core polyelectrolyte nanocarriers: From controlling physical state and stability to biological impact. Adv. Colloid Interface Sci. 2015, 222, 678–691. [Google Scholar] [CrossRef] [PubMed]
- Conn, A.R.; Scheinberg, K.; Vicente, L.N. Introduction to Derivative-Free Optimization; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009; ISBN 0898716683. [Google Scholar]
- Dutta, S. Trust-Region Methods. In Optimization in Chemical Engineering; Cambridge University Press: Cambridge, UK, 2016; pp. 74–85. [Google Scholar]
- Yuan, Y.X. Recent advances in trust region algorithms. Math. Program. 2015, 151, 249–281. [Google Scholar] [CrossRef]
- Drude, P. The Theory of Optics; Longmans, Green, and Co.: New York, NY, USA, 1902; ISBN 0548647755. [Google Scholar]
- Nagle, J.F.; Scott, H.L. Lateral compressibility of lipid mono- and bilayers. Theory of membrane permeability. BBA Biomembr. 1978, 513, 236–243. [Google Scholar] [CrossRef]
- Daillant, J.; Bosio, L.; Benattar, J.J.; Meunier, J. Capillary waves and bending elasticity of monolayers on water studied by X-ray reflectivity as a function of surface pressure. Europhys. Lett. 1989, 8, 458. [Google Scholar] [CrossRef]
- Brumm, T.; Naumann, C.; Sackmann, E.; Rennie, A.R.; Thomas, R.K.; Kanellas, D.; Penfold, J.; Bayerl, T.M. Conformational changes of the lecithin headgroup in monolayers at the air/water interface. Eur. Biophys. J. 1994, 23, 289–295. [Google Scholar] [CrossRef]
- De Feijter, J.A.; Benjamins, J.; Veer, F.A. Ellipsometry as a Tool to Study the adsorption behavior of synthetic and biopolymers at the air- water interface. Biopolymers 1978, 17, 1759–1772. [Google Scholar] [CrossRef]
- Bringezu, F.; Majerowicz, M.; Wen, S.; Reuther, G.; Tan, K.T.; Kuhlmann, J.; Waldmann, H.; Huster, D. Membrane binding of a lipidated N-Ras protein studied in lipid monolayers. Eur. Biophys. J. 2007, 36, 491–498. [Google Scholar] [CrossRef]
- Thoma, M.; Möhwald, H. Monolayers of dipalmitoylphosphatidylcholine at the oil-water interface. Colloids Surfaces A Physicochem. Eng. Asp. 1995, 95, 193–200. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Elsevier/Academic Press: Cambridge, MA, USA, 2011; ISBN 9780123751829. [Google Scholar]
- Lu, J.R.; Thomas, R.K.; Penfold, J. Surfactant layers at the air/water interface: Structure and composition. Adv. Colloid Interface Sci. 2000, 84, 143–304. [Google Scholar] [CrossRef]
- Barradas, N.P.; Keddie, J.L.; Sackin, R. Bayesian inference analysis of ellipsometry data. Phys. Rev. E Stat. Physics Plasmas Fluids Relat. Interdiscip. Top. 1999, 59, 6138–6151. [Google Scholar] [CrossRef] [PubMed]

| Fixed Parameters | h-DPPC | cm-DPPC | d62-DPPC |
|---|---|---|---|
| Vm_heads (Å3) | 319 | 319 | 319 |
| Σbhead (10−5 Å) | 60.06 | 60.06 | 60.06 |
| SLDhead (10−6 Å−2) | 1.88 | 1.88 | 1.88 |
| Vm_tails (Å3) | 825 | 825 | 825 |
| Σbtail (10−5 Å) | −32.50 | 0 | 612.98 |
| SLDtails (10−6 Å−2) | −0.39 | 0 | 7.43 |
| ftails (%) | 100 | 100 | 100 |
| Fitting Parameters | h-DPPC, cm-DPPC, Π = 30 mN·m−1 |
|---|---|
| theads (Å) | 8.5 |
| ttails (Å) | 15.0 ± 0.5 |
| fheads (%) | 68 ± 1 |
| Atails (Å2) | 55.2 ± 0.3 |
| Aheads* (Å2) | 55.2 ± 0.3 |
| Γtails (µmol·m−2) | 3.0 ± 0.1 |
| Γheads (µmol·m−2) | 3.0 ± 0.1 |
| r (Å) | 3.0 ± 0.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrascosa-Tejedor, J.; Santamaria, A.; Pereira, D.; Maestro, A. Structure of DPPC Monolayers at the Air/Buffer Interface: A Neutron Reflectometry and Ellipsometry Study. Coatings 2020, 10, 507. https://doi.org/10.3390/coatings10060507
Carrascosa-Tejedor J, Santamaria A, Pereira D, Maestro A. Structure of DPPC Monolayers at the Air/Buffer Interface: A Neutron Reflectometry and Ellipsometry Study. Coatings. 2020; 10(6):507. https://doi.org/10.3390/coatings10060507
Chicago/Turabian StyleCarrascosa-Tejedor, Javier, Andreas Santamaria, Daniel Pereira, and Armando Maestro. 2020. "Structure of DPPC Monolayers at the Air/Buffer Interface: A Neutron Reflectometry and Ellipsometry Study" Coatings 10, no. 6: 507. https://doi.org/10.3390/coatings10060507
APA StyleCarrascosa-Tejedor, J., Santamaria, A., Pereira, D., & Maestro, A. (2020). Structure of DPPC Monolayers at the Air/Buffer Interface: A Neutron Reflectometry and Ellipsometry Study. Coatings, 10(6), 507. https://doi.org/10.3390/coatings10060507






