Abstract
In this mathematical study, magnetohydrodynamic, time-independent nanofluid flow over a stretching sheet by using the Cattaneo–Christov heat flux model is inspected. The impact of the thermal, solutal boundary and gravitational body forces with the effect of double stratification on the mass flow and heat transfer phenomena is also observed. The temperature-dependent viscosity impact on heat transfer through a moving sheet with capricious heat generation in nanofluids have studied, and the viscosity of the fluid is presumed to deviate as the inverse function of temperature. With the appropriate transformations, the system of partial differential equations is transformed into a system of nonlinear ordinary differential equations. By applying the variational finite element method, the transformed system of equations is solved. The properties of the several parameters for buoyancy, velocity, temperature, stratification, and Brownian motion parameters have examined. The enhancement in the concentration and thermal boundary layer thickness of the nanofluid sheet due to the increment in the viscosity parameter, also increased the temperature and concentration of nanoparticles. Moreover, the fluid temperature declined with the increasing values of thermal relaxation parameter. This displays that the Cattaneo–Christov heat flux model provides a better assessment of temperature distribution. Moreover, confirmation of the code and precision of the numerical method has inveterate with the valuation of the presented results with previous studies.
1. Introduction
In recent years, the dynamic research work associated with the problems of heat transfer has based on constant physical characteristics of ambient fluids. However, it is known that these characteristics might be variate with temperature, particularly for fluid viscosity. For the accurate predictions of heat transfer and flow rates, it is compulsory to take into consideration this alteration in the viscosity. The flow through a stretching sheet is a momentous problem in various engineering processes with applications in different industries, such as melt-spinning, glass fiber manufacturing, rubber sheet, plastic manufacturing, wire drawing, and metallic plates cooling in baths. Sakiadis [1] and Crane [2] described the stretching problems and fluid flow with constant temperature. Grubka, and Bobba [3] have evaluated the stretching problems for the surfaces moving with a linear velocity and with variant temperature. Banks et al. [4] inspected the flow field of a stretching wall with the power-law velocity variation. El-Hakiem [5] has deliberated the impacts of transverse flow along with variable viscosity in a micropolar fluid. Elbashbeshy et al. [6] premeditated the consequences of temperature-dependent viscosity on heat transfer through an incessant moving sheet.
In view of all the abovementioned studies, the viscidness of the fluid has been supposed to be fixed. Alhough it is well known that this physical property might be variate expressively along with the temperature, to precisely visualize the flow demeanor, it is compulsory to know this disparity of the viscosity. In earlier times, water was used as the refrigerator of fluid, but then, it did not appear that water was an impeccable refrigeration fluid after scrutinizing the required properties of the final products. Furthermore, many researchers have investigated various physical parameters such as magnetic field, injection/suction, production of heat, thermal radiation, and different types of fluids. Christov [7] added the heat flux time-derivative and reformulated the law in a hyperbolic energy equation. Recently, many researchers in the current literature on the boundary layer flow of the stretching sheet have used the non-Fourier energy equation. Salahuddin et al. [8] explored the temperature profile for the magnetohydrodynamic flow of Williamson fluid by fluctuating thickness, which displayed a decrement by the heat flux model associated with the conventional energy model. Hayat et al. [9] deliberated the stagnation point flow of Jeffrey fluid towards a nonlinearly stretching sheet. The fluid temperature reduced with the growing values of the thermal relaxation parameter. Malik et al. [10] inspected the magnetohydrodynamic Casson fluid flow and recognized that the temperature depreciated with the non-Fourier energy model. Rehman et al. [11] scrutinized the Buongiornio model and exposed the characteristics of the heat transfer and forced convective flow in the permeable stretching plate in the existence of second-order slip conditions at the interface. The Cattaneo–Christov model was accomplished by Zampoli and Tibullo [12] for an incompressible fluid. Lie et al. [13] found that the influence of the Cattaneo–Christov model for Maxwell hydro-magnetic fluid originated from the vertically moving sheet.
Nanofluids are a modern type of heat transfer fluids that have been subject to emerging research in different and innovative extents of the exploration. Nanofluids are perceived as boosting the thermal conductivity of the base fluid. The transference of heat is an elementary feature of the enormous utilization via applications that are subjected to the thermal conductivity of operational liquids as a procedure to determine the capability of thermal utilization and erection. There are a lot of periodicals on nanofluids that are apprehensive of identifying their behaviors as this could be exploited when the transfer of heat enrichment intervenes, as in quite a lot of industrial utilizations like transportation, nuclear-power reactors, electricity, as well as in bio-medicine and nutrition. Nanofluids have been confirmed where heat transfer might be truncated or enlarged. Khan et al. [14] have examined the nonlinear radiation effects on the magnetohydrodynamics flow of nanofluid through a nonlinear stretching/shrinking wedge. Bagh et al. [15] scrutinized the effect of unsteady magnetohydrodynamic nanofluid flow through a radially nonlinear stretching sheet with a viscosity-dependent temperature, convective boundary conditions, and thermo-diffusion. Alsarraf et al. [16] have explored the effect of a nanoadditive shape on the fluid flow and heat transfer aspects of -AlOOH nano-fluid flowing through a sinusoidal wavy channel. Sarafraz et al. [17] computed the heat transfer coefficient (HTC) of Fe3O4 aqueous nano-suspension at several mass concentrations of –. Asadi et al. [18] deliberated the recent advances in the preparation methods and thermophysical properties measurements of oil-based nanofluids. Pourmehran et al. [19] have investigated the nanofluid flow and heat transfer between two contracting and rotating disks. Liaqat et al. [20] described the effect of a magnetic dipole on the heat transfer phenomenon of various nanoparticles on the micropolar fluid flow through a stretching sheet. Yulin et al. [21] investigated the natural convective heat transfer of water/AlO nano-fluid in an inclined square. Sarafraz et al. [22] represented the results of various experiments conducted on the thermal performance and efficiency of an evacuated tube solar collector (ETSC). Tian et al. [23] examined the nanofluid rheological behavior of nanoparticles CuO/MWCNTs incorporated with base fluid water/ (70:30) at the temperature 20–60 C. Alsarraf et al. [24] investigated the impact of the nanoparticle shape on the fluid flow features of boehmite alumina nanofluid in a horizontal double-pipe minichannel heat exchanger. Liaqat et al. [25] explored the influence of multiple slips and the solutal boundary condition on magnetohydrodynamic unsteady bioconvective micropolar nanofluid-restrictive gyrotactic microbes, mass, and heat transference impact through the sheet. Ibrahim and Shankar [26] revealed that the heat transfer and the magnetohydrodynamic boundary layer flow of nanofluids via infiltration was able to stretch the sheet in velocity, thermal, and solutal-slip boundary conditions. Ranjbarzadeh et al. [27] in an experimental study, used an eco-friendly process to produce silica nanoparticles. Moreover, the surface and atomic structures of the nanoparticles were explored through SEM and FTIR tests. Sarafraz et al. [28] explored the flow boiling heat transfer properties of MgO/therminol nanofluid as a potential coolant on a copper-made disc. Moradikazerouni et al. [29] investigated the optimal artificial neural network (ANN) designed to evaluate the thermal conductivity enhancement of SWCNTs/EG-water nanofluid using experimental data. Das [30] investigated, through an imperative mathematical analysis on the convective heat transference narration of nanofluids through an infiltrate-able stretching sheet, the existence of partially slip, thermal buoyancy, and internal heat development/captivation. Sarafraz et al. [31] conducted an experimental study to quantify the heat transfer coefficient, thermal resistance and the thermal performance of a thermosyphon heat pipe charged with zirconia-acetone nanofluid. Sohaib et al. [32] investigated the multislip impacts of a magneto-hydrodynamic mixed convection unsteady flow of micropolar nanofluid through a stretching sheet on radiation and the heat source. Uddin et al. [33] deliberated whether free convective boundary layer flow of nanofluid through an infiltrate would be able to ascend a horizontal plate in permeable medium under thermal convective boundary conditions. Sarafraz et al. [34] explored the thermal conductivity, viscosity, and boiling heat transfer coefficient of a biologically produced nano-coolant.
The above literature remains limited regarding to investigations that is explored the influence of temperature-dependent viscosity on magneto-hydrodynamic boundary layer flow to analyze the heat transfer with double stratification through a stretching sheet in nanofluids. However, no studies have investigated the effect of temperature-dependent viscosity on magneto-hydrodynamic boundary layer nanofluid flow with double stratification using the Cattaneo–Christov heat flux model. The significance of this model is that it provides a better assessment of temperature distribution. The viscosity of the fluid is presumed to deviate as the inverse function of temperature and according to this framework, Reynold’s exponential viscosity model has been considered. The variational finite element technique has been applied to find the solution of transformed assembly equations, also using MATLAB software for programming. The aims of the present study is to scrutinize the behavior of several types of existing parameters and thermal conductivity clearly through detailed discussion. Furthermore, a numeral valuation of the existing results is displayed and reflected in figures.
2. Problem Description
Two-dimensional magnetohydrodynamic incompressible boundary layer nanofluid flow through electrically navigated elongating surface of a stretching sheet was investigated in this paper. Here, a two-coordinate system was chosen with the intention of the dimensions of the surface being designated along the x-axis and y-axis. is the velocity of the sheet, as shown in Figure 1. The stretching gives the impression that the sheet is proportionate to the distance from the origin.With the assumption that the Reynolds number is very small, a uniform magnetic of strength has been appllying perpendicularly to the sheet so that the induced magnetic field could be omitted. The wall temperature was which is given as , the concentration was , where and . The stratification temperature is and the concentration is given as where and are the area the ambient temperature and concentration of the nanofluid, respectively.
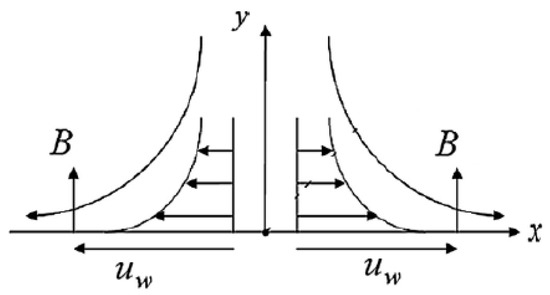
Figure 1.
Configuration of Flow.
According to the boundary layer conventions, the principal equations for flow can be inscribed as [35];
where
and , where is the thermal conductivity of the fluid and is specific heat and the proportion of capacitance of nanoparticles to the warmness capacitance of base fluid is . The velocity compartments laterally to the x-axis and y-axis are u, and v, nanofluid temperature is T, the nanoparticles volume fraction is C, the thermal relaxation time is , the electric conductivity of fluid is , the dynamic viscosity is , is the density of the base fluid, is the nanoparticles’ density, is the Brownian diffusion coefficient, and thermal diffusibility is . The coundary conditions of the above mathematical model are given as [35];
where , , and are the allusion temperature and the dimensionless quantities, respectively. The temperature at the surface, is the curie temperature and is the temperature of the fluid away from the surface. The viscosity of fluid in Equation (2), which is temperature-dependent and thus might fluctuate exponentially, can be mathematically expressed as [36] (Reynolds viscosity model), where H denotes its strength that depends on and T, where denotes the viscosity of the fluid at temperature . Normally, the stream function is stated as, and . To solve the system of Equations (1)–(4) with boundary conditions (5), we substitute the similarity transformations as shown below [37];
The components of velocity for the stream function are
By applying similarities (6) and (7) and then using Maclaurin’s series, we attain the expression as [36]
According to similarity transformations (6) and (7), the following dimensionless system is now accomplished.
where
Moreover, the boundary conditions are
The dimensionless parameters involved in Equations (9)–(11) are describes as
It can be noticed that in the case of the un-stratification of nanofluids, the system of Equations (9)–(11) is reduced to the model and the most substantial corporeal measurements are the skin friction coefficient, the Nusselt number, the Sherwood number and the explanation of these dimensionless corporal measurements is given as (Akbar et al. [38])
3. Interpretation of Method
An efficient scheme, that is, the finite element technique, was executed to find the mathematical resolution of the nonlinear scheme of differential Equations (9)–(11) by using the boundary conditions (12). This method is more efficient and reliable than other numerical techniques, such as the Adomian decomposition method (ADM), the homotopy perturbation method (HPM), and the finite-difference method (FDM). Additionally, it is very proficient and has been applied to study miscellaneous problems in fluid mechanics and computational fluid dynamics, solid mechanics, mass transfer, heat transfer, and in many other fields. The inclusive features of the finite element method are described by Reddy [39] and Gupta et al. Swapna et al. [40,41] described that with the finite element technique, a boundary value problem can be solved efficiently and accurately. To resolve the scheme of Equations (9)–(11), firstly we have to consider
Equations (9)–(11) are converted into the following form:
The correspondent boundary conditions are abbreviated to the subsequent form:
3.1. Variational Formulations
The variational form of Equations (13)–(16) over a typical two-nodded domain can be described as
where are the arbitrary weight functions that may be observed as variation in , , , , respectively and the domain represents the length of the boundary layer region.
3.2. Finite Element Formulation
Let the domain be described into the three-noded quadratic element of the finite element technique which is obtained from Equations (18)–(21) by bartering the FEM estimations as follows:
with and the quadratic shape functions are given as;
The FEM model equations are in matrix form, therefore given by
where and ( = 1,2,3,4,5) are defined as
and
where are considered to be unknown. Subsequently, the accumulation of element equations, a substantial system of nonlinear equations, is achieved. Moreover, an iterative structure is needed to resolve the system of nonlinear differential equations for an efficacious solution. At an inferior level of iterations, the functions , , , and are assumed to be known to linearize the framework and need to be accepted and proceeded for high levels until the exactness of is achieved. To accomplish autonomous work, a mesh affect-ability repetition was made. Table 1 shows the concurrence of the consequences; it is intended to enhance the number of components that are prolonged as (n = 60, 100, 180, 300, 420, 500 and 700). From the results shown in Table 1, there is no substantial disparity in the output of functions , , , and with the increasing number of components beyond 500; thus, the last results are stated for (n = 500) elements.

Table 1.
FEM convergence results of , , , and for a different number of elements when , , , , , , , .
4. Results and Discussion
This section was prepared to inspect the presentation of the dimensionless axial velocity profile , and the temperature distribution together with the concentration profile , under the influence of different emerging parameters such as the viscosity parameter , Hartman number M, Grashof number , thermophoresis parameter , Brownian motion parameter , Lewis number , and Prandtl number as shown in all the graphs. Furthermore, the acquired results of Skin friction and the Nusselt number were compared with the existing results of [42,43,44,45] and presented in the form of tables. Moreover, all the other using parameters are preserved to be fixed throughout the problem as , , , , , , . The aspect of the existing outputs and assessment of skin friction was done with accurate results that confirm the legitimacy of the finite element technique. Table 2 shows the results of heat transference proportion which were assimilated through the finite element technique and are compared with the results of previous studies as well as with the exact solutions of [42,43,44]. To ensure the accuracy of the current precise values, the conclusions attained by the finite element method for the Nusselt number for the unsteady and steady flow were compared with the calculated results from earlier studies, are shown in Table 3, which shows the current results, that is, creditable conventionality supported by current results and earlier available research that approves the intensity and exactness of the current results that were attained by the finite element method (FEM). To determine the consistency and corroborations of the results, the existing results were comprehensively assesses with [42,44,45,46] and were efficaciously simulated, as shown in Table 3.

Table 2.
Assessment of skin friction coefficient for different values of M, when , , , , , , , .

Table 3.
Comparison of for various values of when , , , , , , , .
Table 4 and Table 5 show the comparison of , and for the doubly stratified and unstratified cases; all the displayed results in this study are applicable to limited cases and are in favorable agreement with the previously published work.Here, it is shown that current results are completely concurrent and the grid invariance test is proficient to endure an exactness up to five decimal digits. The velocity profile in Figure 2 illustrates the impacts of the viscosity parameters and M on the velocity profile for both the linear and nonlinear sheets.

Table 4.
Comparison of , and for different values of when , , , , , , , .

Table 5.
Comparison of , and for different values of and when , , , , , , , ,
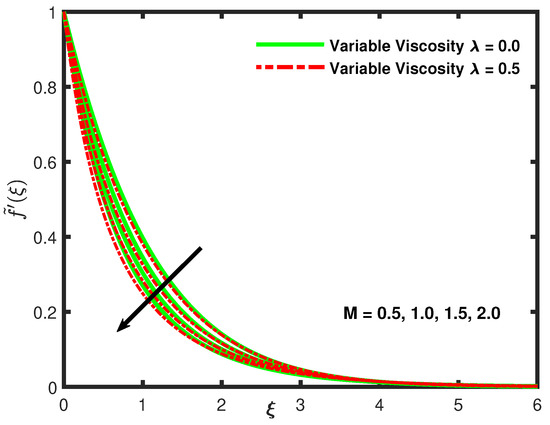
Figure 2.
The influence of Magnetic penetrability on Velocity profile.
With the increasing values of M, the velocity profile declines but there is an opposite effect on concentration and temperature profiles that can be seen from Figure 3 and Figure 4. The declaration in the velocity field is due to magnetic field that generally induces Lorentz forces which act as resistive forces and consequently oppose the fluid motion. Moreover, there is an increment in the concentration of nanoparticles and temperature; the main reason for this is the enhancement in the viscous effect with the higher viscosity, which consequently causes decrements in the fluid velocity [50].
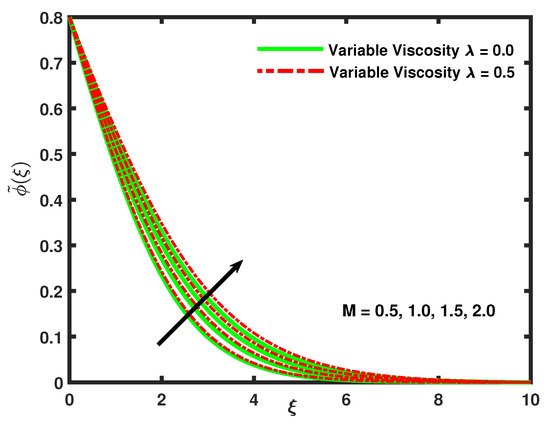
Figure 3.
The influence of Magnetic penetrability on concentration profile.

Figure 4.
The influence of Magnetic penetrability on Temperature profile.
Figure 5 clearly shows that the temperature profile declines as there is an increment in values of up to a certain distance while the momentum boundary layer thickness increases so that the heat transference process from the sheet to fluid decreases with increasing values of . Figure 6 and Figure 7 demonstrate that the temperature and nanoparticle concentration decline with the increasing values of thermal and solutal stratification parameters , and , while the thickness of the thermal boundary layer increases maximally [36].
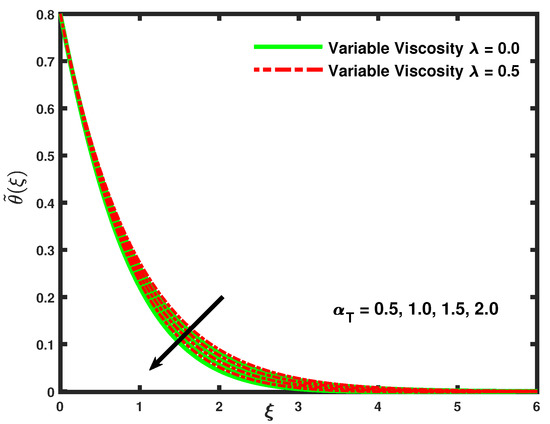
Figure 5.
The influence of thermal relaxation parameter on Temperature profile.

Figure 6.
The influence of Thermal Stratification on Temperature profile.

Figure 7.
The influence of Solutal Stratification on Concentration profile.
It is clear that with the increasing values of and , the decrement in temperature is possible so it can be controlled by controlling the values of the stratification parameters. Figure 8 and Figure 9 show the impact of the viscosity parameter and on the concentration and temperature profiles; by increasing the values of the Brownian motion parameter, the thermal boundary layer thickness increases in both cases while the effect is opposite in the concentration and temperature profiles, as in the presence of nanoparticles, the nanofluids have a better thermal conductivity compared to water as the base fluid [37].

Figure 8.
The influence of the Brownian motion parameter on the Concentration profile.

Figure 9.
The influence of the Brownian motion parameter on the Temperature profile.
From Figure 10, it can be seen that as the values of the thermophoresis parameter increase, a remarkable increment in the concentration profile is seen, and this was found throughout the boundary layer. The thermophoretic forces under the steady temperature gradient are produced by the motion of the particle and the natural phenomenon of the molecules moving from the hotter area towards the cooler region, so as a result, the temperature of the fluid increases.

Figure 10.
The influence of the thermophoresis parameter on the Concentration profile.
Figure 11 shows the impact of the thermophoresis parameter and the viscosity parameter on the dimensionless temperature profile. For the different values of the viscosity parameter, for constant viscosity parameter () and for (), with the increasing viscosity, the temperature profile shows an intensifying performance [5].
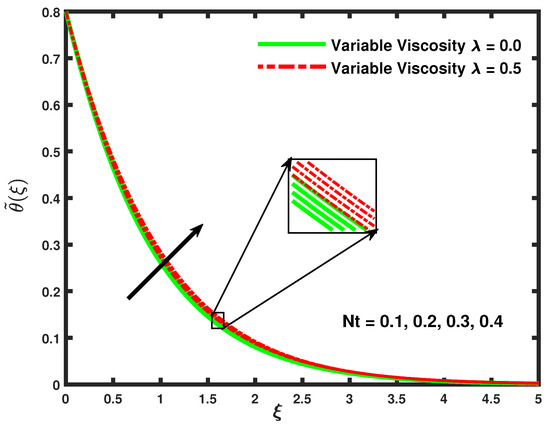
Figure 11.
The influence of thermophoresis parameter on Temperature profile.
From Figure 12 and Figure 13 one can perceive an intensification in the velocity profile as the values of the buoyancy parameters and are cumulative. Nevertheless, the extensiveness of the momentum boundary layer deteriorates. For , the buoyancy forces associated with the nanoparticle types in Equation (13) reduce. However, the non zero values of show that the velocity profile is exceedingly close to the stretching wall. Thus, in turn, the momentum grows inside the boundary layer so that it elevates the fluid velocity. Moreover, from Figure 12 and Figure 13, the elevation in the viscid parameter creates an obstacle in the fluid motion and because of this, the fluid velocity declines and the thickness of the momentum boundary layer increases. Figure 14, Figure 15 and Figure 16 reveals the impact of the magnetic parameter M and the viscosity parameter on the Nusselt number (Nur), Sherwood number (Shr) and on the Skin friction. It can be seen that with the increasing values of the magnetic parameter M, the values of the Nusselt number (Nur), the Sherwood number (Shr), and the Skin friction coefficient decrease. Moreover, this reduces the thermal boundary layer in the case of the Nusselt number (Nur) and the Sherwood number (Shr) but the effect is opposite on the Skin friction coefficient. The magnetic parameter M is characteristic of fluid flow, which causes instantaneous heat and mass transferences by convection. Lastly, it was found that the heat transfer rate declines as the values of the magnetic parameter M increase. The observed decrement in temperature profile is due to temperature difference reasonably decaying between the surface and away from the sheet. Thus, the change in values of the thermal stratification parameter causes an increase in the density of the fluid layers, which leads the dense particles toward the surface and creates more magnetohydrodynamic interaction, due to which a decrement occurs in heat transference.

Figure 12.
The influence of the Buoyancy parameter on the Velocity profile.

Figure 13.
The influence of the Buoyancy parameter on the Velocity profile.

Figure 14.
The influence of Magnetic penetrability on Nusselt number.
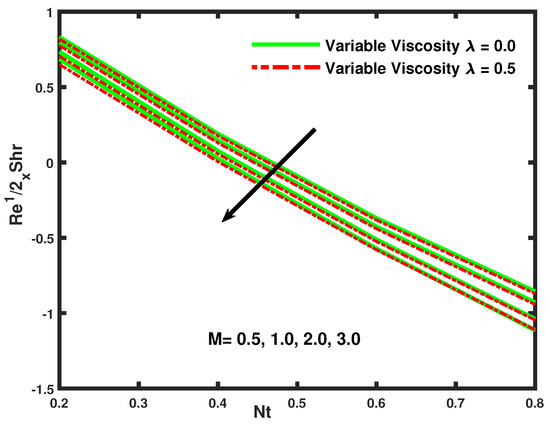
Figure 15.
The influence of Magnetic penetrability on the Sherwood number.

Figure 16.
The influence of Magnetic penetrability on Skin friction.
5. Concluding Remarks
This article incorporates the theoretical study associated with the magnetohydrodynamic flow and heat transfer of the doubly stratified nanofluid with buoyancy forces and temperature-dependent viscosity impacts and also used a Cattaneo–Christov Heat flux model. The mathematical model (partial differential equations) was transformed into the system of ordinary differential equations by using the suitable transformations. The finite element method (FEM) was selected to solve the consequential boundary value problem and the subsequent results were compared with the previous studies. Furthermore, the graphical pictures demonstrating the influence of numerous evolving parameters on the momentum, mass, and heat transference properties were discussed. Below are the foremost conclusions from this study:
- The increasing values of M and the viscosity parameter decrease the nanofluid velocity magnitude; however, there is a contrary impact on the concentration and temperature distributions.
- The increase in the concentration and thermal boundary layer thickness of the nanofluid sheet due to the increment in the viscosity parameter also increases the temperature and concentration of nanoparticles.
- Fluid temperature declines with increasing values of the thermal relaxation parameter. This shows that the Cattaneo–Christov heat flux model provides a better assessment of temperature distribution.
- The magnitude of the Nusselt number and the Sherwood number declines, and the thermal boundary layer thickness is reduced with increasing values of magnetic M and viscosity parameters.
- The increasing values of the Brownian motion parameter cause a decline in the nanoparticle concentration profile whereas for thermophoresis parameter , the results are contrary.
- The thermal relaxation parameter effectively increases the rate of heat transfer of the flow.
Author Contributions
L.A. modeled the problem and wrote the manuscript. X.L. thoroughly checked the mathematical modeling and English corrections. B.A. helped in MATLAB coding. X.L. contributed to the results and discussions. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 51676152) and Fundamental Research Funds for the Central Universities (No. zrzd2017012).
Acknowledgments
The first author acknowledge with thanks Xiaomin Liu for his continuous guidance throughout the work at Xi’an Jiaotong University, Xi’an, China.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Viscosity of fluid | |
| Thermal Stratification | |
| Solutal Stratification | |
| Dimensionless parameters | |
| Buoyancy parameters | |
| Brownian diffusion coefficient | |
| Brownian motion parameter | |
| Curie temperature | |
| Lewis number | |
| Thermal conductivity of fluid | |
| Nanoparticle’s density | |
| Specific heat | |
| Prandtl number | |
| Thermal Grashof number | |
| Thermophoresis parameter | |
| Thermal relaxation parameter | |
| Thermal diffusibility | |
| Velocity components | |
| Velocity of sheet | |
| Temperature at surface | |
| Local Reynold number | |
| T | Non-dimensional temperature |
| M | Magnetic penetrability |
| Conductivity of fluid | |
| Thermal relaxation parameter | |
| Variable viscosity parameter | |
| Fluid density | |
| Temperature away from the surface |
References
- Sakiadis, B. Boundary-layer behavior on continuous solid surfaces: II. The boundary layer on a continuous flat surface. AiChE J. 1961, 7, 221–225. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Für Angew. Math. Und Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Grubka, L.; Bobba, K. Heat transfer characteristics of a continuous, stretching surface with variable temperature. J. Heat Transf. 1985, 107, 248–250. [Google Scholar] [CrossRef]
- Banks, W.; Zaturska, M. Eigensolutions in boundary-layer flow adjacent to a stretching wall. IMA J. Appl. Math. 1986, 36, 263–273. [Google Scholar] [CrossRef]
- El-Hakiem, M. Effects of a transverse flows with variable viscosity in micropolar fluids. Heat Mass Transf. 1998, 34, 91–99. [Google Scholar] [CrossRef]
- Elbashbeshy, E.; Bazid, M. The effect of temperature-dependent viscosity on heat transfer over a continuous moving surface. J. Phys. D Appl. Phys. 2000, 33, 2716. [Google Scholar] [CrossRef]
- Christov, C. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Salahuddin, T.; Malik, M.Y.; Hussain, A.; Bilal, S.; Awais, M. MHD flow of Cattanneo–Christov heat flux model for Williamson fluid over a stretching sheet with variable thickness: Using numerical approach. J. Magn. Magn. Mater. 2016, 401, 991–997. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Alsaedi, A.; Waqas, M.; Yasmeen, T. Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Transf. 2016, 99, 702–710. [Google Scholar] [CrossRef]
- Malik, M.; Khan, M.; Salahuddin, T.; Khan, I. Variable viscosity and MHD flow in Casson fluid with Cattaneo–Christov heat flux model: Using Keller box method. Eng. Sci. Technol. Int. J. 2016, 19, 1985–1992. [Google Scholar] [CrossRef]
- Rahman, M.; Roşca, A.; Pop, I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking/stretching surface with second order slip using Buongiorno’s model. Int. J. Heat Mass Transf. 2014, 77, 1133–1143. [Google Scholar] [CrossRef]
- Tibullo, V.; Zampoli, V. A uniqueness result for the Cattaneo–Christov heat conduction model applied to incompressible fluids. Mech. Res. Commun. 2011, 38, 77–79. [Google Scholar] [CrossRef]
- Li, J.; Zheng, L.; Liu, L. MHD viscoelastic flow and heat transfer over a vertical stretching sheet with Cattaneo-Christov heat flux effects. J. Mol. Liq. 2016, 221, 19–25. [Google Scholar] [CrossRef]
- Khan, U.; Ahmed, N.; Mohyud-Din, S.T.; Bin-Mohsin, B. Nonlinear radiation effects on MHD flow of nanofluid over a nonlinearly stretching/shrinking wedge. Neural Comput. Appl. 2017, 28, 2041–2050. [Google Scholar] [CrossRef]
- Ali, B.; Naqvi, R.A.; Nie, Y.; Khan, S.A.; Sadiq, M.T.; Rehman, A.U.; Abdal, S. Variable Viscosity Effects on Unsteady MHD an Axisymmetric Nanofluid Flow over a Stretching Surface with Thermo-Diffusion: FEM Approach. Symmetry 2020, 12, 234. [Google Scholar] [CrossRef]
- Vo, D.D.; Alsarraf, J.; Moradikazerouni, A.; Afrand, M.; Salehipour, H.; Qi, C. Numerical investigation of γ-AlOOH nano-fluid convection performance in a wavy channel considering various shapes of nanoadditives. Powder Technol. 2019, 345, 649–657. [Google Scholar] [CrossRef]
- Sarafraz, M.; Pourmehran, O.; Yang, B.; Arjomandi, M.; Ellahi, R. Pool boiling heat transfer characteristics of iron oxide nano-suspension under constant magnetic field. Int. J. Therm. Sci. 2020, 147, 106131. [Google Scholar] [CrossRef]
- Asadi, A.; Aberoumand, S.; Moradikazerouni, A.; Pourfattah, F.; Żyła, G.; Estellé, P.; Mahian, O.; Wongwises, S.; Nguyen, H.M.; Arabkoohsar, A. Recent advances in preparation methods and thermophysical properties of oil-based nanofluids: A state-of-the-art review. Powder Technol. 2019, 352, 209–226. [Google Scholar] [CrossRef]
- Pourmehran, O.; Sarafraz, M.; Rahimi-Gorji, M.; Ganji, D. Rheological behaviour of various metal-based nano-fluids between rotating discs: A new insight. J. Taiwan Inst. Chem. Eng. 2018, 88, 37–48. [Google Scholar] [CrossRef]
- Ali, L.; Liu, X.; Ali, B.; Mujeed, S.; Abdal, S.; Khan, S.A. Analysis of Magnetic Properties of Nano-Particles Due to a Magnetic Dipole in Micropolar Fluid Flow over a Stretching Sheet. Coatings 2020, 10, 170. [Google Scholar] [CrossRef]
- Ma, Y.; Shahsavar, A.; Moradi, I.; Rostami, S.; Moradikazerouni, A.; Yarmand, H.; Zulkifli, N.W.B.M. Using finite volume method for simulating the natural convective heat transfer of nano-fluid flow inside an inclined enclosure with conductive walls in the presence of a constant temperature heat source. Phys. A Stat. Mech. Appl. 2019, 123035. [Google Scholar] [CrossRef]
- Sarafraz, M.; Safaei, M.R. Diurnal thermal evaluation of an evacuated tube solar collector (ETSC) charged with graphene nanoplatelets-methanol nano-suspension. Renew. Energy 2019, 142, 364–372. [Google Scholar] [CrossRef]
- Tian, Z.; Rostami, S.; Taherialekouhi, R.; Karimipour, A.; Moradikazerouni, A.; Yarmand, H.; Zulkifli, N.W.B.M. Prediction of rheological behavior of a new hybrid nanofluid consists of copper oxide and multi wall carbon nanotubes suspended in a mixture of water and ethylene glycol using curve-fitting on experimental data. Phys. A Stat. Mech. Appl. 2020, 124101. [Google Scholar] [CrossRef]
- Alsarraf, J.; Moradikazerouni, A.; Shahsavar, A.; Afrand, M.; Salehipour, H.; Tran, M.D. Hydrothermal analysis of turbulent boehmite alumina nanofluid flow with different nanoparticle shapes in a minichannel heat exchanger using two-phase mixture model. Phys. A Stat. Mech. Appl. 2019, 520, 275–288. [Google Scholar] [CrossRef]
- Ali, L.; Liu, X.; Ali, B.; Mujeed, S.; Abdal, S. Finite Element Simulation of Multi-Slip Effects on Unsteady MHD Bioconvective Micropolar nanofluid Flow Over a Sheet with Solutal and Thermal Convective Boundary Conditions. Coatings 2019, 9, 842. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids 2013, 75, 1–10. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Moradikazerouni, A.; Bakhtiari, R.; Asadi, A.; Afrand, M. An experimental study on stability and thermal conductivity of water/silica nanofluid: Eco-friendly production of nanoparticles. J. Clean. Prod. 2019, 206, 1089–1100. [Google Scholar] [CrossRef]
- Sarafraz, M.; Arya, H.; Saeedi, M.; Ahmadi, D. Flow boiling heat transfer to MgO-therminol 66 heat transfer fluid: Experimental assessment and correlation development. Appl. Therm. Eng. 2018, 138, 552–562. [Google Scholar] [CrossRef]
- Moradikazerouni, A.; Hajizadeh, A.; Safaei, M.R.; Afrand, M.; Yarmand, H.; Zulkifli, N.W.B.M. Assessment of thermal conductivity enhancement of nano-antifreeze containing single-walled carbon nanotubes: Optimal artificial neural network and curve-fitting. Phys. A Stat. Mech. Appl. 2019, 521, 138–145. [Google Scholar] [CrossRef]
- Das, K. Slip flow and convective heat transfer of nanofluids over a permeable stretching surface. Comput. Fluids 2012, 64, 34–42. [Google Scholar] [CrossRef]
- Sarafraz, M.; Pourmehran, O.; Yang, B.; Arjomandi, M. Assessment of the thermal performance of a thermosyphon heat pipe using zirconia-acetone nanofluids. Renew. Energy 2019, 136, 884–895. [Google Scholar] [CrossRef]
- Abdal, S.; Ali, B.; Younas, S.; Ali, L.; Mariam, A. Thermo-Diffusion and Multislip Effects on MHD Mixed Convection Unsteady Flow of Micropolar Nanofluid over a Shrinking/Stretching Sheet with Radiation in the Presence of Heat Source. Symmetry 2020, 12, 49. [Google Scholar] [CrossRef]
- Uddin, M.J.; Khan, W.; Ismail, A.M. Free convection boundary layer flow from a heated upward facing horizontal flat plate embedded in a porous medium filled by a nanofluid with convective boundary condition. Transp. Porous Media 2012, 92, 867–881. [Google Scholar] [CrossRef]
- Sarafraz, M.; Arya, A.; Nikkhah, V.; Hormozi, F. Thermal performance and viscosity of biologically produced silver/coconut oil nanofluids. Chem. Biochem. Eng. Q. 2016, 30, 489–500. [Google Scholar] [CrossRef]
- Besthapu, P.; Haq, R.U.; Bandari, S.; Al-Mdallal, Q.M. Mixed convection flow of thermally stratified MHD nanofluid over an exponentially stretching surface with viscous dissipation effect. J. Taiwan Inst. Chem. Eng. 2017, 71, 307–314. [Google Scholar] [CrossRef]
- Disu, A.; Dada, M. Reynold’s model viscosity on radiative MHD flow in a porous medium between two vertical wavy walls. J. Taibah Univ. Sci. 2017, 11, 548–565. [Google Scholar] [CrossRef][Green Version]
- Akbar, N.S.; Tripathi, D.; Khan, Z.H.; Bég, O.A. A numerical study of magnetohydrodynamic transport of nanofluids over a vertical stretching sheet with exponential temperature-dependent viscosity and buoyancy effects. Chem. Phys. Lett. 2016, 661, 20–30. [Google Scholar] [CrossRef]
- Akbar, N.S. Ferromagnetic CNT suspended H2O+ Cu nanofluid analysis through composite stenosed arteries with permeable wall. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 72, 70–76. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method; TMH: New York, NY, USA, 1993. [Google Scholar]
- Gupta, D.; Kumar, L.; Beg, O.A.; Singh, B. Finite Element Analysis of Transient Heat and Mass Transfer in Mircostructural Boundary layer Flow from a Porous Stretching Sheet. Comput. Therm. Sci. Int. J. 2014, 6, 155–169. [Google Scholar] [CrossRef]
- Swapna, G.; Kumar, L.; Rana, P.; Singh, B. Finite element modeling of a double-diffusive mixed convection flow of a chemically-reacting magneto-micropolar fluid with convective boundary condition. J. Taiwan Inst. Chem. Eng. 2015, 47, 18–27. [Google Scholar] [CrossRef]
- Ali, L.; Liu, X.; Ali, B.; Mujeed, S.; Abdal, S. Finite Element Analysis of Thermo-Diffusion and Multi-Slip Effects on MHD Unsteady Flow of Casson Nano-Fluid over a Shrinking/Stretching Sheet with Radiation and Heat Source. Appl. Sci. 2019, 9, 5217. [Google Scholar] [CrossRef]
- Jalil, M.; Asghar, S.; Yasmeen, S. An exact solution of MHD boundary layer flow of dusty fluid over a stretching surface. Math. Probl. Eng. 2017, 2017, 2307469. [Google Scholar] [CrossRef]
- Ali, B.; Nie, Y.; Khan, S.A.; Sadiq, M.T.; Tariq, M. Finite Element Simulation of Multiple Slip Effects on MHD Unsteady Maxwell Nanofluid Flow over a Permeable Stretching Sheet with Radiation and Thermo-Diffusion in the Presence of Chemical Reaction. Processes 2019, 7, 628. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Boundary layer flow and heat transfer over an unsteady stretching vertical surface. Meccanica 2009, 44, 369–375. [Google Scholar] [CrossRef]
- Pal, D. Combined effects of non-uniform heat source/sink and thermal radiation on heat transfer over an unsteady stretching permeable surface. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1890–1904. [Google Scholar] [CrossRef]
- Abbasi, F.; Shehzad, S.; Hayat, T.; Alhuthali, M. Mixed convection flow of jeffrey nanofluid with thermal radiation and double stratification. J. Hydrodyn. Ser. B 2016, 28, 840–849. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Anwar, M.; Khan, I.; Sharidan, S.; Salleh, M. Conjugate effects of heat and mass transfer of nanofluids over a nonlinear stretching sheet. Int. J. Phys. Sci. 2012, 7, 4081–4092. [Google Scholar] [CrossRef]
- Anantha Kumar, K.; Ramadevi, B.; Sugunamma, V. Impact of Lorentz force on unsteady bio convective flow of Carreau fluid across a variable thickness sheet with non-Fourier heat flux model. In Defect and Diffusion Forum; Trans Tech Publ: Zurich, Switzerland, 2018; Volume 387, pp. 474–497. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).