Abstract
The cold spray coating properties and performances are largely affected by feedstock characteristics and the employed processing parameters. Starting from experimental results obtained from the bibliographic data, the relationships between starting particles, processing conditions, and coating properties obtained by cold gas spray were analyzed. The relationships among these properties and particle velocity were described for various material systems. The effect on particle flattening, hardness, and porosity were largely described. Finally, the influence of the different parameters on the process output and on the coating properties was analytically defined through the employment of the multi-objective simulation tool modeFRONTIER. The analysis of data from the bibliography is a new trend that can also be applied to cold spray in order to analyze the effect of powder properties and spraying parameters on the cold spray (CS) process.
1. Introduction
Cold spray (CS), developed and studied over the last 15 years, has been established as a very powerful additive manufacturing technology for coatings or bulk production [1]. Among its many applications, cold spray has become very effective in modern industries for repairing tasks [2]. Despite the availability of different commercial cold spray machines, there is still great interest in studying the in-flight behavior and the deformation mechanisms of feedstock particles during the process in order to extend cold spray technology to different metals and alloys. For this, the deposit formation must be considered to occur in two consecutive steps. In the initial stage, the first impacting particles adhere to the substrate; in the following step, a coating layer is grown due to the further adhesion of particles to this first layer of adhered particles [3]. In both steps, different microstructural mechanisms, such as atomic and metallurgical bonding as well as interparticle cohesion, are a consequence of the severe plastic deformation and adiabatic shear instability of particles experienced during the impact. However, knowledge of bonding mechanisms in CS remains an interesting and open field of research [4]. It is widely accepted that adhesion of the sprayed particles to the substrate is due to the phenomenon of heteroepitaxy (one kind of crystal is grown upon the surface of a different type) and adiabatic shearing. These phenomena lead to dynamic recrystallization that causes metallurgical bonding, mechanical anchoring, mechanical interlocking, and interfacial mixing, as well as the formation of hard amorphous layers at the substrate-coating interfaces [5,6,7,8].
Given that many types of materials can be deposited through cold spray, and that many new and promising examples are continuously presented in the literature, various processing routes have been investigated to optimize the overall process. It is known that the nozzle dimensions (short or long) and materials (such as WC, glass, or SiC), the propellant gas (N2 or He), the spraying temperature, and the pressure, as well as the powder particles’ morphology and density, directly influence gas flow inside the nozzle. Thus, many spraying parameters are involved in the in-flight behavior and the impact conditions of particles [9].
Particle impact velocity is recognized as one of the most relevant parameters (among all processing conditions) governing cold sprayed deposit formation, growth, and final mechanical and microstructural properties. For this reason, many diagnostic tools have been developed to monitor this parameter based on in-flight particle behavior [10]. Many finite element modeling (FEM) studies that predict the in-flight and impact conditions for various cold spray settings can be found in the literature [11,12]. In these studies, the gas–particle interaction and impact conditions are modeled by means of complex equations as a function of physical parameters such as the gas densities, particle morphology, mechanical properties, and microstructure of coatings and/or substrate influence [13,14].
In these models, the equations can be solved by the force and momentum balances for every single particle [13,14]. Another important aspect of cold spray is heat transfer during particle deformation. Many scientific studies highlight that this heat transfer is directly dependent on the impact velocity, which also influences the final coating hardness and porosity [15,16]. Thus, many complex models capable of accurately predicting particle velocity, as an explicit function of different spraying parameters (mainly pressure, temperature, and particle morphology), can be found in the literature [17,18]. The coatings’ microstructure and properties can be largely modified by tuning all the involved processing parameters [19,20].
The aim of the present study is to analyze the relationships between processing parameters and coating properties in cold spray to obtain a simple model capable of describing coating properties as a function of different process parameters. This is possible by employing the well-known multi-objective simulation tool modeFRONTIER. modeFRONTIER is an integration platform for multi-objective and multi-disciplinary optimization. It provides seamless coupling with third-party engineering tools, enables automation of the design simulation process, and facilitates analytic decision making. This powerful workflow enables the execution of complex chains of design optimization, innovative algorithms that determine the set of best possible solutions by combining opposing objectives, and post-processing tools that allow the user to perform sophisticated statistical analysis and data visualization.
The coating formation analyses were carried out for the main metals and alloys used in cold spray technology based on the experimental data described in the literature. For this reason, the present work uses a broad range of materials, with different densities, particle dimensions, and spraying parameters. Analysis of data from the bibliography is a new trend that can also be applied to cold spray in order to analyze the effect of powder properties and spraying parameters on the CS process. On the one hand, experimental data gathered from the literature has the advantage of being able to process large amounts of data; on the other hand, special attention must be paid to the heterogeneity of these data. In this bibliographic research, there are several sources of uncertainty (using different equipment and nozzles for example). In this study, we propose new combinations of parameters that would allow us to simplify the understanding of the data.
2. Materials and Methods
The material properties and processing parameters considered for this study for all material systems are listed in Table 1. This table presents the large amount of experimental data collected from the literature for this study in order to achieve a good relationship between the processing parameters and coating properties in cold spray for as many materials as possible.

Table 1.
Materials and processing conditions employed for the present study.
For the calculations, only experimental measurements or calculations supported by experimental validation were recorded. Thus, data from finite element models were not used for the calculation carried out in this study.
It has been demonstrated that irregularly shaped powders show broader distributions of particle impact velocity than spherical particles [67]. For this reason, only spherical particles were considered for the calculations in this study. The spraying temperature and pressure were considered as the main parameters for evaluating the effects of the spraying parameters on impact velocity. Notably, experimental results using nitrogen, helium, air, argon, and/or a mixture of these gases as propellant gases were employed for the calculations. Propellant gas properties are crucial for achieving high deposition efficiency and high-quality coatings by cold spray. Thus, temperature and pressure were considered to calculate the gas properties (mainly density) during spray in every situation, and the values of the different gas densities as a function of their temperature were used for building the database.
The database was built by introducing the input parameters, the corresponding output for each processing condition to be experimentally analyzed, and the physical correlations between the different conditions. The overall process is outlined in the workflow for the analysis carried out by modeFRONTIER (version 5.6.0.1, Figure 1).
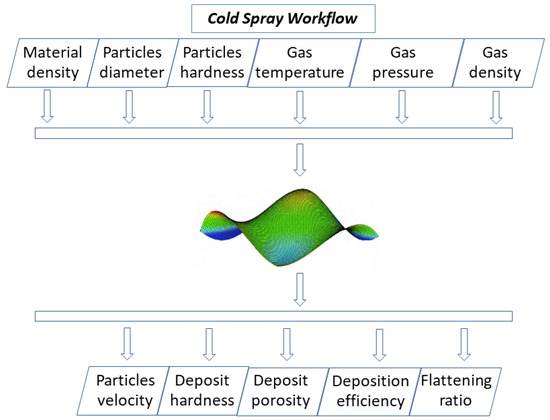
Figure 1.
Workflow of the performed analyses.
modeFRONTIER enables multidisciplinary engineering practices to consolidate specialized expertise and streamline teamwork by allocating software resources where needed. Depending on the step of the engineering problem at hand, it is possible to access different functionalities within the same installation through dedicated modules or directly in modeFRONTIER, according to the profile of the user. The workflow is divided into data flow and logic flow, which have a common node (calculator node), in which the mathematical functions representative of the process are introduced. In the data flow, all the parameters that should be analyzed in numerical simulations are introduced: material density, particle dimensions, particle hardness, gas temperature, gas pressure, and gas density. The output variables have multipurpose definitions and have been minimized or maximized considering some constraints or limitations typical of the actual process. Here, the nodes that comprise the logic flow of numerical analysis are defined [68,69]. The first node is the design of experiments (DoE), which is the set of designs from which the different possible working conditions are analyzed. This means achieving a set number of designs that will be used by the scheduler (the node where the best algorithm is introduced) for optimization. In the present case, the most appropriate method of assessment is the fractional factorial method. This is a very common method that assumes high order interactions are not significant. The core workflow is a specific response surface, which is the only node in common between the logical flow and data flow. For each output variable to be minimized, it is necessary to create a response surface. The next step is to evaluate the performance surface and use it as a node operator in our workflow. The available tools are the ones offered by modeFRONTIER, including the response surface method (RSM) distance, the RSM residual, and RSM function plot. After an analysis of all areas, carried out through the different tools proposed in the design space of the mF panel, the optimal condition for the analysis of all output variables can be chosen. Specifically, once the individual objectives would be unable to attain their own optimum levels; here, a set of best possible compromises between them represents the optimum, and the locus of these solutions is known as the Pareto frontier. After the RSM has been built for the output variables, it is possible to use the surrogate model to evaluate the performance of pins instead of the real solver. Since the design evaluation using RSM is very fast, a massive optimization of the design space is performed by using the response surface. Thus, virtual optimization is the optimization carried out by running the problem on the surrogate model. At the end of the virtual optimization, the best so-far designs (those that belong to the Pareto frontier) are re-calculated by running the real solver. This process is named validation of the response surface (Figure 2).
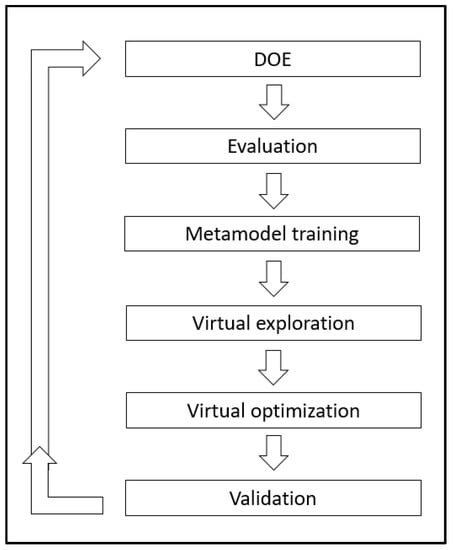
Figure 2.
Calculations schematic.
These choices lead to the use of radial basis function (RBF)-type surfaces with the MultiQuadrics Hardy’s radial function. New designs fill the entire range of analysis. For each objective and each constraint, a different set of RSM is trained, whose fitness quality is checked independently to guarantee the usage of the best RSM in every single case. These designs are introduced to the response surface established in the first step of the study. In this way, mF generates a determined number of working parameters that lead to a particular goal. At this point, the user has to choose the set of inputs that optimizes the value of each output, considering the physical and technological constraints. Specifically, the network is capable of identifying significant inputs through a simple probabilistic procedure. The computation starts with a population of neural networks, each having a different topology and combination of weights, and the same data set is run through them. The algorithm includes also a local refinement around the best solutions to improve the accuracy of the solutions. At this point, the best solutions thus obtained, pertaining to the Pareto frontier, can be validated through real-time expensive simulations, updating in this way the database used for the RSM training. At each iteration the newly evaluated designs enrich the training database, permitting a more and more accurate RSM to be built in an adaptive and iterative way.
The main goal of these analyses is to calculate the weights that each parameter has for one selected output. The methodological approach used was an empirical approach without a pre-allocated analytical framework. The experimental data, after being appropriately filtered and reordered, are then processed to build metamodels representative of the n-dimensional phenomena by referring to an experimental database. This meta-model can be considered a black box capable of providing the desired output values of the variables following the introduction of the input variables. Through the use of the evolutionary design (ED) algorithm, which provides the output’s analytical expression, the equations simulating the processes have been obtained and validated.
3. Results and Discussion
The aim of this study was to obtain the simple correlation between the impact particle velocity and all the spraying parameters affecting in-flight particle behavior. For this correlation, it was necessary to design a parameter called the “process parameter” that incorporates the main properties of the materials being propelled and the gas propellant, as well as the particles’ morphologies. In this way, a simple parameter can take into consideration the most important variables related to spray behavior, and this parameter allows both the particles and the gas properties to be concentrated. Thus, the process parameter was developed considering the densities of the gas and materials, the particles’ diameters, and was calculated according to Equation (1):
where ρp is the material density, d is the particle diameter, P is the gas pressure, and ρg is the gas density in the spray conditions.
Figure 3 shows the evolution of impact velocity particles for the selected cold sprayed materials as a function of the “process parameter”. As stated above, the data considered to calculate the process parameter are included in Table 1.
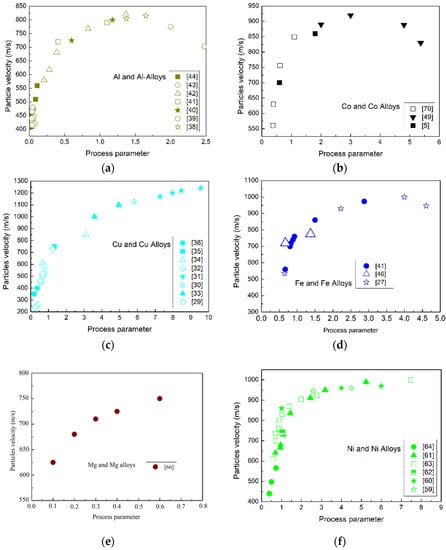
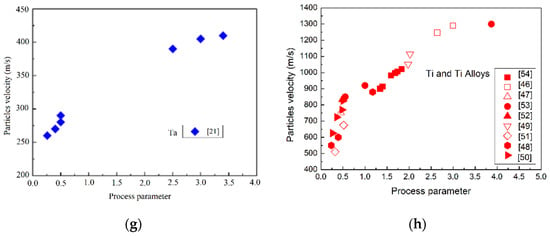
Figure 3.
Particle velocity vs. process parameter for the different pure metals and alloys analyzed in the present study. (a) Al and Al Alloys [38,39,40,41,42,43,44], (b) Co and Co Alloys [5,49,70], (c) Cu and Cu Alloys [29,30,31,32,33,34,35,36], (d) Fe and Fe Alloys [27,41,46], (e) Mg and Mg Alloys [66], (f) Ni and Ni Alloys [59,60,61,62,63,64], (g) Ta [21], (h) Ti and Ti Alloys [46,47,48,49,50,51,52,53,54].
In these figures, it can be observed that, independent of the alloys, all the plots show a similar correlation between the particle impact velocity and the process parameter. Thus, in all these profiles, a sharp increase in the particles’ impact velocities are observed by increasing the process parameter up to a maximum value for particle impact velocity. After this maximum, the particle velocity decreases according to higher values of the process parameter.
It is accepted that deposition behavior has been always related to the impact velocity of cold spray. High impact velocity is considered to favor adiabatic shear instability during impact. This phenomenon leads to optimal material deformation and facilitates particle–interface bonding due to the interlocking between the particles and metallurgical junctions. Bonding is achieved once an impacting particle accelerates over the previously established critical velocity. In this way, it is possible to identify a process window able to produce particle bonding by coupling both the impact temperature and velocity [71,72,73]. These plots show that the particle velocity is managed by spraying parameters (the material and gas properties and spraying pressure and temperature). On the one hand, the particle acceleration in the nozzle scales with gas density. For this reason, a particle acceleration limit has been found in cold spray when N2 and air are used as propellant gases. This limit, however, can be overcome by employing a mix with He gas or pure He as carrier [74]. Additionally, particle sizes are not totally homogeneous in feedstock materials, and, as a result, particle temperature changes with the particle dimensions. All these properties are included in the process parameter and the plots show that when the spraying parameter is not correct, deposition leads to the incomplete bonding of all the particles, which directly affects deposition efficiency, as will be shown in the following.
As expected, despite the fact that all the materials show a similar correlation between the impact velocity and the new process parameter, in these figures, it can be observed that there are some differences among the materials used for this study for the maximum impact velocity position and/or the growth of impact velocity as a function of the process parameter. To facilitate understanding of this comparison, Figure 4 presents a summary of the cold sprayed impact velocity as a function of the process parameter (Equation (1)), for all the studied materials.
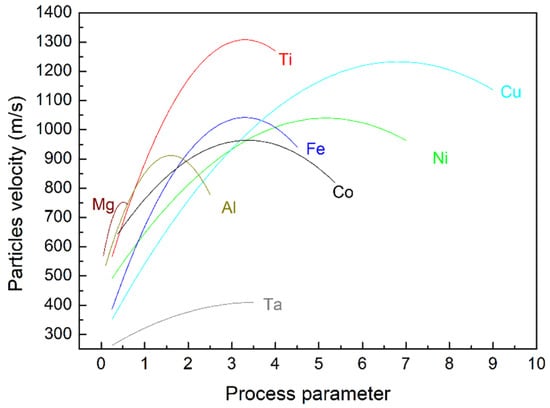
Figure 4.
Particle impact velocity as a function of the process parameter for all the studied alloys [71,72,73,75,76].
The particle impact velocity seems to drastically increase for the light materials (Mg, Al, Ti, and their alloys) and for low process parameters values. Furthermore, for these materials, the particle velocity decreases very rapidly after reaching the maximum value of particle velocity. These results indicate that as material density increases, a higher process parameter is needed to increase the particle velocity. However, for materials with high density, there is a broad range of process parameters for which the impact velocity is close to the maximum value.
As noted by many researchers, the dependence of particle velocity on processing conditions does not follow a linear behavior [75,76]. For this reason, research on the effects of spraying conditions on overall process behavior and coating formation remains incomplete from many perspectives. In addition, many interesting results have emerged from finite element modeling studies. Many of these models are conducted by simplifying the parameters used during spray, yielding results that are not always close to the experimental conditions. Consequently, the present study has chosen to use only data belonging to experimental observations.
In order to eliminate the effect of the density of the sprayed material on this relationship, the process parameter was normalized with respect to the material density; the correlation of the normalized process parameter and particle velocities are included in Figure 5a. This allowed us to obtain a common fitting curve capable of predicting the particles’ in-flight and impact behavior under a wide range of spraying conditions. A similar approach was employed in [18], where the authors considered that by multiplying the particle diameter by the material density, it is possible to obtain a material independent parameter, which could be directly related to the particle velocity.
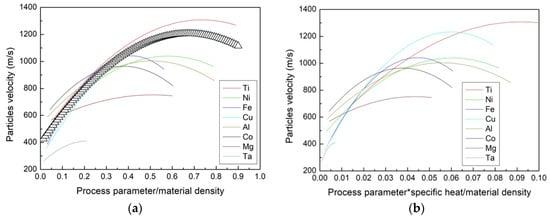
Figure 5.
(a) Relationship between the particle velocity and (b) the process parameter normalized over the particle density. The black triangles define the common fitting curve.
In addition, the authors estimated that the squared particle diameter multiplied by the material density and specific heat could be considered a material independent combination parameter, which could be related to the particle temperature. For comparison, the data used in this study have also been plotted while taking into consideration the sprayed material’s specific heat expressed in kcal/(kg·°C) (Figure 5b). It is known that the rate at which a material loses heat after impact plays an important role in bonding. In this sense, the cooling rate of the material is affected by particle size, the heat capacity of the spraying material, and its thermal conductivity. The cooling rate should be “low enough” to promote shear instability but “high enough” to allow the interface to cool down quickly and complete the bonding process. Shear instability can be hindered in small particles due to high thermal gradients with their surroundings [20,77].
The deposition efficiency of the selected data (Table 1) was plotted as a function of the process parameter and as a function of the process parameter normalized to the material density (Figure 6). Deposition efficiency increases with both the process parameter and the normalized values up to a maximum; then, it decreases for all materials, showing behavior similar to the behavior previously described for the particle velocity. This result can be explained by the increase of no-bonded particles as the impact velocity is outside of the optimal processing window, which indicates when the impact velocity is lower or higher than the critical velocity. In cold spray, not all particles can be accelerated to critical velocity; due to the heterogeneity of the powder particle size, large and small particles often do not attain critical velocity and bounce off the surface [78]. On the other hand, a very high particle velocity leads to erosion of the surface or of previously deposited material [79].
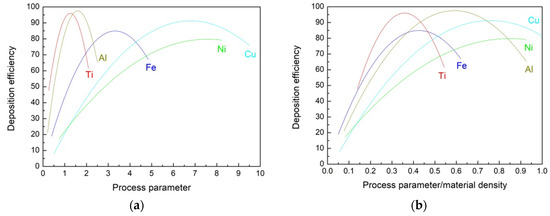
Figure 6.
Deposition efficiency as a function of (a) the process parameter and (b) the process parameter normalized to the material density.
For all these reasons, many scientists suggest caution when interpreting deposition efficiency without taking into consideration the particle size distribution of the feedstock material. Thus, further investigations on the relationships between processing parameters, particle size, and coating properties would be very useful for an in-depth understanding of the overall cold spray process. For instance, a very interesting study coupling all these issues is presented for the IN718 alloy in [80].
At this point, an analysis of the correlation between particle size distribution and the deposition efficiency has been carried out. In order to get a parameter that represents the size distribution of a powder, laser-scattering characterization was carried out. From the results obtained (Figure 7), the area below the size distribution curve was measured. The calculated area was divided for the mean particle diameter in order to obtain a representative parameter of the particle powder size.
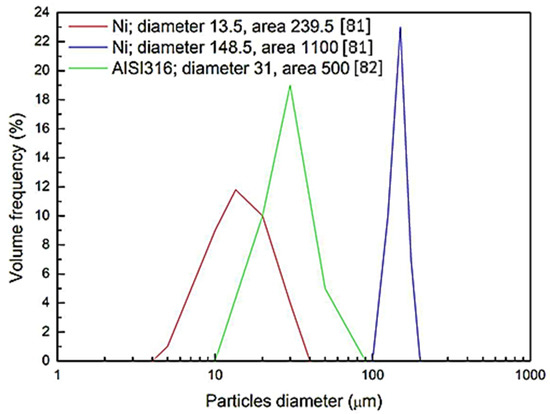
Figure 7.
Particles size and distribution of selected examples [81,82].
The “velocity parameter” was calculated as described in Equation (2) as a process parameter. In this parameter, particle velocity, particle density, and particle size are included:
where A is the area (under the curve particles diameter volume frequency) and Vp the particle velocity. The summary for the studied alloys is shown in Figure 8.
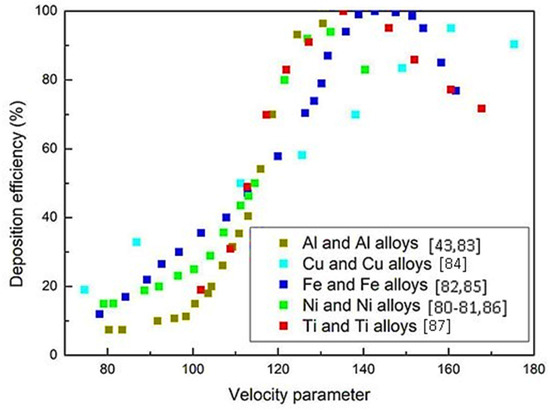
Figure 8.
Deposition efficiency as a function of the velocity parameter for different alloys [43,80,81,82,83,84,85,86,87].
As a general trend, the deposition efficiency increases with the velocity parameter up to a maximum, then the efficiency starts to decrease for many materials and different particle sizes and distributions. Different processing conditions were employed to validate the results. These spray conditions can be observed in Figure 9a,b. By focusing the analyses on Ni, Fe and Ni, and Fe alloys (Figure 9a,b), the behavior was confirmed for a very wide range of particle dimensions and distributions (listed in Table 2).
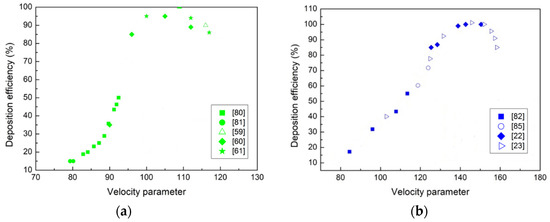
Figure 9.
Deposition efficiency as a function of the velocity parameter for Ni (a) [59,60,61,80,81] and Fe [22,23,82,85] (b) alloys.

Table 2.
Parameters for Fe and Fe alloys and Ni and Ni alloys.
The flattening ratio as a function of the particle velocity is shown in Figure 10. The flattening ratio is defined [17,88] by considering the larger over the smaller particle dimension of the splats within a coating.
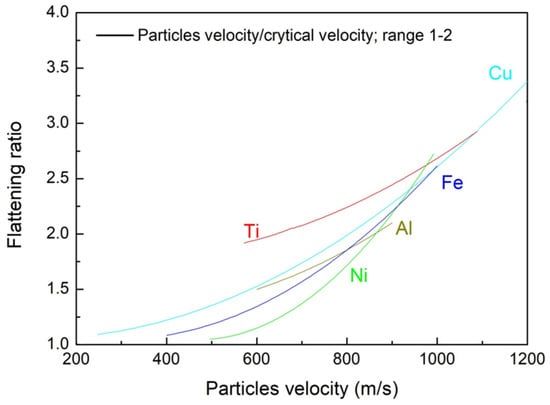
Figure 10.
Flattening ratio as a function of the particle velocity.
The particle velocity data were also normalized by the critical velocity. The flattening ratio increases with the particle velocity and with the particle velocity over the critical velocity. The flattening ratio provides the severity of how particles deform during impact. Generally, higher flattening indicates lower porosity results. A higher flattering ratio involves large particle deformations and thus leads to optimal pore filling [89,90]. This ratio is considered a very important parameter for the quality monitoring of cold sprayed coatings, which are principally dependent on the particle velocity as confirmed by the following numerical analyses. The coating material hardens because of the continuous impact and flattening. This leads to an increase in the coating hardness. This hardening behavior, under optimal impact velocity conditions, makes the coating hardness remarkably higher than the correspondent cold-worked material [90]. As previously mentioned, the flattening behavior also influences the deposit porosity. To evaluate the cold sprayed coatings’ hardness as a function of particle velocity, another parameter was developed. This “hardness to porosity” is related to the particle velocity and the results were plotted in Figure 11.

Figure 11.
Particle velocity as a function of the hardness to porosity parameter.
The hardness to porosity was calculated by employing Equation (3).
In Equation (3), Hc is the coating hardness, p is the coating porosity, and Hp is the particle hardness.
All data were deeply analyzed through modeFRONTIER. In the present analysis, it was necessary to employ a “scatter matrix” that allows immediate recognition of how strongly the different variables are correlated to each other. The parameters are strongly correlated if the corresponding value in the table is distant from zero in a range between −1 and 1. If the value is 1, the parameters are directly proportional, while if the value is −1, the parameters are inversely proportional. A summary of the present study is given in Table 3 based on this matrix. It is also possible to observe the different weights of all the parameters. The more the value differs from 0, the more it influences the corresponding variable.

Table 3.
Correlation behavior among the different input/output employed in the present study.
A database, adapted by including the defined “process parameter”, as well as the correlation among the different parameters while considering the provided analytical solutions, has been developed. The correlations among the employed parameters belonging to the modeFRONTIER analyses are summarized in Table 4.

Table 4.
Correlation behavior among the different input/output (taking into account the defined process parameter) employed in the present study.
Based on the performed analyses, it is evident how the particles’ velocity (and the particles’ impact conditions) are mainly dependent based on gas pressure and gas temperature (both related to gas density). With a remarkable inverse dependence, a particle’s velocity is related to a particle’s diameter; with a lower weight, the impact velocity is dependent on the material density with an inverse relationship. The variation in deposit variation is primarily dependent on the particle velocity. Secondarily, this variation is dependent on gas density, with an inverse relationship. Porosity is mainly related to particle velocity and gas pressure. Deposition efficiency shows a direct pronounced dependence on particle velocity, as well as on particle density, with an inverse dependence on gas density. The flattening ratio is mainly dependent on the particles’ velocity and the gas temperature. All these results are consistent with the deformation mechanisms acting during cold spray. First, the dependence of flattening ratio on the gas temperature is consistent with the fact that the higher the gas temperature, the higher the particles’ temperature results during impact; this allows for a more pronounced deformation leading to a high flattening of the particles. Obviously, severe plastic deformation is directly dependent on the particles’ velocity, which locally governs the strain rate leading to the sprayed material’s dynamic recrystallization. In addition, a higher particle velocity leads to an increase in the heat generated upon impact favoring this process [17,91]. Thus, bonding quality increases with particle size under the same impact velocities because the maximum temperature and corresponding bonding time are both increased [20]. How each fundamental mechanical or microstructural property of the deposits is governed by different processing parameters must be noted. In this scenario, it is possible to tune the processing parameters in order to optimize one of the mechanical or microstructural properties without worsening the coating performance. A multi-objective optimization tool allows us to optimize the output parameters. The results indicated which processing parameters should be tuned and also the ranges of modification inside the design space.
4. Conclusions
Bibliographic data were employed to build a database to be analyzed through a multi-objective optimization software (modeFRONTIER) to develop a provisional simple model capable of simulating the coating properties as a function of different processing parameters. Using a variety of state-of-the-art optimization techniques ranging from gradient-based methods to genetic algorithms, users can optimize their process or design by specifying their objectives and defining variables that affect factors such as operating conditions. modeFRONTIER is very effective in performing the optimization by modifying the value assigned to the input variables and monitoring the outputs.
The results confirm that using a large experimental dataset makes it possible to analyze the cold spray process. The relationships for many metals systems have been analytically described in the present study. Simple parameters that consider the effect of temperature and pressure on the employed gas density, as well as the effects of powder properties, have been related to the particle velocity and to the coating properties of the sprayed deposits. As expected, the model confirms that the particles’ velocity is dependent on the gas pressure and gas temperature. There is also an inverse dependence of particle velocity with particle diameter. Moreover, to a lesser extent, the impact velocity is dependent on material density, with an inverse relationship. Deposition efficiency shows a direct dependency with particle velocity as well as with the particle density, and has an inverse dependency with gas density.
The calculated process parameter is related to the main properties of the materials, such as the carrier’s gas pressure and temperature (both leading to gas density variation), as well as to the particles’ densities and dimensions. It was shown that the impact velocity increases by increasing the process parameter. By defining a velocity parameter, the dependence of the deposition efficiency on the particle dimensions and size distribution was calculated.
This study allowed us to develop a very broad experimental space capable of including all the most crucial processing conditions for the actual cold spray technologies used in many material systems. This procedure allows us to simulate the actual process using physical laws with appropriately calibrated coefficients. The different weights of the processing parameters affecting the mechanical and microstructural properties of the deposits were calculated.
The number of process parameter could be decreased in order to analyze their effect on the process if a high level of correlation for the defined process parameter is considered (Table 5 and Table 6).

Table 5.
Correlation behavior among the different input/output.

Table 6.
Correlation behavior among the process parameter and the coating properties.
The approach of using data analysis on multiple and disperse data gathered from bibliography has thus proven consistent with the expected trends dictated by previous knowledge, thereby opening the door to more complex data analysis in the future.
Author Contributions
Conceptualization, P.D.C.; investigation, A.S., V.A. and A.M.; writing—original draft preparation, A.S., P.D.C., V.A. and A.M.; writing—review and editing, S.D. and I.G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors thank the Spanish government for support under MAT2016-76928-C2-2-R.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Raoelison, R.N.; Xie, Y.; Sapanathan, T.; Planche, M.P.; Kromer, R.; Costil, S.; Langlade, C. Cold gas dynamic spray technology: A comprehensive review of processing conditions for various technological developments till to date. Addit. Manuf. 2018, 19, 134–159. [Google Scholar] [CrossRef]
- Yin, S.; Cavaliere, P.; Aldwell, B.; Jenkins, R.; Liao, H.; Lid, W.; Lupoi, R. Cold spray additive manufacturing and repair: Fundamentals and applications. Addit. Manuf. 2018, 21, 628–650. [Google Scholar] [CrossRef]
- Ichikawa, Y.; Tokoro, R.; Tanno, M.; Ogawa, K. Elucidation of cold-spray deposition mechanism by auger electron spectroscopic evaluation of bonding interface oxide film. Acta Mater. 2019, 164, 39–49. [Google Scholar] [CrossRef]
- Hassani-Gangaraj, M.; Veysset, D.; Champagne, V.K.; Nelson, K.A.; Schuh, C.A. Adiabatic shear instability is not necessary for adhesion in cold spray. Acta Mater. 2018, 158, 430–439. [Google Scholar] [CrossRef]
- Grujicic, M.; Saylor, J.R.; Beasley, D.E.; De Rosset, W.S.; Helfritch, D. Computational analysis of the interfacial bonding between feed-powder particles and the substrate in the cold-gas dynamic-spray process. Appl. Surf. Sci. 2003, 219, 211–227. [Google Scholar] [CrossRef]
- Cavaliere, P.; Perrone, A.; Silvello, A. Crystallization evolution of cold-sprayed pure Ni coatings. J. Therm. Spray Technol. 2016, 25, 1158–1167. [Google Scholar] [CrossRef]
- Rafaja, D.; Schucknecht, T.; Klemm, V.; Paul, A.; Berek, H. Microstructural characterisation of titanium coatings deposited using cold gas spraying on Al2O3 substrates. Surf. Coat. Technol. 2009, 203, 3206–3213. [Google Scholar] [CrossRef]
- Theimer, S.; Graunitz, M.; Schulze, M.; Gaertner, F.; Klassen, T. Optimization adhesion in cold spraying onto hard substrates: A case study for brass coatings. J. Therm. Spray Technol. 2019, 28, 124–134. [Google Scholar] [CrossRef]
- Cavaliere, P.; Silvello, A. Fatigue behavior of cold sprayed metals and alloys: A critical review. Surf. Eng. 2016, 32, 631–640. [Google Scholar] [CrossRef]
- Yin, S.; Meyer, M.; Li, W.; Liao, H.; Lupoi, R. Gas flow, particle acceleration, and heat transfer in cold spray: A review. J. Therm. Spray Technol. 2016, 25, 874–896. [Google Scholar] [CrossRef]
- Prisco, U. Size-dependent distributions of particle velocity and temperature at impact in the cold-gas dynamic-spray process. J. Mater. Proc. Technol. 2015, 216, 302–314. [Google Scholar] [CrossRef]
- Ozdemir, O.C.; Widener, C.A. Influence of powder injection parameters in high-pressure cold spray. J. Therm. Spray Technol. 2017, 26, 1411–1422. [Google Scholar] [CrossRef]
- Krull, F.; Hesse, R.; Breuninger, P.; Antonyuk, S. Impact behaviour of microparticles with microstructured surfaces: Experimental study and DEM simulation. Chem. Eng. Res. Des. 2018, 175–184. [Google Scholar] [CrossRef]
- Leitz, K.H.; O’Sullivan, M.; Plankensteiner, A.; Lichtenegger, T.; Pirker, S.; Kestler, H.; Sigl, L.S. CFDEM modelling of particle heating and acceleration in cold spraying. Int. J. Refr. Met. Hard Mat. 2018, 73, 192–198. [Google Scholar] [CrossRef]
- Assadi, H.; Kreye, H.; Gartner, F.; Klassen, T. Cold spraying—A materials perspective. Acta Mater. 2016, 116, 382–407. [Google Scholar] [CrossRef]
- Champagne, V.K.; Helfritch, D.J.; Trexler, M.D.; Gabriel, B.M. The effect of cold spray impact velocity on deposit hardness. Modell. Simul. Mater. Sci. Eng. 2010, 18, 065011. [Google Scholar] [CrossRef]
- Assadi, H.; Schmidt, T.; Richter, H.; Kliemann, J.-O.; Binder, K.; Gärtner, F.; Klassen, T.; Kreye, H. On parameter selection in cold spraying. J. Therm. Spray Technol. 2010, 20, 1161–1176. [Google Scholar] [CrossRef]
- Katanoda, H.; Fukuhara, M.; Iino, N. Numerical study of combination parameters for particle impact velocity and temperature in cold spray. J. Therm. Spray Technol. 2007, 16, 627–633. [Google Scholar] [CrossRef]
- Lee, C.; Kim, J. Microstructure of kinetic spray coatings: A review. J. Therm. Spray Technol. 2015, 24, 592–610. [Google Scholar] [CrossRef]
- Rokni, M.R.; Nutt, S.R.; Widener, C.A.; Champagne, V.K.; Hrabe, R.H. Review of relationship between particle deformation, coating microstructure, and properties in high-pressure cold spray. J. Therm. Spray Technol. 2017, 26, 1308–1355. [Google Scholar] [CrossRef]
- Maestracci, R.; Sova, A.; Jeandin, M.; Malhaire, J.-M.; Movchan, I.; Bertrand, P.H.; Smurov, I. Deposition of composite coatings by cold spray using stainless steel 316L, copper and tribaloy T-700 powder mixtures. Surf. Coat. Technol. 2016, 287, 1–8. [Google Scholar] [CrossRef]
- Huang, J.; Ma, W.; Xie, Y.; Fukanum, H.; Zhang, K.; Wang, G.; Huang, R. Influence of cold gas spray processing conditions on the properties of 316L stainless steel coatings. Surf. Eng. 2019, 1–8. [Google Scholar] [CrossRef]
- Coddet, P.; Verdy, C.; Coddet, C.; Debray, F.; Lecouturier, F. Mechanical properties of thick 304L stainless steel deposits processed by He cold spray. Surf. Coat. Technol. 2015, 277, 74–80. [Google Scholar] [CrossRef]
- Concustell, A.; Henao, J.; Dosta, S.; Cinca, N.; Cano, I.G.; Guilemany, J.M. On the formation of metallic glass coatings by means of cold gas spray technology. J. Alloys Compd. 2015, 651, 764–772. [Google Scholar] [CrossRef]
- Luzin, V.; Spencer, K.; Zhang, M.-X. Residual stress and thermo-mechanical properties of cold spray metal coatings. Act. Mater. 2011, 59, 1259–1270. [Google Scholar] [CrossRef]
- Cavaliere, P. Cold-Spray Coatings: Recent Trends and Future Perspectives; Springer: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Gilmore, D.L.; Dykhuizen, R.C.; Neiser, R.A.; Roemer, T.J.; Smith, M.F. Particle velocity and deposition efficiency in the cold spray process. J. Therm. Spray Technol. 1999, 8, 576–582. [Google Scholar] [CrossRef]
- McCune, R.C.; Donlon, W.T.; Popoola, O.O.; Cartwright, E.L. Characterization of copper layers produced by cold gas-dynamic spraying. J. Therm. Spray Technol. 2000, 5, 73–82. [Google Scholar] [CrossRef]
- Chavan, N.M.; Kumar, M.V.; Phani, S.P.; Pant, P.; Sundararajan, G. Influence of nozzle throat dimension on microstructure and properties of cold sprayed coatings. J. Therm. Spray Technol. 2019, 28, 1718–1729. [Google Scholar] [CrossRef]
- Huang, R.; Fukanuma, H. Study of the influence of particle velocity on adhesive strength of cold spray deposits. J. Therm. Spray Technol. 2012, 21, 541–549. [Google Scholar] [CrossRef]
- Huang, R.; Ma, W.; Fukanuma, H. Development of ultra-strong adhesive strength coatings using cold spray. Surf. Coat. Technol. 2014, 258, 832–841. [Google Scholar] [CrossRef]
- Zahiri, S.H.; Fraser, D.; Gulizia, S.; Jahedi, M. Effect of processing conditions on porosity formation in cold gas dynamic spraying of copper. J. Therm. Spray Technol. 2006, 15, 422–430. [Google Scholar] [CrossRef]
- Yin, S.; Liu, Q.; Liao, H.; Wang, X. Effect of injection pressure on particle acceleration, dispersion and deposition in cold spray. Comput. Mater. Sci. 2014, 90, 7–15. [Google Scholar] [CrossRef]
- Taylor, K.; Jodoin, B.; Karov, J. Particle loading effect in cold spray. J. Therm. Spray Technol. 2006, 15, 273–279. [Google Scholar] [CrossRef]
- Goupil, G.; Jucken, S.; Poirier, D.; Legoux, J.G.; Irissou, E.; Davis, B.; Guay, D.; Roué, L. Cold sprayed Cu–Ni–Fe anode for Al production. Corrosion Sci. 2015, 90, 259–265. [Google Scholar] [CrossRef]
- Li, W.-Y.; Li, C.-J.; Wang, H.-T.; Li, C.-X.; Bang, H.-S. Measurement and numerical simulation of particle velocity in cold spraying. J. Therm. Spray Technol. 2006, 15, 559–562. [Google Scholar] [CrossRef]
- Spencer, K.; Luzin, V.; Matthews, N.; Zhang, M.-X. Residual stresses in cold spray Al coatings: The effect of alloying and of process parameters. Surf. Coat. Technol. 2012, 206, 4249–4255. [Google Scholar] [CrossRef]
- Choi, W.B.; Li, L.; Luzin, V.; Neiser, R.; Gnäupel-Herold, T.; Prask, H.J.; Sampath, S.; Gouldstone, A. Integrated characterization of cold sprayed aluminum coatings. Acta Mater. 2007, 55, 857–866. [Google Scholar] [CrossRef]
- Van Steenkiste, T.H.; Smith, J.R.; Teets, R.E. Aluminum coatings via kinetic spray with relatively large powder particles. Surf. Coat. Technol. 2002, 154, 237–252. [Google Scholar] [CrossRef]
- De Force, B.S.; Eden, T.J.; Potter, J.K. Cold spray Al-5% mg coatings for the corrosion protection of magnesium alloys. J. Therm. Spray Technol. 2011, 20, 1352–1358. [Google Scholar] [CrossRef]
- Sova, A.; Doubenskaia, M.; Grigoriev, S.; Okunkova, A.; Smurov, I. Parameters of the gas-powder supersonic jet in cold spraying using a mask. J. Therm. Spray Technol. 2013, 22, 551–556. [Google Scholar] [CrossRef]
- Ozdemir, O.C.; Widener, C.A.; Helfritch, D.; Delfanian, F. Estimating the effect of helium and nitrogen mixing on deposition efficiency in cold spray. J. Therm. Spray Technol. 2016, 25, 660–671. [Google Scholar] [CrossRef]
- Ning, X.-J.; Jang, J.-H.; Kim, H.-J.; Li, C.-J.; Lee, C. Cold spraying of Al–Sn binary alloy: Coating characteristics and particle bonding features. Surf. Coat. Technol. 2008, 202, 1681–1687. [Google Scholar] [CrossRef]
- Li, W.-Y.; Zhang, C.; Guo, X.P.; Zhang, G.; Liao, H.L.; Coddet, C. Deposition characteristics of Al–12Si alloy coating fabricated by cold spraying with relatively large powder particles. Appl. Surf. Sci. 2007, 253, 7124–7130. [Google Scholar] [CrossRef]
- Zahiri, S.H.; Antonio, C.I.; Jahedi, M. Elimination of porosity in directly fabricated titanium via cold gas dynamic spraying. J. Mater. Proc. Technol. 2009, 209, 922–929. [Google Scholar] [CrossRef]
- Goldbaum, D.; Shockley, J.M.; Chromik, R.R.; Rezaeian, A.; Yue, S.; Legoux, J.-G.; Irissou, E. The effect of deposition conditions on adhesion strength of Ti and Ti6Al4V cold spray splats. J. Therm. Spray Technol. 2011, 21, 288–303. [Google Scholar] [CrossRef]
- Wong, W.; Irissou, E.; Ryabinin, A.N.; Legoux, J.-G.; Yue, S. Influence of helium and nitrogen gases on the properties of cold gas dynamic sprayed pure titanium coatings. J. Therm. Spray Technol. 2010, 20, 213–226. [Google Scholar] [CrossRef]
- Li, C.-J.; Li, W.-Y. Deposition characteristics of titanium coating in cold spraying. Surf. Coat. Technol. 2003, 167, 278–283. [Google Scholar] [CrossRef]
- Marrocco, T.; McCartney, D.G.; Shipway, P.H.; Sturgeon, A.J. Production of titanium deposits by cold-gas dynamic spray: Numerical modeling and experimental characterization. J. Therm. Spray Technol. 2006, 15, 263–272. [Google Scholar] [CrossRef]
- Goldbaum, D.; Chromik, R.R.; Yue, S.; Irissou, E.; Legoux, J.-G. Mechanical property mapping of cold sprayed Ti splats and coatings. J. Therm. Spray Technol. 2010, 20, 486–496. [Google Scholar] [CrossRef]
- Kim, K.H.; Kuroda, S.; Watanabe, M.; Huang, R.Z.; Fukanuma, H.; Katanoda, H. Comparison of oxidation and microstructure of warm-sprayed and cold-sprayed titanium coatings. J. Therm. Spray Technol. 2011, 21, 550–560. [Google Scholar] [CrossRef]
- Vo, P.; Irissou, E.; Legoux, J.-G.; Yue, S. Mechanical and microstructural characterization of cold-sprayed Ti–6Al–4V after heat treatment. J. Therm. Spray Technol. 2013, 22, 954–964. [Google Scholar] [CrossRef]
- Khun, N.W.; Tan, A.W.Y.; Bi, K.J.W.; Liu, E. Effects of working gas on wear and corrosion resistances of cold sprayed Ti–6Al–4V coatings. Surf. Coat. Technol. 2016, 302, 1–12. [Google Scholar] [CrossRef]
- Bhattiprolu, V.S.; Johnson, K.W.; Ozdemir, O.C.; Crawford, G.A. Influence of feedstock powder and cold spray processing parameters on microstructure and mechanical properties of Ti–6Al–4V cold spray depositions. Surf. Coat. Technol. 2018, 335, 1–12. [Google Scholar] [CrossRef]
- Ajdelsztajn, L.; Jodoin, B.; Schoenung, J.M. Synthesis and mechanical properties of nanocrystalline Ni coatings produced by cold gas dynamic spraying. Surf. Coat. Technol. 2006, 201, 1166–1172. [Google Scholar] [CrossRef]
- Richer, P.; Zúñiga, A.; Yandouzi, M.; Jodoin, B. CoNiCrAlY microstructural changes induced during cold gas dynamic spraying. Surf. Coat. Technol. 2008, 203, 364–371. [Google Scholar] [CrossRef]
- Cavaliere, P.; Perrone, A.; Silvello, A. Cold-sprayed nanostructured pure cobalt coatings. J. Therm. Spray Technol. 2016, 25, 1168–1176. [Google Scholar] [CrossRef]
- Seraj, R.A.; Abdollah-zadeha, A.; Dosta, S.; Canales, H.; Assadi, H.; Cano, I.G. The effect of traverse speed on deposition efficiency of cold sprayed stellite 21. Surf. Coat. Technol. 2019, 366, 24–34. [Google Scholar] [CrossRef]
- Wong, W.; Irissou, E.; Vo, P.; Sone, M.; Bernier, F.; Legoux, J.-G.; Fukanuma, H.; Yue, S. Cold spray forming of inconel 718. J. Therm. Spray Technol. 2012, 22, 413–421. [Google Scholar] [CrossRef]
- Ma, W.; Xie, Y.; Chen, C.; Fukanuma, H.; Wang, J.; Ren, Z.; Huang, R. Microstructural and mechanical properties of high-performance Inconel 718 alloy by cold spraying. J. Alloys Compd. 2019, 792, 456–467. [Google Scholar] [CrossRef]
- Cavaliere, P.; Silvello, A.; Cinca, N.; Canales, H.; Dosta, S.; Cano, I.G.; Guilemany, J.M. Microstructural and fatigue behavior of cold sprayed Ni-based superalloys coatings. Surf. Coat. Technol. 2017, 324, 390–402. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Raghupathy, Y.; Srinivasan, D.; Suwas, S.; Srivastava, C. Microstructural evolution of cold-sprayed Inconel 625 superalloy coatings on low alloy steel substrate. Acta Mater. 2017, 129, 11–25. [Google Scholar] [CrossRef]
- Luo, X.-T.; Li, Y.-J.; Li, C.-X.; Yang, G.-J.; Li, C.-J. Effect of spray conditions on deposition behavior and microstructure of cold sprayed Ni coatings sprayed with a porous electrolytic Ni powder. Surf. Coat. Technol. 2016, 289, 85–93. [Google Scholar] [CrossRef]
- Xie, Y.; Planche, M.-P.; Raoelison, R.; Hervé, P.; Suo, X.; He, P.; Liao, H. Investigation on the influence of particle preheating temperature on bonding of cold-sprayed nickel coatings. Surf. Coat. Technol. 2017, 318, 99–105. [Google Scholar] [CrossRef]
- Van Steenkiste, T.; Gorkiewicz, D.W. Analysis of tantalum coatings produced by the kinetic spray process. J. Therm. Spray Technol. 2003, 13, 265–273. [Google Scholar] [CrossRef]
- Suo, X.; Yin, S.; Planche, M.-P.; Liu, T.; Liao, H. Strong effect of carrier gas species on particle velocity during cold spray processes. Surf. Coat. Technol. 2015, 268, 90–93. [Google Scholar] [CrossRef]
- Wong, W.; Rezaeian, A.; Irissou, E.; Legoux, J.G.; Yue, S. Cold spray characteristics of commercially pure Ti and Ti–6Al–4V. Adv. Mater. Res. 2010, 89, 639–644. [Google Scholar] [CrossRef]
- Cavaliere, P.; Perrone, A.; Silvello, A. Multi-objective optimization of steel nitriding. Eng. Sci. Technol. 2016, 19, 292–312. [Google Scholar] [CrossRef]
- Cavaliere, P.; Perrone, A.; Silvello, A. Steel nitriding optimization through multi-objective and FEM analysis. J. Comput. Des. Eng. 2016, 3, 71–90. [Google Scholar] [CrossRef][Green Version]
- Karimi, M.; Rankin, G.W.; Fartaj, A. Parametric study of exhaust pattern in cold spray using CFD and particle-wall impact analysis. J. Appl. Fluid Mech. 2014, 7, 75–87. [Google Scholar]
- Stoltenhoff, T.; Kreye, H.; Richter, H.J. An analysis of the cold spray process and its coatings. J. Therm. Spray Technol. 2002, 11, 542–550. [Google Scholar] [CrossRef]
- Kosarev, V.F.; Klinkov, S.V.; Alkimov, A.P.; Papyrin, A.N. On Some aspects of gas dynamics of the cold spray process. J. Therm. Spray Technol. 2003, 12, 265–281. [Google Scholar] [CrossRef]
- Grujicic, M.; Zhao, C.L.; Tong, C.; DeRosset, W.S.; Helfritch, D. Analysis of the impact velocity of powder particles in the cold-gas dynamic-spray process. Mater. Sci. Eng. 2004, 368, 222–230. [Google Scholar] [CrossRef]
- Koivuluoto, H.; Matikainen, V.; Larjo, J.; Vuoristo, P. Novel online diagnostic analysis for in-flight particle properties in cold spraying. J. Therm. Spray Technol. 2018, 27, 423–432. [Google Scholar] [CrossRef]
- Borchers, C.; Schmidt, T.; Gärtner, F.; Kreye, H. High strain rate deformation microstructures of stainless steel 316L by cold spraying and explosive powder compaction. Appl. Phys. 2008, 90, 517–526. [Google Scholar] [CrossRef]
- Bae, G.; Kang, K.; Na, H.; Kim, J.-J.; Lee, C.H. Effect of particle size on the microstructure and properties of kinetic sprayed nickel coatings. Surf. Coat. Technol. 2010, 204, 3326–3335. [Google Scholar] [CrossRef]
- Lange, F.F. Powder processing science and technology for increased reliability. J. Am. Ceram. Soc. 1989, 72, 3–15. [Google Scholar] [CrossRef]
- Champagne, V.; Helfritch, D. The unique abilities of cold spray deposition. Int. Mater. Rev. 2016, 61, 437–455. [Google Scholar] [CrossRef]
- Klinkov, S.V.; Kosarev, V.F. Measurements of cold spray deposition efficiency. J. Therm. Spray Technol. 2006, 15, 364–371. [Google Scholar] [CrossRef]
- Mauer, G.; Singh, R.; Rauwald, K.-H.; Schrüfer, S.; Wilson, S.; Vaßen, R. Diagnostics of cold-sprayed particle velocities approaching critical deposition conditions. J. Therm. Spray Technol. 2017, 26, 1423–1433. [Google Scholar] [CrossRef]
- Luo, X.-T.; Yao, M.-L.; Ma, N.; Takahashi, M.; Li, C.-J. Deposition behavior, microstructure and mechanical properties of an in-situ micro-forging assisted cold spray enabled additively manufactured Inconel 718 alloy. Mater. Des. 2018, 155, 384–395. [Google Scholar] [CrossRef]
- Fukanuma, H.; Ohno, N.; Sun, B.; Huang, R. In-flight particle velocity measurements with DPV-2000 in cold spray. Surf. Coat. Technol. 2006, 201, 1935–1941. [Google Scholar] [CrossRef]
- Wu, J.; Fang, H.; Yoon, S.; Kim, H.J.; Lee, C. Measurement of particle velocity and characterization of deposition in aluminum alloy kinetic spraying process. Appl. Surf. Sci. 2005, 252, 1368–1377. [Google Scholar] [CrossRef]
- Li, Y.-J.; Luo, X.-T.; Li, C.-J. Dependency of deposition behavior, microstructure and properties of cold sprayed Cu on morphology and porosity of the powder. Surf. Coat. Technol. 2017, 328, 304–312. [Google Scholar] [CrossRef]
- Chu, X.; Che, H.; Vo, P.; Chakrabarty, R.; Sun, B.; Song, J.; Yue, S. Understanding the cold spray deposition efficiencies of 316L/Fe mixed powders by performing splat tests onto as-polished coatings. Surf. Coat. Technol. 2017, 304, 353–360. [Google Scholar] [CrossRef]
- Jodoin, B.; Raletzb, T.F.; Vardelle, M. Cold spray modeling and validation using an optical diagnostic method. Surf. Coat. Technol. 2006, 200, 4424–4432. [Google Scholar] [CrossRef]
- Luo, X.-T.; Wei, Y.-K.; Wang, Y.; Li, C.-J. Microstructure and mechanical property of Ti and Ti6Al4V prepared by an in-situ shot peening assisted cold spraying. Mater. Des. 2015, 85, 527–533. [Google Scholar] [CrossRef]
- Wong, W.; Vo, P.; Irissou, E.; Ryabinin, A.N.; Legoux, J.-G.; Yue, S. Effect of particle morphology and size distribution on cold-sprayed pure titanium coatings. J. Therm. Spray Technol. 2013, 22, 1140–1153. [Google Scholar] [CrossRef]
- Dykhuizen, R.C.; Smith, M.F.; Neiser, R.A.; Gilmore, D.L.; Jiang, X.; Sampath, S. Impact of high velocity cold spray particles. J. Therm. Spray Technol. 1998, 8, 559–564. [Google Scholar] [CrossRef]
- Hall, A.; Brewer, L.; Roemer, T. Preparation of aluminum coatings containing homogenous nanocrystalline microstructures using the cold spray process. J. Therm. Spray Technol. 2008, 17, 352–359. [Google Scholar] [CrossRef]
- Assadi, H.; Gärtner, F.; Stoltenhoff, T.; Kreye, H. Bonding mechanism in cold gas spraying. Acta Mater. 2003, 51, 4379–4394. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).