Percolation Model for Renewable-Carbon Doped Functional Composites in Packaging Application: A Brief Review
Abstract
1. Introduction
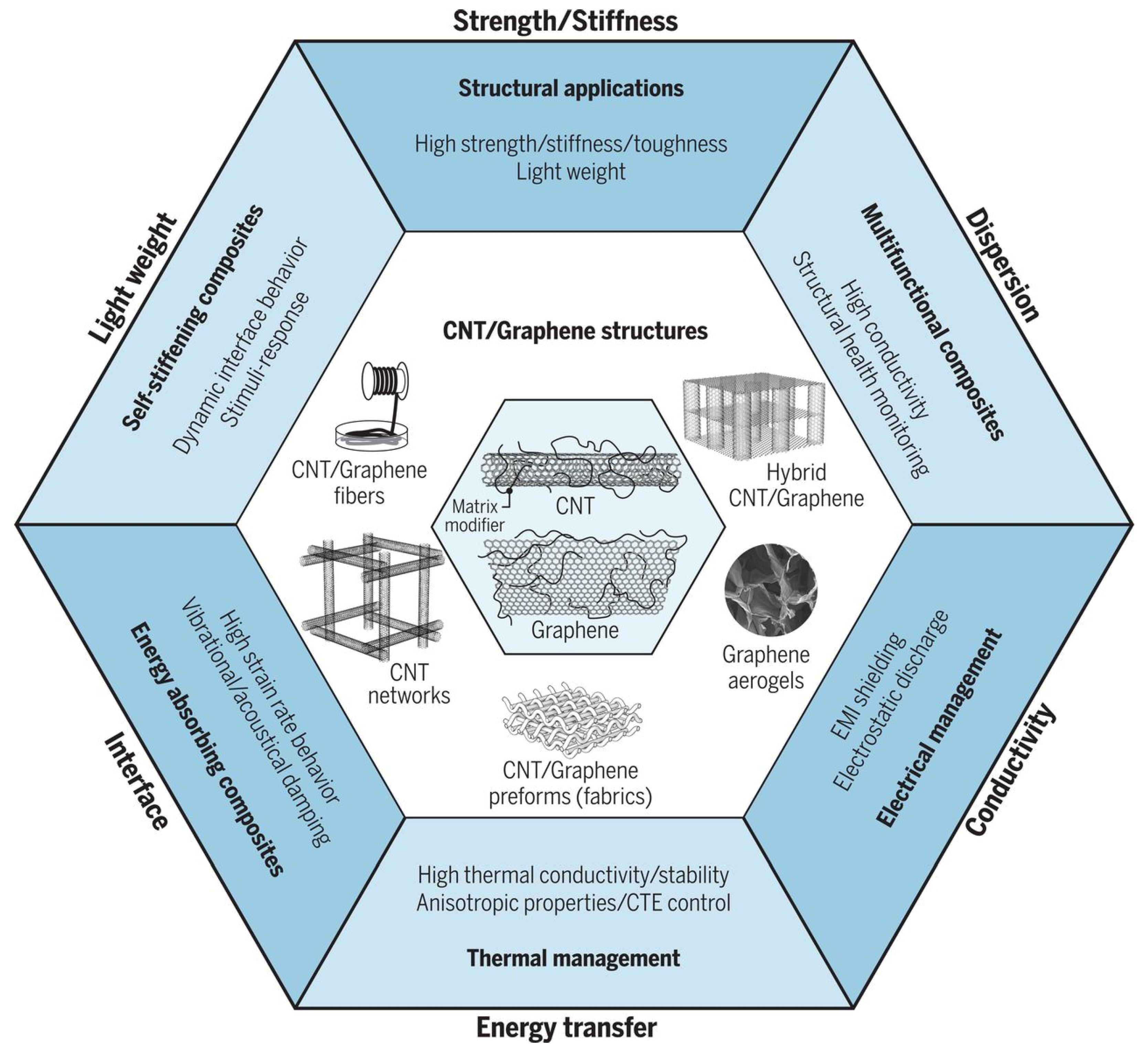
2. Renewable Carbon/Carbon Complex
2.1. Classification of Renewable Carbon
2.1.1. Granular Renewable Carbon
2.1.2. Powdered Renewable Carbon
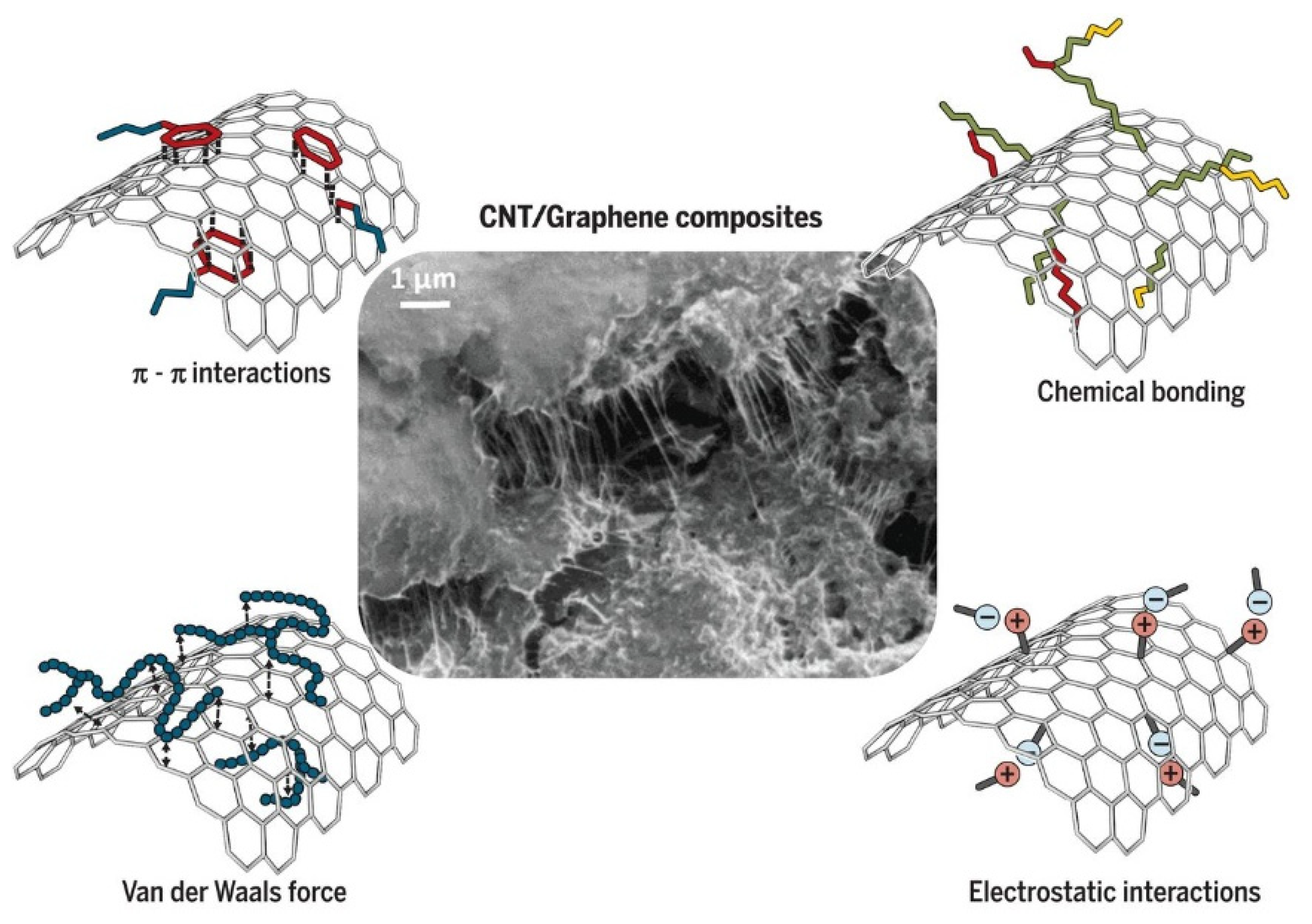
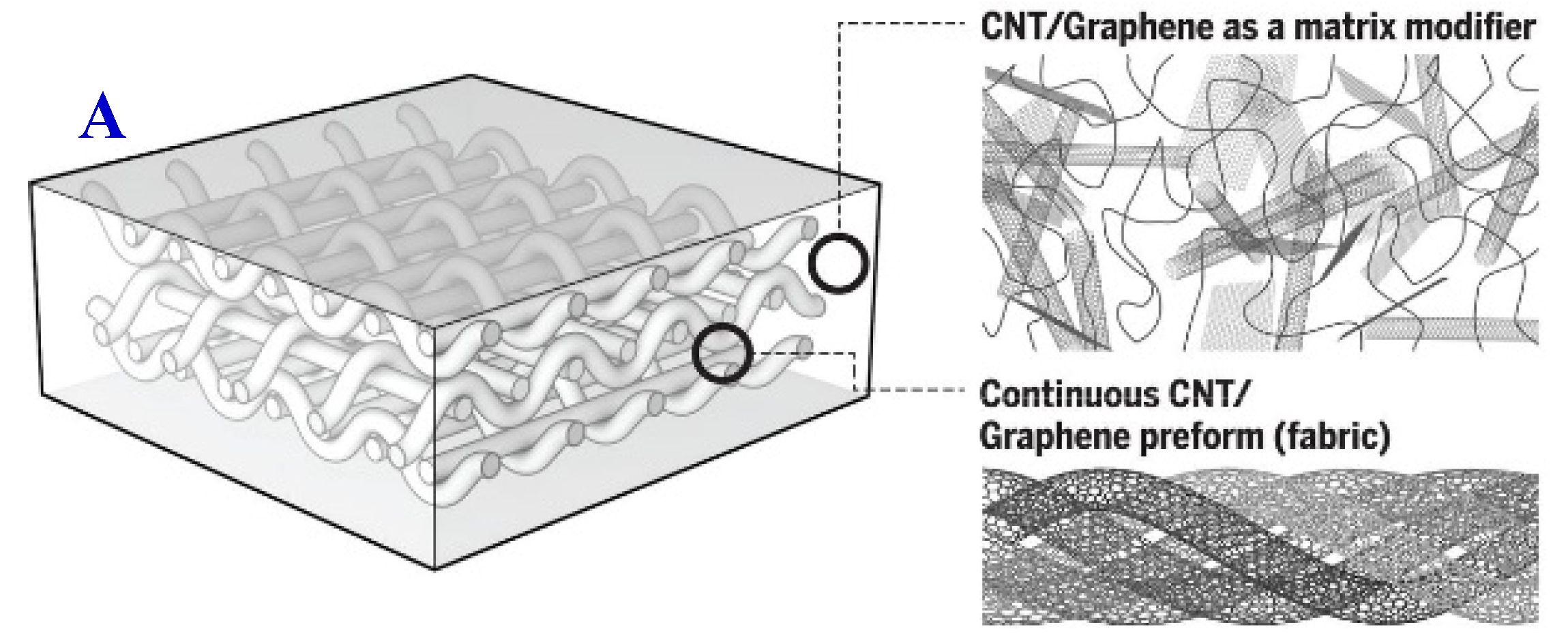
2.2. Use of Renewable Carbon in the Reinforced Packaging Polymeric Composites
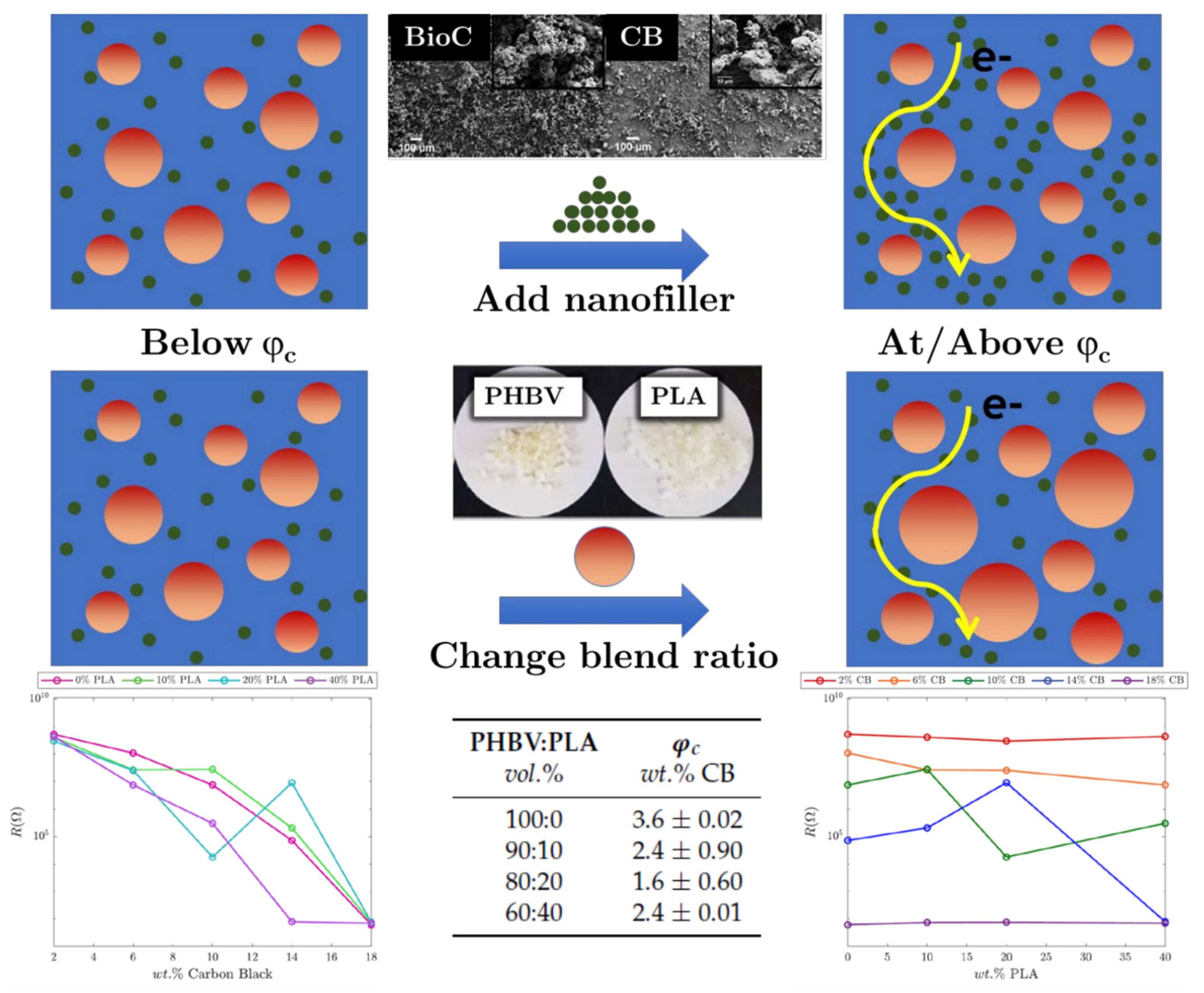
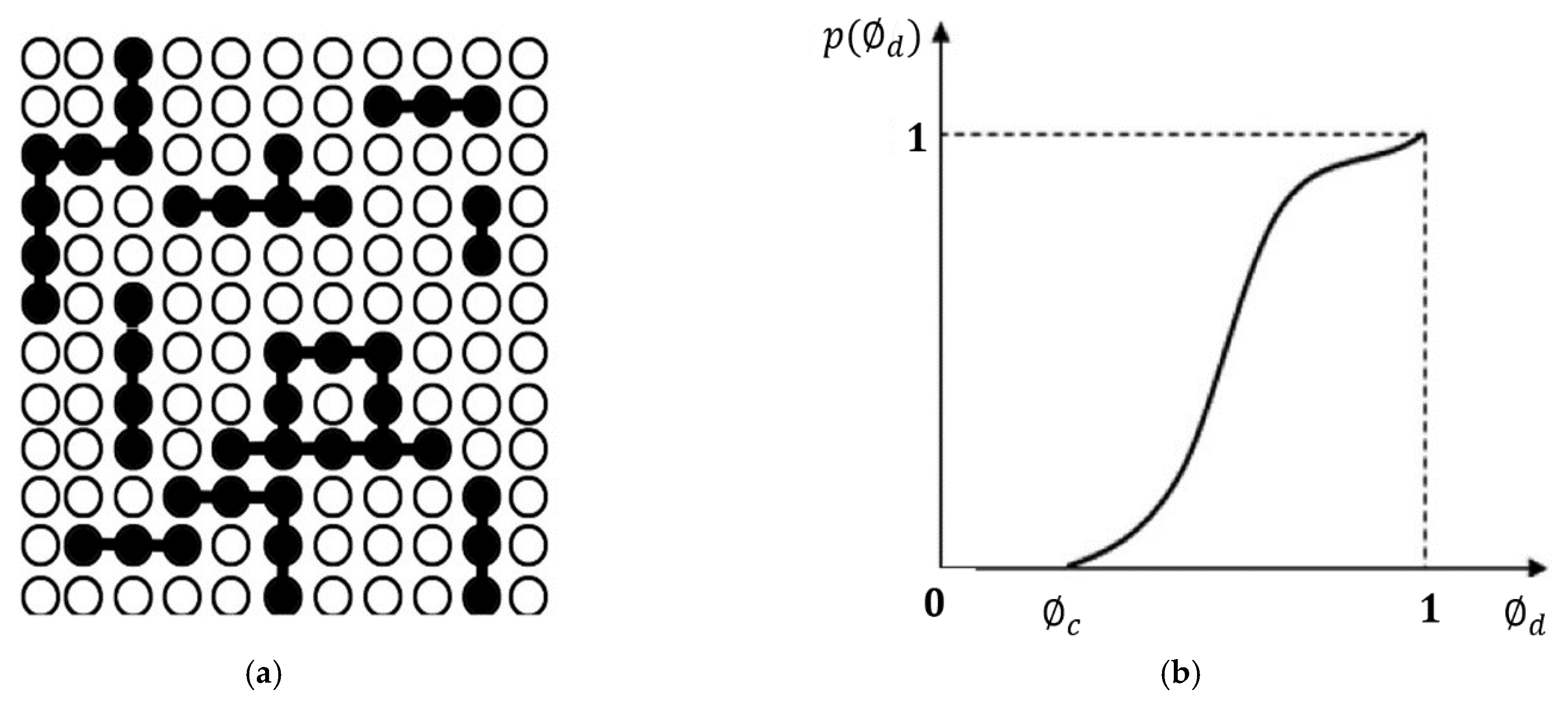
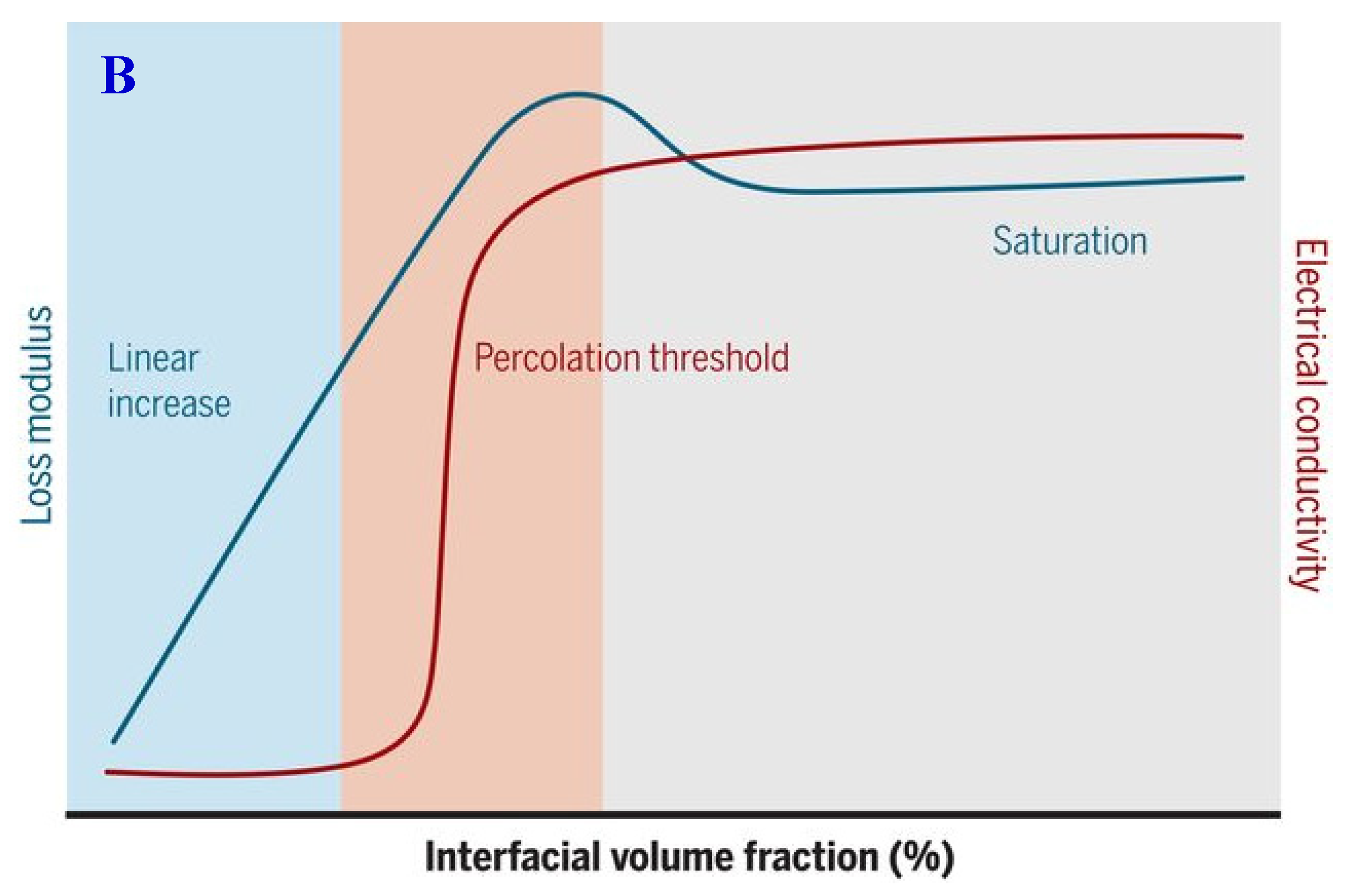
3. Percolation Theory
4. The Effect of Renewable Carbon Characteristics on Its Percolation Behavior
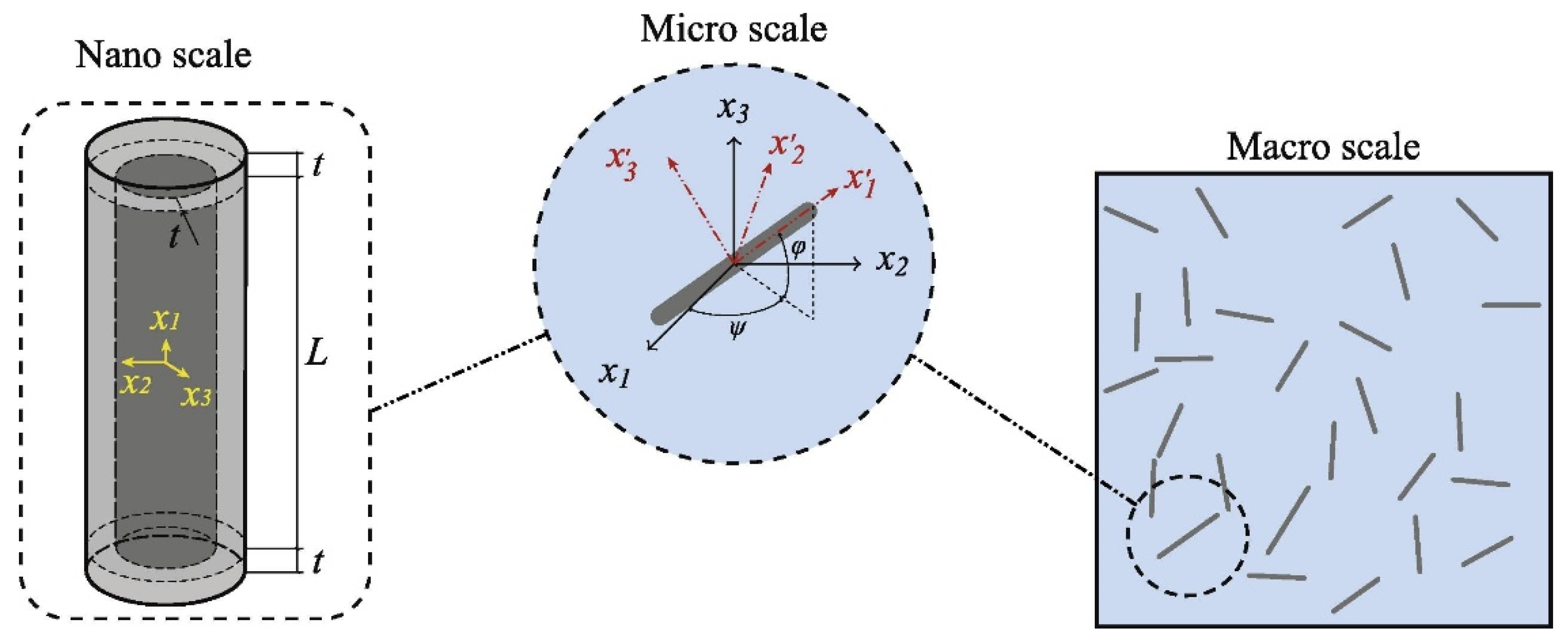
4.1. Geometry of Renewable Carbon
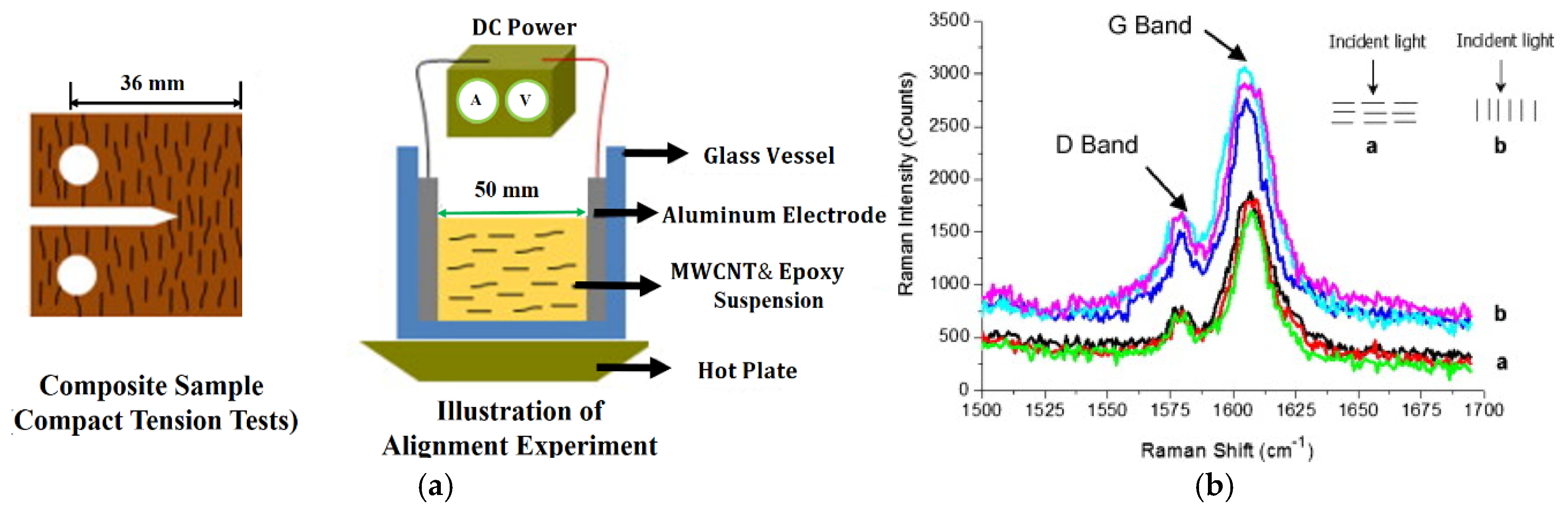
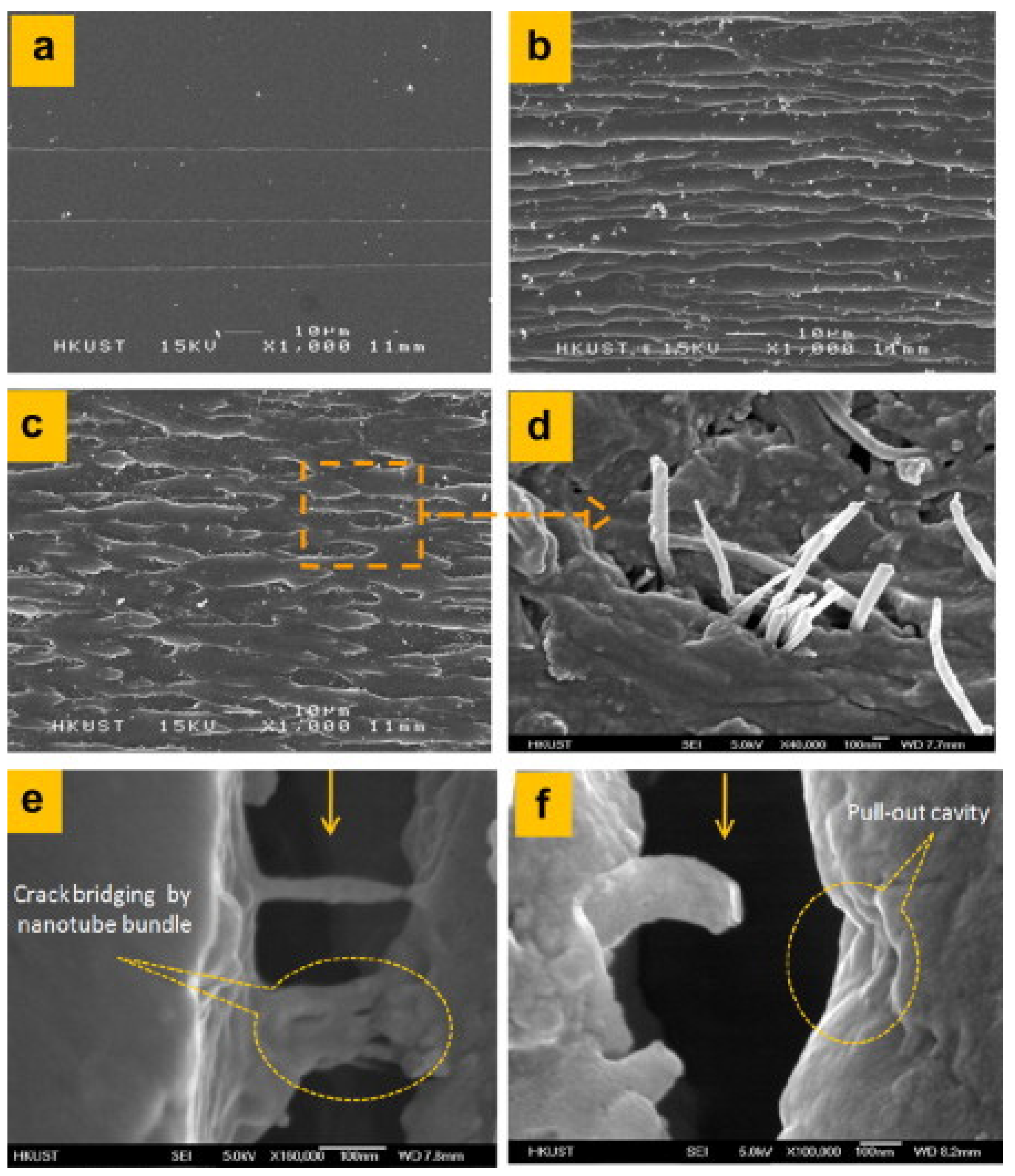
4.2. Alignment of Renewable Carbon
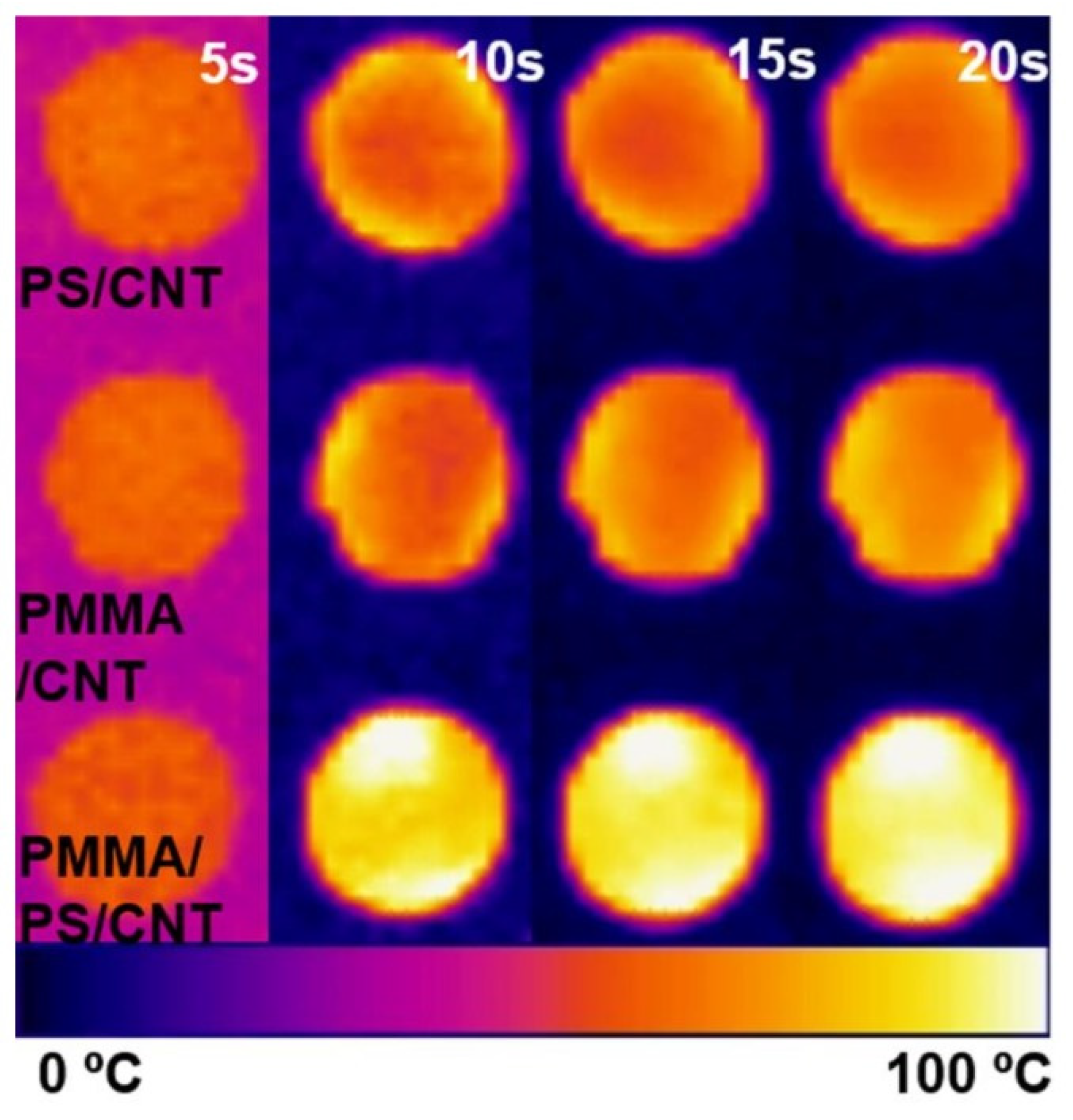
4.3. Surface Property of Renewable Carbon
5. Percolation Models
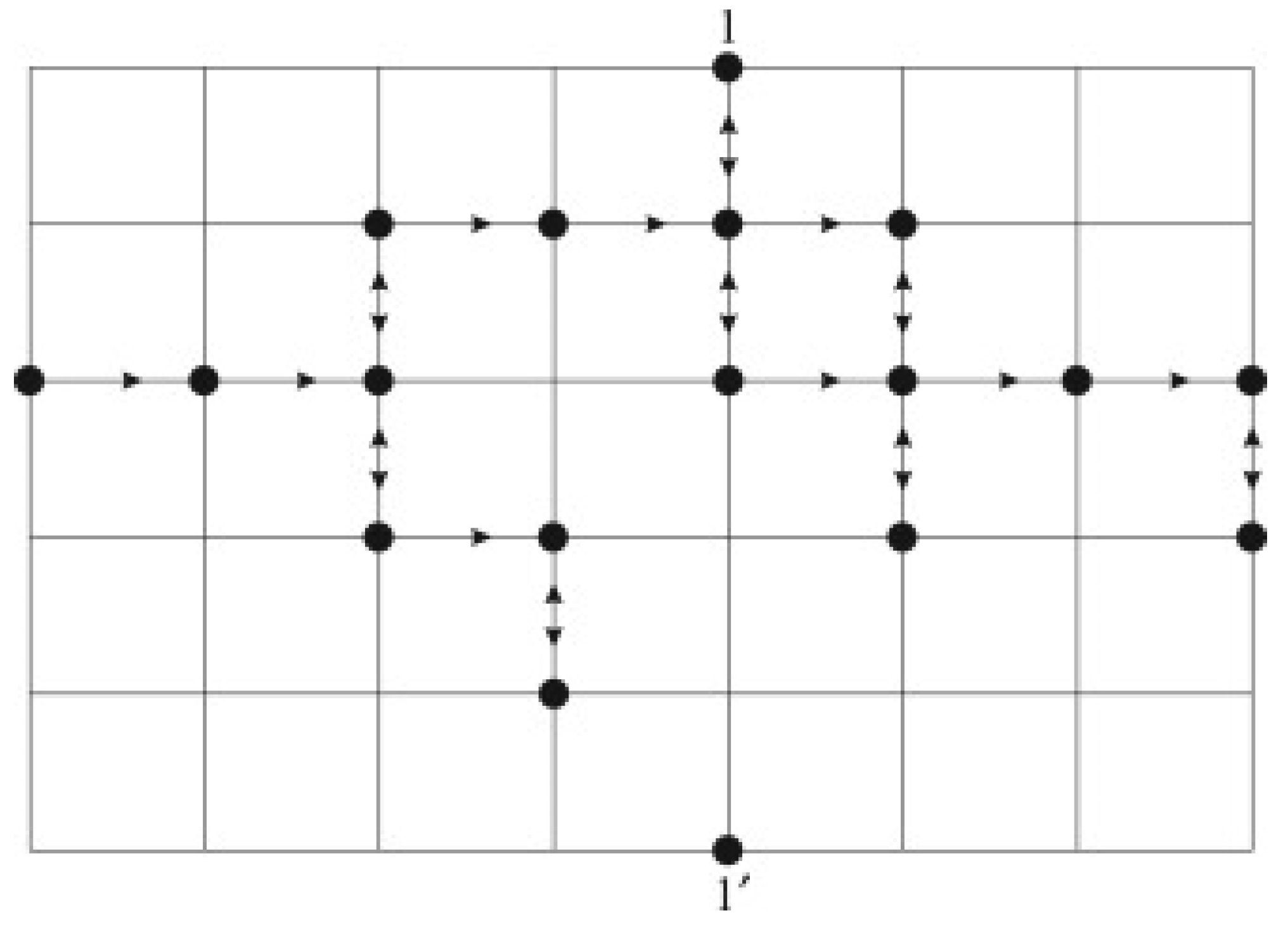
5.1. Directed Percolation and Semi-directed Percolation
5.2. Tunneling Percolation
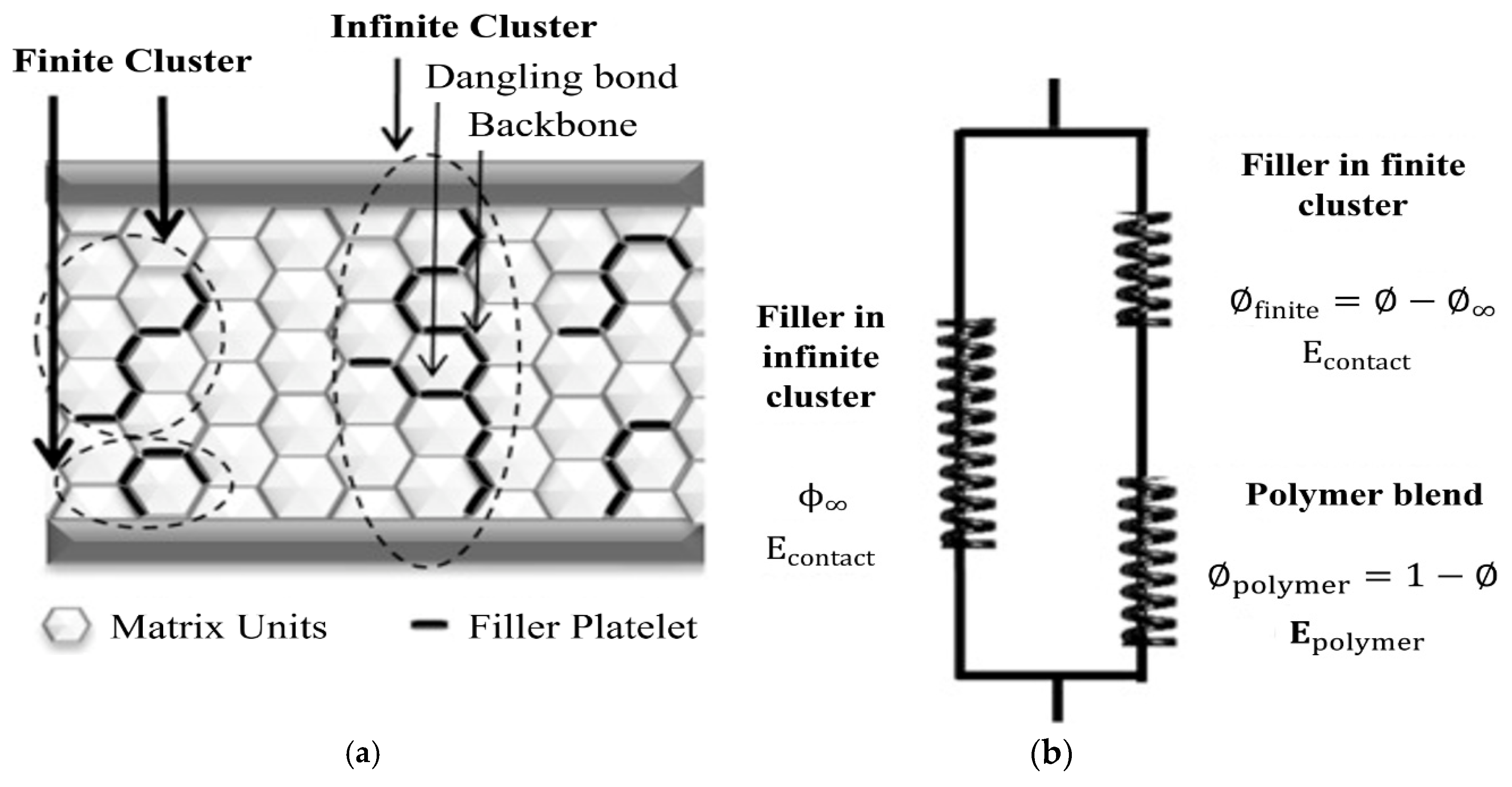
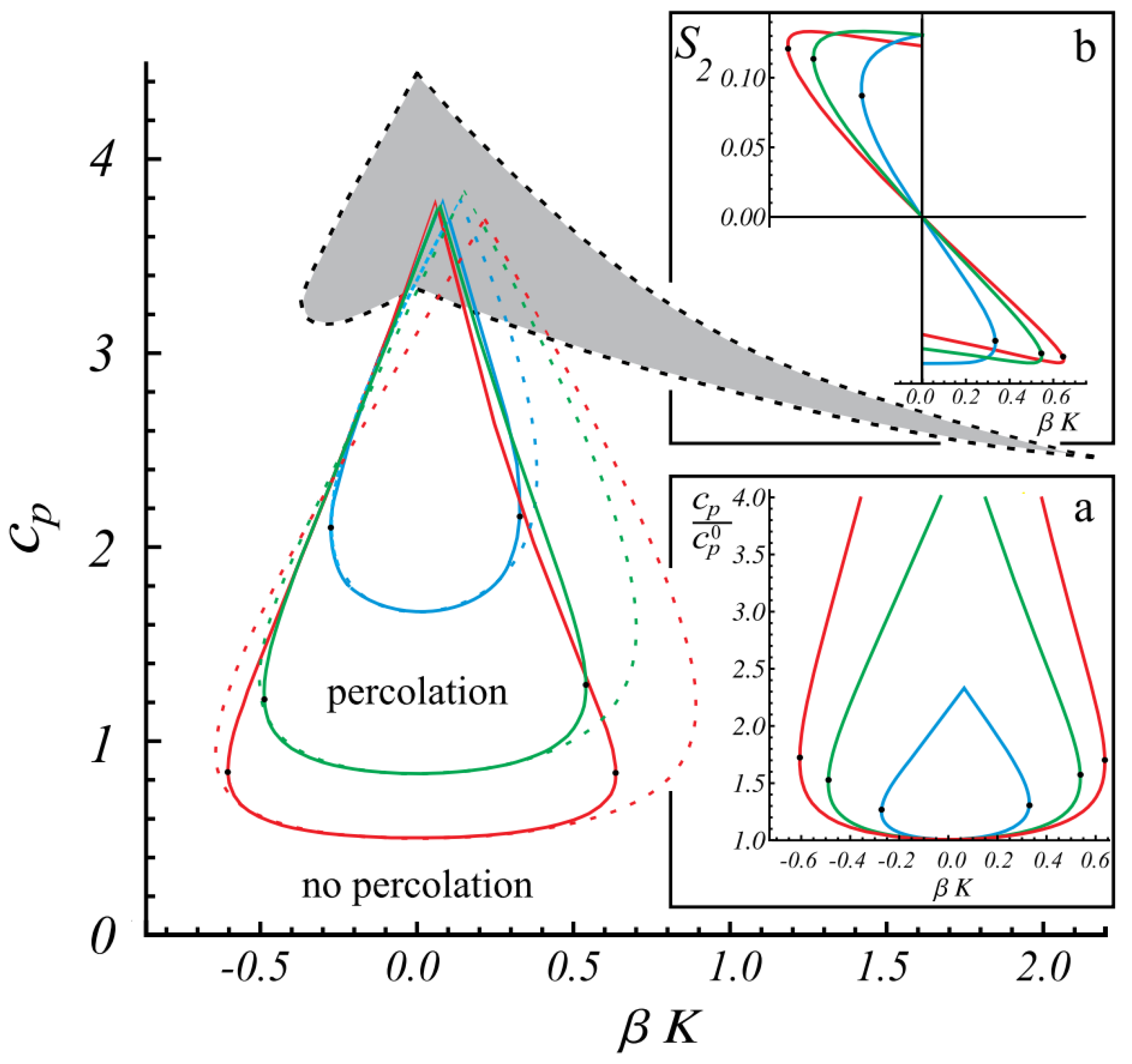
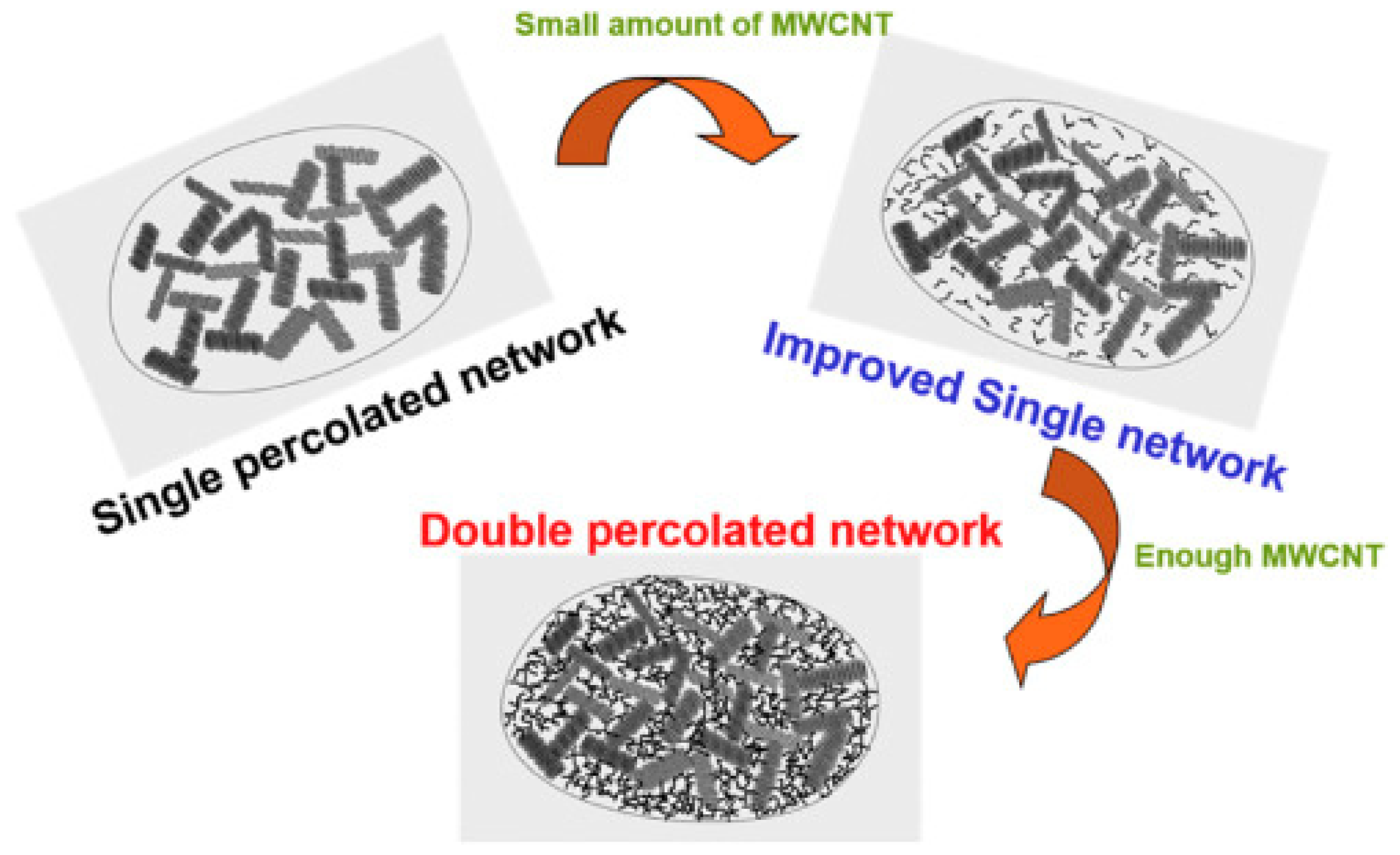
5.3. Dual Percolation
5.4. Other Models
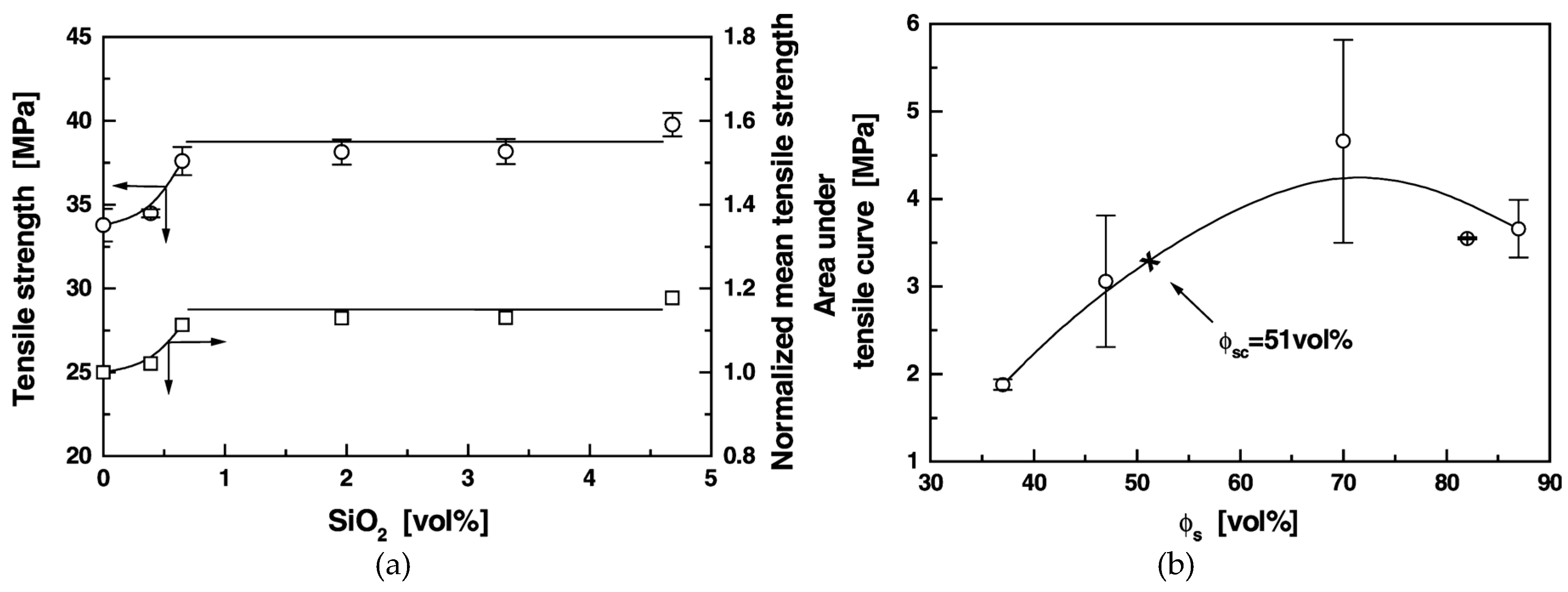
5.4.1. Halpin–Tsai Model
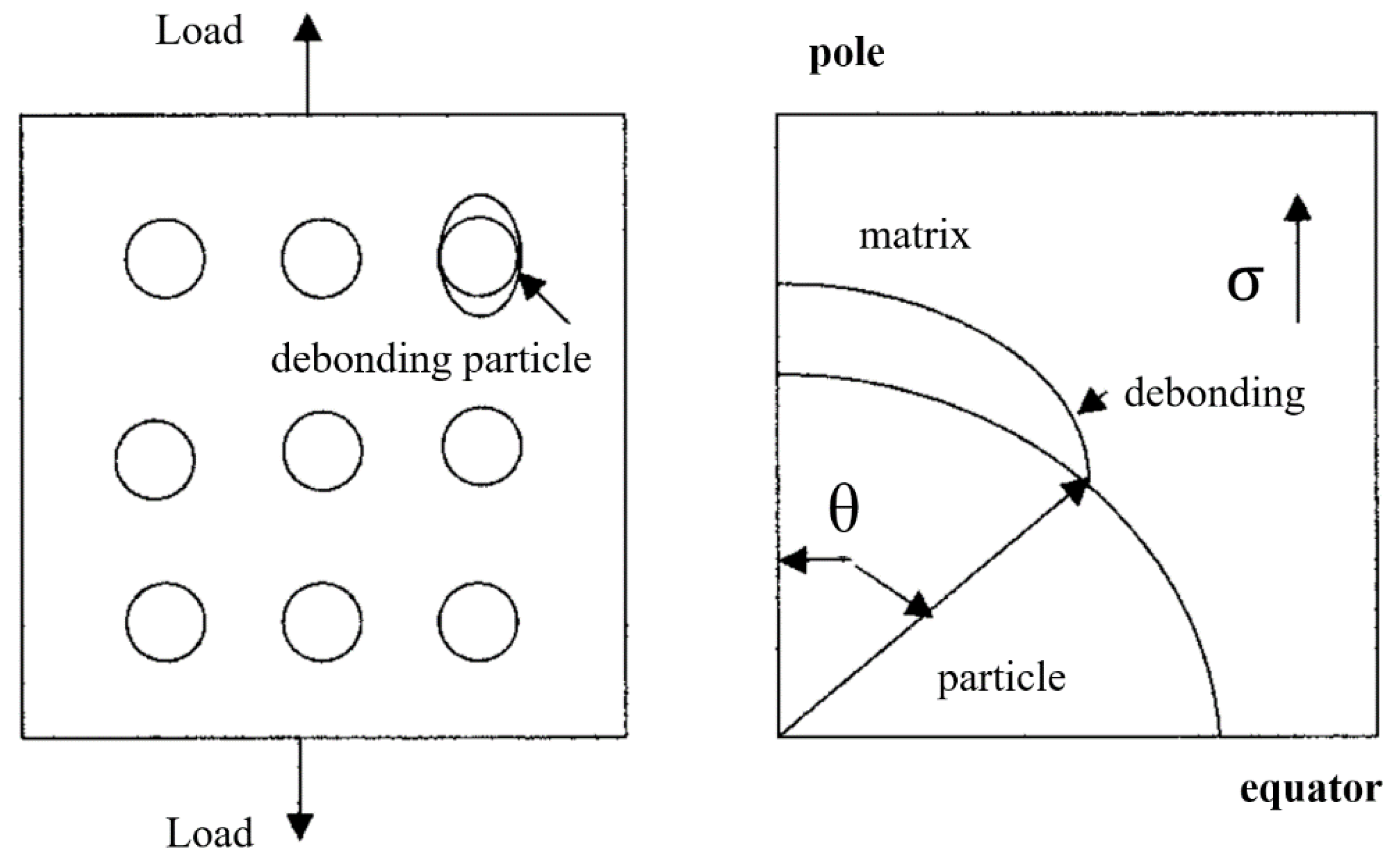
5.4.2. Debonding Model
5.4.3. Generalized Method of Cells (GMC) Model
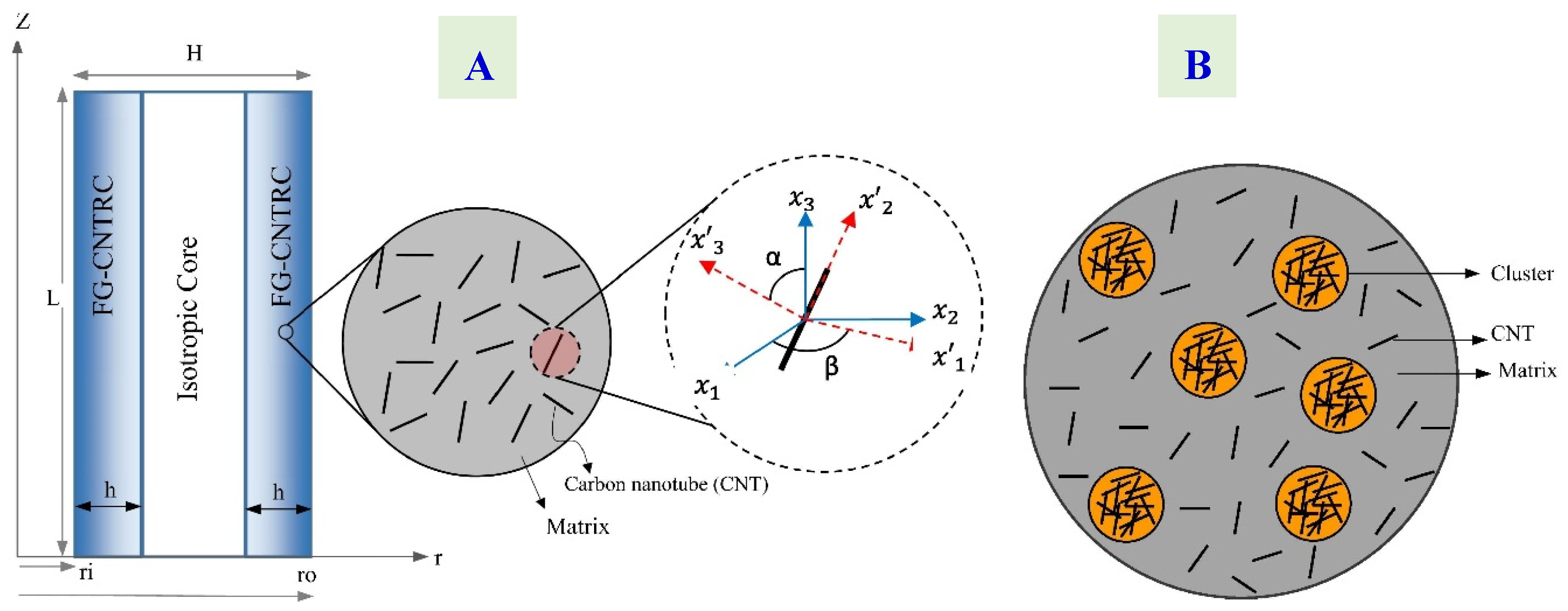
5.4.4. Other Micromechanics Models
6. Nanocellulose: Carbon-Based Reinforcing Filler
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Väisänen, T.; Das, O.; Tomppo, L. A review on new bio-based constituents for natural fiber-polymer composites. J. Clean. Prod. 2017, 149, 582–596. [Google Scholar] [CrossRef]
- Jasim, S.M.; Ali, N.A. Properties characterization of plasticized polylactic acid/Biochar (bio carbon) nano-composites for antistatic packaging. Iraqi J. Phys. 2019, 17, 13–26. [Google Scholar]
- Ulaeto, S.B.; Rajan, R.; Pancrecious, J.K.; Rajan, T.; Pai, B. Developments in smart anticorrosive coatings with multifunctional characteristics. Prog. Org. Coat. 2017, 111, 294–314. [Google Scholar] [CrossRef]
- Ouadil, B.; Cherkaoui, O.; Safi, M.; Zahouily, M. Surface modification of knit polyester fabric for mechanical, electrical and UV protection properties by coating with graphene oxide, graphene and graphene/silver nanocomposites. Appl. Surf. Sci. 2017, 414, 292–302. [Google Scholar] [CrossRef]
- Ceran, Ö.B.; Şimşek, B.; Doruk, S.; Uygunoğlu, T.; Şara, O.N. Effects of dispersed and powdered silver nanoparticles on the mechanical, thermal, electrical and durability properties of cementitious composites. Constr. Build. Mater. 2019, 222, 152–167. [Google Scholar] [CrossRef]
- Vivek, R.; Kumar, A.; Chaturvedi, T.P.; Prakash, R. Mechanical and Wear Properties of Nano Titanium Based Dental Composite Resin, in Materials for Biomedical Engineering; Elsevier: Amsterdam, The Netherlands; pp. 441–462.
- Sun, B.; Hou, Q.; Liu, Z.; He, Z.; Ni, Y. Stability and efficiency improvement of ASA in internal sizing of cellulosic paper by using cationically modified cellulose nanocrystals. Cellulose 2014, 21, 2879–2887. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, M.; Hou, Q.; Liu, R.; Wu, T.; Si, C. Further characterization of cellulose nanocrystal (CNC) preparation from sulfuric acid hydrolysis of cotton fibers. Cellulose 2016, 23, 439–450. [Google Scholar] [CrossRef]
- Sun, B.; Wang, W.; Zhang, M.; Sain, M. Biomass-based edible film with enhanced mass barrier capacity and gas permeable selectivity. Cellulose 2018, 25, 5919–5937. [Google Scholar] [CrossRef]
- Fatehi, P.; Ryan, J.; Ni, Y. Adsorption of lignocelluloses of model pre-hydrolysis liquor on activated carbon. Bioresour. Technol. 2013, 131, 308–314. [Google Scholar] [CrossRef]
- Oubagaranadin, J.; Murthy, Z. Activated carbons: Classifications, properties and applications. Activated Carbon: Classifications, Properties and Applications; Nova Science Publishers Inc.: Hauppauge, NY, USA, 2011; pp. 239–266. [Google Scholar]
- Kinloch, I.A.; Suhr, J.; Lou, J.; Young, R.J.; Ajayan, P.M. Composites with carbon nanotubes and graphene: An outlook. Science 2018, 362, 547–553. [Google Scholar] [CrossRef]
- Qiu, G.; Guo, M. Quality of poultry litter-derived granular activated carbon. Bioresour. Technol. 2010, 101, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Deng, S.; Nie, Y.; Du, Z.; Huang, Q.; Meng, P.; Wang, B.; Huang, J.; Yu, G. Enhanced adsorption of perfluorooctane sulfonate and perfluorooctanoate by bamboo-derived granular activated carbon. J. Hazard. Mater. 2015, 282, 150–157. [Google Scholar] [CrossRef] [PubMed]
- Aziz, N.A.A.; Mohamed, M.; Mohamad, M.; Amini, M.H.M.; Abdul, M.; Aziz, M.; Yusoff, H.; Rizman, Z. Influence of activated carbon filler on the mechanical properties of wood composites. Arpn J. Eng. Appl. Sci. 2015, 10, 376–386. [Google Scholar]
- Yang, Y.; Zhang, Y.; Li, Z.; Zhao, Z.; Quan, X.; Zhao, Z. Adding granular activated carbon into anaerobic sludge digestion to promote methane production and sludge decomposition. J. Clean. Prod. 2017, 149, 1101–1108. [Google Scholar] [CrossRef]
- Fuertes, A.B.; Sevilla, M. High-surface area carbons from renewable sources with a bimodal micro-mesoporosity for high-performance ionic liquid-based supercapacitors. Carbon 2015, 94, 41–52. [Google Scholar] [CrossRef]
- Partlan, E.; Davis, K.; Ren, Y.; Apul, O.G.; Mefford, O.T.; Karanfil, T.; Ladner, D.A. Effect of bead milling on chemical and physical characteristics of activated carbons pulverized to superfine sizes. Water Res. 2016, 89, 161–170. [Google Scholar] [CrossRef]
- Bandosz, T.J.; Bagreev, A.; Adib, F.; Turk, A. Unmodified versus caustics-impregnated carbons for control of hydrogen sulfide emissions from sewage treatment plants. Environ. Sci. Technol. 2000, 34, 1069–1074. [Google Scholar] [CrossRef]
- Moreno-Castilla, C.; Pérez-Cadenas, A. Carbon-based honeycomb monoliths for environmental gas-phase applications. Materials 2010, 3, 1203–1227. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, S.; Hu, Y.; Li, L.; Yan, T.; Yang, G.; Ji, D.; Srinivasan, M.; Pan, Z.; Ramakrishna, S. Cobalt nanoparticles encapsulated in carbon nanotube-grafted nitrogen and sulfur co-doped multichannel carbon fibers as efficient bifunctional oxygen electrocatalysts. J. Mater. Chem. A 2017, 5, 4949–4961. [Google Scholar] [CrossRef]
- Neisiany, R.E.; Khorasani, S.N.; Naeimirad, M.; Lee, J.K.Y.; Ramakrishna, S. Improving mechanical properties of carbon/epoxy composite by incorporating functionalized electrospun polyacrylonitrile nanofibers. Macromol. Mater. Eng. 2017, 302, 1600551. [Google Scholar] [CrossRef]
- Chapman, M.; Dhakal, H.N. Effects of hybridisation on the low velocity falling weight impact and flexural properties of flax-carbon/epoxy hybrid composites. Fibers 2019, 7, 95. [Google Scholar] [CrossRef]
- Arroyo, J.; Ryan, C. Incorporation of carbon nanofillers tunes mechanical and electrical percolation in PHBV: PLA blends. Polymers 2018, 10, 1371. [Google Scholar] [CrossRef] [PubMed]
- Meincke, O.; Kaempfer, D.; Weickmann, H.; Friedrich, C.; Vathauer, M.; Warth, H. Mechanical properties and electrical conductivity of carbon-nanotube filled polyamide-6 and its blends with acrylonitrile/butadiene/styrene. Polymer 2004, 45, 739–748. [Google Scholar] [CrossRef]
- Gubbels, F.; Jérôme, R.; Vanlathem, E.; Deltour, R.; Blacher, S.; Brouers, F. Kinetic and thermodynamic control of the selective localization of carbon black at the interface of immiscible polymer blends. Chem. Mater. 1998, 10, 1227–1235. [Google Scholar] [CrossRef]
- Wu, S. Chain structure, phase morphology, and toughness relationships in polymers and blends. Polym. Eng. Sci. 1990, 30, 753–761. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Cheng, P. Application of continuum percolation theory for modeling single-and two-phase characteristics of anisotropic carbon paper gas diffusion layers. Journal of Power Sources. 2016, 307, 613–623. [Google Scholar] [CrossRef]
- Noël, A.; Faucheu, J.; Chenal, J.-M.; Viricelle, J.-P.; Bourgeat-Lami, E. Electrical and mechanical percolation in graphene-latex nanocomposites. Polymer 2014, 55, 5140–5145. [Google Scholar] [CrossRef]
- Moore, C.; Newman, M.E. Epidemics and percolation in small-world networks. Phys. Rev. E 2000, 61, 5678. [Google Scholar] [CrossRef]
- Yang, X.; Liang, C.; Ma, T.; Guo, Y.; Kong, J.; Gu, J.; Chen, M.; Zhu, J. A review on thermally conductive polymeric composites: Classification, measurement, model and equations, mechanism and fabrication methods. Adv. Compos. Hybrid Mater. 2018, 1, 207–230. [Google Scholar] [CrossRef]
- Pan, L.; Ge, C.; Lu, L.; Wang, J. An oxygen permeability predictive model without geometric factors for immiscible polymer blended films based on fractal and percolation theory. Food Packag. Shelf Life 2019, 22, 100335. [Google Scholar] [CrossRef]
- Ouali, N.; Cavaillé, J.; Perez, J. Elastic, viscoelastic and plastic behavior of multiphase polymer blends. Plastics. Rubber Compos. Rubber Compos. Process. Appl. (Uk) 1991, 16, 55–60. [Google Scholar]
- Yi, Y.; Tawerghi, E. Geometric percolation thresholds of interpenetrating plates in three-dimensional space. Phys. Rev. E 2009, 79, 041134. [Google Scholar] [CrossRef] [PubMed]
- Mathew, M.; Schilling, T.; Oettel, M. Connectivity percolation in suspensions of hard platelets. Phys. Rev. E 2012, 85, 061407. [Google Scholar] [CrossRef] [PubMed]
- Ambrosetti, G.; Johner, N.; Grimaldi, C.; Danani, A.; Ryser, P. Percolative properties of hard oblate ellipsoids of revolution with a soft shell. Phys. Rev. E 2008, 78, 061126. [Google Scholar] [CrossRef] [PubMed]
- Ambrosetti, G.; Grimaldi, C.; Balberg, I.; Maeder, T.; Danani, A.; Ryser, P. Solution of the tunneling-percolation problem in the nanocomposite regime. Phys. Rev. B 2010, 81, 155434. [Google Scholar] [CrossRef]
- Otten, R.H.; van der Schoot, P. Connectedness percolation of elongated hard particles in an external field. Phys. Rev. Lett. 2012, 108, 088301. [Google Scholar] [CrossRef]
- Chatterjee, A.P. Percolation in polydisperse systems of aligned rods: A lattice-based analysis. J. Chem. Phys. 2014, 140, 204911. [Google Scholar] [CrossRef]
- Kale, S.; Sabet, F.A.; Jasiuk, I.; Ostoja-Starzewski, M. Effect of filler alignment on percolation in polymer nanocomposites using tunneling-percolation model. J. Appl. Phys. 2016, 120, 045105. [Google Scholar] [CrossRef]
- Khan, S.U.; Pothnis, J.R.; Kim, J.-K. Effects of carbon nanotube alignment on electrical and mechanical properties of epoxy nanocomposites. Compos. Part A: Appl. Sci. Manuf. 2013, 49, 26–34. [Google Scholar] [CrossRef]
- Jalal, M.; Moradi-Dastjerdi, R.; Bidram, M. Big data in nanocomposites: ONN approach and mesh-free method for functionally graded carbon nanotube-reinforced composites. J. Comput. Des. Eng. 2019, 6, 209–223. [Google Scholar] [CrossRef]
- Shi, D.L.; Feng, X.Q.; Huang, Y.Y.; Hwang, K.C.; Gao, H. The effect of nanotube waviness and agglomeration on the elastic property of carbon nanotube-reinforced composites. J. Eng. Mater. Technol. 2004, 126, 250–257. [Google Scholar] [CrossRef]
- Mitchell, C.A.; Bahr, J.L.; Arepalli, S.; Tour, J.M.; Krishnamoorti, R. Dispersion of functionalized carbon nanotubes in polystyrene. Macromolecules 2002, 35, 8825–8830. [Google Scholar] [CrossRef]
- Saini, P.; Sharma, B.; Singh, M.; Tandon, R.P.; Singh, S.P.; Mahapatro, A.K. Electrical Properties of Self Sustained Layer of Graphene Oxide and Polyvinylpyriodine Composite. Integr. Ferroelectr. 2019, 202, 197–203. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282. [Google Scholar] [CrossRef] [PubMed]
- Nawaz, K.; Khan, U.; Ul-Haq, N.; May, P.; O’Neill, A.; Coleman, J.N. Observation of mechanical percolation in functionalized graphene oxide/elastomer composites. Carbon 2012, 50, 4489–4494. [Google Scholar] [CrossRef]
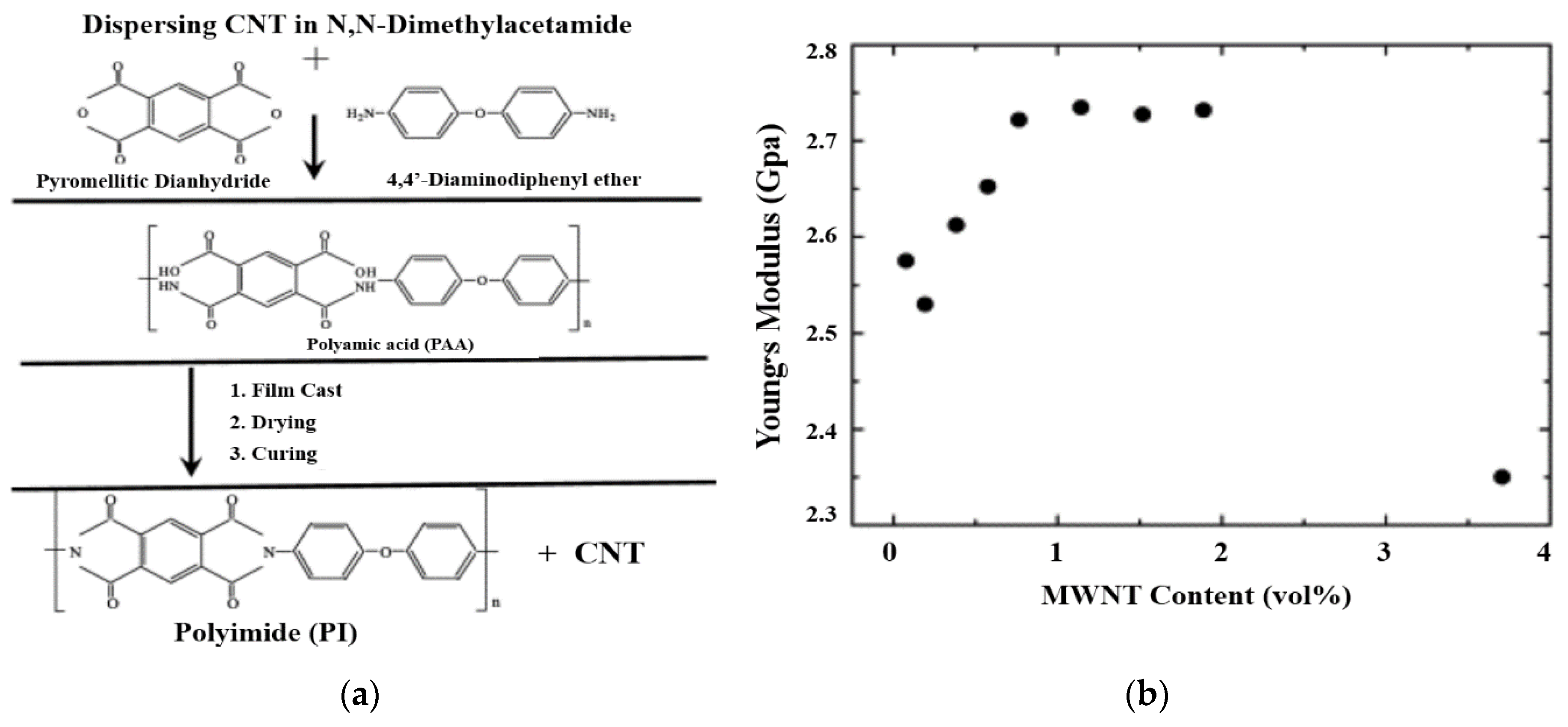
- Jiang, X.; Bin, Y.; Matsuo, M. Electrical and mechanical properties of polyimide–carbon nanotubes composites fabricated by in situ polymerization. Polymer 2005, 46, 7418–7424. [Google Scholar] [CrossRef]
- Shaffer, M.S.; Windle, A.H. Fabrication and characterization of carbon nanotube/poly (vinyl alcohol) composites. Adv. Mater. 1999, 11, 937–941. [Google Scholar] [CrossRef]
- Oskouyi, A.; Sundararaj, U.; Mertiny, P. Tunneling conductivity and piezoresistivity of composites containing randomly dispersed conductive nano-platelets. Materials 2014, 7, 2501–2521. [Google Scholar] [CrossRef]
- Hicks, J.; Behnam, A.; Ural, A. A computational study of tunneling-percolation electrical transport in graphene-based nanocomposites. Appl. Phys. Lett. 2009, 95, 213103. [Google Scholar] [CrossRef]
- Lemoult, G.; Shi, L.; Avila, K.; Jalikop, S.V.; Avila, M.; Hof, B. Directed percolation phase transition to sustained turbulence in Couette flow. Nat. Phys. 2016, 12, 254. [Google Scholar] [CrossRef]
- Privman, V.; Švrakić, N.M. Directed Models of Polymers, Interfaces, and Clusters: Scaling and Finite-Size Properties; Springer: Berlin, Germany, 1989. [Google Scholar]
- Knežević, D.; Knežević, M. Semi-directed percolation in two dimensions. Physica A Stat. Mech. Appl. 2016, 444, 560–565. [Google Scholar]
- Grimaldi, C.; Maeder, T.; Ryser, P.; Strässler, S. Piezoresistivity and conductance anisotropy of tunneling-percolating systems. Phys. Rev. B 2003, 67, 014205. [Google Scholar] [CrossRef]
- Silva, J.; Ribeiro, S.; Lanceros-Mendez, S.; Simões, R. The influence of matrix mediated hopping conductivity, filler concentration, aspect ratio and orientation on the electrical response of carbon nanotube/polymer nanocomposites. Compos. Sci. Technol. 2011, 71, 643–646. [Google Scholar] [CrossRef][Green Version]
- White, S.I.; DiDonna, B.A.; Mu, M.; Lubensky, T.C.; Winey, K.I. Simulations and electrical conductivity of percolated networks of finite rods with various degrees of axial alignment. Phys. Rev. B 2009, 79, 024301. [Google Scholar] [CrossRef]
- Wu, K.; Xue, Y.; Yang, W.; Chai, S.; Chen, F.; Fu, Q. Largely enhanced thermal and electrical conductivity via constructing double percolated filler network in polypropylene/expanded graphite–multi-wall carbon nanotubes ternary composites. Compos. Sci. Technol. 2016, 130, 28–35. [Google Scholar] [CrossRef]
- Wie, J.; Kim, J. Thermal Conductivity Enhancement Derived from Poly (Methyl Methacrylate)-Grafted Carbon Nanotubes in Poly (Methyl Methacrylate)/Polystyrene Blends. Polymers 2019, 11, 1347. [Google Scholar] [CrossRef]
- Rong, M.Z.; Zhang, M.Q.; Zheng, Y.X.; Zeng, H.M.; Friedrich, K. Improvement of tensile properties of nano-SiO2/PP composites in relation to percolation mechanism. Polymer 2001, 42, 3301–3304. [Google Scholar] [CrossRef]
- Nikfar, N.; Zare, Y.; Rhee, K.Y. Dependence of mechanical performances of polymer/carbon nanotubes nanocomposites on percolation threshold. Phys. B Condens. Matter 2018, 533, 69–75. [Google Scholar] [CrossRef]
- Halpin, J.C. Effects of Environmental Factors on Composite Materials; Air Force Materials Lab Wright-Patterson AFB OH: Wright-Patterson AFB, OH, USA, 1969.
- Sun, L.-H.; Ounaies, Z.; Gao, X.-L.; Whalen, C.A.; Yang, Z.-G. Preparation, characterization, and modeling of carbon nanofiber/epoxy nanocomposites. J. Nanomater. 2011, 2011. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y.; Park, S.-J. A developed equation for electrical conductivity of polymer carbon nanotubes (CNT) nanocomposites based on Halpin-Tsai model. Results Phys. 2019, 14, 102406. [Google Scholar] [CrossRef]
- Wu, D.; Wu, L.; Zhou, W.; Sun, Y.; Zhang, M. Relations between the aspect ratio of carbon nanotubes and the formation of percolation networks in biodegradable polylactide/carbon nanotube composites. J. Polym. Sci. Part B Polym. Phys. 2010, 48, 479–489. [Google Scholar] [CrossRef]
- Yeh, M.-K.; Tai, N.-H.; Liu, J.-H. Mechanical behavior of phenolic-based composites reinforced with multi-walled carbon nanotubes. Carbon 2006, 44, 1–9. [Google Scholar] [CrossRef]
- Liang, J.Z. Toughening and reinforcing in rigid inorganic particulate filled poly (propylene): A review. J. Appl. Polym. Sci. 2002, 83, 1547–1555. [Google Scholar] [CrossRef]
- Liang, J.; Li, R. Mechanical properties and morphology of glass bead–filled polypropylene composites. Polym. Compos. 1998, 19, 698–703. [Google Scholar] [CrossRef]
- Baxter, S.C.; Robinson, C.T. Pseudo-percolation: Critical volume fractions and mechanical percolation in polymer nanocomposites. Compos. Sci. Technol. 2011, 71, 1273–1279. [Google Scholar] [CrossRef]
- Snipes, J.; Robinson, C.; Baxter, S. Effects of scale and interface on the three-dimensional micromechanics of polymer nanocomposites. J. Compos. Mater. 2011, 45, 2537–2546. [Google Scholar] [CrossRef]
- Fralick, B.S.; Gatzke, E.P.; Baxter, S.C. Three-dimensional evolution of mechanical percolation in nanocomposites with random microstructures. Probabilistic Eng. Mech. 2012, 30, 1–8. [Google Scholar] [CrossRef][Green Version]
- Xu, W.; Wu, F.; Jiao, Y.; Liu, M. A general micromechanical framework of effective moduli for the design of nonspherical nano-and micro-particle reinforced composites with interface properties. Mater. Des. 2017, 127, 162–172. [Google Scholar] [CrossRef]
- Bernard, O.; Ulm, F.-J.; Lemarchand, E. A multiscale micromechanics-hydration model for the early-age elastic properties of cement-based materials. Cem. Concr. Res. 2003, 33, 1293–1309. [Google Scholar] [CrossRef]
- Xu, W.; Ma, H.; Ji, S.; Chen, H. Analytical effective elastic properties of particulate composites with soft interfaces around anisotropic particles. Compos. Sci. Technol. 2016, 129, 10–18. [Google Scholar] [CrossRef]
- Underwood, B.S.; Kim, Y.R. A four phase micro-mechanical model for asphalt mastic modulus. Mech. Mater. 2014, 75, 13–33. [Google Scholar] [CrossRef]
- Ngabonziza, Y.; Li, J.; Barry, C. Electrical conductivity and mechanical properties of multiwalled carbon nanotube-reinforced polypropylene nanocomposites. Acta Mech. 2011, 220, 289–298. [Google Scholar] [CrossRef]
- Taya, M. Micromechanics modeling of smart composites. Compos. Part A Appl. Sci. Manufac. 1999, 30, 531–536. [Google Scholar] [CrossRef]
- Loos, M.R.; Manas-Zloczower, I. Reinforcement efficiency of carbon nanotubes–myth and reality. Macromol. Theory Simul. 2012, 21, 130–137. [Google Scholar] [CrossRef]
- García-Macías, E.; D’Alessandro, A.; Castro-Triguero, R.; Pérez-Mira, D.; Ubertini, F. Micromechanics modeling of the uniaxial strain-sensing property of carbon nanotube cement-matrix composites for SHM applications. Compos. Struct. 2017, 163, 195–215. [Google Scholar] [CrossRef]
- Feng, C.; Jiang, L. Micromechanics modeling of the electrical conductivity of carbon nanotube (CNT)–polymer nanocomposites. Compos. Part A Appl. Sci. Manufac. 2013, 47, 143–149. [Google Scholar] [CrossRef]
- Jarali, C.S.; Patil, S.F.; Pilli, S.C. Hygro-thermo-electric properties of carbon nanotube epoxy nanocomposites with agglomeration effects. Mech. Adv. Mater. Struc. 2015, 22, 428–439. [Google Scholar] [CrossRef]
- Kim, S.Y.; Noh, Y.J.; Yu, J. Prediction and experimental validation of electrical percolation by applying a modified micromechanics model considering multiple heterogeneous inclusions. Compos. Sci. Technol. 2015, 106, 156–162. [Google Scholar] [CrossRef]
- Sun, B.; Wang, W.; He, Z.; Zhang, M.; Kong, F.; Sain, M. Biopolymer Substrates in Buccal Drug Delivery: Current Status and Future Trend. Curr. Med. Chem. 2019. [Google Scholar] [CrossRef]
- Sun, B.; Wang, W.; He, Z.; Zhang, M.; Kong, F.; Sain, M.; Ni, Y. Improvement of Stability of Tea Polyphenols: A Review. Curr. Pharm. Des. 2018, 24, 3410–3423. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, M.; Ni, Y. Use of sulfated cellulose nanocrystals towards stability enhancement of gelatin-encapsulated tea polyphenols. Cellulose 2018, 25, 5157–5173. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, M.; He, Z.; Zheng, L.; Shen, J.; Ni, Y. Towards greener and more sustainable cellulose-based hand sanitizer products. J. Bioresour. Bioprod. 2017, 2, 56–60. [Google Scholar]
- Sun, B.; Zhang, M.; Shen, J.; He, Z.; Fatehi, P.; Ni, Y. Applications of cellulose-based materials in sustained drug delivery systems. Curr Med Chem. 2019, 26, 2485–2501. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Hou, Q.; He, Z.; Liu, Z.; Ni, Y. Cellulose nanocrystals (CNC) as carriers for a spirooxazine dye and its effect on photochromic efficiency. Carbohydr. Polym. 2014, 111, 419–424. [Google Scholar] [CrossRef] [PubMed]
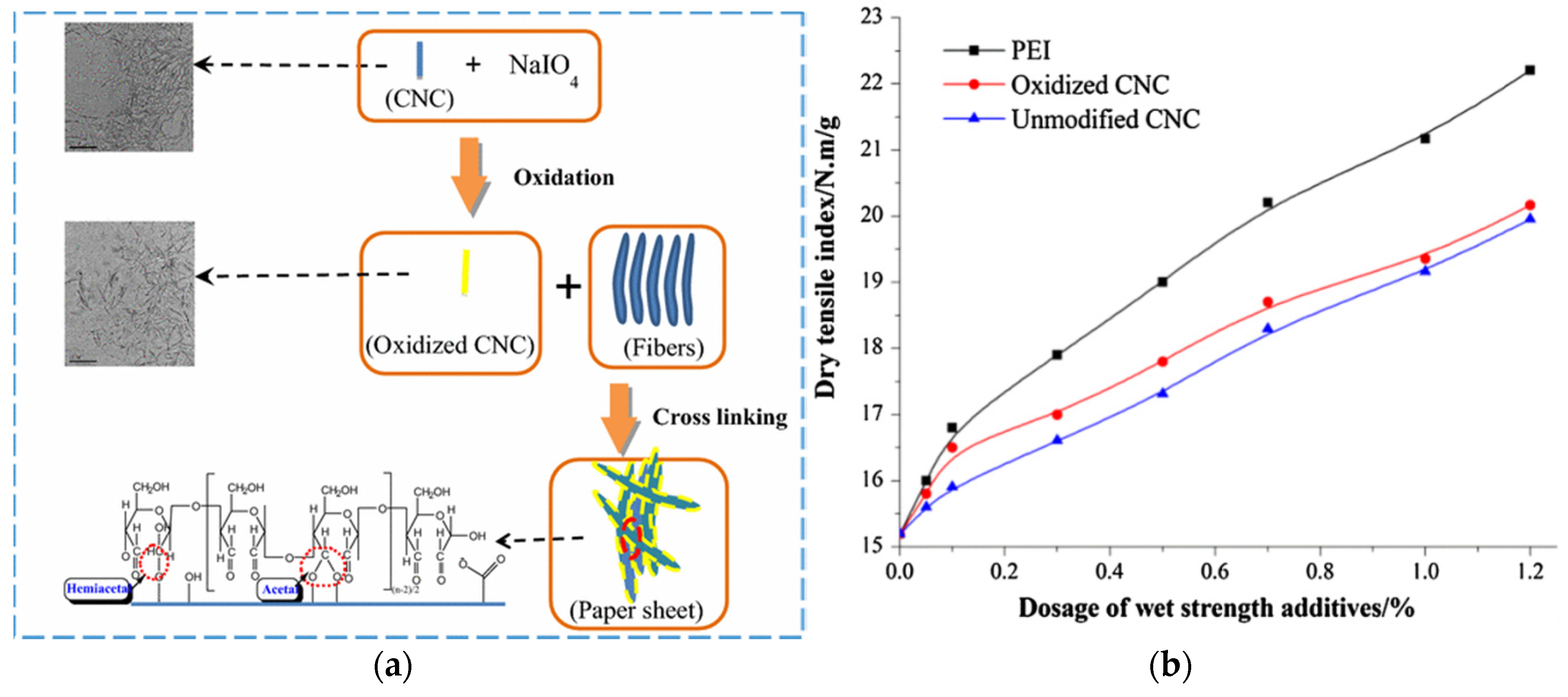
- Sun, B.; Hou, Q.; Liu, Z.; Ni, Y. Sodium periodate oxidation of cellulose nanocrystal and its application as a paper wet strength additive. Cellulose 2015, 22, 1135–1146. [Google Scholar] [CrossRef]
- Loos, M.; Manas-Zloczower, I. Micromechanical models for carbon nanotube and cellulose nanowhisker reinforced composites. Polym. Eng. Sci. 2013, 53, 882–887. [Google Scholar] [CrossRef]


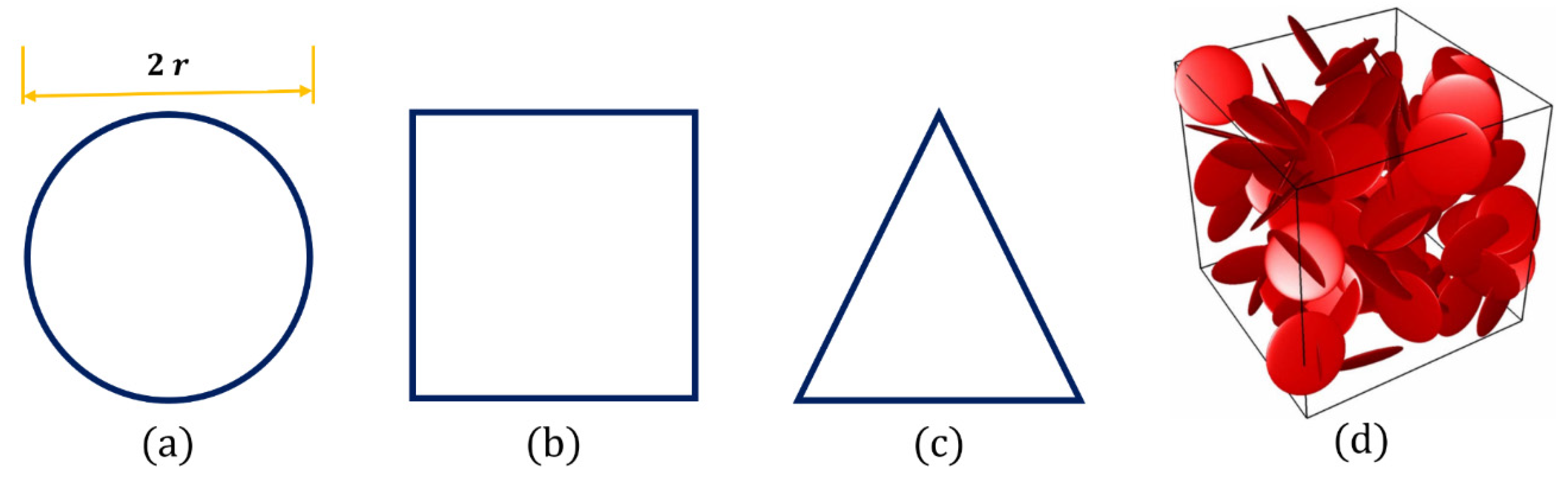


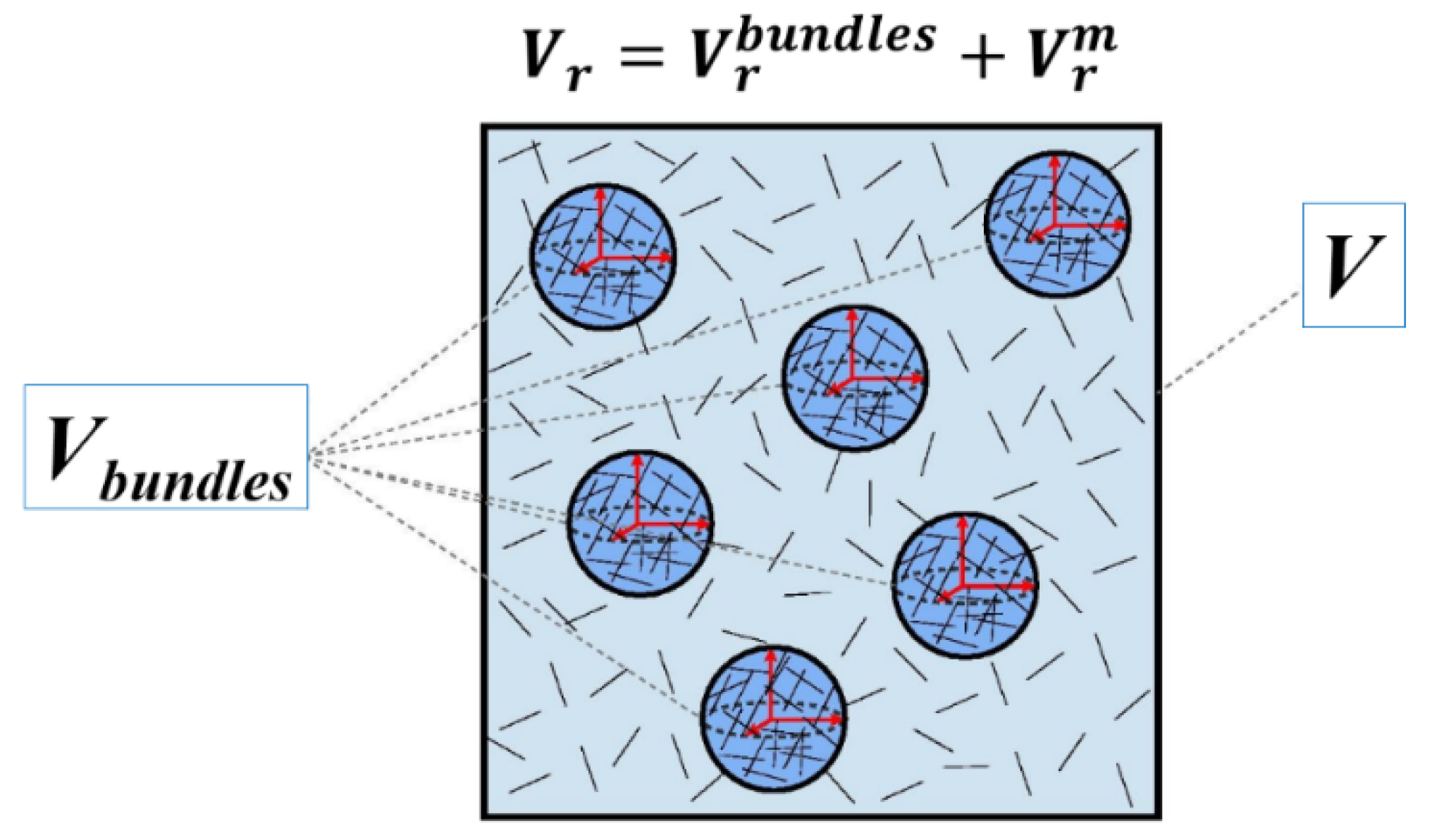
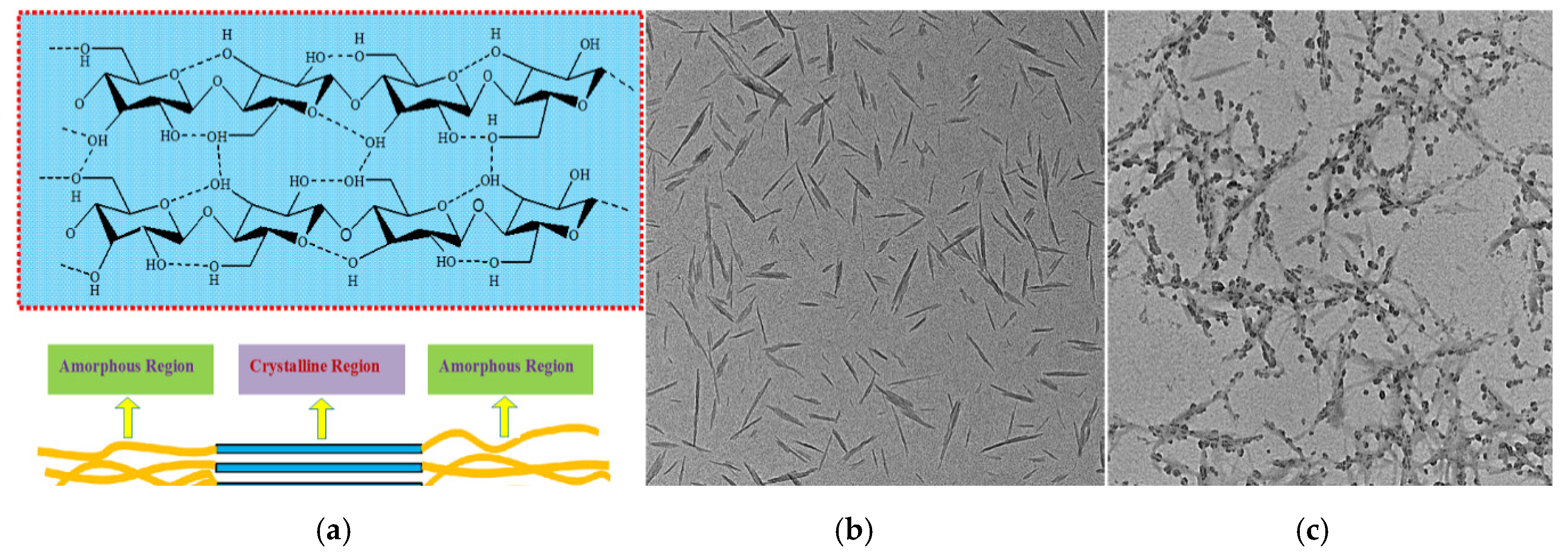
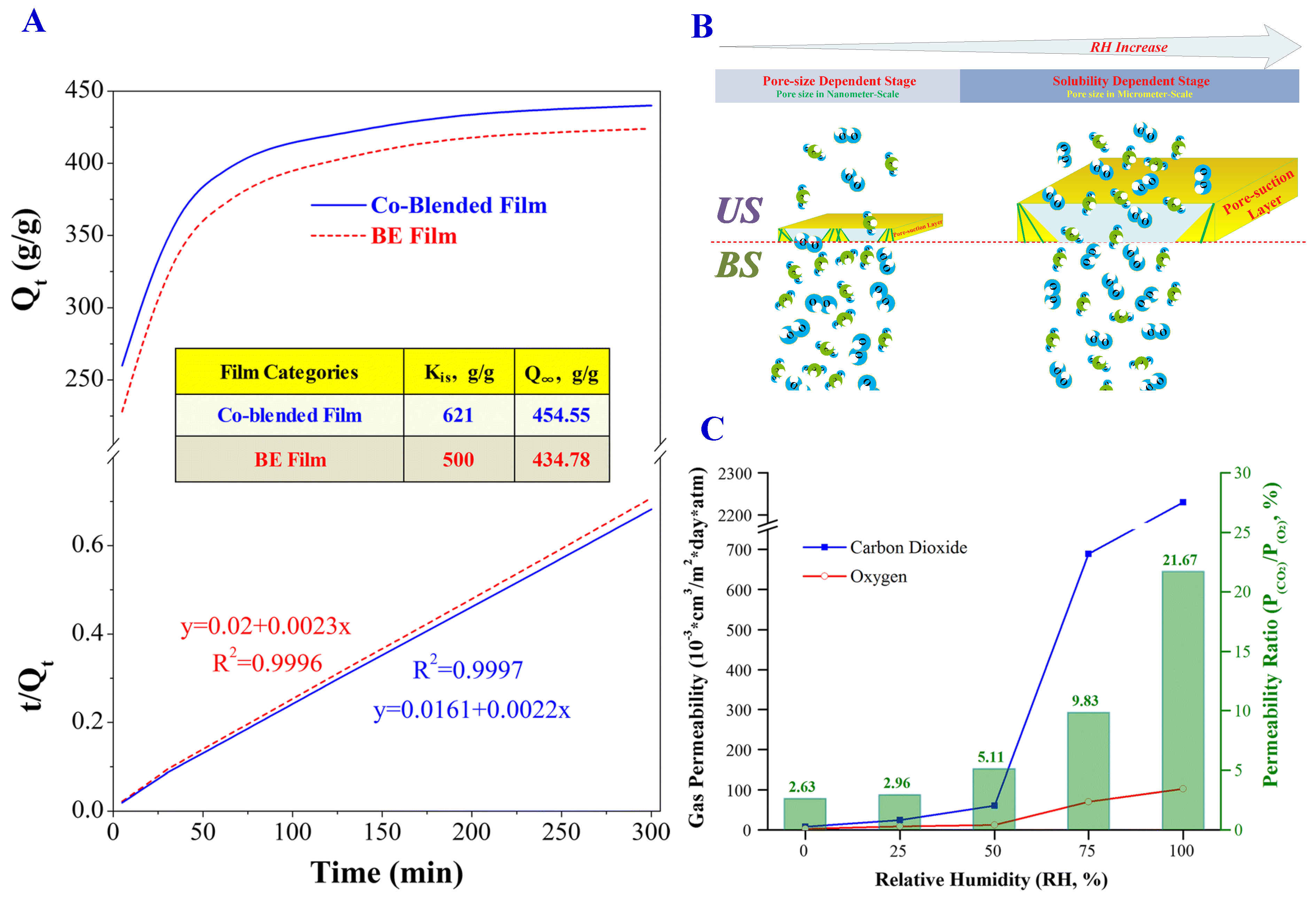
| Geometry | Circular Plates | Square Plates | Triangular Plates |
|---|---|---|---|
| ηc | 0.9614 | 0.8647 | 0.7295 |
| Error | ± 0.0005 | ±0.0006 | ±0.0006 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Kong, F.; Zhang, M.; Wang, W.; KC, B.S.; Tjong, J.; Sain, M. Percolation Model for Renewable-Carbon Doped Functional Composites in Packaging Application: A Brief Review. Coatings 2020, 10, 193. https://doi.org/10.3390/coatings10020193
Sun B, Kong F, Zhang M, Wang W, KC BS, Tjong J, Sain M. Percolation Model for Renewable-Carbon Doped Functional Composites in Packaging Application: A Brief Review. Coatings. 2020; 10(2):193. https://doi.org/10.3390/coatings10020193
Chicago/Turabian StyleSun, Bo, Fangong Kong, Min Zhang, Weijun Wang, Birat Singh KC, Jimi Tjong, and Mohini Sain. 2020. "Percolation Model for Renewable-Carbon Doped Functional Composites in Packaging Application: A Brief Review" Coatings 10, no. 2: 193. https://doi.org/10.3390/coatings10020193
APA StyleSun, B., Kong, F., Zhang, M., Wang, W., KC, B. S., Tjong, J., & Sain, M. (2020). Percolation Model for Renewable-Carbon Doped Functional Composites in Packaging Application: A Brief Review. Coatings, 10(2), 193. https://doi.org/10.3390/coatings10020193





