Application of Rank Annihilation Factor Analysis for Antibacterial Drugs Determination by Means of pH Gradual Change-UV Spectral Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Instruments
2.2. Chemicals and Reagents
2.3. Standard Solutions
2.4. Treatment of Real Samples
2.5. Spectrophotometric Analysis of Sulfamethoxazole and Trimethoprim in Laboratory-Prepared Mixtures
2.6. Theory of Rank Annihilation Factor Analysis
2.7. Chemometrics Models
3. Results and Discussion
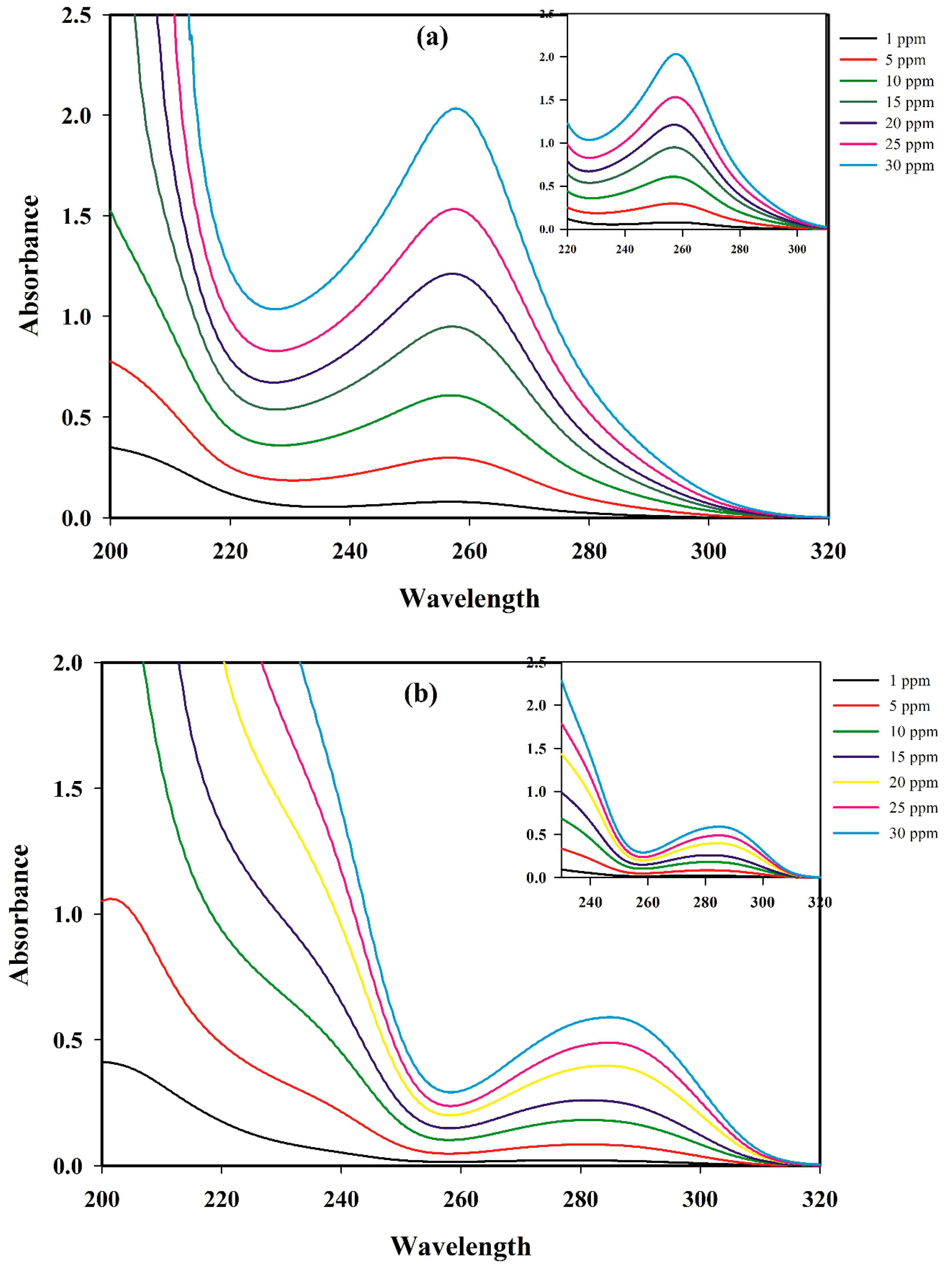
3.1. Linear Calibration Models for A Single Component
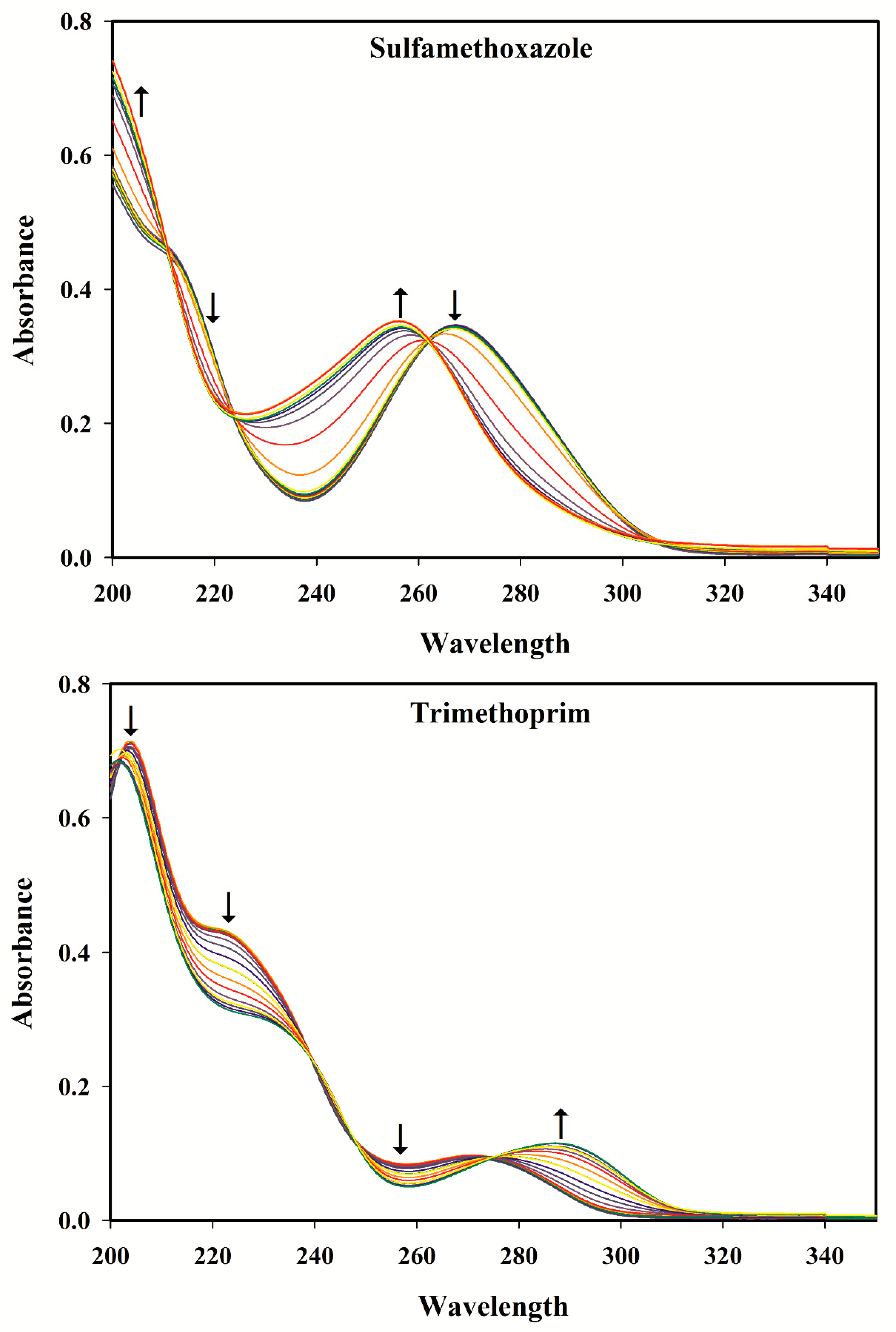
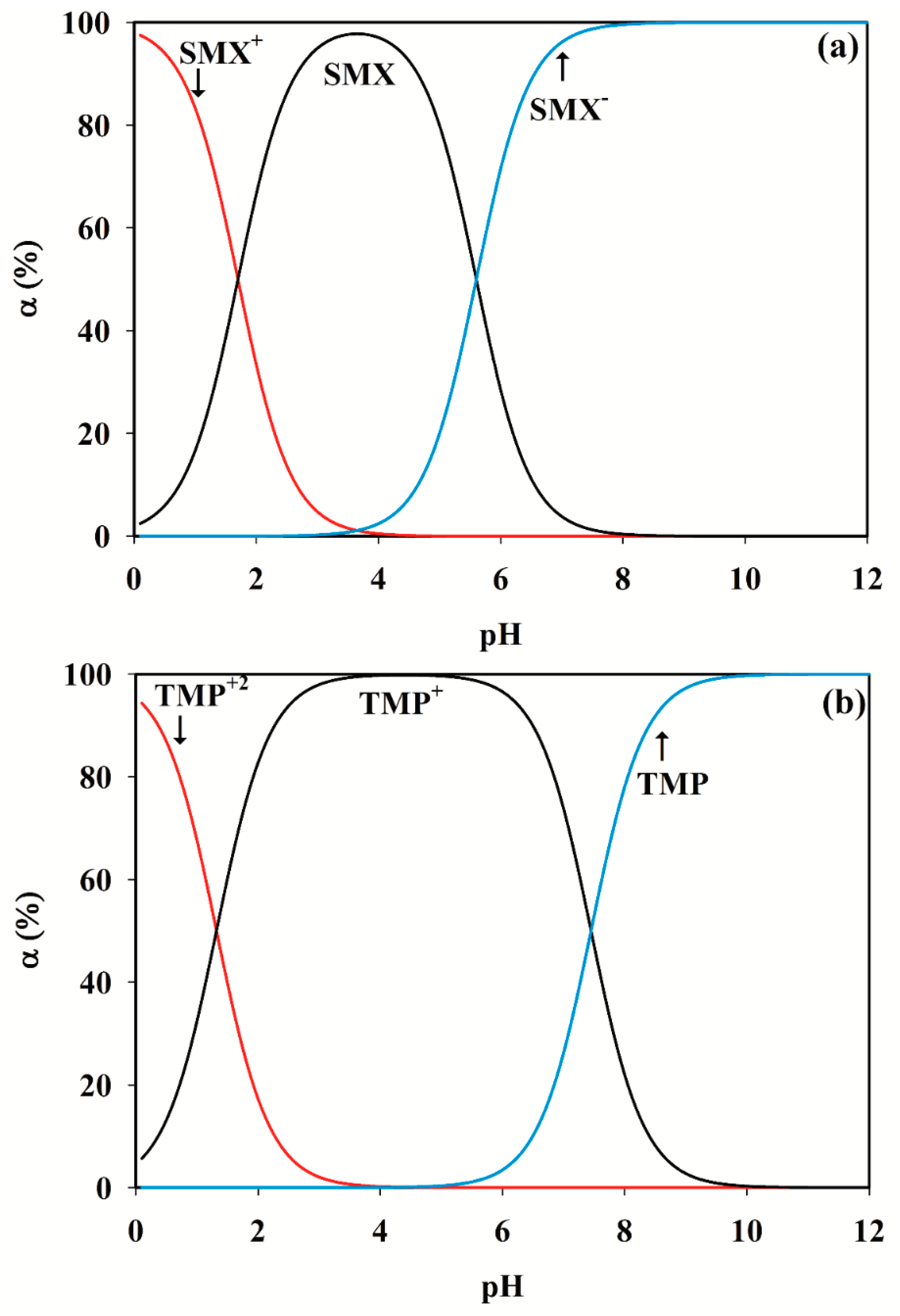
3.2. Selection of the pH Range
3.3. pH-Spectral Absorbance Data: Bilinearity, Trilinearity and Rank Deficiency
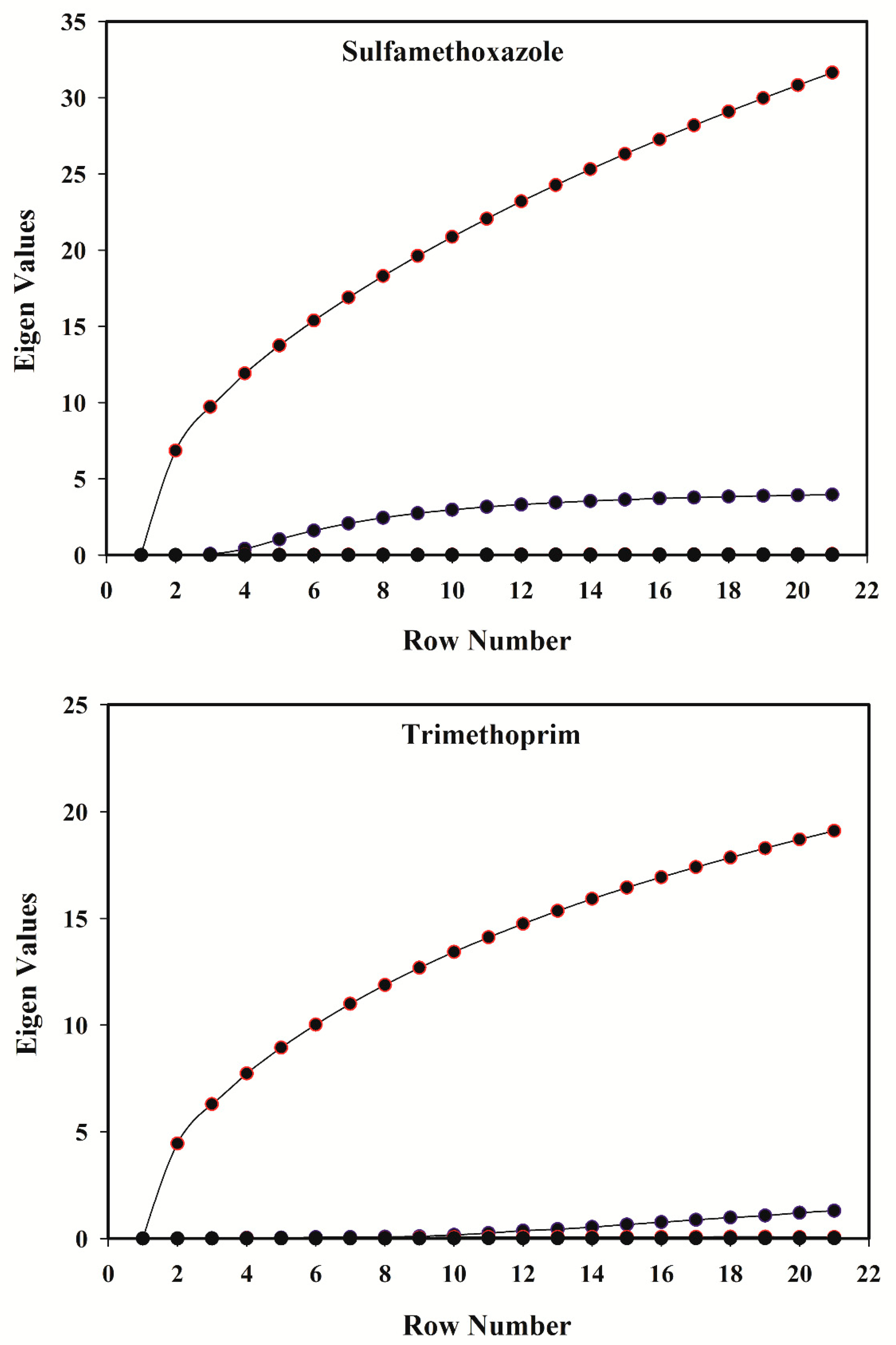
3.4. Rank Analysis
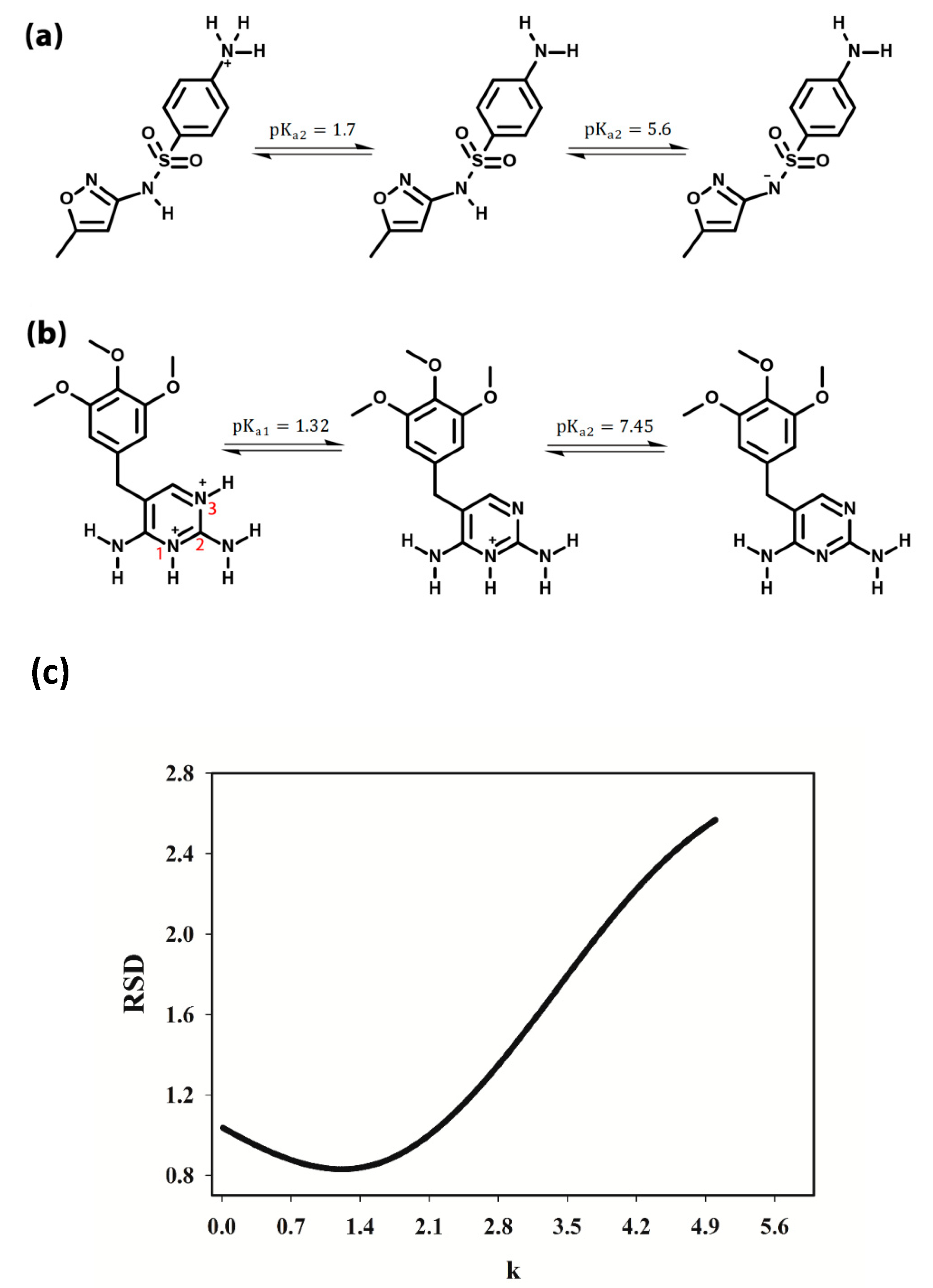
SMX + H2O ⇆ SMX− + H3O+
SMX+ + H2O ⇆ SMX + H3O+
TMP+ + H2O ⇆ TMP + H3O+ pKa2 = 7.45
3.5. Determination of SMX and TMP in Validation Samples
3.6. Determination of SMX and TMP in Real Samples
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ma, R.; Wang, Y.; Zou, X.; Hu, K.; Sun, B.; Fang, W. Pharmacokinetics of sulfamethoxazole and trimethoprim in Pacific white shrimp, Litopenaeus vannamei, after oral administration of single-dose and multiple-dose. Environ. Toxicol. Pharmacol. 2017, 52, 90–98. [Google Scholar] [CrossRef]
- Tungsanga, K.; Chongthaleong, A.; Udomsantisuk, N.; Petcharabutr, O.A.; Sitprija, V.; Wong, E.C.K. Norfloxacin versus co-trimoxazole for the treatment of upper urinary tract infections: A double blind trial. Scand. J. Infect. Dis. Suppl. 1988, 20, 28–34. [Google Scholar]
- Cooper, J.; McGillion, F.B. Treatment of acute exacerbations of chronic bronchitis. A double-blind trial of cotrimoxazole and cephalexin. Practitioner 1978, 221, 428–432. [Google Scholar]
- Feldman, W.; Richardson, H.; Rennie, B.; Dawson, P. A trial comparing cefaclor with co-trimoxazole in the treatment of acute otitis me. Arch. Dis. Child. 1982, 57, 594–596. [Google Scholar] [CrossRef]
- Sayar, E.; Sahin, S.; Cevheroglu, S.; Hincal, A. Development and validation of an HPLC method for simultaneous determination of trimethoprim and sulfamethoxazole in human plasma. Eur. J. Drug Metab. Pharmacokinet. 2010, 35, 41–46. [Google Scholar] [CrossRef]
- Ayejuyo, O.O.; Nwoko, C.; Hamed, M. Liquid Chromatographic Technique for the Simeltaneous Dtermination of Sulphamethoxazole and Trimethoprim in Pharmaceutical Formulations. UNILAG J. Med. Sci. Technol. 2016, 4, 120–132. [Google Scholar]
- Bedor, D.C.G.; Gonçalves, T.M.; Ferreira, M.L.L.; de Sousa, C.E.M.; Menezes, A.L.; Oliveira, E.J.; de Santana, D.P. Simultaneous determination of sulfamethoxazole and trimethoprim in biological fluids for high-throughput analysis: Comparison of HPLC with ultraviolet and tandem mass spectrometric detection. J. Chromatogr. B 2008, 863, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, I.S.; Vidal, D.T.R.; Do Lago, C.L.; Angnes, L. Fast simultaneous determination of trimethoprim and sulfamethoxazole by capillary zone electrophoresis with capacitively coupled contactless conductivity detection. J. Sep. Sci. 2013, 36, 1405–1409. [Google Scholar] [CrossRef] [PubMed]
- Pereira, P.F.; da Silva, W.P.; Muñoz, R.A.A.; Richter, E.M. A simple and fast batch injection analysis method for simultaneous determination of phenazopyridine, sulfamethoxazole, and trimethoprim on boron-doped diamond electrode. J. Electroanal. Chem. 2016, 766, 87–93. [Google Scholar] [CrossRef]
- Gonzalez, D.; Melloni, C.; Poindexter, B.B.; Yogev, R.; Atz, A.M.; Sullivan, J.E.; Mendley, S.R.; Delmore, P.; Delinsky, A.; Zimmerman, K.; et al. Simultaneous determination of trimethoprim and sulfamethoxazole in dried plasma and urine spots. Bioanalysis 2015, 7, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Sgobbi, L.F.; Razzino, C.A.; Machado, S.A.S. A disposable electrochemical sensor for simultaneous detection of sulfamethoxazole and trimethoprim antibiotics in urine based on multiwalled nanotubes decorated with Prussian blue nanocubes modified screen-printed electrode. Electrochim. Acta 2016, 191, 1010–1017. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Hu, X.L.; Bao, Y.F.; Yin, D.Q. Simultaneous determination of 29 pharmaceuticals in fish muscle and plasma by ultrasonic extraction followed by SPE–UHPLC–MS/MS. J. Sep. Sci. 2018, 41, 2139–2150. [Google Scholar] [CrossRef] [PubMed]
- Amini, H.; Ahmadiani, A. Rapid and simultaneous determination of sulfamethoxazole and trimethoprim in human plasma by high-performance liquid chromatography. J. Pharm. Biomed. Anal. 2007, 43, 1146–1150. [Google Scholar] [CrossRef] [PubMed]
- Teshima, D.; Otsubo, K.; Makino, K.; Itoh, Y.; Oishi, R. Simultaneous determination of sulfamethoxazole and trimethoprim in human plasma by capillary zone electrophoresis. Biomed. Chromatogr. 2004, 18, 51–54. [Google Scholar] [CrossRef]
- Afkhami, A.; Khalafi, L. Spectrophotometric investigation of the effect of β-cyclodextrin on the intramolecular cyclization reaction of catecholamines using rank annihilation factor analysis. Anal. Chim. Acta 2007, 599, 241–248. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Wang, Y.; Xu, M.; Hu, X. UV–Vis spectroscopy combined with chemometric study on the interactions of three dietary flavonoids with copper ions. Food Chem. 2018, 263, 208–215. [Google Scholar] [CrossRef]
- Esteki, M.; Nouroozi, S.; Amanifar, S.; Shahsavari, Z. A Simple and Highly Sensitive Method for Quantitative Detection of Methyl Paraben and Phenol in Cosmetics Using Derivative Spectrophotometry and Multivariate Chemometric Techniques. J. Chin. Chem. Soc. 2017, 64, 152–163. [Google Scholar] [CrossRef]
- Esteki, M.; Nouroozi, S.; Shahsavari, Z. A fast and direct spectrophotometric method for the simultaneous determination of methyl paraben and hydroquinone in cosmetic products using successive projections algorithm. Int. J. Cosmet. Sci. 2016, 38. [Google Scholar] [CrossRef]
- Bro, R. Multivariate calibration: What is in chemometrics for the analytical chemist? Anal. Chim. Acta 2003, 500, 185–194. [Google Scholar] [CrossRef]
- Othman, S. Multicomponent derivative spectroscopic analysis of sulfamethoxazole and trimethoprim. Int. J. Pharm. 1990, 63, 173–176. [Google Scholar] [CrossRef]
- Nevado, J.J.B.; Gallego, J.M.L.; Penalvo, G.C. Determination of sulfamethoxazole and trimethoprim by ratio spectra derivative spectrophotometry. Fresenius J. Anal. Chem. 1992, 342, 723–728. [Google Scholar] [CrossRef]
- López-Martínez, L.; López-de-Alba, P.L.; de-León-Rodríguez, L.M.; Yepez-Murrieta, M.L. Simultaneous determination of binary mixtures of trimethoprim and sulfamethoxazole or sulphamethoxypyridazine by the bivariate calibration spectrophotometric method. J. Pharm. Biomed. Anal. 2002, 30, 77–85. [Google Scholar] [CrossRef]
- Navarro, M.V.; Cabezón, M.A.; Damiani, P.C. Simultaneous Determination of Pesticides in Fruits by Using Second-Order Fluorescence Data Resolved by Unfolded Partial Least-Squares Coupled to Residual Bilinearization. J. Chem. 2018, 2018, 3217465. [Google Scholar] [CrossRef]
- Nikpour, H.; Mousavi, M.; Asadollahzadeh, H. Using inclusion complexes for achieving second-order advantage: A novel technique for cinnamic acid derivatives analysis with second-order calibration methods. J. Chemom. 2019. [Google Scholar] [CrossRef]
- Olivieri, A.C. On a versatile second-order multivariate calibration method based on partial least-squares and residual bilinearization: Second-order advantage and precision properties. J. Chemom. 2005, 19, 253–265. [Google Scholar] [CrossRef]
- El-Sheikh, A.H.; Al-Degs, Y.S. Spectrophotometric determination of food dyes in soft drinks by second order multivariate calibration of the absorbance spectra-pH data matrices. Dye Pigment. 2013, 97, 330–339. [Google Scholar] [CrossRef]
- Ho, C.N.; Christian, G.D.; Davidson, E.R. Application of the method of rank annihilation to quantitative analyses of multicomponent fluorescence data from the video fluorometer. Anal. Chem. 1978, 50, 1108–1113. [Google Scholar] [CrossRef]
- Hemmateenejad, B.; Yousefinejad, S. Multivariate standard addition method solved by net analyte signal calculation and rank annihilation factor analysis. Anal. Bioanal. Chem. 2009, 394, 1965–1975. [Google Scholar] [CrossRef]
- Etezadi, H.; Sajjadi, S.M.; Maleki, A. Crucial successes in drug delivery systems using multivariate chemometric approaches: Challenges and opportunities. New J. Chem. 2019. [Google Scholar] [CrossRef]
- Benvidi, A.; Dadras, A.; Abbasi, S.; Tezerjani, M.D.; Rezaeinasab, M.; Tabaraki, R. Experimental and computational study of the pKa of coumaric acid derivatives. J. Chin. Chem. Soc. 2019. [Google Scholar] [CrossRef]
- Alizadeh, S.; Moghtader, M.; Aliasgharlou, N. Rank Annihilation Factor Analysis for Spectrophotometric Study of Morphine Based on AuNPs Aggregation Using Multivariate Curve Resolution. Sens. Lett. 2019, 17, 337–343. [Google Scholar] [CrossRef]
- Mita, H.; Mansur, U.; Sartika, J. Optimation and Validation of Analytical Method of Cotrimoxazole in Tablet and Plasma In vitro by High Performance Liquid Chromatography. J. Bioanal. Biomed. 2012, 04, 26–29. [Google Scholar] [CrossRef]
- Bahram, M.; Mabhooti, M. Rank annihilation factor analysis using mean centering of ratio spectra for kinetic–spectrophotometric analysis of unknown samples. Anal. Chim. Acta 2009, 639, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Meloun, M.; Čapek, J.; Mikšík, P.; Brereton, R.G. Critical comparison of methods predicting the number of components in spectroscopic data. Anal. Chim. Acta 2000, 423, 51–68. [Google Scholar] [CrossRef]
- Abdollahi, H.; Safavi, A.; Zeinali, S. Model-based rank annihilation factor analysis for quantitative analysis of mixtures of monoprotic acids using multivariate spectrophotometric acid-base titrations. Chemom. Intell. Lab. Syst. 2008, 94, 112–117. [Google Scholar] [CrossRef]
- Zhou, W.; Moore, D.E. Photosensitizing activity of the anti-bacterial drugs sulfamethoxazole and trimethoprim. J. Photochem. Photobiol. B Biol. 1997, 39, 63–72. [Google Scholar] [CrossRef]
- Faber, N.M.; Buydens, L.M.C.; Kateman, G. Generalized rank annihilation method. I: Derivation of eigenvalue problems. J. Chemom. 1994, 8, 147–154. [Google Scholar] [CrossRef]
- Olivieri, A.C.; Wu, H.-L.; Yu, R.-Q. MVC2: A MATLAB graphical interface toolbox for second-order multivariate calibration. Chemom. Intell. Lab. Syst. 2009, 96, 246–251. [Google Scholar] [CrossRef]
- Smilde, A.K.; Tauler, R.; Saurina, J.; Bro, R. Calibration methods for complex second-order data. Anal. Chim. Acta 1999, 398, 237–251. [Google Scholar] [CrossRef]
- Rodríguez-Cuesta, M.; Boqué, R.; Xavier, R.F. Influence of selectivity and sensitivity parameters on detection limits in multivariate curve resolution of chromatographic second-order data. Anal. Chim. Acta 2003, 476, 111–122. [Google Scholar] [CrossRef]
- Goicoechea, H.C.; Olivieri, A.C. New Robust Bilinear Least Squares Method for the Analysis of Spectral-pH Matrix Data. Appl. Spectrosc. 2005, 59, 926–933. [Google Scholar] [CrossRef] [PubMed]
- Amrhein, M.; Srinivasan, B.; Bonvin, D.; Schumacher, M.M. On the rank deficiency and rank augmentation of the spectral measurement matrix. Chemom. Intell. Lab. Syst. 1996, 33, 17–33. [Google Scholar] [CrossRef]
- Keller, H.R.; Massart, D.L. Evolving factor analysis. Chemom. Intell. Lab. Syst. 1991, 12, 209–224. [Google Scholar] [CrossRef]
- Babić, S.; Horvat, A.J.M.; Mutavdžić Pavlović, D.; Kaštelan-Macan, M. Determination of pKa values of active pharmaceutical ingredients. TrAC Trends Anal. Chem. 2007, 26, 1043–1061. [Google Scholar] [CrossRef]
- Chen, H.; Gao, B.; Li, H.; Ma, L.Q. Effects of pH and ionic strength on sulfamethoxazole and ciprofloxacin transport in saturated porous media. J. Contam. Hydrol. 2011, 126, 29–36. [Google Scholar] [CrossRef]
- Qiang, Z.; Adams, C. Potentiometric determination of acid dissociation constants (pKa) for human and veterinary antibiotics. Water Res. 2004, 38, 2874–2890. [Google Scholar] [CrossRef]
- Mikes, O.; Trapp, S. Acute Toxicity of the Dissociating Veterinary Antibiotics Trimethoprim to Willow Trees at Varying pH. Bull. Environ. Contam. Toxicol. 2010, 85, 556–561. [Google Scholar] [CrossRef]
- Effect of Water Quality on Rejection of Selected Human and Veterinary Antibiotics by Nanofiltration and Reverse Osmosis Membranes—Semantic Scholar. Membr. Technol. Conf.; Phoenix: International Water Association: London, UK, 2005; pp. 1–7.
- Cocco, L.; Roth, B.; Temple, C.; Montgomery, J.A.; London, R.E.; Blakley, R.L. Protonated state of methotrexate, trimethoprim, and pyrimethamine bound to dihydrofolate reductase. Arch. Biochem. Biophys. 1983, 226, 567–577. [Google Scholar] [CrossRef]
- Cao, J.; Cross, R.F. The separation of dihydrofolate reductase inhibitors and the determination of pKa,1 values by capillary zone electrophoresis. J. Chromatogr. A 1995, 695, 297–308. [Google Scholar] [CrossRef]
- Schwalbe, C.H.; Cody, V. Trimethoprim analysis. In Proceedings of the 7th International Symposium Structure Study on Antifolate Drugs; Blair, J.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1983; pp. 511–515. [Google Scholar]
- Perrin, D. Dissociation Constants of Organic Bases in Aqueous Solution; Butterworths: London, UK, 1965. [Google Scholar]
- Javier, S.; Santiago, H.-C.; Romà, T.A.; Izquierdo-Ridorsa, A. Procedure for the Quantitative Determination of Mixtures of Nucleic Acid Components Based on Multivariate Spectrophotometric Acid−Base Titrations. Anal. Chem. 1999, 71, 126–134. [Google Scholar] [CrossRef]
| Parameters | Sulfamethoxazole | Trimethoprim |
|---|---|---|
| Linear range (µg mL−1) | 1.0–30.0 | 1.0–30.0 |
| Correlation coefficient | 0.994 | 0.996 |
| Intercept | −0.0196 ± 0.0033 (n = 3) | −0.0121 ± 0.0025 (n = 3) |
| Slope (mL−1 µg) | 0.0632 ± 0.0028 (n = 3 ) | 0.0197 ± 0.0020 (n = 3) |
| Detection limit (µg mL−1) | 0.25 | 0.38 |
| Sample No. | SMX | TMP | ||||||
|---|---|---|---|---|---|---|---|---|
| Actual (µg mL−1) | Predicted (µg mL−1) | Error (µg mL−1) | RSD (%, n = 3) | Actual (µg mL−1) | Predicted (µg mL−1) | Error (µg mL−1) | RSD (%, n = 3) | |
| 1 | 1 | 0.91 | −0.09 | 3.1 | 1 | 1.03 | 0.03 | 2.78 |
| 2 | 6 | 5.65 | −0.35 | 2.32 | 1 | 0.98 | −0.02 | 2.12 |
| 3 | 13 | 14.59 | 1.59 | 1.51 | 1 | 0.95 | −0.05 | 2.98 |
| 4 | 20 | 20.18 | 0.18 | 3.20 | 1 | 1.08 | 0.08 | 3.15 |
| 5 | 30 | 30.55 | 0.55 | 0.55 | 1 | 0.96 | −0.04 | 3.19 |
| 6 | 1 | 0.89 | −0.11 | 1.68 | 6 | 5.66 | −0.34 | 1.59 |
| 7 | 6 | 6.58 | 0.58 | 2.32 | 6 | 6.12 | 0.12 | 2.31 |
| 8 | 13 | 12.77 | −0.23 | 1.98 | 6 | 6.23 | 0.23 | 1.66 |
| 9 | 20 | 19.32 | −0.68 | 1.33 | 6 | 5.89 | −0.11 | 1.45 |
| 10 | 30 | 28.51 | −1.49 | 2.52 | 6 | 6.08 | 0.08 | 1.98 |
| 11 | 1 | 1.05 | 0.05 | 2.31 | 13 | 13.78 | 0.78 | 1.32 |
| 12 | 6 | 6.87 | 0.87 | 1.56 | 13 | 12.32 | −0.68 | 1.75 |
| 13 | 13 | 13.88 | 0.88 | 1.23 | 13 | 12.42 | −0.58 | 2.13 |
| 14 | 20 | 21.89 | 1.89 | 1.32 | 13 | 13.88 | 0.88 | 1.55 |
| 15 | 30 | 29.12 | −0.88 | 1.45 | 13 | 13.59 | 0.59 | 1.32 |
| 16 | 1 | 1.10 | 0.1 | 1.05 | 20 | 20.13 | 0.13 | 2.62 |
| 17 | 6 | 5.64 | −0.36 | 1.23 | 20 | 21.16 | 1.16 | 1.78 |
| 18 | 13 | 14.02 | 1.02 | 2.12 | 20 | 19.55 | −0.45 | 3.21 |
| 19 | 20 | 22.21 | 2.21 | 1.21 | 20 | 19.17 | −0.83 | 2.17 |
| 20 | 30 | 28.65 | −1.35 | 1.59 | 20 | 21.21 | 1.21 | 2.79 |
| 21 | 1 | 0.99 | −0.01 | 2.32 | 30 | 32.42 | 2.42 | 1.98 |
| 22 | 6 | 5.22 | −0.78 | 1.48 | 30 | 30.67 | 0.67 | 3.31 |
| 23 | 13 | 14.65 | 1.65 | 1.75 | 30 | 29.10 | −0.9 | 2.78 |
| 24 | 20 | 20.03 | 0.03 | 0.75 | 30 | 31.78 | 1.78 | 1.44 |
| 25 | 30 | 31.22 | 1.22 | 0.89 | 30 | 32.52 | 2.52 | 1.32 |
| Drug | SMX | TMP | ||||
|---|---|---|---|---|---|---|
| Approximate Doses (mg) | Proposed Method (mg) | HPLC (mg) | Approximate Doses (mg) | Proposed Method (mg) | HPLC (mg) | |
| Co-trimoxazole adult tablet | 400 | 403 ± 4.3 | 402 ± 5.2 | 80 | 78.3 ± 2.6 | 79.6 ± 3.1 |
| Co-trimoxazole pediatric tablet | 100 | 98.23 ± 3.7 | 97.3 ± 4.1 | 20 | 22.3 ± 3.1 | 24.8 ± 4.1 |
| Co-trimoxazole oral suspension | 200 | 197.56 ± 4.9 | 198.4 ± 4.7 | 40 | 38.5 ± 4.5 | 38.1 ± 4.3 |
| Co-trimoxazole intravenous infusion | 400 | 398.91 ± 4.2 | 400.1 ± 5.1 | 80 | 82.8 ± 5.2 | 81.6 ± 6.1 |
| SMX | ||||||||
| Samples | Proposed Method | HPLC | ||||||
| Added (µg mL−1) | Found (µg mL−1) | Recovery (%) | RSD (%, n = 3) | Added (µg mL−1) | Found (µg mL−1) | Recovery (%) | RSD (%, n = 3) | |
| Serum | 10 | 10.98 | 109.8 | 5.54 | 10 | 9.3 | 93.0 | 6.5 |
| 20 | 19.10 | 95.5 | 6.32 | 20 | 19.05 | 95.2 | 6.95 | |
| 30 | 32.31 | 107.7 | 3.52 | 30 | 33.05 | 110.1 | 5.32 | |
| Plasma | 10 | 9.23 | 92.3 | 4.21 | 10 | 9.35 | 93.5 | 5.62 |
| 20 | 21.56 | 107.8 | 3.11 | 20 | 19.32 | 96.6 | 4.73 | |
| 30 | 29.11 | 97.0 | 4.63 | 30 | 32.15 | 107.2 | 6.72 | |
| TMP | ||||||||
| Samples | Proposed Method | HPLC | ||||||
| Added (µg mL−1) | Found (µg mL−1) | Recovery (%) | RSD (%, n = 3) | Added (µg mL−1) | Found (µg mL−1) | Recovery (%) | RSD (%, n = 3) | |
| Serum | 20 | 20.89 | 104.4 | 4.62 | 20 | 21.65 | 108.2 | 5.97 |
| 10 | 9.05 | 90.5 | 5.31 | 10 | 10.21 | 102.1 | 4.78 | |
| 25 | 24.32 | 97.3 | 4.65 | 25 | 23.65 | 94.6 | 5.64 | |
| Plasma | 20 | 19.52 | 97.6 | 3.12 | 20 | 19.23 | 96.15 | 4.68 |
| 10 | 10.23 | 102.3 | 2.65 | 10 | 9.53 | 95.3 | 6.28 | |
| 25 | 26.14 | 104.6 | 4.77 | 25 | 27.15 | 108.6 | 6.89 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esteki, M.; Dashtaki, E.; Heyden, Y.V.; Simal-Gandara, J. Application of Rank Annihilation Factor Analysis for Antibacterial Drugs Determination by Means of pH Gradual Change-UV Spectral Data. Antibiotics 2020, 9, 383. https://doi.org/10.3390/antibiotics9070383
Esteki M, Dashtaki E, Heyden YV, Simal-Gandara J. Application of Rank Annihilation Factor Analysis for Antibacterial Drugs Determination by Means of pH Gradual Change-UV Spectral Data. Antibiotics. 2020; 9(7):383. https://doi.org/10.3390/antibiotics9070383
Chicago/Turabian StyleEsteki, Mahnaz, Elham Dashtaki, Yvan Vander Heyden, and Jesus Simal-Gandara. 2020. "Application of Rank Annihilation Factor Analysis for Antibacterial Drugs Determination by Means of pH Gradual Change-UV Spectral Data" Antibiotics 9, no. 7: 383. https://doi.org/10.3390/antibiotics9070383
APA StyleEsteki, M., Dashtaki, E., Heyden, Y. V., & Simal-Gandara, J. (2020). Application of Rank Annihilation Factor Analysis for Antibacterial Drugs Determination by Means of pH Gradual Change-UV Spectral Data. Antibiotics, 9(7), 383. https://doi.org/10.3390/antibiotics9070383






