A Theoretical Study of Surface Mode Propagation with a Guiding Layer of GaN/Sapphire Hetero-Structure in Liquid Medium
Abstract
1. Introduction
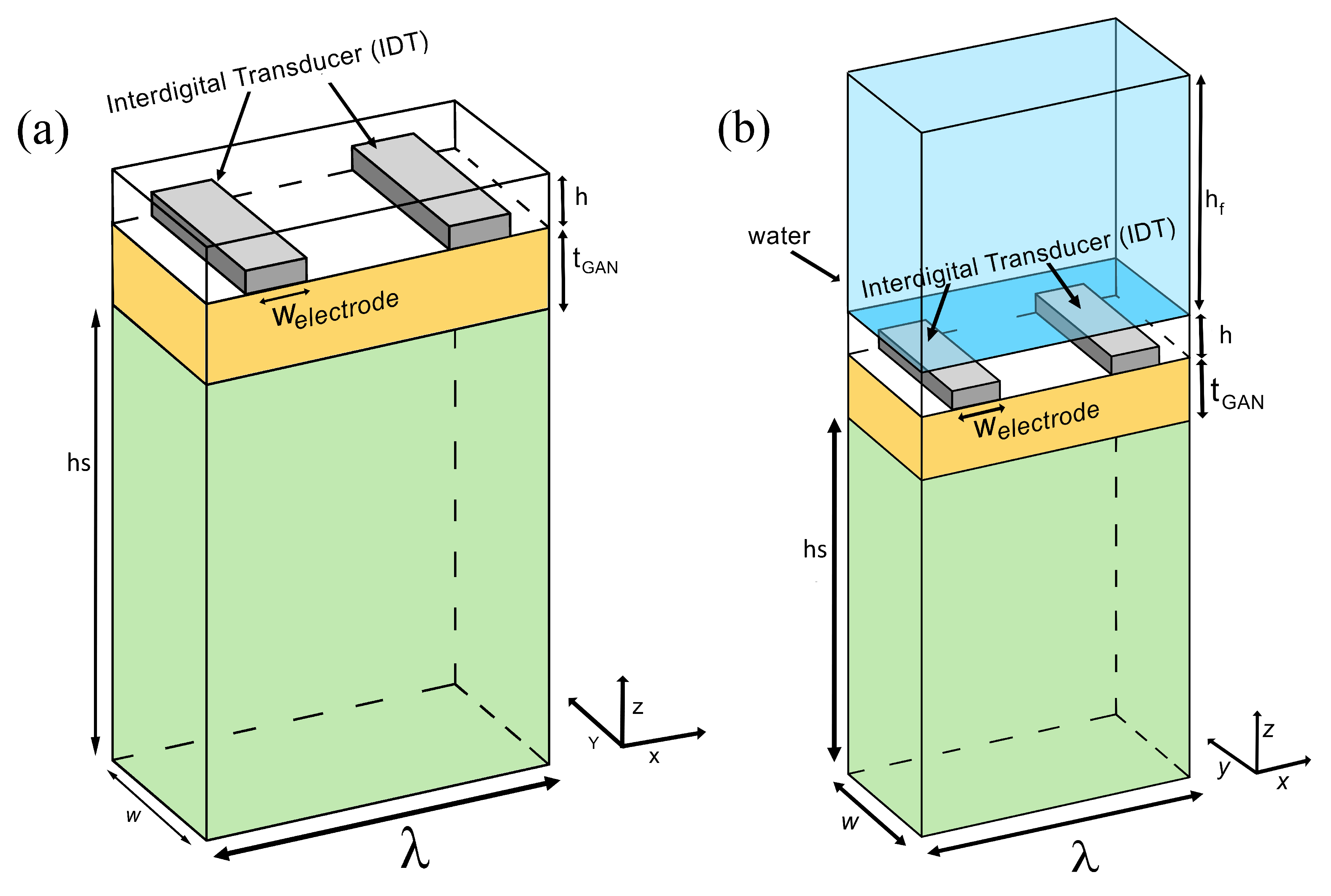
2. Simulation of Surface Wave Phase Velocity
3. Results and Discussion
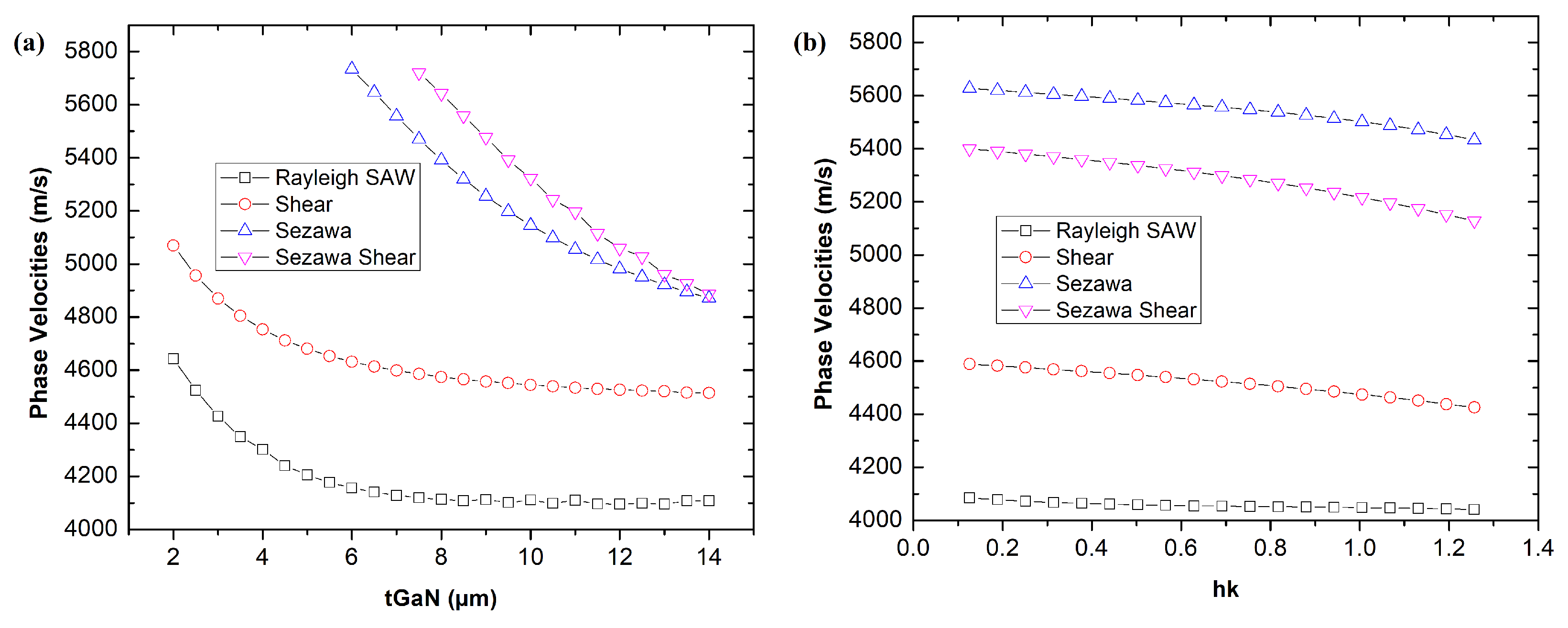
3.1. Phase Velocities
3.2. The Displacement Field
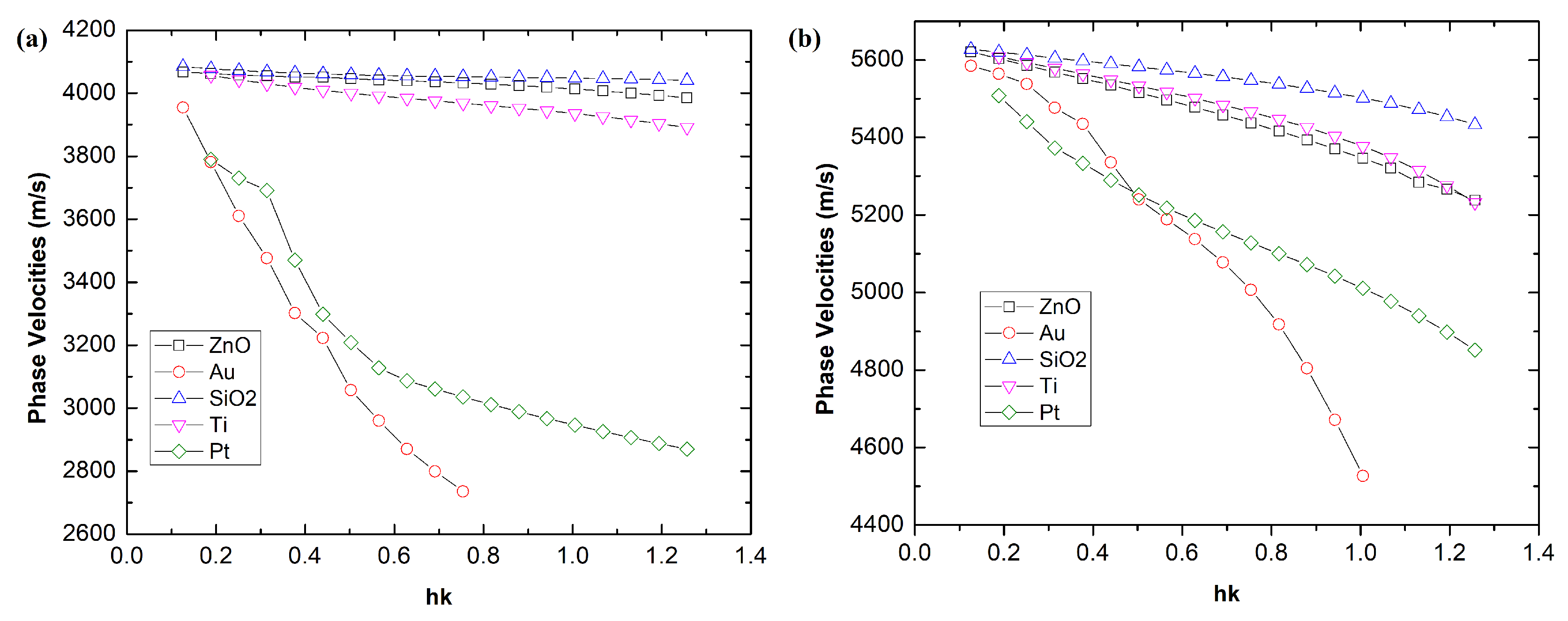
3.3. Investigating Different Materials as Guiding and Sensing Layers
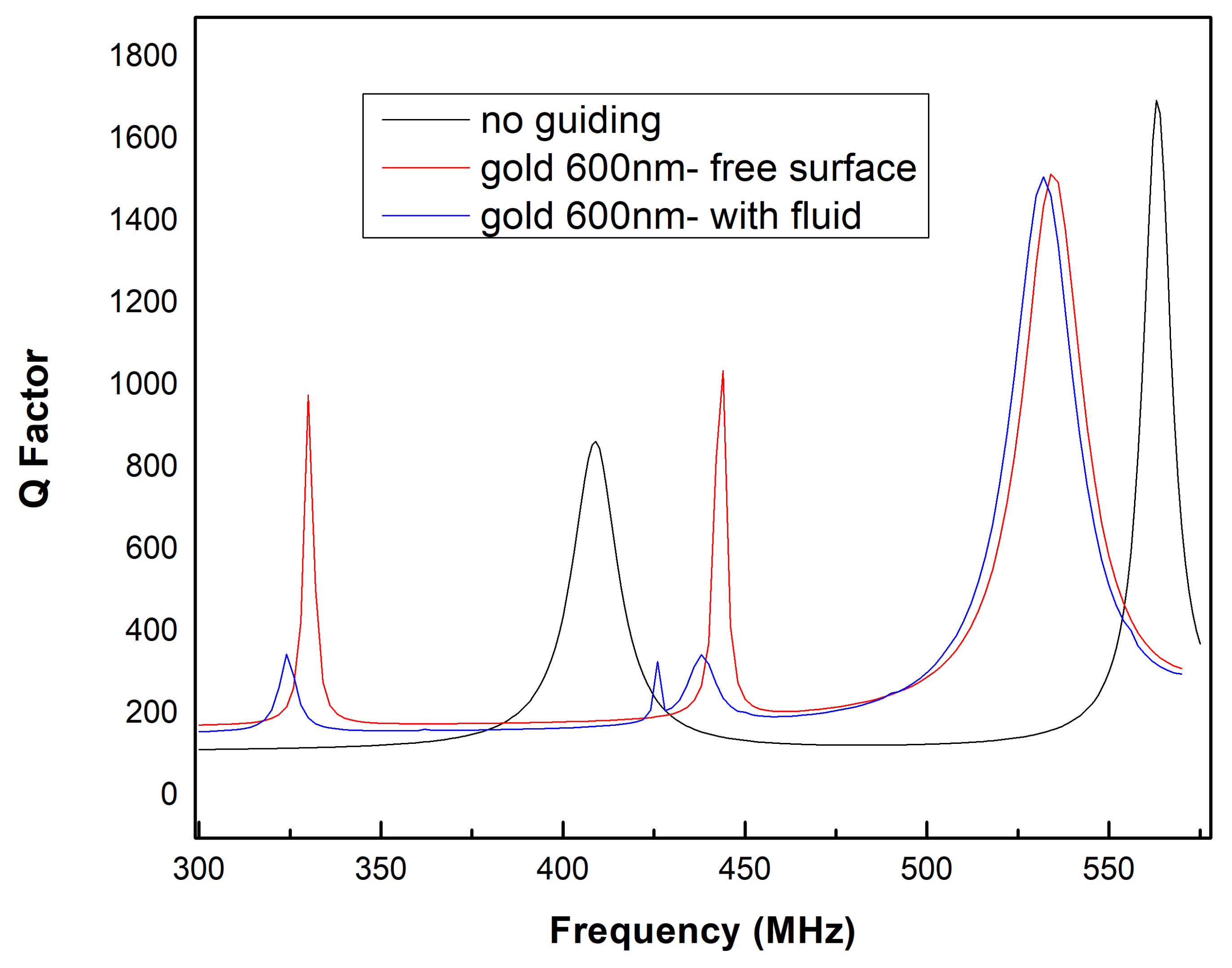
3.4. Q-Factor for Free Surface and Under Liquid Loading
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lu, C.C.; Liao, K.H.; Udrea, F.; Covington, J.A.; Gardner, J.W. Multi-field simulations and characterization of CMOS-MEMS high-temperature smart gas sensors based on SOI technology. J. Micromech. Microeng. 2008, 18, 075010. [Google Scholar] [CrossRef]
- Stefanescu, A.; Müller, A.; Giangu, I.; Dinescu, A.; Konstantinidis, G. Influence of Au-based metallization on the phase velocity of GaN on Si surface acoustic wave resonators. IEEE Electron Device Lett. 2016, 37, 321–324. [Google Scholar] [CrossRef]
- Ding, X.; Li, P.; Lin, S.C.S.; Stratton, Z.S.; Nama, N.; Guo, F.; Slotcavage, D.; Mao, X.; Shi, J.; Costanzo, F.; et al. Surface acoustic wave microfluidics. Lab Chip 2013, 13, 3626–3649. [Google Scholar] [CrossRef] [PubMed]
- An, Y.K.; Kim, M.; Sohn, H. 4-Piezoelectric transducers for assessing and monitoring civil infrastructures. In Sensor Technologies for Civil Infrastructures; Wang, M., Lynch, J., Sohn, H., Eds.; Woodhead Publishing: Cambridge, UK, 2014; pp. 86–120. [Google Scholar]
- Uchino, K. Glory of piezoelectric perovskites. Sci. Technol. Adv. Mater. 2015, 16, 046001. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, K.Y.; Hashimoto, K.Y. Surface Acoustic Wave Devices in Telecommunications; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Müller, A.; Konstantinidis, G.; Giangu, I.; Buiculescu, V.; Dinescu, A.; Stefanescu, A.; Stavrinidis, A.; Stavrinidis, G.; Ziaei, A. GaN-based SAW structures resonating within the 5.4–8.5 GHz frequency range, for high sensitivity temperature sensors. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Hudgins, J.L.; Simin, G.S.; Santi, E.; Khan, M.A. An assessment of wide bandgap semiconductors for power devices. IEEE Trans. Power Electron. 2003, 18, 907–914. [Google Scholar] [CrossRef]
- Cai, Y.; Cheng, Z.; Yang, Z.; Tang, C.W.; Lau, K.M.; Chen, K.J. High-Temperature Operation of AlGaN/GaN HEMTs Direct-Coupled FET Logic (DCFL) Integrated Circuits. IEEE Electron Device Lett. 2007, 28, 328–331. [Google Scholar] [CrossRef]
- Pedrós, J.; Calle, F.; Grajal, J.; Riobóo, R.J.; Takagaki, Y.; Ploog, K.; Bougrioua, Z. Anisotropy-induced polarization mixture of surface acoustic waves in Ga N/c-sapphire heterostructures. Phys. Rev. B 2005, 72, 075306. [Google Scholar] [CrossRef]
- Wright, J.; Lim, W.; Gila, B.; Pearton, S.; Johnson, J.L.; Ural, A.; Ren, F. Hydrogen sensing with Pt-functionalized GaN nanowires. Sens. Actuators B Chem. 2009, 140, 196–199. [Google Scholar] [CrossRef]
- Kim, S.S.; Park, J.Y.; Choi, S.W.; Kim, H.S.; Na, H.G.; Yang, J.C.; Lee, C.; Kim, H.W. Room temperature sensing properties of networked GaN nanowire sensors to hydrogen enhanced by the Ga2Pd5 nanodot functionalization. Int. J. Hydrogen Energy 2011, 36, 2313–2319. [Google Scholar] [CrossRef]
- Johnson, J.L.; Choi, Y.; Ural, A.; Lim, W.; Wright, J.; Gila, B.; Ren, F.; Pearton, S. Growth and characterization of GaN nanowires for hydrogen sensors. J. Electron. Mater. 2009, 38, 490–494. [Google Scholar] [CrossRef]
- Lim, W.; Wright, J.; Gila, B.; Johnson, J.L.; Ural, A.; Anderson, T.; Ren, F.; Pearton, S. Room temperature hydrogen detection using Pd-coated GaN nanowires. Appl. Phys. Lett. 2008, 93, 072109. [Google Scholar] [CrossRef]
- Müller, A.; Giangu, I.; Stavrinidis, A.; Stefanescu, A.; Stavrinidis, G.; Dinescu, A.; Konstantinidis, G. Sezawa propagation mode in GaN on Si surface acoustic wave type temperature sensor structures operating at GHz frequencies. IEEE Electron Device Lett. 2015, 36, 1299–1302. [Google Scholar] [CrossRef]
- Pearton, S.J.; Kang, B.S.; Kim, S.; Ren, F.; Gila, B.P.; Abernathy, C.R.; Lin, J.; Chu, S.N.G. GaN-based diodes and transistors for chemical, gas, biological and pressure sensing. J. Phys. Cond. Matter 2004, 16, R961. [Google Scholar] [CrossRef]
- Wong, K.; Tang, W.; Lau, K.M.; Chen, K.J. Planar Two-dimensional Electron Gas (2DEG) IDT SAW Filter on AlGaN/GaN Heterostructure. In Proceedings of the 2007 IEEE/MTT-S International Microwave Symposium, Honolulu, HI, USA, 3–8 June 2007; pp. 2043–2046. [Google Scholar] [CrossRef]
- Petroni, S.; Tripoli, G.; Combi, C.; Vigna, B.; De Vittorio, M.; Todaro, M.; Epifani, G.; Cingolani, R.; Passaseo, A. GaN-based surface acoustic wave filters for wireless communications. Superlattices Microstruct. 2004, 36, 825–831. [Google Scholar] [CrossRef]
- Muller, A.; Neculoiu, D.; Konstantinidis, G.; Deligeorgis, G.; Dinescu, A.; Stavrinidis, A.; Cismaru, A.; Dragoman, M.; Stefanescu, A. SAW devices manufactured on GaN/Si for frequencies beyond 5 GHz. IEEE Electron Device Lett. 2010, 31, 1398–1400. [Google Scholar] [CrossRef]
- Müller, A.; Konstantinidis, G.; Buiculescu, V.; Dinescu, A.; Stavrinidis, A.; Stefanescu, A.; Stavrinidis, G.; Giangu, I.; Cismaru, A.; Modoveanu, A. GaN/Si based single SAW resonator temperature sensor operating in the GHz frequency range. Sens. Actuators A Phys. 2014, 209, 115–123. [Google Scholar] [CrossRef]
- Palacios, T.; Calle, F.; Grajal, J.; Monroy, E.; Eickhoff, M.; Ambacher, O.; Omnes, F. High frequency SAW devices on AlGaN: fabrication, characterization and integration with optoelectronics. In Proceedings of the Ultrasonics Symposium, Munich, Germany, 8–11 October 2002; Volume 1, pp. 57–60. [Google Scholar]
- Chen, Y.C.; Chang, W.T.; Cheng, C.C.; Shen, J.Y.; Kao, K.S. Development of human IgE biosensor using Sezawa-mode SAW devices. Curr. Appl. Phys. 2014, 14, 608–613. [Google Scholar] [CrossRef]
- Shiokawa, S.; Moriizumi, T. Design of SAW sensor in liquid. Jpn. J. Appl. Phys. 1988, 27, 142. [Google Scholar] [CrossRef]
- Herrmann, F.; Weihnacht, M.; Buttgenbach, S. Properties of sensors based on shear-horizontal surface acoustic waves in LiTaO3//SiO2 and quartz SiO2 structures. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 268–273. [Google Scholar] [CrossRef]
- Brookes, J.; Bufacchi, R.; Kondoh, J.; Duffy, D.M.; McKendry, R.A. Determining biosensing modes in SH-SAW device using 3D finite element analysis. Sens. Actuators B Chem. 2016, 234, 412–419. [Google Scholar] [CrossRef]
- Li, R.; Reyes, P.I.; Ragavendiran, S.; Shen, H.; Lu, Y. Tunable surface acoustic wave device based on acoustoelectric interaction in ZnO/GaN heterostructures. Appl. Phys. Lett. 2015, 107, 073504. [Google Scholar] [CrossRef]
- Aslam, M.Z.; Jeoti, V.; Karuppanan, S.; Malik, A.F.; Iqbal, A. FEM Analysis of Sezawa Mode SAW Sensor for VOC Based on CMOS Compatible AlN/SiO2/Si Multilayer Structure. Sensors 2018, 18, 1687. [Google Scholar] [CrossRef] [PubMed]
- Kondoh, J. Theoretical consideration of high-sensitivity biosensor using shear horizontal acoustic waves in layered structures. Electron. Commun. Jpn. 2012, 95, 27–32. [Google Scholar] [CrossRef]
- Pomorska, A.; Shchukin, D.; Hammond, R.; Cooper, M.A.; Grundmeier, G.; Johannsmann, D. Positive frequency shifts observed upon adsorbing micron-sized solid objects to a quartz crystal microbalance from the liquid phase. Anal. Chem. 2010, 82, 2237–2242. [Google Scholar] [CrossRef]
- Mohanan, A.A.; Islam, M.S.; Ali, S.H.M.; Parthiban, R.; Ramakrishnan, N. Investigation into mass loading sensitivity of sezawa wave mode-based surface acoustic wave sensors. Sensors 2013, 13, 2164–2175. [Google Scholar] [CrossRef]
- Tetelin, A.; Blanc, L.; Tortissier, G.; Dejous, C.; Rebière, D.; Boissière, C. Guided SH-SAW characterization of elasticity variations of mesoporous TiO2 sensitive films during humidity sorption. In Proceedings of the Sensors, Kona, HI, USA, 1–4 November 2010; pp. 2136–2140. [Google Scholar]
- Su, H.; Williams, P.; Thompson, M. Platinum anticancer drug binding to DNA detected by thickness-shear-mode acoustic wave sensor. Anal. Chem. 1995, 67, 1010–1013. [Google Scholar] [CrossRef]

| Parameter | Value | |
|---|---|---|
| Substrate thickness | 40 m | |
| GaN thickness | 8 m | |
| Wavelength | 10 m | |
| finger width | 2.5 m | |
| Width | W | 2 m |
| Sensing layer thickness | h | 100–2000 nm |
| Fluid domain thickness | hf | 20 m |
| Properties | Gold | Platinum | Titanium | ZnO | SiO |
|---|---|---|---|---|---|
| Density (kg/m) | 19,300 | 21,450 | 4940 | 5676 | 2200 |
| Young Modulus (GPa) | 70 | 168 | 105 | 210 | 70 |
| Poisson ratio | 0.44 | 0.33 | 0.38 | 0.33 | 0.17 |
| Shear velocity (m/s) | 1122 | 2827 | 1685 | 2747 | 3766 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohd Razip Wee, M.F.; Jaafar, M.M.; Faiz, M.S.; Dee, C.F.; Yeop Majlis, B. A Theoretical Study of Surface Mode Propagation with a Guiding Layer of GaN/Sapphire Hetero-Structure in Liquid Medium. Biosensors 2018, 8, 124. https://doi.org/10.3390/bios8040124
Mohd Razip Wee MF, Jaafar MM, Faiz MS, Dee CF, Yeop Majlis B. A Theoretical Study of Surface Mode Propagation with a Guiding Layer of GaN/Sapphire Hetero-Structure in Liquid Medium. Biosensors. 2018; 8(4):124. https://doi.org/10.3390/bios8040124
Chicago/Turabian StyleMohd Razip Wee, M. F., Muhammad Musoddiq Jaafar, Mohd Syafiq Faiz, Chang Fu Dee, and Burhanuddin Yeop Majlis. 2018. "A Theoretical Study of Surface Mode Propagation with a Guiding Layer of GaN/Sapphire Hetero-Structure in Liquid Medium" Biosensors 8, no. 4: 124. https://doi.org/10.3390/bios8040124
APA StyleMohd Razip Wee, M. F., Jaafar, M. M., Faiz, M. S., Dee, C. F., & Yeop Majlis, B. (2018). A Theoretical Study of Surface Mode Propagation with a Guiding Layer of GaN/Sapphire Hetero-Structure in Liquid Medium. Biosensors, 8(4), 124. https://doi.org/10.3390/bios8040124





